Calculations of theoretical efficiencies for electrochemically-mediated tandem solar water splitting as a function of bandgap energies and redox shuttle potential†
Sam
Keene
a,
Rohini
Bala Chandran
b and
Shane
Ardo
 *cd
*cd
aDepartment of Physics, University of California Irvine, Irvine, CA 92697-2025, USA
bDepartment of Mechanical Engineering, University of Michigan, Ann Arbor, MI 48109-2125, USA
cDepartment of Chemistry, University of California Irvine, Irvine, CA 92697-2025, USA. E-mail: ardo@uci.edu
dDepartment of Chemical Engineering and Materials Science, University of California Irvine, Irvine, CA 92697-2025, USA
First published on 16th October 2018
Abstract
Tandem Z-scheme solar water splitting devices composed of two light-absorbers that are connected electrochemically by a soluble redox shuttle constitute a promising technology for cost-effective solar hydrogen production. Herein, efficiency limits of these devices are modeled by combining the detailed-balance model of the light-absorbers with Butler–Volmer electron-transfer kinetics. The impacts of the redox shuttle thermodynamic potential, light-absorber bandgaps, and electrocatalytic parameters on the solar-to-hydrogen conversion (STH) efficiency are modeled. We report that the thermodynamic potential of the redox shuttle with respect to the hydrogen and oxygen evolution potentials has a direct effect on both the STH efficiency and the optimal tandem light-absorber bandgaps needed to achieve the maximum possible STH efficiency. At 1 sun illumination and assuming ideal and optimally selective electrocatalytic parameters, the STH efficiency varies from a minimum of 21%, for a redox shuttle potential of 0 V vs. the reversible hydrogen electrode (RHE), to a maximum of 34%, for a redox shuttle potential of either 0.36 V or 1.06 V vs. RHE. To attain the maximum possible STH efficiency of 34%, the light-absorber bandgaps must be 1.53 eV and 0.75 eV, yet the optimal redox shuttle potential depends on whether the hydrogen-evolving or oxygen-evolving light-absorber has the larger bandgap. Results also underscore the importance of optimizing the absorptance of the top light-absorber, which enables large STH efficiencies to be achieved with a wider range of bandgap combinations. Moreover, given the large overpotentials for the oxygen evolution reaction and reasonably low overpotentials for most redox shuttle reactions, the tandem design is more efficient than a single light-absorber design even when the potential of the redox shuttle exceeds 1.23 V vs. RHE. When the exchange current density of the redox shuttle reactions is as low as 10−5 mA cm−2, STH efficiencies as large as 22% are still achievable as long as selective catalysis and optimal redox shuttle potential are assumed, suggesting that even slow redox shuttle reactions may not limit the practicality of these devices.
Introduction
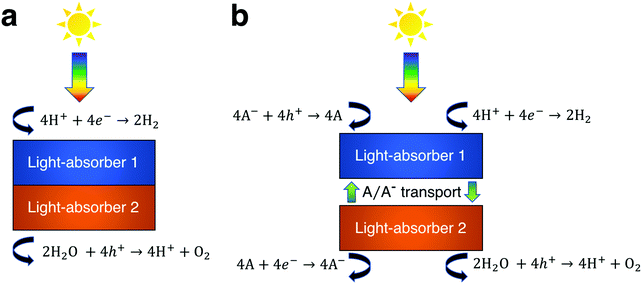
The process of solar water splitting provides renewable and storable energy in the chemical bonds of hydrogen and oxygen gas. This process is initiated through sunlight absorption by at least one light-absorber, which for the purpose of this work is a material that absorbs light and generates mobile charge carriers that ultimately participate in water electrolysis redox reactions either with or without co-catalysts. The photovoltage required to effectively drive water electrolysis at 25 °C under standard-state conditions is the sum of the thermodynamic potential difference between the two half reactions (1.23 V), overpotentials, and resistive losses, which based on state-of-the-art electrocatalysts equals at least 1.6 V.1 In order to provide this photovoltage with a single light-absorber its bandgap must exceed ∼1.9 eV. However, this is inefficient, because a ∼1.9 eV bandgap light-absorber is not optimum for maximum power-conversion efficiency, which instead occurs for a single light-absorber with a bandgap of 1.1–1.4 eV.2 A common solution to this energetic discrepancy is to use two or more light-absorbers in tandem, i.e. optically in series, that together generate the required photovoltage. In the vast majority of demonstrations of tandem solar water electrolysis, the light-absorbers are connected electronically in series (Fig. 1a).3 Under illumination, electrons in one light-absorber reduce protons, or water, to hydrogen via the hydrogen evolution reaction (HER) while holes at the other light-absorber oxidize water, or hydroxide, to oxygen via the oxygen evolution reaction (OER). The other electronic charge carriers recombine at low-resistance contacts to maintain charge balance. These electronically-connected tandem devices are often challenging to fabricate as they typically require high-quality metallurgical junctions between light-absorbers,4–9 and they have been described and modeled extensively in the literature.10–20Another approach to tandem solar water electrolysis replaces electronic connection(s) between the light-absorbers with electrochemical connection(s) (Fig. 1b). These electrochemically-connected tandem devices use redox shuttles (denoted by A/A− in Fig. 1b) that are oxidized by holes from the H2-evolving light-absorber and that are reduced by electrons from the O2-evolving light-absorber. An example of an electrochemically-connected tandem device is the redox-shuttle-mediated Z-scheme particle suspension reactor for solar water electrolysis, which facilitates H2 evolution and O2 evolution in separate compartments and does not require the use of an ion-selective membrane, like Nafion.21–25 This design maximizes light-absorption by stacking the compartments optically in series, and by evolving H2 and O2 in separate compartments, avoids explosive hazards. As a result, techno-economic projections suggest that Z-scheme particle suspension reactors for plant-scale production of H2 are a scalable technology that can be cost-competitive with H2 generated by steam methane reforming, provided that photocatalyst materials, redox shuttles, and additional reactor components are discovered that are efficient, durable, and inexpensive.21,24,26–30 However, there are still challenges for this concept, because experimental demonstrations of electrochemically-connected tandem devices for solar water electrolysis often exhibit <1% STH efficiency,24 as compared to the large number of demonstrations with >10% STH efficiency for the electronically-connected tandem devices.3,4 Recently, our group developed transport and kinetic models for Z-scheme particle suspension reactors that established that passive diffusive species transport with IO3−/I− and quinone/hydroquinone (Q/QH2) redox shuttles can sustain up to a 4% solar-to-hydrogen conversion (STH) efficiency in centimeter-tall reactors.27 In that work, we identified optimal reactor designs and operating conditions by investigating the impacts of light absorption, species transport, and electrokinetics for a few commonly investigated semiconductor materials (TiO2, BiVO4 and Rh-doped SrTiO3) and plausible redox shuttles (Fe3+/Fe2+, IO3−/I−, Q/QH2). That work did not optimize the STH efficiency for the bandgap combinations of the photocatalysts or the redox shuttle potentials of the electrolyte, in part because of the complexity of the model, which had many adjustable parameters.
Evaluation of theoretical limiting efficiencies for solar energy conversion processes as a function of the bandgap of the light-absorbers is a critical step toward identifying the primary factors that influence device performance. While numerous studies have reported the Shockley–Queisser detailed-balance efficiency limits for solar water electrolysis using electronically-connected tandem devices,10–15,20 such predictions are not available for electrochemically-connected tandem devices. To establish theoretical STH efficiency limits and design requirements for redox-shuttle-mediated electrochemically-connected tandem devices for solar water electrolysis, herein we present a comprehensive numerical analysis as a function of light-absorber bandgaps, redox shuttle potential, and redox shuttle electrocatalytic parameters. Notably, we found that the thermodynamic potential of the redox shuttle and the light-absorber bandgaps each influence the maximum possible STH efficiency. The resulting optimal bandgap combinations differ from combinations previously deduced from models of electronically-connected tandem designs, which further supports the merit in this work. We also determine that the range of redox shuttle potentials for the electrochemically-connected tandem design to outperform the performance of a single light-absorber depends on the exchange current densities modeled for the redox shuttle.
Numerical model
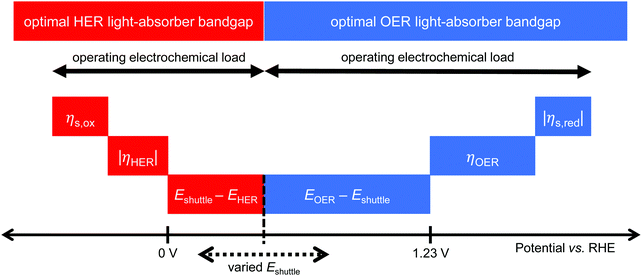
Models for electronically-connected tandem devices for solar water electrolysis that are positioned optically and electronically in series (Fig. 1a) are well known.10–15,20 Electrochemically-connected devices (Fig. 1b) are more complex due to additional constraints imposed by electrochemical reactions with the redox shuttle. Therefore, equations for the electronically-connected tandem devices are presented first, followed by several modifications required to describe the electrochemically-connected tandem devices. For the electronically-connected devices, the sum of the photovoltages generated by the light-absorbers must equal the electrochemical load, which is defined as the difference of the thermodynamic reaction potentials plus the overpotentials as follows,| Vtop + Vbottom = (EOER − EHER) + ηOER + |ηHER| | (1) |
For the electrochemically-connected tandem devices charge is mediated between the two light-absorbers by a soluble redox shuttle, A/A− (Fig. 1b). In these devices, the photovoltage generated by each light-absorber must equal the electrochemical load for its associated oxidation and reduction half-reactions as follows,
| Vbottom/top = (EOER − Eshuttle) + ηOER + |ηshuttle,red| | (2) |
| Vtop/bottom = (Eshuttle − EHER) + ηshuttle,ox + |ηHER| | (3) |
All model calculations were performed using MATLAB 2017b and numeric solutions to coupled equations were found using the vpasolve function. Several assumptions are made in the model including a standard temperature of 300 K, unity activity for H2 and O2 gases such that (EOER − EHER) = 1.23 V, unity activity for redox shuttle species that each react by an outer-sphere single-electron transfer mechanism, no parasitic light absorption by the redox shuttle species, no ohmic resistance/ion migration losses, and no concentration overpotentials due to species concentration gradients from finite rates of mass transport. Additionally, we assume that the device configuration and selection of light-absorbers and any additional co-catalysts are such that the band edges at the active surfaces straddle the appropriate redox potentials as required for device operation. This means that for each light-absorber, the potential of the valence-band edge is larger than the corresponding potential of the oxidation reaction and the potential of the conduction band edge is smaller than the corresponding potential of the reduction reaction.
Each light-absorber is modeled as an ideal photodiode via the typical areal current-density vs. voltage (j–V) relationship,15,16,31,32
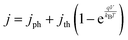 | (4) |
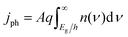 | (5) |
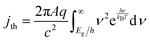 | (6) |
The frequency-independent absorptance (A) is included in eqn (5) to consider partial absorption of above-bandgap photons by the top light-absorber, and therefore, partial transmission of the incident photons to the bottom light-absorber. Likewise, eqn (6) guarantees that the rate of radiative recombination equals the rate of blackbody photon absorption at thermal radiative equilibrium, as mandated by the principle of detailed balance.2,33 The benefit of partial absorption of above-bandgap light is that with appropriately chosen absorptance values, a larger range of bandgap combinations results in large STH efficiencies, as shown previously for electronically-connected tandem devices.9,34 Absorptance/emittance is typically a frequency-dependent quantity that depends on the optical absorption coefficient of the light-absorber and the pathlength that light travels within the light-absorber.35 In electronically-connected tandem devices, the absorptance/emittance can be varied by altering the thickness of the nanometers-to-microns thick light-absorber and/or by altering its frequency-dependent absorption coefficient. In electrochemically-connected tandem particle suspension reactors, the absorptance/emittance can be varied through facile variations in the height of the suspension-filled reactor, the particle concentration, or the particle size.27 Because these facile variations are most likely to be incorporated in actual reactors and they result in frequency-independent variations in A, we incorporated frequency-independent values for the absorptance/emittance in the model.
For most cases, A is set equal to one for all photons with energy larger than the light-absorber bandgap. However, when the absorbed photon flux by the bottom light-absorber limits the overall operating current density of the tandem device, Atop is allowed to vary between 0 and 1 to enforce current-matching between the top and bottom light-absorbers, by a process that we term absorptance optimization. Absorptance optimization is not useful for the bottom light-absorber, because there is no benefit in transmitting photons through the bottom light-absorber. Moreover, when the overall operating current density of the tandem device is limited by the absorbed photon flux by the top light-absorber, absorptance optimization is also not useful, and in this case, the largest STH efficiency occurs when Atop = 1 and no photons whose energy is larger than the bandgap of the top light-absorber can be absorbed by the bottom light-absorber.
The electrocatalytic behavior of the two coupled redox reactions that occur at each light-absorber surface are modeled by the Butler–Volmer equation,
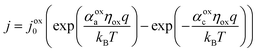 | (7) |
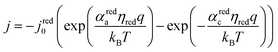 | (8) |
Experimentally-measured kinetic parameters for state-of-the-art RuO2 OER electrocatalysts and state-of-the-art Pt HER electrocatalysts,36,37 which were used in previous models of electronically-connected tandem devices,15 are incorporated herein for conditions of net production of O2 and H2, respectively, but with optimal selectivity such that α for the undesired reactions are set equal to zero (j0,HER = 0.147 mA cm−2; j0,OER = 3.26 × 10−6 mA cm−2; αa,HER = 0; αc,HER = 1.97; αa,OER = 1.60; αc,OER = 0). While convenient, the assumption of optimal selectivity for OER and HER electrocatalysis are inconsequential to the outcomes of the simulations; when perfectly symmetric non-selective electrocatalytic behavior is simulated using αa,HER = αc,HER = 1.97 and αc,OER = αa,OER = 1.60, the maximum calculated STH efficiency changed by <0.15% from the value obtained for the case of optimal selectivity (33.82% vs. 33.96%). Kinetic parameters for the redox shuttle reactions were chosen so that the reactions were modeled as being rapid, which was implemented by setting the exchange current density to an arbitrarily chosen large value such that the overpotentials were effectively equal to zero. In addition, all redox shuttle reactions were assumed to have optimal selectivity, which was implemented by setting the charge-transfer coefficients for the desired redox shuttle reactions to one and the charge-transfer coefficients for the undesired reactions to zero. The significance of selective, asymmetric redox shuttle electrocatalysis and optimal redox shuttle kinetic parameters were discussed in our prior work.27
The relationship between the operating voltage and the overpotentials are described by eqn (2) and (3) for the light-absorbers that perform the OER and the HER, respectively. In the absence of absorptance optimization, Atop is set equal to one and eqn (2) or (3) and (4), (7), and (8) are numerically solved for each light-absorber to obtain the operating current density and voltage. To enforce current-matching, the smaller of the two current densities is selected as the overall operating current density. When absorptance optimization is used, eqn (2) and (3) and one set of eqn (4), (7), and (8) for each light-absorber are simultaneously solved under the constraint of current-matching, i.e. jtop = jbottom, and with Atop as a free parameter. Other designs can also be modeled using similar procedures. In the model of an electronically-connected tandem device, eqn (1), (7), and (8), and two versions of eqn (4), one for each light-absorber, are simultaneously solved to obtain the overall operating current density. For the single light-absorber design, eqn (1), (7), and (8), and one version of eqn (4) are simultaneously solved to obtain the overall operating current density. For a side-by-side electrochemically-connected tandem design, where the light-absorbers are positioned optically in parallel, eqn (2) or (3), and (4), (7), and (8), are solved for each light-absorber. In this case, n(ν) for each light-absorber is set equal to the solar photon flux and A is set equal to one, but the current density of each light-absorber is multiplied by the fraction of the area it occupies out of the total area of the tandem design. In the base case, this fraction is set equal to 0.5 for both light-absorbers and the smaller of the two current densities is selected as the overall operating current density to enforce current matching. In the optimized case, the fractions are allowed to vary between 0 and 1 under the restriction that the two fractions sum to 1, and eqn (2) and (3) and one set of eqn (4), (7), and (8) for each light-absorber are simultaneously solved under the constraint of current-matching.
The ultimate performance metric is the STH efficiency,
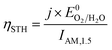 | (9) |
Results and discussion
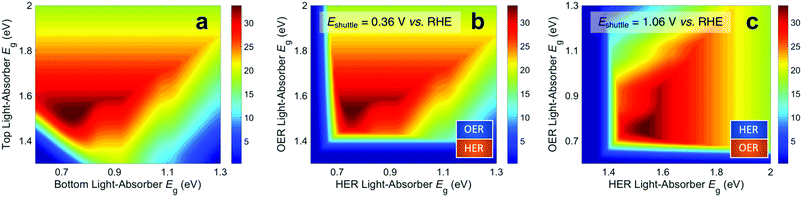
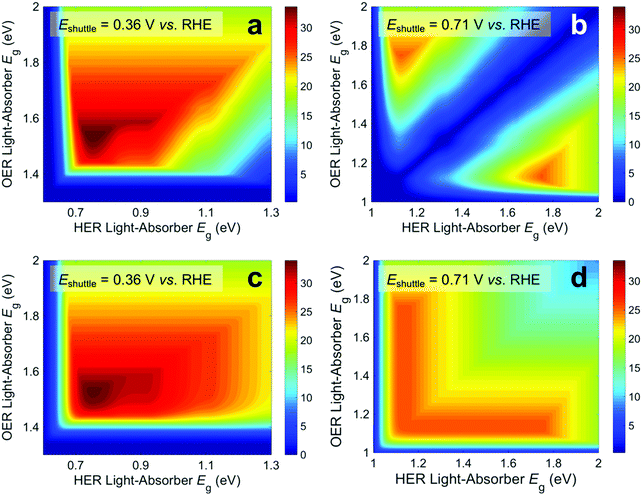
Fig. 3 presents STH efficiencies for the electronically-connected and electrochemically-connected tandem devices as a function of the light-absorber bandgaps. For the electronically-connected devices (Fig. 3a) the predicted maximum STH efficiency is 34%, which occurs for light-absorber bandgaps of 1.53 eV and 0.75 eV. This STH efficiency is slightly larger than the value of 30% obtained by Hu et al.,15 because of additional solution resistance terms that were included in their work. Fig. 3b and c depict the STH efficiencies for electrochemically-connected tandem designs for the specific cases of Eshuttle = 0.36 V and Eshuttle = 1.06 V vs. the reversible hydrogen electrode (RHE), redox shuttle potentials that lead to maximum STH efficiencies equal to that of the electronically-connected devices.For Eshuttle = 0.36 V (Fig. 3b), the minimum electrochemical load for the light-absorber driving the HER and redox shuttle oxidation (labeled as HER light-absorber) is 0.36 V (0.36 V – 0 V), whereas the minimum electrochemical load for the light-absorber driving the redox shuttle reduction and the OER (labeled as OER light-absorber) is 0.87 V (1.23 V – 0.36 V). In an optimal configuration the OER light-absorber has the larger bandgap and generates the larger photovoltage and is thus positioned on top of the HER light-absorber. For Eshuttle = 1.06 V (Fig. 3c), the minimum electrochemical load for the HER light-absorber is 1.06 V (1.06 V – 0 V), whereas the minimum electrochemical load for the OER light-absorber is 0.17 V (1.23 V – 1.06 V). Even with OER overpotentials of 0.3–0.4 V, the HER light-absorber has the larger bandgap and thus in an optimal configuration it is positioned on top of the OER light-absorber. Because of the important distinction between the HER light-absorber and the OER light-absorber in these two cases, the axes in Fig. 3b and c are labeled as HER and OER light-absorber bandgaps as opposed to the usual convention of bottom and top light-absorber bandgaps, as in Fig. 3a. Because of this reason, the data in Fig. 3b and c are transposes of each other. This is evident based on the maximum possible STH efficiency of 34%, which is achieved with an HER light-absorber bandgap of 0.75 V and an OER light-absorber bandgap of 1.53 V in Fig. 3b, and with an HER light-absorber bandgap of 1.53 V and an OER light-absorber bandgap of 0.75 V in Fig. 3c.
Fig. 3 illustrates that the predicted STH efficiencies for electrically-connected and electrochemically-connected tandem devices largely follow similar trends, except when one light-absorber bandgap is too small to supply the minimum electrochemical load of its desired half reactions, as seen in Fig. 3b and c for an HER light-absorber bandgap of <0.7 V or an OER light-absorber bandgap of <1.4 V. In the electronically-connected case, the same phenomena is observed, but within a smaller region bounded by the diagonal line that satisfies the condition that the sum of the light-absorber bandgaps is <1.7 V, and is therefore too small to supply the minimum electrochemical load for overall water electrolysis. The two values of Eshuttle selected for Fig. 3b and c are the only cases where the maximum possible STH efficiency for the electronically-connected device equals the maximum possible STH efficiency for the electrically-connected device. In general, the redox shuttle potential affects the distribution of STH efficiency values in the contour plot and in most cases the maximum STH efficiency is not the same.
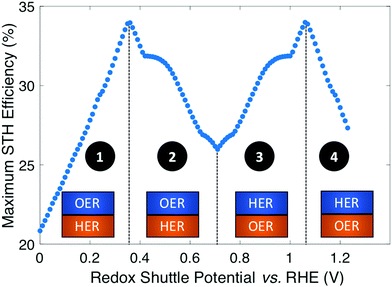
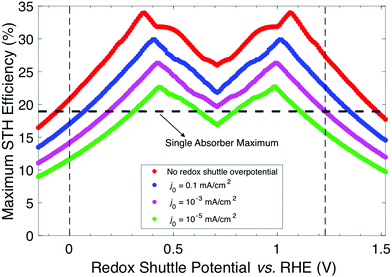
Plotting the maximum possible STH efficiency from each contour plot as a function of the redox shuttle potential generates Fig. 4. The observed trend results because the redox shuttle potential determines how the electrochemical loads (eqn (2) and (3)) are split between the two light-absorbers, and each light-absorber must generate a photovoltage in excess of its electrochemical load. This trend is present irrespective of whether redox shuttle reactions require a large kinetic overpotential. Large electrochemical loads require large photovoltages which are obtained using large bandgap light-absorbers; these light-absorbers inherently absorb less sunlight than small bandgap light-absorbers, and in turn generate smaller photocurrents than small bandgap light-absorbers. Because the photocurrent density is directly related to the STH efficiency (eqn (9)), the STH efficiency is maximized when the bandgap energy is small while still allowing the light-absorber to attain the photovoltage required to drive its electrochemical load at a fast rate. This requirement results in four distinct regions to the data shown in Fig. 4 that each define which light-absorber limits the STH efficiency and how this limitation changes with respect to the potential of the redox shuttle. For regions 1 and 2, the top light-absorber drives the OER and reduction of the redox shuttle while the bottom light-absorber drives the HER and oxidation of the redox shuttle; for regions 3 and 4 the locations of the redox reactions are switched.
As the redox shuttle potential is increased from its smallest value of 0 V to 0.36 V vs. RHE, the electrochemical load for the OER light-absorber decreases (eqn (2)), while the electrochemical load for the HER light-absorber increases (eqn (3)), all while Vtop > Vbottom. In this region, the electrochemical load on the top OER light-absorber is still substantially larger than the electrochemical load on the bottom HER light-absorber, forcing the bandgap of the top light-absorber to be large, and ranging from ∼2.0 eV to ∼1.5 eV; requiring such large bandgaps to overcome the minimum load of 0.87 V (1.23 V – 0.36 V) is an outcome of the slow OER kinetics. The large bandgap of the OER light-absorber means that it absorbs incident photons poorly, which results in a photocurrent that is always smaller than the photocurrent possible from an optimal bottom HER light-absorber. In region 1, there are no conditions where the electrochemical load on the bottom HER light-absorber becomes so large that its bandgap does not allow for sufficient absorption of transmitted sunlight to current-match with the top OER light-absorber. Even when the redox shuttle potential is as large as 0.36 V, the increase in the electrochemical load for the HER in this region does not negatively influence the predicted STH efficiencies because the relatively large top light-absorber bandgap still limits the net photocurrent. Therefore, in this region the STH efficiency increases with Eshuttle until it equals 0.36 V, a condition where the STH efficiency reaches a global maximum value of 34%.
In region 2, the electrochemical load is split more evenly between the two light-absorbers. Excluding the overpotentials, the minimum load on the HER light-absorber increases from 0.36 V to 0.71 V, while the load on the OER light-absorber decreases from 0.87 V to 0.52 V. Therefore, the minimum bandgap required for the top OER light-absorber to generate a photovoltage in excess of its electrochemical load is not prohibitively large, meaning that fewer photons are transmitted to the bottom light-absorber. This effect, combined with the increase in the electrochemical load on the bottom light-absorber compared to region 1, causes photon absorption by the bottom light-absorber to limit the STH efficiency. Therefore, a decrease in STH efficiency is observed with increasing value of Eshuttle until a local minimum in STH efficiency is observed at Eshuttle = 0.71 V. At this point, the operating electrochemical load is equal for the two light-absorbers, and therefore this is the only condition where the location of the HER and OER light-absorbers is interchangeable. This redox shuttle potential also results in the condition where the optimum bandgap of the bottom light-absorber is the largest.
In regions 3 and 4, Eshuttle > 0.71 V and thus, the electrochemical load on the HER light-absorber is larger than the electrochemical load on the OER light-absorber; the HER light-absorber is positioned on top of the OER light-absorber. The trend in STH efficiency as a function of Eshuttle mirrors the trend in regions 2 and 1, because of the explanations above, but with the HER light-absorber exposed to sunlight first. The STH efficiency again reaches a global maximum of 34%, but this time when Eshuttle equals 1.06 V. As in region 1, when Eshuttle > 1.06 V (region 4), STH efficiency decreases because the electrochemical load on the top HER light-absorber limits its bandgap to large values and thus its poor light absorption limits the photocurrent and therefore the STH efficiency. The reason why Eshuttle = 1.23 V results in a substantially larger STH efficiency compared to Eshuttle = 0 V (27% compared to 21%) is because the Pt HER electrocatalyst is at least four orders of magnitude faster than the RuO2 OER electrocatalyst for the same magnitude of overpotential. This difference in reactivity is widely observed and the underlying causes of this disparate behavior are the subject of substantial ongoing research efforts.38–40 Therefore, in region 4, relatively smaller bandgap requirements are placed on the top, HER light-absorber compared to in region 1 for the top, OER light-absorber.
In summary, the maximum STH efficiency for each value of Eshuttle is limited by photon absorption, and therefore photocurrent (eqn (9)), dictated by the electrochemical load of the light-absorbers: in regions 1 and 4, the large electrochemical load on the top light-absorber limits its absorption of incident solar photons while in regions 2 and 3, the bottom light-absorber has fewer solar photons transmitted to it and its electrochemical load limits its onset of absorption of transmitted light. In Fig. 4 there are several regions where the plot changes curvature, roughly at 0.4–0.5 V, 0.65–0.75 V, and 0.9–1.0 V. These sharp changes are a consequence of the irregular shape of the AM 1.5G solar spectrum with abrupt changes in the photon fluxes. Fig. S1 (ESI†) shows an analogous plot to Fig. 4 that uses an analytical, smooth blackbody spectrum with temperature of 5800 K instead of the AM 1.5G spectrum. The overall shape of the plot is the same but the sharp changes in curvature are not present.
When the STH efficiency is limited by photon absorption by the bottom light-absorber, the absorptance of the top light-absorber can be decreased from unity to better optimize the STH efficiency. Fig. 5 presents the contour plots of STH efficiency as a function of bandgap combination without so-called absorptance optimization (Fig. 5a and b) and with absorptance optimization (Fig. 5c and d) at two values of Eshuttle: Eshuttle = 0.36 V (Fig. 5a and c) is a redox potential that results in a global maximum for STH efficiency and Eshuttle = 0.71 V (Fig. 5b and d) is a redox potential that results in a local minimum in STH efficiency and where the location of the OER and the HER are interchangeable. Without absorptance optimization (Fig. 5a and b) there exists a single bandgap combination for each value of Eshuttle that results in its maximum STH efficiency: for Eshuttle = 0.36 V, the bandgaps are 1.53 eV and 0.75 eV for a 34% STH efficiency, and for Eshuttle = 0.71 V, the bandgaps are 1.75 eV and 1.13 eV for a 26% STH efficiency. When absorptance optimization is used, a single bandgap combination also maximizes STH efficiency for Eshuttle = 0.36 V. However, the range of bandgap combinations that produce a near-optimal STH efficiency is slightly larger, as seen by the small expansion of higher efficiency contours in the lower right-hand-side of Fig. 5c, which represent combinations where the two bandgaps are similar. Without absorptance optimization, these combinations have low efficiency because there is very little light that is absorbed by the bottom light-absorber but not by the top light-absorber, causing the bottom light-absorber to limit the overall current. For Eshuttle = 0.71 V, which resulted in equal operating electrochemical loads for both light-absorbers, absorptance optimization allows a larger range of bandgap combinations to produce a near-optimal STH efficiency value of 26%. Disregarding small fluctuations in the AM 1.5G solar spectrum by analyzing conditions that result in at least 99% of this maximum STH efficiency value, absorptance optimization allows the top light-absorber bandgap to range from 1.75 eV to 1.13 eV, with Atop ranging from 0.5 to 1, and with the bottom light-absorber bandgap fixed at 1.13 eV. In every case all photons with energy >1.13 eV are absorbed such that the photocurrent of each light-absorber is the same. Although absorptance optimization increases the number of high-efficiency bandgap combinations, it does not increase the maximum STH efficiency for a given value of Eshuttle. This is expected because whether or not absorptance optimization is used, the ideal bandgap combination results in absorption of all photons above the minimum allowable bandgap, which is dictated by the electrochemical load on the bottom light-absorber, in a way that matches the current between the two light-absorbers.
From a practical standpoint, having a larger range of useable bandgaps is desired because there is only a limited number of high-performance materials to choose from,24 and the bandgaps of these materials are often difficult to adjust without negatively affecting other photocatalytic properties. Additionally, for all values of Eshuttle, absorptance optimization enables a nonzero STH efficiency for the configuration in which both light-absorbers have the same bandgap. The case where both bandgaps are equal is also the condition of maximum STH efficiency for the tandem design where the light-absorbers are positioned side-by-side and optically in parallel (Fig. S2, ESI†) instead of being stacked on top of each other and optically in series. Reactor designs incorporating tandem light-absorbers positioned optically in parallel were considered in initial techno-economic analyses of Z-scheme particle suspension reactors for solar water electrolysis.28,29 For all other values of Eshuttle, and in the limit of key model assumptions including no gas crossover and no ohmic resistance/ion migration losses for both designs, the stacked tandem design can achieve a larger STH efficiency than the side-by-side tandem design for a fixed geometric area. The same conclusion was also observed from numerical device physics modeling of electronically-connected tandem devices.19 Similar to absorptance optimization for the stacked tandem design, by allowing the relative areas of the two light-absorbers in the side-by-side design to differ, the maximum STH efficiency can be improved for all values of Eshuttle ≠ 0.71 V, however, the maximum STH efficiency is still smaller than for the stacked tandem design, as shown in Fig. S2 (ESI†).
Fig. 6 builds on Fig. 4 and 5 and shows the bandgap combinations that result in near-optimal values for STH efficiency, which we define as within 99% of the maximum STH efficiency, for all values of Eshuttle between 0 V and 1.23 V. The effect of absorptance optimization on the results is distinct under different regions. In regions 1 and 4, where the bandgap for the top light-absorber limits the maximum STH efficiency and therefore Atop = 1 is optimal, absorptance optimization does not affect the results and therefore, a range of bandgaps for the bottom light-absorber results in the maximum STH efficiency for each value of Eshuttle. The minimum bandgap in the range is set by the electrochemical load and the maximum bandgap in the range is constrained by the condition of current-matching with the top light-absorber, which converge to a single bandgap combination at Eshuttle values of 0.36 V and 1.06 V. In regions 2 and 3, which are bracketed by Eshuttle values of 0.36 V and 1.06 V, the bottom light-absorber limits the STH efficiency and therefore absorptance optimization has a dramatic impact on the possible combinations of bandgaps that yield near-optimal values for STH efficiency. When the absorptance of the top light-absorber is not optimized (Fig. 6a), there is only a single combination of bandgaps that maximizes the STH efficiency, and therefore an extremely narrow range of bandgap combinations, spanning only <0.05 eV, results in STH efficiencies that are within 99% of their maximum value. When the absorptance of the top light-absorber is optimized (Fig. 6b), the bandgap of the top light-absorber can range from a maximum value when Atop = 1 to a minimum value fixed by its electrochemical load. Atop values resulting in near-optimal STH efficiencies increase to a maximum range of 0.5–1 as Eshuttle approaches the condition where a local minimum in STH efficiency occurs, at Eshuttle = 0.71 V. In summary, in regions 1 and 4 absorptance optimization has no effect on bandgap combinations that result in near-optimal values for STH efficiency, but in regions 2 and 3, absorptance optimization allows for a larger range of bandgap combinations that result in near-optimal values for STH efficiency, especially close to the boundary between these two regions at Eshuttle = 0.71 V.
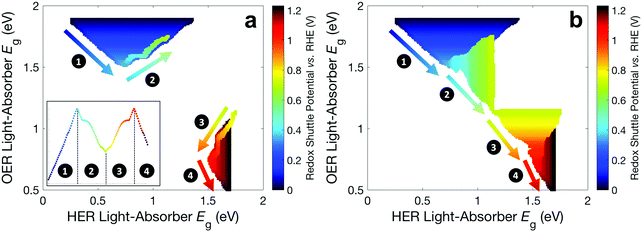 | ||
| Fig. 6 Bandgap combinations that result in an STH efficiency that is within 99% of the maximum STH efficiency for each value of Eshuttle (a) without absorptance optimization and (b) with absorptance optimization. Marker color signifies the value of Eshuttle. The inset in panel a is a reproduction of Fig. 4 using the same color scheme as in this figure. | ||
For the results in Fig. 3–6, the exchange current density of the redox shuttle was assumed to be effectively infinite, causing the redox shuttle reactions to contribute no kinetic overpotentials to the electrochemical load. Fig. 7 shows the STH efficiency vs. Eshuttle for a range of values of the exchange current density of the redox shuttle, j0,shuttle, and still assuming selective catalysis toward the desired reactions. As j0,shuttle decreases, additional overpotential is required to drive redox shuttle electrocatalysis, meaning that there is an increased electrochemical load and therefore requires additional photovoltage and a larger bandgap for both light-absorbers for any value of Eshuttle. This results in a decrease in the maximum STH efficiency, which is found to have an approximately logarithmic dependence on j0,shuttle. This logarithmic trend can be explained by eqn (7) and (8) which dictate that the electrocatalytic overpotential scales logarithmically with j0,shuttle. For large enough values of j0,shuttle (>102 mA cm−2) the overpotential is effectively zero and the maximum STH efficiency plateaus, as shown in Fig. S4 (ESI†); however, as j0,shuttle decreases the two redox shuttle potentials that result in a maximum STH efficiency converge slightly. For example, for j0,shuttle = 10−4 mA cm−2 the maximum STH efficiency occurs for Eshuttle = 1.00 V and 0.43 V, instead of for Eshuttle = 1.06 V and 0.36 V when j0,shuttle is nearly infinite. This is because at smaller values of j0,shuttle the overpotential for redox shuttle reactions represents a larger fraction of the electrochemical loads and therefore the electrochemical loads on each light-absorber are more similar in value. The local minimum in STH efficiency always occurs at Eshuttle = 0.71 V, which is the condition where the operating electrochemical loads on each light-absorber are equal. When j0,shuttle for the redox shuttle reactions decreases, each light-absorber requires the same additional overpotential and thus Eshuttle = 0.71 V is still the condition where the operating electrochemical loads on each light-absorber are equal.
In Fig. 7, the STH efficiency is plotted for Eshuttle values that extend beyond the water stability window of 0 V to 1.23 V as indicated by vertical dashed lines. For Eshuttle < 0 V, the minimum electrochemical load for the top OER light-absorber, i.e. (1.23 V – Eshuttle) in region 1 by eqn (2), exceeds the minimum electrochemical load for overall water electrolysis, 1.23 V (1.23 V – 0 V) by eqn (1), while for Eshuttle > 1.23 V, the minimum electrochemical load for the top HER light-absorber, i.e. (Eshuttle – 0 V) in region 4 by eqn (3), also exceeds the minimum electrochemical load for overall water electrolysis. It is apparent from Fig. 7 that the maximum STH efficiency of the tandem device exceeds that of a non-tandem device that incorporates a single light-absorber, as indicated by the horizontal dashed line; intersections of the colored plots with the horizontal dashed line represent conditions where the maximum STH efficiencies are the same for the two designs (Fig. S3, ESI† shows the relationship between STH efficiency and bandgap for a single light-absorber design that uses the same OER and HER electrocatalytic parameters as the tandem design). This phenomenon occurs because, while the minimum electrochemical load on the top light-absorber in the tandem design is always larger than the minimum electrochemical load for overall water electrolysis, the operating electrochemical load is not necessarily larger than the operating electrochemical load for overall water electrolysis. This enables the tandem design to have a larger maximum STH efficiency than the single light-absorber design even when Eshuttle values extend beyond the water stability window. This occurs when |ηshuttle,red| < |ηHER| in region 1 and ηshuttle,ox < ηOER in region 4 and is a consequence of the relative values for the exchange current densities of each reaction.
Because each light-absorber must catalyze two different redox reactions simultaneously, it may be necessary to utilize multiple co-catalysts each with fine-tuned electrocatalytic properties. Thus it is of practical importance to understand how the redox shuttle exchange current density, j0,shuttle, affects STH efficiency. Practically, a wide range of factors can affect j0,shuttle, including the material and surface properties of the co-catalyst(s) used, ion concentrations including the solution pH for proton-coupled electron-transfer reactions, and the number of electrons involved in the redox reaction.41–44 Because optimizing a device requires consideration of the HER, the OER, and the redox shuttle reactions, a wide range of j0,shuttle values is expected. As j0,shuttle decreases from its nearly infinite value (red) to a value similar that of j0,HER(Pt) (blue) and ultimately to a value that is similar to that of j0,OER(RuO2) (green), the range of values for Eshuttle where the tandem design is more efficient than the single light-absorber design narrows. When j0,shuttle is large (≥0.1 mA cm−2), the maximum STH efficiency for the tandem design exceeds that for the single light-absorber design over a significant range of Eshuttle values larger than 1.23 V (up to 1.35 V for j0,shuttle = 0.1 mA cm−2). Because the value of j0,shuttle is large, the electrochemical load on the top light-absorber is predominantly affected by the overpotential for either the HER or the OER, and to a lesser extent the overpotential for the redox shuttle reaction. This is in contrast to the design with the single light-absorber, which must supply the overpotential for both the HER and the OER and therefore leads to a larger electrochemical load and lower maximum STH efficiency for the single light-absorber design. However, for j0,shuttle < 0.1 mA cm−2 there are conditions where the single light-absorber maximum STH efficiency exceeds that of the tandem light-absorber maximum STH efficiency even when Eshuttle is within the water stability window. This occurs when the sum of the thermodynamic potentials and overpotentials for the redox shuttle reaction and either the HER or the OER (eqn (2) or (3)) for the top light-absorber is larger than the sum of the thermodynamic potentials (1.23 V) and overpotentials for overall water electrolysis, such that the operating electrochemical load on the top light-absorber in the tandem device is larger than the operating electrochemical load on the single light-absorber.
We have clearly shown that the value of Eshuttle substantially impacts the STH efficiency of electrochemically-connected tandem devices for solar water electrolysis. In practice, the optical and transport properties of the redox shuttle are also important; the shuttle must not competitively absorb sunlight and must transport rapidly between the two reactor compartments. In our previous work, we identified two candidate redox shuttles that had these beneficial properties, IO3−/I− and Q/QH2, and predicted that a steady-periodic STH efficiency of ∼4% was possible when either was used.27 The thermodynamic potentials of these redox shuttles, 1.085 V for IO3−/I− and 0.7 V for Q/QH2, lie near the predicted global maximum and local minimum in the STH efficiencies reported herein, respectively. Thus, we anticipate that the IO3−/I− redox shuttle is a more promising choice for a reactor, assuming that it is implemented in a device with nearly ideal HER and OER electrocatalysts and nearly ideal light-absorbers with bandgaps near 1.53 eV and 0.75 eV. Methylammonium lead triiodide perovskite or amorphous silicon is a close match for the larger bandgap while germanium or iron pyrite is a close match for the smaller bandgap. The Q/QH2 redox shuttle could also be effectively utilized in a device with STH efficiency between 20% and 26%, for a wide range of bandgap combinations when absorptance optimization is used (Fig. 6b). In this case, crystalline silicon could possibly be used for both light-absorbers. The other commonly considered redox shuttles, Fe3+/Fe2+ and I3−/I−, with thermodynamic potentials of 0.77 V and 0.536 V, respectively, also lie near the predicted local minimum STH efficiencies, where implementing absorptance optimization can extend the range of effective light-absorber bandgaps that can be used to attain near-optimal STH efficiencies.
Conclusions
Presented herein are calculations of the theoretical STH efficiency limits of electrochemically-connected tandem solar water splitting devices with soluble redox shuttles mediating charge transport between the OER and the HER light-absorbers. The behavior of these devices is fundamentally different from the relatively well-understood electrically-connected tandem structures. The analyses showed that the thermodynamic potential of the redox shuttle reaction has a significant impact on the maximum possible STH efficiency and thus selection of the redox shuttle is as important as selection of the light-absorbers and co-catalysts.For redox shuttles exhibiting zero kinetic overpotentials, optimally selective catalysis, and optimal redox potentials of Eshuttle = 0.36 V or Eshuttle = 1.06 V vs. RHE, electrochemically-connected tandem devices can attain the same maximum STH efficiency of 34% as possible with electronically-connected tandem devices. The total number of absorbed photons is maximized by splitting the electrochemical loads unevenly between the two light-absorbers. This study also demonstrated the influence of other design parameters on STH efficiency, including absorptance of the top light-absorber and exchange current density of the redox shuttle. Optical absorptance was determined to be a crucial parameter to widen the range of the top and bottom light-absorber bandgaps that attain near-optimal STH efficiencies, especially for redox shuttle potentials between 0.36 V and 1.06 V. As the exchange current density of the redox shuttle decreased, the maximum STH efficiency decreased and redox shuttle potentials to attain this STH efficiency converged toward the local minimum in STH efficiency, which occurs at a redox shuttle potential of 0.71 V. Results indicate that even with slow redox shuttle electrocatalysis, e.g. j0,shuttle = 10−5 mA cm−2, STH efficiencies above the single light-absorber limit of 19% can still be achieved with a tandem device as long as the redox shuttle potential is in the range of 0.3–0.6 V or 0.8–1.1 V. Moreover, results prove that for optimal and selective redox shuttle electrocatalysis, the electrochemically-connected tandem design is more efficient than the single light-absorber design even when redox shuttle potentials lie outside of the water stability window.
Based on the predicted results in this work, and favorable optical and transport behavior revealed in prior work,27 we expect that the IO3−/I− redox shuttle with a potential of 1.085 V exhibits great promise to achieve close to maximum STH efficiencies with optimally chosen light-absorber bandgaps of 1.53 eV and 0.75 eV. Collectively, these results provide insights to the broader community of researchers on the complex interplay between the numerous parameters in electrochemically-connected tandem devices for solar water electrolysis.
Conflicts of interest
There are no conflicts to declare.Acknowledgements
This work was supported by the U.S. Department of Energy, Office of Energy Efficiency and Renewable Energy, Fuel Cell Technologies Incubator Program under Award No. DE-EE0006963. The authors also thank Dr Adam Weber (Lawrence Berkeley National Laboratory) and Dr Chengxiang Xiang (California Institute of Technology) for helpful discussions related to this work.References
- C. C. L. McCrory, S. Jung, I. M. Ferrer, S. Chatman, J. C. Peters and T. F. Jaramillo, J. Am. Chem. Soc., 2015, 137, 4347–4357 CrossRef CAS PubMed.
- W. Shockley and H. J. Queisser, J. Appl. Phys., 1961, 32, 510–519 CrossRef CAS.
- J. W. Ager, M. R. Shaner, K. A. Walczak, I. D. Sharp and S. Ardo, Energy Environ. Sci., 2015, 8, 2811–2824 RSC.
- J. Jia, L. C. Seitz, J. D. Benck, Y. Huo, Y. Chen, J. W. D. Ng, T. Bilir, J. S. Harris and T. F. Jaramillo, Nat. Commun., 2016, 7, 13237 CrossRef CAS PubMed.
- S. Licht, B. Wang, S. Mukerji, T. Soga, M. Umeno and H. Tributsch, J. Phys. Chem. B, 2000, 104, 8920–8924 CrossRef CAS.
- G. Peharz, F. Dimroth and U. Wittstadt, Int. J. Hydrogen Energy, 2007, 32, 3248–3252 CrossRef CAS.
- K. Fujii, S. Nakamura, M. Sugiyama, K. Watanabe, B. Bagheri and Y. Nakano, Int. J. Hydrogen Energy, 2013, 38, 14424–14432 CrossRef CAS.
- E. Verlage, S. Hu, R. Liu, R. J. R. Jones, K. Sun, C. Xiang, N. S. Lewis and H. A. Atwater, Energy Environ. Sci., 2015, 8, 3166–3172 RSC.
- J. L. Young, M. A. Steiner, H. Döscher, R. M. France, J. A. Turner and T. G. Deutsch, Nat. Energy, 2017, 2, 17028 CrossRef CAS.
- J. R. Bolton, S. J. Strickler and J. S. Connolly, Nature, 1985, 316, 495–500 CrossRef CAS.
- M. C. Hanna and A. J. Nozik, J. Appl. Phys., 2006, 100, 074510 CrossRef.
- L. C. Seitz, Z. Chen, A. J. Forman, B. A. Pinaud, J. D. Benck and T. F. Jaramillo, ChemSusChem, 2014, 7, 1372–1385 CrossRef CAS PubMed.
- K. T. Fountaine, H. J. Lewerenz and H. A. Atwater, Nat. Commun., 2016, 7, 13706 CrossRef CAS PubMed.
- M. T. Winkler, C. R. Cox, D. G. Nocera and T. Buonassisi, Proc. Natl. Acad. Sci. U. S. A., 2013, 110, E1076–E1082 CrossRef CAS.
- S. Hu, C. Xiang, S. Haussener, A. D. Berger and N. S. Lewis, Energy Environ. Sci., 2013, 6, 2984 RSC.
- S. Haussener, S. Hu, C. Xiang, A. Z. Weber and N. S. Lewis, Energy Environ. Sci., 2013, 6, 3605 RSC.
- G. Liu, K. Du, S. Haussener and K. Wang, ChemSusChem, 2016, 9, 2878–2904 CrossRef CAS PubMed.
- C. Xiang, A. Z. Weber, S. Ardo, A. Berger, Y. Chen, R. Coridan, K. T. Fountaine, S. Haussener, S. Hu, R. Liu, N. S. Lewis, M. A. Modestino, M. M. Shaner, M. R. Singh, J. C. Stevens, K. Sun and K. Walczak, Angew. Chem., Int. Ed., 2016, 55, 12974–12988 CrossRef CAS PubMed.
- S. Haussener, C. Xiang, J. M. Spurgeon, S. Ardo, N. S. Lewis and A. Z. Weber, Energy Environ. Sci., 2012, 5, 9922 RSC.
- H. Döscher, J. F. Geisz, T. G. Deutsch and J. A. Turner, Energy Environ. Sci., 2014, 7, 2951–2956 RSC.
- T. Hisatomi, J. Kubota and K. Domen, Chem. Soc. Rev., 2014, 43, 7520–7535 RSC.
- K. Maeda and K. Domen, J. Phys. Chem. Lett., 2010, 1, 2655–2661 CrossRef CAS.
- F. E. Osterloh, Chem. Soc. Rev., 2013, 42, 2294–2320 RSC.
- D. M. Fabian, S. Hu, N. Singh, F. A. Houle, T. Hisatomi, K. Domen, F. E. Osterloh and S. Ardo, Energy Environ. Sci., 2015, 8, 2825–2850 RSC.
- A. Kudo and Y. Miseki, Chem. Soc. Rev., 2009, 38, 253–278 RSC.
- H. Li, W. Tu, Y. Zhou and Z. Zou, Adv. Sci., 2016, 3, 1500389 CrossRef PubMed.
- R. Bala Chandran, S. Breen, Y. Shao, S. Ardo and A. Z. Weber, Energy Environ. Sci., 2018, 11, 115–135 RSC.
- B. D. James, G. N. Baum, J. Perez and K. N. Baum, Technoeconomic Analysis of Photoelectrochemical (PEC) Hydrogen Production, Virginia, 2009, http://energy.gov/eere/fuelcells/downloads/technoeconomic-analysis-photoelectrochemical-pec-hydrogen-production Search PubMed.
- B. A. Pinaud, J. D. Benck, L. C. Seitz, A. J. Forman, Z. Chen, T. G. Deutsch, B. D. James, K. N. Baum, G. N. Baum, S. Ardo, H. Wang, E. Miller and T. F. Jaramillo, Energy Environ. Sci., 2013, 6, 1983 RSC.
- https://www.hydrogen.energy.gov/pdfs/review17/pd125_ardo_2017_o.pdf .
- M. R. Shaner, K. T. Fountaine and H.-J. Lewerenz, Appl. Phys. Lett., 2013, 103, 143905 CrossRef.
- Y. Surendranath, D. K. Bediako and D. G. Nocera, Proc. Natl. Acad. Sci. U. S. A., 2012, 109, 15617–15621 CrossRef CAS PubMed.
- C. H. Henry, J. Appl. Phys., 1980, 51, 4494–4500 CrossRef CAS.
- B. Seger, O. Hansen and P. C. K. Vesborg, Sol. RRL, 2017, 1, e201600013 CrossRef.
- M. F. Modest, Radiative Heat Transfer, Academic Press, 2nd edn, 2003 Search PubMed.
- S. Trasatti, J. Electroanal. Chem. Interfacial Electrochem., 1972, 39, 163–184 CrossRef CAS.
- G. Lodi, E. Sivieri, A. De Battisti and S. Trasatti, J. Appl. Electrochem., 1978, 8, 135–143 CrossRef CAS.
- J. K. Nørskov, J. Rossmeisl, A. Logadottir, L. Lindqvist, J. R. Kitchin, T. Bligaard and H. Jónsson, J. Phys. Chem. B, 2004, 108, 17886–17892 CrossRef.
- I. C. Man, H.-Y. Su, F. Calle-Vallejo, H. A. Hansen, J. I. Martínez, N. G. Inoglu, J. Kitchin, T. F. Jaramillo, J. K. Nørskov and J. Rossmeisl, ChemCatChem, 2011, 3, 1159–1165 CrossRef CAS.
- A. Kulkarni, S. Siahrostami, A. Patel and J. K. Nørskov, Chem. Rev., 2018, 118, 2302–2312 CrossRef CAS PubMed.
- Y. Sasaki, A. Iwase, H. Kato and A. Kudo, J. Catal., 2008, 259, 133–137 CrossRef CAS.
- H. Kato, Y. Sasaki, N. Shirakura and A. Kudo, J. Mater. Chem. A, 2013, 1, 12327 RSC.
- Y. Miseki, S. Fujiyoshi, T. Gunji and K. Sayama, Catal. Sci. Technol., 2013, 3, 1750 RSC.
- H. Suzuki, O. Tomita, M. Higashi and R. Abe, Catal. Sci. Technol., 2015, 5, 2640–2648 RSC.
Footnote |
| † Electronic supplementary information (ESI) available. See DOI: 10.1039/c8ee01828f |
| This journal is © The Royal Society of Chemistry 2019 |