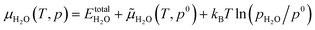Molecular or dissociative adsorption of water on clean and oxygen pre-covered Ni(111) surfaces†
Ling
Zhu
abc,
Chunli
Liu
abc,
Xiaodong
Wen
 ab,
Yong-Wang
Li
ab and
Haijun
Jiao
ab,
Yong-Wang
Li
ab and
Haijun
Jiao
 *ad
*ad
aState Key Laboratory of Coal Conversion, Institute of Coal Chemistry, Chinese Academy of Sciences, Taiyuan, 030001, China
bNational Energy Center for Coal to Liquids, Synfuels China Co., Ltd, Huairou District, Beijing, 101400, China
cUniversity of Chinese Academy of Sciences, No. 19A Yuquan Road, Beijing, 100049, PR China
dLeibniz-Institut für Katalyse e.V. an der Universität Rostock, Albert-Einstein Strasse 29a, 18059 Rostock, Germany. E-mail: haijun.jiao@catalysis.de
First published on 27th November 2018
Abstract
Water adsorption and dissociation on clean and oxygen pre-covered Ni(111) surfaces have been computed systematically by using density functional theory and ab initio atomistic thermodynamics. The adsorption of H, O and OH prefers 3-fold faced centered cubic hollow sites, and that of H2O prefers the top site. For (H2O)n aggregation, direct O–Ni interaction and H-bonding synergistically determine the adsorption energy, which is structure insensitive for large adsorbed clusters. At low coverage (θ ≤ 0.25 ML), OH adsorbs perpendicularly and prefers remote distribution without H-bonding, and the OH saturation coverage should be 0.625 ML on the basis of H2O dissociative adsorption. The adsorption configuration for 4O (0.25 ML) prefers a p(2 × 2) structure, in agreement with the experiment, and the O saturation coverage should be 0.25 ML based on H2O dissociative adsorption. On the 0.25 ML O pre-covered Ni(111), H2O greatly prefers molecular adsorption [4O + 4H2O(s)] over dissociative adsorption [8OH] thermodynamically, and this is in agreement with the photoelectron spectroscopy results and in disagreement with previously and recently proposed results from single crystal adsorption calorimetry of D2O adsorption. It is noted that the computed bond energy and formation enthalpy of the supposed surface hydroxyls on the basis of the molecular adsorbed state [4O + 4H2O(s)] are much closer to the experimentally estimated results than those computed on the basis of the dissociatively adsorbed state [8OH]. Furthermore, the computed H2O desorption temperature on the basis of the molecular adsorbed state [4O + 4H2O(s)] is in excellent agreement with experimental results (284 vs. 275–300 K), while that from the dissociatively adsorbed state [8OH] differs strongly (197 K). All these support H2O molecular adsorption instead of dissociative adsorption, and this needs further experimental investigations and confirmations. The vibrational frequencies of 4O, 4O + 4H2O and 8OH adsorption configurations have been computed to aid experimental studies.
Introduction
The interaction of water and solid surfaces plays an important role in many industrial processes, e.g. catalysis, corrosion, electrochemistry, environmental chemistry and materials science.1–4 Nickel catalysts have been widely used in methanation [CO + 3H2 = CH4 + H2O],5–8 methane steam reforming [CH4 + H2O = CO + 3H2],9–18 methane dry reforming [CH4 + CO2 = 2CO + 2H2]19,20 and methane partial oxidation [2CH4 + 3O2 = 2CO + 4H2O].21 Since water, as either a product or reactant, is involved in these reactions, it is essential to study the reaction of H2O formation or dissociation on nickel surfaces.Using electron stimulated desorption (ESD) ion angular distribution, low-energy electron diffraction (LEED) and temperature programmed thermal desorption (TPD), Madey et al.22 studied H2O adsorption on clean and O-pre-covered Ni(111) surfaces from the lowest to the saturation coverage. On the clean surface, they found the desorption peak at 165–170 K, which is actually due to H2O molecules in the first monolayer (ML) and the attractive H-bonding among these H2O molecules, and the adsorption energy of a single molecule is 0.44 eV. On the O-pre-covered surface (≤0.05 ML) at low H2O coverage (≤0.08 ML), there are two desorption peaks at 180–200 K and at 275–300 K, where the higher temperature peaks were supposed to be a consequence of the formation [O + H2O(s) = 2OH] of surface OH at low temperature (≥120 K) and their subsequent disproportionation to yield surface O and gaseous H2O at high temperature (≥200 K). Increasing the O pre-coverage from 0.05 to 0.25 ML at constant H2O coverage (∼0.3 ML), the H2O desorption rate and H2O coverage are virtually unchanged in the temperature range of 250–300 K. Using TPD and ESD, Stulen and Thiel23 studied H2O adsorption on clean and O pre-covered Ni(111) surfaces and found that on the clean surface the desorption of the first layer chemisorbed H2O has a first order kinetics with a desorption energy of about 0.42 eV; on the O-pre-covered surface (≈0.07 ML) the high temperature desorption (180–260 K) is due to the dissociative recombination from 2OH disproportionation.
Using TPD, angle resolved ultraviolet photoelectron spectroscopy (UPS), X-ray photoelectron spectroscopy (XPS) and LEED, Pache et al.24 studied H2O adsorption on clean as well as 0.25 ML O pre-covered Ni(111) surfaces. On the clean Ni(111) surface, they found that the saturation coverage of chemisorbed H2O is 0.66 ± 0.05 ML by XPS and the desorption temperature of 171, 152 and 158 K comes from the chemisorbed bilayer, transition layer and condensed water, respectively; the adsorption energy of the chemisorbed layer is 0.59 ± 0.05 eV. On the O pre-covered surface (0.25 ML), an additional peak is observed in TPD of water at low coverage reaching from 180 to 260 K saturating at a coverage of 0.25 ± 0.04 ML; this desorption peak is attributed to the molecularly adsorbed H2O on the surface and no evidence is found for H2O dissociation and OH formation from work function and angle resolved UPS measurement. Using TPD and XPS at 10−5 mbar and low coverage, Schulze et al.25 studied H2O adsorption on clean and O pre-covered Ni(111) surfaces. On the clean surface two adsorption states were observed; the first adsorbed layer with a maximum coverage of 0.42 ML has an adsorption energy of 0.54 ± 0.03 eV as well as a desorption peak at about 163 K at low coverage, and this peak shows saturation with increasing coverage; at coverage larger than 0.42 ML, the desorption energy is about 0.40 eV. On the 0.2 ML O pre-covered surface, photoelectron spectroscopy shows that the adsorbed H2O remains in the molecular state and does not desorb at 156 K, while it desorbs only at higher temperatures of 180 to 260 K. The UPS and XPS results24,25 contradict H2O formation from 2OH disproportionation as proposed by Madey et al.22 Further TPD studies of H2O on the clean Ni(111) surface confirms desorption temperature of about 170 K for the first layer adsorbed H2O molecules.26–28
Recently, Zhao et al.29 measured the heats of adsorption of D2O on clean and O pre-covered Ni(111) surfaces by single crystal adsorption calorimetry. On the clean surface at 100 K, the differential heat of adsorption of D2O starts at 0.56 eV and slightly increases up to ∼0.3 ML due to the intermolecular H-bonding; the integral heat of molecular adsorption is 0.56 eV for the most stable adlayer at 0.5 ML. On the 0.25 ML O pre-covered surface, D2O prefers molecular adsorption at 100 K with an integral heat of 0.58 eV, which is slightly higher than that on the clean surface by 0.02 eV. At 170 K, D2O was proposed to favor dissociative adsorption producing surface OH up to 0.23 ML D2O coverage. The differential heat starts from ∼0.73 eV and the decreases to 0.68 eV at 0.23 ML D2O saturation coverage. The integral heat is 0.70 eV at saturation coverage, which, in turn, gives an enthalpy of formation and bond energy of surface hydroxyls of −2.88 and 3.27 eV, respectively.
Theoretically, many studies reported H2O adsorption and dissociation on Ni(111) and found H2O adsorption at the top site with O–H bonds nearly parallel to the flat surface. As listed in Table 1, different models and methods gave different dissociation barriers, while coverage dependent H2O adsorption and dissociation are missing despite the fact that H2O prefers H-bonding and interacts with pre-covered oxygen atoms. By constructing a new nine-dimensional potential energy surface based on density functional theory points,30,31 Jiang and Guo studied water dissociation on Ni(111) and found their results to be in better agreement with the experiment.
| Size | Method | E a | E r | d O–H | Ref. |
|---|---|---|---|---|---|
| a This work. | |||||
| H2O = OH + H | |||||
| 4 × 4 (4T/2R) | PBE-D3 | 0.68 | −0.56 | 1.503 | |
| 3 × 3 (3T/2R) | PBE | 0.97 | −0.22 | 32 | |
| 2 × 2 (4T/2R) | PBE | 0.67 | −0.20 | 33 | |
| 3 × 3 (4T/2R) | RPBE | 0.90 | −0.28 | 34 | |
| 2 × 2 (3T/1R) | RPBE | 0.92 | −0.10 | 35 | |
| 2 × 2 (4T/2R) | PBE | 0.90 | −0.24 | 1.586 | 36 |
| 2 × 2 (4T/2R) | PBE | 0.69 | −0.18 | 1.538 | 37 |
| 3 × 3 (4T/2R) | PBE | 0.88 | −0.19 | 1.55 | 38 |
| 3 × 3 (3T/1R) | PW91 | 0.96 | −0.26 | 1.56 | 39 |
| 2 × 2 (3T/1R) | PBE | 0.89 | −0.16 | 40 | |
| 2 × 2 (4T/2R) | PW91 | 0.80 | −0.41 | 41 | |
| 3 × 2 | PBE | 0.74 | −0.56 | 1.881 | 42 |
| 2 × 2 | PW91 | 0.77 | −0.26 | 1.60 | 43 |
| OH = O + H | |||||
| 4 × 4 (4T/2R) | PBE-D3 | 1.25 | −0.18 | 1.378 | |
| 3 × 3 (3T/2R) | PBE | 1.19 | −0.17 | 32 | |
| 2 × 2 (4T/2R) | PBE | 0.79 | −0.03 | 33 | |
| 3 × 3 (4T/2R) | RPBE | 0.85 | −0.20 | 34 | |
| 2 × 2 (3T/1R) | RPBE | 0.85 | −0.34 | 35 | |
| 2 × 2 (4T/2R) | PBE | 1.01 | −0.06 | 1.374 | 36 |
| 2 × 2 (4T/2R) | PBE | 0.80 | −0.03 | 1.340 | 37 |
| 3 × 3 (3T/1R) | PW91 | 1.03 | −0.04 | 1.35 | 39 |
| 2 × 2 (3T/1R) | PBE | 0.97 | −0.33 | 40 | |
| 2 × 2 (4T/2R) | PW91 | 0.97 | −0.36 | 41 | |
| 3 × 2 | PBE | 0.65 | −0.29 | 1.465 | 42 |
| 3 × 3 (4T/2R) | RPBE | 1.03 | 1.59 | 30 | |
| 3 × 3 (4T/2R) | PW91 | 0.67 | 1.56 | 30 | |
| O + H2O = 2OH | |||||
| 4 × 4 (4T/2R) | PBE-D3 | 0.46 | 0.14 | 1.558 | |
| 3 × 3 (3T/2R) | PBE | 0.66 | 0.38 | 32 | |
| 2 × 2 (4T/2R) | PW91 | 0.72 | 0.30 | 41 | |
| 2H2O = OH + H + H2O | |||||
| 4 × 4 (4T/2R) | PBE-D3 | 0.68 | −0.25 | 1.475 | |
| 3 × 3 (3T/2R) | PBE | 0.82 | 0.09 | 32 | |
| 3 × 3 (4T/2R) | PBE | 0.81 | 0.22 | 1.45 | 38 |
To study the interaction of H2O and Ni(111) systematically, we computed H2O adsorption and dissociation on clean and oxygen pre-covered Ni(111) surfaces. Our main concerns are coverage dependent adsorption and dissociation, surface oxygen mediated reactions and H2O desorption temperatures on different surfaces. Systematic and comparative results are reported. To aid the experimental studies, the vibrational frequencies of 4O, 4O + 4H2O and 8OH adsorption have been computed.
Computational methods and models
Density functional theory calculations were performed with the plane wave based pseudo-potential code in the Vienna ab initio simulation package (VASP).44,45 The electron–ion interaction is described with the projector augmented wave method (PAW).46,47 The exchange and correction energies are described within generalized gradient approximation using the Perdew–Burke–Ernzerhof formulation (GGA-PBE).48 To include van der Waals interaction, which is known to play an important role in weak interaction systems,49,50 we included the D3 correction of Grimme.51 All structures were optimized with PBE including D3 correction (PBE-D3). The plane wave cutoff energy was specified by 400 eV, and the electron smearing method with σ = 0.20 eV was used to ensure energies with errors due to smearing of less than 1 meV per unit cell. The convergence criteria for geometry optimizations of total energy and forces were 10−4 eV and 0.02 eV Å−1. Spin polarization was included. The transition state was identified using the climbing image nudged elastic band (CI-NEB) method.52 For the bulk structure, the face centered cubic crystal structure was used and the reciprocal space is sampled with a 12 × 12 × 12 k-point grid using the Monkhorst–Pack method.53 The calculated lattice constant (3.525 Å) and magnetic moment (0.64 μB) are close to the experimental values (3.52 Å54 and 0.61 μB![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 55). For Ni(111), to avoid interactions among slabs, the vacuum layer between periodically repeated slabs was set at 15 Å. The (4 × 4) slab model consists of four layers containing a total of 64 Ni atoms, where the top two layers including adsorbates were relaxed and the bottom two layers were fixed in their bulk positions. The 3 × 3 × 1 Monkhorst–Pack k-point sampling was used.
55). For Ni(111), to avoid interactions among slabs, the vacuum layer between periodically repeated slabs was set at 15 Å. The (4 × 4) slab model consists of four layers containing a total of 64 Ni atoms, where the top two layers including adsorbates were relaxed and the bottom two layers were fixed in their bulk positions. The 3 × 3 × 1 Monkhorst–Pack k-point sampling was used.
The adsorption energy (Eads) was defined as Eads = E(X/slab) − E(slab) − E(X), where E(X/slab) is the total energy of the slab with adsorbates on the surface in equilibrium; E(slab) is the energy of the clean Ni(111) surface; E(X) is the energy of the free adsorbed molecule in the gas phase. The more negative the Eads, the stronger the adsorption. The desorption energy Edes is the negative of the adsorption energy, Edes = −Eads. All relative energies include the correction of zero point energies (ZPE). The activation barrier (Ea) is defined as Ea = ETS − EIS, and the reaction energy (Er) is defined as Er = EFS − EIS, where EIS, EFS and ETS are the energies of the corresponding initial state (IS), final state (FS) and transition state (TS). The stepwise adsorption energy was defined as ΔEads = E((n + 1)X/slab) − E(nX/slab) − E(X), where a position ΔEads for (n + 1) adsorbed X species indicates the saturation adsorption with nX species. In addition, we carried out revised PBE (RPBE56) single-point energy calculation with dispersion correction on the basis of PBE optimized structures (RPBE-D3) and ZPE correction from PBE.
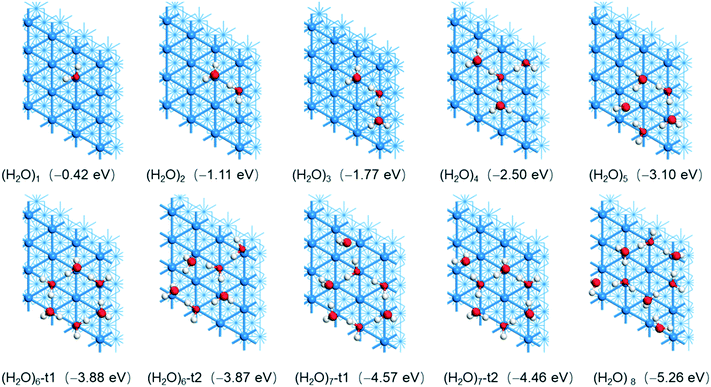
Further we used ab initio atomistic thermodynamics57,58 to model the H2O desorption temperature under given conditions. There are many related examples for the adsorption and desorption of H2, H2O, CO and other small molecules by using this method.59–64 According to previous work, we took H2O desorption on the Ni(111) surface: H2O/Ni → Ni + H2O(g) as an example; the change of Gibbs free energy (ΔG) for this reaction can be described as eqn (1):
| ΔG = G[Ni(111)] + Ggas(H2O) − G[{H2O}/Ni(111)] | (1) |
In this equation, G[Ni(111)] is the Gibbs free energy of the Ni(111) surface. G[{H2O}/Ni(111)] is the Gibbs free energy of the Ni(111) surface with the H2O molecule. We apply the DFT calculated total energy to replace the Gibbs free energy of the solid surfaces.65 The Ggas(H2O) term is equal to μ(H2O). The H2O chemical potential can be described as
 is the DFT calculated energy of the isolated H2O molecule (including zero point energy), the
is the DFT calculated energy of the isolated H2O molecule (including zero point energy), the 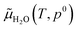 term is the chemical potential at different temperatures, which can be found in thermodynamic tables; and kBT
term is the chemical potential at different temperatures, which can be found in thermodynamic tables; and kBT![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) ln(pH2O/p0) is the contribution of temperature and H2O partial pressure to the H2O chemical potential. Therefore eqn (1) can be rewritten as
ln(pH2O/p0) is the contribution of temperature and H2O partial pressure to the H2O chemical potential. Therefore eqn (1) can be rewritten as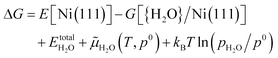 | (2) |
Results and discussion
(a) Adsorption of H, O, OH and H2O
For H, O, OH and H2O adsorption on Ni(111), the top (T), bridge (B), 3-fold hexagonal close-packed (hcp-3H) and 3-fold face centered-cubic (fcc-3F) sites have been considered with different initial configurations. The most stable adsorption configurations are shown in Fig. 1 and the related parameters are listed in Table 2.| (mT/nR) | Method | E ads | d X–Ni | Ref. |
|---|---|---|---|---|
| a This work. b On the basis of gaseous H2 and O2. | ||||
| H (fcc-3F) | ||||
| 4 × 4 (4T/2R) | PBE-D3 | −0.62b (−2.91) | 1.708 | |
| 4 × 4 (4T/2R) | RPBE-D3 | −0.59b (−2.83) | 1.708 | |
| 4 × 4 (4T/2R) | PBE | −0.53b (−2.65) | ||
| 2 × 2 (4T/2R) | PBE | −2.65 | 33 | |
| 2 × 2 (3T/1R) | RPBE | −2.8 | 35 | |
| 2 × 2 (4T/2R) | PBE | −2.77 | 36 | |
| 2 × 2 (4T/2R) | PBE | −2.66 | 1.71 | 37 |
| 2 × 2 (3T/1R) | PBE | −2.78 | 40 | |
| 2 × 2 (4T/2R) | PW91 | −2.77 | 0.896 | 41 |
| 2 × 2 (3T/1R) | PBE | −2.80 | 66 | |
| O (fcc-3F) | ||||
| 4 × 4 (4T/2R) | PBE-D3 | −2.44b (−5.78) | 1.840 | |
| 4 × 4 (4T/2R) | RPBE-D3 | −2.27b (−5.47) | 1.840 | |
| 4 × 4 (4T/2R) | PBE | −2.33b (−5.67) | ||
| 2 × 2 (4T/2R) | PBE | −5.30 | 33 | |
| 2 × 2 (3T/1R) | RPBE | −4.5 | 35 | |
| 2 × 2 (4T/2R) | PBE | −4.81 | 36 | |
| 2 × 2 (4T/2R) | PBE | −5.31 | 1.84 | 37 |
| 3 × 3 (3T/1R) | PW91 | −2.14b | 39 | |
| 2 × 2 (3T/1R) | PBE | −5.50 | 40 | |
| 2 × 2 (4T/2R) | PW91 | −5.43 | 1.129 | 41 |
| 2 × 2 (3T/1R) | PBE | −5.39 | 66 | |
| OH (fcc-3F) | ||||
| 4 × 4 (4T/2R) | PBE-D3 | −3.16 | 1.971 | |
| 4 × 4 (4T/2R) | RPBE-D3 | −2.61 | 1.971 | |
| 4 × 4 (4T/2R) | PBE | −3.07 | ||
| 2 × 2 (4T/2R) | PBE | −3.10 | 33 | |
| 2 × 2 (3T/1R) | RPBE | −2.5 | 35 | |
| 2 × 2 (4T/2R) | PBE | −3.34 | 36 | |
| 2 × 2 (4T/2R) | PBE | −3.08 | 1.98 | 37 |
| 3 × 3 (3T/1R) | PW91 | −3.12 | 39 | |
| 2 × 2 (3T/1R) | PBE | −3.14 | 40 | |
| 2 × 2 (4T/2R) | PW91 | −3.06 | 1.360 | 41 |
| 2 × 2 (3T/1R) | PBE | −3.27 | 66 | |
| H2O (T) | ||||
| 4 × 4 (4T/2R) | PBE-D3 | −0.42 | 2.156 | |
| 4 × 4 (4T/2R) | RPBE-D3 | −0.52 | 2.156 | |
| 4 × 4 (4T/2R) | PBE | −0.25 | ||
| 3 × 3 (3T/2R) | PBE | −0.40 | 32 | |
| 2 × 2 (4T/2R) | PBE | −0.19 | 33 | |
| 2 × 2 (4T/2R) | PBE | −0.47 | 36 | |
| 2 × 2 (4T/2R) | PBE | −0.20 | 2.23 | 37 |
| 3 × 3 (4T/2R) | PBE | −0.16 | 2.17 | 38 |
| 3 × 3 (3T/1R) | PW91 | −0.29 | 2.19 | 39 |
| 2 × 2 (3T/1R) | PBE | −0.25 | 2.24 | 40 |
| 2 × 2 (4T/2R) | PW91 | −0.04 | 2.216 | 41 |
| 3 × 3 (4T/2R) | RPBE | −0.03 | 2.81 | 30 |
| 3 × 3 (4T/2R) | PW91 | −0.24 | 2.25 | 30 |
| 2 × 2 (3T/1R) | PBE | −0.27 | 66 | |
As shown in Fig. 1, H2O adsorption prefers the top site with an adsorption energy of −0.42 eV, and the adsorption of H, O and OH prefers the fcc-3F site with an adsorption energy of −0.62, −2.44 and −3.16 eV, respectively. It is noted that OH adsorbs vertically to the surface and H2O adsorbs nearly parallel to the surface plane. As shown in Table 2, different methods and models give different adsorption energies for each surface species despite the same adsorption site and configuration. We found that the computed H2O adsorption including dispersion correction agrees with the experimentally determined value (−0.42 vs. −0.44,22 −0.42,23 −0.5425 and −0.56 eV29). We further computed H2O adsorption using the RPBE method including dispersion correction with the PBE structure, and the estimated H2O adsorption is −0.52 eV, more close to the experimental values. For H2 adsorption, only the PBE computed adsorption energy agrees very well with the experimental values (−1.07 vs. −1.0,67 −0.90,68 −0.84 to −1.0,69 and −0.92 eV70), while the PBE-D3 and RPBE-D3 computed values (−1.24 and −1.18 eV, respectively) are slightly higher.
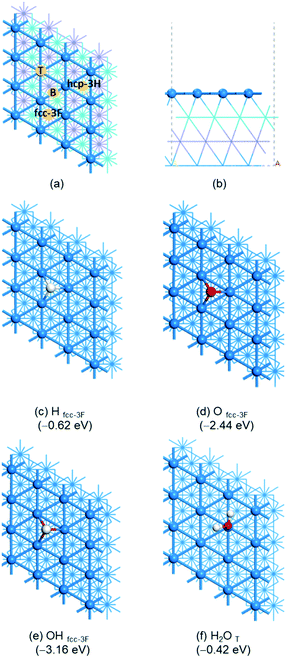
(b) Surface H2O aggregation
Due to the interaction of H2O and Ni(111) as well as H-bonding among adsorbed H2O molecules, we used the stepwise adsorption energy to find the most stable adsorption configurations of (H2O)n, where one H2O molecule was added to the previous one which is the most stable after considering both interactions. The most stable adsorption configurations of (H2O)n (n = 1–8) by using PBE-D3 are given in Fig. 2 and the relevant adsorption energies and bond parameters are listed in the ESI† (Table S1). The adsorption energies by using RPBE-D3 of (H2O)n (n = 1–8) are given in the ESI† (Fig. S1).For 2H2O co-adsorption, one H2O prefers the top site with an O–Ni distance of 2.061 Å, shorter than that of single H2O adsorption (2.156 Å), and the second adsorbed H2O has a very long O–Ni distance (3.031 Å). The first adsorbed H2O provides a H atom and the second adsorbed H2O provides an O atom for H-bonding (1.687 Å). The total adsorption energy is −1.11 eV, larger than double that of single H2O adsorption (−0.84 eV). The average adsorption energy is −0.56 eV, and the stepwise adsorption energy is −0.69 eV. To verify the synergy effect of both interactions, we computed the gas phase single-point energies of the co-adsorbed 2H2O as well as the two individual H2O molecules from their co-adsorbed states. It is found that the resulting H-bonding energy is −0.19 eV, weaker than the stepwise adsorption energy by 0.50 eV. This indicates that the stepwise adsorption energy (−0.69 eV) comes from the synergy effect of both interactions.
For 3H2O co-adsorption in a bent shape, the middle H2O adsorbs at the top site and provides both H atoms for H-bonding. The O–Ni distance is 2.005 Å, shorter than that of 2H2O and H2O adsorption (2.061 and 2.156 Å, respectively), and the O–Ni distance of the other two H2O molecules is 3.028 and 3.026 Å, respectively. The H-bonding distances are 1.727 Å, longer than that of the co-adsorption of 2H2O (1.687 Å). The total adsorption energy is −1.77 eV, larger than triple that of single H2O adsorption (−1.26 eV). The average adsorption energy is −0.59 eV, and the stepwise adsorption energy is −0.66 eV, close to that for the second H2O stepwise adsorption.
For 4H2O co-adsorption, the most stable adsorption configuration has a star-like structure, in which the middle H2O adsorbs at the top site with an O–Ni distance of 2.101 Å and provides both H atoms for H-bonding (1.668 Å) to two H2O molecules. In addition, the O–Ni distance of these two H2O molecules is 2.910 and 2.924 Å, respectively. The last H2O molecule provides a H atom for H-bonding to the central H2O molecule (1.678 Å) and the O–Ni distance is 2.065 Å. The total adsorption energy is −2.50 eV, larger than four-fold that of single H2O adsorption (−1.68 eV). The average adsorption energy is −0.63 eV, and the stepwise adsorption energy is −0.73 eV. This shows that two H2O molecules, which provide H atoms for H-bonding, interact directly with surface Ni atoms, and the other two H2O molecules, which provide O atoms for H-bonding, are stabilized by H-bonding.
On the basis of these results, we build large H2O clusters by considering O–Ni and H-bonding interactions. For the co-adsorption of 5H2O, the most stable adsorption configuration has a cyclic structure, where one H2O molecule provides both H atoms for H-bonding (1.681 and 1.698 Å) with two neighboring H2O molecules and the O–Ni distance is 1.990 Å. In turn, these two neighboring H2O molecules interact with their next neighboring H2O molecules via H-bonding (1.919 and 1.859 Å). The last two H2O molecules also interact via H-bonding (1.749 Å). It is noted that the last H2O has one O–H bond to the surface rather than the O atom. The total adsorption energy is −3.10 eV, the stepwise adsorption energy is −0.60 eV and the average adsorption energy is −0.62 eV.
For the co-adsorption of 6H2O, we computed a hexagonal adsorption configuration with three short (1.567 Å) and three long H-bonds (1.796, 1.798 and 1.797 Å). Each H2O molecule adsorbs at the top site, and the O–Ni distances are 2.149, 2.150, 2.151, 2.984, 2.972, and 2.978 Å, indicating that there are three strong and three weak O–Ni interactions. The total adsorption energy is −3.88 eV, the stepwise adsorption energy is −0.78 eV and the average adsorption energy is −0.65 eV. On the basis of the cyclic (H2O)5, we computed another (H2O)6 structure with an exocyclic H2O and the total adsorption energy is −3.87 eV. This indicates that the adsorption energy is not structure sensitive for large adsorbed clusters. This is probably due to the same number of Ni–O and H-bonding interactions. Indeed, ring-like hexamer D2O clusters on Ni(111) were observed in wide coverage ranges at 20 K by infrared reflection absorption spectroscopy.71 In addition, we computed the O–H stretching and bending frequencies for (H2O)n (Table S6†). It is found that the O–H stretching frequencies are shifted to lower wavenumbers with the formation of H-bonding. Taking the (H2O)6 ring hexamer as an example, the O–H stretching frequencies are in the range of about 3650 to 2560 cm−1, and this differs strongly from the monomeric H2O adsorption at 3700 and 3584 cm−1. In contrast, the O–H bending frequencies are shifted to higher wavenumbers compared with that of single H2O adsorption (1635–1574 vs. 1556 cm−1).
On the basis of the hexagonal structure of (H2O)6, we added next exocyclic H2O molecules. The two (H2O)7 structures have close adsorption energies (−4.57 and −4.46 eV, respectively), the stepwise adsorption energy is −0.69 and −0.58 eV, respectively, and the average adsorption energy is −0.65 and −0.64 eV, respectively. For the monolayer (H2O)8, on the basis of the more stable (H2O)7 with another exocyclic H2O molecule, the total adsorption energy is −5.26 eV, the stepwise adsorption energy is −0.69 eV and the average adsorption energy is −0.66 eV.
On the basis of these results, one can expect that H2O adsorption on Ni(111) can have simple structures at very low coverage and very complex structures at high coverage; both direct O–Ni and H-bonding synergistically determine the total adsorption energy. It is also interesting to note that the stepwise adsorption energy has an average value of −0.69 eV.
(c) Surface H2O dissociation
As listed in Table 1, there are many computational studies about H2O dissociative adsorption on Ni(111). Although all these studies gave the same qualitative trend, they differ quantitatively from different methods and models. For example, some studies showed that the first step H–O dissociation has a lower barrier than the second step, while some studies gave disordered results. In addition, the computed dissociation energies also differ strongly. The optimized geometries of the initial, transition and final states are shown in Fig. 3. Relevant structural parameters are listed in Table 2. The reaction barriers, reaction energies and relevant structural parameters of the transition state are listed in the ESI† (Table S3). The potential energy surface is shown in Fig. 4.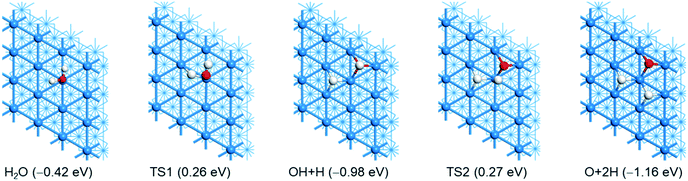 | ||
| Fig. 3 Adsorption configuration and energy (eV, PBE-D3) of H2O dissociation (Ni/blue; O/red; H/white). | ||
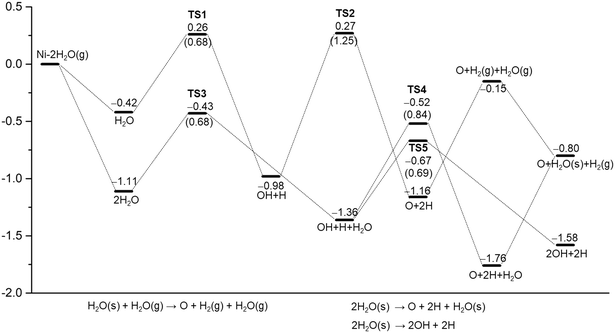 | ||
| Fig. 4 Potential energy surfaces for H2O and (H2O)2 dissociative adsorption on Ni(111) using PBE-D3 (the barrier of elementary steps in parentheses, s for surface species, g for gas phase species). | ||
Starting with H2O adsorbed at the top site, the first H–O dissociation has a barrier of 0.68 eV and is exothermic by 0.56 eV. In the transition state, the breaking O–H distance is 1.544 Å. In the final state, both OH and H are located at the fcc-3F site. Starting with the co-adsorbed OH + H, the second H–O dissociation has a barrier of 1.25 eV and is exothermic by 0.18 eV. This indicates that the second H–O dissociation has a higher barrier than the first one and is less exothermic than the first one. The total reaction is exothermic by 1.16 eV on the basis of gaseous H2O or exothermic by 0.74 eV on the basis of adsorbed H2O.
By consideration of gaseous H2O (Fig. 4), both steps have very close apparent barriers (0.26 and 0.27 eV, respectively). On the basis of the adsorbed H2O and O + 2H, gaseous H2 evolution is endothermic by 0.27 and 1.01 eV, respectively. However, gaseous H2 evolution becomes exothermic by 0.15 eV on the basis gaseous H2O. Experimentally, it is found that D2O forms adsorbed clusters at first at 80 K and then dissociates at 165 K; the dissociation temperature becomes high with an increase in coverage.71
Due to the H-bonding in co-adsorbed (H2O)2, we computed the H-bonding mediated H2O dissociation. The optimized structures of the initial, transition and final states are shown in the ESI† (Fig. S2). Relevant structural parameters are listed in Table S2.† The reaction barriers and reaction energies as well as relevant structural parameters of the transition state are listed in the ESI† (Table S3). The potential energy surface is shown in Fig. 4.
At first, we computed the dissociation of the H2O molecule with the longer Ni–O bond distance. The first H–O dissociation has a barrier of 0.68 eV and is exothermic by 0.25 eV. In the transition state, the breaking O–H distance is 1.475 Å. For the first H–O dissociation of the H2O molecule with the shorter Ni–O bond distance, the barrier is 0.95 eV and the reaction is exothermic by 0.26 eV. The breaking O–H distance in the transition state is 1.348 Å.
In the second H–O dissociation, we considered two competitive reactions. The reaction OH + H + H2O = O + 2H + H2O has a barrier of 0.84 eV and is exothermic by 0.40 eV. In the transition state, the breaking O–H distance is 1.478 Å, and the forming H–Ni distance is 1.528 Å. The reaction OH + H + H2O = 2OH + 2H has a barrier of 0.69 eV and is exothermic by 0.22 eV. In the transition state, the breaking O–H distance is 1.512 Å. As shown in Fig. 4, the co-adsorbed H2O molecule did not significantly affect the first step dissociation barrier of the H2O molecule, but obviously boosted the dissociation barrier of OH. This is due to the H-bonding (1.687 Å) in the transition states. Therefore, we computed the surface O promoted H2O dissociation.
(d) Surface O assisted H2O dissociation
To study the effect of surface O on H2O dissociation, the H2O dissociative adsorption on the O pre-covered Ni(111) surface is computed with a sequential increase of the H2O molecule and the evolution of gaseous H2, nO + H2O(g) = (n + 1)O + H2(g) (n = 1–4). The optimized configurations for the stationary points of the initial, transition and finial states (Fig. S3–S6†), as well as the structural parameters of the initial and final states are listed in the ESI† (Table S4). The energy barriers, reaction energies and related critical bond distances of the transition states are listed in the ESI† (Table S5). The whole potential energy surface is shown in Fig. 5 and the ESI† (Fig. S7).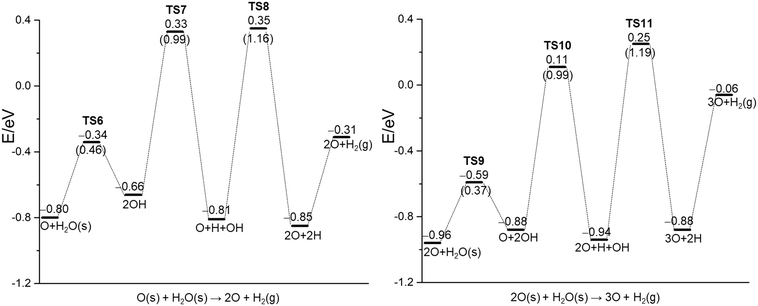 | ||
| Fig. 5 H2O dissociation on nO (n = 1–2) pre-covered Ni(111) using PBE-D3 (the barrier of elementary steps in parentheses, s for surface species, g for gas phase species). | ||
At first, we computed the H2O dissociative adsorption on one oxygen pre-covered Ni(111) surface (0.0625 ML), which is close to the oxygen coverage used in the experiment (θ ≤ 0.05 ML).22 Starting with the co-adsorption of one adsorbed surface O atom and one gaseous H2O molecule, the adsorption energy of H2O is −0.65 eV, higher than that on the clean surface (−0.42 eV); this increase of adsorption is due to the enhanced H-bonding (1.908 Å). For H2O dissociation [O + H2O = 2OH], the barrier is 0.46 eV and the reaction is endothermic by 0.14 eV. In the transition state, the breaking O–H distance is 1.558 Å. For the reverse reaction [2OH = H2O + O], the barrier is 0.32 eV and the reaction is exothermic by 0.14 eV. Similar results were also reported by Wang et al.,42i.e., the reaction has a barrier of 0.65 eV and is endothermic by 0.29 eV. This indicates that H2O adsorption on the O pre-covered surface does not prefer dissociation; applying the energy difference of 0.14 eV gives a ratio much higher than 99.99% in preferring molecular H2O, and this agrees with the XPS results of Pache et al.24 and Schulze et al.,25 where the adsorbed H2O does not dissociate and remains in its molecular state, while it disagrees with the proposal of Madey et al.,22 where the adsorbed dissociates into surface OH.
For the reaction [2OH = O + H + OH], the barrier is 0.99 eV and the reaction is exothermic by 0.15 eV. The breaking O–H distance in the transition state is 1.490 Å. For the next dissociation [O + H + OH = 2O + 2H], the barrier is 1.16 eV and the reaction is nearly thermal neutral (−0.04 eV). In the transition state, the breaking O–H distance is 1.486 Å. Finally, we computed the H2 desorption energy, which is exothermic by 0.16 eV on the basis of gaseous H2O [O + H2O(g)], and endothermic by 0.49 eV on the basis of adsorbed H2O [O + H2O(s)]. On the basis of co-adsorbed O and H [2O + 2H], the computed H2 desorption energy is 0.54 eV.
For H2O dissociation on the nO pre-covered Ni(111) surface (n = 2–4), the potential energy surface is similar to that of O assisted H2O dissociation (Fig. S3–S6†). The H2O adsorption energies are in the range of −0.65 to −0.67 eV, very close to that of n = 1 (−0.65 eV). For the first step dissociation, nO + H2O = (n − 1)O + 2OH, the barrier is 0.37, 0.45 and 0.46 eV, respectively, and the reaction is endothermic by 0.08, 0.18 and 0.14 eV, respectively, in favor of molecular adsorption instead of dissociative adsorption of H2O. In the transition state, the breaking O–H distance is 1.530, 1.698 and 1.507 Å, respectively. For the second step, (n − 1)O + 2OH = nO + H + OH, the barriers are around 0.90–0.99 eV, and the reaction is nearly thermal neutral (−0.06 eV) for n = 2, and slightly endothermic (0.18 and 0.09 eV, respectively) for n = 3 and 4. For the last step dissociation, nO + H + OH = (n + 1)O + 2H, the barrier is 1.19, 1.29 and 1.19 eV, respectively, and the reaction is endothermic by 0.06, 0.12 and 0.21 eV, respectively. All these show that higher O pre-coverage does not promote H2O dissociative adsorption, and the adsorbed H2O remains in the molecular state.
(e) High coverage adsorption of OH and O on Ni(111)
The most stable OH adsorption configurations at different coverages on Ni(111) are shown in Fig. 6a. For 2OH, we computed two adsorption configurations (Fig. S8†): a remote one and an adjacent one, and both have OH perpendicularly adsorbed at the fcc-3F sites without H-bonding. In addition, the remote one is more stable than the adjacent one by 0.17 eV. For 4OH (0.25 ML), we computed five combined adsorption configurations (Fig. S9†) and found the remote regularly distributed p(2 × 2) configuration with all OH perpendicularly adsorbed at the fcc-3F sites without H-bonding to be the most stable, and the linear one with all OH at the bridge sites with H-bonding to be the least stable; the energy difference between these two adsorption configurations is 0.41 eV, indicating the strong lateral repulsive interaction despite the H-bonding in the linear one. The energies of the other configurations are in between.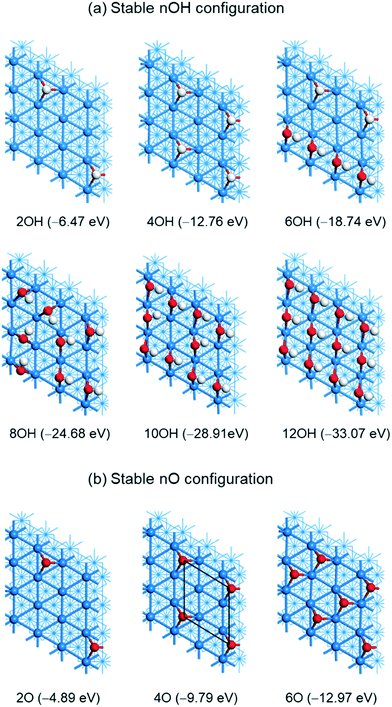 | ||
| Fig. 6 The most stable geometries and adsorption energies (eV, PBE-D3) of different coverages of (a) OH and (b) O on the Ni(111) surface (Ni/blue; O/red; H/white). | ||
For 6OH, we computed eight adsorption configurations by considering the remote adsorption and H-bonding (Fig. S10†). The most stable one has 4OH at the bridge sites that form a line with H-bonding (1.640, 1.637 and 1.637 Å) and the other two OH are remote at two fcc-3F sites. Several other configurations are less stable by less than 0.1 eV. This might reveal the flexibility of the adsorption configurations at high OH coverage, and random adsorption under given conditions becomes possible.
Next, we computed six adsorption configurations for 8OH (0.5 ML, Fig. S11†). In contrast to the expected regular structures, the most stable one has all OH at the bridge sites and each OH interacts with another OH via H-bonding. The least stable one with one 4OH line and one 3OH line at the bridge site via H-bonding with another one OH at the fcc-3F site is less stable by 0.40 eV. Despite the repulsive interaction among the adsorbed OH groups at high coverage, we computed the adsorption configuration for 10OH with two parallel 4OH lines and one 2OH line in between, for 12OH (0.75 ML) with three parallel 4OH lines and 16OH (1 ML) with four parallel 4OH lines, where the H-bonding is between two OH lines instead within one line (Fig. S12†).
The average adsorption energy decreases with the increase of OH coverage from −3.16 eV (OH), −3.23 eV (2OH) to −2.30 (16OH). On the basis of gaseous H2O [nH2O(g) = nOH(s) + (n/2)H2(g)], the adsorption of 8OH (0.5 ML) and 10OH (0.625 ML) is exothermic by 2.10 eV and 0.69 eV, respectively, while the adsorption of 12OH (0.75 ML) and 16OH becomes endothermic by 0.79 and 8.37 eV, respectively. This indicates that the saturation coverage of OH adsorption should be 0.625 ML on the basis of H2O dissociative adsorption, and it is not possible to get 1 ML OH coverage.
The most stable adsorption configurations of O atoms with different coverages on Ni(111) are shown in Fig. 6b; all O atoms are adsorbed at fcc-3F sites. The adsorption energy of one O atom is −2.44 eV, and that of the remote 2O is higher than that of the adjacent 2O (−4.89 vs. −4.55 eV), indicating the lateral repulsive interaction between two adjacent O atoms by 0.34 eV, and this energy difference is much higher than that of 2OH adsorption (0.17 eV). It is noted that the adsorption energy of the remote 2O is double that of single O adsorption (−4.89 eV); therefore we optimized high coverage O adsorption with remote O atoms. For 4O adsorption (0.25 ML), the adsorption energy (−9.79 eV) is four-fold that of single O adsorption (−9.74 eV). This shows that there is no lateral repulsive interaction among these 4O atoms at 0.25 ML, and the adsorption configuration has a p(2 × 2) structure, in agreement with the experimental observation.72 On the basis of the 4O adsorption configuration, we computed 6O adsorption and the adsorption energy is −12.97 eV, which is lower than that of six-fold of single O adsorption (−14.64 eV), indicating the lateral repulsive interaction by 1.67 eV. Since high coverage O adsorption will result in surface oxidation and reconstruction,72 we did not consider even higher coverage O adsorption. For comparison we also computed the most stable configuration for n = 8, 12, 16 in the ESI† (Fig. S13); the repulsive interaction is 3.81, 11.44 and 23.96 eV, respectively.
On the basis of gaseous H2O [nH2O(g) = nO(s) + nH2(g)], the adsorption is exothermic by 0.14, 0.31 and 0.61 eV for nO (n = 1, 2, 4), respectively, while endothermic by 0.80 eV for n = 6. Therefore, the oxygen saturation coverage on the basis of gaseous H2O should be 4O (0.25 ML).
(f) H2O desorption on Ni(111)
On the basis of the most stable adsorption structures, we computed the H2O desorption temperature under certain pressure (1 × 10−5 mbar25 for H2O in the experiment) by using ab initio atomistic thermodynamics. Table 3 lists the experimentally estimated H2O desorption temperature, and the computed H2O desorption temperatures are shown in Table 4.| Reaction | PBE-D3 | RPBE-D3 |
|---|---|---|
| H2O(s) = H2O(g) | 140 | 174 |
| 2OH(s) = O(s) + H2O(g) | 191 | 60 |
| (H2O)n(s) = nH2O(g) (n = 1–8) | 184–211 | 196–214 |
| nO + H2O(s) = nO + H2O(g) (n = 1–4) | 212–219 | 247–259 |
| 4O + 4H2O(s) = 4O + 4H2O(g) | 245 | 284 |
| 4O + 4H2O(s) = 4O + 3H2O(s) + H2O(g) | 237 | 283 |
| 4O + 3H2O(s) = 4O + 2H2O(s) + H2O(g) | 236 | 279 |
| 4O + 2H2O(s) = 4O + H2O(s) + H2O(g) | 254 | 291 |
| 4O + H2O(s) = 4O + H2O(g) | 254 | 282 |
| 8OH = 4O + 4H2O(g) | 129 | 197 |
For the desorption of an adsorbed single H2O molecule [H2O(s) = H2O(g)], the calculated desorption temperature is 140 K by using PBE-D3 adsorption energy and 174 K by using RPBE-D3 adsorption energy; the latter is closer to the detected 163,25 164,24 165,22 and 168 K23 at low coverage. In addition, we computed the desorption temperature of the adsorbed (H2O)n clusters, which is in the range of 184–211 K by using PBE-D3 and 196–214 K by using RPBE-D3.
For H2O desorption from OH disproportionation [2OH → O(s) + H2O(g)], the calculated desorption temperature is 191 K by using PBE-D3 and 60 K by using RPBE-D3; both are far away from the detected range of 275–300 K. This shows that H2O does not come from OH disproportionation. Indeed, UPS and XPS studies did not support the supposed formation of surface OH from H2O adsorption on the O pre-covered surface. Using the adsorption energy of H2O on the O pre-covered surface [O + H2O(s)], however, the computed H2O desorption temperature is 212 K by using PBE-D3 and 247 K by using RPBE-D3; the latter is closer to the experimental value than the former.
Since the experimental study used the 0.25 ML O pre-covered p(2 × 2) surface and the adsorbed H2O has 0.25 ML, we optimized the proposed structure of Pache et al.,24 where each surface O interacts with two adjacent H2O molecules via H-bonding in a zigzag manner, and H2O molecules adsorbed at hollow sites (Fig. 7a). The computed average adsorption energy is −0.35 and −0.39 eV by using PBE-D3 and RPBE-D3, respectively, and the corresponding desorption temperature is 123 and 135 K, respectively. They disagree with the experiment because H2O molecules have very weak interaction with the surface.
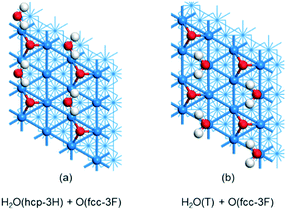 | ||
| Fig. 7 H2O adsorption (0.25 ML) on 0.25 ML O pre-covered Ni(111): (a) H2O at the hollow site; (b) H2O at the top site. | ||
By considering both interaction of H2O with the surface and H-bonding with surface O, we designed a new structure, where H2O molecules are adsorbed at top sites and have H-bonding with surface O atoms (Fig. 7b). The computed average adsorption energy is −0.76 and −0.90 eV by using PBE-D3 and PRBE-D3, respectively. In turn, the computed corresponding desorption temperature is 245 and 284 K, respectively, which are much closer to the experimental values,24 in particular, the one by using RPBE-D3. Our new structure with adsorbed H2O at the top sites is supported by X-ray diffraction and infrared reflection absorption spectroscopy.73
In addition to the concerted desorption of all 4H2O on the 4O pre-covered surface, we computed H2O stepwise desorption, and the desorption temperature is 254, 254, 236, and 237 K by using PBE-D3 and 282, 291, 279, and 283 K by using RPBE-D3, indicating that it is possible for H2O desorption to proceed in either a stepwise or a concerted way, since the desorption temperature is 275–300 K on the 0.25 ML O pre-covered p(2 × 2) surface and the 0.25 ML adsorbed H2O molecule.24
Recently, Zhao et al.29 reported a single crystal adsorption calorimetry study of D2O adsorption on clean and 0.25 ML O pre-covered Ni(111) surfaces. This is very related to our study of H2O adsorption, particularly, with the co-adsorption of 0.25 ML O (4O) and 0.25 ML H2O (4H2O) on a p(4 × 4) slab model. This provides a chance for direct comparison between experimental and DFT computation.
At first, the computed average H2O adsorption energy at 0.5 ML coverage on the clean Ni(111) surface (−0.66 and −0.65 eV by using PBE-D3 and RPBE-D3, respectively) is slightly larger than the determined value (−0.56 eV) for D2O adsorption at 0.5 ML coverage and at 100 K by about 0.1 eV.
Next, we computed the OH average bond energy at 0.5 ML OH coverage (8OH), which is 3.09 and 3.06 eV using PBE-D3 and RPBE-D3, respectively, lower than the estimated value for D2O at 170 K (3.26 eV) by 0.17–0.20 eV. Further, we estimated the surface OH enthalpy of formation on the basis of 4H2(g) + 4O2(g) = 8OH, and the computed value is −5.11 and −5.09 eV, respectively, using PBE-D3 and RPBE-D3, also lower than the estimated −5.77 eV. All these show a difference of 0.66–0.68 eV.
Since the computed OH bond energy and enthalpy of formation differ from the experimental values on the basis of the supposed OH formation, we are wondering if the adsorbed H2O prefers molecular adsorption over dissociative adsorption. On the basis of the molecular adsorbed state [4O(s) + 4H2O(s)], the dissociation of surface adsorbed H2O [4O(s) + 4H2O(s) = 8OH(s)] is endothermic by 1.57 and 1.19 eV, respectively, using PBE-D3 and RPBE-D3, and the corresponding stoichiometric value is endothermic by 0.39 and 0.30 eV, respectively. This indicates that H2O dissociative adsorption is unlikely, and the expected equilibrium greatly favors H2O molecular adsorption (≫99.99%) over dissociation adsorption. This agrees with the UPS results of Pache et al.24 and XPS results of Schulze et al.,25 where the adsorbed H2O does not dissociate and remains in its molecular state, while it disagrees with the proposal of Madey et al.,22 where the adsorbed dissociates into surface OH.
Taking the co-adsorbed 4O(s) + 4H2O(s) as a reference, the supposed surface hydroxyls have an enthalpy of formation from 4H2(g) + 4O2(g) of −5.51 and −5.38 eV, respectively, using PBE-D3 and RPBE-D3, which are closer to the estimated −5.77 eV. Further taking the adsorbed 4O(s) + 4H2O(s) as a reference, the supposed surface hydroxyls have a bond energy of 3.28 and 3.21 eV, respectively, using PBE-D3 and RPBE-D3, which are also closer to the estimated value of 3.26 eV at 170 K.
Since the computed bond energy and enthalpy of formation of surface hydroxyls support the molecular and non-dissociative adsorption of H2O on the O pre-covered surface, we computed the desorption temperature of the molecularly adsorbed H2O [4O(s) + 4H2O(s) = 4O(s) + 4H2O(g)] (Table 4). Indeed, the computed H2O desorption temperature agrees excellently with the experimentally determined range (284 vs. 275–300 K). In contrast, the calculated desorption temperature of H2O from surface hydroxyl disproportionation [8OH = 4O(s) + 4H2O(g)] is much lower (129 and 197 K). These results indicate once again the molecular state of the adsorbed H2O on the 0.25 ML O pre-covered surface.
All these results prefer H2O molecular adsorption on the 0.25 ML O pre-covered Ni(111) surface, and this is in agreement with the UPS and XPS studies,24,25 while in disagreement with the recently supposed H2O dissociative adsorption from the single crystal adsorption calorimetry study29 and previous results.22,23 This disagreement encourages further experimental investigations and confirmations.
On the basis of the disagreement in dissociative and molecular adsorption of H2O on the 0.25 ML O pre-covered surface, we computed vibrational frequencies to aid further experimental investigation (Table S6†). On the surface with the increase of OH coverage up to 0.25 ML, where all adsorbed OH species have vertical configurations, the O–H vibrational frequencies are about 3700 cm−1. For 0.5 ML OH coverage (8OH), where the adsorbed OH species interact via H-bonding, the O–H vibrational frequencies are shifted to lower wavenumbers, i.e., in the range of 3642–3422 cm−1, lower than those in vertical adsorption configurations. For the co-adsorbed 4O + 4H2O, the O–H vibrational frequencies are in the range of 3552–3440 cm−1, although somewhat lower than those of the OH that interact via H-bonding in the high wavenumber region, they also exhibit an overlap in the low wavenumber region. The characteristic feature of molecular H2O adsorption can come from the O–H bending frequencies in the range of 1551–1537 cm−1. All these need experimental investigation and confirmation.
Conclusion
In this work, we investigated the dissociative adsorption of H2O on clean and oxygen pre-covered Ni(111) surfaces on the basis of density functional theory and ab initio atomistic thermodynamics systematically. Due to the importance of water chemistry in Ni-based catalysts, there are intensive experimental and theoretical investigations. However, there are discrepancies among the experimental results and also differences among computational results, where different computational models and methods have different results. In addition, there are deficits in understanding H2O dissociative adsorption regarding hydrogen-bonding interaction at high coverage.On the clean Ni(111) surface, the most stable adsorption configuration of H, O, and OH prefers the 3-fold face centered-cubic site and that of H2O prefers the top site. The computed adsorption energies of H2O by using PBE and RPBE including dispersion are close to the reported experimental results, while that of H2 using only PBE is closer to the experimental value than the corresponding PBE and PPBE values including dispersion.
For the adsorption of (H2O)n clusters (n = 2–8), both direct O–Ni and H-bonding synergistically determine the total adsorption energy. H2O adsorption on Ni(111) have simple structures at very low coverage, and very complex structures at high coverage, and the adsorption energy is structurally insensitive for large adsorbed clusters. The stepwise adsorption energy has an average value of −0.69 eV.
At low coverage (θ ≤ 0.25 ML), OH adsorbs perpendicularly and prefers remote distribution without H-bonding among OH groups, the OH saturation coverage is 0.625 ML on the basis of H2O dissociative adsorption and H2 evolution [nH2O(g) = nOH(s) + (n/2)H2(g)] and it is not possible to get 1 ML OH coverage. The adsorption configuration for 4O (0.25 ML) prefers a p(2 × 2) structure, in agreement with the experiment, and the O saturation coverage is 0.25 ML on the basis of H2O dissociative adsorption and H2 evolution [nH2O(g) = nO(s) + nH2(g)].
For one H2O dissociative adsorption, the first H–O dissociation is favored both thermodynamically and kinetically, but the second H–O dissociation has a higher barrier and is less exothermic than the first one. On the basis of the gaseous H2O, both steps have close apparent barriers (0.26 and 0.27 eV, respectively). For (H2O)2 dissociation, the co-adsorbed H2O molecules do not significantly affect the first step dissociation barrier of the H2O molecule, but obviously boost the dissociation barrier of OH due to the H-bonding in the transition states.
The co-adsorption of O and H2O each at 0.25 ML prefers a p(2 × 2) structure, in which top site H2O interacts with two hollow site oxygen atoms via H-bonding, which is energetically more stable than the previously proposed one by 0.51 eV; in the latter, the adsorbed H2O molecules are proposed to be over the hollow sites.
On the 0.25 ML O pre-covered Ni(111), H2O greatly prefers molecular adsorption [4O + 4H2O(g) → 4O + 4H2O(s)] over dissociative adsorption [4O + 4H2O(g) → 8OH] thermodynamically by 0.30 eV, and this is in agreement with the UPS and XPS results and in disagreement with previous results as well as recent results from the single crystal adsorption calorimetry study of D2O.
It is noted that the computed bond energy (3.06 eV) and formation enthalpy (−5.09 eV) of the supposed surface hydroxyls on the basis of the dissociatively adsorbed state [8OH] differ from the experimentally estimated values (3.26 and −5.77 eV, respectively), while those (3.21 and −5.38 eV, respectively) on the basis of the molecular adsorbed state [4O + 4H2O(s)] are closer to the experimentally obtained values. This further supports H2O molecular adsorption.
The definitive support of H2O molecular adsorption [4O + 4H2O(s)] comes from the computed H2O desorption temperature, which is in excellent agreement with the experimental result (284 vs. 275–300 K), while that from the dissociatively adsorbed state [8OH] differs strongly (197 K).
All these support H2O molecular adsorption instead of dissociative adsorption, which needs further experimental investigations and confirmations. Despite these results, the vibrational frequencies of the adsorbed OH species for dissociative adsorption as well as molecularly adsorbed H2O on the 0.25 ML O pre-covered surface have been computed to aid experimental investigations. The characteristic difference between the molecular and dissociative H2O adsorption comes from the O–H bending of molecularly adsorbed H2O in the range of 1551–1537 cm−1. Our systematic study provides insights into the water-involved reactions catalyzed by nickel particularly and broadens our fundamental understanding of water interaction with metal surfaces generally.
Conflicts of interest
There are no conflicts to declare.Acknowledgements
This work was supported by the National Natural Science Foundation of China (no. 21673268) and the Chinese Academy of Sciences and Synfuels CHINA. Co., Ltd. We also acknowledge general financial support from the BMBF and the state of Mecklenburg-Vorpommern.References
- J. Carrasco, A. Hodgson and A. Michaelides, A Molecular Perspective of Water at Metal Interfaces, Nat. Mater., 2012, 11, 667–674 CrossRef CAS.
- K.-R. Hwang, C.-B. Lee and J.-S. Park, Advanced Nickel Metal Catalyst for Water–Gas Shift Reaction, J. Power Sources, 2011, 196, 1349–1352 CrossRef CAS.
- A. Hodgson and S. Haq, Water Adsorption and the Wetting of Metal Surfaces, Surf. Sci. Rep., 2009, 64, 381–451 CrossRef CAS.
- J. R. Rostrup-Nielsen, Activity of Nickel Catalysts for Steam Reforming of Hydrocarbons, J. Catal., 1973, 31, 173–199 CrossRef CAS.
- P. Sabatier and J. Senderens, New synthesis of methane, C. R. Hebd. Seances Acad. Sci., 1902, 134, 514–516 CAS.
- P. Sabatier and J. Senderens, Direct Hydrogenation of Oxides of Carbon in Presence of Various Finely Divided Metals, C.R. Acad. Sci., 1902, 134, 689–691 Search PubMed.
- D. W. Goodman, R. D. Kelley, T. E. Madey and J. T. Yates, Kinetics of the Hydrogenation of CO over a Single Crystal Nickel Catalyst, J. Catal., 1980, 63, 226–234 CrossRef CAS.
- J. Sehested, S. Dahl, J. Jacobsen and J. R. Rostrup-Nielsen, Methanation of CO over Nickel: Mechanism and Kinetics at High H2/CO Ratios, J. Phys. Chem. B, 2005, 109, 2432–2438 CrossRef CAS.
- J. Sehested, Four Challenges for Nickel Steam-Reforming Catalysts, Catal. Today, 2006, 111, 103–110 CrossRef CAS.
- H. S. Bengaard, J. K. Nørskov, J. Sehested, B. S. Clausen, L. P. Nielsen, A. M. Molenbroek and J. R. Rostrup-Nielsen, Steam Reforming and Graphite Formation on Ni Catalysts, J. Catal., 2002, 209, 365–384 CrossRef CAS.
- J. G. Xu and G. F. Froment, Methane Steam Reforming, Methanation and Water-Gas Shift: I. Intrinsic Kinetics, AIChE J., 1989, 35, 88–96 CrossRef CAS.
- K. H. Hou and R. Hughes, The Kinetics of Methane Steam Reforming over a Ni/α-Al2O catalyst, Chem. Eng. J., 2001, 82, 311–328 CrossRef CAS.
- H. S. Bengaard, J. K. Nørskov, J. Sehested, B. S. Clausen, L. P. Nielsen, A. M. Molenbroek and J. R. Rostrup-Nielsen, Steam Reforming and Graphite Formation on Ni Catalysts, J. Catal., 2002, 209, 365–384 CrossRef CAS.
- C. Pistonesi, A. Juan, B. Irigoyen and N. Amadeo, Theoretical and Experimental Study of Methane Steam Reforming Reactions over Nickel Catalyst, Appl. Surf. Sci., 2007, 253, 4427–4437 CrossRef CAS.
- G. Jones, J. Jakobsen, S. Shim, J. Kleis, M. Andersson, J. Rossmeisl, F. Abildpedersen, T. Bligaard, S. Helveg and B. Hinnemann, First Principles Calculations and Experimental Insight into Methane Steam Reforming over Transition Metal Catalysts, J. Catal., 2008, 259, 147–160 CrossRef CAS.
- D. W. Blaylock, T. Ogura, W. H. Green and G. J. O. Beran, Computational Investigation of Thermochemistry and Kinetics of Steam Methane Reforming on Ni(111) under Realistic Conditions, J. Phys. Chem. C, 2009, 113, 4898–4908 CrossRef CAS.
- N. Eranda, S. Johannes and L. Suljo, Comparative Study of the Kinetics of Methane Steam Reforming on Supported Ni and Sn/Ni Alloy Catalysts: The Impact of the Formation of Ni Alloy on Chemistry, J. Catal., 2009, 263, 220–227 CrossRef.
- D. W. Blaylock, Y. A. Zhu and W. H. Green, Computational Investigation of the Thermochemistry and Kinetics of Steam Methane Reforming over a Multi-Faceted Nickel Catalyst, Top. Catal., 2011, 54, 828–844 CrossRef CAS.
- J. J. Guo, H. Lou, H. Zhao, D. F. Chai and X. M. Zheng, Dry Reforming of Methane over Nickel Catalysts Supported on Magnesium Aluminate Spinels, Appl. Catal., A, 2004, 273, 75–82 CrossRef CAS.
- Y. A. Zhu, D. Chen, X. G. Zhou and W. K. Yuan, DFT Studies of Dry Reforming of Methane on Ni Catalyst, Catal. Today, 2009, 148, 260–267 CrossRef CAS.
- Y. H. Hu and E. Ruckenstein, Catalytic Conversion of Methane to Synthesis Gas by Partial Oxidation and CO2 Reforming, Adv. Catal., 2004, 48, 297–345 CAS.
- T. E. Madey and F. P. Netzer, The Adsorption of H2O on Ni(111); Influence of Preadsorbed Oxygen on Azimuthal Ordering, Surf. Sci., 1982, 117, 549–560 CrossRef CAS.
- R. H. Stulen and P. A. Thiel, Electron-Stimulated Desorption and Thermal Desorption Spectrometry of H, H2O on Nickel(111), Surf. Sci., 1985, 157, 99–118 CrossRef CAS.
- T. Pache, H. P. Steinrück, W. Huber and D. Menzel, The Adsorption of H2O on Clean and Oxygen Precovered Ni(111) Studied by ARUPS and TPD, Surf. Sci., 1989, 224, 195–214 CrossRef CAS.
- M. Schulze, R. Reißner, K. Bolwin and W. Kuch, Interaction of Water with Clean and Oxygen Precovered Nickel Surfaces, Fresenius' J. Anal. Chem., 1995, 353, 661–665 CrossRef CAS.
- M. E. Gallagher, S. Haq, A. Omer and A. Hodgson, Water Monolayer and Multilayer Adsorption on Ni(111), Surf. Sci., 2007, 601, 268–273 CrossRef CAS.
- J. Shan, J. F. M. Aarts, A. W. Kleyn and L. B. F. Juurlink, The Interaction of Water with Ni(111) and H/Ni(111) Studied by TPD and HREELS, Phys. Chem. Chem. Phys., 2008, 10, 2227–2232 RSC.
- J. Shan, A. W. Kleyn and L. B. F. Juurlink, Identification of Hydroxyl on Ni(111), ChemPhysChem, 2009, 10, 270–275 CrossRef CAS PubMed.
- W. Zhao, S. J. Carey, Z. Mao and C. T. Campbell, Adsorbed Hydroxyl and Water on Ni(111): Heat of Formation by Calorimetry, ACS Catal., 2018, 8, 1485–1489 CrossRef CAS.
- B. Jiang and H. Guo, Towards An Accurate Specific Reaction Parameter Density Functional for Water Dissociation on Ni(111): RPBE Versus PW91, Phys. Chem. Chem. Phys., 2016, 18, 21817–21824 RSC.
- B. Jiang and H. Guo, Dynamics of Water Dissociative Chemisorption on Ni(111): Effects of Impact Sites and Incident Angles, Phys. Rev. Lett., 2015, 114, 166101 CrossRef PubMed.
- Z. Y. Du, Y. X. Ran, Y. P. Guo, J. Feng and W. Y. Li, A Theoretical Study on the Role of Water and its Derivatives in Acetic Acid Steam Reforming on Ni(111), Appl. Surf. Sci., 2017, 419, 114–125 CrossRef CAS.
- A. Mohsenzadeh, T. Richards and K. Bolton, DFT Study of the Water Gas Shift Reaction on Ni(111), Ni(100) and Ni(110) surfaces, Surf. Sci., 2016, 644, 53–63 CrossRef CAS.
- D. W. Blaylock, Y. A. Zhu and W. H. Green, Computational Investigation of the Thermochemistry and Kinetics of Steam Methane Reforming over A Multi-Faceted Nickel Catalyst, Top. Catal., 2011, 54, 828–844 CrossRef CAS.
- D. W. Blaylock, T. Ogura, W. H. Green and G. J. O. Beran, Computational Investigation of Thermochemistry and Kinetics of Steam Methane Reforming on Ni(111) under Realistic Conditions, J. Phys. Chem. C, 2009, 113, 4898–4908 CrossRef CAS.
- R. C. Catapan, A. A. M. Oliveira, Y. Chen and D. G. Vlachos, DFT Study of the Water−Gas Shift Reaction and Coke Formation on Ni(111) and Ni(211) Surfaces, J. Phys. Chem. C, 2012, 116, 20281–20291 CrossRef CAS.
- A. Mohsenzadeh, K. Bolton and T. Richards, DFT Study of the Adsorption and Dissociation of Water on Ni(111), Ni(110) and Ni(100) surfaces, Surf. Sci., 2014, 627, 1–10 CrossRef CAS.
- Y. C. Huang, C. Y. Ling, M. Jin, J. Y. Du, T. Zhou and T. S. Wang, Water Adsorption and Dissociation on Ni surface: Effects of Steps, Dopants, Coverage and Self-Aggregation, Phys. Chem. Chem. Phys., 2013, 15, 17804 RSC.
- A. A. Phatak, W. N. Delgass, F. H. Ribeiro and W. F. Schneider, Density Functional Theory Comparison of Water Dissociation Steps on Cu, Au, Ni, Pd, and Pt, J. Phys. Chem. C, 2009, 113, 7269–7276 CrossRef CAS.
- M. Pozzo, G. Carlini, R. Rosei and D. Alfè, Comparative Study of Water Dissociation on Rh(111) and Ni(111) Studied with First Principles Calculations, J. Chem. Phys., 2007, 126, 164706 CrossRef PubMed.
- W. Wang and G. Wang, A Theoretical Study of Water Adsorption and Dissociation on Ni(111) Surface During Oxidative Steam Reforming and Water Gas Shift Processes, J. Energy Inst., 2015, 88, 112–117 CrossRef CAS.
- G.-C. Wang, S.-X. Tao and X.-H. Bu, A Systematic Theoretical Study of Water Dissociation on Clean and Oxygen-Preadsorbed Transition Metals, J. Catal., 2006, 244, 10–16 CrossRef CAS.
- P. M. Hundt, B. Jiang, M. E. van Reijzen, H. Guo and R. D. Beck, Vibrationally Promoted Dissociation of Water on Ni(111), Science, 2014, 344, 504–507 CrossRef CAS.
- G. Kresse and J. Furthmüller, Efficiency of Ab-initio Total Energy Calculations for Metals and Semiconductors Using A Plane-Wave Basis Set, Comput. Mater. Sci., 1996, 6, 15–50 CrossRef CAS.
- G. Kresse and J. Furthmüller, Efficient Iterative Schemes for Ab Initio Total-energy Calculations Using A Plane-Wave Basis Set, Phys. Rev. B: Condens. Matter, 1996, 54, 11169–11186 CrossRef CAS.
- P. E. Blöchl, Projector Augmented-Wave Method, Phys. Rev. B, 1994, 50, 17953–17979 CrossRef.
- G. Kresse and D. Joubert, From Ultrasoft Pseudopotentials to the Projector Augmented-Wave Method, Phys. Rev. B: Condens. Matter Mater. Phys., 1999, 59, 1758–1775 CrossRef CAS.
- J. P. Perdew, K. Burke and M. Ernzerhof, Generalized Gradient Approximation Made Simple, Phys. Rev. Lett., 1996, 77, 3865–3868 CrossRef CAS.
- J. L. F. Da Silva, C. Stampfl and M. Scheffler, Adsorption of Xe Atoms on Metal Surfaces: New Insights from First-Principles Calculations, Phys. Rev. Lett., 2003, 90, 066104 CrossRef.
- J. L. F. Da Silva, C. Stampfl and M. Scheffler, Xe Adsorption on Metal Surfaces: First-principles Investigations, Phys. Rev. B: Condens. Matter Mater. Phys., 2005, 72, 075424 CrossRef.
- S. Grimme, J. Antony, S. Ehrlich and H. Krieg, A Consistent and Accurate Ab Initio Parametrization of Density Functional Dispersion Correction (DFT-D) for the 94 elements H-Pu, J. Chem. Phys., 2010, 132, 154104 CrossRef.
- G. Henkelman, B. P. Uberuaga and H. Jónsson, A Climbing Image Nudged Elastic Band Method for Finding Saddle Points and Minimum Energy Paths, J. Chem. Phys., 2000, 113, 9901–9904 CrossRef CAS.
- H. J. Monkhorst and J. D. Pack, Special Points for Brillouin-Zone Integrations, Phys. Rev. B: Solid State, 1976, 13, 5188–5192 CrossRef.
- A. Taylor, Lattice Parameters of Binary Nickel Cobalt Alloys, J. Jpn. Inst. Met., 1950, 77, 585–594 CAS.
- C. Kitte, Introduction to Solid State Physics, Wiley, New York, 7th edn, 1996 Search PubMed.
- B. Hammer, L. B. Hansen and J. K. Nørskov, Improved Adsorption Energetics within Density-Functional Theory Using Revised Perdew–Burke–Ernzerhof Functionals, Phys. Rev. B: Condens. Matter Mater. Phys., 1999, 59, 7413–7421 CrossRef.
- K. Reuter and M. Scheffler, Composition, Structure, and Stability of RuO2(110) as a Function of Oxygen Pressure, Phys. Rev. B: Condens. Matter Mater. Phys., 2001, 65, 035406 CrossRef.
- K. Reuter and M. Scheffler, Composition and Structure of the RuO2(110) Surface in an O2 and CO Environment: Implications for the Catalytic Formation of CO2, Phys. Rev. B: Condens. Matter Mater. Phys., 2003, 68, 045407 CrossRef.
- T. Wang, X. W. Liu, S. G. Wang, C. F. Huo, Y. W. Li, J. G. Wang and H. J. Jiao, Stability of β-Mo2C Facets from Ab Initio Atomistic Thermodynamics, J. Phys. Chem. C, 2011, 115, 22360–22368 CrossRef CAS.
- F. Zasada, W. Piskorz, S. Cristol, J. F. Paul, A. Kotarba and Z. Sojka, Periodic Density Functional Theory and Atomistic Thermodynamic Studies of Cobalt Spinel Nanocrystals in Wet Environment: Molecular Interpretation of Water Adsorption Equilibria, J. Phys. Chem. C, 2010, 114, 22245–22253 CrossRef CAS.
- T. Wang, S. G. Wang, Y. W. Li, J. Wang and H. J. Jiao, Adsorption Equilibria of CO Coverage on β-Mo2C Surfaces, J. Phys. Chem. C, 2012, 116, 6340–6348 CrossRef CAS.
- W. X. Li, C. Stampfl and M. Scheffler, Insights into the Function of Silver as an Oxidation Catalyst by Ab Initio Atomistic Thermodynamics, Phys. Rev. B: Condens. Matter Mater. Phys., 2003, 68, 165412 CrossRef.
- W. Piskorz, J. Gryboś, F. Zasada, P. Zapała, S. Cristol, J. F. Paul and Z. Sojka, Periodic DFT Study of the Tetragonal ZrO2 Nanocrystals: Equilibrium Morphology Modeling and Atomistic Surface Hydration Thermodynamics, J. Phys. Chem. C, 2012, 116, 19307–19320 CrossRef CAS.
- S. L. Liu, Y. W. Li, J. G. Wang and H. J. Jiao, Mechanisms of H2O and CO2 Formation from Surface Oxygen Reduction on Co(0001), J. Phys. Chem. C, 2016, 120, 19265–19270 CrossRef CAS.
- T. Zeng, X. D. Wen, Y.-W. Li and H. J. Jiao, Density Functional Theory Study of Triangular Molybdenum Sulfide Nanocluster and CO Adsorption on It, J. Phys. Chem. B, 2005, 109, 13704–13710 CrossRef CAS PubMed.
- M. Zhou and B. Liu, First-Principles Investigation of Adsorbate−Adsorbate Interactions on Ni(111), Ni(211), and Ni(100) Surfaces, Ind. Eng. Chem. Res., 2017, 56, 5813–5820 CrossRef CAS.
- K. Christmann, O. Schober, G. Ertl and M. Neumann, Adsorption of Hydrogen on Nickel Single Crystal Surfaces, J. Chem. Phys., 1974, 60, 4528–4540 CrossRef CAS.
- K. Christmann, R. J. Behm, G. Ertl, M. A. Van Hove and W. H. Weinberg, Chemisorption Geometry of Hydrogen on Ni(111): Order and Disorder, J. Chem. Phys., 1979, 70, 4168–4184 CrossRef CAS.
- A. Winkler and K. D. Rendulic, Adsorption Kinetics for Hydrogen Adsorption on Nickel and Coadsorption of Hydrogen and Oxygen, Surf. Sci., 1982, 118, 19–31 CrossRef CAS.
- Y. Hong and J. L. Whitten, Dissociative Adsorption of H2 on Ni(111), J. Chem. Phys., 1993, 98, 5039–5049 CrossRef.
- M. Nakamura and M. Ito, Ring Hexamer Like Cluster Molecules of Water Formed on A Ni(111) Surface, Chem. Phys. Lett., 2004, 384, 256–261 CrossRef CAS.
- A. R. Kortan and R. L. Park, Phase Diagram of Oxygen Chemisorbed on Nickel (111), Phys. Rev. B: Condens. Matter Mater. Phys., 1981, 23, 6340–6347 CrossRef CAS.
- M. Nakamura, M. Tanaka, M. Ito and S. Sakata, Water Adsorption on A p(2×2)-Ni(111)-O Surface Studied by Surface X-ray Diffraction and Infrared Reflection Absorption Spectroscopy at 25 and 140 K, J. Chem. Phys., 2005, 122, 224703 CrossRef CAS PubMed.
Footnote |
| † Electronic supplementary information (ESI) available: Adsorption energies and structural parameters of (H2O)n adsorption (Table S1, Fig. S1); dissociation energetics of H2O and (H2O)2 on the clean surface (Tables S2 and S3; Fig. S2 and S3) as well as on the oxygen pre-covered surface (Tables S4 and S5; Fig. S4–S6); stretching and bending frequencies of 4O, (OH)n, 4O + 4H2O and (H2O)n on Ni(111) (Table S6); potential energy surface of H2O dissociative adsorption on 3O and 4O pre-covered surfaces (Fig. S7); high coverage OH and O adsorption configurations and energies (Fig. S8–S12; Fig. S13). See DOI: 10.1039/c8cy02198h |
| This journal is © The Royal Society of Chemistry 2019 |