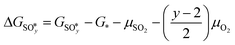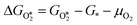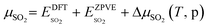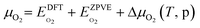Sulfation of a PdO(101) methane oxidation catalyst: mechanism revealed by first principles calculations
Ryan Lacdao
Arevalo
 a,
Susan Meñez
Aspera
a and
Hiroshi
Nakanishi
*abc
a,
Susan Meñez
Aspera
a and
Hiroshi
Nakanishi
*abc
aNational Institute of Technology, Akashi College, 679-3 Nishioka, Uozumi, Akashi, Hyogo 674-8501, Japan. E-mail: nakanishi@akashi.ac.jp
bGraduate School of Engineering, Osaka University, 2-1 Yamadaoka, Suita, Osaka 565-0871, Japan
cInstitute of Industrial Science, The University of Tokyo, Meguro, Tokyo 153-8505, Japan
First published on 10th December 2018
Abstract
PdO efficiently catalyzes the oxidation of methane but suffers tremendously from sulfur poisoning that lowers its catalytic activity. In this work, first principles calculations were performed to reveal the mechanism of PdO(101) sulfation and how the active sites for methane activation are altered upon the formation of SOy (y = 2 to 4) species on the surface. The results suggest that under typical experimental conditions with a high O2/SO2 gas ratio, the formation of SO4-decorated PdO(101) is favored and contributes significantly to the poisoning of PdO(101) as it blocks the coordinatively unsaturated Pd atoms that were identified to play a crucial role in the activation of methane. At a low temperature regime, SO2 oxidation forming SO3 and SO4 species is highly exothermic via the Eley–Rideal and Langmuir–Hinshelwood mechanisms but is limited by the high activation barrier for O2 dissociation. On the other hand, the Mars–van Krevelen mechanism has low exothermicity but provides facile elementary steps. From these results, insights into the design of PdO-based sulfur poisoning-resistant methane oxidation catalysts were drawn.
1. Introduction
Catalyst poisoning is a long-standing problem in the heterogeneous catalysis of a wide range of reactions such as oxidation, hydrogenation, reforming of hydrocarbons, and ammonia production.1 It often involves compounds that strongly bond with the active sites of catalysts, thereby decreasing the catalytic activity and/or selectivity. Over the past years, many research studies were conducted to understand the mechanism of various catalyst poisoning reactions to provide insights into the design of poison-resistant catalysts and optimization of processes to prevent or reduce catalyst deactivation.1–8Sulfur poisoning is a major concern in the catalytic oxidation of methane.9–11 It is due mainly to sulfur contained in the natural gas itself (as an odorizer) or from engine lubricating oil in combustion systems.9 Over the past decades, experiments were conducted to understand the mechanism of this reaction on various supported and unsupported catalysts such as mono and bimetallic Pt and Pd on Al2O3, CeO2, ZrO2, SiO2, Y2O3, and La2O3, using techniques such as X-ray photoelectron spectroscopy (XPS), Fourier transform infrared spectroscopy (FT-IR), X-ray diffraction (XRD), scanning transmission electron microscopy (STEM), and operando X-ray absorption near edge spectroscopy (XANES), among others.9,11–19 These studies sought to identify the effects of support,12,16,17 catalyst size and composition,11,16,18,20 various experimental conditions,14,15 and catalyst regeneration.17,18,21
Pd-Based catalysts have excellent activity for methane oxidation under net oxidizing conditions but suffer tremendously from sulfur poisoning.12,15–19 A general consensus suggests that Pd exists in the form of an oxide when methane oxidation proceeds under oxygen-rich conditions and at temperatures below 950 K.22,23In situ XRD and XPS measurements showed that PdO(101) develops preferentially during the oxidation of Pd(100).24–26 Its formation coincides with the increased rates of methane oxidation,26 suggesting PdO formation to be responsible for the exceptional activity of Pd catalysts for the catalytic combustion of methane.27,28 Because of this, significant experimental efforts were directed toward understanding the mechanism of sulfur poisoning of PdO methane oxidation catalysts.
Experiments reveal the formation of sulfites and sulfates on Pd catalysts, which are believed to poison or deactivate the active sites for methane oxidation.12,15–19 Lampert et al. confirmed through the XPS of unsupported PdO treated with SO2 or SO3 the formation of a surface layer of SO42− and the increase in the degree of Pd oxidation as evidenced by the increase in the Pd 3d5/2 electron binding energy.16 From these results, it was inferred that the deactivation of PdO by SO2 may be due to both the decrease in the chemisorption of methane as a surface sulfate layer is formed, and the decrease in the availability of oxygen from PdO due to an increase in the Pd oxidation state. In more recent XPS, FT-IR, and XRD experiments on unsupported PdO, Mowery et al. similarly found a rapid, permanent, and complete deactivation of PdO due to the sulfation of the surface layer. Furthermore, XRD of deactivated catalysts indicates the presence of Pd0, which was proposed to form through the oxidation of SO2 to SO3.15 Recently, a theoretical study showed that the formation of PdSO4 and adsorption of SO3 and oxygen species are highly favored on clean and oxidized Pd surfaces under typical temperature and pressure conditions.10
As the literature is scarce on the theoretical studies of the sulfation of PdO as the methane oxidation catalyst, a molecular understanding on how SO4 forms on the surface of PdO remains speculative. In particular, it is imperative to identify the mechanistic paths toward SO4 formation on the PdO(101) surface and describe how the active sites for methane activation are altered by the adsorption and subsequent oxidation of SO2. In this contribution, first principles calculations based on density functional theory with van der Waals correction were used to reveal the mechanism of PdO(101) sulfation in relation to the activation of methane. In the first part, the electronic structure of PdO(101) is presented to predict the reactive sites on the surface and identify the relevant components of the Pd d band in the bonding of molecules on the surface. In the second part, methane activation on PdO(101) is revisited to clarify and expound the literature-proposed mechanism of C–H bond activation by the coordinatively unsaturated Pd atom. In the last part, a mechanistic study of SO2 oxidation is presented and discussed in relation to methane activation and insights into catalyst design.
2. Results and discussion
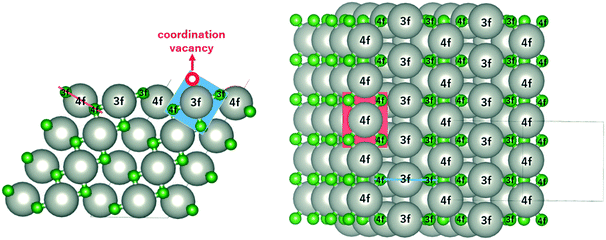
The monoxide compound PdO (space group 131, P42/mmc) is the only known stable oxide of Pd.10 Its calculated lattice constants are a = 3.06 Å and c/a = 1.77, which are in excellent agreement with those in experiments (a = 3.04 Å and c/a = 1.75).29,30Fig. 1 shows the side and top views of the PdO(101) surface, which was modeled using a slab with four Pd layers in a 1 × 2 supercell (16 Pd and 16 O atoms) with ca. 12 Å of vacuum space. The Pd atoms on the surface are labelled as either 3f or 4f to denote the 3-fold and 4-fold coordinated Pd atoms, which are respectively referred to in this paper as Pd3f and Pd4f atoms. Pd forms a square planar coordination with the O atoms as shown by the red and blue planes in Fig. 1. Pd3f is coordinatively unsaturated (cus) with a coordination vacancy on top of the Pd3f atom. The O atoms on the surface are also labelled as either 3f or 4f based on their coordination with the Pd atoms, which are also referred to in this paper as O3f and O4f, respectively. The O3f atoms protrude out of the surface while the O4f atoms bond with the subsurface atoms. The coordination plane of the unsaturated Pd3f atom is perpendicular to the surface, while that of the Pd4f atom is tilted with respect to the (101) surface.2.1 Electronic structure of PdO(101)
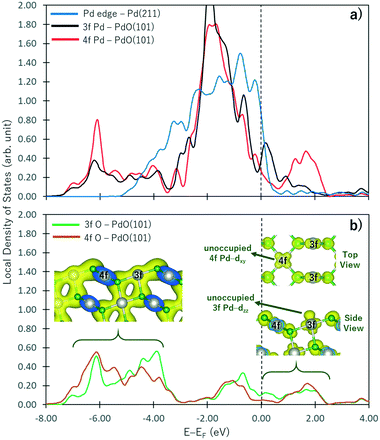
In PdO, the Pd atoms oxidized while the O atoms reduced. As shown by the Bader charges reported in Table 1, the Pd4f atoms have lost more electrons than Pd3f because more O atoms are coordinated to the Pd4f atom. Correspondingly, more electrons are gained by O4f than O3f because of the difference in their coordination with the Pd atoms. These observations correspond to the change in the electronic structure of a non-oxide Pd atom shown in Fig. 2a as it forms an oxide. In this figure, the projected local density of states on the d band of the Pd atom at the step edge of the Pd(211) surface (representing a pure Pd metal) and the Pd3f and Pd4f atoms of the PdO(10) surface are shown by blue, black, and red curves, respectively. Correspondingly, the sp states of the O3f and O4f atoms are shown in Fig. 2b. With respect to the d band of the non-oxide Pd(211), there is an emergence of unoccupied states above the Fermi level in the d band of both the Pd3f and Pd4f atoms of PdO(101). A broader unoccupied state is seen for Pd4f, corroborating its notable greater electron loss in the Bader charge analysis. In the energy range below −4.00 eV, new states are formed in the d band of the Pd3f and Pd4f atoms with respect to the d band of the pure Pd atom. These states hybridize with the sp states of O shown in Fig. 2b, indicating the Pd-d and O-sp bonding states. The projected partial charge density plot in this energy range (left inset figure in Fig. 2b) shows the covalent bond between the Pd and O atoms.| Pd | O | ||
|---|---|---|---|
| 3f | 4f | 3f | 4f |
| +0.76 | +0.98 | −0.85 | −0.96 |
Interestingly, the projected partial charge density plots in the energy range above the Fermi level (right inset in Fig. 2b) show the different characteristics of the unoccupied states of the Pd3f and Pd4f atoms. For the Pd3f atoms, the unoccupied state has a dzz character, which stems from the presence of an O atom directly below the Pd3f atom. This unoccupied dzz state of Pd3f hints its higher affinity toward electron donation from the σ-type molecular orbital of adsorbates. Assigning the Pd3f coordination plane as the xz plane, the corresponding occupied states of the Pd3f d band has a dyz character. On the other hand, in the case of Pd4f, similar analysis indicates that the unoccupied states of its d band have dxy characteristics. Because the Pd4f atoms are rectangularly coordinated to 4 O atoms on the xy plane, its dxy orbital is depopulated. Correspondingly, the dzz orbital of Pd4f is occupied, which is expected to result in a repulsive interaction toward the σ-type molecular orbital of the adsorbates. As the Pd atoms in PdO are oxidized, they have higher affinities for electron donation from the adsorbates and reduced tendencies for back-donation. By its spatial distribution, the Pd3f–dzz can facilitate electron donation, resulting in the greater reactivity of Pd3f compared to Pd4f.
2.2 Revisiting methane activation on PdO(101)
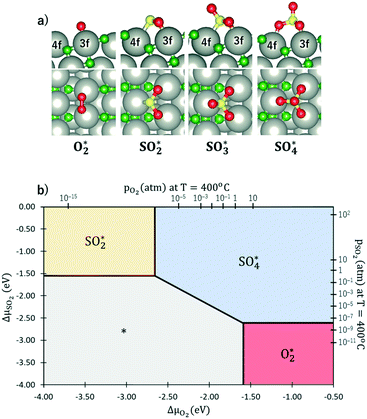
Methane activation and oxidation on PdO(101) were studied recently using DFT calculations.30–32 Though the methane oxidation pathway is a subject of an ongoing debate, there is a general consensus that the initial C–H bond activation of methane is the main limiting step.31,32 Weaver et al. proposed that methane forms dative bonds with the coordinately unsaturated Pd atoms, resulting in a σ complex whose bonding involves electron donation and back-donation.31 However, considering that the charge density difference only accounts for the initial and final states of the system, developing a model for this donor–acceptor interaction remains a challenge from their analysis of the charge density difference upon CH4 adsorption on PdO(101). Bossche and Gronbeck used the first principles kinetic modeling of methane oxidation over PdO(101) and revealed that oxidation steps subsequent to the initial methane activation take place through the Mars–van Krevelen mechanism.32 Nevertheless, as mentioned earlier that experiments predicted PdO deactivation by SO2 originating from the decrease of CH4 chemisorption on the surface, a confirmation of the active sites for CH4 activation is an important step in understanding the mechanism of the sulfur poisoning of a PdO(101) methane oxidation catalyst.Fig. 3a shows the optimal adsorption configuration of CH4 on PdO(101). The two C–H bonds are coordinated with the Pd3f atom while the other two C–H bonds point away from the surface. This confirms the earlier predicted reactivity of Pd3f from the analysis of its electronic structure. Considering the identified unoccupied dzz and occupied dyz states of the Pd3f atom mentioned earlier, the mechanism of electron donation and back-donation between CH4 and Pd3f can be drawn. The highest occupied molecular orbital of CH4 is a three-fold degenerate σ-type molecular orbital (1t2), as shown in Fig. 3b. This filled molecular orbital can donate electrons to the unoccupied dzz state of Pd3f. The occupied Pd3f–dyz orbital can facilitate the back-donation to an unfilled σ* molecular orbital of CH4. Considering the phase and spatial configurations of the unfilled CH4 molecular orbitals, the 2t2 molecular orbital can facilitate the back-donation from the occupied Pd3f–dyz orbital, as shown in Fig. 3b. This back-donation results in the weakening of the two C–H bonds coordinated to the Pd3f atom. We found that these “activated” C–H bonds are elongated by 21 mÅ with respect to the gas-phase C–H bonds of methane. The charge density difference plot in Fig. 3c shows an accumulation of charges between CH4 and Pd3f, which Weaver et al. attributed to a dative covalent bond.31
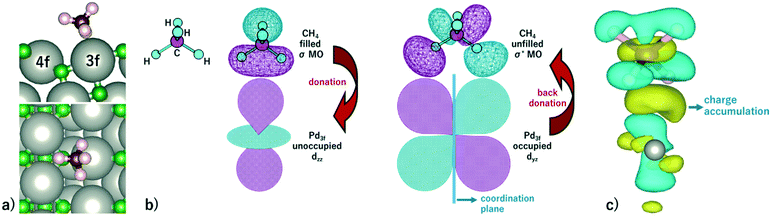 | ||
Fig. 3 a) Optimal adsorption configuration of CH4 on the PdO(101) surface. b) Mechanism of electron donation and back-donation between CH4 and the coordinatively unsaturated Pd atom. Lobes of the same color denote the same phase of the wave function. The molecular orbitals of the gas phase CH4 were calculated using the GAUSSIAN code55 with the B3LYP functional with 6-31G(d,p) basis sets. c) Charge density difference upon the adsorption of CH4 on PdO(101) was computed using 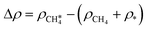 , where each term to the right denotes the charge density of the CH4 + slab complex, and the summed charge densities of the isolated CH4 gas and slab. Yellow and cyan colors represent charge accumulation and depletion, respectively, rendered using VESTA.56 , where each term to the right denotes the charge density of the CH4 + slab complex, and the summed charge densities of the isolated CH4 gas and slab. Yellow and cyan colors represent charge accumulation and depletion, respectively, rendered using VESTA.56 | ||
Fig. 4 shows the energy profile for the dissociation of CH4 into CH3 + H. At the final state, CH3 bonds with the Pd3f atom while the O3f atom acts as the H acceptor, forming CH3–Pd3f and H–O3f moieties. The transition states were calculated using the dimer method, with the initial direction along the dimer generated based on the initial and final states.33–36 The activated (TS1) and non-interacting (TS2) C–H bonds required activation barriers of 0.66 eV and 1.72 eV, respectively. For comparison, the values calculated by Weaver et al. using DFT without van der Waals correction are 0.67 eV and 1.73 eV for TS1 and TS2 activation barriers, respectively, while that by Chin et al. is 0.64 eV for the TS1 activation barrier using ultrasoft pseudopotentials.37,38 This confirms the weakening of the Pd3f coordinated C–H bonds through back-donation to the CH4–σ* molecular orbital. The C–H bond activation of methane on IrO2(110) was also attributed by Wang et al. on the σ–d interaction of CH4 and the coordinatively unsaturated Ir atom.39 Following the initial activation of methane, DFT-based microkinetic modeling and kinetic isotope studies found that the subsequent reactions with O follow the Mars–van Krevelen mechanism, where the O atoms from the substrates are used to produce carbon dioxide and water.32,40
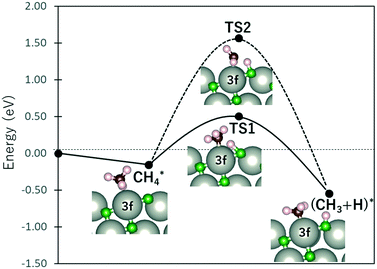 | ||
| Fig. 4 Energy profile of CH4 dissociation. TS1 and TS2 denote the transition states for the cleaving of the Pd-coordinated (“activated”) and non-interacting C–H bonds, respectively. | ||
2.3 SO2 oxidation on PdO(101)
The results from the previous section have shown that the Pd3f and O3f atoms on PdO(101) play important roles in the activation of methane. It can be argued that blocking these active sites with other adsorbates can decrease the activity of the catalyst for methane activation. As shown in Fig. 5a, the adsorption of SOy (y = 2 to 4) molecules involves both the Pd3f and Pd4f atoms, suggesting a possible poisoning of the Pd3f site. SO2 forms two O–Pd3f and one S–Pd4f bonds on the surface, with an adsorption energy of −1.74 eV. This value of adsorption energy is more than ten times greater than that of CH4 (−0.16 eV). This explains why sulfur poisoning is still prominent despite its very low concentration (1 ppm or less) under typical experimental conditions.9 It can be noted that another DFT calculation showed that water molecules also block the Pd sites on PdO(101) with a sizeable adsorption energy (ca. −1.3 eV), which explains the experimentally observed water inhibition of methane adsorption on the surface.32 SO3 and SO4 have similar bonding characteristics on the surface, i.e., forming bonds with two Pd3f and one Pd4f atoms. The calculated Bader charges of S in SO2, SO3, and SO4 adsorbed on the surface are +3.2e, +4.9e, and +6.0e, respectively, indicating the different oxidation states of S on these systems. Correspondingly, O gained electrons because of its high electronegativity. The stabilities of adsorbed species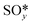 (y = 2, 3, 4) and
(y = 2, 3, 4) and 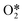 were compared by calculating their free energy change with respect to gas-phase O2, SO2, and the clean PdO(101) surface. That is:
were compared by calculating their free energy change with respect to gas-phase O2, SO2, and the clean PdO(101) surface. That is:The asterisk “*” denotes surface-bound species, while the molecules with no asterisk denote the gas-phase species. The chemical potentials μ of gas-phase species SO2 and O2 were computed by adding the DFT calculated total energy, zero-point vibrational energy, and the temperature and pressure-dependent parts of the chemical potential:
The temperature dependence of free energies for the condensed phases (i.e., 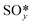 ,
, 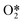 and slab) was shown to have no significant impact on constructing phase diagrams and is thus ignored in this calculation.10
and slab) was shown to have no significant impact on constructing phase diagrams and is thus ignored in this calculation.10
Fig. 5b shows the phase diagram with the clean PdO(101) surface (denoted by asterisks to indicate an “empty” site), and the PdO(101) surface with adsorbed O2, SO2, SO3, and SO4 in the given range of SO2 and O2 chemical potentials, which are translated into a pressure range at T = 400 °C. Essentially, the figure shows the most stable (i.e., the one with the lowest free energy) 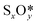 species for a given chemical potential of SO2 and O2. Under typical experimental conditions9 where the chemical potential of O2 is ca. −1.7 eV, the phase diagram shows the preference towards the bare PdO surface for a SO2 chemical potential lower than ca. −2.5 eV. For the same O2 chemical potential, increasing the SO2 chemical potential to values typical in experiments (ca. −2.3 eV corresponding to ca. 10−6 atm at 400 °C), SO4 formation on the surface is favored, which indicates the facile oxidation of SO2 given the high O2/SO2 gas ratio. Correspondingly, for a typical SO2 chemical potential of ca. −2.3 eV in experiments, increasing the chemical potential of O2 up to ca. −1.9 eV favors the formation of adsorbed SO4 over the bare surface. These results explain why, under typical experimental conditions for methane oxidation (e.g., O2 and SO2 partial pressures of 0.20 atm and 5 × 10−6 atm, respectively), the SO4-decorated PdO(101) surface is detected.9,16
species for a given chemical potential of SO2 and O2. Under typical experimental conditions9 where the chemical potential of O2 is ca. −1.7 eV, the phase diagram shows the preference towards the bare PdO surface for a SO2 chemical potential lower than ca. −2.5 eV. For the same O2 chemical potential, increasing the SO2 chemical potential to values typical in experiments (ca. −2.3 eV corresponding to ca. 10−6 atm at 400 °C), SO4 formation on the surface is favored, which indicates the facile oxidation of SO2 given the high O2/SO2 gas ratio. Correspondingly, for a typical SO2 chemical potential of ca. −2.3 eV in experiments, increasing the chemical potential of O2 up to ca. −1.9 eV favors the formation of adsorbed SO4 over the bare surface. These results explain why, under typical experimental conditions for methane oxidation (e.g., O2 and SO2 partial pressures of 0.20 atm and 5 × 10−6 atm, respectively), the SO4-decorated PdO(101) surface is detected.9,16
Considering that the SO4-decorated surface is highly favored under typical experimental conditions, it is imperative to describe the reaction mechanism of its formation from SO2. Fig. 6 shows the free energy profile for SO2 oxidation to SO4 on PdO(101) via the Eley–Rideal (red curve followed by black curve), Langmuir–Hinshelwood (black curve), and Mars–van Krevelen (blue curve) mechanisms, at temperatures of 0 K (to show the energy profile without entropic correction) and 673.15 K or 400 °C (a typical temperature in experiments where CH4 conversion is observed).9 The top panel in Fig. 6 shows the optimal adsorption configurations of the molecules on the surface. Briefly, in the Langmuir–Hinshelwood (LH) mechanism, both SO2 and O2 first adsorb onto the surface before the reaction takes place. In the Eley–Rideal (ER) mechanism, only O2 adsorbs onto the surface, after which SO2 interacts with the adsorbed O. Finally, in the Mars–van Krevelen (MK) mechanism, SO2 forms a chemical bond with the surface O atoms of PdO(101), generating an O vacancy site upon the production of SO3 and SO4.
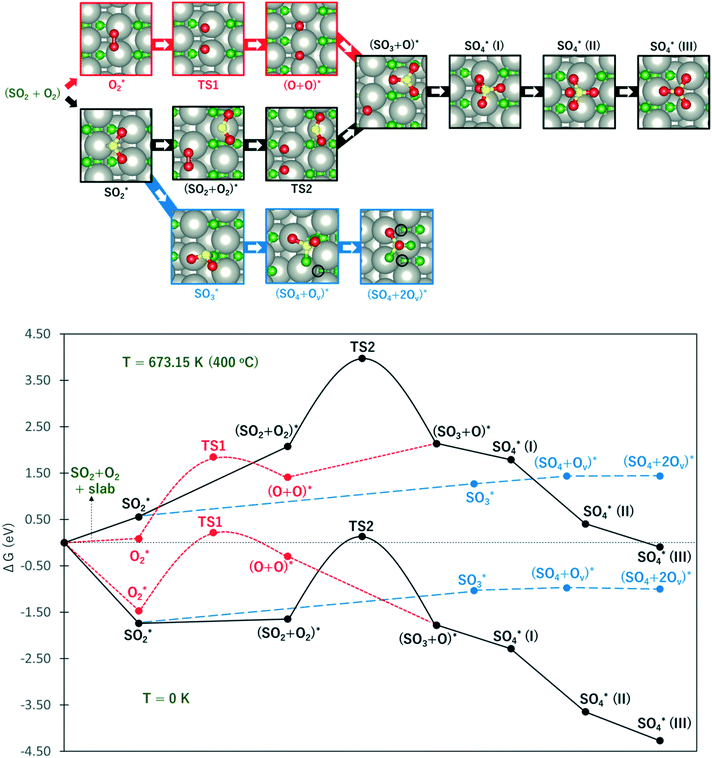 | ||
Fig. 6 The upper panel shows the optimal adsorption configuration of the states depicted in the energy profile at the lower panel. The energy diagram shows the Eley–Rideal (red curve followed by black curve), Langmuir–Hinshelwood (black curve), and Mars–van Krevelen (blue curve) mechanisms, evaluated at temperatures of 0 K and 673.15 K (or 400 °C), and O2 and SO2 partial pressures of 0.20 atm and 5 × 10−6 atm, respectively. 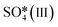 corresponds to corresponds to 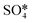 in Fig. 5a while Ov denotes an O-vacancy site. in Fig. 5a while Ov denotes an O-vacancy site. | ||
The Gibbs free energy GA* of the adsorbed species A* (“*” denotes surface-bound species) was calculated by adding the zero-point vibrational energy (ZPVE), vibrational energy change for temperature increased from 0 to T K (ΔEvib,0→T), and subtracting the vibrational entropy, as previously described in our previous studies:59,60
| GA* = EDFT + EZPVE + ΔEvib,0→T − SvibT |
The free energies were referenced to the chemical potentials of gas-phase SO2 and O2, and the free energy of the slab.
It can be observed from Fig. 6 that compared to the 0 K case, the free energy profile at T = 400 °C displays higher activation energies and more endothermic reaction energies. This is due to the large increase in the entropy of gas-phase O2 and SO2 (i.e., more negative chemical potential) which are used for reference energy. However, considering the large increase in the temperature from 0 to 400 °C, the rate constant for the elementary steps are expected to increase largely, as described by the Arrhenius equation.
At this point, the energy profile in the 0 K case is first described. As shown by the red curve in the ER path, the activation of O2 requires an activation barrier of 1.68 eV (TS1). Subsequent to the dissociation of O2, SO2 from the gas can form a SO3 + O co-adsorption state where SO3 binds at the Pd4f atom with a planar structure. Further S–O bond formation between SO3 and O toward the SO4 product proceeds thermodynamically downhill in energy. As shown in Fig. 5, the tridentate SO4 is the most stable, followed by the bidentate and monodentate structures. The reaction energy for the overall process of adsorbed SO4 formation from the reference state is −4.27 eV.
In the LH path, SO2 adsorbs on the surface with greater adsorption energy than molecular O2. The co-adsorption state SO2 + O2 is only slightly downhill in energy from adsorbed SO2. This state is expected to have a lower energy in the zero-coverage limit as the lateral interaction between SO2 and O2 becomes negligible. From the SO2 + O2 co-adsorption state, the activation of O2 requires a higher energy barrier of 1.79 eV (TS2) compared to TS1, indicating a contribution from the lateral interaction between SO2 and O + O. The subsequent S–O bond formation toward the SO3 + O state is inferred to be barrierless as the optimization of co-adsorbed SO2 + O + O readily yields SO3 + O.
The blue curve in Fig. 6 shows the MK path where the oxidation of SO2 required the formation of O vacancies on the surface. The adsorbed SO2 diffuses to a nearby O3f atom to form an SO3 species. This process is 0.71 eV endothermic. From here, the adsorbed SO3 diffuses to the adjacent O3f site forming an O vacancy and adsorbed SO4, which is only 0.06 eV endothermic. Finally, a slightly exothermic process proceeds, where another O vacancy is formed as SO4 adsorbs in a tridentate structure on three coordinatively unsaturated Pd atoms. The overall process for this MK mechanism has a reaction energy of −1.00 eV with respect to the reference state.
These results show that despite the highly exothermic SO2 oxidation on PdO(101) via the ER and LH mechanisms, its kinetics can be limited by the high barrier for O2 dissociation. On the other hand, the MK mechanism has low exothermicity for the overall SO2 oxidation process but is expected to promote more favorable kinetics because of the relatively facile elementary steps. In the 400 °C case, it can be noted that the energy profile gives the same preference towards the MK mechanism. The ER and LH paths are still limited by the earlier noted activation of O2. Similar to the 0 K case, the formation of SO3 and SO4 on the surface proceeds downhill subsequent to the activation of O2 for both the ER and LH mechanisms.
From these results, insights into avoiding the sulfur poisoning of PdO(101) can be drawn. Considering that CH4 activation only involves the Pd3f site while SO2 adsorption and subsequent oxidation to SO3 and SO4 involve both the Pd3f and Pd4f sites on the PdO(101) surface, it can be argued that the Pd4f site is an important element to consider in weakening/avoiding the adsorption of SOy (x = 2 to 4) species while at the same time retaining the catalytic activity of the Pd3f site for methane activation. One approach is to find an adsorbate that selectively blocks the Pd4f sites without compromising the activity of the Pd3f sites. Another approach is to replace the Pd4f atoms with other elements that weakly interact with SOy species. These proposed approaches to catalyst design are challenged by the discovery of specific additives and impurities that would yield sulfur poisoning-resistant PdO without compromising its remarkable activity for methane oxidation. It is hoped that these insights will stimulate further research interest into the design of poison-free and efficient methane oxidation catalysts.
3. Conclusion
van der Waals-corrected density functional theory-based first principles calculations were performed to determine the mechanism of PdO(101) sulfation in relation to the poisoning of the active sites for methane activation. Methane was found to adsorb at the coordinatively unsaturated Pd atom on the surface, with two C–H bonds coordinated to the Pd atom and the other two C–H bonds pointing away from the surface. The unoccupied dzz state of the unsaturated Pd atom facilitates the electron donation from the filled σ molecular orbital of CH4, while its occupied dyz orbital facilitates back-donation to the unfilled σ anti-bonding CH4 molecular orbital, resulting in the elongation and weakening of the Pd-coordinated C–H bonds. SOy (y = 2 to 4) species block this active site for methane activation, with the SO4 species predicted to be the most favoured under typical conditions in the experiments. The formation of SO3 and SO4 on the surface from the oxidation of SO2 is highly exothermic via the Eley–Rideal and Langmuir–Hinshelwood mechanisms but is limited by the high activation barrier for O2 dissociation. A more kinetically feasible path for SO2 oxidation is the less exothermic Mars–van Krevelen mechanism that can provide more facile elementary steps. The results suggest that efforts in designing sulfur poisoning-resistant PdO should be aimed at blocking or substituting the four-fold coordinated Pd atom without compromising the activity of the coordinatively unsaturated three-fold Pd atom.Computational model
Spin-polarized DFT calculations were carried out using the Vienna ab initio simulation package (VASP).42–45 The exchange–correlation term was described using generalized gradient approximation (GGA) based on the Perdew–Burke–Ernzerhof (PBE) functional,48–51 with van der Waals correction (D3) by Grimme.52 A comparison of standard GGA-DFT and GGA+U calculations for the adsorption of molecules such as H2O, H2, and alkanes on PdO(101) has shown similar conclusions and trends about the relative stabilities of these species on the surface.31,57,58 Moreover, the adsorption energies and barriers of the elementary processes determined through temperature programmed desorption (TPD) have a better quantitative agreement with values calculated using the standard GGA-DFT without the +U implementation. Thus, inclusion of the +U correction to the standard GGA is expected to yield the same trend for adsorption energies of the molecules and barriers for surface reactions, which is the primary interest in this paper. The interaction between ions and electrons was described using the projector augmented wave (PAW) method.46,47 Plane wave basis sets were employed with an energy cut-off of 400 eV. The surface Brillouin zone integrations were performed on a grid of 6 × 6 × 1 Monkhorst–Pack k-points53 using Methfessel–Paxton smearing54 of σ = 0.2 eV.The optimal adsorption configuration of the molecules on the surface was explored using a number of different possible orientations on one side of the slab model with dipole correction to avoid spurious electrostatic interactions between periodic images. The gas-phase molecules were modeled using one free molecule inside a 25 × 25 × 25 Å3 unit cell. Optimizations were performed using a conjugate gradient algorithm41 within a force tolerance of 0.05 eV Å−1. The adsorption energies of the molecules were calculated by taking the difference between the total energy of the adsorbate–slab system in the lowest energy adsorption configuration and the summed energies of the optimized clean surface and the gas-phase molecule.
Conflicts of interest
All the authors declare that they have no competing interests.Acknowledgements
This work is supported in part by JST ACCEL grant number JPMJAC1501 “Creation of the Functional Materials on the Basis of the Inter-Element-Fusion Strategy and their Innovative Applications”, MEXT Grant-in-Aid for Scientific Research (16K04876), and JST CREST Innovative Catalysts and Creation Technologies for the Utilization of Diverse Natural Carbon Resources: in situ atomic characterization of catalytic reactions for the development of Innovative Catalysts (No. 17942262). Some of the numerical calculations presented here were done using the computer facilities at the following institutes: High Energy Accelerator Research Organization (KEK), Institute for Solid State Physics (ISSP, University of Tokyo), Yukawa Institute for Theoretical Physics (YITP, Kyoto University), and the National Institute for Fusion Science (NIFS). The authors acknowledge the support of Prof. Hideaki Kasai, President of the National Institute of Technology, Akashi College.Notes and references
- C. H. Bartholomew, Appl. Catal., A, 2001, 212, 17 CrossRef CAS.
- M. D. Argyle and C. H. Bartholemew, Catalysts, 2015, 5, 145 CrossRef CAS.
- J. P. Lange, Angew. Chem., Int. Ed., 2015, 54, 13186 CrossRef CAS PubMed.
- E. Rytter and A. Holmen, Catalysts, 2015, 5, 478 CrossRef CAS.
- S. M. Sadrameli, Fuel, 2016, 173, 285 CrossRef CAS.
- I. Sadaba, M. L. Granados, A. Riisager and E. Taarning, Green Chem., 2015, 17, 4133 RSC.
- S. Ronsch, J. Schneider, S. Matthischke, M. Schluter, M. Gotz, J. Lefebvre, P. Prabhakaran and S. Bajohr, Fuel, 2016, 166, 276 CrossRef.
- R. L. Arevalo, S. M. Aspera, M. C. S. Escano, H. Nakanishi and H. Kasai, Sci. Rep., 2017, 7, 13963 CrossRef PubMed.
- P. Gelin and M. Primet, Appl. Catal., B, 2002, 39, 1 CrossRef CAS.
- H. N. Sharma, V. Sharma, A. B. Mhadeshwar and R. Ramprasad, J. Phys. Chem. Lett., 2015, 6, 1140 CrossRef CAS PubMed.
- A. Gremminger, P. Lott, M. Merts, M. Casapu, J.-D. Grunwaldt and O. Deutschmann, Appl. Catal., A, 2017, 218, 833 CrossRef CAS.
- S. Colussi, F. Arosio, T. Montanari, G. Busca, G. Groppi and A. Trovarelli, Catal. Today, 2010, 155, 59 CrossRef CAS.
- S. Ordonez, P. Hurtado and F. V. Diez, Catal. Lett., 2005, 100, 27 CrossRef CAS.
- M. Happel, Y. Lykhach, N. Tsud, T. Skala, V. Johanek, K. C. Prince, V. Matolin and J. Libuda, J. Phys. Chem. C, 2012, 116, 10959 CrossRef CAS.
- D. Mowery and R. L. McCormick, Appl. Catal., B, 2001, 34, 287 CrossRef CAS.
- J. K. Lampert, M. Shahjahan Kazi and R. J. Farrauto, Appl. Catal., B, 1997, 14, 211 CrossRef CAS.
- L. J. Hoyos, H. Praliaud and M. Primet, Appl. Catal., A, 1993, 98, 125 CrossRef CAS.
- M. S. Wilburn and W. S. Epling, Appl. Catal., A, 2017, 206, 589 CrossRef CAS.
- V. Meeyoo and D. L. Trimm, Appl. Catal., B, 1998, 16, L101 CrossRef CAS.
- P. Briot and M. Primet, Appl. Catal., 1991, 68, 301 CrossRef CAS.
- J. M. Jones, V. A. Dupont, R. Brydson, D. J. Fullerton, N. S. Nasri, A. B. Ross and A. V. K. Westwood, Catal. Today, 2003, 81, 589 CrossRef CAS.
- D. Ciuparu, M. R. Lyubovsky, E. Altman, L. D. Pfefferle and A. Datye, Catal. Rev.: Sci. Eng., 2002, 44, 593 CrossRef CAS.
- S. K. Matam, M. H. Aguirre, A. Weidenkaff and D. Ferri, J. Phys. Chem. C, 2010, 114, 9439 CrossRef CAS.
- R. Westerstrom, M. E. Messing, S. Blomberg, A. Hellman, H. Gronbeck, J. Gustafson, N. M. Martin, O. Balmes, R. van Rijn, J. N. Andersen, K. Deppert, H. Bluhm, Z. Liu, E. Grass, M. Havecker and E. Lundgren, Phys. Rev. B: Condens. Matter Mater. Phys., 2011, 83, 115440 CrossRef.
- R. van Rijn, O. Balmes, A. Resta, D. Wermeille, R. Westerstrom, J. Gustafson, R. Felici, E. Lundgren and J. W. M. Frenken, Phys. Chem. Chem. Phys., 2011, 13, 13167 RSC.
- A. Hellman, A. Resta, N. M. Martin, J. Gustafson, A. Trinchero, P.-A. Carlsson, O. Balmes, R. Felici, R. van Rijn, J. W. M. Frenkeni, J. N. Andersen, E. Lundgren and H. Gronbeck, J. Phys. Chem. Lett., 2012, 3, 678 CrossRef CAS PubMed.
- J. F. Weaver, C. Hakanogly, A. Antony and A. Asthagiri, Chem. Soc. Rev., 2014, 43, 7536 RSC.
- J. G. McCarty, Catal. Today, 1995, 26, 283 CrossRef CAS.
- C.-J. Huang, F.-M. Pan, T.-C. Tzeng, L. Chang and J.-T. Sheu, J. Electrochem. Soc., 2009, 156, J28 CrossRef CAS.
- H. H. Kan and J. F. Weaver, Surf. Sci., 2008, 602, L53 CrossRef CAS.
- J. F. Weaver, C. Hakanoglu, J. M. Hawkins and A. Asthagiri, J. Chem. Phys., 2010, 132, 024709 CrossRef PubMed.
- M. Van den Bossche and H. Gronbeck, J. Am. Chem. Soc., 2015, 137, 12035 CrossRef PubMed.
- P. Xiao, D. Sheppard, J. Rogal and G. Henkelman, J. Chem. Phys., 2014, 140, 174104 CrossRef PubMed.
- J. Kastner and P. Sherwood, J. Chem. Phys., 2008, 128, 014106 CrossRef PubMed.
- A. Heyden, A. T. Bell and F. J. Keil, J. Chem. Phys., 2005, 123, 224101 CrossRef PubMed.
- G. Henkelman and H. Jonsson, J. Chem. Phys., 1999, 111, 7010 CrossRef CAS.
- J. F. Weaver, J. A. Hinojosa, C. Hakanogly, A. Antony, J. M. Hawkins and A. Asthagiri, Catal. Today, 2011, 160, 213 CrossRef CAS.
- Y.-H. Chin, C. Buda, M. Neurock and E. Iglesia, J. Am. Chem. Soc., 2013, 135, 15425 CrossRef CAS PubMed.
- C.-C. Wang, S. S. Siao and J.-C. Jiang, J. Phys. Chem. C, 2012, 116, 6367 CrossRef CAS.
- J. Au-Yeng, K. Chen, A. T. Bell and E. Iglesia, J. Catal., 1999, 188, 132 CrossRef.
- I. Stich, R. Car, M. Parrinello and S. Baroni, Phys. Rev. B: Condens. Matter Mater. Phys., 1989, 39, 4997 CrossRef CAS.
- G. Kresse and J. Furthmuller, Phys. Rev. B: Condens. Matter Mater. Phys., 1996, 54, 11169 CrossRef CAS.
- G. Kresse and J. Furthmuller, Comput. Mater. Sci., 1996, 6, 15 CrossRef CAS.
- G. Kresse and J. Hafner, Phys. Rev. B: Condens. Matter Mater. Phys., 1993, 47, 558 CrossRef CAS.
- G. Kresse and J. Hafner, Phys. Rev. B: Condens. Matter Mater. Phys., 1994, 49, 14251 CrossRef CAS.
- P. Blochl, Phys. Rev. B: Condens. Matter Mater. Phys., 1999, 59, 17953 Search PubMed.
- G. Kresse and J. Joubert, Phys. Rev. B: Condens. Matter Mater. Phys., 1999, 59, 1758 CrossRef CAS.
- J. Perdew, K. Burke and M. Ernzerhof, Phys. Rev. Lett., 1996, 77, 3865 CrossRef CAS PubMed.
- J. Perdew and K. Burke, Phys. Rev. B: Condens. Matter Mater. Phys., 1996, 54, 16533 CrossRef CAS.
- A. Becke, Phys. Rev. A: At., Mol., Opt. Phys., 1988, 38, 3098 CrossRef CAS.
- C. Lee, W. Yang and R. Parr, Phys. Rev. B: Condens. Matter Mater. Phys., 1988, 37, 785 CrossRef CAS.
- S. Grimme, J. Comput. Chem., 2004, 25, 1463 CrossRef CAS PubMed.
- H. Monkhorst, Phys. Rev. B: Solid State, 1976, 13, 5188 CrossRef.
- M. Methfessel and A. Paxton, Phys. Rev. B, 1989, 470, 3616 CrossRef.
- M. J. Frisch, et al., Gaussian 09, Gaussian, Inc., Wallingford CT, 2009 Search PubMed.
- K. Momma and F. Izumi, J. Appl. Crystallogr., 2011, 44, 1272 CrossRef CAS.
- C. Hakanoglu, J. M. Hawkins, A. Asthagiri and J. F. Weaver, J. Phys. Chem. C, 2010, 114, 11485 CrossRef CAS.
- H. H. Kan, R. C. Colmyer, A. Asthagiri and J. F. Weaver, J. Phys. Chem. C, 2009, 113, 1495 CrossRef CAS.
- R. L. Arevalo, M. C. S. Escano and H. Kasai, ACS Catal., 2013, 3, 3031 CrossRef CAS.
- R. L. Arevalo, M. C. S. Escano, A. Y.-S. Wang and H. Kasai, Dalton Trans., 2013, 42, 770 RSC.
| This journal is © The Royal Society of Chemistry 2019 |