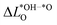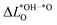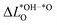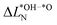Open Access Article
Open Access ArticleCreative Commons Attribution 3.0 Unported Licence
The role of metastability in enhancing water-oxidation activity†
Nathalie
Vonrüti
and
Ulrich
Aschauer
 *
*
Department of Chemistry and Biochemistry, University of Bern, Freiestrasse 3, CH-3012 Bern, Switzerland. E-mail: ulrich.aschauer@dcb.unibe.ch
First published on 23rd October 2019
Abstract
While metastability enhanced water-oxidation activity was experimentally reported, the reason behind this effect is still unclear. We determine here, using density functional theory calculations, oxygen evolution reaction overpotentials for a variety of defective (001) surfaces of three different perovskite materials. For all three, we find a large range of overpotentials for different reaction sites including also overpotentials at the top of the activity volcano. Assuming that these sites dominate the apparent catalytic activity, this implies that a large number of geometrically different reaction sites, as they occur when a catalyst is operated at the border of its stability conditions, can lead to a strong enhancement of the apparent activity. This also implies that a pre-treatment of the catalyst creating a variety of different reactive sites could lead to superior catalytic activities for thermodynamically stable materials.
Introduction
Hydrogen fuel production by (photo)electrochemical water splitting has been intensively studied as a route to convert electrical or solar energy to chemical energy. The bottleneck in (photo)electrochemical water splitting is the oxygen evolution reaction (OER). Previous studies of metal1 and oxide2 catalysts proposed a likely OER reaction mechanism to consist of four consecutive proton-coupled one-electron transfer (PCET) steps with reaction intermediates *OH, *O and *OOH as shown in eqn (1)–(4).| * + H2O(l) → *OH + H+ + e− | (1) |
| *OH → *O + H+ + e− | (2) |
| *O + H2O(l) → *OOH + H+ + e− | (3) |
| *OOH → * + O2(g) + H+ + e− | (4) |
Several experimental studies found an inverse correlation between the activity and the stability of catalyst materials for the OER. Markovic and co-workers investigated activity–stability trends of the OER for crystalline and amorphous RuO23,4 as well as for different surface orientations of the perovskite SrRuO3.5 Based on the concentration of dissolved metal ions, they found a higher activity for less stable surfaces of both materials and concluded that a highly active OER catalyst should balance activity and stability. A mechanistic understanding of a catalyst's stability in enhancing the OER activity is however still elusive and actively debated. It was suggested that the OER activity is controlled by the density of surface defects rather than by the binding energy of the reaction intermediates on the perfect surface and that it may be linked to changes in oxidation state of Ru ions close to defects.5 A very recent study on RuO2 thin films did, however, not find such a fundamental relationship between a material's stability and its activity.6 While a correlation between the dissolution and the activity for different surface orientations was initially observed, it was also shown that the active OER sites are decoupled from the fastest-corroding Ru sites.6
To fully understand the activity–stability relationship one would ideally study the OER on specific reaction sites of defective dissolving materials. Experimentally it is, however, very challenging to characterize the geometry and activity of specific reaction sites since spectroscopic methods probe the average state of a catalyst. Computationally, one could readily calculate the overpotential and hence the activity of a given reaction site with a specific local geometry, but there exists no well-established method to determine the surface structure of a material with a low stability under OER conditions. For materials with a thermodynamically stable bulk, reasonable surface structures can be determined from the surface energy as a function of the applied potential and the pH by means of so-called surface Pourbaix diagrams (SPD).7 For thermodynamically unstable materials, on the other hand, one can only investigate the stability of the bulk with respect to competing phases,8,9 while a SPD would yield the surface with the minimal number of atoms as most stable, indicating that the thermodynamic equilibrium is the fully dissolved state. Nevertheless, in practice the dissolution may be kinetically slow and still allow these materials to be used as catalysts.8 We refer here to such materials, that are thermodynamically unstable under OER conditions and for which we therefore cannot determine their surface structure by means of SPDs, as metastable materials.
The aim of the present work is to obtain a density functional theory (DFT) description of the OER on surfaces of metastable materials and to reveal how metastability can increase the performance of a catalyst. Computational studies for different oxides have, so far, mainly compared the OER activity of ideal stoichiometric, clean10 or adsorbate-covered,11 low-index surfaces which are unlikely to be good approximations for surfaces of a metastable material that may slowly dissolve under OER conditions.8 Few studies reported the theoretical activity for reaction sites in the vicinity of point defects, steps or kinks,7,12–14 however without linking such structures to metastability. Our approach to account for metastability is to study the OER on a large variety of different reaction sites by sampling many defective surface structures that should be representative for a slowly dissolving metastable material. We study the effect of metastability on the OER for three chemically very different perovskite structured catalysts, which enables us to distinguish between effects resulting from intrinsic material properties and effects of specific reaction sites. We compare LaTiO2N (LTON) and SrRuO3 (SRO), which differ by their d0 respectively d4 d-electron occupation and their insulating respectively metallic character. LTON is the best studied member of the family of perovskite oxynitrides that by virtue of their smaller band gap than oxides are considered promising photocatalysts.15 Calculations16 and experimentally observed nitrogen loss17 indicate that LTON is metastable under OER conditions and SRO was also reported to be metastable.5,8 As these two materials differ not only in their metallic respectively insulating behaviour but also in their cation composition, we complement the set of materials with SrTiO3 (STO), which shares properties with both LTON and SRO: like SRO it is a pure oxide but like LTON it is a d0 insulator. Moreover, it shares the same A and B site with SRO and LTON respectively but unlike the other two materials STO was not reported to be metastable.
Computational approach
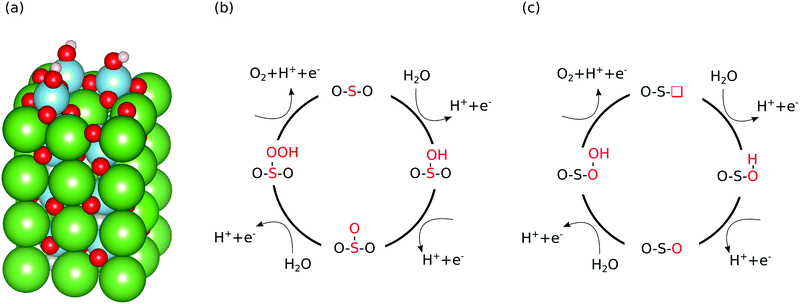
For all three materials we investigate both the AO and BO2 terminated (001) surface, assuming that for a metastable or unstable material both terminations will be exposed as dissolution proceeds. For the oxynitride we also have to consider the anion order, which is different in the surface and the bulk: LaTiO2N assumes a cis anion order in the bulk to maximize the overlap between the N 2p and the Ti 3d orbitals18 but the (001) surface prefers a non-polar trans anion order.19 We therefore perform calculations on the trans surface but to account for the metastability-induced dissolution of the thin trans layer20 also investigate the OER on a cis ordered surface. As we find no significant difference between the two anion orders regarding OER reaction free energies, we do however not distinguish between them in our results.Our stoichiometric and clean surface slabs contain four surface cation sites and we create defective surfaces with between one and four nitrogen, titanium, ruthenium, lanthanum or strontium vacancies in the surface layer (see Fig. 1a for an example). We do not explicitly consider oxygen vacancies, since these are unlikely to exist on the surface under oxidizing OER conditions.11,21 Occasionally, during surface relaxation – in particular for high cation-vacancy concentrations – either O2 or N2 recombine and desorb. In these cases, we stop the calculation and remove the desorbed molecules before continuing the calculation, which can in effect lead to oxygen vacancies. Since potentials relevant for (photo)electrochemical water splitting often lead to formation of oxidising surface species,11 we also cover surface metal sites with either zero or one monolayer of OH or O in top position in the case of Ti and Ru as well as in the bridge position for La and Sr (see Fig. 1a, as well as ESI,† Fig. S1 and S2 for examples of different surface structures). For these surfaces we calculate the OER free energy profile on symmetrically inequivalent titanium, ruthenium, lanthanum and strontium reaction sites in the topmost formula-unit layer – meaning that for example on a defective BO2 terminated surface also an A atom could become the reaction site.
We consider here only the conventional OER mechanism with four PCET steps (see eqn (1)–(4)) that is depicted in Fig. 1(b) as we want to study the influence of different reaction sites irrespective of the reaction mechanism. This conventional mechanism does normally not include oxygen ions that are part of the slab. However, in the vicinity of defects and adsorbates it is not always clear if an oxygen originated as part of the adsorbate or the slab and whether the conventional mechanism depicted in Fig. 1b can be applied or not. Therefore, we also include the OER mechanism shown in Fig. 1c which is mathematically equivalent to the conventional mechanism shown in Fig. 1b but operates on an oxygen deficient surface. This so-called lattice oxygen evolution22 was experimentally observed23–25 and also explained by basic thermodynamic concepts.26 Alternative lattice oxygen evolution mechanisms have been proposed,27,28 which are however mathematically different from the conventional mechanism (eqn (1)–(4)) and were therefore not included in this study.
In total we calculate the OER on 778 symmetrically inequivalent reaction sites (327 trans LTON, 143 cis LTON, 176 STO, 132 SRO) on 106 LTON, 35 STO and 39 SRO defective (001) surface models. The larger number of reaction sites on the oxynitride stems from anion-induced symmetry breaking. For roughly 3/4 of the reaction sites either the *OOH or *OH intermediate was not stable and we exclude these cases from our analysis.
We calculate the change in free energy (ΔG) of the four reaction steps (1)–(4) using the computational hydrogen electrode (CHE),29 where the energy of a proton and an electron equals half the energy of a hydrogen molecule. As the theoretical overpotential is not dependent on the pH or the potential2 we perform our calculations at standard conditions (pH = 0, T = 298.15 K) and U = 0 V. Zero-point energies (ZPE) and entropies (S) of the reaction intermediates were included as detailed elsewhere.30 In contrast to other studies, where ZPE was calculated for reaction intermediates in different environments (bridge vs. top site),30 we always use the ZPE at the top site. Given that for defective surfaces a full ZPE evaluation would be computationally prohibitively expensive and that previously reported changes in ZPE were minor,30 this approach will yield correct trends for defective surfaces.
We estimate the activity of a specific reaction site by the largest step in its OER free energy profile:
| ΔGOER = max[ΔG01,ΔG02,ΔG03,ΔG04] | (5) |
| ηOER = (ΔGOER)/e − 1.23 V | (6) |
| ΔGads = Gads+slab − Gslab − nGH2O − mGH2 | (7) |
We further compare the calculated overpotential ηOER with the overpotential ηOERD predicted by the single descriptor ΔG02: it was established that there exists a universal scaling relation between the adsorption energies of the reaction intermediates *OH and *OOH, their difference being approximatively 3.2 eV for metal and oxide surfaces irrespective of the reaction site.31 Since the overpotential for oxides and metals is generally determined by either step 2 (ΔG02) or 3 (ΔG03 = 3.2 eV − ΔG02), the former is often a suitable descriptor of the OER activity that determines the overpotential:2
| ηOERD = max[ΔG02, 3.2 eV − ΔG02]/e − 1.23 V, | (8) |
| ΔG02 = ΔGO − ΔGOH | (9) |
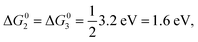 | (10) |
Results and discussion
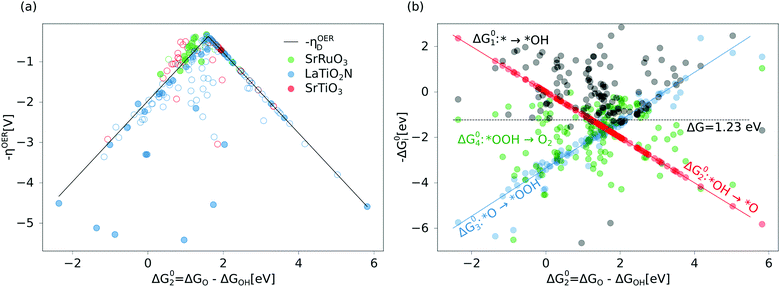
We begin our analysis by comparing the calculated overpotentials ηOER with the overpotentials determined via the single descriptor ηOERD and find in general a good agreement for the majority of the calculated overpotentials (see Fig. 2a). Most remarkable is the fact that we find for all three materials a continuous distribution of overpotentials within a large range of the descriptor ΔG02, including also the top of the volcano. The complex dissolution kinetics, make it difficult to determine with certainty which sites will be predominantly present on a dissolving surface, yet we can attempt to distinguish between reactive sites occurring more likely (filled circles in Fig. 2a) and less likely (empty circles in Fig. 2a) based on thermodynamic and kinetic considerations: From surface Pourbaix diagrams (see ESI,† Section S2 for details) we see, in agreement with experimental studies,32,33 that A sites dissolve more readily and therefore B sites represent likelier OER reactive sites. Moreover, the Bell–Evans–Polanyi principle34,35 implies that the formation of B-site vacancies is also kinetically less likely than the formation of A-site vacancies. Since under OER conditions surfaces are normally oxidized,11 we consider B sites oxidized either by an OH or O species to be the thermodynamically and kinetically most likely OER reaction sites. For LTON we consider the trans anion order to be more likely due to electrostatic considerations19 and for STO we only consider the O covered defect free TiO2 termination as likely since the material is stable. When considering only the overpotentials of these likely reactive sites we still find a continuous distribution of overpotentials, many of them at the top of the activity volcano. Since many of the less likely (less stable) sites also have overpotentials close to the top of the volcano, this implies, in agreement with recent experiments,6 that there exists no correlation between the stability of a single site and its catalytic activity and that the activity–stability relations must have a different origin.Given the large number of likely sites close to the top of the volcano, we can assume that some of these will at least be transiently present. Since we omitted combinations of different defects types and considered only zero or full adsorbate coverage, the actual variety of reaction sites should be even larger. Together with alternative reaction mechanisms that could be active, we thus expect even more sites with small overpotentials on a metastable catalyst. Since the activity of a catalyst depends exponentially on the overpotential, even a small number of highly-active sites can dominate the apparent activity.14,36,37 We therefore postulate that in operando, surface dissolution can lead to the appearance of highly active sites, resulting in an enhanced apparent activity of the catalyst. In other words, the less a material is stable, the higher should be the diversity of reaction sites and the higher the chance of finding highly active reaction sites, which we believe to be the origin of the activity–stability relations. We stress that at this point the proposed activity improvement requires the material to be metastable under the chosen conditions. However, metastable materials such as LTON and SRO can of course only benefit from this proposed activity enhancement if the dissolution is slow enough for the material to still sustain extended periods of operation.
Previous studies suggest that active dissolution of the material results in the best activities.3–5 Our results, however, suggest that an activity enhancement can also be achieved by an initial dissolution, for example by exposing the catalyst to conditions that render it unstable, to create a variety of reaction sites but that the dissolution does not have to continue for high OER activities. Such a preconditioning approach would yield a large variety of sites, some of which are likely highly active, while preventing continuous dissolution and hence maintaining long-term operability of the catalyst. This agrees with recent experimental findings for RuO2 thin films, which show that while the surface orientation with the initially highest dissolution rate results in the best activities, an ongoing dissolution is not necessary for highly active surfaces.6
The similarity of the overpotential distribution of LTON, SRO and STO implies further that the high activity does not originate purely from the bulk electronic structure of the catalyst as is often assumed, but that reaction sites with geometries that enable a lower overpotential can form on any of the investigated materials. This is supported by the experimental finding that perovskite oxide electrocatalysts with structural flexibility can lead to superior activity.38 We were not able to correlate catalytic activity with geometrical descriptors or simple structural features such as the reaction site species, angles and bond lengths of reaction intermediates or the adsorbate coverages to mention only a few. We also find no correlation with global properties such as the dipole moment of the slab or the nominal charge of the atoms. However, in agreement with other studies,13,39,40 a preliminary analysis that will be reported elsewhere41 hints at a correlation of ΔG02 with the electronic structure and in particular the centre of the O2p band of the oxygen adsorbate.
We continue by predicting the minimum overpotentials of the three materials. From the relation between the adsorption energies of the *OH and *OOH intermediates, we predict minimum overpotentials of 0.23 V for STO, 0.26 V for SRO and 0.40 V for LTON, the two former being smaller than the 0.37 V predicted by the scaling relations, while the latter is larger. Despite these differences, we do for STO and SRO not find actual reaction sites with overpotentials smaller than 0.37 V. This is in line with the observation that breaking the universal scaling relation between *OOH and *OH is a necessary but not sufficient condition to optimize the OER.42 Further, while there are only small differences between the two oxides that show a rather good agreement between the calculated ηOER and the single-descriptor overpotentials ηOERD, for LTON we find a not insignificant number of reaction sites that show large deviations from ηOERD. A more detailed analysis of the reaction free energies of the four charge transfer steps ΔG0i for LTON (see Fig. 2b), reveals that while for most reactions ΔG02 or ΔG03 (blue and red data points) have the largest free-energy change, there are some reactions where ΔG04 (green data points) has the largest free energy change and is the limiting step. This implies that for the oxynitride the step from *OOH to O2 is energetically less favourable while at the same time the formation of *OH is more favourable. This difference with respect to oxides2 suggests a stronger adsorption of *OOH on the oxynitride. The larger deviation from the perfect scaling relations (i.e., single-descriptor overpotentials ηOERD) for some of the OERs on LTON compared to the oxides thus stems from differences in adsorption energetics, likely induced by less symmetric reaction sites (due to both O and N neighbors) for LTON.
From the volcano plot in Fig. 2a we can see a further difference between the two oxides and the oxynitride: While for the oxynitride the descriptor value ΔG02 ranges from −2 eV to 6 eV, the two oxides seem to have a much smaller range of ΔG02 and their overpotentials are therefore more concentrated around the top of the volcano. The spread in ΔG02 is important for the apparent activity. A catalyst with an activity of the perfect surface far from the top of the volcano would benefit from a large spread to increase the number of highly active sites. An already good catalyst located not far from the top of the volcano, on the other hand, would benefit from a small spread to have a large proportion of highly active sites. We can explain the difference in the ΔG02 range between oxides and oxynitrides by analysing the charge transfer between oxygen and nitrogen anions, in particular for the *OH → *O reaction step. To do so, we look at the change of average Löwdin charges43 of the anions for different reaction steps. While all charge partitioning methods have their advantages and drawbacks, the Löwdin charge analysis uses the same atomic orbitals we project on to obtain partial density of states (used in descriptor searches), thus enabling a direct comparison between these quantities. We find the best correlations of the Löwdin charges with ΔG02 if we include all anions (meaning all the atoms of the slab including the adsorbates) and not only surface atoms. This might stem from the fact that energy changes for these highly defective surfaces are not only related to the change in adsorbates and their electronic structure but also to movements of other surface and bulk atoms that affect the electronic structure. We compute differences between element-averaged Löwdin charges for the different reaction steps:
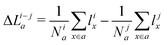 | (11) |
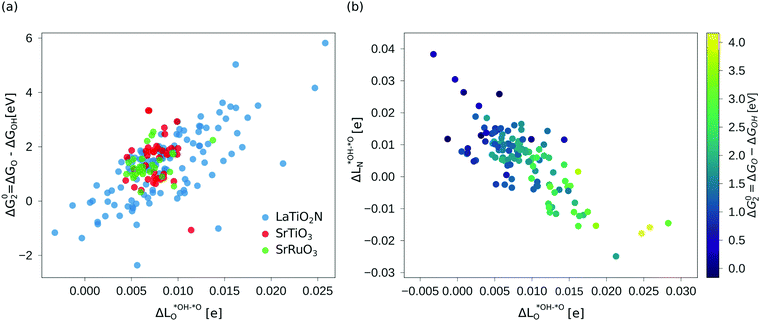
As we show in Fig. 3a, there is a direct correlation between the descriptor ΔG02 and the average change in Löwdin charge of the oxygen ions 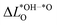 for LTON. We do, however, not see a correlation for STO or SRO, which may be related to the smaller range of ΔG02 for these materials.
for LTON. We do, however, not see a correlation for STO or SRO, which may be related to the smaller range of ΔG02 for these materials. 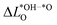 is generally positive, meaning that the average Löwdin charge of oxygen is higher for the *OH than for the *O intermediate, which we can relate to the fact that oxygen in *OH attracts electrons from the hydrogen atom and all non-oxygen atoms of the slab whereas *O attracts electrons only from all non-oxygen atoms of the slab. A smaller
is generally positive, meaning that the average Löwdin charge of oxygen is higher for the *OH than for the *O intermediate, which we can relate to the fact that oxygen in *OH attracts electrons from the hydrogen atom and all non-oxygen atoms of the slab whereas *O attracts electrons only from all non-oxygen atoms of the slab. A smaller 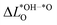 therefore signifies less charge transfer from the non-oxygen atoms of the slab to the oxygen atoms (including the oxygen adsorbate) during deprotonation. This implies that the oxygen atoms attract a similar number of electrons in both cases, which results in an energetically more favourable deprotonation and a smaller ΔG02, giving a physical interpretation to the correlation in Fig. 3a.
therefore signifies less charge transfer from the non-oxygen atoms of the slab to the oxygen atoms (including the oxygen adsorbate) during deprotonation. This implies that the oxygen atoms attract a similar number of electrons in both cases, which results in an energetically more favourable deprotonation and a smaller ΔG02, giving a physical interpretation to the correlation in Fig. 3a.
For the oxides SRO and STO the range of 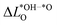 is much smaller than for LTON leading to a smaller range in ΔG02. We can explain this difference between oxides and oxynitrides by relating the average change in Löwdin charge of oxygen
is much smaller than for LTON leading to a smaller range in ΔG02. We can explain this difference between oxides and oxynitrides by relating the average change in Löwdin charge of oxygen 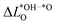 to the one of nitrogen
to the one of nitrogen 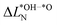 . As shown in Fig. 3b we find an inverse correlation between these charge differences, suggesting a charge transfer from N to O. From the colour coding of the data points, we see that ΔG02 is generally smaller when nitrogen loses more electrons (large positive
. As shown in Fig. 3b we find an inverse correlation between these charge differences, suggesting a charge transfer from N to O. From the colour coding of the data points, we see that ΔG02 is generally smaller when nitrogen loses more electrons (large positive 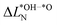 ), while the charge variation on the oxygen atoms is small. From these observations we propose that nitrogen can act as an electron reservoir: The reaction from *OH to *O is favoured if nitrogen ions provide electrons, resulting in a lower descriptor value ΔG02, while reaction sites, where this charge transfer is not possible, result in larger ΔG02s. More generally, this implies that a more flexible valence-band electronic structure, for example in mixed-anion materials, can yield a larger variety of ΔG02s.
), while the charge variation on the oxygen atoms is small. From these observations we propose that nitrogen can act as an electron reservoir: The reaction from *OH to *O is favoured if nitrogen ions provide electrons, resulting in a lower descriptor value ΔG02, while reaction sites, where this charge transfer is not possible, result in larger ΔG02s. More generally, this implies that a more flexible valence-band electronic structure, for example in mixed-anion materials, can yield a larger variety of ΔG02s.
Conclusions
In summary, we have shown for three electronically different perovskite materials that the structural variety of reaction sites on dissolving heterogeneous catalysts will, for some sites, lead to overpotentials close to the top of the activity volcano. Given that reaction sites with low overpotentials will dominate the apparent activity, this implies that, independent of the bulk electronic properties, operating a heterogeneous catalyst at the border of its stability region can lead to an increased apparent activity due to the increased variety of geometrically different reaction sites. Also preconditioning catalysts under metastable conditions before operation under stable conditions should result in the same activity enhancement.While we find the single-descriptor approach to generally work well for these highly defective surfaces, we observe that the strong binding of the *OOH and *OH intermediates on LaTiO2N can lead to different limiting steps and larger deviations from the descriptor-based overpotential than for oxides. We find only minor differences in activity between metallic SrRuO3 and insulating SrTiO3 but show that a flexible valence band structure as it occurs in LaTiO2N yields a larger variety of ΔG02 values.
Methods
We determine energies of the various adsorbate covered, defective surfaces by density functional theory (DFT) calculations using the Quantum ESPRESSO44 package at the GGA+U level of theory with the PBE45 exchange–correlation functional and a Hubbard U46 of 3 eV19,47 applied to the titanium 3d states. We do not apply a Hubbard U on ruthenium 4d orbitals as this setup results in the best agreements with experimentally measured magnetic moments and the density of states at the Fermi energy. We use ultrasoft pseudopotentials48 with La(5s,5p,5d,6s), Sr(4s,4p,5s), Ti(3s,3p,3d,4s), Ru(4d,5s,5p), O(2s,2p) and N(2s,2p) electrons as valence states to describe the interaction between electrons and nuclei and perform spin-polarized calculations in the case of SrRuO3. The cutoff for the plane-wave basis set is 40 Ry and 320 Ry for the kinetic energy and the augmented density respectively for LaTiO2N and SrTiO3, while for SrRuO3 we use slightly higher cutoffs of 50 Ry and 500 Ry respectively. We start our calculations from a 40-atom pseudo-cubic perovskite cell and create asymmetric 1 × 1 × 2 (001) surface slabs (see Fig. 1a) with at least 10 Å vacuum, two fixed atomic layers at the bottom of the slab and a dipole correction in the vacuum layer.49 The Brillouin zone is sampled with a 4 × 4 × 1 Monkhorst–Pack50k-point grid for LaTiO2N and SrTiO3 and a 6 × 6 × 1 grid for SrRuO3. We relax ionic positions until forces converge below 0.05 eV Å−1 and total energies change by less than 1.4 × 10−5 eV.Conflicts of interest
There are no conflicts to declare.Acknowledgements
This research was funded by the SNF Professorship Grant PP00P2_157615. Calculations were performed on UBELIX (http://www.id.unibe.ch/hpc), the HPC cluster at the University of Bern, the Swiss National Supercomputing Centre (CSCS) under project s766 and SuperMUC at GCS@LRZ, Germany, for which we acknowledge PRACE for awarding us access.References
- J. Rossmeisl, A. Logadottir and J. K. Nørskov, Chem. Phys., 2005, 319, 178–184 CrossRef CAS.
- I. C. Man, H.-Y. Su, F. Calle-Vallejo, H. A. Hansen, J. I. Martinez, N. G. Inoglu, J. Kitchin, T. F. Jaramillo, J. K. Nørskov and J. Rossmeisl, ChemCatChem, 2011, 3, 1159–1165 CrossRef CAS.
- S. H. Chang, J. G. Connell, N. Danilovic, R. Subbaraman, K.-C. Chang, V. R. Stamenkovic and N. M. Markovic, Faraday Discuss., 2014, 176, 125–133 RSC.
- N. Danilovic, R. Subbaraman, K.-C. Chang, S. H. Chang, Y. J. Kang, J. Snyder, A. P. Paulikas, D. Strmcnik, Y.-T. Kim, D. Myers, V. R. Stamenkovic and N. M. Markovic, J. Phys. Chem. Lett., 2014, 5, 2474–2478 CrossRef CAS PubMed.
- S. H. Chang, N. Danilovic, K.-C. Chang, R. Subbaraman, A. P. Paulikas, D. D. Fong, M. J. Highland, P. M. Baldo, V. R. Stamenkovic, J. W. Freeland, J. A. Eastman and N. M. Markovic, Nat. Commun., 2014, 5, 4191 CrossRef CAS PubMed.
- C. Roy, R. R. Rao, K. A. Stoerzinger, J. Hwang, J. Rossmeisl, I. Chorkendorff, Y. Shao-Horn and I. E. L. Stephens, ACS Energy Lett., 2018, 3, 2045–2051 CrossRef CAS.
- X. Rong and A. M. Kolpak, J. Phys. Chem. Lett., 2015, 6, 1785–1789 CrossRef CAS PubMed.
- B.-J. Kim, D. F. Abbott, X. Cheng, E. Fabbri, M. Nachtegaal, F. Bozza, I. E. Castelli, D. Lebedev, R. Schäublin, C. Copéret, T. Graule, N. Marzari and T. J. Schmidt, ACS Catal., 2017, 7, 3245–3256 CrossRef CAS.
- A. K. Singh, L. Zhou, A. Shinde, S. K. Suram, J. H. Montoya, D. Winston, J. M. Gregoire and K. A. Persson, Chem. Mater., 2017, 29, 10159–10167 CrossRef CAS.
- J. H. Montoya, A. D. Doyle, J. K. Nørskov and A. Vojvodic, Phys. Chem. Chem. Phys., 2018, 20, 3813–3818 RSC.
- J. H. Montoya, M. Garcia-Mota, J. K. Nørskov and A. Vojvodic, Phys. Chem. Chem. Phys., 2015, 17, 2634–2640 RSC.
- C. F. Dickens and J. K. Nørskov, J. Phys. Chem. C, 2017, 121, 18516–18524 CrossRef CAS.
- C. F. Dickens, J. H. Montoya, A. R. Kulkarni, M. Bajdich and J. K. Nørskov, Surf. Sci., 2019, 681, 122–129 CrossRef CAS.
- L. C. Seitz, C. F. Dickens, K. Nishio, Y. Hikita, J. Montoya, A. Doyle, C. Kirk, A. Vojvodic, H. Y. Hwang, J. K. Norskov and T. F. Jaramillo, Science, 2016, 353, 1011–1014 CrossRef CAS PubMed.
- A. Kasahara, K. Nukumizu, T. Takata, J. N. Kondo, M. Hara, H. Kobayashi and K. Domen, J. Phys. Chem. B, 2003, 107, 791–797 CrossRef CAS.
- I. E. Castelli, K. S. Thygesen and K. W. Jacobsen, Top. Catal., 2014, 57, 265–272 CrossRef CAS.
- A. Kasahara, K. Nukumizu, G. Hitoki, T. Takata, J. N. Kondo, M. Hara, H. Kobayashi and K. Domen, J. Phys. Chem. A, 2002, 106, 6750–6753 CrossRef CAS.
- M. Yang, J. Oró-Solé, J. A. Rodgers, A. B. Jorge, A. Fuertes and J. P. Attfield, Nat. Chem., 2011, 3, 47–52 CrossRef CAS PubMed.
- S. Ninova and U. Aschauer, J. Mater. Chem. A, 2017, 5, 11040–11046 RSC.
- S. Ninova and U. Aschauer, J. Mater. Chem. A, 2019, 7, 2129–2134 RSC.
- H. Ouhbi and U. Aschauer, ACS Mater. Lett., 2019, 1, 52–57 CrossRef CAS.
- E. Fabbri and T. J. Schmidt, ACS Catal., 2018, 8, 9765–9774 CrossRef CAS.
- M. Wohlfahrt-Mehrens and J. Heitbaum, J. Electroanal. Chem. Interfacial Electrochem., 1987, 237, 251–260 CrossRef CAS.
- S. Fierro, T. Nagel, H. Baltruschat and C. Comninellis, Electrochem. Commun., 2007, 9, 1969–1974 CrossRef CAS.
- O. Diaz-Morales, F. Calle-Vallejo, C. de Munck and M. T. M. Koper, Chem. Sci., 2013, 4, 2334–2343 RSC.
- T. Binninger, R. Mohamed, K. Waltar, E. Fabbri, P. Levecque, R. Kötz and T. J. Schmidt, Sci. Rep., 2015, 5, 12167 CrossRef CAS PubMed.
- A. Grimaud, O. Diaz-Morales, B. Han, W. T. Hong, Y.-L. Lee, L. Giordano, K. A. Stoerzinger, M. T. M. Koper and Y. Shao-Horn, Nat. Chem., 2017, 9, 457–465 CrossRef CAS PubMed.
- J. S. Yoo, X. Rong, Y. Liu and A. M. Kolpak, ACS Catal., 2018, 8, 4628–4636 CrossRef CAS.
- J. K. Nørskov, J. Rossmeisl, A. Logadottir, L. Lindqvist, J. R. Kitchin, T. Bligaard and H. Jonsson, J. Phys. Chem. B, 2004, 108, 17886–17892 CrossRef.
- Á. Valdés, Z.-W. Qu, G.-J. Kroes, J. Rossmeisl and J. K. Nørskov, J. Phys. Chem. C, 2008, 112, 9872–9879 CrossRef.
- M. T. M. Koper, J. Electroanal. Chem., 2011, 660, 254–260 CrossRef CAS.
- J. H. Adair, J. Crampo, M. M. Mandanas and E. Suvaci, J. Am. Ceram. Soc., 2006, 89, 1853–1860 CrossRef CAS.
- J. G. Connell, B. J. Isaac, G. B. Ekanayake, D. R. Strachan and S. S. A. Seo, Appl. Phys. Lett., 2012, 101, 251607 CrossRef.
- R. P. Bell, Proc. R. Soc. London, Ser. A, 1936, 154, 414–429 CrossRef.
- M. G. Evans and M. Polanyi, Trans. Faraday Soc., 1936, 32, 1333 RSC.
- G. Sun and P. Sautet, J. Am. Chem. Soc., 2018, 140, 2812–2820 CrossRef CAS PubMed.
- T. A. Batchelor, J. K. Pedersen, S. H. Winther, I. E. Castelli, K. W. Jacobsen and J. Rossmeisl, Joule, 2019, 3, 834–845 CrossRef CAS.
- E. Fabbri, M. Nachtegaal, T. Binninger, X. Cheng, B.-J. Kim, J. Durst, F. Bozza, T. Graule, R. Schäublin, L. Wiles, M. Pertoso, N. Danilovic, K. E. Ayers and T. J. Schmidt, Nat. Mater., 2017, 6, 8106–8108 Search PubMed.
- A. Vojvodic and J. K. Nørskov, Science, 2011, 334, 1355–1356 CrossRef CAS PubMed.
- J. K. Nørskov, F. Abild-Pedersen, F. Studt and T. Bligaard, Proc. Natl. Acad. Sci. U. S. A., 2011, 108, 937–943 CrossRef PubMed.
- N. Vonrüti, R. R. Rao, L. Giordano, Y. Shao-Horn and U. Aschauer, in preparation.
- N. Govindarajan, J. M. Garcia-Lastra, E. J. Meijer and F. Calle-Vallejo, Curr. Opin. Electrochem., 2018, 8, 110–117 CrossRef CAS.
- P. O. Löwdin, J. Chem. Phys., 1950, 18, 365–375 CrossRef.
- P. Giannozzi, S. Baroni, N. Bonini, M. Calandra, R. Car, C. Cavazzoni, D. Ceresoli, G. L. Chiarotti, M. Cococcioni, I. Dabo, A. Dal Corso, S. de Gironcoli, S. Fabris, G. Fratesi, R. Gebauer, U. Gerstmann, C. Gougoussis, A. Kokalj, M. Lazzeri, L. Martin-Samos, N. Marzari, F. Mauri, R. Mazzarello, S. Paolini, A. Pasquarello, L. Paulatto, C. Sbraccia, S. Scandolo, G. Sclauzero, A. P. Seitsonen, A. Smogunov, P. Umari and R. M. Wentzcovitch, J. Phys.: Condens. Matter, 2009, 21, 395502 CrossRef PubMed.
- J. P. Perdew, K. Burke and M. Ernzerhof, Phys. Rev. Lett., 1996, 77, 3865–3868 CrossRef CAS PubMed.
- V. I. Anisimov, J. Zaanen and O. K. Andersen, Phys. Rev. B: Condens. Matter Mater. Phys., 1991, 44, 943–954 CrossRef CAS PubMed.
- N. Vonrüti and U. Aschauer, Phys. Rev. Lett., 2018, 120, 046001 CrossRef PubMed.
- D. Vanderbilt, Phys. Rev. B: Condens. Matter Mater. Phys., 1990, 41, 7892–7895 CrossRef PubMed.
- L. Bengtsson, Phys. Rev. B: Condens. Matter Mater. Phys., 1999, 59, 12301 CrossRef CAS.
- H. J. Monkhorst and J. D. Pack, Phys. Rev. B: Solid State, 1976, 13, 5188–5192 CrossRef.
Footnote |
| † Electronic supplementary information (ESI) available: Surface structure examples and surface stability analysis. See DOI: 10.1039/c9cp04859f |
| This journal is © the Owner Societies 2019 |