Theoretical investigations of a platinum–water interface using quantum-mechanics-molecular-mechanics based molecular dynamics simulations†
Abstract
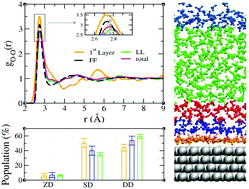
Pt–water interfaces have been of immense interest in the field of energy storage and conversion. Studying this interface using both experimental and theoretical tools is challenging. On the theoretical front, typically one uses classical molecular dynamics (MD) simulations to handle large system sizes or time scales while for a more accurate quantum mechanical description Born Oppenheimer MD (BOMD) is typically used. The latter is limited to smaller system sizes and time-scales. In this study using quantum-mechanics-molecular-mechanics (QMMM), we have performed atomistic MD simulations to have a microscopic understanding of the structure of the Pt–water interface using a system size that is much larger than that accessible when using BOMD simulations. In contrast to recent reports using BOMD simulations, our study reveals that the water molecules typically form two distinct layers above the Pt-surface before they form bulk like structures. Further, we also find that a significant fraction of the water molecules at the interface are pointed towards the surface thereby disrupting the H-bond network. Consistent with this observation, the layer resolved oxygen–oxygen radial distribution function for the water molecules belonging to the solvating water layer shows a high density liquid like behaviour even though the overall water behaves like a low density liquid. A charge transfer analysis reveals that this solvating water layer donates electrons to the Pt atoms in contact with it thereby resulting in the formation of an interface dipole that is pointing towards the surface. Our results suggest that, using QMMM-MD, on one hand it is possible to study more realistic models of solid–liquid interfaces that are inaccessible with BOMD, while on the other hand one also has access to information about such systems that are not obtained from conventional classical MD simulations.
- This article is part of the themed collection: 2019 PCCP HOT Articles


 Please wait while we load your content...
Please wait while we load your content...