The reassigned pseudo Wigner–Ville transform in electrochemical noise analysis
Abstract
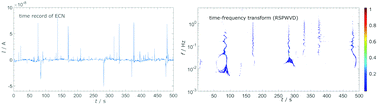
Several different time–frequency transforms from signal processing were used to analyze electrochemical noise data to determine frequency components contained within the noise record and their time evolution. Bilinear time–frequency representations (TFR) based on the Wigner–Ville distribution (WVD) were compared with a special focus on the reassigned smoothed pseudo WVD (RSPWVD). Spectra obtained with WVD were compared with traditional linear time–frequency representations, such as short time Fourier transform and wavelet transform. Comparison to other TFRs showed that the RSPWVD suppressed artifacts, provided better resolution of the time–frequency analysis in both time and frequency domains, and improved the overall readability of a representation. The obtained spectra from RSPWVD were consistent with the results from DWT, but permitted a more comprehensive analysis of transients. Consequently, RSPWVD is suitable for electrochemical noise analysis. In the presence of Cl−, RSPWVD showed that the passivity of Al was compromised, as evidenced by the presence of various current transients in the frequency range from 10−2 to 1 Hz.
- This article is part of the themed collection: 2019 PCCP HOT Articles


 Please wait while we load your content...
Please wait while we load your content...