Open Access Article
Open Access ArticleCreative Commons Attribution 3.0 Unported Licence
Considerable matrix shift in the electronic transitions of helium-solvated cesium dimer cation Cs2He+n†
Lorenz
Kranabetter
 a,
Nina K.
Bersenkowitsch
a,
Paul
Martini
a,
Michael
Gatchell
a,
Nina K.
Bersenkowitsch
a,
Paul
Martini
a,
Michael
Gatchell
 ab,
Martin
Kuhn
a,
Felix
Laimer
ab,
Martin
Kuhn
a,
Felix
Laimer
 a,
Arne
Schiller
a,
Martin K.
Beyer
a,
Arne
Schiller
a,
Martin K.
Beyer
 a,
Milan
Ončák
a,
Milan
Ončák
 *a and
Paul
Scheier
*a and
Paul
Scheier
 *a
*a
aInstitut für Ionenphysik und Angewandte Physik, Universität Innsbruck, Technikerstr. 25, A-6020 Innsbruck, Austria. E-mail: Milan.Oncak@uibk.ac.at; Paul.Scheier@uibk.ac.at
bDepartment of Physics, Stockholm University, 106 91 Stockholm, Sweden
First published on 8th November 2019
Abstract
We investigate the photodissociation of helium-solvated cesium dimer cations using action spectroscopy and quantum chemical calculations. The spectrum of Cs2He+ shows three distinct absorption bands into both bound and dissociative states. Upon solvation with further helium atoms, considerable shifts of the absorption bands are observed, exceeding 0.1 eV (850 cm−1) already for Cs2He10+, along with significant broadening. The shifts are highly sensitive to the character of the excited state. Our calculations show that helium atoms adsorb on the ends of Cs2+. The shifts are particularly pronounced if the excited state orbitals extend to the area occupied by the helium atoms. In this case, Pauli repulsion leads to a deformation of the excited state orbitals, resulting in the observed blue shift of the transition. Since the position of the weakly bound helium atoms is ill defined, Pauli repulsion also explains the broadening.
Introduction
Vibrationally resolved electronic spectroscopy in combination with theoretical calculations is a powerful technique to determine details of the geometrical arrangement and electronic structure of molecules or clusters. The quality of vibrationally resolved spectra depends critically on the temperature, as recently demonstrated for the assignment of the structure of Au4+.1 This has triggered the development of several cryogenic techniques, i.e., molecular beams,2,3 matrix isolation,4,5 helium droplets,6,7 cryogenic traps8–20 and cryogenic storage rings.21–25 The low density of ionic targets requires special techniques, such as cavity ring down26 or action spectroscopy.27,28 Tagging of ions with a weakly bound messenger turns out to be particularly suitable to measure absorption lines of ions, albeit leading to a matrix shift.10,29 The binding energy of helium to ions is lower than for any other atom or molecule, leading to a minimum matrix shift.30Whereas only very few He atoms can be attached to singly-charged ions in cold traps, ions can be solvated with almost any number of He atoms when formed in doped helium nanodroplets. In the case of C60+, a remarkable linear red-shift of the absorption lines for the first 32 He atoms attached could be used to extrapolate to the absorption line of the bare ion.31–33 In combination with theory, the experimental results of the matrix shift as well as the width of the absorption lines provide unprecedented insight into the details of the solvation of ions with helium, including phase transitions and isomeric effects.
Alkali metal atoms reside on dimples at the surface of helium droplets, as shown in numerous experimental21,34–40 and theoretical studies.41–46 Alkali metal clusters, however, are submerged into the cluster above a critical cluster size.46–48 The groups of Ernst and Stienkemeier investigated photoionization of Cs atoms and the submersion of Cs+ into He droplets.34,39 Chen et al. managed to solvate Cs+ ions with several million helium atoms via pickup of Cs+ formed upon thermionic emission into large He droplets.49 Dopant ions ejected from charged helium droplets are sometimes complexed with a few helium atoms when recorded via mass spectrometry. The first solvation layer is particularly strongly bound, and its closure is typically reflected as a clear intensity drop of the ion series MHe+n (with M+ the alkali metal ion) in mass spectra.48,50–52 Path integral or basin-hopping methods reproduce the experiments very well.44,45 It was also shown previously that helium adsorption might lead to appreciable spectral shifts.53
Spectroscopic properties of the Cs2+ ion were investigated previously in experimental54,55 and theoretical studies56–58 within the series of alkali metal dimers, assigning the lowest electronically excited states. In the present study, we explore photodissociation of Cs2He+nvia action spectroscopy to assess helium solvation effects in a seemingly simple diatomic system. Single-reference and multi-reference ab initio calculations including spin–orbit coupling reproduce the experimental results and provide an assignment of the electronic transitions. A pronounced blue-shift of more than 0.1 eV (850 cm−1) for absorption into the 12Σ+u state for Cs2He+n with n = 10 provides clear evidence that the He atoms preferentially occupy positions along the axis of the cesium dimer cation.
Methods
CsmHe+n ions are formed upon electron irradiation (85 eV, 260 μA) of Cs doped He nanodroplets (average size about 105 atoms, 2.7 MPa, 9.95 K expansion conditions). Penning ionization via electronically excited He* will be the dominant ionization channel for the heliophobic cesium atoms.7,59–61 Ionized cesium atoms and clusters have a substantially stronger interaction with the He matrix than their corresponding neutral precursors, thus leading to their submersion into the droplet.46 Low-mass ions ejected from the large multiply charged droplet are deflected by 90 degrees relative to the neutral beam via electro-static lenses. The beam is guided into the extraction region of a high-resolution time of flight mass spectrometer, where it is merged with a laser beam from a pulsed tuneable light source (EKSPLA NT 242, 210–2600 nm). Every tenth extraction pulse of the mass spectrometer operated at 10 kHz is irradiated with the laser (repetition rate 1 kHz), thereby enabling simultaneous measurement of mass spectra with and without laser light. Upon photon absorption, all adsorbed He atoms are typically lost from CsmHe+n, and an optical photodissociation spectrum is derived from the depletion signal. A detailed description of the experiment can be found in the ESI† (Fig. S9) and elsewhere.62To obtain a quantum chemical description of the optical spectra, ground state structures of Cs2He+n ions were first modelled at the coupled cluster singles doubles (CCSD) level with the def2QZVP basis set on Cs and def2TZVP on He. The position of the weakly bound He atoms, residing in shallow potential wells, is very sensitive to the quality of the basis set used on Cs. With the triple-zeta quality basis set def2TZVP used on Cs, a bent structure is predicted for Cs2He+; a linear Cs2He+ structure is obtained with the def2QZVP basis set on Cs and def2TZVP on He, and this does not change when the def2QZVPPD basis set is used on both Cs and He. To validate the theory as much as possible, excited states were modelled on various theory levels: time-dependent density functional theory (TDDFT) with the CAM-B3LYP functional; equation of motion – CCSD (EOM-CCSD); multi-reference configuration interaction (MRCI) with an active space of one electron in 5 or 17 orbitals, MRCI(1,5) and MRCI(1,17), respectively; def2QZVPPD basis set was used on all atoms for excited state calculations. Spin–orbit coupling was calculated using the state-interacting method as implemented in the Molpro program63,64 along with the ECP46MDF basis set.65 The D2h symmetry group was used for calculations; irreducible representations (IRs) in the D∞h symmetry group were reconstructed from the respective IRs in D2hD2h. “Very Tight” optimization criteria were used for optimization; for optimization in the floppy excited state in Cs2He+, even stricter criteria for solving the EOM-CCSD equations were used, with convergence criteria of 10−9, 10−11 and 10−10 for energy, wavefunction and CCSD and ground-state Z-vector iterations, respectively. In all calculations, only 17 electrons in Cs2+ were treated explicitly, with the rest described within an effective core pseudopotential (ECP).
Purely dissociative as well as bound excited states are encountered in Cs2+. The absorption spectra of the dissociative states were modeled using the linear reflection principle (LRP) within the harmonic approximation66–68 and by the standard reflection principle projecting the vibrational wavefunction (calculated for the Cs2+ potential on a grid) onto the excited state potential energy surface. The spectra of the bound states were calculated using the Franck–Condon approximation within the harmonic regime as implemented in the Gaussian software69 or directly by calculating the overlap of the ground state vibrational wavefunction in the electronic ground state with both ground and excited vibrational wavefunctions in the electronically excited state.
Gaussian 16 was used for TDDFT and (EOM-)CCSD calculations, Molpro for MRCI and spin–orbit calculations.
Results and discussion
Let us start with the photodissociation spectrum of Cs2He+ (Fig. 1a). Upon electronic excitation, the He atom is lost, and the spectrum is recorded following the depletion of the ion signal. There are four clearly observed absorption bands at about 1.4, 1.55, 1.60 and 2.8 eV (Table 1). The band at 2.8 eV is further split, with spacing of about 40 meV (300 cm−1). The band at 1.60 eV has pronounced vibrational structure, with a spacing of 22 cm−1 (Fig. 1b); the broad bands at 1.4 and 2.8 eV are, on the other hand, structureless.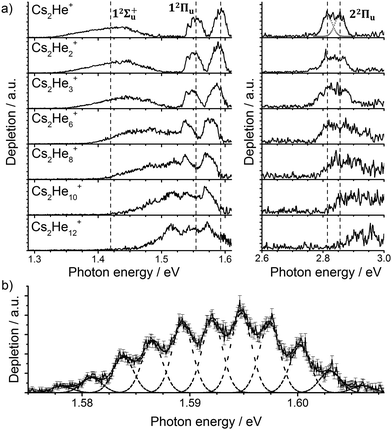 | ||
| Fig. 1 (a) Photodissociation spectra of Cs2He+n ions, n = 1, 2, 3, 6, 8, 10, 12 obtained as a differential spectrum with and without laser irradiation of clusters and scaled with laser power (see ESI† for details). A fit of the peak at 2.8 eV by two Gaussian functions is shown for n = 1. Band centers for Cs2He+ are marked by vertical lines to guide the eye. Electronic state assignment is based on calculations (Table 1). (b) Multiple Gaussian fit to the vibrational progression of the transition into the 12Πu state in Cs2He+ and determination of the vibrational spacing. | ||
For a more quantitative interpretation and reliable assignment of these features, we performed EOM-CCSD and MRCI calculations and analyzed the contribution of spin–orbit coupling effects. Fig. 2 shows the potential energy curves of Cs2+. The Cs2+ ion has D∞h symmetry and, when disregarding spin–orbit coupling, its ground electronic state is 12Σ+g. From this state, the only symmetry allowed transitions are perpendicular and parallel transitions into 2Πu and 2Σ+u states, respectively. Within 3 eV, two 2Σ+u and two 2Πu states can be found. Among these states, only the 12Πu state is bound, the others are dissociative. When accounting for spin–orbit effects (see Table S3 in the ESI†), the Σ states are only slightly affected, with shifts of up to 5 meV. However, the doubly-degenerate Π states split into two states, separated by ∼10–35 meV (80–280 cm−1).
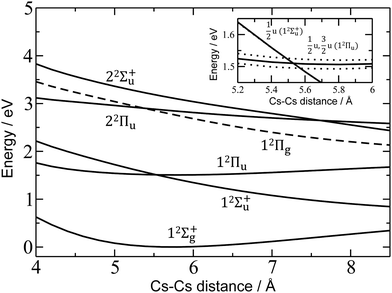 | ||
| Fig. 2 Potential energy curves in Cs2+ calculated at the EOM-CCSD/def2QZVPPD level. Excited states to which electronic transitions are allowed from the ground state are shown with full lines, forbidden ones with dashed lines. In the inset, the vicinity of the 12Πu minimum is shown, along with states including spin–orbit coupling (dotted lines, calculated at the MRCI(1,17)/ECP46MDF level of theory). Only selected states are shown. See the ESI† for excluded electronic states and method benchmarking. | ||
Comparison of the calculations with experiment, summarized in Table 1, allows us to assign the three main bands observed in the experiment as 12Σ+u, 12Πu, and 22Πu, reproducing the excitation energy to within 0.1 eV. The fourth allowed transition into 22Σ+u at ∼3.1 eV (see Table S2, ESI†) is not observed in the experiment due to insufficient laser power in this region. For the dissociative states 12Σ+u and 22Πu, calculations within the reflection principle approximation also predict a realistic width of the observed bands, see Table 1.
| State | 12Σ+u | 12Πu | 22Πu | |
|---|---|---|---|---|
| Experiment, Cs2He+ | E | 1.41 | 1.55; 1.59 | 2.82; 2.86 |
| w | 83 | — | 39; 30 | |
| ΔEsplit | — | 39 | 42 | |
| Theory, Cs2+ | E | 1.43 | 1.51 | 2.85 |
| w | 64 | — | 26 | |
| ΔESO | — | 28 | 13 | |
| Theory, Cs2He+ | E | 1.44 | 1.51 | 2.84 |
| ΔESO | — | 28 | 14 | |
As mentioned above, the 12Πu state is bound and, therefore, the measured photodissociation spectrum reflects its vibrational structure. The 12Πu state is calculated to have a very similar equilibrium distance as the 12Σ+g ground state (Fig. 2). The excited state potential well is less steep, reflected in the calculated harmonic vibrational frequencies of 30 and 20 cm−1 for the 12Σ+g and 12Πu state, respectively, for Cs2+ (at the (EOM-)CCSD/def2QZVPPD level). The respective values for Cs2+He are 31 and 19 cm−1, with a stronger Cs2+–He interaction in the excited states, shortening the Cs–He distance from 4.4 Å in the 12Σ+g state to 4.0 Å in 12Πu. The harmonic Cs2+⋯He vibration is located at 30 cm−1. The calculated frequency in the 12Πu state of 19 cm−1 fits well to the measured spacing of 22 cm−1. Note that only the higher 3/2u(12Πu) state shows clear vibrational resolution shown in Fig. 1b. The 1/2u(12Πu) state interacts with the repulsive 1/2u(12Σ+u) state, and the potential energy surface will be deformed due to the avoided crossing of the states. From a computational perspective, the equilibrium distance in the 12Πu state depends heavily on the choice of the basis set (Fig. S4, ESI†). As a direct consequence, our attempts to reproduce the experimental spectrum shown in Fig. 1b using Franck–Condon simulations failed to grasp correctly the relative intensity of the contributing peaks (see the ESI† for details).
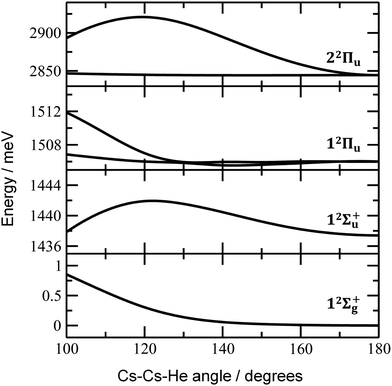
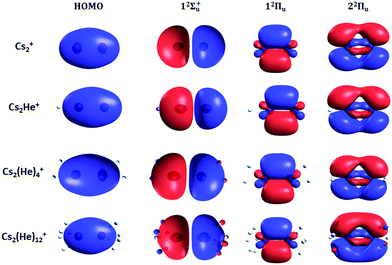
Finally, the calculated weak spin–orbit splitting of the 2Πu states results into two states 1/2u and 3/2u with a different Ω value following Hund's rule 3. The splitting is well reproduced for 12Πu (see also inset in Fig. 2). For 22Πu, the calculated spin–orbit splitting is significantly smaller than the experimentally observed splitting. These observations can be rationalized if one takes into account the additional splitting induced by the asymmetric distribution of the He atom relative to the singly occupied molecular orbital (SOMO) in the excited state. Fig. 3 illustrates how the energy of the several electronic states in Cs2He+ depends on the position of the He atom in Cs2He+. For this calculation, the Cs–Cs–He angle is fixed, and the Cs–Cs and Cs–He distances are optimized in the electronic ground state, 12Σ+g. From 180° to 150°, the ground state energy hardly changes, i.e. the He atom moves more or less freely in this range of Cs–Cs–He angles. The repulsive 12Σ+u state reacts more sensitively to the position of the He atom, and this effect contributes to the broadening of the absorption band, which is 19 meV larger than expected from the linear reflection principle approximation, Table 1. For the 12Πu and 22Πu states, the degeneracy of the two contributing π orbitals (see Fig. 4) is lifted by the presence of the He atom, which leads to an additional splitting. For 12Πu, this effect is negligible down to 150° Cs–Cs–He angle, because the He atom does occupy the same space as the singly occupied π orbitals. In contrast, the SOMO of the 22Πu state is much more diffuse, and in one of the two orientations exhibits significant overlap with the position of the He atom. The splitting of the two orientations of the SOMO in the 22Πu state amounts to 31 meV at 150°, which constitutes the dominant contribution to the experimentally observed splitting. For larger clusters, the same effect is responsible for the significant broadening of the 22Πu band.
Let us now concentrate on the shift of the spectra induced by solvation, i.e. the He matrix shift. As shown in Fig. 1a and Table 2, pronounced shifts to higher energies are recorded for the 12Σ+u and 22Πu states, reaching values of more than 0.1 eV already for Cs2He10+. Note also that the shift in the 12Σ+u state exceeds the He binding energy. In the n = 1–10 range, the energy of the 12Σ+u state shifts linearly with solvation by 12 meV (100 cm−1) per helium atom. The 22Πu band at ∼2.8 eV seems to shift slightly non-linearly, its structure is however not well resolved in the experiment for larger ions. The 12Πu state at 1.6 eV, on the other hand, is shifted only by ∼20 meV (160 cm−1) to lower energies within n = 1–12 (Table 2).
| Experiment | Theory | |||
|---|---|---|---|---|
| n He | 12Σ+u | 12Πu | 12Σ+u | 12Πu |
| 2 | 11 | −3.4; −3.7 | 6 | −0.8 |
| 3 | 23 | −6.1; −6.6 | 15 | −2.1 |
| 6 | 59 | −13.3; −15.2 | 41 | −6.1 |
| 10 | 98 | −9.2; −19.3 | 96 | −12.0 |
| 12 | 124 | −18.5; −41.0 | 109 | −14.2 |
The shifts can be directly connected to the interplay between the position of He atoms around the Cs2+ ion and the character of the respective excited state. Our calculations show that Cs2+ is preferentially solvated by He atoms on its ends, along the Cs–Cs axis for the smallest ions (see Fig. 4). For Cs2He+ and Cs2He2+, the most stable configuration is linear, but deformation from linearity down to a Cs–Cs–He angle of 150° requires very little energy, see Fig. 3; in Cs2He12+, conformations with six and five/seven He atoms on each end are the most stable ones (Table S1, ESI†). As expected, the binding energy of helium atoms is low, within 2.4–3.1 meV He−1 for up to 12 helium atoms. In addition to the shifts, the presence of a large variety of almost isoenergetic isomers leads to significant broadening of the spectra upon solvation (see Fig. S1, ESI†).
Due to Pauli repulsion, the presence of He atoms deforms the orbitals of both ground and excited electronic states that extend along the Cs–Cs axis, shifting them to higher energy. This is the case for the HOMO orbital as well as the orbitals corresponding to excitations into the 12Σ+u and 22Πu states (Fig. 4). The diffuse orbitals in the excited state are deformed more than the HOMO orbital, shifting the excitation energy considerably to higher values (Fig. 1a). The π orbital corresponding to the excitation into the 12Πu state at 1.6 eV represents a different case. Here, the surrounding helium atoms do not approach the orbital and the shift to lower energies reflects the slight destabilization of the HOMO orbital. Our calculations can reproduce the shifts for excitations into 12Σ+u and underestimate those observed for 12Πu (Table 2); for n = 12, the sudden increase observed in the 12Πu experimental shift might be induced by the fitting procedure (see Fig. S12, ESI†) or appearance of new isomers. This is most likely caused by the neglect of He delocalization around the Cs2+ core due to zero-point motion and the presence of multiple isomers.
Conclusions
In contrast to photodissociation of bare Cs2+, helium tagging gives experimental access to the 3/2u component of the 12Πu state, which features a pronounced vibrational progression with a Cs–Cs frequency of 22 cm−1 in the excited state. According to quantum chemical calculations, He considerably changes the spectrum already for the Cs2He+ ion, inducing splitting of bands due to both solvation and dynamic effects. When more helium atoms are added, shifts exceeding 0.1 eV, i.e. almost 1000 cm−1, are induced, and the 22Πu significantly broadens. The magnitude and even direction of the shift are extremely sensitive to both the nature of the electronic transition as well as the position of the solvating atoms. Our calculations show that the shifts are particularly pronounced if He occupies a position in the electronic ground state that carries large electron density in the excited state. Despite its extremely weak interaction, He is capable of inducing significant matrix shifts in electronic excitation spectra, due to Pauli repulsion, as already pointed out before.70,71 This effect is used to derive information both on the shape of excited state molecular orbitals as well as solvation patterns.Conflicts of interest
There are no conflicts to declare.Acknowledgements
This work was supported by the Austrian Science Fund FWF, project numbers W1259 (DK-ALM), P29174 and P31149, and the Swedish Research Council, contract number 2016-06625. The tunable OPO system is part of the Innsbruck Laser Core Facility, financed by the Austrian Federal Ministry of Science, Research and Economy. The computational results presented have been achieved using the HPC infrastructure LEO of the University of Innsbruck.References
- M. Förstel, W. Schewe and O. Dopfer, Angew. Chem., Int. Ed., 2019, 58, 3356–3360 CrossRef PubMed.
- J. Jankunas and A. Osterwalder, Annu. Rev. Phys. Chem., 2015, 66, 241–262 CrossRef CAS PubMed , and references therein.
- D. H. Levy, Annu. Rev. Phys. Chem., 1980, 31, 197–225 CrossRef CAS , and references therein.
- V. E. Bondybey, A. M. Smith and J. Agreiter, Chem. Rev., 1996, 96, 2113–2134 CrossRef CAS PubMed , and references therein.
- V. A. Apkarian and N. Schwentner, Chem. Rev., 1999, 99, 1481–1514 CrossRef CAS PubMed , and references therein.
- J. P. Toennies and A. F. Vilesov, Angew. Chem., Int. Ed., 2004, 43, 2622–2648 CrossRef CAS PubMed , and references therein.
- A. Mauracher, O. Echt, A. M. Ellis, S. Yang, D. K. Bohme, J. Postler, A. Kaiser, S. Denifl and P. Scheier, Phys. Rep., 2018, 751, 1–90 CrossRef CAS , and references therein.
- E. J. Bieske and O. Dopfer, Chem. Rev., 2000, 100, 3963–3998 CrossRef CAS PubMed , and references therein.
- J. A. Fournier, C. J. Johnson, C. T. Wolke, G. H. Weddle, A. B. Wolk and M. A. Johnson, Science, 2014, 344, 1009–1012 CrossRef CAS PubMed.
- E. K. Campbell, M. Holz, D. Gerlich and J. P. Maier, Nature, 2015, 523, 322–323 CrossRef CAS PubMed.
- E. K. Campbell, M. Holz and J. P. Maier, Astrophys. J., Lett., 2016, 826, L4 CrossRef.
- E. K. Campbell, M. Holz, J. P. Maier, D. Gerlich, G. A. H. Walker and D. Bohlender, Astrophys. J., 2016, 822, 17 CrossRef.
- J. P. Maier and E. K. Campbell, Philos. Trans. R. Soc., A, 2016, 374, 20150316 CrossRef PubMed.
- J. Roithova, A. Gray, E. Andris, J. Jasik and D. Gerlich, Acc. Chem. Res., 2016, 49, 223–230 CrossRef CAS PubMed.
- O. Asvany, S. Brünken, L. Kluge and S. Schlemmer, Appl. Phys. B: Lasers Opt., 2014, 114, 203–211 CrossRef CAS.
- O. Asvany, K. M. T. Yamada, S. Brünken, A. Potapov and S. Schlemmer, Science, 2015, 347, 1346–1349 CrossRef CAS PubMed.
- O. Lakhmanskaya, M. Simpson, S. Murauer, M. Notzold, E. Endres, V. Kokoouline and R. Wester, Phys. Rev. Lett., 2018, 120, 253003 CrossRef CAS PubMed.
- R. L. Wong, K. Paech and E. R. Williams, Int. J. Mass Spectrom., 2004, 232, 59–66 CrossRef CAS.
- O. P. Balaj, C. B. Berg, S. J. Reitmeier, V. E. Bondybey and M. K. Beyer, Int. J. Mass Spectrom., 2009, 279, 5–9 CrossRef CAS.
- S. Dillinger, M. P. Klein, A. Steiner, D. C. McDonald, M. A. Duncan, M. M. Kappes and G. Niedner-Schatteburg, J. Phys. Chem. Lett., 2018, 9, 914–918 CrossRef CAS PubMed.
- R. D. Thomas, H. T. Schmidt, M. Gatchell, S. Rosen, P. Reinhed, P. Lofgren, L. Brannholm, M. Blom, M. Bjorkhage, E. Backstrom, J. D. Alexander, S. Leontein, D. Hanstorp, H. Zettergren, M. Kaminska, R. Nascimento, L. Liljeby, A. Kallberg, A. Simonsson, F. Hellberg, S. Mannervik, M. Larsson, W. D. Geppert, K. G. Rensfelt, A. Paal, M. Masuda, P. Hallden, G. Andler, M. H. Stockett, T. Chen, G. Kallersjo, J. Weimer, K. Hansen, H. Hartman and H. Cederquist, EPJ Web Conf., 2015, 84, 01004 CrossRef.
- M. Gatchell, H. T. Schmidt, R. D. Thomas, S. Rosen, P. Reinhed, P. Lofgren, L. Brannholm, M. Blom, M. Bjorkhage, E. Backstrom, J. D. Alexander, S. Leontein, D. Hanstorp, H. Zettergren, L. Liljeby, A. Kallberg, A. Simonsson, F. Hellberg, S. Mannervik, M. Larsson, W. D. Geppert, K. G. Rensfelt, H. Danared, A. Paal, M. Masuda, P. Hallden, G. Andler, M. H. Stockett, T. Chen, G. Kallersjo, J. Weimer, K. Hansen, H. Hartman and H. Cederquist, J. Phys.: Conf. Ser., 2014, 488, 012040 CrossRef.
- R. D. Thomas, H. T. Schmidt, J. Gurell, N. Haag, A. I. S. Holm, H. A. B. Johansson, G. Kallersjo, M. Larsson, S. Mannervik, D. Misra, A. Orban, P. Reinhed, K. G. Rensfelt, S. Rosen, F. Seitz, J. Weimer, H. Zettergren, G. Andler, H. Danared, S. Das, L. Liljeby, M. Bjorkhage, M. Blom, L. Brannholm, P. Hallden, F. Hellberg, A. Kallberg, S. Leontein, P. Lofgren, B. Malm, A. Paal, A. Simonsson and H. Cederquist, J. Phys.: Conf. Ser., 2011, 300, 012011 CrossRef.
- R. von Hahn, A. Becker, F. Berg, K. Blaum, C. Breitenfeldt, H. Fadil, F. Fellenberger, M. Froese, S. George, J. Gock, M. Grieser, F. Grussie, E. A. Guerin, O. Heber, P. Herwig, J. Karthein, C. Krantz, H. Kreckel, M. Lange, F. Laux, S. Lohmann, S. Menk, C. Meyer, P. M. Mishra, O. Novotny, A. P. O'Connor, D. A. Orlov, M. L. Rappaport, R. Repnow, S. Saurabh, S. Schippers, C. D. Schroter, D. Schwalm, L. Schweikhard, T. Sieber, A. Shornikov, K. Spruck, S. S. Kumar, J. Ullrich, X. Urbain, S. Vogel, P. Wilhelm, A. Wolf and D. Zajfman, Rev. Sci. Instrum., 2016, 87, 063115 CrossRef CAS PubMed.
- Y. Nakano, Y. Enomoto, T. Masunaga, S. Menk, P. Bertier and T. Azuma, Rev. Sci. Instrum., 2017, 88, 033110 CrossRef CAS PubMed.
- G. Berden, R. Peeters and G. Meijer, Int. Rev. Phys. Chem., 2000, 19, 565–607 Search PubMed , and references therein.
- T. D. Fridgen, Mass Spectrom. Rev., 2009, 28, 586–607 CrossRef CAS PubMed , and references therein.
- N. C. Polfer and J. Oomens, Mass Spectrom. Rev., 2009, 28, 468–494 CrossRef CAS PubMed , and references therein.
- M. Straka, E. Andris, J. Vicha, A. Ruzicka, J. Roithova and L. Rulisek, Angew. Chem., Int. Ed., 2019, 58, 2011–2016 CrossRef CAS PubMed.
- G. T. Pullen, P. R. Franke, Y. P. Lee and G. E. Douberly, J. Mol. Spectrosc., 2018, 354, 7–14 CrossRef CAS.
- M. Kuhn, M. Renzler, J. Postler, S. Ralser, S. Spieler, M. Simpson, H. Linnartz, A. G. G. M. Tielens, J. Cami, A. Mauracher, Y. Wang, M. Alcamí, F. Martín, M. K. Beyer, R. Wester, A. Lindinger and P. Scheier, Nat. Commun., 2016, 7, 13550 CrossRef CAS PubMed.
- S. Spieler, M. Kuhn, J. Postler, M. Simpson, R. Wester, P. Scheier, W. Ubachs, X. Bacalla, J. Bouwman and H. Linnartz, Astrophys. J., 2017, 846, 168 CrossRef.
- A. Kaiser, J. Postler, M. Oncak, M. Kuhn, M. Renzler, S. Spieler, M. Simpson, M. Gatchell, M. K. Beyer, R. Wester, F. A. Gianturco, P. Scheier, F. Calvo and E. Yurtsever, J. Phys. Chem. Lett., 2018, 9, 1237–1242 CrossRef CAS PubMed.
- F. Stienkemeier, J. Higgins, C. Callegari, S. I. Kanorsky, W. E. Ernst and G. Scoles, Z. Phys. D: At., Mol. Clusters, 1996, 38, 253–263 CrossRef CAS.
- J. Higgins, C. Callegari, J. Reho, F. Stienkemeier, W. E. Ernst, M. Gutowski and G. Scoles, J. Phys. Chem. A, 1998, 102, 4952–4965 CrossRef CAS.
- J. H. Reho, J. Higgins, M. Nooijen, K. K. Lehmann, G. Scoles and M. Gutowski, J. Chem. Phys., 2001, 115, 10265–10274 CrossRef CAS.
- G. E. Douberly and R. E. Miller, J. Phys. Chem. A, 2007, 111, 7292–7302 CrossRef CAS PubMed.
- J. Tiggesbäumker and F. Stienkemeier, Phys. Chem. Chem. Phys., 2007, 9, 4748–4770 RSC.
- M. Theisen, F. Lackner and W. E. Ernst, J. Chem. Phys., 2011, 135, 074306 CrossRef PubMed.
- M. Renzler, M. Daxner, L. Kranabetter, A. Kaiser, A. W. Hauser, W. E. Ernst, A. Lindinger, R. Zillich, P. Scheier and A. M. Ellis, J. Chem. Phys., 2016, 145, 181101 CrossRef PubMed.
- E. Cheng, M. W. Cole, W. F. Saam and J. Treiner, Phys. Rev. Lett., 1991, 67, 1007–1010 CrossRef CAS PubMed.
- F. Ancilotto, E. Cheng, M. W. Cole and F. Toigo, Z. Phys. B: Condens. Matter, 1995, 98, 323–329 CrossRef CAS.
- F. Ancilotto, A. M. Sartori and F. Toigo, Phys. Rev. B: Condens. Matter Mater. Phys., 1998, 58, 5085–5092 CrossRef CAS.
- A. Nakayama and K. Yamashita, J. Chem. Phys., 2000, 112, 10966–10975 CrossRef CAS.
- A. Nakayama and K. Yamashita, AIP Conf. Proc., 2001, 559, 265–272 CrossRef CAS.
- C. Stark and V. V. Kresin, Phys. Rev. B: Condens. Matter Mater. Phys., 2010, 81, 085401 CrossRef.
- L. An der Lan, P. Bartl, C. Leidlmair, H. Schöbel, R. Jochum, S. Denifl, T. D. Märk, A. M. Ellis and P. Scheier, J. Chem. Phys., 2011, 135, 044309 CrossRef PubMed.
- L. An der Lan, P. Bartl, C. Leidlmair, H. Schöbel, S. Denifl, T. D. Märk, A. M. Ellis and P. Scheier, Phys. Rev. B: Condens. Matter Mater. Phys., 2012, 85, 115414 CrossRef.
- L. Chen, J. Zhang, W. M. Freund and W. Kong, J. Chem. Phys., 2015, 143, 074201 CrossRef PubMed.
- M. Rastogi, C. Leidlmair, L. An der Lan, J. O. de Zarate, R. P. de Tudela, M. Bartolomei, M. I. Hernandez, J. Campos-Martinez, T. Gonzalez-Lezana, J. Hernandez-Rojas, J. Breton, P. Scheier and M. Gatchell, Phys. Chem. Chem. Phys., 2018, 20, 25569–25576 RSC.
- L. Kranabetter, M. Goulart, A. Aleem, T. Kurzthaler, M. Kuhn, E. Barwa, M. Renzler, L. Grubwieser, M. Schwärzler, A. Kaiser, P. Scheier and O. Echt, J. Phys. Chem. C, 2017, 121, 10887–10892 CrossRef CAS.
- R. Pérez de Tudela, P. Martini, M. Goulart, P. Scheier, F. Pirani, J. Hernandez-Rojas, J. Breton, J. Ortiz de Zárate, M. Bartolomei, T. Gonzalez-Lezana, M. I. Hernandez, J. Campos-Martinez and P. Villarreal, J. Chem. Phys., 2019, 150, 154304 CrossRef PubMed.
- H. Kohguchi, P. Jusko, K. M. T. Yamada, S. Schlemmer and O. Asvany, J. Chem. Phys., 2018, 148, 144303 CrossRef PubMed.
- H. Helm, P. C. Cosby and D. L. Huestis, J. Chem. Phys., 1983, 78, 6451–6454 CrossRef CAS.
- H. Helm and R. Möller, Phys. Rev. A: At., Mol., Opt. Phys., 1983, 27, 2493–2502 CrossRef CAS.
- M. Aymar, S. Azizi and O. Dulieu, J. Phys. B: At., Mol. Opt. Phys., 2003, 36, 4799–4812 CrossRef CAS.
- A. Jraij, A. R. Allouche, M. Korek and M. Aubert-Frecon, Chem. Phys., 2005, 310, 145–151 CrossRef CAS.
- H. Silberbach, P. Schwerdtfeger, H. Stoll and H. Preuss, J. Phys. B: At., Mol. Opt. Phys., 1986, 19, 501–510 CrossRef CAS.
- A. Scheidemann, B. Schilling and J. P. Toennies, J. Phys. Chem., 1993, 97, 2128–2138 CrossRef CAS.
- R. Fröchtenicht, U. Henne, J. P. Toennies, A. Ding, M. Fieber-Erdmann and T. Drewello, J. Chem. Phys., 1996, 104, 2548–2556 CrossRef.
- A. C. LaForge, M. Shcherbinin, F. Stienkemeier, R. Richter, R. Moshammer, T. Pfeifer and M. Mudrich, Nat. Phys., 2019, 15, 247–250 Search PubMed.
- M. Gatchell, P. Martini, F. Laimer, M. Goulart, F. Calvo and P. Scheier, Faraday Discuss., 2019, 217, 276–289 RSC.
- H.-J. Werner, P. J. Knowles, G. Knizia, F. R. Manby, M. Schütz, P. Celani, T. Korona, R. Lindh, A. Mitrushenkov, G. Rauhut, K. R. Shamasundar, T. B. Adler, R. D. Amos, A. Bernhardsson, A. Berning, D. L. Cooper, M. J. O. Deegan, A. J. Dobbyn, F. Eckert, E. Goll, C. Hampel, A. Hesselmann, G. Hetzer, T. Hrenar, G. Jansen, C. Köppl, Y. Liu, A. W. Lloyd, R. A. Mata, A. J. May, S. J. McNicholas, W. Meyer, M. E. Mura, A. Nicklass, D. P. O'Neill, P. Palmieri, D. Peng, K. Pflüger, R. Pitzer, M. Reiher, T. Shiozaki, H. Stoll, A. J. Stone, R. Tarroni, T. Thorsteinsson and M. Wang, MOLPRO, version 2012.1, a package of ab initio programs, 2012.
- H. J. Werner, P. J. Knowles, G. Knizia, F. R. Manby and M. Schutz, Wiley Interdiscip. Rev.: Comput. Mol. Sci., 2012, 2, 242–253 CAS.
- I. S. Lim, P. Schwerdtfeger, B. Metz and H. Stoll, J. Chem. Phys., 2005, 122, 104103 CrossRef PubMed.
- S. Y. Lee, R. C. Brown and E. J. Heller, J. Phys. Chem., 1983, 87, 2045–2053 CrossRef CAS.
- M. K. Prakash, J. D. Weibel and R. A. Marcus, J. Geophys. Res.: Atmos., 2005, 110, D21315 CrossRef.
- M. Oncak, L. Sistik and P. Slavicek, J. Chem. Phys., 2010, 133, 174303 CrossRef PubMed.
- M. J. Frisch, G. W. Trucks, H. B. Schlegel, G. E. Scuseria, M. A. Robb, J. R. Cheeseman, G. Scalmani, V. Barone, G. A. Petersson, H. Nakatsuji, X. Li, M. Caricato, A. V. Marenich, J. Bloino, B. G. Janesko, R. Gomperts, B. Mennucci, H. P. Hratchian, J. V. Ortiz, A. F. Izmaylov, J. L. Sonnenberg, D. Williams-Young, F. Ding, F. Lipparini, F. Egidi, J. Goings, B. Peng, A. Petrone, T. Henderson, D. Ranasinghe, V. G. Zakrzewski, J. Gao, N. Rega, G. Zheng, W. Liang, M. Hada, M. Ehara, K. Toyota, R. Fukuda, J. Hasegawa, M. Ishida, T. Nakajima, Y. Honda, O. Kitao, H. Nakai, T. Vreven, K. Throssell, J. A. Montgomery, Jr., J. E. Peralta, F. Ogliaro, M. J. Bearpark, J. J. Heyd, E. N. Brothers, K. N. Kudin, V. N. Staroverov, T. A. Keith, R. Kobayashi, J. Normand, K. Raghavachari, A. P. Rendell, J. C. Burant, S. S. Iyengar, J. Tomasi, M. Cossi, J. M. Millam, M. Klene, C. Adamo, R. Cammi, J. W. Ochterski, R. L. Martin, K. Morokuma, O. Farkas, J. B. Foresman and D. J. Fox, Gaussian 16, Revision A.03, Gaussian, Inc., Wallingford CT, 2016 Search PubMed.
- M. Ratschek, J. V. Pototschnig, A. W. Hauser and W. E. Ernst, J. Phys. Chem. A, 2014, 118, 6622–6631 CrossRef CAS PubMed.
- T. J. O. P. C. A. Messner, A. Schiffmann, J. V. Pototschnig, M. Lasserus, M. Schnedlitz, F. Lackner and W. E. Ernst, J. Chem. Phys., 2018, 149, 024305 CrossRef PubMed.
Footnote |
| † Electronic supplementary information (ESI) available: Relative stabilities of calculated isomers, method benchmarks, spin–orbit couplings, complete experimental spectra, Cartesian coordinates. See DOI: 10.1039/c9cp04790e |
| This journal is © the Owner Societies 2019 |