Open Access Article
Open Access ArticleCreative Commons Attribution 3.0 Unported Licence
How to calculate charge mobility in molecular materials from surface hopping non-adiabatic molecular dynamics – beyond the hopping/band paradigm
Antoine
Carof
 *a,
Samuele
Giannini
*a,
Samuele
Giannini
 a and
Jochen
Blumberger
a and
Jochen
Blumberger
 *ab
*ab
aDepartment of Physics and Astronomy, University College London, London WC1E 6BT, UK. E-mail: j.blumberger@ucl.ac.uk; antoine.carof@gmail.com; Fax: +44-(0)20-7679-7148; Tel: +44-(0)20-7679-4373
bInstitute for Advanced Study, Technische Universität München, Lichtenbergstrasse 2 a, D-85748 Garching, Germany
First published on 20th November 2019
Abstract
Charge transport in high mobility organic semiconductors is in an intermediate regime between small polaron hopping and band transport limits. We have recently shown that surface hopping non-adiabatic molecular dynamics is a powerful method for prediction of charge transport mechanisms in organic materials and for near-quantitative prediction of charge mobilities at room temperature where the effects of nuclear zero-point motion and tunneling are still relatively small [S. Giannini et al., Nat. Commun., 2019, 10, 3843]. Here we assess and critically discuss the extensions to Tully's original method that have led to this success: (i) correction for missing electronic decoherence, (ii) detection of trivial crossings and (iii) removal of decoherence correction-induced spurious charge transfer. If any one of these corrections is not included, the charge mobility diverges with system size, each for different physical reasons. Yet if they are included, convergence with system size, detailed balance and good internal consistency are achieved.
1 Introduction
Organic semiconductors are promising materials for a large range of electronic applications.1–4 Their flexibility and tunability are advantageous for organic photovoltaics or diodes, but their charge carrier mobility is still moderate compared to inorganic semiconductors.5 The experimental and computational quest for OSs with larger mobility is hampered by insufficient knowledge of the charge transport (CT) mechanism in such materials. The parameters determining the CT usually range in a regime where the standard transport theories (band theory and the hopping model) fail.6 Without an existing model at hand, a direct propagation of electron-nuclear dynamics is required. While improved theoretical models have recently been proposed, e.g., transient localization theory,7–9 explicit propagation of coupled electron-nuclear dynamics is arguably the most promising method to reveal the true nature of charge carriers in organic semiconductor materials. The explicit propagation is founded on rigorous quantum mechanical principles, is free of many of the assumptions that limit the predictitive power of theoretical models, and thus encompasses a wide range of possible transport mechanisms.Among the numerous existing methods to propagate nuclei and electrons in a non-adiabatic framework at a molecular scale (e.g., ab initio multiple spawning,10,11 exact factorization,12–14 Ehrenfest dynamics15), Tully's fewest switches surface hopping (FSSH) has become one of the most popular methods.16,17 The FSSH algorithm relies on the usual molecular dynamics (MD) framework and additionally integrates electronic dynamics explicitly solving the time-dependent Schrödinger equation. By allowing instantaneous vertical transitions (hops) between potential energy surfaces, FSSH also includes the feedback between nuclei and electrons. The classical treatment of the nuclei and the ad hoc – but based on physical arguments – probability for hops between electronically excited states permits a fast, yet accurate, propagation of the dynamics in many situations. The properties required for FSSH (excited state energies, forces and non-adiabatic coupling vectors) can be calculated on-the-fly using time-dependent density functional theory11,18,19 or semi-empirical Hamiltonians.20–25 The latter approach renders FSSH attractive for study of condensed matter problems and large systems.26,27 Moreover, FSSH has a number of desirable attributes: it conserves total energy and it was shown to obey detailed balance to a good approximation.25,28–33 However, this method also has a number of well-known shortcomings and a plethora of variants appeared in the literature since the original work of Tully to address them.34–38
Among these various intrinsic issues, some shortcomings hinder particularly the simulation of charge transport: (i) the decay of the electronic coherences between adiabatic states (decoherence) is missing in the original formulation,39 (ii) undetected trivial crossings may lead to unphysical long-range charge transfers, (iii) the common decoherence correction schemes induce spurious long-range charge transfers and (iv) nuclear quantum effects that are particularly important at low temperatures, such as zero-point energy and tunneling, are missing. In this paper we investigate in detail how issues (i)–(iii) affect the FSSH simulation of charge transport in organic materials and we analyse the performance of various correction schemes to mitigate these shortcomings. For inclusion of nuclear quantum effects in the surface hopping simulation of electron transfer, we refer to a recent publication.40 The aim is to identify the best “set-up” or “flavour” of FSSH simulations for reliable calculation of charge mobilities in molecular materials.
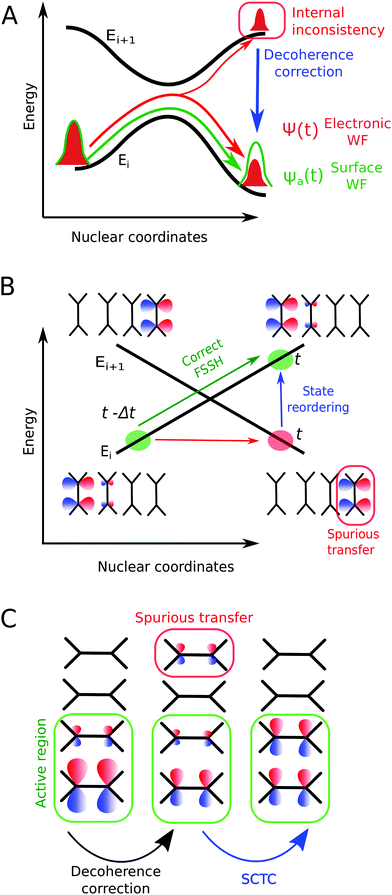
Fig. 1 illustrates issues (i)–(iii). The lack of an inherent decoherence mechanism within FSSH (see Fig. 1(A)) is a well-known issue, often raised in the literature when studying excited states and relaxation processes.41 Without a correction to enforce a decoherence, the electronic dynamics is strongly biased and that impacts the charge transfer rate.42 Numerous correction schemes have been developed,21,43–51 yet several open questions remain, especially in relation to charge transport simulations. What is the impact of the different decoherence schemes on the equilibrium distribution of states? How important is the decoherence to calculate the electronic mobility using FSSH simulations? On the other hand, the correct detection of trivial crossings has been often an overlooked problem, though it limits substantially the accuracy of charge transport simulations via FSSH. When a trivial crossing occurs, it must be taken care of with an update of state indices, otherwise unphysical charge transfer will occur (see Fig. 1(B)). But such events are often undetected by the original FSSH algorithm, due to the finite MD timestep of the simulation. Different approaches have been developed to detect trivial crossings and to update the state indices accordingly.52–57 Finally, Fig. 1(C) shows another source of spurious transfer recently pointed out by our group26 and Wang and coworkers.58 This transfer is induced by the common decoherence correction schemes, and, if not removed, will render any mobility calculation erroneous.
The goal of this paper is to establish the best practice for FSSH simulation of charge transport in real materials by determining the best set-up in terms of decoherence correction, elimination of spurious long-range charge transfers, detection of trivial crossings and appropriate definition of mean-square-displacement for mobility calculation. We present here a thorough study of the role of the decoherence correction schemes in both equilibrium and transport properties. We assess the necessity of a state-tracking algorithm to detect and to take care of the trivial crossings and of a correction to remove the spurious charge transfers induced by the decoherence correction schemes. We also discuss the definitions of electronic populations (somewhat ambiguous in FSSH due to the simultaneous propagation of quantum and surface states59) and we compare different definitions for the mean-square displacement calculation. To test these various corrections and set-ups and explore the role of decoherence and state-tracking algorithms in large molecular systems, we needed an efficient method to propagate surface hopping trajectories. We relied on our recently developed fragment-orbital based surface hopping (FOB-SH),25,60 a semi-empirical approach that is designed to determine efficiently and yet accurately the electronic Hamiltonian and nuclear derivatives (forces, non-adiabatic coupling vectors) in large organic crystals. We conclude that a combination of a decoherence scheme, a trivial crossing detection and a correction of spurious long-range transfer permits converging the electronic mobility with system size and MD timestep.
This paper is organized as follows. In Section 2, we provide a short summary of the FOB-SH method followed by a discussion of the different existing decoherence schemes, a detailed description of the trivial crossing issue and the state-tracking algorithm used in this work. We also outline the spurious charge transfer correction developed by us. We present the alternative electronic propagation proposed by Hammes-Schiffer to deal with the presence of forbidden transitions (elimination of classically forbidden hops, EFH) and we discuss the different electronic populations commonly used in the literature and the various MSD definitions. We then provide in Section 3 the details of the molecular systems (force field and parameters) we have used to study equilibrium and dynamical properties. Our results are discussed in Section 4: we first investigate the impact of decoherence on equilibrium properties for chains of ethylene-like molecules of different lengths and test the EFH propagation to improve the internal consistency. We then focus on the effect of the state-tracking algorithm and the decoherence correction scheme on electronic mobility and the inverse participation ratio (IPR, a measure of the size of the charge carrier) in an embedded chain of real anthracene molecules. We conclude our work in Section 5.
2 Theory
2.1 Fragment-orbital based surface hopping
To simulate the transport of excess charge carriers in molecular systems, we have recently developed an efficient fragment orbital based surface hopping (FOB-SH) framework. In this section, we will summarize the main elements of FOB-SH and its strengths. In Fig. 2 we report a simplified flowchart of the FOB-SH algorithm to help in discussing its fundamental features. For a more detailed consideration of FOB-SH, we refer to our previous publications.24–26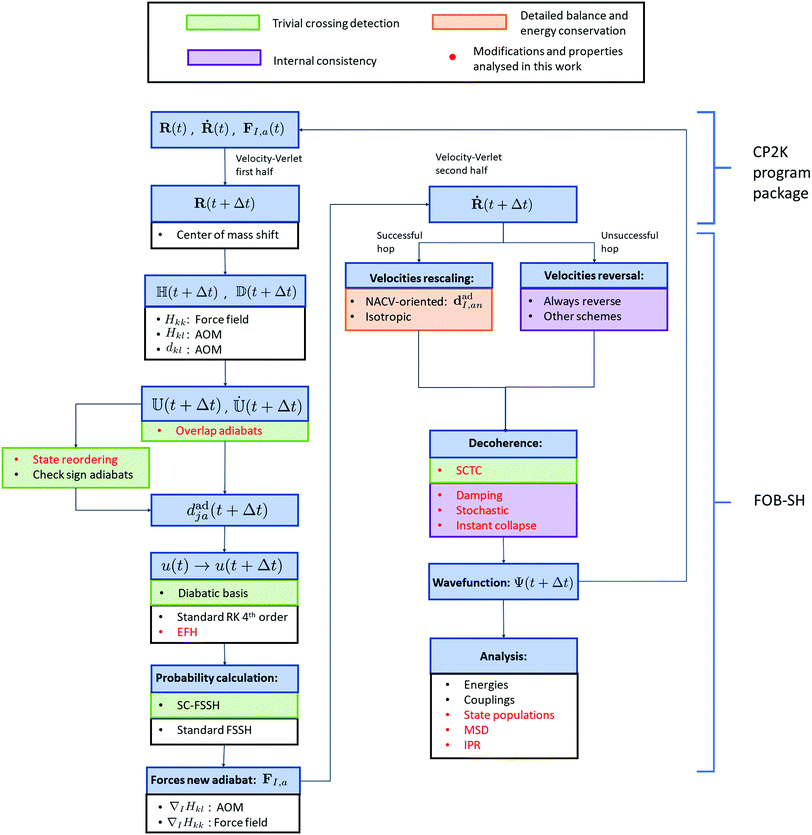 | ||
| Fig. 2 Scheme of the FOB-SH (fragment orbital-based surface hopping) algorithm. Different colors represent improvements of the algorithm necessary to fulfil: trivial crossing detection, detailed balance and energy conservation and internal consistency. In red are reported modifications and properties that have been analysed in the present work. Symbols are defined according to equations in the text. RK: Runge–Kutta algorithm, EFH: elimination of forbidden hops, AOM: analytic overlap method, SC-FSSH: self-consistent fewest switches surface hopping, FSSH: fewest switches surface hopping, NACV: non-adiabatic coupling vector, SCTC: spurious charge transfer correction, MSD: mean squared displacement (eqn (30)), IPR: inverse participation ratio (eqn (35)). | ||
The FOB-SH method is based on the following assumptions. (i) The full many-body electronic wavefunction is replaced by a one-particle wavefunction Ψ(t) for the excess charge carrier. (ii) The excess charge wavefunction Ψ(t) can be expanded in a localized, non-orthogonal basis set made up of fragment orbitals that mediate its transport in the system (usually these orbitals are SOMOs of the isolated molecules {φm}). Ψ(t) takes the form:
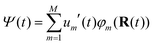 | (1) |
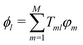 | (2) |
![[Doublestruck S]](https://www.rsc.org/images/entities/char_e176.gif) −1/2]ml, with
−1/2]ml, with ![[Doublestruck S]](https://www.rsc.org/images/entities/char_e176.gif) the overlap matrix of the fragment orbital basis set (
the overlap matrix of the fragment orbital basis set (![[S with combining macron]](https://www.rsc.org/images/entities/i_char_0053_0304.gif) ml = 〈φm|φn〉). The excess charge wavefunction is now:
ml = 〈φm|φn〉). The excess charge wavefunction is now: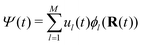 | (3) |
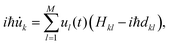 | (4) |
![[small phi, Greek, dot above]](https://www.rsc.org/images/entities/i_char_e0a3.gif) l〉 the non-adiabatic coupling elements (NACEs) of the localized orthogonal basis set. As those NACEs are generally close to zero, we label the orthogonal localized basis as a diabatic basis.
l〉 the non-adiabatic coupling elements (NACEs) of the localized orthogonal basis set. As those NACEs are generally close to zero, we label the orthogonal localized basis as a diabatic basis.
To carry out simulations on large systems and long time scales, we designed a parametrized approach to determine the electronic Hamiltonian Hkl, thus avoiding explicit expensive electronic structure calculations. The diagonal elements Hkk = 〈ϕk|H|ϕk〉, which corresponds to the energy of a charge localized on molecule k, are calculated via a classical force field where molecule k is charged and all the other M − 1 molecules are neutral. The off-diagonal elements Hkl = 〈ϕk|H|ϕl〉, which correspond to the electronic coupling matrix elements or transfer integral, are calculated using our recently developed analytic overlap method (AOM).61 This method relies on the assumption of a linear relationship between off-diagonal elements Hkl and ![[S with combining macron]](https://www.rsc.org/images/entities/i_char_0053_0304.gif) kl (i.e., the overlap between the fragment orbitals (φk,φl) projected into Slater-type functions), namely Hkl = C
kl (i.e., the overlap between the fragment orbitals (φk,φl) projected into Slater-type functions), namely Hkl = C![[S with combining macron]](https://www.rsc.org/images/entities/i_char_0053_0304.gif) kl. C is a fitting parameter and can be obtained by correlating the overlap
kl. C is a fitting parameter and can be obtained by correlating the overlap ![[S with combining macron]](https://www.rsc.org/images/entities/i_char_0053_0304.gif) kl with high quality DFT calculations.61 This method allows the calculation of Hkl for a cost several orders of magnitude lower than that of explicit electronic structure calculations. It was found that errors are less than a factor of 2 with respect to reference coupling values, obtained with approximate coupled cluster (SCS-CC2)/Generalized Mulliken Hush calculations,62 which spanned 5 orders of magnitude. We refer to our previous paper61 for a more detailed description of the AOM. It is worth noting the analogy between the calculation of the FOB-SH electronic Hamiltonian and the empirical valence bond approach of Warshel and co-workers,63 where the electronic Hamiltonian is also built from the classical force field for the diagonal elements and different parametrizations for the off-diagonal elements. As indicated in Fig. 2 this Hamiltonian is a key feature of the FOB-SH method that allows fast computation.
kl with high quality DFT calculations.61 This method allows the calculation of Hkl for a cost several orders of magnitude lower than that of explicit electronic structure calculations. It was found that errors are less than a factor of 2 with respect to reference coupling values, obtained with approximate coupled cluster (SCS-CC2)/Generalized Mulliken Hush calculations,62 which spanned 5 orders of magnitude. We refer to our previous paper61 for a more detailed description of the AOM. It is worth noting the analogy between the calculation of the FOB-SH electronic Hamiltonian and the empirical valence bond approach of Warshel and co-workers,63 where the electronic Hamiltonian is also built from the classical force field for the diagonal elements and different parametrizations for the off-diagonal elements. As indicated in Fig. 2 this Hamiltonian is a key feature of the FOB-SH method that allows fast computation.
Besides the electronic Hamiltonian matrix elements, the time-dependent Schrödinger equation (eqn (3)) requires the determination of the NACEs dkl which can be related to the non-orthogonal NACEs 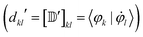 ,
,
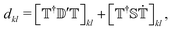 | (5) |
Both ![[Doublestruck D]](https://www.rsc.org/images/entities/char_e167.gif) kl′ and
kl′ and  are obtained from the finite difference between t and t + Δt. We have taken special care that the nuclear positions Rt and Rt+Δt are translated within the center-of-mass frame at each timestep. Otherwise, in the case of non-zero center-of-mass nuclear velocities, the overlap element 〈φk(Rt)|φl(Rt+Δt)〉 would have arbitrary values.
are obtained from the finite difference between t and t + Δt. We have taken special care that the nuclear positions Rt and Rt+Δt are translated within the center-of-mass frame at each timestep. Otherwise, in the case of non-zero center-of-mass nuclear velocities, the overlap element 〈φk(Rt)|φl(Rt+Δt)〉 would have arbitrary values.
We now turn to the propagation of the nuclei according to the velocity-Verlet as shown in Fig. 2 and to the force calculation. In the FSSH algorithm, the nuclei evolve on one adiabatic energy surface Ea (where Ea = [![[Doublestruck H]](https://www.rsc.org/images/entities/char_e16b.gif) ad]aa, with
ad]aa, with ![[Doublestruck H]](https://www.rsc.org/images/entities/char_e16b.gif) ad =
ad = ![[Doublestruck U]](https://www.rsc.org/images/entities/char_e178.gif) †
†![[Doublestruck H]](https://www.rsc.org/images/entities/char_e16b.gif)
![[Doublestruck U]](https://www.rsc.org/images/entities/char_e178.gif) and
and ![[Doublestruck U]](https://www.rsc.org/images/entities/char_e178.gif) the unitary transformation matrix that diagonalizes
the unitary transformation matrix that diagonalizes ![[Doublestruck H]](https://www.rsc.org/images/entities/char_e16b.gif) to
to ![[Doublestruck H]](https://www.rsc.org/images/entities/char_e16b.gif) ad). It is worth noticing that before starting the electronic integration, the phase of the eigenvectors forming
ad). It is worth noticing that before starting the electronic integration, the phase of the eigenvectors forming ![[Doublestruck U]](https://www.rsc.org/images/entities/char_e178.gif) must be checked and made consistent along the trajectory for an accurate calculation of
must be checked and made consistent along the trajectory for an accurate calculation of 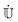 at a later stage of the algorithm (eqn 8). Since
at a later stage of the algorithm (eqn 8). Since ![[Doublestruck H]](https://www.rsc.org/images/entities/char_e16b.gif) and
and ![[Doublestruck U]](https://www.rsc.org/images/entities/char_e178.gif) are real, this amounts to a check of the sign of the eigenvectors (“check sign” in Fig. 2).64 From
are real, this amounts to a check of the sign of the eigenvectors (“check sign” in Fig. 2).64 From ![[Doublestruck U]](https://www.rsc.org/images/entities/char_e178.gif) , we can define the adiabatic wavefunctions ψi,
, we can define the adiabatic wavefunctions ψi, 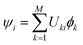 , that form the adiabatic basis. The nuclear force acting on nucleus I is FI,a = −∇IEa and can be obtained from the Hellmann–Feynman theorem:
, that form the adiabatic basis. The nuclear force acting on nucleus I is FI,a = −∇IEa and can be obtained from the Hellmann–Feynman theorem:
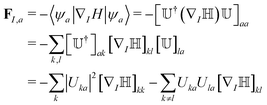 | (6) |
![[Doublestruck H]](https://www.rsc.org/images/entities/char_e16b.gif) ]kl = ∇I〈ϕk|H|ϕl〉. We refer to our previous paper25 for the derivation of eqn (6). The gradients of the electronic Hamiltonian matrix diagonal elements are obtained directly from the classical force field, whereas a finite difference approach is used for the matrix off-diagonal elements based on the AOM.60 We note that the finite difference for the off-diagonal gradients requires an order of NatomM calculations of Hkl elements that would make explicit electronic structure calculations unaffordable. The nuclear forces on a given adiabatic state a obtained in eqn (6) consist of a linear combination of the diagonal and off-diagonal forces on the diabats, with a weighting that is proportional to the projection of the adiabats on the diabats – the weighting takes into account the effect of charge delocalization on the adiabatic forces.
]kl = ∇I〈ϕk|H|ϕl〉. We refer to our previous paper25 for the derivation of eqn (6). The gradients of the electronic Hamiltonian matrix diagonal elements are obtained directly from the classical force field, whereas a finite difference approach is used for the matrix off-diagonal elements based on the AOM.60 We note that the finite difference for the off-diagonal gradients requires an order of NatomM calculations of Hkl elements that would make explicit electronic structure calculations unaffordable. The nuclear forces on a given adiabatic state a obtained in eqn (6) consist of a linear combination of the diagonal and off-diagonal forces on the diabats, with a weighting that is proportional to the projection of the adiabats on the diabats – the weighting takes into account the effect of charge delocalization on the adiabatic forces.
Finally, the core of the FSSH method is the choice of active surface Ea on which the nuclei evolve and the feedback of the electronic dynamics onto the nuclear motion. In Tully's approach,39 the active surface is decided in two steps: (i) a new state is chosen via a stochastic process and (ii) the energy conservation requirement is applied to determine whether the change in active state is energetically possible. The stochastic process (i) is based on the hopping probabilities calculated at each timestep t between the active surface and all the other states j:
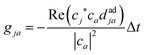 | (7) |
![[small psi, Greek, dot above]](https://www.rsc.org/images/entities/i_char_e0a5.gif) a〉 are the adiabatic NACEs, which are calculated from the diabatic NACEs (dkl ≡ [
a〉 are the adiabatic NACEs, which are calculated from the diabatic NACEs (dkl ≡ [![[Doublestruck D]](https://www.rsc.org/images/entities/char_e167.gif) ]kl),
]kl),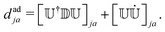 | (8) |
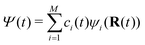 . The probability to remain in state a is simply
. The probability to remain in state a is simply 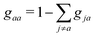 . After the calculation of the probability gja, a random number is drawn to decide whether a hop can be attempted to a new state n. If so, the following condition should hold to ensure energy conservation,
. After the calculation of the probability gja, a random number is drawn to decide whether a hop can be attempted to a new state n. If so, the following condition should hold to ensure energy conservation,| Etot(R) = Ta(R) + Ea(R) = Tn(R) + En(R) | (9) |
However, the rejection of hops causes an inconsistency in FSSH populations. Tully's hopping probability (eqn (7)) was designed to ensure for a model two-state system that – on average – the wavefunction Ψ(t) is similar to the adiabatic active state. On the other hand, the energy conservation criterion leads to rejecting some classical nuclear hops along the dynamics. Without any correction, the electronic wavefunction will over-populate excited states that are high in energy and therefore unreachable for the classical nuclei. This yields the so-called FSSH internal inconsistency, i.e., a divergence between Ψ(t) and ψa(t) (as illustrated in Fig. 1(A)).
Due to this internal inconsistency, two different adiabatic populations coexist in the FSSH algorithm, the quantum amplitude averaged over the trajectory, 〈|ci(t)|2〉trj and the surface population,
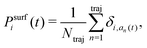 | (10) |
2.2 Decoherence corrections
The lack of an inherent decoherence mechanism is a long-standing issue of FSSH, already mentioned in Tully's original paper39 and often advocated in the literature when studying excited state dynamics and relaxation processes.41 After leaving an avoided crossing where the adiabatic states mix, the full electronic-nuclear wavefunction splits into two sub-wavepackets χi(R) and χj(R), which evolve on different adiabatic surfaces Ei and Ej. Immediately after the crossing, the center and/or the phase of each wavepacket may diverge in phase space, decreasing the wavefunction coherence between surfaces i and j,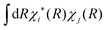 . This effect is not taken into account in standard FSSH, where the coherence term (i.e., ci*cj) remains finite. The lack of decoherence ruins the dynamics of the system, leading to the failures of FSSH for some important processes. Rossky and co-workers41 found that, in the absence of decoherence, decay rates from excited states to the ground state are too fast, yielding incorrect excited state dynamics. Landry and Subotnik42,68 have later shown that the decay in the charge transfer rate between two molecules obtained with FSSH does not follow the behaviour predicted by Marcus theory.
. This effect is not taken into account in standard FSSH, where the coherence term (i.e., ci*cj) remains finite. The lack of decoherence ruins the dynamics of the system, leading to the failures of FSSH for some important processes. Rossky and co-workers41 found that, in the absence of decoherence, decay rates from excited states to the ground state are too fast, yielding incorrect excited state dynamics. Landry and Subotnik42,68 have later shown that the decay in the charge transfer rate between two molecules obtained with FSSH does not follow the behaviour predicted by Marcus theory.
Since the pioneering work of Rossky and collaborators,43 numerous correction schemes have been suggested in the literature to tackle the decoherence problem. The most common can be divided into three main categories. (i) Collapsing approaches, in which the electronic wavefunction is reset to the active state Ψ(t) = ψa(t) when a given criterion is fulfilled. Criteria suggested in the literature rely on collapsing events after each attempted or successful hop, after each successful hop50 or when the adiabatic NACEs fall below a threshold.44 (ii) Exponential damping approaches, in which all non-active adiabatic populations ci are damped at each time step ci → ci![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) exp(−Δt/τia), while the active state population is scaled to ensure norm conservation. τia is the decoherence time.45,47 (iii) Stochastic damping approaches that rely on random numbers to determine whether the wavefunction is collapsed.42,51,69 In the last category, each component of the wave-vector containing the expansion coefficients ci with i ≠ a (where a is the active state index) is reset to zero whenever the collapsing probability is larger than a given random number (η ∈ [0,1]) drawn at each time step. The relative population is transferred to the active state in order to conserve the norm. Within this method, the probability of a collapsing event can be expressed as γcollapsei = Δt/τia in which Δt is the MD timestep. A longer decoherence time τia results in a lower probability to collapse γcollapsei.
exp(−Δt/τia), while the active state population is scaled to ensure norm conservation. τia is the decoherence time.45,47 (iii) Stochastic damping approaches that rely on random numbers to determine whether the wavefunction is collapsed.42,51,69 In the last category, each component of the wave-vector containing the expansion coefficients ci with i ≠ a (where a is the active state index) is reset to zero whenever the collapsing probability is larger than a given random number (η ∈ [0,1]) drawn at each time step. The relative population is transferred to the active state in order to conserve the norm. Within this method, the probability of a collapsing event can be expressed as γcollapsei = Δt/τia in which Δt is the MD timestep. A longer decoherence time τia results in a lower probability to collapse γcollapsei.
As far as we know, no exact expression was derived in the literature to calculate the decoherence time τia in the context of mixed-quantum classical approaches. However, different formulations were either proposed based on physically grounded justifications45,46 or derived using approximations for the evolution of nuclear wavepackets.41,43,48 More recently, using controlled approximations, a decoherence time has been derived from quantum classical Liouville equation (QCLE) formalisms.36 Those expressions rely on the absence of decoherence when the potential energy surfaces are close to each other or when nuclei are fixed. The energy based-decoherence time (EDC) proposed by Persico and Granucci (starting from an original expression suggested by Truhlar and co-workers45,46) has the aforementioned characteristics and is widely used in the literature:
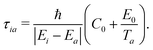 | (11) |
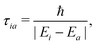 | (12) |
Other expressions for the decoherence time, derived for condensed phase systems and frozen Gaussians travelling on different potential energy surfaces, involve nuclear forces rather than the energy. For instance, Rossky and co-workers41,43 derived:
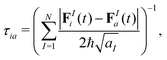 | (13) |
Finally, Subotnik and co-workers developed an extension of FSSH, the augmented-FSSH (A-FSSH), directly from QCLEs to incorporate the decoherence mechanism more rigorously. New dynamical variables are propagated along the nuclear and electronic degrees of freedom to calculate an instantaneous decoherence time.42,49 Yet propagation with this method is more expensive than FSSH and might not be suitable to study large systems with several hundred molecules.
2.3 Trivial crossings and state tracking
The presence of trivial (or unavoided) crossing becomes a substantial limitation in performing charge transport simulations with FSSH. A trivial crossing event occurs when two energy surfaces cross with zero couplings between them, leading to an actual reordering of the state indices (as shown in Fig. 1(B)). Physically, such crossings occur when the adiabats are not interacting, i.e., when the adiabatic wavefunctions are localized in distant regions in space. If the state reordering is not taken care of, the dynamics is continued on the wrong surface, leading to spurious charge transfer that biases any mobility calculation (see Fig. 1(B)). The problem is greatly amplified in systems with many adiabatic states in a narrow energy band (e.g., in OSs), where adiabatic energy surfaces can frequently cross each other.In practice, the FSSH algorithm is implemented with a finite timestep, meaning that the trivial crossing and index update may be missed. Moreover, the distinction between a trivial crossing and an avoided crossing with a very small energy gap is unclear with a finite timestep. This inherent issue of the FSSH algorithm was often overlooked, as it only arises for systems with many adiabatic states and more strikingly for charge transport. Recently, different solutions emerged in the literature to tackle the missed trivial crossings. Most of them resort to a state tracking algorithm. At each MD timestep, a map is drawn between the indexes of the adiabatic states at time t − Δt and at time t. To build that map, Thiel and co-workers relied on energy criteria and the maximum of overlap between adiabats at time t − Δt and time t,52 whereas Tretiak and co-workers used the more sophisticated min-cost algorithm.53,54
Another innovative approach, suggested by Wang and Beljonne, is their flexible surface hopping method (FSH), where the size of the “active” region of the OS that transports the charge evolves at each MD timestep.55 Such an approach not only permits maintaining the relatively small number of adiabatic states (provided that the charge carrier remains localized in space) and diminishing the number of trivial crossings, but also requires new criteria and rules to decide at each MD timestep which part of the OS should be included in the active region. Recently, Wang and co-workers proposed to use the overlap between adiabats at time t − Δt and at time t to classify the surface crossings in different types to determine how to calculate the hopping probability and whether the adiabats’ indexes must be updated.56 They also combined this classification approach with a restriction to hop only to adiabats with a large enough adiabatic population,57 which strays, however, from the spirit of Tully's original FSSH.
An alternative route would be to improve the calculation of the hopping probability to capture such trivial crossings. A norm-preserving interpolation of the adiabats between time t − Δt and time t can provide a better estimation of the NACV dadij.70 Subotnik and co-workers generalized the norm-preserving interpolation to multiple states crossing using the logarithm of the overlap matrix (eqn (16)).51 They extended this approach very recently to ensure phase consistency and trivial crossing correction.71 Wang and Prezhdo proposed a few years ago an alternative straightforward improvement of the probability to hop.72 They invoked the exact sum rule,
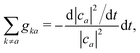 | (14) |
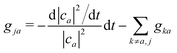 | (15) |
In this work, we opt for a combination of the mapping approach and the self-consistent correction (eqn (15)) for surface hopping. We build the map ![[scr M, script letter M]](https://www.rsc.org/images/entities/char_e145.gif) between the adiabatic states j at time t and adiabatic states i at time t − Δt with a maximum overlap criterion. First, we calculate the overlap Oij,
between the adiabatic states j at time t and adiabatic states i at time t − Δt with a maximum overlap criterion. First, we calculate the overlap Oij,
| Oij = 〈ψi(t − Δt)|ψj(t)〉. | (16) |
![[scr M, script letter M]](https://www.rsc.org/images/entities/char_e145.gif) is a bijection between states at t and states at t − Δt, the reverse map
is a bijection between states at t and states at t − Δt, the reverse map ![[scr M, script letter M]](https://www.rsc.org/images/entities/char_e145.gif) −1 (which associates states at t − Δt with states at t) is easily found. We can track the index of the active state at t, knowing its value at t − Δt, at =
−1 (which associates states at t − Δt with states at t) is easily found. We can track the index of the active state at t, knowing its value at t − Δt, at = ![[scr M, script letter M]](https://www.rsc.org/images/entities/char_e145.gif) −1(at−Δt). This step permits changing the index of the active state without hopping. We stress that our algorithm maps all the states at t with the states at t − Δt, not only the active state, as required by the calculation of the NACEs (eqn (17)). We also note that our mapping criterion produces a unique map and that the algorithm can be run over the states in any order. After the mapping, we make the phase of the eigenvectors consistent along the trajectory by checking the sign of the overlap matrix element Oi,
−1(at−Δt). This step permits changing the index of the active state without hopping. We stress that our algorithm maps all the states at t with the states at t − Δt, not only the active state, as required by the calculation of the NACEs (eqn (17)). We also note that our mapping criterion produces a unique map and that the algorithm can be run over the states in any order. After the mapping, we make the phase of the eigenvectors consistent along the trajectory by checking the sign of the overlap matrix element Oi,![[scr M, script letter M]](https://www.rsc.org/images/entities/char_e145.gif) (i) and by reversing the sign of ψi if Oi,
(i) and by reversing the sign of ψi if Oi,![[scr M, script letter M]](https://www.rsc.org/images/entities/char_e145.gif) (i) < 0 (as we discussed in Section 2.1 and underlined in Fig. 2 with the comment “check sign”). We finally determine the correct hopping probability (eqn (7)), which requires the adiabatic NACEs (eqn (8)) and in particular the second term
(i) < 0 (as we discussed in Section 2.1 and underlined in Fig. 2 with the comment “check sign”). We finally determine the correct hopping probability (eqn (7)), which requires the adiabatic NACEs (eqn (8)) and in particular the second term 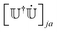 . As suggested by Hammes-Schiffer and Tully,67 we take advantage of the anti-symmetry of this term. After mapping, this term now is,
. As suggested by Hammes-Schiffer and Tully,67 we take advantage of the anti-symmetry of this term. After mapping, this term now is,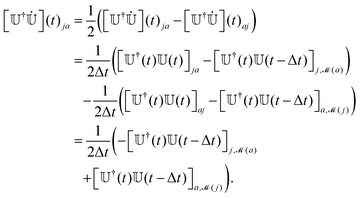 | (17) |
2.4 Spurious charge transfer
Although the decoherence correction is paramount to maintain the internal consistency of the FSSH algorithm as discussed in Section 2.2, it may create an undesirable charge displacement in the cases of large systems and high densities of states. In those systems, a surface hop between adiabatic states localized in different regions of space is unlikely but still possible in the FSSH algorithm (due to the stochasticity of the hopping algorithm). After an unlikely hop, the decoherence correction scheme (damping-based or collapsing-based) will move the electronic wavefunction Ψ(t) closer to the new active state ψa(t), thus leading to unphysical charge transfer, as illustrated in Fig. 1(C). This problem was recently pointed out by our group26 and Wang and coworkers.58 We labelled such events decoherence correction-induced spurious charge transfers (DCICTs). They arise because the different decoherence correction schemes act on the adiabatic (i.e., non-local) representation. Note that, since the mean-squared displacement (MSD) depends on the square of the distance, this will have a strong impact on the diffusion coefficient and on the mobility (see Section 2.7).Recently, Wang and collaborators proposed to switch off the decoherence correction when the surface population is below a certain threshold and showed that the spurious transfer is indeed alleviated.58 However, this formulation can reduce the internal consistency of surface hopping as some decoherence events are actually removed. Independently from the latter study, we have developed a three-step strategy to remove the DCICTs as illustrated in Fig. 1(C): (i) at each timestep, an “active” region that encloses 99.9% of the electronic density |Ψ(t)|2 is determined, (ii) the decoherence correction is applied and (iii) any change in the diabatic population Δ|ul|2 outside the active region is reset to zero, while the diabatic populations inside the active region are scaled accordingly to preserve the norm. We call this strategy spurious charge transfer correction (SCTC, previously termed SPTC in our previous paper26). In practice, it amounts to a local decoherence correction within the active region, while outside the active region the diabatic populations remain unchanged. All DCICTs are removed, while decoherence correction is still applied at each timestep. Note that the propagation of the wave function according to eqn (4) remains unaffected by the presence of the active region.
2.5 Elimination of forbidden hops
As discussed in Section 2.1, a key issue in FSSH simulation is the internal inconsistency between the surface population and the wavefunction population. One of the main reasons for this discrepancy is the lack of an intrinsic decoherence mechanism, as detailed in Section 2.2. Another source of internal inconsistency is attributed to forbidden hops, namely attempted hops triggered by the stochastic FSSH algorithm (probability to hop in eqn (7)) but that do not fulfil the conservation energy requirement (eqn (9)).73 Although frustrated hops are actually essential to maintain detailed balance as pointed out by Tully,29,74 they can be a source of internal inconsistency. When such forbidden hops are encountered, NACEs between the active state and those classically forbidden states are finite and the TDSE (eqn (4)) will transfer a small amount of the electronic wavefunction Ψ(t) to those states. In some cases an ad hoc decoherence scheme cannot completely correct the problem especially when the electronic coupling is high (i.e., when a large number of forbidden transitions are present because the surfaces are distant from each other). This problem has been partially overlooked in the literature as most applications of surface hopping are related to fast relaxation processes from excited states to low-energy states.44,48,50 In this case, almost all transitions are downward (thus allowed) and a simple decoherence scheme is sufficient to reach a satisfactory internal consistency.At the early stage of FSSH development, Hammes-Schiffer and co-workers already suggested a route to ensure internal consistency even in the presence of a great number of forbidden transitions.44,73 They proposed to remove the undesired population transfers, by setting the corresponding NACEs/NACVs to classically forbidden states to zero in the TDSE. In this work, we call their approach elimination of forbidden hop (EFH). In this approach the FSSH algorithm is modified in the following way: (i) at each timestep, one first determines which transitions are energetically forbidden between the active state and the excited states using the energy conservation criterion in eqn (9), (ii) for such forbidden transitions, the corresponding adiabatic NACEs/NACVs are exactly set to zero and (iii) one propagates the modified electronic TDSE (analogue to eqn (4)) that, in the adiabatic basis, now reads,
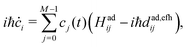 | (18) |
![[Doublestruck D]](https://www.rsc.org/images/entities/char_e167.gif) ad,efh. This matrix is now sparse as certain transitions are forbidden. In our implementation, the electronic propagation (eqn (4)) is carried out in the diabatic basis, which gives better numerical stability.25,75 For this reason, eqn (18) can be transformed in the diabatic basis:
ad,efh. This matrix is now sparse as certain transitions are forbidden. In our implementation, the electronic propagation (eqn (4)) is carried out in the diabatic basis, which gives better numerical stability.25,75 For this reason, eqn (18) can be transformed in the diabatic basis: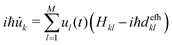 | (19) |
![[Doublestruck D]](https://www.rsc.org/images/entities/char_e167.gif) efh]kl and
efh]kl and ![[Doublestruck D]](https://www.rsc.org/images/entities/char_e167.gif) efh is the NACE matrix in the diabatic basis. The latter can be written in terms of the adiabatic NACE matrix
efh is the NACE matrix in the diabatic basis. The latter can be written in terms of the adiabatic NACE matrix ![[Doublestruck D]](https://www.rsc.org/images/entities/char_e167.gif) ad,efh as (see eqn (8)),
ad,efh as (see eqn (8)),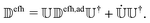 | (20) |
 and the adiabatic NACE between two subsequent nuclear time steps. As discussed in Section 2.3, especially near crossing points, NACEs have sharp localized peaks resembling Dirac delta functions that can be easily missed. However, as we show in the following,
and the adiabatic NACE between two subsequent nuclear time steps. As discussed in Section 2.3, especially near crossing points, NACEs have sharp localized peaks resembling Dirac delta functions that can be easily missed. However, as we show in the following, 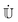 can be eliminated from eqn (20). In its final form
can be eliminated from eqn (20). In its final form ![[Doublestruck D]](https://www.rsc.org/images/entities/char_e167.gif) efh only contains the smooth NACEs between the active state and the energetically forbidden states that are high in energy. To this end, we write
efh only contains the smooth NACEs between the active state and the energetically forbidden states that are high in energy. To this end, we write ![[Doublestruck D]](https://www.rsc.org/images/entities/char_e167.gif) efh in the following way:
efh in the following way:![[Doublestruck D]](https://www.rsc.org/images/entities/char_e167.gif) efh = efh = ![[Doublestruck D]](https://www.rsc.org/images/entities/char_e167.gif) + ( + (![[Doublestruck D]](https://www.rsc.org/images/entities/char_e167.gif) efh − efh − ![[Doublestruck D]](https://www.rsc.org/images/entities/char_e167.gif) ), ), | (21) |
![[Doublestruck D]](https://www.rsc.org/images/entities/char_e167.gif) is the matrix of diabatic NACEs with elements
is the matrix of diabatic NACEs with elements 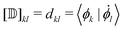 that appear in the unmodified Schrödinger, eqn (4). Substituting eqn (20) in eqn (21) and defining
that appear in the unmodified Schrödinger, eqn (4). Substituting eqn (20) in eqn (21) and defining 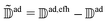 ,
, 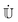 is eliminated from eqn (20),
is eliminated from eqn (20), | (22) |
We will discuss in Section 4.1 the effects of this alternative electronic propagation on the internal consistency and the equilibrium properties.
2.6 Electronic populations
Our objective is to calculate the electronic mobility from FOB-SH simulations. Electronic-based properties are, however, ambiguous in FSSH, as different definitions can be found for the electronic population. Landry and Subotnik provided a detailed account of the existing definitions in ref. 59 and they highlighted that these populations can produce divergent properties. In the most common approach (“Method 1” in ref. 59 or the “surface method”) electronic properties are calculated using the active adiabatic state ψa(t). To avoid confusion, we prefer to call this population a projected active state population (PAS). The electronic population on site k is| PPASk = |〈ϕk(t)|ψa(t)〉|2 = |Uka|2(t). | (23) |
| Pwfk = |〈ϕk(t)|Ψ(t)〉|2 = |uk|2(t). | (24) |
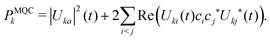 | (25) |
As mentioned before, the projected active state method has the advantage of giving the correct detailed balance distribution (the electronic state distribution follows an approximately Boltzmann population in FSSH). However, this method is also more sensitive to trivial crossings, as any trivial crossing missed will instantaneously modify ψa(t). In contrast, Ψ(t) (in “Method 2”) would not be directly impacted by a missed trivial crossing, although in the long term there will be a bias in the dynamics.
2.7 Mean-square displacement
In the literature, the charge mobility μ is often obtained from the diffusion coefficient D by means of the Einstein equation: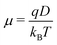 | (26) |
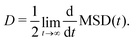 | (27) |
![[x with combining macron]](https://www.rsc.org/images/entities/i_char_0078_0304.gif) (t) = 〈Ψ(t)|x|Ψ(t)〉, and then to use it within the classical definition to obtain:
(t) = 〈Ψ(t)|x|Ψ(t)〉, and then to use it within the classical definition to obtain: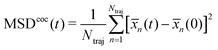 | (28) |
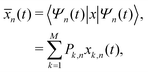 | (29) |
![[x with combining macron]](https://www.rsc.org/images/entities/i_char_0078_0304.gif) (0))2 (with
(0))2 (with ![[x with combining macron]](https://www.rsc.org/images/entities/i_char_0078_0304.gif) (0) = 〈Ψ(0)|x|Ψ(0)〉) and to average the expectation value of such an operator in the following manner:
(0) = 〈Ψ(0)|x|Ψ(0)〉) and to average the expectation value of such an operator in the following manner: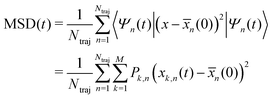 | (30) |
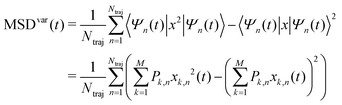 | (31) |
The three definitions are of course related, MSD = MSDcoc + MSDvar. The MSD (eqn (30)) is preferable because it accounts for both the motion of the center of charge and the spreading of the wavefunction. Therefore it can be used for both extremes, small polaron hopping and pure wavefunction spreading, and all intermediate cases. We will analyse the two different contributions MSDcoc and MSDvar in Section 4.2.
3 Numerical details
3.1 Chains of ethylene-like molecules
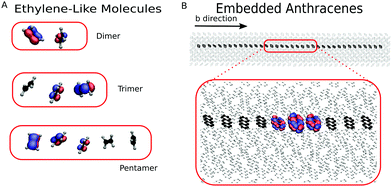
To investigate the detailed balance of FOB-SH, we used one-dimensional chains of two (dimer), three (trimer) and five (pentamer) ethylene-like molecules (ELMs), as shown in Fig. 3(A). The name “ethylene-like” stresses that only the nuclear geometries correspond to a real ethylene molecule, while the CT parameters (namely the reorganization energy λ and the AOM scaling value C) are chosen freely to explore a large range of physical behaviours. Within a chain, the ELMs are spaced by 4 Å and a weak center of mass restraint potential (force constant = 11 kcal mol−1 Å−2) is applied to keep the chain straight. Because the NVE ensemble is used in all our FOB-SH simulations to avoid any dynamical bias introduced by the thermostat, the chain is embedded in a bath of neon atoms that mimics the role of a thermostat and reduces the fluctuations of the temperature (especially for the short chains with few degrees of freedom). The simulation boxes are cubic with size a = 60 Å and contain one chain of ELMs and 123 neon atoms (124 for the dimer). Periodic boundary conditions are applied in all directions of the simulation box. We insist, however, that the electronic propagation occurring within the chain of ELMs is not periodic: when the charge reaches the edges of the chain, it is scattered backward and it does not continue at the other end of the chain.In the present model, hole transfer is mediated by a set of (orthogonalized) HOMOs of the ethylene molecules, ϕk, k = 1, M, that are used to construct the electronic Hamiltonian ![[Doublestruck H]](https://www.rsc.org/images/entities/char_e16b.gif) . Diagonalization of the Hamiltonian
. Diagonalization of the Hamiltonian ![[Doublestruck H]](https://www.rsc.org/images/entities/char_e16b.gif) gives the M adiabatic electronic states. For a detailed explanation of how the orbitals ϕi(R(t)) are reconstructed along the trajectory we refer to ref. 60. The diagonal elements Hkk are calculated with a force field energy function whose parameters for neutral and positively charged ELMs are chosen as in our previous work.25,60 For charged ELMs, the equilibrium distance of the C
gives the M adiabatic electronic states. For a detailed explanation of how the orbitals ϕi(R(t)) are reconstructed along the trajectory we refer to ref. 60. The diagonal elements Hkk are calculated with a force field energy function whose parameters for neutral and positively charged ELMs are chosen as in our previous work.25,60 For charged ELMs, the equilibrium distance of the C![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) C bond is displaced (1.387 Å) with respect to the one in the neutral state (1.324 Å) corresponding to the reorganization energy for hole transfer between two ELMs of λ = 200 meV. Such reorganization energies are typical for organic semiconductors and an order of magnitude smaller than those, e.g., for redox processes in aqueous solution79–81 or oxide materials.82 Intra-molecular interactions for neutral ELMs are taken from the Generalized Amber Force Field (GAFF).83 The intermolecular interactions among the ELMs and between ELMs and Ne atoms are modelled by Lennard-Jones terms with parameters taken again from the GAFF database for neutral and charged ELMs and from ref. 84 for Ne and applying the Lorentz–Berthelot mixing rules. Electrostatic interactions in the form of fixed point charges do not significantly alter the energetics of this system because only one ELM carries a net charge and the other ELMs and Ne are charge neutral. Hence, for convenience, electrostatic interactions were switched off in all simulations.
C bond is displaced (1.387 Å) with respect to the one in the neutral state (1.324 Å) corresponding to the reorganization energy for hole transfer between two ELMs of λ = 200 meV. Such reorganization energies are typical for organic semiconductors and an order of magnitude smaller than those, e.g., for redox processes in aqueous solution79–81 or oxide materials.82 Intra-molecular interactions for neutral ELMs are taken from the Generalized Amber Force Field (GAFF).83 The intermolecular interactions among the ELMs and between ELMs and Ne atoms are modelled by Lennard-Jones terms with parameters taken again from the GAFF database for neutral and charged ELMs and from ref. 84 for Ne and applying the Lorentz–Berthelot mixing rules. Electrostatic interactions in the form of fixed point charges do not significantly alter the energetics of this system because only one ELM carries a net charge and the other ELMs and Ne are charge neutral. Hence, for convenience, electrostatic interactions were switched off in all simulations.
The initial configurations are built with the investigated chain in its energy-minimized geometry and the neon atoms positioned on a regular grid. The system is equilibrated with a 1 ns NVT run at 298 K using a Nosé–Hoover thermostat85,86 and using a force field energy function where the first molecule of the chain is charged. From the last configuration of the NVT run, 100 ps Born–Oppenheimer molecular dynamics (BOMD) trajectories are started for each adiabatic electronic state (two, three and five states for the dimer, trimer and pentamer, respectively). This is done for each of the six AOM scaling values C that determine the strength of electronic coupling according to Hkl = C![[S with combining macron]](https://www.rsc.org/images/entities/i_char_0053_0304.gif) kl. For the dimer and trimer, we choose C = 14, 82, 272, 381, 816 and 1360 meV that correspond to average coupling values
kl. For the dimer and trimer, we choose C = 14, 82, 272, 381, 816 and 1360 meV that correspond to average coupling values 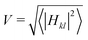 of about 2, 10, 34, 51, 130 and 220 meV. For the pentamer, we choose C = 14, 82, 272, 381, 544 and 816 meV that correspond to V = 2, 10, 34, 49, 72, and 111 meV. We remove the first 20 ps where the system equilibrates and use the last 180 ps of the BO trajectories in the different states to calculate free energy differences for consecutive adiabatic electronic states, depending on the size of the system: ΔAi,i−1(C) = −kBT
of about 2, 10, 34, 51, 130 and 220 meV. For the pentamer, we choose C = 14, 82, 272, 381, 544 and 816 meV that correspond to V = 2, 10, 34, 49, 72, and 111 meV. We remove the first 20 ps where the system equilibrates and use the last 180 ps of the BO trajectories in the different states to calculate free energy differences for consecutive adiabatic electronic states, depending on the size of the system: ΔAi,i−1(C) = −kBT![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) ln〈exp[−(Ei − Ei−1)/kBT]〉Ei−1, where i represents the given state, for each scaling value C. The corresponding “exact” excited state populations are determined according to the Boltzmann population of each state i:
ln〈exp[−(Ei − Ei−1)/kBT]〉Ei−1, where i represents the given state, for each scaling value C. The corresponding “exact” excited state populations are determined according to the Boltzmann population of each state i:
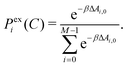 | (32) |
For each set of parameters (chain length, C value, decoherence correction), we generated 1000 independent FOB-SH trajectories starting from the initial configuration evenly sampled from the corresponding BOMD trajectories. Each trajectory is run for 10 ps in the NVE ensemble. The nuclear dynamics is propagated with the velocity-Verlet algorithm with forces calculated according to eqn (6) and with a MD timestep Δt = 0.1 fs. The wavefunction of the excess charge carrier Ψ(t) was propagated by integrating eqn (4) using the Runge–Kutta algorithm of 4th order and an electronic timestep δt = Δt/5 = 0.02 fs. An interpolation scheme is used to calculate the Hamiltonian matrix elements at each electronic timestep.60 Error bars were determined by block averaging over the 1000 trajectories with a block size of 200 independent runs.
3.2 Chains of embedded anthracenes
To investigate the mobility and IPR of a real system, we have modelled an electron hole transfer in a chain of electronically active anthracene molecules, embedded in a larger crystal comprised of electronically inactive anthracene molecules, see Fig. 3(B). We have compared 4 chains of different lengths: 12, 24, 36 and 48 molecules. The simulation boxes are monoclinic, with angles α = 90.0°, β = 124.7° and γ = 90.0° and with dimensions a = 8.562 Å and c = 11.184 Å. We have adapted the box length in the b direction to ensure that the distance between the chain and the edges of the box is above 8 Å. Periodic boundary conditions are applied in all directions of the crystal, but, similarly to the chains of ELMs, the electronic dynamics occurs along non-periodic chains. To check the convergence of mobility with respect to the length of the chain, different numbers of molecules of chains are investigated. Table 1 presents the total number of molecules and the length b for the different chain lengths.| Number of active molecules | Total number of anthracene molecules | b (Å) |
|---|---|---|
| 12 | 256 | 97.3 |
| 24 | 448 | 170.2 |
| 36 | 640 | 243.2 |
| 48 | 832 | 316.2 |
As for the ELM model system described in the previous section, we assume that the electron hole transfer is mediated by the HOMOs of the anthracene molecules that form the basis functions for the excess charge expansion (eqn (1)). The M diagonal elements Hkk are, again, estimated using M classical force field energy functions. In the kth energy functions, anthracene molecule k is positively charged, while all the others are neutral. Intra-molecular interactions for the neutral anthracene molecule are taken from the Generalized Amber Force Field (GAFF).83 These intramolecular parameters are used also for the charged anthracene, except for the carbon–carbon bond length which was chosen instead to reproduce the reorganization energy λ. The reorganization energy is determined using four DFT calculations on neutral and charge anthracene molecules in both neutral and charged geometries as:
| λ = [EC(RN) + EN(RC)] − [EC(RC) + EN(RN)] | (33) |
The off-diagonal elements of the electronic Hamiltonian Hkl are calculated using the AOM.61 First, the HOMO of anthracene (which is non-degenerate) is projected onto an atomic Slater basis consisting of one atomic p orbital per carbon atom. The calculation of the HOMO and its projection are done using CPMD software88 using the PBE exchange–correlation functional.89 Core electrons are described by Goedecker–Teter–Hutter (GTH) pseudo-potentials,90 and the valence electrons are expanded in plane waves with a reciprocal space plane wave cutoff of 90 Ry. The dimers are centered in a simulation box with dimensions of 12 × 40 × 40 Å3. After that, the electronic coupling HDFTkl is calculated using the FODFT method62 for four different dimers extracted from the crystal structure, while the HOMO–HOMO overlap ![[S with combining macron]](https://www.rsc.org/images/entities/i_char_0053_0304.gif) kl = 〈φk|φl〉 is calculated using the AOM for the same four dimers. The FODFT couplings are scaled by a constant 1.348 as recommended in ref. 62. A linear regression is applied between HDFTkl and
kl = 〈φk|φl〉 is calculated using the AOM for the same four dimers. The FODFT couplings are scaled by a constant 1.348 as recommended in ref. 62. A linear regression is applied between HDFTkl and ![[S with combining macron]](https://www.rsc.org/images/entities/i_char_0053_0304.gif) kl to determine the AOM scaling value C = 3.09 eV.
kl to determine the AOM scaling value C = 3.09 eV.
Each FOB-SH simulation involves 1000 independent trajectories initialized from 100 different initial conditions (10 trajectories repeated with a different random seed for each initial condition). Starting from the crystal structure, the system is equilibrated for 500 ps in the NVT ensemble using a Nosé–Hoover thermostat.85,86 Then a MD run of length 500 ps is carried out in the NVE ensemble from which 100 configurations are chosen at equidistant intervals. These configurations are used as the initial configurations for subsequent FOB-SH runs. The initial wavefunction is fully localized on the first molecule of the chain, Ψ(t = 0) = ϕ1(0), and the initial active state is randomly drawn from all adiabatic states with a probability 〈ψi(0)|ϕ1(0)〉2. Each trajectory is then run for 2 ps in the NVE ensemble. We opt for the NVE ensemble to avoid any artificial thermostat that may bias the calculation of the electronic mobility. The large number of degrees of freedom due to the “inactive” part (inactive for electronic propagation, as depicted in Fig. 3) of the anthracene crystal plays the role of a thermostat and ensures small temperature fluctuations. The nuclear dynamics is propagated using the velocity-Verlet algorithm and different MD timesteps are tested to check for convergence (Δt = 0.025, 0.05, 0.1 and 0.5 ps). The electronic wavefunction is propagated using the Runge–Kutta algorithm of 4th order and electronic timestep δt = Δt/5.
4 Results
4.1 Energy conservation, detailed balance and internal consistency
Before investigating charge transport properties, we focus here on the influence of various decoherence correction schemes and the treatment of classically forbidden hops on key equilibrium properties such as energy conservation, detailed balance and internal consistency. In this section, we exclude analysis of trivial crossings or DCICTs, as these issues arise only when considering large systems and transport properties.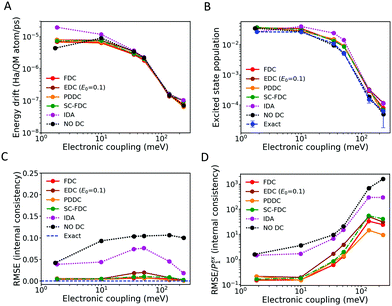 | ||
| Fig. 4 Properties of a FOB-SH simulation for an ethylene-like molecule (ELM) dimer cation with a total of two electronic states at T = 300 K. The conserved energy drift (A), excited state population (B) and internal consistency (C and D) are shown as functions of the diabatic electronic coupling strength between the two ELMs. Different electronic decoherence corrections (DCs) are compared: damping of adiabatic electronic populations with force-based (FDC, eqn (13)), stochastic force-based (SC-FDC), energy-based (EDC, eqn (11)), and pure dephasing decoherence times (PDDC, eqn (12)), instant collapse (IDA) and no DC. Exact populations in (B) are obtained as described in Section 3.1. The internal consistency in (C) is measured in terms of the root-mean-square error (RMSE, eqn (34)), and divided by the excited state population Pex1 in (D). | ||
A similar conclusion holds for the detailed balance. In Fig. 4(B), we show the electronic population of the excited state, averaged over the 1000 trajectories and over time, against the time average electronic coupling. The exact result obtained from the BOMD simulations as described in Section 3.1 is also indicated. Since the work of Tully and collaborators,29,74 the ability of the “vanilla” FSSH (i.e., without decoherence correction) to reach detailed balance is well-known. We recently reinforced the point that the NACV-oriented adjustment of velocities after a hop is paramount for this agreement to hold.25 Remarkably, we find here that the bias introduced by the decoherence correction in the electronic dynamics is almost negligible in terms of equilibrium distribution. This can be readily explained in the cases of EDC, PDDC and FDC, for which the decoherence time is small (i.e., fast decoherence) far from the crossing region and it is large (i.e., slow decoherence) within the crossing region. For this reason, such corrections have only a minor effect in the proximity of an avoided crossing, which is where the probability for hops sharply increases and the thermal equilibration between the electronic states occurs. Thus, decoherence only affects the dynamics away from the crossing region, where, in any case, the surfaces are quite well separated in energy and the number of hops is small. Therefore, damping-based schemes maintain the correct flux between states and do not ruin the detailed balance.
It is important to notice that such an argument does not apply to instantaneous decoherence algorithms. These algorithms require the nuclei to be in the crossing region in order to trigger the decoherence event (i.e. there must be either an attempted or a successful hop in order to collapse the wavefunction) and they do not depend on any decoherence time. This explains why for the latter algorithms we can observe larger deviations for both energy drift and excited state population, even though the bias is still small due to the small number of collapsing events with respect to the total number of steps in the dynamics.
We conclude that all the decoherence schemes investigated here can reach approximately the detailed balance, meaning that the bias introduced in the electronic dynamics does not affect the flux between adiabatic states.
While the different decoherence algorithms give virtually identical results for energy drift and detailed balance, they give very different results for internal consistency. We measure the latter by calculating the time-averaged root mean square error between the surface population and the quantum amplitude of the excited state i, Psurfi(t) (eqn (10)) and 〈|ci(t)|2〉trj, respectively,
 | (34) |
However, Fig. 4(D) reveals that the internal consistency, normalized with respect to the excited state population Pexi, deteriorates with increasing coupling strength. The quantum populations of excited states are generally overestimated in this regime. In our previous paper,25 we showed that for couplings V > kBT/2, adiabatic NACEs still transfer the electronic population from the ground state to the excited state, while attempted hops become increasingly energy-forbidden. Therefore, the wavefunction population in the excited state is overestimated compared to the surface population. While for no DC and collapse the error is substantial to the extent that there is no longer any consistency between quantum and surface amplitudes in the high coupling regime, the damping methods significantly improve on this situation, albeit not perfectly. For a large coupling value of 100 meV, the excited state surface population is about 10−4 (Fig. 4(B)), while the quantum populations are about 10−3, giving RMSE1/Pex1 ≈ 10. While this deviation may not be relevant in many practical situations, it is desirable to investigate further possible improvements to internal consistency such as elimination of energy forbidden hops.
 | ||
| Fig. 5 Excited state population (A) and internal consistency (B) from FOB-SH simulations for an ELM-dimer cation with a total of two electronic states, at T = 300 K. Decoherence correction (DC) and decoherence correction with the elimination of forbidden hops (DC + EFH) are compared to simulations without decoherence correction (no DC). The DC method used is damping with force-based decoherence time (FDC, eqn (13)). Internal consistency is measured by the relative root-mean-square error defined in eqn (34). The exact result for the excited state population is obtained as described in Section 3.1. Error bars are obtained by block-averaging over five independent blocks of 200 trajectories each. | ||
 | ||
| Fig. 6 Excited state population and internal consistency of FOB-SH simulations for an ELM trimer-cation (A and B) and an ELM pentamer-cation (C and D), as functions of the diabatic electronic coupling strength between the monomers, at T = 300 K. Simulations are carried out with DC (damping with force-based decoherence time, eqn (13)) and with DC + elimination of forbidden hops (DC + EFH). Exact populations are calculated as described in Section 3.1. The first, second, third and fourth excited states are shown as solid, dashed–dotted, dashed and dotted lines, respectively. Error bars represent standard deviations over five independent blocks of 200 trajectories each. | ||
In conclusion, EFH greatly improves the internal consistency; nevertheless, it biases the hopping probability and produces a worse agreement with the exact equilibrium population when compared with the standard FSSH propagation. It is worth noting that in large organic semiconductors the density of states in a given band is quite high, most of the hops are allowed and the most important source of internal inconsistency is the wavefunction branching rather than the presence of frustrated hops. For these reasons we will not consider further this correction to investigate dynamical properties and charge transport.
4.2 Charge mobility
We now focus on building and describing the best FOB-SH set-up to calculate the mobility and delocalization of a charge carrier in organic semiconductors. We make use of the system described in Section 3.2, a hole diffusing in a chain of anthracene molecules embedded in a larger crystal. Several parameters and set-ups need to be assessed: the role of the state tracking algorithm and/or the spurious transfer correction, the size of the system, the MD timestep, the decoherence correction scheme, the population definition, the MSD definition and finally the length and the number of trajectories. | ||
| Fig. 7 (A) Mean-square-displacement (MSD) and (B) inverse participation ratio (IPR, eqn (35)) for hole transport in anthracene, from FOB-SH simulations. In (A) the MSD (eqn (30)) is broken down into the MSD for the centre of charge, MSDcoc (eqn (28)), and the MSD due to the changes in the spread or variance of the wavefunction, MSDvar (eqn (31)). FOB-SH simulations were carried out for an embedded chain of 48 anthracene molecules, applying a MD timestep of 0.1 fs. Error bars are obtained by block-averaging over five independent blocks of 200 trajectories each. | ||
As described in Section 2.7, the mobility is related via the diffusion coefficient (eqn (26)) to the slope of the MSD at long times (eqn (27)). In Fig. 7(A), the best linear fits are indicated by black dashed lines for all three MSD definitions. We conclude that to determine the mobility, both MSDcoc and MSD will give the same value for the diffusion constant, whereas MSDvar will give a zero value for this coefficient and so for the mobility.
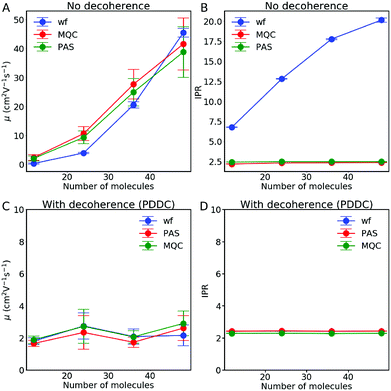
Besides the mobility, it is also interesting to measure the delocalization of the wavefunction. Rather than using the wavefunction spreading, MSDvar, we prefer to follow ref. 55 and to calculate the inverse participation ratio (IPR):
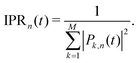 | (35) |
 | ||
| Fig. 8 Importance of state reordering and spurious charge transfer correction in FOB-SH simulations of hole transport along embedded chains of anthracene molecules. (A–C) MSDs (eqn (30)) for hole transport with chain lengths as indicated (12, 24, 36 and 48 molecules). (D–F) Time evolution of the hole carrier wavefunction population (Pwfk, eqn (24)) along a representative FOB-SH trajectory. The MSDs and the wavefunction populations are compared for three different set-ups: (A and D) adiabatic electronic states are reordered using the state tracking algorithm (see Section 2.3) and the decoherence-induced spurious charge transfer correction is active (SCTC, see Section 2.4); (B and E) state reordering is active, and SCTC is switched off; and (C and F) state ordering and SCTC are switched off. Note that the MSD is independent of system size only in (A). For all set-ups, decoherence keeps the charge localized over about 2 molecules (consistently with Fig. 7(B)). Long-range spurious transfer events are highlighted with red arrows in (E) and (F); note that the charge transport in (C) is completely biased by unphysical jumps of the charge. The MD timestep is 0.1 fs and the decoherence correction is damping with pure dephasing decoherence time. Error bars represent standard deviations over five independent blocks of 200 trajectories each. | ||
 | ||
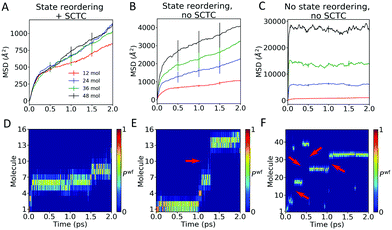
| Fig. 9 (A and C) Hole mobility μ and (B and D) time-averaged inverse participation ratio (IPR) with respect to (A and B) the number of FOB-SH trajectories and (C and D) the MD timestep. FOB-SH simulations were carried out for an embedded chain of 48 anthracene molecules, with pure dephasing decoherence correction (PDDC, eqn (12)). In (C and D), error bars are obtained by block-averaging over five independent blocks of 200 trajectories each. | ||
 | ||
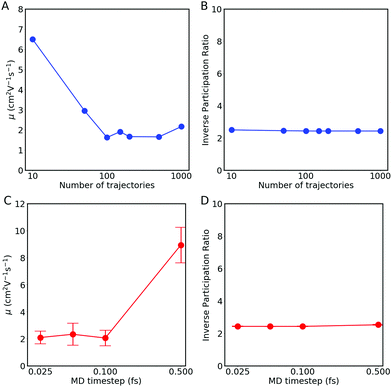
| Fig. 10 Importance of decoherence correction for the convergence of charge mobility with respect to system size. No decoherence correction is applied in (A) and (B) and the pure dephasing decoherence correction (PDDC, eqn (12)) scheme is applied in (C) and (D). Results are shown for different choices for the diabatic populations used to calculate the charge mobility μ and the inverse participation ratio (IPR): wavefunction (Pwf, eqn (24)), active state (PPAS, eqn (23)) and mixed quantum-classical populations (PMQC, eqn (25)). The data were obtained from FOB-SH simulations of hole transport along an embedded chain of anthracene molecules with a MD timestep of 0.1 fs. Error bars are obtained by block-averaging over five independent blocks of 200 trajectories each. | ||
The mobility and IPR obtained with a decoherence correction (pure-dephasing correction) are shown in Fig. 10(C) and (D) respectively. In contrast to the results obtained without decoherence, the mobility is well converged with respect to chain length. Adding a decoherence correction permits localizing (in adiabatic and diabatic space) the electronic wavefunction Ψ(t), to eliminate the undesired hops present without decoherence and to converge with system size. The decoherence correction also ensures the internal consistency of the method, explaining why the three population definitions behave similarly. The IPR results are similar to the ones for the mobility: convergence for the different system sizes and similar values for all three population definitions. Although, in general, we recommend using the wavefunction population (Pwf, eqn (24)) as it is generally less affected by potentially undetected trivial crossings. Based on these results, we conclude that a decoherence correction is mandatory for the calculation of mobility and the IPR.
5 Conclusion
In the present work, we have employed the fragment-orbital based surface hopping (FOB-SH) approach that is a powerful tool to perform atomistic non-adiabatic dynamics in large realistic molecular systems. We have explored and discussed several possible improvements applicable to any surface hopping code when calculating equilibrium and dynamical properties, i.e., decoherence correction with various decoherence times, spurious charge transfer correction (SCTC), electronic propagation with the elimination of classically forbidden transitions (EFH), trivial crossing correction and state tracking. The correct way to retrieve important observables from FSSH simulations such as electronic populations, mean-square displacement and electronic mobility has also been discussed.Using an organic semiconductor model formed by chains of ethylene-like molecules, we have first looked at equilibrium properties (i.e., energy conservation, detailed balance and internal consistency) over three orders of magnitude of electronic coupling and different system sizes. We have shown that good energy conservation and detailed balance is obtained regardless of the decoherence time and algorithm used. In fact, generally speaking, the decoherence biases the dynamics only away from the crossing region and it does not significantly modify the flux between adiabatic states. On the other hand, when comparing the effects of different decoherence corrections in restoring the consistency between surface and wavefunction populations, we have shown that the damping-based algorithms with fast decoherence times produce far better results than instantaneous collapsing events and maximize internal consistency across several orders of coupling strengths. However, for small systems, some degrees of internal inconsistency can still be seen when electronic coupling is large due to the presence of a significant number of forbidden transitions and the inability of the ad hoc damping procedure to correct for such cases. Therefore, to further reduce the internal inconsistency in this coupling region, we have explored an alternative electronic propagation (called the elimination of classically forbidden hops – EFH) in which electronic population transfer between adiabatic states is removed in the case of classically forbidden transitions for the nuclei. Although the algorithm massively improves internal consistency at high couplings, the agreement with the detailed balance deteriorates due to the bias introduced in the electronic dynamics.
Then, focussing on charge transport in a real organic crystal (i.e., anthracene), we have studied two fundamental properties related to the actual efficiency of organic semiconductors: the electronic mobility and the inverse participation ratio (the latter measures the size of the charge carrier). We have found that charge carriers propagate through OSs as polarons via diffusive jumps, somewhat in analogy with the diffusion of gas molecules in a complex environment,95,96 though with the sizes and shapes of the polarons strongly fluctuating in time. We have also found that a state-tracking algorithm is mandatory in the case of a large number of states to detect the trivial crossings and to map the adiabatic states between two different MD timesteps, thus improving the electronic and nuclear dynamics and avoiding spurious long-range charge transfers. Without a state-tracking procedure, the mean-square displacement does not reach a diffusive linear regime, prohibiting mobility calculation. In addition, to ensure the convergence of the electronic mobility with the size of the system and the number of excited states, we have shown that a combination of the decoherence correction scheme and decoherence-induced spurious charge transfer correction is required.
Besides those paramount improvements to the surface hopping algorithm, we have also compared different definitions used in the literature for the mean-square displacement and for the electronic population definition. We have shown that the two commonly used definitions for the mean-square displacement (MSD and MSDcoc) give the same diffusion coefficient and the same mobility, whereas the third one (MSDvar), which is related to the spreading of the wavefunction, rather than to the diffusion of the charge carrier, yields always a zero slope as the polaron reaches a finite equilibrium size and does not grow indefinitely. Regarding the choice of electronic population to use in FSSH, we have compared the three definitions suggested in the literature (Pwf, PPAS and PMQC) and we have shown that these definitions coincide when a decoherence scheme is active.
In conclusion, we have established a well-founded set-up to run fewest switches surface hopping simulation of charge transport that converges electronic mobilities for different timesteps and different system sizes and that achieves detailed balance and good internal consistency.
Conflicts of interest
There are no conflicts to declare.Acknowledgements
A. C. and S. G. were supported by the European Research Council (ERC) under the European Union, Horizon 2020 Research and Innovation Programme (grant agreement no. 682539/SOFTCHARGE). Via our membership of the UK's HEC Materials Chemistry Consortium, which is funded by EPSRC (EP/L000202 and EP/R029431), this work used the ARCHER UK National Supercomputing Service (http://www.archer.ac.uk). In addition, the authors want to thank Hui Yang for the force field parametrization, Matthew Ellis for the development of a wavefunction visualization code and Guido von Rudorff for code improvements.Notes and references
- M. J. Malachowski and J. Zmija, Opto-Electron. Rev., 2010, 18, 121–136 CAS.
- B. Kippelen and J.-L. Brédas, Energy Environ. Sci., 2009, 2, 251 RSC.
- W. Tress, K. Leo and M. Riede, Phys. Rev. B: Condens. Matter Mater. Phys., 2012, 85, 1–11 CrossRef.
- M. Slawinski, M. Weingarten, M. Heuken, A. Vescan and H. Kalisch, Org. Electron., 2013, 14, 2387–2391 CrossRef CAS.
- C. Wang, H. Dong, L. Jiang and W. Hu, Chem. Soc. Rev., 2018, 47, 422–500 RSC.
- A. Troisi, Chem. Soc. Rev., 2011, 40, 2347 RSC.
- S. Fratini, D. Mayou and S. Ciuchi, Adv. Funct. Mater., 2016, 26, 2292–2315 CrossRef CAS.
- S. Fratini, S. Ciuchi, D. Mayou, G. T. de Laissardière and A. Troisi, Nat. Mater., 2017, 16, 998–1002 CrossRef CAS PubMed.
- T. Nematiaram, S. Ciuchi, X. Xie, S. Fratini and A. Troisi, J. Phys. Chem. C, 2019, 123, 6989–6997 CrossRef CAS.
- T. J. Martínez, M. Ben-Nun and R. D. Levine, J. Phys. Chem., 1996, 100, 7884–7895 CrossRef.
- T. J. Martínez, Acc. Chem. Res., 2006, 39, 119–126 CrossRef PubMed.
- A. Abedi, N. T. Maitra and E. K. U. Gross, Phys. Rev. Lett., 2010, 105, 123002 CrossRef.
- A. Abedi, N. T. Maitra and E. K. U. Gross, J. Chem. Phys., 2012, 137, 22A530 CrossRef.
- F. Agostini, A. Abedi and E. K. U. Gross, J. Chem. Phys., 2014, 141, 214101 CrossRef.
- P. Ehrenfest, Z. Phys. A, 1927, 45, 455–457 Search PubMed.
- R. Crespo-Otero and M. Barbatti, Chem. Rev., 2018, 118, 7026–7068 CrossRef CAS.
- M. Persico and G. Granucci, Theor. Chem. Acc., 2014, 133, 1–28 Search PubMed.
- B. F. E. Curchod, I. Tavernelli and U. Rothlisberger, Phys. Chem. Chem. Phys., 2011, 13, 3231 RSC.
- H. Tamura and I. Burghardt, J. Am. Chem. Soc., 2013, 135, 16364–16367 CrossRef CAS PubMed.
- F. Sterpone and P. J. Rossky, J. Phys. Chem. B, 2008, 112, 4983–4993 CrossRef CAS PubMed.
- M. J. Bedard-Hearn, F. Sterpone and P. J. Rossky, J. Phys. Chem. A, 2010, 114, 7661–7670 CrossRef CAS PubMed.
- T. Nelson, S. Fernandez-Alberti, V. Chernyak, A. E. Roitberg and S. Tretiak, J. Phys. Chem. B, 2011, 115, 5402–5414 CrossRef CAS PubMed.
- T. Nelson, S. Fernandez-Alberti, A. E. Roitberg and S. Tretiak, Acc. Chem. Res., 2014, 47, 1155–1164 CrossRef CAS PubMed.
- J. S. Spencer and A. J. W. Thom, J. Chem. Phys., 2016, 144, 084108 CrossRef.
- A. Carof, S. Giannini and J. Blumberger, J. Phys. Chem., 2017, 147, 214113 CrossRef.
- S. Giannini, A. Carof and J. Blumberger, J. Phys. Chem. Lett., 2018, 9, 3116–3123 CrossRef CAS.
- S. Pal, D. J. Trivedi, A. V. Akimov, B. Aradi, T. Frauenheim and O. V. Prezhdo, J. Chem. Theory Comput., 2016, 12, 1436–1448 CrossRef CAS PubMed.
- D. F. Coker and L. Xiao, J. Chem. Phys., 1995, 102, 496–510 CrossRef CAS.
- P. V. Parandekar and J. C. Tully, J. Chem. Phys., 2005, 122, 094102 CrossRef.
- J. Schmidt, J. Hutter, H.-W. Spiess and D. Sebastiani, ChemPhysChem, 2008, 9, 2313–2316 CrossRef CAS.
- A. Jain and J. E. Subotnik, J. Chem. Phys., 2015, 143, 134107 CrossRef PubMed.
- A. Jain, M. F. Herman, W. Ouyang and J. E. Subotnik, J. Chem. Phys., 2015, 143, 134106 CrossRef.
- A. E. Sifain, L. Wang and O. V. Prezhdo, J. Chem. Phys., 2016, 144, 211102 CrossRef.
- H. M. Jaeger, S. Fischer and O. V. Prezhdo, J. Chem. Phys., 2012, 137, 22A545 CrossRef PubMed.
- P. Shushkov, R. Li and J. C. Tully, J. Chem. Phys., 2012, 137, 22A549 CrossRef PubMed.
- J. E. Subotnik, W. Ouyang and B. R. Landry, J. Chem. Phys., 2013, 139, 214107 CrossRef.
- L. Wang, A. E. Sifain and O. V. Prezhdo, J. Phys. Chem. Lett., 2015, 6, 3827–3833 CrossRef CAS.
- L. Wang, A. Akimov and O. V. Prezhdo, J. Phys. Chem. Lett., 2016, 7, 2100–2112 CrossRef CAS.
- J. C. Tully, J. Chem. Phys., 1990, 93, 1061 CrossRef CAS.
- S. Ghosh, S. Giannini, K. Lively and J. Blumberger, Faraday Discuss., 2019 10.1039/C9FD00046A.
- O. V. Prezhdo and P. J. Rossky, J. Chem. Phys., 1997, 107, 5863–5878 CrossRef CAS.
- B. R. Landry and J. E. Subotnik, J. Chem. Phys., 2012, 137, 22A513 CrossRef PubMed.
- E. R. Bittner and P. J. Rossky, J. Chem. Phys., 1995, 103, 8130 CrossRef CAS.
- J.-Y. Fang and S. Hammes-Schiffer, J. Phys. Chem. A, 1999, 103, 9399–9407 CrossRef CAS.
- C. Zhu, S. Nangia, A. W. Jasper and D. G. Truhlar, J. Chem. Phys., 2004, 121, 7658 CrossRef CAS PubMed.
- C. Zhu, A. W. Jasper and D. G. Truhlar, J. Chem. Phys., 2004, 120, 5543–5557 CrossRef CAS PubMed.
- G. Granucci and M. Persico, J. Chem. Phys., 2007, 126, 134114 CrossRef.
- G. Granucci, M. Persico and A. Zoccante, J. Chem. Phys., 2010, 133, 134111 CrossRef PubMed.
- J. E. Subotnik and N. Shenvi, J. Chem. Phys., 2011, 134, 2011 Search PubMed.
- T. Nelson, S. Fernandez-Alberti, A. E. Roitberg and S. Tretiak, J. Chem. Phys., 2013, 138, 224111 CrossRef.
- A. Jain, E. Alguire and J. E. Subotnik, J. Chem. Theory Comput., 2016, 12, 5256–5268 CrossRef CAS.
- E. Fabiano, T. Keal and W. Thiel, Chem. Phys., 2008, 349, 334–347 CrossRef CAS.
- S. Fernandez-Alberti, A. E. Roitberg, T. Nelson and S. Tretiak, J. Chem. Phys., 2012, 137, 014512 CrossRef PubMed.
- T. Nelson, S. Fernandez-Alberti, A. E. Roitberg and S. Tretiak, Chem. Phys. Lett., 2013, 590, 208–213 CrossRef CAS.
- L. Wang and D. Beljonne, J. Phys. Chem. Lett., 2013, 4, 1888–1894 CrossRef CAS PubMed.
- J. Qiu, X. Bai and L. Wang, J. Phys. Chem. Lett., 2018, 9, 4319–4325 CrossRef CAS PubMed.
- J. Qiu, X. Bai and L. Wang, J. Phys. Chem. Lett., 2019, 10, 637–644 CrossRef.
- X. Bai, J. Qiu and L. Wang, J. Chem. Phys., 2018, 148, 104106 CrossRef PubMed.
- B. R. Landry, M. J. Falk and J. E. Subotnik, J. Chem. Phys., 2013, 139, 211101 CrossRef.
- J. Spencer, F. Gajdos and J. Blumberger, J. Chem. Phys., 2016, 145, 064102 CrossRef.
- F. Gajdos, S. Valner, F. Hoffmann, J. Spencer, M. Breuer, A. Kubas, M. Dupuis and J. Blumberger, J. Chem. Theory Comput., 2014, 10, 4653–4660 CrossRef CAS PubMed.
- A. Kubas, F. Hoffmann, A. Heck, H. Oberhofer, M. Elstner and J. Blumberger, J. Chem. Phys., 2014, 140, 104105 CrossRef PubMed.
- A. Warshel and R. M. Weiss, J. Am. Chem. Soc., 1980, 102, 6218–6226 CrossRef CAS.
- S. Mai, P. Marquetand and L. González, Int. J. Quantum Chem., 2015, 115, 1215–1231 CrossRef CAS.
- P. Pechukas, Phys. Rev., 1969, 181, 174 CrossRef CAS.
- M. F. Herman, J. Chem. Phys., 1984, 81, 754–763 CrossRef CAS.
- S. Hammes-Schiffer and J. C. Tully, J. Chem. Phys., 1994, 101, 4657–4667 CrossRef CAS.
- B. R. Landry and J. E. Subotnik, J. Chem. Phys., 2011, 135, 191101 CrossRef.
- M. J. Bedard-Hearn, R. E. Larsen and B. J. Schwartz, J. Chem. Phys., 2005, 123, 234106 CrossRef PubMed.
- G. A. Meek and B. G. Levine, J. Phys. Chem. Lett., 2014, 5, 2351–2356 CrossRef CAS.
- Z. Zhou, Z. Jin, T. Qiu, A. M. Rappe and J. E. Subotnik, 2019, arXiv:199.11157v1[physics.chem-ph].
- L. Wang and O. V. Prezhdo, J. Phys. Chem. Lett., 2014, 5, 713–719 CrossRef CAS PubMed.
- J.-Y. Fang and S. Hammes-Schiffer, J. Chem. Phys., 1999, 110, 11166–11175 CrossRef CAS.
- J. R. Schmidt, P. V. Parandekar and J. C. Tully, J. Chem. Phys., 2008, 129, 044104 CrossRef CAS PubMed.
- G. Granucci, M. Persico and A. Toniolo, J. Chem. Phys., 2001, 114, 10608–10615 CrossRef CAS.
- A. Heck, J. J. Kranz, T. Kubař and M. Elstner, J. Chem. Theory Comput., 2015, 11, 5068–5082 CrossRef CAS.
- A. Heck, J. J. Kranz and M. Elstner, J. Chem. Theory Comput., 2016, 12, 3087–3096 CrossRef CAS.
- A. Troisi, Adv. Mater., 2007, 19, 2000–2004 CrossRef CAS.
- R. Seidel, M. Faubel, B. Winter and J. Blumberger, J. Am. Chem. Soc., 2009, 131, 16127 CrossRef CAS.
- J. Moens, R. Seidel, P. Geerlings, M. Faubel, B. Winter and J. Blumberger, J. Phys. Chem. B, 2010, 114, 9173 CrossRef CAS.
- R. Seidel, S. Thurmer, J. Moens, P. Geerlings, J. Blumberger and B. Winter, J. Phys. Chem. B, 2011, 115, 11671 CrossRef CAS PubMed.
- J. Blumberger and K. McKenna, Phys. Chem. Chem. Phys., 2013, 15, 2184 RSC.
- D. Case, T. Darden, T. Cheatham III, C. Simmerling, J. Wang, R. Duke, R. Luo, M. Crowley, R. Walker and W. E. A. Zhang, Amber10 Search PubMed.
- C. P. Herrero, Phys. Rev. B: Condens. Matter Mater. Phys., 2001, 65, 2001 CrossRef.
- S. Nosé, Mol. Phys., 1984, 52, 255–268 CrossRef.
- S. Nosé, J. Chem. Phys., 1984, 81, 511 CrossRef.
- A. D. Becke, J. Chem. Phys., 1993, 98, 5648–5652 CrossRef CAS.
- CPMD Version 4.1, the CPMD consortium, http://www.cpmd.org, MPI für Festkörperforschung and the IBM Zurich Research Laboratory, 2015.
- J. P. Perdew, K. Burke and M. Ernzerhof, Phys. Rev. Lett., 1996, 77, 3865 CrossRef CAS PubMed.
- S. Goedecker, M. Teter and J. Hutter, Phys. Rev. B: Condens. Matter Mater. Phys., 1996, 54, 1703–1710 CrossRef CAS PubMed.
- S. Giannini, A. Carof, M. Ellis, H. Yang, O. G. Ziogos, S. Ghosh and J. Blumberger, Nat. Commun., 2019, 10, 3843 CrossRef PubMed.
- H. Matsui, A. S. Mishchenko and T. Hasegawa, Phys. Rev. Lett., 2010, 104, 1–4 CrossRef PubMed.
- T. Sakanoue and H. Sirringhaus, Nat. Mater., 2010, 9, 736–740 CrossRef CAS PubMed.
- J. F. Chang, T. Sakanoue, Y. Olivier, T. Uemura, M. B. Dufourg-Madec, S. G. Yeates, J. Cornil, J. Takeya, A. Troisi and H. Sirringhaus, Phys. Rev. Lett., 2011, 107, 1–4 Search PubMed.
- P. Wang, R. B. Best and J. Blumberger, J. Am. Chem. Soc., 2011, 133, 3548 CrossRef CAS PubMed.
- P. Wang and J. Blumberger, Proc. Natl. Acad. Sci. U. S. A., 2012, 109, 6399 CrossRef CAS PubMed.
| This journal is © the Owner Societies 2019 |