Atomistic insights into the screening and role of oxygen in enhancing the Li+ conductivity of Li7P3S11−xOx solid-state electrolytes†
Abstract
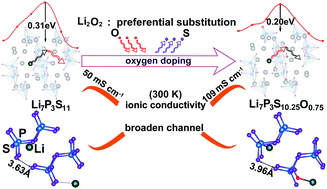
Herein, we implement first-principles calculations to design Li7P3S11−xOx at an atomic scale, aiming to obtain stable Li7P3S11−xOx-type solid electrolyte materials with good Li+ conductivity. After searching for chemical potentials, Li2O2 is expected to be the potential raw material, and it can afford the most favorable growth environment for the synthesis of Li7P3S11−xOx (x = 0.25, 0.50, 0.75 and 1). Among these compounds, it is found that Li7P3S10.25O0.75 exhibits the most desirable Li+ conductivity of 109 mS cm−1 at 300 K, which is far higher than that of Li7P3S11 (50 mS cm−1 at 300 K). By structural analysis, it is demonstrated that the Li diffusion pathway in Li7P3S10.25O0.75 is significantly broadened relative to that in Li7P3S11 (71.38 Å3vs. 69.48 Å3), which breaks the bottleneck during Li diffusion. Moreover, the resistance of Li ion diffusion in Li7P3S10.25O0.75 decreases due to the balance of interactions between Li and its neighbouring atoms at the transition state, which induces a much lesser energy barrier of Li7P3S10.25O0.75 than that of Li7P3S11 (0.20 eV vs. 0.31 eV). Moreover, introducing Li vacancies is unlikely to alter the essence of the inherent superionic conductivity of Li7P3S10.25O0.75. Furthermore, Li7P3S10.25O0.75 can maintain good thermal stability and similar electrochemical stability to Li7P3S11. This study successfully clarifies the role of oxygen in enhancing the Li+ conductivity of Li7P3S11−xOx. Moreover, it affords a new strategy to design other solid-state electrolytes with good Li+ conductivity.
- This article is part of the themed collection: 2019 PCCP HOT Articles


 Please wait while we load your content...
Please wait while we load your content...