Open Access Article
Open Access ArticleCreative Commons Attribution 3.0 Unported Licence
NMR relaxation and modelling study of the dynamics of SF6 and Xe in porous organic cages†
Pär
Håkansson
 *a,
Muhammad Asadullah
Javed
*a,
Muhammad Asadullah
Javed
 a,
Sanna
Komulainen
a,
Sanna
Komulainen
 a,
Linjiang
Chen
a,
Linjiang
Chen
 b,
Daniel
Holden
b,
Tom
Hasell
b,
Daniel
Holden
b,
Tom
Hasell
 b,
Andrew
Cooper
b,
Andrew
Cooper
 b,
Perttu
Lantto
b,
Perttu
Lantto
 a and
Ville-Veikko
Telkki
a and
Ville-Veikko
Telkki
 a
a
aNMR Research Unit, University of Oulu, P. O. Box 3000, 90014 Oulu, Finland. E-mail: par.hakanson@oulu.fi
bDepartment of Chemistry and Centre for Materials Discovery, University of Liverpool, Crown Street, Liverpool L69 7ZD, UK
First published on 22nd October 2019
Abstract
The porous solid formed from organic CC3 cage molecules has exceptional performance for rare gas separation. NMR spectroscopy provides a way to reveal the dynamical details by using experimental relaxation and diffusion measurements. Here, we investigated T1 and T2 relaxation as well as diffusion of 129Xe and SF6 gases in the CC3-R molecular crystal at various temperatures and magnetic field strengths. Advanced relaxation modelling made it possible to extract various important dynamical parameters for gases in CC3-R, such as exchange rates, activation energies and mobility rates of xenon, occupancies of the cavities, rotational correlational times, effective relaxation rates, and diffusion coefficients of SF6.
1 Introduction
Porous materials are solids that exhibit networks of pores and cavities and that have a much larger internal surface area as compared to the external surface area. Porous solids are ubiquitous and have widespread applications, such as molecular separation, purification, catalysis, chromatography, fluid transport, energy storage etc.1,2 They also provide promising opportunities to capture greenhouse gases by adsorption,3 such as CO2, CH4, as well as noble gases4,5 (Xe, Ar, Kr). Various extended porous networks have been developed for these applications, such as activated carbons,6 zeolites,7 metal organic frameworks (MOFs),8 covalent organic frameworks (COFs)9 and porous polymers.10Nuclear magnetic resonance (NMR) relaxation and diffusion experiments provide extraordinarily versatile information about dynamics of fluid molecules in porous media.11,12 Combined with a molecular level modelling, a detailed picture about the gas and framework dynamics can be revealed.13 The modelling provides deep explanations for the observations and, overall, the analysis may guide in further system design.
This study focuses on the dynamics of sulphur hexafluoride (SF6) and Xe gas in porous organic cages. SF6 is a gas that has long atmospheric life span. It absorbs infrared light that makes it a potent greenhouse gas.14 SF6 acts as an excellent insulator for electrical equipment, thermos-acoustic insulator for windows, contrast agent in medical applications, and etchant plasma in semi-conductor industry.15,16 However, due to its high global warming potential—23![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 900 times higher than CO2 over a hundred year span17—it should be handled careful and recovered and stored in industrial usage.16 Many techniques, including pressure swing adsorption/desorption processes, have been proposed to separate SF6 from other gas mixtures and prevent its release to the atmosphere but the process requires high size selectivity and adsorption capacity of adsorbents.18 Several extended porous solids19,20 have been utilised for the separation and adsorption of SF6. Moreover, cucurbituril in aqueous solution21 has also been utilised for the reversible trapping of SF6.
900 times higher than CO2 over a hundred year span17—it should be handled careful and recovered and stored in industrial usage.16 Many techniques, including pressure swing adsorption/desorption processes, have been proposed to separate SF6 from other gas mixtures and prevent its release to the atmosphere but the process requires high size selectivity and adsorption capacity of adsorbents.18 Several extended porous solids19,20 have been utilised for the separation and adsorption of SF6. Moreover, cucurbituril in aqueous solution21 has also been utilised for the reversible trapping of SF6.
Xenon is used in light appliances due to its glow effects and in medical imaging field. The inertness of Xe and its low abundance in air (0.087 ppm by volume)22 makes it commercially expensive. Due to its inert nature, a precise size selectivity is required to capture xenon gas in porous materials.23
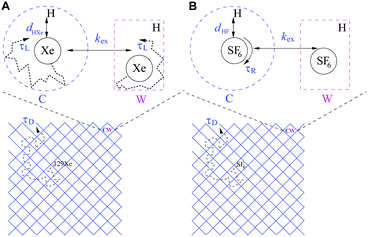
Porous organic cages are discrete cage molecules having permanent internal voids accessed by well-defined windows that provide porosity for guest molecules.24 These cages provide a way for the analytical separation of rare gases and chiral molecules by selective bindings.25 It has been shown that one of the organic cage molecules, CC3,26 exhibits extraordinary characteristics for the selective separation of rare gases and SF6 over gas mixtures.26,27 The tetrahedral CC3 cage is composed of imine bonds that connect the rigid aromatic rings to the flexible cyclohexane linkers (Fig. 1A). These cages pack into a crystalline structure to form an interconnected 3D pore structure accessible via windows of the cages (Fig. 1B). The size of cage cavities is 4.4 Å while the narrowest point between the cage and window cavities is 3.6 Å in diameter. Adsorbed xenon (with diameter of 4.3 Å) was shown to have fast exchange, on the order of 108 s−1, between these cavities,28 and even SF6 with kinetic diameter of 5.5 Å can enter the cage through the window cavity because of thermal and vibrational motion of the porous organic crystals.27
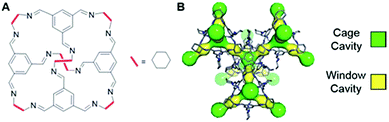 | ||
| Fig. 1 (A) Chemical structure of CC3 cage. (B) 3D crystal and cavity structure of CC3 material. The cage and window cavities are illustrated by green and yellow, respectively. | ||
The fluorine atoms in SF6 have an NMR active 19F isotope with spin-1/2, high gyromagnetic ratio and 100% natural abundance. The presence of six magnetically equivalent 19F atoms in each SF6 molecule makes the spin density of the gas high. The stable isotopes of S have a spin zero and natural abundance of 99.2%. Chemically SF6 is inert, non-toxic, non-explosive, incombustible and thermally stable, which makes it a suitable NMR probe in various applications in chemistry, materials science and medicine.29 It has been utilized for the investigation of porous media,30 MRI of lungs,31 liquid crystals,32 and ethylene-propylene rubbers.29 In addition, it has been used also as a spy molecule for highlighting the cavities in proteins.33
Xenon has an NMR active 129Xe isotope with spin-1/2 nucleus and relatively high natural abundance (26%). It is an inert, monoatomic noble gas with an easily polarizable electron cloud, which renders its chemical shifts extremely sensitive to the local environments. The sensitivity of the adsorbed 129Xe can be enhanced by several orders of magnitude by applying a spin-exchange optical pumping (SEOP) hyperpolarization technique. Therefore, it is widely used in NMR and magnetic resonance imaging (MRI) applications in chemistry, biochemistry, materials science and medicine.34 It has been used in MRI of lungs,35 microfluidic flow imaging,36 investigation of liquid crystals,37 polymers,38 cements and shales39 and ionic liquids,40 for the determination of pore sizes of porous networks41,42 and also as an biosensors.43,44
In our previous work,28 we performed a thorough 129Xe NMR analysis of adsorption and dynamical phenomena of xenon in CC3. We calculated chemical shifts of 129Xe in cage and window cavities, and, based on a simple two-site exchange model, we were able to interpret observed exchange averaged chemical shifts and T2 relaxation times as well as extract populations of cage and window cavities and exchange rates.
In the present work, we extend the previous work by investigating T1, T2 and diffusion of both Xe and SF6 in homochiral CC3-R material (see Note on cage nomenclature and chirality in ESI†). Quantitative insights on the gas-mobility in CC3-R are deduced by analysing the data with a relaxation and diffusion model. We perform a global analysis of T1, T2 and diffusion data using an extensive set of relaxation mechanisms for 129Xe and SF6. The model benefits from a reduced number of adjustable parameters by incorporating quantum chemical information and configurational sampling. Three main aspects are covered here: first, extraction detailed information on the dynamics of the xenon and SF6 gases in CC3-R; second, exploration of a model development where a reduced set of adjustable parameters are required by making use of potential energy surface (PES) to precompute relaxation model parameters; finally, we show how global analysis in the parameter estimation is performed with Bayesian Monte Carlo approach.45
2 Materials and methods
2.1 Samples
Two CC3-R samples with different SF6 loadings were prepared. The sample was inserted into a 5 mm glass tube and SF6 gas was condensed in it by using liquid nitrogen. Thereafter, the tube was sealed with flame. The SF6![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) CC3-R molar ratio for the low loading (LL) and middle loading (ML) samples were 0.18
CC3-R molar ratio for the low loading (LL) and middle loading (ML) samples were 0.18![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1, 0.53
1, 0.53![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1, respectively. Three CC3-R samples with different xenon loadings were prepared as well in the similar way as the SF6 samples by using enriched 129Xe gas (91%). The Xe
1, respectively. Three CC3-R samples with different xenon loadings were prepared as well in the similar way as the SF6 samples by using enriched 129Xe gas (91%). The Xe![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) CC3-R molar ratios were 0.10
CC3-R molar ratios were 0.10![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1, 0.52
1, 0.52![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1 and 2.4
1 and 2.4![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1 for the low loading (LL), middle loading (ML) and high loading (HL) samples, respectively. The last sample represents an almost fully saturated material, in which nearly all three binding sites (one in each cage cavity plus four shared (equals to two) in the surrounding window cavities) are occupied by xenon. The adsorption rate of Xe sample was remarkably higher as compared to larger SF6 molecules.
1 for the low loading (LL), middle loading (ML) and high loading (HL) samples, respectively. The last sample represents an almost fully saturated material, in which nearly all three binding sites (one in each cage cavity plus four shared (equals to two) in the surrounding window cavities) are occupied by xenon. The adsorption rate of Xe sample was remarkably higher as compared to larger SF6 molecules.
2.2 NMR measurements
19F and 129Xe NMR experiments were carried out using Bruker Avance 400 and 600 MHz spectrometers with the magnetic field strengths of 9.4 and 14.1 T, respectively. Resonance frequencies of 19F are 376 and 564 MHz and 129Xe are 111 and 166 MHz.3 Relaxation models
3.1 Xenon
An introduction of 129Xe relaxation mechanisms is provided, following the scheme in Fig. 2A. The relaxation contributions may be discussed in terms of amplitudes governed by the spin-interaction strengths of the mechanisms (amplitude) and modulation, i.e. time constants of molecular processes causing the relaxation, summarized in Table 1. The details of the computation of relaxation rate amplitudes are described in Section 3.4. The ambition is to find as complete relaxation representation as possible with limited number of adjustable parameters that explains the experimental features in Fig. 3C and D.| Mechanism | DDinter | Shift-ex | DDHXe-ex | DDHXe-L | CSA-L |
|---|---|---|---|---|---|
| Amplitude | d HXe, NH | Δδ, XS, B0 | X S, bexHXe | X S, bexHXe | X S, ΔσS, B0 |
| Modulation | τ D | (kex)−1 | (kex)−1 | τ L | τ L |
The diffusion of gas molecules is a molecular process causing intermolecular dipole–dipole relaxation (DDinter) due to the interaction with the protons of the organic structure. This is illustrated with motion between unit cells in Fig. 2A, lower panel. The DDinter 129Xe–H relaxation model was originally derived for liquid state relaxation.46,47 In the implementation, the protons of the CC3-R structure are assumed to be fixed in space with the proton spin density of NH (computed in ESI†). The model assumes hard sphere diffusion with the spin located at the centre of a sphere, which is reasonable for 129Xe. The amplitude of the DDinter interaction (see Table 1) depends on the length of closest distance (dHXe) between 1H and 129Xe spins (in the liquid state derivation),47 which can be explicitly computed by eqn (4). The DDinter mechanism is dependent on diffusion correlation time τD = d2HXe/D, where D is the experimentally known 129Xe translational diffusion constant (see Fig. 3D).
The chemical shift difference of 129Xe in the cage and window cavities (Δδ = δC − δW)28 provides the shift-ex mechanism48 that has a dominant role in T2 relaxation. The amplitude (Table 1) is determined by Δδ, the cavity molar fractions of 129Xe (XS, S = C, W) and the strength of external magnetic field (B0). The relaxation is modulated by the exchange rate (kex).
There are two local dipole–dipole mechanisms. The first one, DDHXe-ex, is due to exchange process and dependent on the bexHXe interaction (see eqn (7)). The second one (DDHXe-L) is modulated by characteristic time τL due to local cavity motion (see Fig. 2A) and is dependent on the in-cavity dipole–dipole interaction (bSHXe, S = C, W; the subscripts refer to the 129Xe–1H pairs in window and cage cavities, see eqn (7)).
The CSA-L mechanism is due to the same local cavity motion (τL) and have amplitude dependent on the chemical shielding anisotropy (ΔσS), populations (XS) and B0.
The relaxation mechanisms are assumed additive (statistically uncorrelated) such that cavity specific relaxation rates (Ti−1)mm = {DDHXe-L, CSA-L}, (i = {1, 2}) are population weighted:
| (Ti−1)m = (Ti−1)m,CXC + (Ti−1)m,WXW. | (1) |
3.2 SF6
The relaxation model for SF6 is illustrated in the scheme in Fig. 2B and the symbols for amplitudes and modulation are shown in Table 2. The intermolecular mechanism DDinter contains the same parameters as in the case of xenon. Since the diffusion measurements were performed at higher temperatures than the relaxation experiments, one Arrhenius model was used for modelling diffusion coefficients in the entire temperature region of the diffusion and relaxation experiments.| Mechanism | DD-inter | DDFF-R | DDFH-R | DDFH-ex | CSA-R | SR |
|---|---|---|---|---|---|---|
| Amplitude | d HF, NH | ScaleR, bCFF, XC | ScaleR, bCHF, XC | b exHF, XC | X C, ΔσC | C SR I, XC |
| Modulation | τ D | τ R | τ R | (kex)−1 | τ R | τ −1R |
Three dipole–dipole mechanisms are included, DDFH-ex, DDFH-R and DDFF-R, where (bexHF), F–H (bCHF) and F–F (bCFF) couplings are considered, respectively. The first accounts for the two-site exchange modulation. The following two mechanisms are local and assumed to be modulated by the rotational motion with correlation time (τR) in the cage cavity (C), weighted by the molar fraction XC. Simulation of SF6 metadynamics in cage structure suggest there is a significant energy barrier and a rotation in passing the window cavity.27 The barrier translates to a low window population and motivates not to include a specific window site relaxation process. The passing through the window cavity is accounted for locally with DDFH-ex and via the proton concentration dependent diffusion process DDinter. The local DD amplitudes have an additional parameter scaleR as compared to 129Xe. Since there is only QC equilibrium and not temperature dependent trajectory information simulated, this parameter serves to rescale F–H and F–F distances in order to resemble the configuration averaged values (see “r” in eqn (7)).
The relatively complex local DDFH interaction is thus modulated by two correlation times due to rotation and site exchange. In the analysis (Section 4.3) the latter is approximated with τD. An additional fast (sub-picoseconds) liberation process can be anticipated, however, is not explicitly included other than in the final DD amplitude. For this process, an effect on the T1 model cannot be ruled out, but a negligible influence on T2 is estimated due to the short timescale.
The chemical shielding anisotropy (CSA-R) with respect to zz axis (along a bond) is large for SF6 as shown by the quantum chemical (QC) calculations (see Section 3.4.2) and the relaxation is modulated by the correlation time (τR) in the cage cavity. For the window cavity no large amplitude modulation is expected, and no CSA mechanism is included. Potential DD-CSA cross correlations are not included in the model as discussed in the ESI† (see Section S2.1).
For similar reason, nuclear spin-rotation (SR) mechanism is estimated for SF6 rotation in the cage cavity following the Hubbard SR model.49 In this case, the modulation is dependent on the inverse rotational correlation time and thus has a reverse temperature dependence. The SR tensors are estimated by using QC calculations (Section 3.4.2).
Strictly speaking, contrary to Xe, SF6 molecule is not a perfect sphere, as the model assumes, and this has some effects on its dynamics in CC3. For example, it has been shown by simulations that, when SF6 exits the cage, it has to align its outermost triangular face with the triangular face of the window. Thereafter a rotation of about 60° is required so that the second face can align the cage window and pass through.27 However, the details of the dynamics in the window cavity is not really important in the relaxation modelling, as the population of SF6 in the window cavity is very low. Furthermore, the transport of SF6 enters the relaxation model via the diffusion coefficients. Thus, the details of SF6 deformations are not explicitly required. Therefore, the spherical approximation should be well justified.
3.3 Spin-system dynamics
The relaxation models for 129Xe and SF6 consider a system with single spin in case of CSA, shift-ex and SR and a two spin system for dipole–dipole relaxation, in the standard perturbative form.48 For completeness the 1/T1 and 1/T2 components are provided by eqn (S1)–(S10) in ESI.† Particular important for 129Xe 1/T2 is the shift-ex mechanism (eqn (S9) in ESI†):| (Tex2(ωA))−1 = (ωAΔδ)2XCXWJex(0); XW = (1 − XC), | (2) |
The latter depends on correlation time τex = 1/kex and in general resonance frequency ωA for spin A. The spectral densities for local DD, CSA and shift-ex are computed as a Lorentzian from the correlation times τY, Y = L, R, ex:
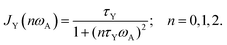 | (3) |
3.4 Computational methods
The computational methods involving QC and PES are outlined together with parameter estimation procedure. The QC and PES computed system properties are directly related to the 129Xe and SF6 relaxation models discussed in previous section.The list of 129Xe relaxation mechanisms is provided in Table 1. In this section the amplitude parametrisation is considered. The computed relaxation amplitudes follow from the hypothesis that there is statistically independent cavity dipole–dipole interaction and exchange and diffusion processes. Reasons for this separation may originate from a separation of timescale as well as approximately orthogonal processes. The latter processes are thus sensitive to averaged interaction tensors. Furthermore, our previous work28 provides the mole fractions of Xe in the cage and window cavities (XC, XW) that are here used as fixed parameters. Thus, the current relaxation model provides a validation of the two-site model used in our previous work.28
In order to compute the estimates of shielding tensors, the Monte Carlo NVT sampling28 was performed at 298 K. The calculations provided spatial Xe configurations and shielding trajectories in the cage and window cavities (not including the loading effect of the neighbouring cavities). The trajectories allow for relaxation modelling with molecular details but only with few adjustable parameters.
For DDinter, the average (denoted with 〈·〉i) of the proton (i) to Xe distance at the equilibrium is computed as:
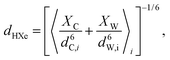 | (4) |
The shift-ex mechanism has a chemical shift difference sampled with the configuration trajectory as:
| Δδ = [〈(δNRC − δNRW)2〉]1/2 + |(δRELC − δRELW)|, | (5) |
To arrive at local DDHXe-ex amplitude for the cage-window exchange process, the starting point is the standard deviation of [(bCHA)2 − (bWHA)2] and, for comparison, computing the ensemble average as a population weighted effective distance:
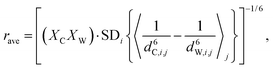 | (6) |
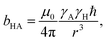 | (7) |
The local cavity interaction (bSHXe, S = C, W) is provided in similar way from the effective distance:
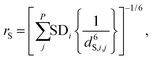 | (8) |
The CSA-L is obtained from shielding tensors trajectory (see page 106 of ref. 48) for the cage and window cavity in crystal frame and compute:
| ΔσS = std[ΔσtrajS]. | (9) |
The nuclear shielding tensors calculations with the Turbomole code were carried out using the B3LYP functional. For S atom in SF6 molecule we used def2-TZVP basis set but for F atoms a completeness-optimized co-r primitive basis set (18s10p6d2f) was used, which provides result for all NMR parameters practically at complete basis set limit for all NMR parameters.56 The def2-SVP basis set was used for the atoms in the surrounding cage/window structure. The obtained shielding tensors were symmetrized and diagonalized with python code to yield the isotropic, anisotropic and asymmetric parts in principal axis system (PAS) of the tensor for the relaxation models. The computed chemical shielding anisotropy (CSA) in the cage cavity was ΔσC = 390 ppm and the chemical shift difference between the cage and window cavities was Δδ = 10.7 ppm (see Table S5 in ESI†).
The nuclear spin-rotation (SR) constant (mean of tensor trace) was computed with DFT vacuum optimized geometry (for details see Section S4 in ESI†). The purpose of SR tensor is to explore the order of magnitude contribution of SR-relaxation of SF6 in the cage.
The relaxation due to F–H dipole–dipole interaction in the cage cavity has a modulation due to overall rotation of SF6 with correlation time τR. The amplitude (bCHF)2 may be computed following eqn (7) and (8), however, with the SD estimation from the fluoride equilibrium positions as opposed to NVT configurations. The effective distance was found to be rC: 2.72 Å. For the F–F interaction (b2FF) the sum over the five intramolecular 1/d6FF distances were computed leading to an effective distance rFF = 1.8 Å, to be compared with the shortest equilibrium F–F distance of 2.2 Å. Thus, the sum of F–F relaxation channels provides an efficient relaxation mechanism. Due to the approximation of equilibrium distances these distances were rescaled with a fitted parameter scaleR. Amplitude for DDFH-ex is obtained from eqn (6), with the mean computed over F-distances.
Related to nuclear spin-rotation (SR) and CSA the QC values (Section 3.4.2) where used.
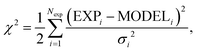 | (10) |
The parameters in x are estimated together with confidence intervals by sampling the so-called posterior probability of the hypothesis x. The form of this distribution is given in Section S3 in ESI.† It consists of the likelihood function, i.e. the negative exponential of eqn (10) constrained by the prior assumptions of x. In practise, the distribution of x is obtained by generating MCMC-trajectories for the four and seven-dimensional parameter space for 129Xe and SF6, respectively.
First the parameters are assumed to be of uniform distribution prior to the study, with their boundaries (cf. Tables S1 and S2 in ESI†), chosen based on physical constraints, for instance shortest plausible atom distance or alternatively, if the computational cost is too large, the boundary domain is reduced. The MCMC sampling was done following the Metropolis–Hastings algorithm,45,57 where initial configurations are generated uniformly and kept within the boundaries (cf. Tables S1 and S2 in ESI†) by implementing reflective boundary condition. After calibrating MCMC step length such that approximately 50% of steps are accepted and simulating an initial “burn in” period the productive estimation follows. For Xe and SF6, 25 and 5 independent trajectories were simulated, with parameters initiated from uniformly distributed random numbers within the boundaries. In order to reduce chance of getting stuck in local minima during the “burn in” sequence an inverse “temperature” (χ2 → β·χ2, β = {10−7, 10−3, 1}) was used. Hence, first an equilibration at “high temperature” (small β) is performed, followed by the sampling of the distribution related to eqn (10) (i.e. β = 1).
Consensus is confirmed between the trajectories (with different starting parameters) in that the distribution of χ2 is similar for each trajectory as well as the trajectories predicts similar parameter distribution. Thus, from multiple trajectories it is seen that the final χ2-distribution does not depend on the initial condition.45 Production run of the trajectories are performed with 106 MCMC steps, as deemed necessary considering the parameter self-correlation in the MCMC-trajectory. The statistically best estimates of parameters are given by the mean over MCMC configurations. Their corresponding 95% confidence interval are estimated by numerically integrating each parameter cumulative probability distribution. Scripts are implemented in MATLAB.
4 Results and discussion
4.1 Overview of NMR observations
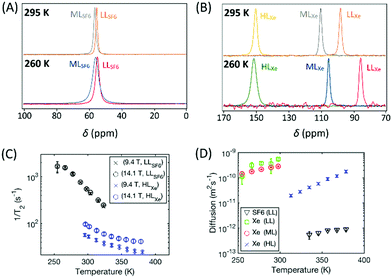
19F and 129Xe NMR spectra of CC3-R with different SF6 and xenon loadings measured at 295 and 260 K at 14.1 T are shown in Fig. 3A and B. The spectra show only one, relatively narrow peak due to fast thermal motion; the random changes in the 19F and 129Xe frequencies due to exchange between cage and window cavity, modulation of dipole–dipole, chemical shift anisotropy interactions, etc. occur much faster than the millisecond NMR-timescale. The chemical shift of 129Xe increases significantly with loading, mostly due to increasing relative occupancy of window cavities, as the chemical shift of 129Xe in the window cavity is much larger (about 210 ppm) than that in the cage cavity (about 20 ppm).28 In the LL and ML samples, the 129Xe chemical shift increases with temperature due to increased relative occupancy of window cavities, while the shift remains constant in the HL sample.28Contrary to the xenon samples, the 19F chemical shift of SF6 does not change almost at all with temperature or loading (see also Fig. S1A in ESI†). According to the quantum chemical calculations described in Section 3.4.2, the 19F chemical shift difference between the cage and window cavities (about 11 ppm, see also Table S5 in ESI†) is much smaller than in the case of 129Xe (about 190 ppm). Furthermore, SF6 (5.5 Å) is larger than Xe (4.3 Å), and therefore it strongly favors the larger cage cavity over the window cavity, and changes in the temperature or loading does not change much the relative occupancies of SF6 in the cavities. Consequently, 19F chemical shift remains almost constant.
The transverse relaxation rate of both 19F and 129Xe decreases with increasing temperature due to the increased mobility (see Fig. 3C). T2 of 129Xe is also strongly dependent on the magnetic field strength whereas T2 of 19F is not. The predominant mechanism of T2 relaxation of 129Xe is the changing chemical shift due to the exchange between the cage and window cavities,28 while in the case of 19F it is intermolecular dipolar mechanism. The former depends on the square of the field strength (cf.eqn (2)), while the latter has vanishing field dependence at the slow 19F mobility and high fields of this study (see eqn (S2) in ESI†). The T2 of 19F is approximately equal for the LL and ML loading (see Fig. S1C in ESI†) suggesting the same homogeneous broadening in their spectra. However, the spectral line width in Fig. 3A is almost double for the ML sample. Considering the few ppm larger chemical shift for gas phase SF6 (QC estimate Table S6 in ESI†), this is consistent with a inhomogeneously broadened ML spectrum due to unresolved gas phase. The longitudinal SF6 relaxation rate goes down by a factor of 5 with increased loading (see Fig. S1B in ESI†), most probably due to the same gas pool. Thus, the T1 values, chemical shifts and linewidths are implying that not all the SF6 molecules are absorbed in CC3-R (see also Section S1.1 in ESI†). As it is an additional complication to consider the effect of non-adsorbed gas, the quantitative modeling was conducted only for the LL SF6 sample.
Fig. 3D shows the self-diffusion coefficients of SF6 and xenon in CC3-R. The diffusion coefficient of SF6 is very low, about 4.8 × 10−13 m2 s−1 at 335 K, and it is almost the same for the LL and ML samples (see also Fig. S2 in ESI†). This reflects very slow diffusional motion of the large SF6 molecule in the small cavities of CC3-R. The diffusion coefficient of xenon in the HL sample is more than an order of magnitude higher than the diffusion coefficient of SF6 because of the smaller size of xenon. On the other hand, the diffusion of xenon in the LL and ML samples is more than an order of magnitude larger than in the HL loading sample, because diffusion of xenon is significantly restricted in the almost saturated HL sample as xenon atoms cannot pass each other in the channels.
4.2 Xenon
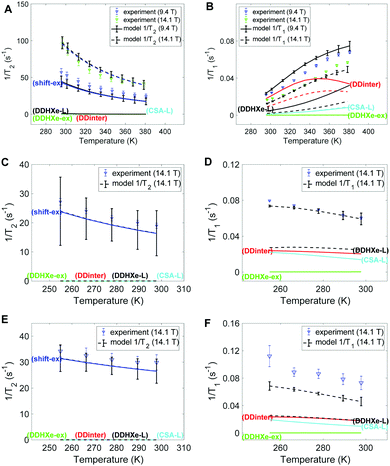
Fig. 4 provides the experimental 129Xe 1/T2 and 1/T1 relaxation rates in left and right columns, respectively, together with the model estimates. Panels A-B, C-D and E-F display the results of HL, ML and LL samples, respectively. The dominant mechanism for T2 relaxation is the shift-ex mechanism for all the three samples, and the contributions of dipolar mechanisms (DDinter, DDHXe-L and DDHXe-ex) as well as CSA-L are negligible. For the DDinter mechanism, the diffusion constants were interpolated from the experimental data (see Fig. S6 in ESI†). Thus, the DDinter mechanism does not have any adjustable parameters. This mechanism has negligible T2 influence due the fast diffusion. The most significant mechanisms to explain 1/T1 are the DDinter, DDHXe-L and CSA-L mechanisms. Table 3 shows the resulting parameters of the Arrhenius model in bold (columns 4–7) with 95% confidence interval in brackets. The values of the cavity correlation time τL and exchange rate kex at 298 K are given in columns 2 and 3 of Table 3. The exchange rates are in close proximity to our previous estimation, in which the chemical shift exchange mechanism was taken into account.28 The exchange rate of the HL sample is 3–5 smaller than in the LL and ML samples, because almost all cage and window cavities are occupied by xenon atoms, restricting significantly the exchange between the cavities. Likewise, the cavity correlation time representing local dynamics show factor 70 slower dynamics at the HL sample than at the other samples. The activation energy is lower for the exchange process as compared to the local cage dynamics.| Gas load | τ L (ns) | k ex (108 s−1) | τ −1ex0 (108 s−1) | E ex (kJ mol−1) | τ −1L0 (1010 s−1) | E L (kJ mol−1) |
|---|---|---|---|---|---|---|
| HL | 25 [23, 29] | 0.8 [0.7, 0.9] | 45 [30, 65] | 9.8 [8.7, 11] | 47 [35, 61] | 23 [22, 24] |
| ML | 0.36 [0.3, 0.4] | 4.9 [4, 6] | 51 [11, 117] | 5.5 [3, 8] | 55 [24, 105] | 13 [11, 14] |
| LL | 0.5 [0.4, 0.7] | 2.9 [2.7, 3.2] | 8.9 [3, 18] | 2.5 [0.7, 4] | 88 [3, 416] | 13 [7, 18] |
The 1/T1 increases with temperature for the HL sample and decreases for the ML and LL samples (see Fig. 4B, D and F). The higher temperature interval for HL cannot be the single explanation. It is found that both diffusion and local cavity dynamics are slower in the HL sample. It is noted that T1 is particularly sensitive to dynamics close to resonance frequency (see eqn (3), with τLω0 ∼ 1). Both the net transport (τ−1D factor 3–5) and local cavity dynamics (cavity correlation time τL factor 70) is decreased by the high loading.
The slow local dynamics at HL and the cause of 1/T1 change of temperature dependence may be rationalized with high pressure increasing the influence of slow crystallite undulations on the shape of cavity. Hence, only at the timescale of these modes can the Xe gas fully explore the cavity, leading to the longer correlation time and increased activation energy. Table 3 shows transition from sub-ns to 25 ns, which is still too fast to provide a large change in 1/T2.
In Fig. 5A–C the exchange and diffusion mobility rates kex and τ−1D of xenon are displayed versus temperature. Both have similar magnitude; however, the temperature dependence is less pronounced for kex. This is also reflected in the activation energies, which are larger for diffusion than for exchange; the experimentally determined diffusion activation energies (see Fig. S6 in ESI†) are 33 ± 1, 11 ± 0.5 and 19 ± 5 kJ mol−1 for the HL, ML and LL samples, respectively, which are larger than the Eex values shown in Table 3.
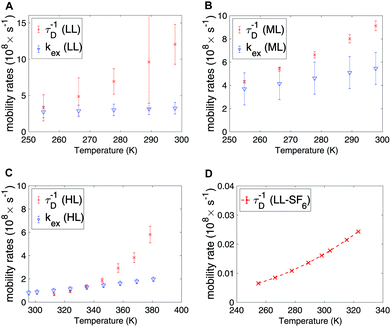 | ||
| Fig. 5 Exchange and diffusion mobility rates for xenon in the (A) LL, (B) ML and (C) HL samples. (D) Diffusion mobility rate for SF6 in the LL sample, extracted from Arrhenius law. | ||
4.3 SF6
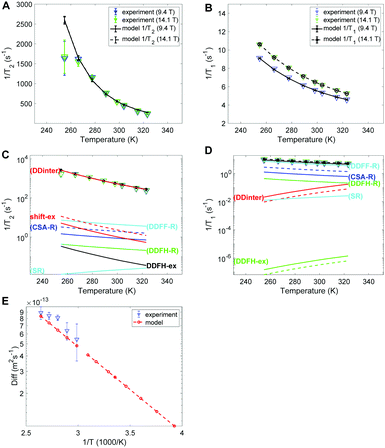
The experimental and modelled 1/T2 and 1/T1 values of SF6 are shown in Fig. 6A and B, respectively. The corresponding individual mechanism are displayed in Fig. 6C and D. The 1/T2 data are explained by the DDinter mechanism. For 1/T1 DDFF-R together with DDFH-R and CSA-R play significant roles. The estimate of SR and DDinter is shown to have negligible contribution. The diffusion data is displayed in Fig. 6E. Due to the very slow diffusion of SF6 in CC3-R, we were able to measure diffusion coefficients only at high temperatures and the relaxation modeling extends the diffusion coefficient range to the lower temperature range. Diffusion is here modeled with one activation energy over the whole temperature range. Considering the ML T1 experimental data (see Fig. S1B in ESI†) it is seen that a factor of 5 change is seen in increasing from LL to ML. This together change in lineshape is explained in terms of some free SF6 gas present in ML sample (see Section 4.1).In Table 4 the estimated parameters are provided with 95% confidence interval. The closest contact H–F spin distance is estimated to be 4.1 Å. This is relatively close to the static QC configuration estimate, 5.7 Å, following eqn (4). For the local DD mechanisms (DDFH and DDFF) the equilibrium distances were scaled down by 43% in the model; this is expected to be within a plausible range of distance deviations due to thermal motion. The SF6 molecule has a rotational correlation time of 6.7 ps and a diffusion constant of 1.08 × 10−13 m2 s−1 at 298 K. These are computed from the estimated Arrhenius parameters (see Table 4). From Fig. 5D it is noted that SF6 has more than two orders of magnitude slower diffusion as compared to the xenon samples. The model predicts 0.999 gas molar fraction of the cage cavity. The computed 19F chemical shift difference between the cage and window cavities of 10.7 ppm together with the uneven populations gives a small shift-ex contribution (Fig. 6C). The Xe study suggest that exchange rate is in the regime of inverse diffusion correlation time (Fig. 5). Hence, kex is approximated as τ−1D in the SF6 shift-ex and DDFH-ex to keep adjustable parameters at a minimum.
| d HF (Å) | ScaleR | X C | τ R (ps) | D (10−13 m2 s−1) |
|---|---|---|---|---|
| 4.09 [4.06, 4.13] | 0.5673 [0.5656, 0.5688] | 0.999 [0.99, 1] | 6.7 [6.6, 6.8] | 1.08 [1.06, 1.1] |
5 Conclusions
In this work, adsorption and dynamics of SF6 and xenon gases in CC3-R organic porous material was studied by 19F and 129Xe relaxation and diffusion NMR. The experiments show that the mobility of xenon decreases significantly close to the saturation of the cage and window cavity sites. Diffusion of SF6 in CC3-R is two orders of magnitude slower than that of xenon due to its larger size. Much more detailed understanding about the dynamics and relaxation mechanism was achieved by building a common model for T1, T2 and diffusion data. The model confirmed that cage to window exchange is a completely dominating mechanisms for 129Xe T2 relaxation (Fig. 4) and the exchange rate is about 108 s−1 (Fig. 5). The T1 relaxation is dominated by the diffusion modulated dipole–dipole (DDinter) relaxation as well as the CSA and DDHXe-L relaxation due to the local cavity mobility (τL). This is in contrast to the low loading SF6T2 data, where the dominating mechanism is diffusion modulated dipole–dipole relaxation (Fig. 6); for T1 the local tumbling of SF6 in the cage cavity is the key dynamics entering the dipole–dipole (DDFF) and CSA mechanisms. The detailed information about gas transport in organic cages is expected to stimulate the design of these systems further for potential applications such as selective separation of noble gases and SF6.Author contributions
P. H. developed the relaxation model and wrote first complete manuscript draft, using the experimental material from M. A. J. and S. K. Xenon trajectories were simulated by P. L., SF6 QC was computed by S. K. NMR experiments were performed by M. A. J. and S. K. The CC3-R material was synthesized by L. C., D. H., T. H. and A. C. Discussion of relaxation model: P. H., P. L., M. A. J., S. K. and V.-V. T. Planning the NMR experiments: V.-V. T. All authors contributed in writing the paper.Conflicts of interest
There are no conflicts to declare.Acknowledgements
This work was supported by innovation programme under the Marie Sklodowska-Curie grant no. 703446, the Kvantum institute (University of Oulu) and the CA15209 COST Action (EURELAX). The financial support of the European Research Council (ERC) under Horizon 2020 (H2020/2018–2022/ERC grant agreement no. 772110), Academy of Finland (grants #289649, 285666, 294027 and 319216) are also acknowledged. We thank the Engineering and Physical Sciences Research Council (EPSRC) for financial support under Grant EP/N004884/1. The computational resources were provided by the CSC – IT Center for Science, Finland and the Finnish Grid and Cloud Infrastructure (FGCI) (urn:nbn:fi:research-infras-2016072533).References
- M. E. Davis, Nature, 2002, 417, 813–821 CrossRef CAS PubMed.
- A. G. Slater and A. I. Cooper, Science, 2015, 348, 988 CrossRef CAS.
- M. von Delius and D. A. Leigh, Chem. Soc. Rev., 2011, 40, 3656–3676 RSC.
- H. Wang, K. Yao, Z. Zhang, J. Jagiello, Q. Gong, Y. Han and J. Li, Chem. Sci., 2014, 5, 620–624 RSC.
- J. J. Perry, S. L. Teich-Mcgoldrick, S. T. Meek, J. A. Greathouse, M. Haranczyk and M. D. Allendorf, J. Phys. Chem. C, 2014, 118, 11685–11698 CrossRef CAS.
- G. L. Bozec, S. Giraudet, L. L. Polles and P. L. Cloirec, Langmuir, 2017, 33, 1605–1613 CrossRef.
- J. Zhao, K. Xie, R. Singh, G. Xiao, Q. Gu, Q. Zhao, G. Li, P. Xiao and P. A. Webley, J. Phys. Chem. C, 2018, 122, 18933–18941 CrossRef CAS.
- A. J. Rieth and M. Dincă, J. Am. Chem. Soc., 2018, 140, 3461–3466 CrossRef CAS PubMed.
- C. S. Diercks and O. M. Yaghi, Science, 2017, 355, 923–931 CrossRef CAS.
- M. Carta, R. Malpass-Evans, M. Croad, Y. Rogan, J. C. Jansen, P. Bernardo, F. Bazzarelli and N. B. McKeown, Science, 2013, 339, 303–307 CrossRef CAS PubMed.
- P. T. Callaghan, Translational Dynamics and Magnetic Resonance: Principles of Pulsed Gradient Spin Echo NMR, Oxford University Press, Oxford, 2011 Search PubMed.
- J. Kärger, D. M. Ruthven and D. N. Theodorou, Diffusion in Nanoporous Materials, Wiley-VCH, Weinheim, 2012 Search PubMed.
- D. Kruk, Understanding Spin Dynamics, Pan Stanford Publishing, Singapore, 2016 Search PubMed.
- A. R. Ravishankara, S. Solomon, A. A. Turnipseed and R. F. Warren, Science, 1993, 259, 194–199 CrossRef CAS PubMed.
- A. A. Lindley and A. McCulloch, J. Fluorine Chem., 2005, 126, 1457–1462 CrossRef CAS.
- I. Senkovska, E. Barea, J. A. R. Navarro and S. Kaskel, Micropor. Mesopor. Mater., 2012, 156, 115–120 CrossRef CAS.
- S. Solomon, D. Qin, M. Manning, Z. Chen, M. Marquis and K. B. Averyt, in Global climate projections, ed. M. Tignor and H. L. Miller, Cambridge University Press, 2007 Search PubMed.
- R. T. Yang, Adsorbents: fundamentals and applications, Hoboken, New Jersey, 2003, vol. 78 Search PubMed.
- D. V. Cao and S. Sircar, Adsorption, 2001, 7, 73–80 CrossRef CAS.
- I. A. Riddell, M. M. J. Smulders, J. K. Clegg and J. R. Nitschke, Chem. Commun., 2011, 47, 457–459 RSC.
- L. Fusaro, E. Locci, A. Lai and M. Luhmer, J. Phys. Chem. B, 2008, 112, 15014–15020 CrossRef CAS PubMed.
- F. G. Kerry, Industrial Gas Handbook: Gas Separation and Purification, CRC Press, Boca Raton, 1st edn, 2007 Search PubMed.
- T. Mitra, K. E. Jelfs, M. Schmidtmann, A. Ahmed, S. Y. Chong, D. J. Adams and A. I. Cooper, Nat. Chem., 2013, 5, 276–281 CrossRef CAS.
- T. Hasell and A. I. Cooper, Nat. Rev. Mater., 2016, 1, 16053 CrossRef CAS.
- L. Chen, P. S. Reiss, S. Y. Chong, D. Holden, K. E. Jelfs, T. Hasell, M. A. Little, A. Kewley, M. E. Briggs, A. Stephenson, K. M. Thomas, J. A. Armstrong, J. Bell, J. Busto, R. Noel, J. Liu, D. M. Strachan, P. K. Thallapally and A. I. Cooper, Nat. Mater., 2014, 13, 954–960 CrossRef CAS PubMed.
- T. Tozawa, J. T. A. Jones, S. I. Swamy, S. Jiang, D. J. Adams, S. Shakespeare, R. Clowes, D. Bradshaw, T. Hasell, S. Y. Chong, C. Tang, S. Thompson, J. Parker, A. Trewin, J. Bacsa, A. M. Z. Slawin, A. Steiner and A. I. Cooper, Porous Organic Cages, Nat. Mater., 2009, 8, 973–978 CrossRef CAS.
- T. Hasell, M. Miklitz, A. Stephenson, M. A. Little, S. Y. Chong, R. Clowes, L. Chen, D. Holden, G. A. Tribello, K. E. Jelfs and A. I. Cooper, Porous Organic Cages for Sulfur Hexafluoride Separation, J. Am. Chem. Soc., 2016, 138, 1653–1659 CrossRef CAS.
- S. Komulainen, J. Roukala, V. V. Zhivonitko, M. A. Javed, L. Chen, D. Holden, T. Hasell, A. Cooper, P. Lantto and V.-V. Telkki, Chem. Sci., 2017, 8, 5721–5727 RSC.
- D. Hoepfel, M. Aluas, M. Terekhov, L. R. Oellrich and S. Neutzler, Magn. Reson. Chem., 2005, 43, 926–936 CrossRef.
- M. J. Paul, S. R. Biegalski and D. A. Haas, Int. J. Mod. Phys.: Conf. Ser., 2018, 48, 1860124 Search PubMed.
- M. J. Couch, I. K. Ball, T. Li, M. S. Fox, B. Biman and M. S. Albert, J. Magn. Reson. Imaging, 2019, 49, 343–354 CrossRef.
- H. Tervonen, J. Saunavaara, L. P. Ingman and J. Jokisaari, J. Phys. Chem. B, 2006, 110, 16232–16238 CrossRef CAS.
- L. Fusaro, E. Locci, A. Lai and M. Luhmer, J. Phys. Chem. B, 2010, 114, 3398–3403 CrossRef CAS PubMed.
- D. A. Barskiy, A. M. Coffey, P. Nikolaou, D. M. Mikhaylov, B. M. Goodson, R. T. Branca, G. J. Lu, M. G. Shapiro, V. V. Telkki, V. V. Zhivonitko, I. V. Koptyug, O. G. Salnikov, K. V. Kovtunov, V. I. Bukhtiyarov, M. S. Rosen, M. J. Barlow, S. Safavi, I. P. Hall, L. Schröder and E. Y. Chekmenev, Chem. – Eur. J., 2017, 23, 725–751 CrossRef CAS PubMed.
- G. W. Miller, K. Ruppert, F. W. Hersman, T. A. Altes, J. Ketel, J. F. Mata, I. M. Dregely, J. P. Mugler, I. C. Ruset and S. Ketel, PNAS, 2010, 107, 21707–21712 CrossRef PubMed.
- V. V. Telkki, C. Hilty, S. Garcia, E. Harel and A. Pines, J. Phys. Chem. B, 2007, 111, 13929–13936 CrossRef CAS PubMed.
- J. Jokisaari, in NMR of Ordered Liquids, ed. E. E. Burnell and C. A. de Lange, Kluwer, Dordrecht, 2003, pp. 109–135 Search PubMed.
- M. Raue, J. Colell, A. Liebisch, B. Blümich, S. Appelt, S. Glöggler, P. Türschmann and T. Mang, ChemPhysChem, 2012, 13, 4120–4123 CrossRef PubMed.
- M. A. Javed, S. Komulainen, H. Daigle, B. Zhang, J. Vaara, B. Zhou and V.-V. Telkki, Micropor. Mesopor. Mater., 2019, 281, 66–74 CrossRef CAS.
- G. Saielli, A. Bagno, F. Castiglione, R. Simonutti, M. Mauri and A. Mele, J. Phys. Chem. B, 2014, 118, 13963–13968 CrossRef CAS.
- V. V. Telkki, J. Lounila and J. Jokisaari, J. Chem. Phys., 2006, 124, 034711 CrossRef.
- E. Weiland, M. A. Springuel-Huet, A. Nossov and A. Gédéon, Microporous Mesoporous Mater., 2016, 225, 41–65 CrossRef CAS.
- G. K. Seward, Y. Bai, N. S. Khan and I. Dmochowski, J. Chem. Sci., 2011, 2, 1103–1110 CAS.
- L. Schröder, Proc. Natl. Acad. Sci. U. S. A., 2014, 111, 11697–11702 CrossRef PubMed.
- U. von Toussaint, Rev. Mod. Phys., 2011, 83, 943–999 CrossRef.
- Y. Ayant, E. Belorizky, J. Alizon and J. Gallice, J. Phys., 1975, 36, 991–1004 CrossRef CAS.
- L.-P. Hwang and J. H. Freed, J. Chem. Phys., 1975, 63, 4017–4025 CrossRef CAS.
- J. Kowalewski and L. Mäler, Nuclear Spin Relaxation in Liquids: Theory, Experiments, and Applications, Taylor & Francis Group, New York, USA, 2006 Search PubMed.
- P. S. Hubbard, Phys. Rev., 1963, 131, 1155–1165 CrossRef CAS.
- TURBOMOLE V7.2 2017, a development of University of Karlsruhe and Forschungszentrum Karlsruhe GmbH, 1989–2007, TURBOMOLE GmbH, since 2007; available from http://www.turbomole.com.
- A. D. Becke, Phys. Rev. A: At., Mol., Opt. Phys., 1988, 38, 3098 CrossRef CAS PubMed.
- C. Lee, W. Yang and R. G. Parr, Phys. Rev. B: Condens. Matter Mater. Phys., 1988, 37, 785 CrossRef CAS PubMed.
- A. D. Becke, J. Chem. Phys., 1993, 98, 5648 CrossRef CAS.
- S. Grimme, J. Antony, S. Ehrlich and H. Krieg, J. Chem. Phys., 2010, 132, 154104 CrossRef PubMed.
- F. Weigend and R. Ahlrichs, Phys. Chem. Chem. Phys., 2005, 7, 3297 RSC.
- J. Vähäkangas, S. Ikäläinen, P. Lantto and J. Vaara, Phys. Chem. Chem. Phys., 2013, 15, 4634 RSC.
- N. Metropolis, A. W. Rosenbluth, M. N. Rosenbluth, A. H. Teller and E. Teller, J. Chem. Phys., 1953, 21, 1087–1092 CrossRef CAS.
Footnote |
| † Electronic supplementary information (ESI) available: Additional details of experimental methods and results as well as computational modelling. See DOI: 10.1039/c9cp04379a |
| This journal is © the Owner Societies 2019 |