Divergent excited state proton transfer reactions of bifunctional photoacids 1-ammonium-2-naphthol and 3-ammonium-2-naphthol in water and methanol†
Abstract
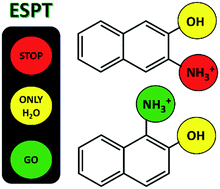
This paper highlights the challenge of predicting the excited state proton transfer (ESPT) reactions of small organic compounds with multiple proton transfer sites. Aminonaphthols, naphthalene compounds with both hydroxyl and amino substituents, can be viewed as a combination of two monoprotic photoacids, naphthol and naphthylammonium. Here, the ESPT reactions of 3-ammonium-2-naphthol (3N2OH) and 1-ammonium-2-naphthol (1N2OH) were studied in water and methanol using a combination of steady-state and time-correlated single-photon counting emission spectroscopy. For 3N2OH, ESPT was observed at the OH site in water but at neither of the sites in methanol; for 1N2OH, ESPT was observed at both the OH and NH3+ sites in water but only at the NH3+ site in methanol. Evidence of ESPT at the NH3+ site is limited for aminonaphthols. The divergent dynamics of 3N2OH and 1N2OH in water and methanol are discussed; dependent on the substitution and solvent, the ESPT reactions were analysed within the frameworks of reference photoacids 2-naphthol and 1-naphthylammonium. The application of crown ether and salt to control the release of select protons in non-aqueous media is also discussed.
- This article is part of the themed collection: 2019 PCCP HOT Articles


 Please wait while we load your content...
Please wait while we load your content...