State-interaction pair density functional theory for locally avoided crossings of potential energy surfaces in methylamine†
Chen
Zhou
 ,
Laura
Gagliardi
,
Laura
Gagliardi
 * and
Donald G.
Truhlar
* and
Donald G.
Truhlar
 *
*
Department of Chemistry, Chemical Theory Center, and Minnesota Supercomputing Institute, University of Minnesota, Minneapolis, Minnesota 55455-0431, USA. E-mail: gagliard@umn.edu; truhlar@umn.edu
First published on 4th June 2019
Abstract
The strong couplings between electronic states in conical intersection regions are among the most challenging problems in quantum chemistry. XMS-CASPT2, a second-order multireference quasidegenerate perturbation theory, has been successful in describing potential energy surfaces near the conical intersections. We have recently proposed a less expensive method for this problem, namely state-interaction pair-density functional theory (SI-PDFT), which considers the coupling between electronic states described by multiconfiguration pair-density functional theory (MC-PDFT). Here we test the accuracy of SI-PDFT for closely coupled potential energy surfaces of methylamine along five different reaction paths for N–H bond fission. We choose paths that pass close to a conical intersection of the ground and first excited states. We find that SI-PDFT predicts potential energy curves and energy splittings near the locally avoided crossing in close proximity to those obtained by XMS-CASPT2. This validates the method for application to photochemical simulations.
1. Introduction
Potential energy surfaces (PESs) are the starting point for studies of molecular energy states and dynamical processes.1 Standard methods of electronic structure theory yield the adiabatic potential energy surfaces; however, the calculations require special care when two or more adiabatic surfaces of the same symmetry are degenerate or nearly degenerate and hence closely coupled. The intersection of multi-dimensional PESs is called a conical intersection, and such intersections are a prominent motif in the photochemistry of chemical and biological processes. Because the internal coordinate space has a dimensionality of (3N − 6), where N is the number of atoms, the conical intersection space of PESs of the same spatial and spin symmetry has dimensionality 3N − 8 or lower.2–5 (We here exclude the cases of linear intersections, which may be glancing rather than conical. Furthermore we note that intersections of states with different symmetry can have dimensionality 3N − 7.) Most trajectories in conical intersection regions do not pass precisely through conical intersection seams but rather close to them where the intersection is avoided along the path; we call this a locally avoided crossing (LAC). Therefore, studies of coupled potential energy surfaces along paths with LACs are of great interest. In regions near a conical intersection, the behavior of the intersecting surfaces is controlled by the conical intersection;6 however the strong couplings between electronic states in such conical intersection regions is one of the most challenging problems in electronic structure theory.Methylamine (CH3NH2) is the smallest amine, and hence serves as a prototype; consequently there are many studies of its PESs, dynamics, and spectroscopy.7–20 Michael and Noyes studied the photochemical decomposition of methylamine and found four major dissociation pathways, among which the N–H dissociation channel was detected to be dominant (∼75%) for excitation by 194–244 nm radiation.7 Kassab et al. showed that the first excited state of methylamine is dominated by the excitation of a lone pair electron of the nitrogen atom to an orbital mixing with Rydberg 3s of N atom and C–N antibonding character; a small barrier for the N–H bond fission surface was discovered and compared with that of C–N bond fission.8 Butler and coworkers studied the emission spectrum of methylamine excited at 222 nm by photofragment kinetic energy distribution measurements, and found that both the N–H and C–N bond fission channels pass the conical intersection seam.9 By performing calculations with complete active space self-consistent-field (CASSCF) and multireference configuration interaction with single and double excitations (MRCISD), Dunn and Morokuma showed that the dissociation of N–H bond yields the ground-state products via decay mediated by the conical intersection, while the dissociation of C–N bond proceeds mostly on the excited surface.11 The excitation spectrum of methylamine and its isotopomers for the first excited state was characterized by Baek et al., and they studied the dynamics for two paths for N–H bond dissociation through the conical intersection region by using the velocity map ion imaging technique as a probe for H or D fragment.12 The tunneling of H (D) atom during N–H (N–D) bond fission for photoexcited methylamine and its isotopomers was studied by Levi et al., and PESs of the ground and first excited states are obtained with MRCI method.15 The N–H bond fission was then shown to be dominated by quantum tunneling.16 Morokuma and coworkers used the anharmonic downward distortion following (ADDF) method and the artificial force induced reaction (AFIR) method to study various reaction pathways starting from the first excited state.19 The dynamics of methylamine studied by Epshtein et al. again demonstrated the importance of the conical intersection in N–H bond fission.20
Due to the involvement of the conical intersection region in the N–H bond fission, computational methods should be chosen carefully. Multireference configuration interaction (MRCI)21 and multireference perturbation theory (complete active space perturbation theory (MS-CASPT2),22,23 extended MS-CASPT2 (XMS-CASPT2)24 multiconfiguration quasidegenerate perturbation theory (MC-QDPT),25 and extended MC-QDPT (XMC-QDPT)26) involving the diagonalization of Hamiltonians approximating the full dynamic correlation have been the methods for choice for describing PESs in the conical intersection region. XMS-CASPT2 differs from MS-CASPT2 in that it includes the entire model-space block of the Fock operator in the reference space in the zeroth-order Hamiltonian rather than just the diagonal elements; this makes it invariant (except for the level shift used to avoid intruder state problems) with respect to a unitary transformation of the reference wave functions, and it corrects a systematic overestimation of the off-diagonal elements of the model-space Hamiltonian in the region of strong state mixing. Shiozaki et al.24 and Sen and Schapiro27 have shown that XMS-CASPT2 is more accurate than MS-CASPT2 both near and far from intersections, and it avoids unphysical artifacts that sometimes occur in MS-CASPT2. (XMC-QDPT should show similar improvement over MC-QDPT, the difference being that XMS-CASPT2 and MS-CASPT2 use internal contraction, whereas XMC-QDPT and MC-QDPT use uncontracted configuration state functions (CSFs).)
The above methods, however, are often too expensive for use in practical calculations. To avoid the high cost, state-interaction pair-density functional theory (SI-PDFT) has recently been proposed.28 SI-PDFT involves diagonalizing a model-space Hamiltonian constructed with the MC-PDFT method,29,30 and has been applied successfully to a few example problems, namely the lithium fluoride dissociation,28 the LAC of the first two singlet states of phenol along two paths for photodissociation of the O–H bond,28 and the PES of a spiro mixed valence compound.31 In the present paper, we will provide additional systematic tests of SI-PDFT by applying it to calculate the PESs of the ground (S0) and first excited (S1) states of N–H bond fission in methylamine and comparing the results to MS-CASPT2 and XMS-CASPT2.
2. Methodology
The CASSCF steps of the SI-PDFT method are designed to calculate a set of orthogonal multi-configuration wave functions and their energies for the N lowest-energy electronic states of a particular spatial and spin symmetry, if spatial symmetry is used, or for the N lowest-energy electronic states of a particular spin symmetry, if spatial symmetry is not present or not used. These N states span a space called the model space, and they do not diagonalize the Hamiltonian in this space; rather they combine a single-state approximation for the ground state with state-averaged approximations for the excited states in a way that can serve as a basis for PDFT calculations on states that may be closely coupled. The method was published in full in a previous paper;28 here we just summarize the procedure.In SI-PDFT, first one calculates a single state-specific CASSCF wave function ψSS for the ground state, and this is written as,
 | (1) |
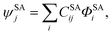 | (2) |
 | (3) |
| Θ1 = A1P|ψSS〉, | (4) |
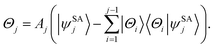 | (5) |
 | (6) |
 is one-body density matrix for state Θi, Eot is the on-top energy computed from the on-top density functional of the density ρΘi and the on-top density ΠΘi. The off-diagonal elements of the model-space Hamiltonian are
is one-body density matrix for state Θi, Eot is the on-top energy computed from the on-top density functional of the density ρΘi and the on-top density ΠΘi. The off-diagonal elements of the model-space Hamiltonian are| Hij = 〈Θi,|H|Θj〉. | (7) |
3. Computational details
The PESs of the S0 and S1 states for N–H bond fission in methylamine molecule are calculated without spatial symmetry (i.e., N = 2 in C1 symmetry). Since the S1 state is dominated by excitation of an electron from the 2pπ lone pair orbital of the nitrogen atom to its 3s Rydberg orbital, the diffuse basis set 6-31++G** is used for all the calculations, in order to describe the Rydberg orbitals correctly.11The MS-CASPT2, XMS-CASPT2, and SI-PDFT calculations are based on an SA-CASSCF wave function with an active space consisting of 6 active electrons on 6 active orbitals. The active electrons are four σ bonding electrons and a pair of 2pπ electrons on the nitrogen atom, while the active orbitals include two σ bonding orbitals, the 2pπ lone-pair orbital on nitrogen and its corresponding 3pπ Rydberg orbital, a 3s Rydberg orbital on nitrogen, and a σ* orbital to describe the dissociation of an N–H bond. The ground-state CASSCF calculations are based on the same active space.
We started with four optimized conformations of methylamine shown in Fig. 1. The H6–C4–N1–H3 dihedral angles of the four conformations are 0°, 90°, 95° and 100°. Methylamine with H6–C4–N1–H3 dihedral angles of 0° and 90° has been investigated in varieties of previous studies,8,11,19 and we denote these conformations here as the eclipsed (0°) and staggered (90°) conformations. The equilibrium geometries of methylamine of these two conformations are optimized at XMS-CASPT2 level with the g4 zeroth-order Hamiltonian32 and a level shift33,34 of 0.3 a.u. by Molpro.35 (The N1–H3 bond length is 1.002 Å for the eclipsed case and 1.015 Å for the staggered case, while the N1–H2 bond length is 1.003 Å for the eclipsed case and 1.015 Å for the staggered case.) The geometries of methylamine with a H6–C4–N1–H3 dihedral angle of 95° and 100° come from rotating the amine group of the staggered conformation without geometry optimization.
 | ||
| Fig. 1 Methylamine molecule with H6–C4–N1–H3 dihedral angles of (a) 0°, (b) 90°, (c) 95° and (d) 100°. For each dihedral angle the figure shows a side view and a view along the N1–C4 bond. | ||
For all reaction paths, one H atom was separated from the amine group along the N–H bond axis with all the other coordinates fixed. Such paths will not go through the conical intersection, but they pass nearby during the dissociation process so there is an LAC along the dissociation path. The energy splitting ΔELAC is defined as the minimum energy difference of the two adiabatic states along a given dissociation path, and we fit the results to quadratic function in the vicinity of this minimum to find the energy splitting and the N–H bond distance (RLAC) at which it occurs.
For each point on the reaction path, we used the orbitals of the previous point as the initial guess orbitals, and in all cases, the orbitals of the SS calculation converged properly to the ground-state orbitals.
All the XMS-CASPT2 calculations are performed with Molpro with the multi-state multi reference23 option. All the MS-CASPT2 and SI-PDFT are performed with the OpenMolcas 8.3 software package36,37 with the previously implemented SI-PDFT module.28 In the MS-CASPT2 calculations, we studied the effect of the IPEA shift38 and real or imaginary level shifts.39 In SI-PDFT calculations, two on-top density functionals, tPBE29 and ftPBE,40 were used, and they are denoted as SI-tPBE and SI-ftPBE.
4. Results and discussion
4.1 Effect of level shifts
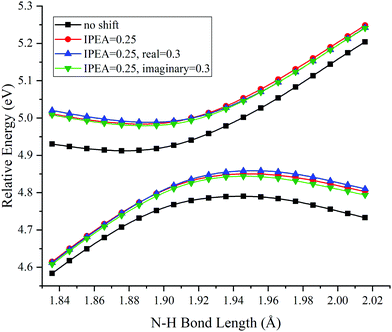
Two choices were examined for carrying out MS-CASPT2 calculations. The first is whether to attempt to improve systematic errors by applying the IPEA shift to modify the energies of active orbitals. The second is whether to minimize intruder state problems by shifting the energy denominators; either real or imaginary level shifts can be used. We made calculations to study the effect of these choices for methylamine with the staggered conformation, and the results are in Table 1 and Fig. 2. Table 1 shows that the shifts have only a small effect on the energy splitting (∼0.01 eV) and its LAC location (∼0.01 A), and Fig. 2 shows that they have only a small effect on the shapes of the potentials.| R LAC | ΔELAC | |
|---|---|---|
| No shift | 1.908 | 0.159 |
| IPEA = 0.25 | 1.916 | 0.168 |
| IPEA = 0.25, real shift = 0.3 | 1.921 | 0.163 |
| IPEA = 0.25, imaginary shift = 0.3 | 1.918 | 0.167 |
Therefore all the remaining calculations are carried out using the values of 0.25 a.u. for IPEA and 0.3 a.u. for real shifts in MS-CASPT2 (the former is the default in OpenMolcas, and the later was used in ref. 19). For XMS-CASPT2, one cannot apply the IPEA shift because of the mixing of the states in this method; we used a real shift of 0.3 a.u. for all XMS-CASPT2 calculations.
4.2 SI-PDFT study for N–H fission passing close to a conical intersection
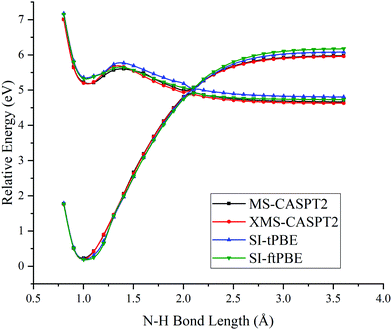
The first case for which we study a dissociation path by using SI-PDFT is the N–H bond fission with the eclipsed geometry. Since the two H atoms of the amine group are inequivalent in the eclipsed conformation, the dissociation of the H3 hydrogen is denoted as the eclipsed-H3 path, and the bond dissociation of the N1–H2 bond is denoted as the eclipsed-H2 path. The PESs calculated for these two N–H fissions by MS-CASPT2, XMS-CASPT2, SI-tPBE, and SI-ftPBE are shown in Fig. 3 and 4. The behavior of the SI-PDFT potentials is quite similar to that of MS-CASPT2 and XMS-CASPT2 for both eclipsed dissociation paths. The LAC of the S0 and S1 states occurs at an N–H bond length in the range 2.00–2.11 Å for all the methods (Table 2). | ||
| Fig. 3 PESs for N–H bond fission of eclipsed-H3 methylamine with various methods. The relative energies are compared with those of the equilibrium geometry for each method. | ||
 | ||
| Fig. 4 PESs for N–H bond fission of eclipsed-H2 methylamine with various methods. The relative energies are compared with those of the equilibrium geometry for each method. | ||
| R LAC | ΔELAC | |
|---|---|---|
| Eclipsed-H3 | ||
| MS-CASPT2 | 2.012 | 0.0002 |
| XMS-CASPT2 | 2.002 | 0.001 |
| SI-tPBE | 2.069 | 0.010 |
| SI-ftPBE | 2.052 | 0.002 |
| Eclipsed-H2 | ||
| MS-CASPT2 | 2.055 | 0.007 |
| XMS-CASPT2 | 2.044 | 0.005 |
| SI-tPBE | 2.111 | 0.008 |
| SI-ftPBE | 2.094 | 0.004 |
| Staggered | ||
| MS-CASPT2 | 1.918 | 0.167 |
| XMS-CASPT2 | 1.903 | 0.207 |
| SI-tPBE | 1.976 | 0.236 |
| SI-ftPBE | 1.970 | 0.260 |
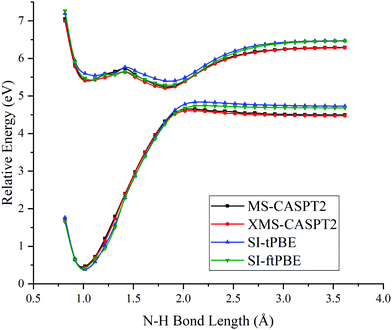
Next we examined the N–H bond fission with the staggered conformation. This is illustrated in Fig. 5. For this staggered conformation, the LAC occurs at a slightly shorter N–H bond length (around 1.9 Å). The SI-PDFT calculations correctly predict that the energy splitting of the S0 and S1 states is larger than for the eclipsed conformation. Table 3 shows better agreement between SI-tPBE and XMS-CASPT2 than the agreement between MS-CASPT2 and XMS-CASPT2.
 | ||
| Fig. 5 PESs for N–H bond fission of staggered methylamine with various methods. The relative energies are compared with those of the equilibrium geometry for each method. | ||
| R LAC | ΔELAC | |
|---|---|---|
| 95° | ||
| MS-CASPT2 | 1.926 | 0.279 |
| XMS-CASPT2 | 1.909 | 0.323 |
| SI-tPBE | 1.981 | 0.327 |
| SI-ftPBE | 1.975 | 0.360 |
| 100° | ||
| MS-CASPT2 | 1.948 | 0.699 |
| XMS-CASPT2 | 1.937 | 0.724 |
| SI-tPBE | 2.005 | 0.708 |
| SI-ftPBE | 1.997 | 0.731 |
Fig. 6 shows closer views of the locally avoided crossing region for the three cases considered so far. The shapes of the potential curves given by SI-PDFT are quite similar to those obtained by XMS-CASPT2, although the N–H bond length at the LAC is longer than that with XMS-CASPT2 by around 0.06 and 0.04 Å for tPBE and ftPBE, respectively. For the two eclipsed conformations, XMS-CASPT2 predicts the splittings to be about 0.01 eV, while SI-PDFT predicts both of them to be less than 0.02 eV. For the staggered conformation, the energy splitting at the LAC is 0.21 eV for XMS-CASPT2 calculation, while energy splittings of 0.24 and 0.26 eV are obtained by SI-tPBE and SI-ftPBE, respectively. We conclude that SI-PDFT gives descriptions of the PESs for the studied N–H bond fissions that are similar to those obtained with XMS-CASPT2, and the accuracy is good enough that SI-PDFT should be useful for photochemical simulations.
4.3 SI-PDFT study for N–H fission with passage farther from the conical intersection
To test the performances of SI-PDFT for N–H bond fission that passes farther away from the conical intersection, we rotated the plane formed by the amine group in staggered methylamine to change the H6–C4–N1–H3 dihedral angle from 90° to 95° and 100°. (The rotation is carried out without geometry optimization.) The potential curves for dissociation with these two dihedral angles are shown in Fig. 7 and 8, which show much larger energy splitting at the LAC than that of eclipsed and staggered conformations. The larger energy splitting can be observed by both SI-PDFT and XMS-CASPT2 calculations. Fig. 9 shows close-ups of the avoided crossing region, and we see good agreement of SI-PDFT with XMS-CASPT2. The good performance of SI-PDFT is also seen in Table 3, where the energy splitting difference of SI-tPBE at the LAC is in excellent agreement with XMS-CASPT2.5. Conclusions
The potential energy curves for five different N–H dissociation paths of methylamine have been studied with the MS-CASPT2, XMS-CASPT2 and SI-PDFT methods. These paths pass the conical intersection by varying amounts of distance. The performance of SI-PDFT, as judged by comparison to XMS-CASPT2, is very good. The minimum splittings along the paths predicted by SI-PDFT with the tPBE on-top functional are close to those calculated by XMS-CASPT2 along all five paths studied, and those predicted by SI-PDFT with the ftPBE on-top functional are also reasonable. With both on-top functionals the deviation of the minimum energy splitting from that predicted by XMS-CASPT2 is less than 0.06 eV for all the five paths. We also find that SI-PDFT predicts the correct shapes for the PESs near the conical intersections. The excitation energies are also quite reasonable.Since the PT2 post-SCF correction to the CASSCF energy is quite demanding in terms of computational time and memory, the economical PDFT methods (whose cost is usually dominated by the CASSCF step rather than the post-SCF steps) are very appealing for large systems or for photochemical simulations requiring long trajectories or a large amount of ensemble averaging. The high accuracy and much lower computational cost than MS-CASPT2 and XMS-CASPT2 make SI-PDFT a promising method to study the challenging systems with strong state interaction that occur in photochemical processes and spectroscopy.
Conflicts of interest
There are no conflicts to declare.Acknowledgements
The authors are grateful to Kelsey Parker for helpful assistance. This work is supported in part by the National Science Foundation under grant no. CHE-1746186.References
- D. G. Truhlar, Potential Energy Surfaces, in The Encyclopedia of Physical Science and Technology, ed. R. A. Meyers, Academic Press, New York, 3rd edn, 2001, vol. 13, pp. 9–13 Search PubMed.
- G. Herzberg and H. C. Longuet-Higgins, Discuss. Faraday Soc., 1963, 35, 77–82 RSC.
- C. A. Mead, J. Chem. Phys., 1979, 70, 2276–2283 CrossRef CAS.
- D. G. Truhlar and C. A. A. Mead, Phys. Rev. A: At., Mol., Opt. Phys., 2003, 68, 032501 CrossRef.
- A. W. Jasper, B. K. Kendrick, C. A. Mead and D. G. Truhlar, Non-Born-Oppenheimer Chemistry: Potential Surfaces, Couplings, and Dynamics, in Modern Trends in Chemical Reaction Dynamics: Experiment and Theory (Part 1), ed. X. Yang and K. Liu, World Scientific, Singapore, 2004, pp. 329–391 Search PubMed.
- T. C. Thompson, D. G. Truhlar and C. A. Mead, J. Chem. Phys., 1985, 82, 2392–2407 CrossRef CAS.
- J. V. Michael and W. A. Noyes, J. Am. Chem. Soc., 1963, 85, 1228–1233 CrossRef CAS.
- E. Kassab, J. Gleghorn and E. Evleth, J. Am. Chem. Soc., 1983, 105, 1746–1753 CrossRef CAS.
- G. Waschewsky, D. Kitchen, P. Browning and L. Butler, J. Phys. Chem., 1995, 99, 2635–2645 CrossRef CAS.
- C. L. Reed, M. Kono and M. N. R. Ashfold, J. Chem. Soc., Faraday Trans., 1996, 92, 4897–4904 RSC.
- K. M. Dunn and K. Morokuma, J. Phys. Chem., 1996, 100, 123–129 CrossRef CAS.
- S. J. Baek, K.-W. Choi, Y. S. Choi and S. K. Kim, J. Chem. Phys., 2003, 118, 11026–11039 CrossRef CAS.
- M. H. Park, K.-W. Choi, S. Choi, S. K. Kim and Y. S. Choi, J. Chem. Phys., 2006, 125, 084311 CrossRef PubMed.
- D.-S. Ahn, J. Lee, J.-M. Choi, K.-S. Lee, S. J. Baek, K. Lee, K.-K. Baeck and S. K. Kim, J. Chem. Phys., 2008, 128, 224305 CrossRef PubMed.
- C. Levi, R. Kosloff, Y. Zeiri and I. Bar, J. Chem. Phys., 2009, 131, 064302 CrossRef PubMed.
- R. Marom, C. Levi, T. Weiss, S. Rosenwaks, Y. Zeiri, R. Kosloff and I. Bar, J. Phys. Chem. A, 2010, 114, 9623–9627 CrossRef CAS PubMed.
- D.-S. Ahn, J. Lee, Y. C. Park, Y. S. Lee and S. K. Kim, J. Chem. Phys., 2012, 136, 024306 CrossRef PubMed.
- J. O. Thomas, K. E. Lower and C. Murray, J. Phys. Chem. Lett., 2012, 3, 1341–1345 CrossRef CAS PubMed.
- H. Xiao, S. Maeda and K. Morokuma, J. Phys. Chem. A, 2013, 117, 5757–5764 CrossRef CAS PubMed.
- M. Epshtein, Y. Yifrach, A. Portnov and I. Bar, J. Phys. Chem. Lett., 2016, 7, 1717–1724 CrossRef CAS PubMed.
- C. Woywod, W. Domcke, A. L. Sobolewski and H. J. Werner, J. Chem. Phys., 1994, 100, 1400–1413 CrossRef CAS.
- J. Finley, P.-Å. Malmqvist, B. O. Roos and L. Serrano-Andrés, Chem. Phys. Lett., 1998, 288, 299–306 CrossRef CAS.
- P. Celani and H.-J. Werner, J. Chem. Phys., 2000, 112, 5546–5557 CrossRef CAS.
- T. Shiozaki, W. Győrffy, P. Celani and H.-J. Werner, J. Chem. Phys., 2011, 135, 081106 CrossRef PubMed.
- H. Nakano, J. Chem. Phys., 1993, 99, 7983–7992 CrossRef CAS.
- A. A. Granovsky, J. Chem. Phys., 2011, 134, 214113 CrossRef PubMed.
- S. Sen and I. Schapiro, Mol. Phys., 2018, 116, 2571–2582 CrossRef CAS.
- A. M. Sand, C. E. Hoyer, D. G. Truhlar and L. Gagliardi, J. Chem. Phys., 2018, 149, 024106 CrossRef PubMed.
- G. Li Manni, R. K. Carlson, S. Luo, D. Ma, J. Olsen, D. G. Truhlar and L. Gagliardi, J. Chem. Theory Comput., 2014, 10, 3669–3680 CrossRef CAS PubMed.
- L. Gagliardi, D. G. Truhlar, G. Li Manni, R. K. Carlson, C. E. Hoyer and J. L. Bao, Acc. Chem. Res., 2017, 50, 66–73 CrossRef CAS PubMed.
- S. S. Dong, K. B. Huang, L. Gagliardi and D. G. Truhlar, J. Phys. Chem. A, 2019, 123, 2100–2106 CrossRef CAS PubMed.
- K. Andersson, Theor. Chim. Acta, 1995, 91, 31–46 CrossRef CAS.
- B. O. Roos and K. Andersson, Chem. Phys. Lett., 1995, 245, 215–223 CrossRef CAS.
- B. O. Roos, K. Andersson, M. P. Fülscher, L. Serrano-Andrés, K. Pierloot, M. Merchán and V. Molina, THEOCHEM, 1996, 388, 257–276 CrossRef CAS.
- H. Werner, P. Knowles, G. Knizia, F. Manby, M. Schütz, P. Celani, W. Györffy, D. Kats, T. Korona and R. Lindh, Molpro, University of Cardiff Chemistry Consultants (UC3), Cardiff, Wales, UK, 2015 Search PubMed.
- S. Vancoillie, M. G. Delcey, R. Lindh, V. Vysotskiy, P.-Å. Malmqvist and V. Veryazov, J. Comput. Chem., 2013, 34, 1937–1948 CrossRef CAS PubMed.
- F. Aquilante, J. Autschbach, R. K. Carlson, L. F. Chibotaru, M. G. Delcey, L. De Vico, I. F. Galván, N. Ferré, L. M. Frutos, L. Gagliardi, M. Garavelli, A. Giussani, C. E. Hoyer, G. Li Manni, H. Lischka, D. Ma, P. Å. Malmqvist, T. Müller, A. Nenov, M. Olivucci, T. B. Pedersen, D. Peng, F. Plasser, B. Pritchard, M. Reiher, I. Rivalta, I. Schapiro, J. Segarra-Martí, M. Stenrup, D. G. Truhlar, L. Ungur, A. Valentini, S. Vancoillie, V. Veryazov, V. P. Vysotskiy, O. Weingart, F. Zapata and R. Lindh, J. Comput. Chem., 2016, 37, 506–541 CrossRef CAS PubMed.
- G. Ghigo, B. O. Roos and P.-Å. Malmqvist, Chem. Phys. Lett., 2004, 396, 142–149 CrossRef CAS.
- N. Forsberg and P.-Å. Malmqvist, Chem. Phys. Lett., 1997, 274, 196–204 CrossRef CAS.
- R. K. Carlson, D. G. Truhlar and L. Gagliardi, J. Chem. Theory Comput., 2015, 11, 4077–4085 CrossRef CAS PubMed.
Footnote |
| † Electronic supplementary information (ESI) available: It contains absolute energies in hartrees of calculations, sample input files, and active orbitals (including geometry and guess orbitals). See DOI: 10.1039/c9cp02240f |
| This journal is © the Owner Societies 2019 |