Photodynamics of alternative DNA base isoguanine

Abstract

Isoguanine is an alternative nucleobase that has been proposed as a component of expanded genetic codes. It has also been considered as a molecule with potential relevance to primordial informational polymers. Here, we scrutinize the photodynamics of isoguanine, because photostability has been proposed as a critical criterion for the prebiotic selection of biomolecular building blocks on an early Earth. We discuss resonance-enhanced multiphoton ionization, IR-UV double resonance spectroscopy and pump–probe measurements performed for this molecule to track the excited-state behaviour of its different tautomeric forms in the gas phase. These experiments, when confronted with highly accurate quantum chemical calculations and nonadiabatic dynamics simulations provide a complete mechanistic picture of the tautomer-specific photodynamics of isoguanine. Our results indicate that UV-excited enol tautomers of isoguanine are relatively short lived and therefore photostable. In contrast, the biologically more relevant keto forms are trapped in dark nπ* states which are sufficiently long lived to participate in destructive photochemistry. The resulting lower photostability compared to canonical nucleobases may have been one of the reasons why isoguanine was not incorporated into DNA and RNA.

---

1 Introduction

Alternative nucleobases have long been considered as potential components of primordial informational polymers. Studies of their possible role on the Archean Earth were largely inspired by substantial difficulties in designing a prebiotically plausible synthesis of a complete set of canonical RNA nucleosides.¹ This resulted in the consideration of nucleobase analogs which undergo efficient glycosidation, namely triaminopyrimidine and barbituric acid, as potential components of a hypothetical predecessor of RNA.^2,3 Presence of extraterrestrial nucleobase analogs was also reported in carbon-rich meteorites including examples like 2,6-diaminopurine, 6,8-diaminopurine, hypoxanthine and xanthine.⁴ Other alternative nucleobases as 2-aminopurine and isocytosine (isoC) were found as the products of formamide condensation catalysed by meteoritic materials,^5–7 which indicates that these compounds could have been delivered to the surface of our planet or otherwise formed locally from readily available prebiotic precursor molecules. The fact that biology has selected a very narrow alphabet of RNA and DNA building blocks raises the question why the remaining nucleobase analogs never constituted biologically relevant nucleosides and were eradicated during the course of abiogenesis.

Recent estimates of plausible solar input and absorption properties of the terrestrial atmosphere in the prebiotic era indicate that UV light could have been a major (if not dominant) source of energy for primordial prebiotic reactions.^8,9 In point of fact, canonical DNA and RNA bases and nucleosides are characterized by remarkable photostability which signifies that their analogs might have been eliminated owing to lower resistance to damage from UV light.^10–12 In particular, photostability is manifested by ultrashort excited-state lifetimes and nearly barrierless photorelaxation pathways which have consistently been reported for all the crucial components of RNA and DNA.^13–20 Recent experimental work by Brister et al.,²¹ showed that two promising candidates for prebiotic ancestors of RNA bases, i.e. 2,4,6-triaminopyrimidine and barbituric acid, exhibit sub-picosecond excited-state lifetimes which could protect their chemical intergrity in UV-rich environments. In contrast, some alternative nucleobases like 2-aminopurine and 2,6-diaminopurine, exhibit longer excited-state lifetimes which could result in fluorescence and are often sufficient to trigger bimolecular destructive photochemical reactions leading to relatively quick depletion of the starting material.^22,23 Nevertheless, the fates of electronically excited states in many non-biological nucleobases were not examined so far.

Experimental and theoretical efforts in understanding the photochemistry and photophysics of isocytosine (isoC) revealed the existence of relatively efficient radiationless deactivation mechanisms in the enol tautomer and a longer-lived S₁(nπ*) state in the keto form.^24–26 However, the photodynamics of its Watson–Crick (WC) partner isoguanine (isoG) has not been investigated yet. It is worth noting, that isoG, also denoted as 2-hydroxy-adenine can be occasionally present in biological DNA as the product of oxidative damage of adenine.²⁷ When incorporated into DNA, isoG could further pair with cytosine (C) in parallel strand orientation, form d(T₄-isoG₄-T₄) tetraplexes, and form anti-parallel strands with isoC by WC base pairing.²⁸ Such WC isoG–isoC base pair was demonstrated to be thermodynamically as stable as the biological G–C WC pair,^29,30 and was also used for expanding the genetic code and incorporating non-biological amino acid L-iodotyrosine into polypeptides by means of ribosome-based translation.^31–33 It is important to note that isoG exists in more than one stable tautomeric form, with evident preference for the enol form in apolar environments.^34–36 This might result in infidelity and might have been one of the reasons why isoG was eventually not utilized by biology.³⁷

In this work, we focused on studying the excited-state dynamics of four different tautomers of isoG in the gas phase from experimental and theoretical perspectives (see Fig. 1). In particular, we investigated the excited-state dynamics of two jet-cooled tautomers of isoG, i.e. keto and enol forms. We identified the absorption spectrum with 2-color R2PI, analyzed these tautomers by means of IR-UV hole burning, and performed pump–probe spectroscopic experiments in the picosecond time regime. For the complete interpretation of the experimental results we further performed static explorations of excited-state (S₁) potential energy (PE) surfaces using the algebraic diagrammatic construction to the second order [ADC(2)]^38–40 method and the more accurate n-electron valence state perturbation theory (NEVPT2) approach for these two tautomers.^41–43 In addition, we performed analogous electronic structure calculations for two keto and enol tautomers which we did not observe in our gas-phase experiments, but which are representative of isoG in nucleic acid polymers. We also performed surface-hopping nonadiabatic molecular dynamics simulations⁴⁴ for two of the enol tautomers of isoG using the ADC(2) method for electronic structure calculations. Our results indicate that keto tautomers of isoG exhibit excited state properties similar to the keto form of cytosine, which are determined by a long lived nπ* excitation,^45–50 while the enol tautomers are characterized by more efficient photorelaxation mechanisms dominated by the lowest-lying singlet ππ* states.

Fig. 1 Different tautomeric forms of isoG considered for the initial determination of the experimentally studied tautomers. The relative energies were calculated at the CCSD(T)/def2-TZVPP level of theory. The photodynamics of the underlined tautomers was investigated in this work.

2 Methods

Experimental section

The experimental methods have been described extensively previously,⁵¹ and only a short description follows. In this study, we used laser desorption, jet-cooling coupled with resonance enhanced multi-photon ionization (REMPI). IsoG was placed on a translating graphite bar and desorbed with a focused Nd:YAG pulse (1064 nm, 1 mJ, 8 ns pulsewidth) from a Continuum Minilite II. The desorbed material was entrained in a supersonic jet expansion of argon gas (8 atm backing pressure, 30 μs pulse width) to achieve jet cooling. The cold, gaseous molecules were resonantly ionized and detected in a reflectron time-of-flight mass spectrometer.

Two-color resonance two-photon ionization (2C-R2PI) is performed using an EKSPLA PL2251 Nd:YAG laser system producing 30 ps pulses. The 355 nm output pumps an optical parametric generator (OPG) (80–120 μJ per pulse) to produce tunable UV pulses, while the unused 1064 nm and 532 nm were combined to harmonically generate 213 nm light (0.3 mJ). The 213 nm pulses were used as the second color for ionization.

IR light was generated in a Laser Vision tunable optical parametric oscillator/optical parametric amplifier (OPO/OPA) (mid-IR output over the range 3200–3800 cm⁻¹ of 1–2 mJ per pulse, 3 cm⁻¹ spectral line width). For IR-UV double resonance spectroscopy, IR light preceded the ionization pulse by 200 ns. The IR laser was scanned across a target wavelength region, while the following ionization pulse was held at a constant R2PI transition for a given tautomer. Whenever the IR pulse excited a resonant vibrational transition, it burned out the cold ground state of the given tautomer, preventing the resonant transition needed for ionization. A resonant vibrational transition was thus detected as a loss in ion signal. All double resonance spectroscopic experiments were digitally chopped to compare the experimental (burn) signal to background (burn laser fired 800 ns after R2PI lasers) signal, with alternating shots collecting burn and background signal.

Pump–probe experiments were conducted by holding the pump pulse on a resonant R2PI transition. The probe (ionization) pulse, was then walked back in time relative to the pump pulse. In this way, a growing delay occurs between excitation and ionization. This delay allows the excited molecule to decay to different states, and will produce less signal as the delay grows. Pump–probe experiments were conducted in the picosecond (ps) and nanosecond (ns) regime. In the ps regime, the pump pulse was generated from the OPG and tuned to a resonant transition and the probe pulse was the harmonically generated 213 nm. The 213 nm pulse was mechanically delayed up to 1.8 ns. In the ns regime, the pump pulse was again generated from the OPG, whereas the probe pulse was generated from a GAM excimer laser (193 nm, 1.5–2 mJ per pulse, 8 ns pulsewidth). Pump–probe experiments were conducted in two different time regimes to account for possible faster and slower processes. The method for deriving lifetimes was based on previous work, and described in detail there.⁵² Briefly, lifetimes were derived from the kinetic equations and solving the system of ordinary differential equations. This involved convolving the instrument response function (IRF) with a monoexponential decay function. The IRF was represented by a Gaussian function centered around t₀.

Computational methods

The minimum-energy ground-state geometries of the enol-N7, enol-N9, keto-N1,9, keto-N3,7, keto-N3,9 and keto-N1,7 tautomers of isoG were optimized with the Kohn–Sham density functional theory (DFT). The two latter tautomers of isoG were not considered in the subsequent excited-state calculations. We applied the B3LYP hybrid functional and B2PLYP double hybrid functional⁵³ for these geometry optimizations. We also performed additional comparative optimizations of the ground-state geometries at the MP2/cc-pVTZ level, which is methodologically consistent with the method [ADC(2)] used for excited-state calculations. The MP2 optimizations yielded virtually identical structures as the two DFT functionals. The geometries obtained with both of the DFT methods were virtually identical and we further performed anharmonic frequency calculations^54,55 using the B2PLYP functional which was suggested to provide highly accurate vibrational frequencies for small and medium sized organic molecules.⁵⁶ The anharmonic vibrational frequencies computed at the B2PLYP/def2-TZVP level were used for the assignment of the tautomers recorded in our experimental setup. While the harmonic vibrational frequencies calculated at the B2PLYP and B3LYP levels were nearly quantitatively consistent, we used the latter set of results for the simulations of UV-vis absorption spectra with the ensemble method.⁵⁷ The relative ground-state energies of all the six tautomers were calculated at the CCSD(T)/def2-TZVPP level of theory. Vertical excitation energies, excited-state geometries, UV absorption spectra, energies and gradients in the surface-hopping nonadiabatic dynamics simulations were all computed employing the algebraic diagrammatic construction to the second order [ADC(2)]^38–40 method and the aug-cc-pVDZ correlation consistent basis set. Vertical excitation energies computed with a larger aug-cc-pVTZ basis set can be found in the ESI,† for comparison.

The minimum-energy crossing points were optimized using our in-house implementation of the protocol proposed by Levine and co-workers,⁵⁸ coupled with the ADC(2) and MP2 methods for energy and gradient calculations and the Broyden–Fletcher–Goldfarb–Shanno quasi-Newton geometry optimization scheme implemented in the Turbomole 7.2 package.^59,60 This protocol was recently tested against multireference methods of quantum chemistry and protocols employing explicit calculation of nonadiabatic couplings, and was shown to provide very accurate geometries of ππ*/S₀ conical intersections.^24,61 We additionally optimized the nπ*/S₀ conical intersections in the keto tautomers of isoG at the MRCIS(6,5)/cc-pVDZ level because of the highly multireference character of the ground-state electronic wave function at these state crossings, which was also reported previously for keto isoC.²⁴

The PE profiles were prepared by linear interpolation in internal coordinates between the crucial stationary points located for each tautomer, i.e. the ground-state geometry, S₁ minimum and the S₁/S₀ conical intersection. Energies of the ground and excited states necessary to construct the PE profiles were calculated at the MP2 and ADC(2) levels respectively. For these PE profiles, we additionally computed NEVPT2^41–43 energies on top of the SA-2-CASSCF(10,9)/cc-pVTZ wave function, in order to test the accuracy of our ADC(2) calculations. The active space used in simulations of all the considered tautomers of isoG comprised of 10 electrons correlated in 9 molecular orbitals, which were selected based on the rules proposed by Veryazov, Malmqvist and Roos.⁶² More precisely, the complete active space (CAS) included orbitals with occupations ranging between 0.02 and 1.98.

We performed the surface-hopping nonadiabatic molecular dynamics simulations using the Tully fewest switches algorithm including the decoherence correction of Granucci and Persico (decoherence parameter was set to 0.1 Hartree). To select the initial conditions we first simulated UV absorption spectra using the nuclear ensemble method,⁵⁷ and generating 600 points for each tautomer based on the Wigner distribution for all vibrational normal modes of the ground-state minimum-energy structures. In the UV absorption spectra simulations we considered 8 lowest-lying excited singlet states, and 4 lowest-lying excited singlet states were considered in the subsequent nonadiabatic molecular dynamics simulations. We simulated 58, 64 and 53 trajectories for the enol-N7, enol-N9 and keto-N1,9 tautomers. These trajectories were initiated in the 4.26 ± 0.05 eV and 4.70 ± 0.05 eV spectral windows in the case of the enol-N7 and enol-N9. The trajectories simulated for the keto-N1,9 form were initiated in the 3.83 ± 0.05 eV spectral window and only the initial stage of the excited-state dynamics of this tautomer was analyzed owing to the incorrect description of the nπ*/S₀ crossing seam at the ADC(2)/MP2 level. In the case of the enol-N7 tautomer 45 and 13 trajectories were initiated in the S₁ and S₂ states, respectively. 55 and 9 trajectories for the enol-N9 tautomer were simulated from the S₁ and S₂ states, respectively. All of the trajectories simulated for the keto-N1,9 form were initiated in the S₁ state. All the trajectories were terminated when the energy gap between the S₁ and S₀ states dropped below 0.15 eV or otherwise propagated for the maximum time of 500 fs. Therefore, nonadiabatic transitions were enabled only between electronically excited states. The classical equations for nuclear motion were propagated with the time step of 0.5 fs, while the semi-classical approximation with the time step of 0.025 fs was applied for the propagation of the electronic time-dependent Schrödinger equation. A similar computational protocol was previously applied for the simulations of the photodynamics of adenine and its reliability was confirmed against surface hopping nonadiabatic molecular dynamics simulations.⁶³

The B3LYP geometries and harmonic vibrational frequencies and all the ADC(2) and MP2 calculations were performed with the Turbomole 7.2 program.^59,60 The B2PLYP geometries, energies and anharmonic vibrational frequencies were computed using the Gaussian09 package.⁶⁴ The NEVPT2 and CCSD(T) calculations were performed with the ORCA 4.0.1 program.⁶⁵ Optimizations of conical intersections at the MRCIS level were carried out using the Columbus 7.0 software.⁶⁶

3 Results and discussion

2C-R2PI spectra

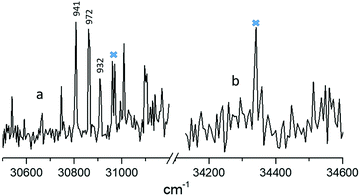
Fig. 2 shows 2C-R2PI spectra (focused) of isoG. We assign the peaks at 30 807 and 34 340 cm⁻¹ as the origin transitions of isoguanine amino-keto (a), and amino-enol (b), based on IR-UV burning as detailed below. The lifetimes of the probed peaks are displayed in ps. Crosses mark peaks for which pump–probe measurements were unsuccessful. The origin peaks are separated by approximately 3500 cm⁻¹ (0.43 eV). Despite thorough searching to the red and blue, no other features were identified. The spectrum between the 30 800 and 34 300 cm⁻¹ region consists of nonresonant signal and is devoid of any indicative features.

Fig. 2 2C-R2PI spectrum (focused) of isoguanine amino-keto (a), and amino-enol (b). Only one repeatable peak was found for the amino-enol tautomer. The lifetimes of the probed peaks are displayed in ps. Pump–probe was unsuccessfully attempted at peaks with crosses above them, owing to low signal-to-noise ratio.

Structural determination

To determine the number and types of tautomers observed experimentally, we conducted IR-UV double resonance spectroscopy measurements (Fig. 3). The experimental data are displayed as the negative log of the raw data, probed at 30 807 cm⁻¹ (red trace) and 34 340 cm⁻¹ (blue trace). Spectra with probe wavelengths set to the other peaks within the 30 800 cm⁻¹ region were practically identical and matched the red trace, confirming that all the peaks within this energy region corresponded to the same tautomer. Comparison of these spectra with the anharmonic vibrational frequencies simulated at the B2PLYP/def2-TZVP level, reveals that they could correspond to one of the keto tautomers with the best agreement for the keto-N3,7 tautomer (where the N3 and N7 heteroatoms of the purine ring are bonded to an H atom; see Fig. 1), with differences within 15–20 cm⁻¹. In contrast, differences between the experimental (red trace) and theoretical vibrational frequencies obtained for the remaining keto tautomers are generally larger and exceed 30 cm⁻¹ in extreme cases.

Fig. 3 IR-UV hole burning results compared to anharmonic vibrational frequency simulations performed using the B2PLYP/def2-TZVP approach.

The double resonant spectrum recorded with the UV probe wavelength fixed at 34 340 cm⁻¹ (blue trace in Fig. 3) is in excellent agreement with the anharmonic vibrational frequencies simulated for the enol-N7 tautomer (having the N7 heteroatom bonded to a hydrogen atom). The anharmonic frequencies calculated for the enol-N9 tautomer contain two groups of nearly overlapping peaks (two peaks in each group) at ∼3505 and ∼3638 cm⁻¹ which is very different from the experimentally determined spectral structure of four well-separated peaks. The peak at 3552 cm⁻¹ of the blue trace is close to the S/N limit and we have carefully determined it to be real based on multiple IR scans and averaging of the results, as shown in Fig. S1 (ESI†). It is also worth noting, that this assignment is further supported by almost identical vibrational frequencies of the NH stretching modes of the N7H and NH₂ groups in the keto-N3,7 and enol-N7 forms. These groups have very similar molecular environments in the assigned tautomers and such similarities in the IR spectra are thus expected.

According to the tautomer energies computed at the CCSD(T)/def2-TZVPP level of theory (Fig. 1) the assigned keto-N3,7 and enol-N7 structures are among the higher energy tautomeric forms of isoG and we were unable to detect the lower energy tautomers in our experiments, i.e. enol-N9, keto-N3,9 and keto-N1,9. However, having detected the higher energy tautomers, we expect that all the lower energy forms should be present in our beam as well. In fact, we cannot predict the plausible distribution of these tautomers, since jet-cooling is a nonequilibrium process. There may be several reasons why the lowest energy tautomers were not detected in our experiments. (1) Laser-desorbed isoG might have been trapped in local minima corresponding to higher energy tautomeric forms during the jet-cooling process, and some of the lower-energy tautomers might not be accessible within the timescales of our measurements. (2) It is likely that some of the tautomers excited with the first photon might not be ionized with the second, for instance when the excited-state lifetime is substantially shorter than the ionizing laser pulse. This behavior is typical for action spectroscopic measurements and was suggested as the reason why low-energy tautomers of guanine were not observed in analogous studies.^25,67 (3) Some of these tautomers might undergo fragmentation upon photoexcitation which could increase the complexity of the action spectrum, particularly since we focused on monitoring the parent ion mass. However, we did not notice any apparent signs of nonstatistical fragmentation.

It is worth noting that the keto-N1,9 form was observed experimentally to exist in neutral aqueous solution, while the lowest energy enol-N9 tautomer is prevalent in apolar solvents.^34,35 In addition, these tautomers are expected as the dominant forms of isoG in a DNA strand,⁶⁸ allowing for wobble base pairing. Therefore, in the subsequent excited-state electronic structure calculations we considered the keto-N3,7 and enol-N7 tautomers identified above, as well as the keto-N1,9 and enol-N9 tautomers more relevant for aqueous environments and modified DNA strands.

Pump–probe measurements

Fig. 4 shows the pump–probe measurements performed for the tautomers assigned above. The excited-state lifetimes are displayed above the probed peaks in Fig. 2. We were able to probe three peaks for the keto-N3,7 form shown in Fig. 2. Pump probe experiments on other peaks in the spectral region corresponding to this keto tautomer were unsuccessful owing to very low singal-to-noise ratio. Similarly none of the peaks of the enol-N7 tautomer could be probed owing to low signal and lack of two-color enhancement. In fact, low signal and the appearance of a single peak followed by spectral broadening indicates that the enol-N7 tautomer exhibits ultrafast excited state dynamics below the probe resolution of 30 ps. Given that R2PI is action spectroscopy, the molecule may not be ionized efficiently, if the probe pulse is significantly longer than the excited-state lifetime. In contrast, the peaks probed for the keto-N3,7 tautomer exhibited a lifetimes of 941, 972 and 932 ps. Our pump–probe measurements of the keto-N3,7 tautomer in the nanosecond regime yielded a trace that matched the instrument response function (IRF = ∼8 ns). The IRF provides an upper limit for the lifetime of the probed transition and which signifies no long-lived state with any appreciable yield was populated in the keto-N3,7 form.

Fig. 4 Pump–probe measurements performed on the three peaks assigned to the keto-N3,7 tautomer. The blue curve is a sum of a Gaussian and mono-exponential functions fitted to the data from the pump–probe measurements, where the Gaussian component represents the instrument response function.

Vertical excitation energies and UV-vis spectra

To characterize the photophysical and photochemical properties of isoG in different contexts we performed excited-state calculations for the biologically more relevant keto-N1,9 and enol-N9 tautomers in addition to the keto-N3,7 and enol-N7 tautomers identified in our IR-UV hole burning experiments. The vertical excitation energies of the six lowest excited singlet states calculated using the ADC(2) method on top of the optimized S₀ geometries are shown in Table 1. In the Franck–Condon regions of all the studied tautomers of isoG, the lowest-lying singlet states can be classified as optically bright ππ* excitations. Similarly to cytosine and isocytosine, the keto-N1,9 and keto-N3,7 tautomers have rather low excitation energies for these ππ* transitions (3.91 and 4.23 eV) which indicates that they could absorb much longer UV wavelengths than the enol-N7 and enol-N9 forms (4.59 and 4.97 eV). Each of these tautomers also displays higher-energy optically bright ππ* excitations which could give rise to additional, higher-energy absorption maxima. Furthermore, both the keto tautomers have low-lying n_Oπ* states which were suggested as important contributors to the photochemistry of nucleobases containing carbonyl groups.^45,48,69 This is particularly evident for the keto-N3,7 tautomer, for which the n_Oπ* is the S₂ state in the Franck–Condon region and this state might participate in the photorelaxation of this tautomeric form upon UV-excitation. While photorelaxation of enol tautomers of nucleobases is usually dominated by ππ* states, both the enol-N7 and enol-N9 forms are also characterized by low-lying n_Nπ* states, which might become important at higher excitation energies.

Table 1 Vertical excitation energies (in eV) of the four considered tautomers of isoG, computed using the ADC(2)/aug-cc-pVDZ method, assuming the ground-state minimum energy structures optimized at the B3LYP/def2-TZVPP level

State/transition		E exc/[eV]	f osc	λ/[nm]
Keto-N1,9
S1	ππ*	3.91	0.141	317.1
S2		4.49	2.40 × 10^−3	276.1
S3	nNπ*	4.96	2.57 × 10^−4	250.0
S4		4.98	1.78 × 10^−4	249.0
S5	nOπ*	5.27	2.14 × 10^−5	235.3
S6	ππ*	5.36	0.171	231.3
Keto-N3,7
S1	ππ*	4.23	0.162	293.8
S2		4.62	1.28 × 10^−3	259.9
S3	nOπ*	4.78	1.52 × 10^−3	256.2
S4	nNπ*	5.15	2.80 × 10^−3	242.6
S5		5.46	5.16 × 10^−3	219.1
S6	ππ*	5.52	0.100	225.0
Enol-N7
S1	ππ*	4.59	0.141	293.1
S2		4.75	9.18 × 10^−3	261.0
S3	nNπ*	4.89	3.02 × 10^−3	253.5
S4		5.52	1.11 × 10^−2	224.6
S5		5.60	3.07 × 10^−3	221.4
S6	ππ*	5.66	6.46 × 10^−2	219.1
Enol-N9
S1	ππ*	4.97	0.191	249.5
S2		5.19	5.09 × 10^−3	238.9
S3	nNπ*	5.40	1.39 × 10^−3	229.6
S4	ππ*	5.47	0.106	226.7
S5		5.52	3.17 × 10^−3	224.6
S6	nNπ*	5.88	7.09 × 10^−3	210.9

---

The UV-absorption spectra simulated using the molecular ensemble method essentially reflect the implications inferred from the analyses of vertical excitations energies (see Fig. 5). Consequently, the onset of the absorption of the two keto tautomers can be observed at approximately 3.2 eV (387.4 nm), which is 0.7 eV lower than for the enol-N7 tautomer. This difference in absorption energies between the keto and enol-N7 is also consistent with the assigned origin transitions in the 2C-R2PI spectra. The enol-N9 tautomer, not observed in our beam absorbs at even higher UV energies, i.e. above 4.2 eV (295 nm). Therefore the keto tautomers of isoG absorb at much longer wavelengths than biologically relevant keto guanine (G), within the UV-A range which is much less efficiently shielded by various atmospheric components and was most likely highly abundant on the Archean Earth. Consequently, if present on the early Earth's surface, isoG would be a better UV absorber than the canonical nucleobases and more prone to deleterious photochemistry in the absence of efficient photodeactivation pathways. As indicated by the shaded areas in Fig. 5, the pump pulses sampled the lower energy bands of the UV-absorption spectra of both keto-N3,7 and enol-N7 forms. Such low-energy excitation predominantly populates the lowest-lying singlet states in each of these tautomers (bright ππ* states). Consequently, we anticipate that the excited-state dynamics of isoG within the experimental setup will be dominated by the S₁ state with a very limited and temporary contribution from higher excitations.

Fig. 5 UV absorption spectra simulated at the ADC(2)/aug-cc-pVDZ method using the nuclear ensemble method.⁵⁷

Minimum energy geometries located in the S₁ state in each of the studied tautomers of isoG using the ADC(2)/aug-cc-pVDZ method

The ADC(2)-optimized minimum-energy geometries of the keto and enol tautomers in their lowest excited singlet states reveal further interesting details of their photochemistry (see Fig. 6). In particular, the S₁ minima of the keto-N1,9 and keto-N3,7 forms have both n_Oπ* character. Therefore, these geometries are characterized by slight pyramidalization of the C6 carbon atoms leading to an out-of-plane tilt of the amino groups and elongation of the C2=O bonds by ∼0.18 Å when compared to the ground-state geometries, i.e. up to 1.39 and 1.40 Å for keto-N1,9 and keto-N3,7 respectively. Geometrically similar S₁(n_Oπ*) minima were also reported for the keto tautomers of C, G and isoC.^{24,45–47,50,70} However, surface-hopping nonadiabatic molecular dynamics simulations executed for G showed that this local minimum is sampled by sparse trajectories and the prevalent photodeactivation channel drives keto-G towards the ππ*/S₀ conical intersection.⁷⁰ Our direct optimization of the S₁ minimum of keto-G initiated from the S₀ geometry also did not stabilize the n_Oπ* state, whereas the same optimization procedure returned the S₁(n_Oπ*) minima for both of the studied keto tautomers of isoG. This result indicates that the dark n_Oπ* states might have a much more significant contribution to the photorelaxation of the keto-N1,9 and keto-N3,7 tautomers of isoG as compared to canonical G.

Fig. 6 Minimum-energy geometries of the studied tautomers of isoG optimized at the ADC(2)/aug-cc-pVDZ level of theory.

Previous investigations of the photochemistry of keto isoC and thiocytosine revealed potential pitfalls of the ADC(2) approach in describing the low-lying n_Oπ* state outside the Franck–Condon region.^24,71 In particular, ADC(2) incorrectly predicted the topography of the n_Oπ* surface between S₁ and the corresponding conical intersection with the ground-state, owing to the multireference character of the electronic ground state for these geometries.²⁴ Therefore, we reoptimized the S₁(n_Oπ*) minima of the keto-N1,9 and keto-N3,7 tautomers at the MRCIS(6,5) level and calculated NEVPT2/SA-CASSCF(10,9) energies to verify whether a similar behavior can be found in isoG. The MRCIS minimum energy geometries optimized for the S₁(n_Oπ*) state were qualitatively consistent with the outcome of ADC(2) calculations (including the extent of ring-puckering and out-of-plane tilting visible in Fig. 6). Nevertheless, we observed an essential difference in the C2=O bond lengths, which were shorter by approximately 0.11 and 0.08 Å in the case of the S₁ minimuma optimized for the keto-N1,9 and keto-N3,7 tautomers at the MRCIS level. Furthermore, the S₁–S₀ energy gap computed at the ADC(2) level for the respective S₁(n_Oπ*) minimima amounts to 0.85 and 1.11 eV, whereas the same quantity calculated with NEVPT2 on top of MRCIS-optimized S₁ minima amounts to 2.92 and 2.68 eV for the keto-N1,9 and keto-N3,7 forms, respectively. These findings indicate that ADC(2) might be an inappropriate method for the description of n_Oπ* states of isoG already in the vicinity of the corresponding S₁ minima.

The excited-state geometry optimizations carried out for the enol-N7 and enol-N9 tautomers returned S₁ minima associated with the optically bright ππ* states. In the case of the enol-N7 tautomer the associated virtual π* molecular orbital has the highest contribution residing on the five-membered imidazole ring. This is reflected by the geometrical changes associated with N7–C8 bond elongation and out-of-plane tilting of the N7–H and C8–H bonds. The vertical S₁–S₀ energy gap at this geometry amounts to 3.12 eV, which indicates that this S₁ minimum is separated from the nearby S₁/S₀ conical intersections by an energy barrier and the enol-N7 tautomer might not exhibit ultrafast excited-state photodeactivation.

In contrast, the geometry in the S₁ minimum of the enol-N9 tautomer is associated with substantial puckering of the pyrimidine ring, which originates from the associated virtual π* molecular orbital located in this part of the molecule. Significant elongation of the C5–C6 bond from 1.41 to 1.51 Å demonstrates that this S₁ should be situated close to a typical ethylenic conical intersection also observed in C and isoC.^24,45 However, unlike the analogous ring-puckered S₁ geometries reported for enol tautomers of C and isoC, the S₁ minimum of enol-N9 practically coincides with the S₁(ππ*)/S₀ conical intersection (ΔE_S1–S0 = 0.03 eV at the ADC(2) level of theory; consistent with NEVPT2 calculations). Good semi-quantitative agreement between the NEVPT2 and ADC(2) results indicate that the ADC(2) method should provide a correct description of excited-state dynamics for the enol tautomers of isoG.

Excited-state PE surfaces

We further explored the PE profiles leading from the Franck–Condon region to the S₁ minima discussed above, and from there to the energetically accessible conical intersections optimized using the ADC(2) and MP2 methods for the S₁ and S₀ states (see Fig. 7). We expect that these pathways should have a substantial contribution to the overall photorelaxation observed in our experiments considering that the irradiation (pump) pulses were targeted near the 0–0 transitions. That is, irradiation near the onset of the absorption of the keto-N3,7 and enol-N7 tautomers likely populates only the lowest-lying excited-singlet states and the consecutive photodeactivation should be largely determined by the associated S₁ minima. We also considered analogous photodeactivation pathways for the keto-N1,9 and enol-N9 tautomers, which would be of relevance to nucleic acid oligomers.

Fig. 7 Potential energy profiles for the predicted dominant photodeactivation pathways of keto and enol isoG NEVPT2/SA-2-CASSCF(10,9)/cc-pVTZ. The inserted structure corresponds to the S₁/S₀ minimum-energy crossing point (MECP) geometry (conical intersections). For an explanation of the difference between the shapes of the ADC(2) and NEVPT2 curves for the keto tautomers, please refer to the text.

Both of the considered keto tautomers could repopulate the electronic ground state through the n_Oπ*/S₀ conical intersections and only insignificant structural changes from the S₁(n_Oπ*) minima lead to the degeneracy with the S₀ state. However, our NEVPT2 calculations show that the n_Oπ*/S₀ minimum-energy crossing points (MECPs) have a clearly sloped topography and are higher in energy than the corresponding S₁ minima. Since the steepness of the slope is not reproduced correctly by the ADC(2) method, we additionally reoptimized these crucial stationary points at the MRCIS level and calculated NEVPT2 energies on top of the resulting structures. These results demonstrate that the n_Oπ*/S₀ conical intersections lie 0.53 eV and 0.98 eV above the S₁ minima in the keto-N1,9 and keto-N3,7 tautomers, respectively. This energy barrier observed in the latter keto tautomer in fact explains the long excited state lifetime of over ∼900 ps. Although we could not determine the excited-state lifetime for the keto-N1,9 form with our pump–probe experiments, we expect a very similar behaviour for this tautomer.

In contrast to the keto tautomers, the ADC(2) method much more accurately describes the photodeactivation mechanisms mediated by the low lying ππ* states of both of the enol forms when compared to the NEVPT2 results. Although there is a systematic energy shift between the two datasets, the shapes of the excited and ground state PE surfaces obtained with both of the methods are in excellent agreement and more importantly, the topographies of the ππ*/S₀ conical intersections are correctly reproduced at the ADC(2)/MP2 levels. This consistency also indicates that the ADC(2) method could be safely applied to nonadiabatic dynamics of the enol forms of isoG. In the case of the enol-N7 tautomer, the lowest energy S₁/S₀ conical intersection can be reached by puckering of the pyrimidine ring driven by ethylenic-like rotation about the C5–C6 bond, pyramidalization of the C6 carbon atom and significant out-of-plane tilting of the amino group. This also means that the ππ* involved in this S₁/S₀ conical intersection has a different orbital character than the S₁(ππ*) minimum of the enol-N7 tautomer. Consequently, the photodeactivation mechanism presented in Fig. 7 requires a molecular orbital change in photoexcited enol-N7 to reach the electronic ground state. This change from the orbital located on the imidazole ring to the with the largest contribution on the pyrimidine ring is also associated with a moderate energy barrier. Since we have not calculated the fully relaxed minimum-energy path between the S₁ minimum and the 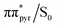conical intersection and we only performed a linear interpolation in internal coordinates between these stationary points we expect the estimated 0.4 eV to be the upper bound to this barrier. The photorelaxation mechanism of the enol-N9 tautomer is an entirely barrierless process starting from the Franck–Condon region and no additional molecular orbital changes of are necessary to reach the conical intersection after the population of the S₁(ππ*) state. This conical intersection is also structurally analogous to the minimum-energy crossing point reported for the enol-N7 tautomer.

In the case of the enol-N7 tautomer we also identified an alternative photodeactivation channel driven by puckering of the imidazole ring which does not entail any change in the molecular orbital character of the 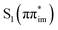state. The associated conical intersection lies 0.33 eV above the S₁ minimum and might be another channel enabling the photodeactivation of the enol-N7 form.

Surface-hopping excited-state dynamics simulations

We further performed surface-hopping nonadiabatic molecular dynamics (NAMD) simulations using the ADC(2) method for electronic structure calculations. We simulated 58 and 64 trajectories for the enol-N7 and enol-N9 tautomers respectively. We also simulated 53 trajectories for the keto-N1,9 tautomer.

The NAMD simulations of the keto-N1,9 tautomer were initiated in the 3.83 ± 0.05 eV spectral window and nearly all of the trajectories initially populated the lowest-lying excited ππ* state. Practically 100% of excited-state population is transferred to the dark n_Oπ* state within the initial 50 fs of the dynamics. Furthermore, the n_Oπ*/S₀ conical intersection is the only photodeactivation channel found in our nondiabatic dynamics simulations. However, as discussed above, the ADC(2) method does not reproduce well the sloped topography of the n_Oπ*/S₀ conical intersection in this tautomer and might overestimate the contribution of this photorelaxation channel. We also expect that the energy difference between this conical intersection and the corresponding S₁ minimum underestimated by the ADC(2) method leads to an artificially short excited-state lifetime of the keto-N1,9 form. Therefore, to keep our interpretation meaningful we limit our discussion of the excited-state dynamics of this tautomer to the initial 50 fs of the simulations. These results clearly demonstrate that the n_Oπ* state is readily populated at the early stages of the photodynamics. Additional information about the excited-state dynamics of the keto-N1,9 tautomer, e.g. the adiabatic electronic state populations can be found in ESI.† Even though ADC(2) would not provide accurate description of the excited-state dynamics of the keto tautomers on longer picosecod timescales, a recent work by Plasser et al. demonstrated that similar photodynamical behavior of alternative nucleobases (e.g. 2-aminopurine) could be correctly described by the linear vibronic coupling model within the surface-hopping regime, parametrized against a higher level electronic structure method.⁷²

Owing to similar ordering of the excited states in the Franck–Condon region of the keto-N3,7 tautomer and even lower vertical excitation energy of the n_Oπ* state, we expect that this dark state could also easily dominate the photodynamics of this form. Nevertheless, owing to the pitfalls of the ADC(2) method in simulating the nπ*/S₀ conical intersections of the keto forms of isoG and substantial costs of surface-hopping nonadiabatic dynamics we did not perform these simulations for the keto-N3,7 tautomer. Instead we focused on simulating the photodynamics of the enol tautomers for which the ADC(2) method provided results consistent with the higher level NEVPT2 calculations.

The trajectories for the enol-N7 and enol-N9 tautomers were propagated until the S₁–S₀ energy gap dropped below 0.15 eV or the maximum simulation time (t_max reached 500 fs). We simulated 58 trajectories for the enol-N7 tautomer from the 4.26 ± 0.05 eV spectral window which corresponds to the energy of the pump pulse applied to this tautomer in our experiments. 14 of these trajectories reached the electronic ground state within the t_max which is ∼25% of all the trajectories (see also Fig. 8). This indicates that the excited-state lifetime of enol-N7 could indeed be significantly below the probe resolution of 30 ps as anticipated in the discussion of the experimental measurements. However, owing to the limited simulation time and statistics we did not estimate this quantity for the enol-N7 tautomer. The most frequent photodeactivation channel observed for this molecule was rupture of the N7–H bond which occurs on the surface of the state⁷³ and was followed by 6 trajectories. In addition, 2 other trajectories associated with dissociation either of the O–H or N_amino–H bonds reached analogous πσ*/S₀ state crossings. Apart from this, 4 trajectories were essentially destructive and resulted in opening of the imidazole ring by breaking the C8–N7 bond on the surface of the state. Finally, 2 trajectories reached the conical intersection by puckering of the pyrimidine ring. The remaining trajectories are transiently trapped in the minimum which is well reflected by the substantial population of the S₁ state (>0.7) and near-zero population of higher singlet excitations after 260 fs of the dynamics.

Fig. 8 Adiabatic populations of electronic states extracted from nonadiabatic molecular dynamics simulations of the enol tautomers of isoG.

Since the enol-N9 tautomer absorbs at slightly higher energies than the enol-N7 form, we initiated the NAMD simulations for the enol-N9 tautomer in the 4.7 ± 0.05 eV spectral window. This higher energy spectral window was necessary to simulate over 50 trajectories (64 in total) to have a good qualitative overview of the photodynamics of this system. Over 85% of these trajectories were initiated in the S₁ state and the contribution of higher energy excitations was fractional and observed only during the initial 180 fs of the dynamics. Notably, 53 of these trajectories reached the S₁/S₀ crossing seam within the t_max which is consistent with the prediction of the barrierless photodeactivation mechanism on the surface. In fact, puckering of the pyrimidine ring is the only photodeactivation channel that we found for the enol-N9 tautomer. This indicates that the electronic ground state of this molecule is most likely populated monoexponentially, and can be fitted with the one-parameter exponential function:

The estimated τ_exp constant amounts to 312 fs, although it should be treated with caution owing to the time frame and limited statistics for which the fitting was performed. However, this result clearly demonstrates that the enol-N9 tautomer has a subpicosecond lifetime and might be the most photostable from all of the studied tautomers of isoG. Such ultrafast photodeactivation of the enol-N9 tautomer could also explain why this molecule was not detected in our IR-UV hole burning experiments, i.e. its lifetime is considerably shorter than the duration’ of the ionizing laser pulse.

4 Conclusions

In summary, we investigated the excited-state dynamics of keto and enol tautomers of isoG in the gas phase, using quantum chemical simulations and pump–probe spectroscopic experiments. Our results show that the keto tautomers of isoG are characterized by long excited-state lifetimes owing to the prevailing population of dark nπ* states after the initial photodynamics in UV-absorbing ππ* states. The pump–probe measurements performed for the keto-N3,7 tautomer excited near its 0–0 transition returned a long lived excited-state decay with a time constant exceeding 900 ps. This can be attributed to the sloped topography of the nπ*/S₀ conical intersection, which is much higher in energy that the respective S₁ minimum (by 0.53 eV). Even though we were not able to detect the biologically more relevant keto-N1,9 tautomer in our experimental setup, our quantum-chemical calculations suggest an even more sloped topography of the analogous nπ*/S₀ conical intersection. In contrast, the excited-state dynamics of the enol tautomers of isoG is controlled by the optically bright ππ* states, which are remarkably short-lived in this particular example. Both our excited state dynamics simulations and PE surface explorations demonstrate a barrierless photodeactivation mechanism in the enol-N9 tautomer. The resulting sub-picosecond excited-state lifetime is shorter than the ionizing laser pulse which explains why the enol-N9 form was so elusive and difficult to detect in our experiments. While a modest energy barrier separates the S₁ minimum and the peaked ππ*/S₀ conical intersection of the remaining enol-N7 tautomer, πσ*-mediated photorelaxation channels involving N–H bond rupture also result in rapid excited-state decay, below the resolution of the probe pulse (<30 ps).

These results have fascinating implications both for the origins of DNA bases on Earth and more general photochemistry and photophysics of nucleobase analogs. In particular, the studied photoexcited keto tautomers of isoG are trapped in long-lived reactive excited states and we expect them to be significantly less photostable than canonical G. The higher photostability of G can be assigned to the radiationless deactivation occurring primarily on the ππ* PE surface, with very limited excited-state population being trapped in long-lived nπ* minima.⁷⁰ In these terms, isoG exhibits very similar photochemistry to the canonical keto tautomer of C which also efficiently populates dark nπ* states.⁴⁵ It is worth noting that dark nπ* states were suggested to promote the formation of nucleobase damage in bulk water, i.e. pyrimidine photohydrates.⁴⁹ Similar excited-state dynamics and lifetimes of ∼1 ns were also reported for jet-cooled 5,6-trimethylenecytosine, which resembles isoG structurally.^74,75 The 5,6-trimethylene-substituent was suggested to lock the planarity of the aromatic pyrimidine ring and hinder ring-puckering motions^74,75 which enable the formation of ππ*/S₀ state crossings in canonical C.⁴⁵ Most importantly, the resulting low photostability of keto isoG is consistent with the prebiotic scenario assuming that intense UV irradiation was one of the crucial selection factors for RNA constituents on an early Earth. This observation, together with the population of multiple tautomeric forms in bulk water and potential wobble base pairing make isoG a much less reliable component of primordial informational polymers than its biological counterpart.

Conflicts of interest

There are no conflicts to declare.

Acknowledgements

This work was supported in part by the National Science Foundation under 1800283, and by a fellowship from the Simons Foundation (494188 to R. S.).

References

1. L. E. Orgel, Crit. Rev. Biochem. Mol. Biol., 2004, 39, 99–123.
2. B. J. Cafferty, I. Gállego, M. C. Chen, K. I. Farley, R. Eritja and N. V. Hud, J. Am. Chem. Soc., 2013, 135, 2447–2450.
3. B. J. Cafferty and N. V. Hud, Isr. J. Chem., 2015, 55, 891–905.
4. M. P. Callahan, K. E. Smith, H. J. Cleaves, J. Ruzicka, J. C. Stern, D. P. Glavin, C. H. House and J. P. Dworkin, Proc. Natl. Acad. Sci. U. S. A., 2011, 108, 13995–13998.
5. R. Saladino, V. Neri, C. Crestini, G. Costanzo, M. Graciotti and E. Di Mauro, J. Am. Chem. Soc., 2008, 130, 15512–15518.
6. R. Saladino, C. Crestini, C. Cossetti, E. Di Mauro and D. Deamer, Origins Life Evol. Biospheres, 2011, 41, 437–451.
7. R. Saladino, G. Botta, M. Delfino and E. Di Mauro, Chem. – Eur. J., 2013, 19, 16916–16922.
8. S. Ranjan and D. D. Sasselov, Astrobiology, 2016, 16, 68–88.
9. S. Ranjan and D. D. Sasselov, Astrobiology, 2017, 17, 169–204.
10. S. Boldissar and M. S. d. Vries, Phys. Chem. Chem. Phys., 2018, 20, 9701–9716.
11. R. J. Rapf and V. Vaida, Phys. Chem. Chem. Phys., 2016, 18, 20067–20084.
12. A. A. Beckstead, Y. Zhang, M. S. d. Vries and B. Kohler, Phys. Chem. Chem. Phys., 2016, 18, 24228–24238.
13. D. Tuna, A. L. Sobolewski and W. Domcke, J. Phys. Chem. A, 2014, 118, 122–127.
14. D. Tuna, A. L. Sobolewski and W. Domcke, J. Phys. Chem. B, 2016, 120, 10729–10735.
15. A. L. Sobolewski and W. Domcke, Europhys. News, 2006, 37, 20–23.
16. C. T. Middleton, K. d. L. Harpe, C. Su, Y. K. Law, C. E. Crespo-Hernández and B. Kohler, Annu. Rev. Phys. Chem., 2009, 60, 217–239.
17. S. D. Camillis, J. Miles, G. Alexander, O. Ghafur, I. D. Williams, D. Townsend and J. B. Greenwood, Phys. Chem. Chem. Phys., 2015, 17, 23643–23650.
18. H. Satzger, D. Townsend, M. Z. Zgierski, S. Patchkovskii, S. Ullrich and A. Stolow, PNAS, 2006, 103, 10196–10201.
19. A. Abo-Riziq, L. Grace, E. Nir, M. Kabelac, P. Hobza and M. S. d. Vries, PNAS, 2005, 102, 20–23.
20. A. L. Sobolewski, W. Domcke and C. Hättig, Proc. Natl. Acad. Sci. U. S. A., 2005, 102, 17903–17906.
21. M. M. Brister, M. Pollum and C. E. Crespo-Hernández, Phys. Chem. Chem. Phys., 2016, 18, 20097–20103.
22. S. Lobsiger, S. Blaser, R. K. Sinha, H.-M. Frey and S. Leutwyler, Nat. Chem., 2014, 6, 989–993.
23. Z. Gengeliczki, M. P. Callahan, N. Svadlenak, C. I. Pongor, B. Sztáray, L. Meerts, D. Nachtigallová, P. Hobza, M. Barbatti, H. Lischka and M. S. d. Vries, Phys. Chem. Chem. Phys., 2010, 12, 5375–5388.
24. R. Szabla, R. W. Góra and J. Šponer, Phys. Chem. Chem. Phys., 2016, 18, 20208–20218.
25. J. A. Berenbeim, S. Boldissar, F. M. Siouri, G. Gate, M. R. Haggmark, B. Aboulache, T. Cohen and M. S. de Vries, J. Phys. Chem. Lett., 2017, 8, 5184–5189.
26. D. Hu, Y. F. Liu, A. L. Sobolewski and Z. Lan, Phys. Chem. Chem. Phys., 2017, 19, 19168–19177.
27. H. Kamiya, Nucleic Acids Res., 2003, 31, 517–531.
28. F. Seela and C. Wei, Helv. Chim. Acta, 1997, 80, 73–85.
29. C. Roberts, R. Bandaru and C. Switzer, J. Am. Chem. Soc., 1997, 119, 4640–4649.
30. X. L. Yang, H. Sugiyama, S. Ikeda, I. Saito and A. H. Wang, Biophys. J., 1998, 75, 1163–1171.
31. J. D. Bain, C. Switzer, R. Chamberlin and S. A. Benner, Nature, 1992, 356, 537–539.
32. S. Hoshika, N. A. Leal, M.-J. Kim, M.-S. Kim, N. B. Karalkar, H.-J. Kim, A. M. Bates, N. E. Watkins, H. A. SantaLucia, A. J. Meyer, S. DasGupta, J. A. Piccirilli, A. D. Ellington, J. SantaLucia, M. M. Georgiadis and S. A. Benner, Science, 2019, 363, 884–887.
33. O. Bande, R. Abu El Asrar, D. Braddick, S. Dumbre, V. Pezo, G. Schepers, V. B. Pinheiro, E. Lescrinier, P. Holliger, P. Marlière and P. Herdewijn, Chem. – Eur. J., 2015, 21, 5009–5022.
34. F. Seela, C. Wei and Z. Kazimierczuk, Helv. Chim. Acta, 1995, 78, 1843–1854.
35. J. Sepioł, Z. Kazimierczuk and D. Shugar, Z. Naturforsch. C, 2014, 31, 361–370.
36. N. B. Karalkar, K. Khare, R. Molt and S. A. Benner, Nucleosides, Nucleotides Nucleic Acids, 2017, 36, 256–274.
37. A. Jaworski, J. S. Kwiatkowski and B. Lesyng, Int. J. Quantum Chem., 1985, 28, 209–216.
38. A. B. Trofimov and J. Schirmer, J. Phys. B: At., Mol. Opt. Phys., 1995, 28, 2299.
39. C. Hättig, Advances in Quantum Chemistry, Academic Press, 2005, vol. 50, pp. 37–60.
40. A. Dreuw and M. Wormit, Wiley Interdiscip. Rev.: Comput. Mol. Sci., 2015, 5, 82–95.
41. C. Angeli, R. Cimiraglia, S. Evangelisti, T. Leininger and J.-P. Malrieu, J. Chem. Phys., 2001, 114, 10252–10264.
42. C. Angeli, R. Cimiraglia and J.-P. Malrieu, J. Chem. Phys., 2002, 117, 9138–9153.
43. C. Angeli, R. Cimiraglia and J.-P. Malrieu, Chem. Phys. Lett., 2001, 350, 297–305.
44. R. Crespo-Otero and M. Barbatti, Chem. Rev., 2018, 118, 7026–7068.
45. M. Barbatti, A. J. A. Aquino, J. J. Szymczak, D. Nachtigallová and H. Lischka, Phys. Chem. Chem. Phys., 2011, 13, 6145–6155.
46. M. Richter, P. Marquetand, J. González-Vázquez, I. Sola and L. González, J. Phys. Chem. Lett., 2012, 3, 3090–3095.
47. S. Mai, P. Marquetand, M. Richter, J. González-Vázquez and L. González, ChemPhysChem, 2013, 14, 2920–2931.
48. P. M. Hare, C. E. Crespo-Hernández and B. Kohler, Proc. Natl. Acad. Sci. U. S. A., 2007, 104, 435–440.
49. R. Szabla, H. Kruse, J. Šponer and R. W. Góra, Phys. Chem. Chem. Phys., 2017, 19, 17531–17537.
50. A. J. Pepino, J. Segarra-Martí, A. Nenov, I. Rivalta, R. Improta and M. Garavelli, Phys. Chem. Chem. Phys., 2018, 20, 6877–6890.
51. G. Meijer, M. S. d. Vries, H. E. Hunziker and H. R. Wendt, Appl. Phys. B, 1990, 51, 395–403.
52. F. M. Siouri, S. Boldissar, J. A. Berenbeim and M. S. de Vries, J. Phys. Chem. A, 2017, 121, 5257–5266.
53. S. Grimme, J. Chem. Phys., 2006, 124, 034108.
54. V. Barone, J. Chem. Phys., 2004, 122, 014108.
55. J. Bloino, J. Phys. Chem. A, 2015, 119, 5269–5287.
56. M. Biczysko, P. Panek, G. Scalmani, J. Bloino and V. Barone, J. Chem. Theory Comput., 2010, 6, 2115–2125.
57. R. Crespo-Otero and M. Barbatti, Theor. Chem. Acc., 2012, 131, 1–14.
58. B. G. Levine, J. D. Coe and T. J. Martínez, J. Phys. Chem. B, 2008, 112, 405–413.
59. R. Ahlrichs, M. Bär, M. Häser, H. Horn and C. Kölmel, Chem. Phys. Lett., 1989, 162, 165–169.
60. TURBOMOLE V7.0 2015, a development of University of Karlsruhe and Forschungszentrum Karlsruhe GmbH, 1989–2007, TURBOMOLE GmbH, since 2007, available from http://www.turbomole.com.
61. D. Tuna, D. Lefrancois, Ł. Wolański, S. Gozem, I. Schapiro, T. Andruniów, A. Dreuw and M. Olivucci, J. Chem. Theory Comput., 2015, 11, 5758–5781.
62. V. Veryazov, P. Å. Malmqvist and B. O. Roos, Int. J. Quantum Chem., 2011, 111, 3329–3338.
63. F. Plasser, R. Crespo-Otero, M. Pederzoli, J. Pittner, H. Lischka and M. Barbatti, J. Chem. Theory Comput., 2014, 10, 1395–1405.
64. M. J. Frisch, G. W. Trucks, H. B. Schlegel, G. E. Scuseria, M. A. Robb, J. R. Cheeseman, G. Scalmani, V. Barone, B. Mennucci, G. A. Petersson, H. Nakatsuji, M. Caricato, X. Li, H. P. Hratchian, A. F. Izmaylov, J. Bloino, G. Zheng, J. L. Sonnenberg, M. Hada, M. Ehara, K. Toyota, R. Fukuda, J. Hasegawa, M. Ishida, T. Nakajima, Y. Honda, O. Kitao, H. Nakai, T. Vreven, J. Montgomery, J. E. Peralta, F. Ogliaro, M. Bearpark, J. J. Heyd, E. Brothers, K. N. Kudin, V. N. Staroverov, R. Kobayashi, J. Normand, K. Raghavachari, A. Rendell, J. C. Burant, S. S. Iyengar, J. Tomasi, M. Cossi, N. Rega, J. M. Millam, M. Klene, J. E. Knox, J. B. Cross, V. Bakken, C. Adamo, J. Jaramillo, R. Gomperts, R. E. Stratmann, O. Yazyev, A. J. Austin, R. Cammi, C. Pomelli, J. W. Ochterski, R. L. Martin, K. Morokuma, V. G. Zakrzewski, G. A. Voth, P. Salvador, J. J. Dannenberg, S. Dapprich, A. D. Daniels, O. Farkas, J. B. Foresman, J. V. Ortiz, J. Cioslowski and D. J. Fox, Gaussian 09, revision C.01, Gaussian Inc., Wallingford CT, 2009.
65. F. Neese, Wiley Interdiscip. Rev.: Comput. Mol. Sci., 2012, 2, 73–78.
66. H. Lischka, R. Shepard, I. Shavitt, R. M. Pitzer, M. Dallos, T. Müller, P. G. Szalay, F. B. Brown, R. Ahlrichs, H. J. Böhm, A. Chang, D. C. Comeau, R. Gdanitz, H. Dachsel, C. Ehrhardt, M. Ernzerhof, P. Höchtl, S. Irle, G. Kedziora, T. Kovar, V. Parasuk, M. J. M. Pepper, P. Scharf, H. Schiffer, M. Schindler, M. Schüler, M. Seth, E. A. Stahlberg, J.-G. Zhao, S. Yabushita, Z. Zhang, M. Barbatti, S. Matsika, M. Schuurmann, D. R. Yarkony, S. R. Brozell, E. V. Beck, J.-P. Blaudeau, M. Ruckenbauer, B. Sellner, F. Plasser and J. J. Szymczak, Columbus, Relase 7.0 2012, an Ab Initio Electronic Structure Program, 2012.
67. M. Y. Choi and R. E. Miller, J. Am. Chem. Soc., 2006, 128, 7320–7328.
68. H. Robinson, Y.-G. Gao, C. Bauer, C. Roberts, C. Switzer and A. H.-J. Wang, Biochemistry, 1998, 37, 10897–10905.
69. R. Szabla, J. Campos, J. E. Šponer, J. Šponer, R. W. Góra and J. D. Sutherland, Chem. Sci., 2015, 6, 2035–2043.
70. M. Barbatti, J. J. Szymczak, A. J. A. Aquino, D. Nachtigallová and H. Lischka, J. Chem. Phys., 2011, 134, 014304.
71. M. J. Janicki, R. Szabla, J. Šponer and R. W. Góra, Chem. Phys., 2018, 515, 502–508.
72. F. Plasser, S. Gómez, M. F. S. J. Menger, S. Mai and L. González, Phys. Chem. Chem. Phys., 2019, 21, 57–69.
73. A. L. Sobolewski, W. Domcke, C. Dedonder-Lardeux and C. Jouvet, Phys. Chem. Chem. Phys., 2002, 4, 1093–1100.
74. M. Z. Zgierski, T. Fujiwara, W. G. Kofron and E. C. Lim, Phys. Chem. Chem. Phys., 2007, 9, 3206–3209.
75. M. A. Trachsel, S. Lobsiger, T. Schär, L. Blancafort and S. Leutwyler, J. Chem. Phys., 2017, 146, 244308.

---

Footnotes

† Electronic supplementary information (ESI) available. See DOI: 10.1039/c9cp01622h

‡ These authors contributed equally to this work.

---