Open Access Article
Open Access ArticleCreative Commons Attribution 3.0 Unported Licence
Ultrahigh binding affinity of a hydrocarbon guest inside cucurbit[7]uril enhanced by strong host–guest charge matching†
Hugues
Lambert
abc,
Neetha
Mohan
ab and
Tung-Chun
Lee
 *ab
*ab
aDepartment of Chemistry, Christopher Ingold Building, University College London (UCL), 20 Gordon Street London WC1H 0AJ, UK. E-mail: tungchun.lee@ucl.ac.uk
bInstitute for Materials Discovery, University College London (UCL), UK
cInstitute of High Performance Computing, 1 Fusionopolis Way, 138632, Singapore
First published on 11th June 2019
Abstract
Cucurbit[7]uril (CB[7]) is an artificial macrocyclic molecule that can form exceptionally strong host–guest complexes with binding constants higher than that of the biotin–avidin complex. Despite notable experimental efforts, there do not exist large-scale computational investigations on finding strongly binding guests of CB[7]. Herein, we develop a computational approach based on large-scale molecular modelling to predict strongly binding hydrocarbon motifs. Our results indicate that an expanded cubane (PubChem ID 101402794) will be the most strongly binding hydrocarbon guest of CB[7] among the hundreds of thousands of hydrocarbons in the PubChem database, achieving a binding affinity significantly stronger than those reported in preceding experimental studies. Our findings highlight the important role of charge complementarity in the form of quadrupole electrostatic interactions in enabling the ultrahigh binding affinity of nonpolar guest molecules with CB[7], in addition to other known contributions such as van der Waals interactions and high-energy water release.
1 Introduction
Cucurbit[n]urils (CB[n], n = 5–8, 10, and 14) are a family of artificial organic macrocycles that have gained increasing attention in recent years, owing to their unique aqueous host–guest chemistry. CB[n] have a rigid molecular construction consisting of a hydrophobic cavity and two symmetric, electron-rich carbonyl portals. They can form host–guest complexes with a range of small guest molecules, showing potential applications in drug delivery,1 sensing,2 and responsive nanomaterials,3 as well as catalysis in solution4 and in the gas phase.5Notably, CBs are known to form highly stable noncovalent complexes compared to other macrocycles such as cyclodextrins, calixarenes and pillarenes.6 In particular, CB[7] and a congressane derivative can form complexes whose binding constant (Ka = 15.3 × 1015 M−1) exceeds that of the well-known biotin–avidin complex, one of the strongest noncovalent bonds found in nature.7
A central quantity that lies at the heart of the chemical properties of CB[n] is their binding free energy  with a specific guest candidate. The quantity
with a specific guest candidate. The quantity 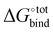 indicates whether a guest@CB[n] complex is stable as well as its relative stability compared to the complexes formed with other competing molecules. In this context, a priori knowledge of
indicates whether a guest@CB[n] complex is stable as well as its relative stability compared to the complexes formed with other competing molecules. In this context, a priori knowledge of 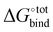 across a range of host–guest complexes would provide useful insights for designing and engineering CB-based supramolecular systems and stimuli-responsive materials. They include supramolecular polymer networks,8 noncovalent ligand immobilisation9 and atypical adhesives,10 all of which typically require strongly binding host–guest moieties for building robust molecular architectures.
across a range of host–guest complexes would provide useful insights for designing and engineering CB-based supramolecular systems and stimuli-responsive materials. They include supramolecular polymer networks,8 noncovalent ligand immobilisation9 and atypical adhesives,10 all of which typically require strongly binding host–guest moieties for building robust molecular architectures.
Fast and accurate evaluation of 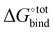 is a challenge often encountered in virtual screening in the field of drug discovery and design. The binding problem can be separated into two parts. First, the optimal conformation of the guest upon complexation with the host needs to be determined, and this step is referred to as docking. Then, the strength of the intermolecular interaction needs to be quantified in an operation called scoring. In practice, some docking algorithms modify the guest's conformation and evaluate on-the-fly its scoring function in iterative steps until a best fit is found.
is a challenge often encountered in virtual screening in the field of drug discovery and design. The binding problem can be separated into two parts. First, the optimal conformation of the guest upon complexation with the host needs to be determined, and this step is referred to as docking. Then, the strength of the intermolecular interaction needs to be quantified in an operation called scoring. In practice, some docking algorithms modify the guest's conformation and evaluate on-the-fly its scoring function in iterative steps until a best fit is found.
A method combining high speed and accuracy together with little need for oversight is however less common, and a trade-off between these desired attributes is often required. Computational methods for estimating 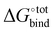 include attach-pull-release, thermodynamical integration, metadynamics and computation of configurational integrals, all of which have been reviewed elsewhere.11 Additional techniques have been used to compute host–guest free binding energies in the SAMPL challenges and in particular for CB[7] in the SAMPL412 challenge. Nevertheless, there do not exist large-scale computational investigations on finding strongly binding guests of CBs in the literature.
include attach-pull-release, thermodynamical integration, metadynamics and computation of configurational integrals, all of which have been reviewed elsewhere.11 Additional techniques have been used to compute host–guest free binding energies in the SAMPL challenges and in particular for CB[7] in the SAMPL412 challenge. Nevertheless, there do not exist large-scale computational investigations on finding strongly binding guests of CBs in the literature.
Herein, we use a classical model based on force fields to screen a large quantity of molecules to predict the most strongly binding hydrocarbon frameworks for CB[7]. Unrecorded strongly binding frameworks are predicted in addition to several derivatives of known high affinity guests such as adamantane, congressane and bicyclo[2.2.2]octane. Furthermore, ab initio calculations on the top ranked host–guest complexes predicted from the force-field methods reveal an expanded cubane to be the most strongly binding hydrocarbon guest for CB[7] with a binding affinity significantly outranking those of all known neutral hydrocarbon frameworks.6 Energy decomposition analysis reveals that the exceptionally strong binding can be attributed to host–guest charge complementarity in the form of electrostatic quadrupole interactions, which provide an additional boost to the binding affinity on top of the classical van der Waals forces. Notably, the strength of the quadrupole interaction (−42.82 kcal mol−1) within the champion complex reaches that of the dispersion component (−53.05 kcal mol−1), which is very rare among neutral nonpolar host–guest systems and is unprecedented for CB complexes, to the best of our knowledge.
2 Method
The overall procedure followed throughout this article is illustrated in Fig. 1. From a skimmed pool of hydrocarbon molecules in Pubchem (Fig. 1A), 200 conformations are generated for each candidate and minimised using MMFF94.13 These conformations are then used to assess the flexibility of the molecules. Only rigid ones are passed to the next stage of the pipeline and other candidates are discarded (Fig. 1B). These molecules are then docked inside CB[7] using AutoDock Vina 1.1.2 (Fig. 1C). For each guest/guest@CB[7] couple, the vacuum binding enthalpy ΔUtotVdW + ΔUtotCoul + ΔUtotval, the configurational entropy change upon binding −TΔStotcfg as well as the polar ΔWtotelec and nonpolar ΔWtotnp solvent contributions to binding are estimated using the Generalised Amber Force Field (GAFF), the Rigid Rotor Harmonic Oscillator (RRHO) approximation and the generalised born implicit solvent and surface area (GBSA) method, respectively (Fig. 1D). Subsequently, the molecules are ranked according to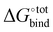 as given by eqn (2). Top ranked candidates are then manually inspected and unphysical molecules are discarded. Finally, the binding affinity of the top 50 molecules as ranked using the force-field based method is evaluated using a density functional theory (DFT) method (Fig. 1E). Individual contributions to binding energy in a vacuum of 10 of the most promising molecules are further characterised using symmetry adapted perturbation theory (SAPT).
as given by eqn (2). Top ranked candidates are then manually inspected and unphysical molecules are discarded. Finally, the binding affinity of the top 50 molecules as ranked using the force-field based method is evaluated using a density functional theory (DFT) method (Fig. 1E). Individual contributions to binding energy in a vacuum of 10 of the most promising molecules are further characterised using symmetry adapted perturbation theory (SAPT).
2.1 Computational details
All screening operations are performed using the force field MMFF94 as implemented in the RDKit.14 The conformers are converged using at most 100![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 000 steps and 10−9 kcal mol−1 as the tolerance criterion on the energy. Molecules that could not be generated using the algorithm are put aside and are not considered further. Molecular volumes are computed using the RDKit.
000 steps and 10−9 kcal mol−1 as the tolerance criterion on the energy. Molecules that could not be generated using the algorithm are put aside and are not considered further. Molecular volumes are computed using the RDKit.
Docking is performed using AutoDock Vina 1.1.2 using the maximum level of exhaustiveness (8). Up to 9 docked poses are generated for each guest. CB[7] is centred at (0, 0, 0) and the search space is centred at (0, 0, 0) with a volume of 24 × 24 × 24 Å3. All other parameters are left to default. Ligand.pdbqt files are generated using the AutoDockTools script prepare_ligand4.py using the Gasteiger charges produced by the same script. The CB[7].pdbqt file is produced using the AutoDockTools GUI.
The contributions to the free energy of binding 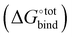 from van der Waals energy (ΔUVdW), Coulomb energy (ΔUCoul) and valence energy (ΔUval) are computed using the General Amber Force Field (GAFF)15 within AMBER 16. The GAFF is expected to perform well in describing noncovalently bound complexes.16 The GAFF parameters are generated using the antechamber from AmberTools16 using the Gasteiger charges. The geometries are subsequently minimised to 10−3 kcal mol−1 using the GBSA implicit solvent model and the conjugated gradient algorithm and to 10−8 kcal mol−1 using the Newton–Raphson algorithm.
from van der Waals energy (ΔUVdW), Coulomb energy (ΔUCoul) and valence energy (ΔUval) are computed using the General Amber Force Field (GAFF)15 within AMBER 16. The GAFF is expected to perform well in describing noncovalently bound complexes.16 The GAFF parameters are generated using the antechamber from AmberTools16 using the Gasteiger charges. The geometries are subsequently minimised to 10−3 kcal mol−1 using the GBSA implicit solvent model and the conjugated gradient algorithm and to 10−8 kcal mol−1 using the Newton–Raphson algorithm.
The generalised Born part is evaluated using the Hawkins, Cramer, and Truhlar's form of pairwise generalised Born model for solvation as implemented in Amber1617 with solute and solvent dielectric constants of, respectively, 1 and 78.5. A non-polar contribution arising from the hydrophobic effect is added as γ*SASA, where γ = 0.005 kcal mol−1 Å−2 is the surface tension of water and SASA is the solvent accessible surface area as approximated using linear combinations of pairwise overlaps18 as implemented in NAB.
The final energy is used in the ranking and its associated geometry is used to estimate the molecular entropy using the RRHO model within Amber16 via the NAB interface.19 The configurational entropy values at 298.15 K are taken as supplied by AmberTools16 and include the translational, rotational and vibrational components of molecular entropy. It is known that a variable number of degrees of freedom, in general, less than 6 including 3 degrees of freedom in translation and 3 in rotation, are lost upon binding.20 Due to the difficulty of systematically estimating the number of degrees of freedom lost upon binding, Amber16 is trusted to select the modes relevant to the estimation of the molecular entropy. The solvent entropy, on the other hand, is mostly contained in the non-polar surface area term of the GBSA evaluation. Indeed, the hydrophobic effect that is evaluated with the non-polar term is mostly entropic in nature.
The endo and exo complexes are distinguished based on two parameters, viz. the distance between the centroid of CB[7] and the centroid of the guest molecule, and the number of atoms of the guest molecule lying within the CB[7] cavity. Hydrogen atoms are not included in the computation of the centroid coordinates. The complex is considered endo if the distance between centroids is less than 4 Å and the number of guest atoms within the CB[7] cavity is greater than or equal to 6.
The distance between centroids is computed using the built-in feature within the RDKit. A heavy atom of the guest is considered to be within the CB[7] cavity if it lies within the convex hull of the heavy atoms of CB[7]. Here, the Delaunay triangulation of CB[7]'s atomic positions is first computed using the SciPy library in Python that uses the qhull algorithm.21 Then, the find_simplex method is used to locate the simplices containing each of the guest's atom. If the procedure is unsuccessful for a given atom, it is assumed to lie outside of CB[7]'s cavity.
Further geometry optimisations and binding energy evaluation of the top 50 ranked host–guest complexes, from the above force-field model, are performed at the ωB97XD/6-31G* level of theory in a vacuum using the Gaussian16 software package22 and cross-validated using the Spartan 16/18 parallel suite. The dispersion-corrected DFT functional ωB97XD23 is chosen to accurately estimate the van der Waals interactions, which are expected to contribute greatly to the stability of these complexes.
Decomposition of interaction energy into its constituent terms using symmetry-adapted perturbation theory (SAPT) analysis24 is performed using PSI4 software25 at the SAPT0 level using the jun-cc-pVDZ basis set.26 SAPT is a perturbative approach that directly computes the interaction energy as a perturbation to the Hamiltonian of the individual monomers and provides a decomposition of the interaction energy into physically meaningful components of electrostatic, exchange, induction, and dispersion. SAPT0 is the simplest and most inexpensive SAPT method that essentially treats the monomers at the Hartree–Fock level and appends explicit dispersion terms obtained from second-order perturbation theory to the electrostatic, exchange, and induction terms from HF dimer treatment.
To obtain the binding enthalpy of a guest in water using an explicit solvent model, the guest, CB[7] and their complex are solvated in 1500 molecules of water using the TIP3P model and a periodic box. The system is first equilibrated to 298.15 K, then the box edges are adapted to equilibrate the pressure to 1 bar. The energy of each subsystem is taken as the time average of the potential energy of the system over a 500 ps simulation. The GAFF is used for the force parameters of CB[7] and the guest. The binding energy is estimated as the difference between the solvated complex and the solvent molecules alone with solvated CB[7] and the solvated guest.
3 Results and discussion
Among the homologues of CB[n], CB[7] is chosen in this study because of its relatively high water solubility and larger inner cavity that allows the encapsulation of a wide variety of guests. Meanwhile, CB[7] is known to form exceptionally strong host–guest complexes owing to a combination of classical and nonclassical hydrophobic effects.27 It is interesting, and perhaps useful, to explore whether there exist other supramolecular forces that can further enhance the noncovalent interactions within CB[7] complexes, potentially leading to record-breaking binding constants.On the other hand, hydrocarbons are chosen as a starting guest pool because of their chemical stability, ease of functionalisation and structural diversity. Their diverse molecular construction can maximise the chance of catching, using the proposed large-scale computational approach, a series of ideal candidates with best possible shape complementarity to the CB[7] cavity. This hypothesis is underpinned by the presence of a few experimentally proven high-affinity guests, such as adamantane derivatives, which are also based on hydrocarbon frameworks. Furthermore, the nonpolar nature of hydrocarbons can also reveal fundamental insights into van der Waals interactions in a CB[7]–guest complex, suggesting new design rules for better guests with exciting new applications.
3.1 Selection of candidates
The initial pool of candidate hydrocarbon guests is obtained from PubChem and contained 238![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 605 hydrocarbon molecules. A filter based on the number of heavy (i.e. carbon) atoms is applied and candidates containing 19 heavy atoms or fewer are retained, yielding a trimmed pool of 132
605 hydrocarbon molecules. A filter based on the number of heavy (i.e. carbon) atoms is applied and candidates containing 19 heavy atoms or fewer are retained, yielding a trimmed pool of 132![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 296 candidates. This prescreening step is justified by the fact that the cavity of CB[7] has total a volume of 242 Å3, which is smaller than the molecular volume of most molecules containing 19 heavy atoms (see the volume distribution shown in Fig. S1, ESI†). Although guests with a volume larger than the CB[7] cavity could still form a host–guest complex with parts sticking out of the cavity, the encapsulated parts can be well-represented by smaller molecular motifs already contained in the trimmed pool. Therefore, we confidently exclude guests that are too large to fit entirely inside the CB[7] cavity. Reactive hydrocarbons containing allenes (C
296 candidates. This prescreening step is justified by the fact that the cavity of CB[7] has total a volume of 242 Å3, which is smaller than the molecular volume of most molecules containing 19 heavy atoms (see the volume distribution shown in Fig. S1, ESI†). Although guests with a volume larger than the CB[7] cavity could still form a host–guest complex with parts sticking out of the cavity, the encapsulated parts can be well-represented by smaller molecular motifs already contained in the trimmed pool. Therefore, we confidently exclude guests that are too large to fit entirely inside the CB[7] cavity. Reactive hydrocarbons containing allenes (C![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) C
C![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) C), three membered rings and charged groups were removed, leaving 110
C), three membered rings and charged groups were removed, leaving 110![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 319 guest candidates for subsequent investigation.
319 guest candidates for subsequent investigation.
We take advantage of the conformational diversity of the conformers generated by the RDKit and generate 200 conformers for each candidate from its SMILES string. The library of conformers generated, though arbitrary, is expected to sample exhaustively the conformational space of a molecule with fewer than 13 rotatable bonds.28 All conformers are then converged using MMFF94. If a given 3D fingerprint computed for each conformer yields sufficiently close values, the molecule is labelled as rigid. In the present case, a molecule is labelled as rigid if the torsion fingerprint deviation29 matrix of its 200 conformers has a single cluster within the Butina clustering algorithm30 provided that a maximum deviation threshold low enough is used. Both operations are carried out using the RDKit implementation with a maximum deviation of 0.01 for the Butina clustering algorithm. It is assumed that if all the 200 conformers generated correspond to the same structure, then the molecule is labelled rigid.
We choose to restrict the search of strongly binding candidates to rigid molecules for two reasons. Firstly, many experimentally observed guests that bind tightly to CB[7] contain rigid hydrocarbon skeletons, such as bicyclo[2.2.2]octane, adamantane or congressane.6 Rigid molecules are expected to possess higher normal mode frequencies and hence are less likely to endure a large entropic penalty upon binding. Secondly, confining the investigation to rigid molecules eliminates the need to consider multiple contributions of different conformers to the change in binding entropy and enthalpy, thereby greatly simplifying the estimation of the free energy of binding that can be computationally demanding even for small systems.31
Determining a priori the rigidity of a molecule is not trivial. For example, an sp3 carbon within a linear alkane can yield a rotatable bond and contribute to the molecular flexibility. On the other hand, an sp3 carbon within a cyclic structure does not indicate the same degree of molecular flexibility. As graph based techniques could prove complex32 with no guarantee of robustness, we choose a statistical method to estimate the rigidity of the small molecules. The method described above is able to distinguish the high flexibility of linear hexane from the limited flexibility of cyclohexane and the high rigidity of benzene. Indeed, it is expected that chair, seesaw and boat conformations will be encountered while enumerating conformers for cyclohexane, indicating its relative molecular flexibility. Cyclohexane is therefore discarded. On the other hand, only one conformer of benzene will be encountered resulting in its labelling as rigid. Moreover, flexible unsaturated molecules are appropriately labelled as flexible while polycyclic saturated structures such as cubane are labelled as rigid. After removing non-rigid molecules, a total of 8999 guest candidates remain and are subject to further study.
3.2 Binding affinity evaluation
Docking is initially performed using AutoDock Vina to obtain a range of starting configurations of each host–guest complex required to estimate the binding affinities. Different guest orientations within the cavity can strongly modulate the computed affinities. Since it is not known a priori which of the docked poses would yield the most negative force-field based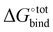 , the free energy of CB[7] complexes are minimised and evaluated for all binding poses. No conformation analysis is required for the free guest molecules owing to the absence of a rotatable bond.
, the free energy of CB[7] complexes are minimised and evaluated for all binding poses. No conformation analysis is required for the free guest molecules owing to the absence of a rotatable bond.
It is noted that, however, the binding affinity predicted by AutoDock Vina is somewhat unreliable for our host–guest system, especially for strongly binding guests. When benchmarking against experimental data (Fig. S2, ESI†), AutoDock Vina tends to underestimate the binding affinity over the entire range, with significant deviation in the slope of the linear fit and in absolute binding affinity for strongly binding guests. For instance, neither bicyclo[2.2.2]octane-1,4-dimethanol [C1CC2(CCC1(CC2)CO)CO], 1-adamantanol [C1C2CC3CC1CC(C2)(C3)O] nor 1-adamantanamine [C1C2CC3CC1CC(C2)(C3)N], with experimental binding affinities in water of respectively 13.44 kcal mol−1, 14.23 kcal mol−1 and 17.34 kcal mol−1, are predicted by AutoDock Vina to have a binding affinity exceeding 10 kcal mol−1. The inability of the software to accurately predict the binding affinities for known strongly binding guests motivates us to employ a more refined force-field based approach for assessing the 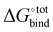 of all the docked poses generated by AutoDock Vina.
of all the docked poses generated by AutoDock Vina.
The free energy of binding 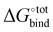 can be decomposed generally in eqn (1)33 and further broken down as shown in eqn (2):34
can be decomposed generally in eqn (1)33 and further broken down as shown in eqn (2):34
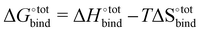 | (1) |
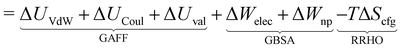 | (2) |
The accuracy of the model has been evaluated by benchmarking a set of experimental binding constants collected from the literature6 against their binding affinity predicted by using the present technique, as shown in Fig. S2 (ESI†). The benchmarking plot shows a Pearson correlation coefficient R2 of 0.49 and a slope of 1.2 where a coefficient R2 of 1 indicates an ideal linear correlation with the experimental data. These parameters are considered reasonable for the given level of theory.34 Nevertheless, it should be noted that the binding affinity 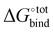 is overestimated. Indeed, the present procedure is known to overestimate the favourable contribution of ΔUVdW and underestimate the unfavourable contribution of −TΔScfg to the binding affinity
is overestimated. Indeed, the present procedure is known to overestimate the favourable contribution of ΔUVdW and underestimate the unfavourable contribution of −TΔScfg to the binding affinity 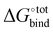 ,34 but not expected to invalidate the consistency of the ranking.
,34 but not expected to invalidate the consistency of the ranking.
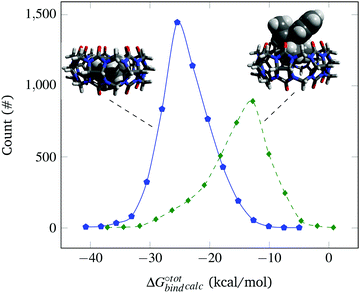
The docked poses of the host–guest complexes can be separated into two groups, namely the endo complexes where the guest molecules lie inside the CB[7] cavity and exo complexes where the guest molecules significantly stick out. As mentioned in the Methods section, a complex is defined as “endo” if the centroid of the atomic coordinates of the guest is less than 4 Å away from the centroid of the atomic coordinates of CB[7] and if at least 6 of the guest's heavy atoms are located inside the cavity. Failure to meet one of these criteria results in the complex being labelled as “exo”. It is observed that the guest molecules that exhibit high binding affinities are predominantly endo complexes. This is well-evident from Fig. 2, which plots the distribution of endo and exo complexes against their binding affinities with CB[7]. This finding can be rationalised by the maximisation of the van der Waals interactions of the guests with the CB[7] cavity, which is consistent with experimental and other computational studies.4
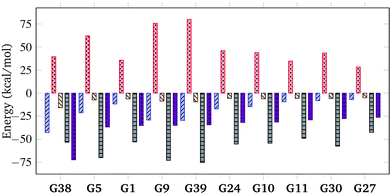
The resultant, force-field based, 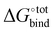 values of the top 100 guests are plotted in Fig. 3, which shows that ΔUCoul + ΔUVdW + ΔUval, as computed by GAFF, together contribute the most to the binding affinity of the top ranked guests in the present model. The van der Waals contribution ΔUVdW is in turn the major contributor to the favourable enthalpic part of the binding affinity (Table S2, ESI†). The presence of the solvent is generally detrimental to binding due to the presence of a mostly positive contribution from ΔWelec. The entropic penalty to binding −TΔScfg as estimated here is relatively small compared to the enthalpy term. For the sake of convenient discussion, guests are labelled as Gx where x stands for their positions in the GAFF-based ranking.
values of the top 100 guests are plotted in Fig. 3, which shows that ΔUCoul + ΔUVdW + ΔUval, as computed by GAFF, together contribute the most to the binding affinity of the top ranked guests in the present model. The van der Waals contribution ΔUVdW is in turn the major contributor to the favourable enthalpic part of the binding affinity (Table S2, ESI†). The presence of the solvent is generally detrimental to binding due to the presence of a mostly positive contribution from ΔWelec. The entropic penalty to binding −TΔScfg as estimated here is relatively small compared to the enthalpy term. For the sake of convenient discussion, guests are labelled as Gx where x stands for their positions in the GAFF-based ranking.
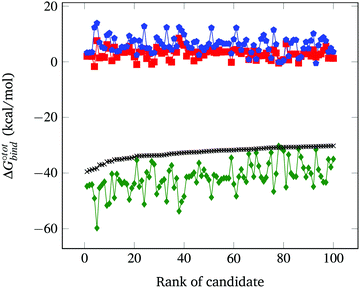 | ||
Fig. 3 Force-field based free energy of binding 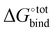 for the top 100 hydrocarbon guests of CB[7] based on our computational approach. The total free energy of binding is indicated by the black ×. The major contributions from the van der Waals ΔUVdW and electrostatic ΔUCoul interactions together with the change in internal energy ΔUval of the molecule, as computed by GAFF, are represented by the green diamonds. Decomposition of the GAFF energy is presented in Table S2 (ESI†). The entropic contribution −TΔScfg at 298.15 K is represented by the blue pentagons. The minor contribution from the solvation energy ΔWnp + ΔWelec is shown by the red squares. for the top 100 hydrocarbon guests of CB[7] based on our computational approach. The total free energy of binding is indicated by the black ×. The major contributions from the van der Waals ΔUVdW and electrostatic ΔUCoul interactions together with the change in internal energy ΔUval of the molecule, as computed by GAFF, are represented by the green diamonds. Decomposition of the GAFF energy is presented in Table S2 (ESI†). The entropic contribution −TΔScfg at 298.15 K is represented by the blue pentagons. The minor contribution from the solvation energy ΔWnp + ΔWelec is shown by the red squares. | ||
The displacement of high-energy water, also known as the nonclassical hydrophobic effect, was previously shown to be the major contributor to the strong binding affinity of CB[7] and CB[n].27 This effect is the consequence of water molecules inside the CB[n] cavity having unsatisfied hydrogen bonds that are able to become satisfied once they leave the cavity and enter the bulk of the solvent. Such an effect is unlikely to be well-captured using an implicit solvent model such as GBSA, where the organisational constraints imposed on the solvent by the solute are mainly accounted for using the term ΔWnp = γ*SASA. Indeed, ΔWnp's continuous description is likely inappropriate to account for the discrete nature of the water molecules that yields this effect. Nevertheless, we argue that for guests big enough to fill the CB[7] cavity, the enthalpic contribution to the removal of the high energy water, though big in absolute terms, should be relatively similar. Implicit solvent models have also been used to estimate host–guest binding affinities in the case of CB[7] with appreciable accuracy.34 The GBSA method is selected here to estimate the solvation contributions ΔWelec and ΔWnp due to its computational speed. As shown in Fig. 3, the contribution of ΔWelec and ΔWnp to 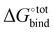 is rather small and shows little variation among the top guest candidates. This can be rationalised by the fact that all guests studied are uncharged hydrocarbons and hence generally hydrophobic. Therefore, the energy difference is insignificant when shifting the guest in a hydrophobic solvent pocket in the bulk to the hydrophobic cavity of CB[7]. The magnitude of ΔWelec and ΔWnp is in reasonable agreement with previously reported values.34
is rather small and shows little variation among the top guest candidates. This can be rationalised by the fact that all guests studied are uncharged hydrocarbons and hence generally hydrophobic. Therefore, the energy difference is insignificant when shifting the guest in a hydrophobic solvent pocket in the bulk to the hydrophobic cavity of CB[7]. The magnitude of ΔWelec and ΔWnp is in reasonable agreement with previously reported values.34
The contribution from the change in configurational entropy −TΔScfg in particular needs to be considered. In the case of the binding of guests with cyclodextrin31 and CB[7],34 it was shown that the unfavourable binding contribution of configurational entropy is of the same order as the favourable van der Waals contribution. Estimating the change in entropy upon binding is not trivial. For instance, in the SAMPL3 challenge35 where diverse research groups attempted to predict the 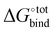 of a range of compounds, the techniques that directly attempted to model the entropic contribution (using the RRHO model for example) performed significantly worse than regression-based approaches that accounted for it implicitly. Entropic contributions can be accounted for accurately using molecular dynamic techniques or end-point approaches similar to RRHO such as HA/MS,36 at the expense of increased computation time. One known shortcoming of the RRHO approximation is that it is only exact for infinitesimally small deformations. In the case of flat energy surfaces such as the case of freely rotatable bonds, marked anharmonicity can occur, yielding inaccurate results.36
of a range of compounds, the techniques that directly attempted to model the entropic contribution (using the RRHO model for example) performed significantly worse than regression-based approaches that accounted for it implicitly. Entropic contributions can be accounted for accurately using molecular dynamic techniques or end-point approaches similar to RRHO such as HA/MS,36 at the expense of increased computation time. One known shortcoming of the RRHO approximation is that it is only exact for infinitesimally small deformations. In the case of flat energy surfaces such as the case of freely rotatable bonds, marked anharmonicity can occur, yielding inaccurate results.36
Since only rigid molecules are considered here, we expect the guests' potential energy surface to be well-described by a harmonic approximation. The entropic contribution to binding is defined as:
| −TΔStotcfg = −TΔScomplexcfg − (−TΔSCB[7]cfg) − (−TΔSguestcfg) | (3) |
Occurrence of the so-called enthalpy–entropy compensation effect37 was checked by plotting the entropic penalty TΔS°![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) bind against the binding enthalpy
bind against the binding enthalpy 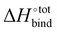 , as shown in Fig. S3 (ESI†). It has been suggested that ultrahigh binding affinity in the case of CB[7] was achievable at least partially through the avoidance of a steep entropic penalty upon binding due to the high intrinsic rigidity of the macrocycle.38
, as shown in Fig. S3 (ESI†). It has been suggested that ultrahigh binding affinity in the case of CB[7] was achievable at least partially through the avoidance of a steep entropic penalty upon binding due to the high intrinsic rigidity of the macrocycle.38
It is interesting to see in Fig. S3 (ESI†) that the highest ranked guests do not exhibit a severe enthalpy–entropy compensation effect, with a regression slope of only 0.686 instead of an expected value of 1 for an ideal manifestation of the effect. The relatively small slope indicates that a large increase in binding enthalpy is less than counterbalanced by the entropic penalty, which helps explain the overall large binding affinities. For the guests ranked between 51 and above (only guests 51 to 200 are displayed), the slope converges towards unity, indicating an increasingly strong enthalpy–entropic compensation effect. It is noteworthy that the enthalpy–entropy compensation effect reported herein arises from the direct computation of 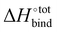 and
and 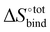 , giving support to the hypothesis of a physical origin of the phenomenon rather than it being a statistical artefact. Indeed, unlike experimental evidence of the effect arising from computation of
, giving support to the hypothesis of a physical origin of the phenomenon rather than it being a statistical artefact. Indeed, unlike experimental evidence of the effect arising from computation of 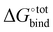 and
and 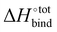 where TΔS°
where TΔS°![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) bind is obtained a posteriori by subtraction, the present vacuum analysis is free from solvent effects and correlated errors.39
bind is obtained a posteriori by subtraction, the present vacuum analysis is free from solvent effects and correlated errors.39
3.3 Ranking
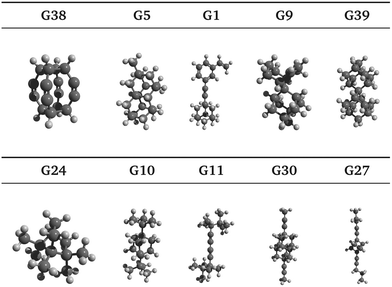
Ten selected guests from the 50 best candidates are shown in Fig. 4 and the references of each of the 100 best candidates are detailed in Table S1 (ESI†). It is noted that several carbon skeletons among the predicted best candidates are already known to bind strongly to CB[7], including guests G1, G9 and G39, which are adamantane40 derivatives, and guests G30 and G10, which are congressane7 and bicyclo[2.2.2]octane34 derivatives, respectively. A guest with a skeleton very similar to G24 has also been reported to bind strongly CB[7].41 It is also worth mentioning guest G27, a cubane derivative similar to those recently reported.42Moreover, we have identified hydrocarbon frameworks that can potentially bind very strongly to CB[7] but have not been reported in such a context, including guests G38, G5 and G11, as shown in Fig. 4. Upon visual inspection of the docked poses, G38 is expected to bind very strongly to CB[7], due to its highly symmetric molecular structure that is complementary to that of the CB[7] cavity, which is also highly symmetric. Guest G3843 appears to have only been studied in silico while G5 was added to PubChem as a part of a patent claim along with over 400 other molecules. To the best of our knowledge, the syntheses of G38 and G5 have not been reported in the literature.
In Section 3.2, we observe that the binding enthalpy in a vacuum (ΔUCoul + ΔUVdW + ΔUval) serves as the major contributor to 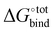 , while the contributions from solvent effects and configurational entropy remain insignificant for our host–guest system of CB[7] and rigid hydrocarbon guests (Fig. 3). In order to better evaluate the vacuum binding energy, DFT optimisation is performed on the host–guest complexes of the top 50 GAFF-based ranked guests. The resultant DFT binding energies are presented in Table S3 in the ESI,† where guests are re-sorted by decreasing magnitude of DFT binding energy. Aligned with our initial hypothesis, guest G38 exhibits the most negative binding energy (−62.78 kcal mol−1) at the ωB97XD/6-31G* level of theory in a vacuum, which exceeds those of other known strongly binding guests such as adamantane (−41.18 kcal mol−1), congressane (−46.79 kcal mol−1) and bicyclo[2.2.2]octane (−34.74 kcal mol−1). Guests G5, G9 and G39 also exhibit strong binding with CB[7] with interaction energy values of −54.34, −48.41 and −49.47 kcal mol−1, respectively.
, while the contributions from solvent effects and configurational entropy remain insignificant for our host–guest system of CB[7] and rigid hydrocarbon guests (Fig. 3). In order to better evaluate the vacuum binding energy, DFT optimisation is performed on the host–guest complexes of the top 50 GAFF-based ranked guests. The resultant DFT binding energies are presented in Table S3 in the ESI,† where guests are re-sorted by decreasing magnitude of DFT binding energy. Aligned with our initial hypothesis, guest G38 exhibits the most negative binding energy (−62.78 kcal mol−1) at the ωB97XD/6-31G* level of theory in a vacuum, which exceeds those of other known strongly binding guests such as adamantane (−41.18 kcal mol−1), congressane (−46.79 kcal mol−1) and bicyclo[2.2.2]octane (−34.74 kcal mol−1). Guests G5, G9 and G39 also exhibit strong binding with CB[7] with interaction energy values of −54.34, −48.41 and −49.47 kcal mol−1, respectively.
To further understand the nature of the exceptionally strong binding of G38, quantitative decomposition of interaction energies into their constituent terms is performed using SAPT on a representative set of 10 top host–guest complexes involving guests G1, G5, G9, G10, G11, G24, G27, G30, G38 and G39. The individual electrostatic, exchange, induction and dispersion components are plotted in Fig. 5 and summarised in Table S4 in the ESI.† The results reveal that the interaction energy typically has the most significant contributions from the dispersion and exchange repulsion terms with the attractive dispersion term outweighing the repulsive exchange term. Notably, however, the exceptionally high binding affinity of G38 can be attributed to its strong electrostatic component in addition to the dispersion contribution, which is uncommon for nonpolar hydrocarbon motifs. The electrostatic component for G38 is −42.82 kcal mol−1, which is comparable to the dispersion component of −53.05 kcal mol−1. Moreover, the relatively small exchange component (+39.49 kcal mol−1) indicates a good shape match between CB[7] and G38.
Upon closer study of the DFT model of the G38@CB[7] host–guest complex, it can be seen in Fig. S4 (ESI†) that the positive regions of the electrostatic potential of G38 located near its hydrogen atoms overlap significantly with the negative regions of the electrostatic potential of CB[7] near its carbonyl portals, while the electron-rich region of the C![[triple bond, length as m-dash]](https://www.rsc.org/images/entities/char_e002.gif) C triple bonds overlaps well with the electron-poor region of the CB cavity, revealing a high degree of electrostatic charge matching between the host and the guest.
C triple bonds overlaps well with the electron-poor region of the CB cavity, revealing a high degree of electrostatic charge matching between the host and the guest.
The extent of charge distribution matching can be quantified, to a first approximation, by considering the molecular electrostatic quadrupole moment θzz, which is defined as the second moment of the charge density44 along the main axis (as defined by component analysis) of a guest molecule or along the axis passing through the centres of both CB[7] portals in the case of CB[7] and its complexes. Despite the possibility of using higher order multipole descriptions, for uncharged, nonpolar molecules (i.e. both monopole and dipole moment = 0), such as hydrocarbons, θzz can serve as a simple and effective measure for assessing the distribution of charge density, as well as for estimating their interaction and matching with each other. As shown in Table 1, G38 has an exceptionally large intrinsic quadrupole moment of 17.69 Buckingham among other top ranked guests, which is followed by G1 (6.66 Buckingham), G11 (8.31 Buckingham), G27 (8.84 Buckingham) and G30 (7.49 Buckingham).
| Label | θ Guest zz | θ Complex zz | θ Complex zz − θCB[7]zz |
|---|---|---|---|
| G1 | 6.6565 | −183.0288 | 9.9537 |
| G5 | −0.6465 | −192.2733 | 0.7092 |
| G9 | −0.877 | −196.8669 | −3.8844 |
| G10 | −0.4871 | −195.6812 | −2.6987 |
| G11 | 8.3143 | −174.0805 | 18.902 |
| G24 | 0.2007 | −190.5710 | 2.4115 |
| G27 | 8.8441 | −184.4205 | 8.5620 |
| G30 | 7.4876 | −185.5569 | 7.4256 |
| G38 | 17.6962 | −172.0938 | 20.8887 |
| G39 | −0.3565 | −190.5165 | 2.4660 |
| Adamantane | −0.0001 | −188.9318 | 4.0507 |
| Congressane | 0.2124 | −191.9764 | 1.0061 |
| Bicyclo[2.2.2]octane | 0.0582 | −183.4338 | 9.5487 |
| CB[7]alone | − | −192.9825 | — |
Nevertheless, a large quadrupole moment of the guest alone is not sufficient to generate significant host–guest electrostatic interactions, while it is also necessary to have quadrupole (or multipole) charge matching between the host and the guest, which can be roughly estimated by the change in θzz of the host upon complexation. In this context, G38 produces the largest change in θzz (= 20.89 Buckingham) upon binding with CB[7], as shown in Table 1. It is noted that, however, the change in θzz does not directly correlate to the degree of charge complementarity. For instance, G1, G11, G27 and G30 also exhibit large intrinsic θzz and can induce significant change in θzz upon complexation despite displaying a negligible electrostatic contribution to binding, as indicated by the SAPT results (Fig. 5). This seemingly paradoxical effect can be attributed to host–guest charge mismatch or the change in θzz being mainly contributed by moieties outside the CB[7] cavity, which might likely be the case for elongated guests, such as G1, G11, G27 and G30. More sophisticated models involving higher order multipole terms would be required to accurately and reliably gauge the mode and the degree of charge complementarity between CB[7] and nonpolar guests.
In order to rule out any overlooked electronic effect during the DFT minimisation, the electronic density ρ of G38@CB[7] was analysed, confirming the absence of charge delocalisation or chemical bonds between CB[7] and G38 (see Fig. S5, ESI†).
A molecular dynamics model based on GAFF with explicit solvent molecules is additionally performed, with the aim to validate the binding enthalpy between CB[7] and G38 in water (see Fig. S6, ESI† for details). The binding enthalpy 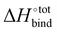 is computed to be −36.24 kcal mol−1, which is significantly higher than any value computed using the same technique or experimentally measured for strongly binding guests; for instance, 1-adamantanol has a binding enthalpy in water of −24.9 kcal mol−1.45 The binding enthalpy in water was also estimated using a DFT implicit solvent model with CPCM/ωB97XD/6-31G*, yielding a value of −46.5 kcal mol−1, comparable to that obtained from the explicit solvent model.
is computed to be −36.24 kcal mol−1, which is significantly higher than any value computed using the same technique or experimentally measured for strongly binding guests; for instance, 1-adamantanol has a binding enthalpy in water of −24.9 kcal mol−1.45 The binding enthalpy in water was also estimated using a DFT implicit solvent model with CPCM/ωB97XD/6-31G*, yielding a value of −46.5 kcal mol−1, comparable to that obtained from the explicit solvent model.
4 Conclusion
In summary, we have developed a force-field based computational approach for finding the most strongly binding hydrocarbon guest for CB[7] from the PubChem database. Top ranked guests are then subjected to further investigation using dispersion-corrected DFT models. An expanded cubane (G38) emerges as the champion, achieving an ultrahigh predicted binding energy of −62.78 kcal mol−1 at the ωB97XD/6-31G* level of theory in a vacuum, which significantly exceeds those of other known strongly binding guests. Notably, this exceptionally strong host–guest binding interaction can be attributed to the excellent complementarity in molecular shape and electrostatic charge, as revealed by the SAPT energy decomposition and the DFT electrostatic potential. The G38@CB[7] complex has been further analysed using molecular quadrupole moment calculations, as well as a molecular dynamics model with explicit solvent molecules and a DFT implicit solvent model.Interestingly, in the champion complex, the strong quadrupole interactions arising from host–guest charge matching serve as a significant driver to supramolecular complexation. This is in contrast to, for example, the situation of the ferrocene@CB[7] system where the quadrupole interactions are only strong enough to modulate the guest's orientation within the cavity.46 Furthermore, our finding extends the relevance of quadrupole interactions to neutral host–guest complexes, in addition to their documented significance in anion47 and cation48 interactions with aromatic hydrocarbons, the efficiency of small graphene sheets exfoliation49 and in the stability of the benzene–hexafluorobenzene complex.50
The presented computational approach can be extended for investigating other rigid host–guest systems beyond CB[n] and hydrocarbons. Meanwhile, our findings highlight the unexpected, yet important, role of charge complementarity for neutral nonpolar molecules, which can potentially be used to further strengthen host–guest interactions on top of hydrophobic effects and van der Waals interactions.
Conflicts of interest
There are no conflicts of interest to declare.Acknowledgements
HL and TCL are grateful to the Studentship funded by the A*STAR-UCL Research Attachment Programme through the EPSRC Centre for Doctoral Training in Molecular Modelling and Materials Science (EP/L015862/1). NM and TCL are grateful to the Research Project Grant (RPG-2016-393) funded by the Leverhulme Trust.References
- D. Jiao, J. Geng, X. J. Loh, D. Das, T.-C. Lee and O. A. Scherman, Angew. Chem., Int. Ed., 2012, 51, 9633–9637 CrossRef CAS PubMed.
- R. W. Taylor, T.-C. Lee, O. A. Scherman, R. Esteban, J. Aizpurua, F. M. Huang, J. J. Baumberg and S. Mahajan, ACS Nano, 2011, 5, 3878–3887 CrossRef CAS PubMed.
- E. Ellis, S. Moorthy, W.-I. K. Chio and T.-C. Lee, Chem. Commun., 2018, 54, 4075–4090 RSC.
- K. I. Assaf and W. M. Nau, Chem. Soc. Rev., 2015, 44, 394–418 RSC.
- T.-C. Lee, E. Kalenius, A. I. Lazar, K. I. Assaf, N. Kuhnert, C. H. Grün, J. Jänis, O. A. Scherman and W. M. Nau, Nat. Chem., 2013, 5, 376–382 CrossRef CAS PubMed.
- S. J. Barrow, S. Kasera, M. J. Rowland, J. del Barrio and O. A. Scherman, Chem. Rev., 2015, 115, 12320–12406 CrossRef CAS PubMed.
- L. Cao, M. Šekutor, P. Y. Zavalij, K. Mlinarić-Majerski, R. Glaser and L. Isaacs, Angew. Chem., Int. Ed., 2014, 53, 988–993 CrossRef CAS PubMed.
- H. Chen, S. Hou, H. Ma, X. Li and Y. Tan, Sci. Rep., 2016, 6, 20722 CrossRef PubMed.
- J. F. Young, H. D. Nguyen, L. Yang, J. Huskens, P. Jonkheijm and L. Brunsveld, ChemBioChem, 2010, 11, 180–183 CrossRef CAS PubMed.
- Y. Ahn, Y. Jang, N. Selvapalam, G. Yun and K. Kim, Angew. Chem., Int. Ed., 2013, 125, 3222–3226 CrossRef.
- D. L. Mobley and M. K. Gilson, Annu. Rev. Biophys., 2017, 46, 531–558 CrossRef CAS PubMed.
- H. S. Muddana, A. T. Fenley, D. L. Mobley and M. K. Gilson, J. Comput.-Aided Mol. Des., 2014, 28, 305–317 CrossRef CAS PubMed.
- T. A. Halgren, J. Comput. Chem., 1996, 17, 553–586 CrossRef CAS.
- G. Landrum, Online, http://www.rdkit.org, (2006), accessed, 3, 2012.
- J. Wang, R. M. Wolf, J. W. Caldwell, P. A. Kollman and D. A. Case, J. Comput. Chem., 2004, 25, 1157–1174 CrossRef CAS PubMed.
- M. Kolář, K. Berka, P. Jurečka and P. Hobza, ChemPhysChem, 2010, 11, 2399–2408 CrossRef PubMed.
- V. Tsui and D. A. Case, Biopolymers, 2000, 56, 275–291 CrossRef CAS.
- J. Weiser, P. S. Shenkin and W. C. Still, J. Comput. Chem., 1999, 20, 217–230 CrossRef CAS.
- D. A. Case, T. E. Cheatham III, T. Darden, H. Gohlke, R. Luo, K. M. Merz Jr., A. Onufriev, C. Simmerling, B. Wang and R. J. Woods, J. Comput. Chem., 2005, 26(16), 1668–1688 CrossRef CAS PubMed.
- A. V. Finkelstein and J. Janin, Protein Eng., Des. Sel., 1989, 3, 1–3 CrossRef CAS.
- C. B. Barber, D. P. Dobkin and H. Huhdanpaa, ACM T. Math. Software, 1996, 22(4), 469–483 CrossRef.
- M. J. Frisch, G. W. Trucks, H. B. Schlegel, G. E. Scuseria, M. A. Robb and J. R. Cheesemanet al., Gaussian 16 Revision B.01, Gaussian Inc., Wallingford CT, 2016 Search PubMed.
- J.-D. Chai and M. Head-Gordon, Phys. Chem. Chem. Phys., 2008, 10, 6615–6620 RSC.
- B. Jeziorski, R. Moszynski and K. Szalewicz, Chem. Rev., 1994, 94, 1887–1930 CrossRef CAS.
- R. M. Parrish, L. A. Burns, D. G. Smith, A. C. Simmonett, A. E. DePrince III, E. G. Hohenstein, U. Bozkaya, A. Y. Sokolov, R. Di Remigio and R. M. Richard, et al. , J. Chem. Theory Comput., 2017, 13, 3185–3197 CrossRef CAS PubMed.
- E. Papajak and D. G. Truhlar, J. Chem. Theory Comput., 2010, 7, 10–18 CrossRef PubMed.
- F. Biedermann, V. D. Uzunova, O. A. Scherman, W. M. Nau and A. De Simone, J. Am. Chem. Soc., 2012, 134, 15318–15323 CrossRef CAS PubMed.
- J.-P. Ebejer, G. M. Morris and C. M. Deane, J. Chem. Inf. Model., 2012, 52, 1146–1158 CrossRef CAS PubMed.
- T. Schulz-Gasch, C. Schärfer, W. Guba and M. Rarey, J. Chem. Inf. Model., 2012, 52, 1499–1512 CrossRef CAS PubMed.
- D. Butina, J. Chem. Inf. Comput. Sci., 1999, 39, 747–750 CrossRef CAS.
- W. Chen, C.-E. Chang and M. K. Gilson, Biophys. J., 2004, 87, 3035–3049 CrossRef CAS PubMed.
- D. J. Jacobs, A. J. Rader, L. A. Kuhn and M. F. Thorpe, Proteins, 2001, 44, 150–165 CrossRef CAS PubMed.
- H.-X. Zhou and M. K. Gilson, Chem. Rev., 2009, 109, 4092–4107 CrossRef CAS PubMed.
- S. Moghaddam, C. Yang, M. Rekharsky, Y. H. Ko, K. Kim, Y. Inoue and M. K. Gilson, J. Am. Chem. Soc., 2011, 133, 3570–3581 CrossRef CAS PubMed.
- H. S. Muddana, C. D. Varnado, C. W. Bielawski, A. R. Urbach, L. Isaacs, M. T. Geballe and M. K. Gilson, J. Comput.-Aided Mol. Des., 2012, 26, 475–487 CrossRef CAS PubMed.
- C.-E. Chang, M. J. Potter and M. K. Gilson, J. Phys. Chem. B, 2003, 107, 1048–1055 CrossRef CAS.
- C. H. Reynolds and M. K. Holloway, ACS Med. Chem. Lett., 2011, 2, 433–437 CrossRef CAS PubMed.
- M. V. Rekharsky, T. Mori, C. Yang, Y. H. Ko, N. Selvapalam, H. Kim, D. Sobransingh, A. E. Kaifer, S. Liu and L. Isaacs, et al. , Proc. Natl. Acad. Sci. U. S. A., 2007, 104, 20737–20742 CrossRef CAS PubMed.
- J. D. Chodera and D. L. Mobley, Annu. Rev. Biophys., 2013, 42, 121–142 CrossRef CAS PubMed.
- S. Liu, P. Y. Zavalij and L. Isaacs, J. Am. Chem. Soc., 2005, 127, 16798–16799 CrossRef CAS PubMed.
- L. Cao and L. Isaacs, Supramol. Chem., 2014, 26, 251–258 CrossRef CAS.
- K. Jelnková, H. Surmová, A. Matelová, M. Rouchal, Z. Prucková, L. Dastychová, M. Nečas and R. Vícha, Org. Lett., 2017, 19, 2698–2701 CrossRef PubMed.
- S. M. Bachrach and D. W. Demoin, J. Org. Chem., 2006, 71, 5105–5116 CrossRef CAS PubMed.
- A. Buckingham, Q. Rev., Chem. Soc., 1959, 13, 183–214 RSC.
- A. T. Fenley, N. M. Henriksen, H. S. Muddana and M. K. Gilson, J. Chem. Theory Comput., 2014, 10, 4069–4078 CrossRef CAS PubMed.
- W. M. Nau, M. Florea and K. I. Assaf, Isr. J. Chem., 2011, 51, 559–577 CrossRef CAS.
- M. R. Jackson, R. Beahm, S. Duvvuru, C. Narasimhan, J. Wu, H.-N. Wang, V. M. Philip, R. J. Hinde and E. E. Howell, J. Phys. Chem. B, 2007, 111, 8242–8249 CrossRef CAS PubMed.
- J. C. Ma and D. A. Dougherty, Chem. Rev., 1997, 97, 1303–1324 CrossRef CAS PubMed.
- M. Kocman, M. Pykal and P. Jurečka, Phys. Chem. Chem. Phys., 2014, 16, 3144–3152 RSC.
- J. Hernández Trujillo, F. Colmenares, G. Cuevas and M. Costas, Chem. Phys. Lett., 1997, 265, 503–507 CrossRef.
Footnote |
| † Electronic supplementary information (ESI) available. See DOI: 10.1039/c9cp01762c |
| This journal is © the Owner Societies 2019 |

![[pentagon open]](https://www.rsc.org/images/entities/char_e1c1.gif) ) and
) and