Physical origin underlying the prenucleation-cluster-mediated nonclassical nucleation pathways for calcium phosphate†
Abstract
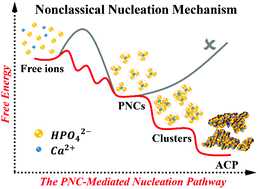
The involvement of prenucleation clusters (PNCs) in crystallization from a supersaturated solution has been recently admitted within the framework of nonclassical nucleation theory; however, little is known about PNCs, at the quantitative level, for their formation mechanism and stability, the new phase formed by them, as well as their impact on nucleation barriers. Herein, using the sophisticated free energy calculations with a cumulative simulation time of over 5 μs, we identify a thermodynamically favored pathway of the PNC-mediated nucleation for calcium phosphate, starting with the ion pair association in solution. We demonstrate that such an ion association occurs not only between cations and anions, but also for the polyatomic species with charges of the same sign, which, in fact, leads to PNC formation via the consecutive coordination of the phosphate ions to calcium. The free energy decomposition calculations illustrate that the water phase is capable to either hinder or promote ion association for the abovementioned processes, and its specific role is intricately related to the characteristics of the hydration shell around calcium ions. The favorable interactions between the highly charged species play a crucial role in stabilizing the PNC complexes and the aggregates formed by PNCs. Furthermore, our present work reveals that the uptake of an extra calcium ion is the first and mandatory step to trigger PNC aggregation into amorphous calcium phosphate (ACP) by eliminating the related free energy barriers. Our theoretical study successfully provides quantitative explanations to a large set of experimental data in the field, which is currently under intense discussions associated with the nonclassical nucleation mechanism. The combination of computational methods developed in our present work offers a feasible and general solution to quantitatively and systematically study ion associations and crystal nucleation/growth in an aqueous solution at the atomic level, which are normally inaccessible to most of the existing experimental acquisitions.


 Please wait while we load your content...
Please wait while we load your content...