High-speed tracking of fast chemical precipitations

Abstract

Heterogeneous reactions taking place in the aqueous phase bear significant importance both in applied and fundamental research. Among others, producing solid catalysts, crystallizing biomorphs or pharmaceutically relevant polymorphs, and yielding bottom-up synthesised precipitate structures are prominent examples. To achieve a better control on product properties, reaction kinetics and mechanisms must be taken into account especially in dynamic systems where transport processes are coupled to chemistry. Since the characteristic time scale of numerous precipitation reactions falls below 1 s within the relevant concentration range, unique experimental protocols are needed. Herein we present a high-speed camera supported experimental procedure capable of determining such characteristic time scales in the range of 10 ms to 1 s. The method is validated both experimentally and by performing 3D hydrodynamic simulations.

---

1 Introduction

Chemical precipitation reactions bear relevance in synthesising nanomaterials^1,2 and catalyst precursors,^3,4 in crystallizing biomorphs^5–7 and polymorphs^8,9 even in the case of pharmaceutically important compounds,^10,11 in nanoparticle-based self-assembly,¹² and also in growing delicate precipitation patterns such as chemical gardens.¹³ In order to enhance productivity, one may make an effort to maintain the most appropriate conditions during reactions. In addition, when intricate structures with tailored properties are targeted via bottom-up synthesis methods, spatial gradients (e.g., pH, concentration, electric field, etc.) and hence transport processes are coupled to chemical reactions.¹⁴

Recently, numerous studies focusing on individual parameters of such complex systems have been published. Although even simple reaction–diffusion systems can produce precipitate structures with hierarchy,¹⁵ flow chemistry may provide even more tempting possibilities.^16–18 Precipitation reactions performed under different flow conditions have been thoroughly investigated, and therefore the effect of different reactants^19–21 and enhanced buoyancy²² and the role of physical parameters, such as oscillatory pressure change during injection²³ and permeability differences of membrane structures,²⁴ are understood. Also, the ion-mobility-dependent unidirectional thickening of 1D precipitate membranes is explained on the basis of the coupling of transport processes and precipitation reactions in a microfluidic channel.^25,26 Maintaining precise control of the formation of such precipitate structures is relevant to corrosion, cement degradation, and inorganic membrane engineering, to name a few.¹³

In this context, the role of reaction kinetics becomes pronounced because successful matching of the time scale with transport processes is required to enhance product properties. Recently, we have elaborated an experimental method for the kinetic characterization of precipitation reactions.²⁷ Our procedure is based on the determination of induction periods, t_ind^28–30 – the time elapsed between the physical contact of reactants and the onset of precipitation on the macroscale – for slow reactions, where the precipitate appears in tens of seconds or even later after bringing the reactants into contact. However, the time scale for most chemical precipitation reactions is significantly shorter than one second under general conditions maintained in order to produce a macroscopic amount of precipitate. In addition, many possible applications corresponding to microfluidic channels (e.g., membrane and crystal growth^18,26) require fast streams and short contact times which calls for precise control over reactions in flow. Since solid particles are produced by chemical precipitation, the traditional stopped-flow technique cannot be applied for kinetic characterisation. A power law has been introduced to describe the dependence of t_ind on reactant concentration.^28,31 The parameters within can play an important role in experimental design because the apparent exponent reflects the changes in the mechanism of crystallization, i.e., crystallization takes place via a mono or polynuclear mechanism. It has also been proven that the characteristic features of precipitation structures obtained by coupling slow precipitation and flow can be tuned via t_ind by adjusting reactant concentrations according to the power law revealed.²⁷

Therefore, there is a need to develop an experimental method to determine induction periods for short (t_ind ≪ 1 s) time scales. Here we apply a high-speed camera (HSC) which has already been proven to be efficient in tracking diversified dynamic phenomena such as combustion flames,^32,33 animals' locomotion,³⁴ planetary milling,³⁵ and aerosol formation.³⁶ Also, the growth of single crystals upon reaching supersaturation by physical effects, e.g., cooling or evaporation, was followed both during levitation and in microfluidic channels.^37,38 However – to the best of our knowledge – it has never been used to measure induction times for the kinetic characterization of fast chemical precipitation reactions on the macroscale. We test and validate our method using the formation of calcium oxalate, a biologically relevant molecule.

2 Experimental

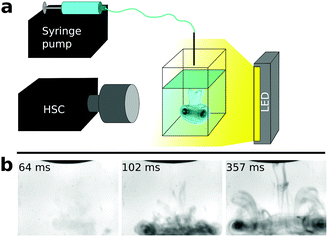
Our kinetic study is based on a high-speed camera (Phantom Miro 110 equipped with a Nikon AF-S 105 mm f/2.8 IF ED VR micro objective) which enables the high temporal resolution monitoring of reaction dynamics. In the experiments, a standard spectrophotometric quartz cuvette containing sodium oxalate solution was placed in front of the camera (Fig. 1a). The other reactant was supplied from above by a syringe pump (KDS Legato 210) equipped with a Hamilton gas tight syringe. Upon injection, one drop (13 ± 2 μL volume) of calcium chloride solution was forced to fall from the tip of a needle placed at a constant distance (∼4 mm) above the pool of oxalate solution. Reactant solutions started to mix immediately after the impact. The dynamics within the field of view (12 × 9 mm) were captured by the HSC (14 000 fps, 320 × 240 px spatial resolution) as shown in Fig. 1b (see also ESI† for the movie). The stock solution concentration for both reactants was varied and was 17.5, 20.0, 22.5, 25.0, 30.0, 35.0, and 40.0 mM. Each experiment was reproduced 10 times to provide reliable results.

Fig. 1 Part a: Sketch of the experimental setup. Part b: Typical moments of dynamics at selected times after the impact of a falling drop. The dark color corresponds to the evolving precipitate. Initial concentration is 40 mM for both reactants.

The instant when the falling drop forces the meniscus of the underlying oxalate pool to move is considered as the beginning of the experiment. Due to the momentum of the drop and the density difference of the reactant solutions, the drop sinks and mixes in the liquid. In the initial stage of the experiment only Schlieren patterns³⁹ are visible and no precipitate is observed. When precipitation starts, the convection pattern becomes more distinct because of the presence of solid particles (Fig. 1b). To determine induction periods, we followed the light intensity change of the black and white experimental images over time. When precipitation takes place, the gray scale steeply decreases because of the light scattering on solid particles. The induction period, t_ind, is defined as the time difference between the impact of the drop and the appearance of the precipitate. Further details about the experiments and the evaluation procedure are in the ESI.†

To validate the HSC method, the kinetics of the same model reaction can also be investigated photometrically with the reactant concentrations sufficiently decreased where t_ind lengthens to the order of ∼10 s. It must be highlighted here that not every precipitation reaction could be used as a model system since the amount of precipitate must be sufficiently large to be detectable even at low concentrations when t_ind is sufficiently long. This is the reason why the HSC method is complementary to the photometric one; most of the reactions cannot be equivalently followed by the two methods. During the photometric experiments, the turbidity (T) change over time (t) can be readily recorded with a spectrophotometer if the amount of product is sufficiently high.²⁷ In the present study we monitored the turbidity change at a wavelength of 340 nm (VWR UV-2100 PC Spectrophotometer) with a 0.5 s time resolution. Unlike during HSC experiments, reactants were premixed with equal volume (1–1 mL) and stock solution concentration (1.000, 1.125, 1.250, 1.375, 1.500, and 1.750 mM) and were continuously stirred (700 rpm) during the photometric measurements. The constructed T–t curves are characterized by a sigmoid shape where t_ind, the steepness of the curve, and also the turbidity at the plateau vary with reactant concentration. Further information about the curves and mixture composition are in the ESI.†

3 Results and discussion

3.1 Determination of local concentrations

The goal of the present study is to elaborate an experimental protocol for the kinetic investigation of fast precipitation reactions with the aid of the calcium-oxalate model reaction by revealing the parameters within the induction period–reactant concentration power law.^27,28 During the photometric experiments, vigorous stirring is maintained to provide a homogeneous reactant mixture before precipitation can take place. In the HSC experiments however t_ind ≪ 1 s which does not allow the assumption of the presence of a homogeneous mixture in terms of concentration distribution even in the vicinity of the sinking drop of CaCl₂ solution. One can estimate local concentrations and the efficiency of mixing by either using light intensity-particle concentration calibrations or performing 3D hydrodynamic simulations.

During our measurements (both HSC and well-stirred photometric ones), the change of light intensity is caused by light scattering on solid particles. Precipitate particles become more numerous and may grow in size as the reaction advances. Both of these effects contribute to the measured signal thus it is not trivial that a measured signal–product concentration calibration can be achieved. Therefore, we have performed calibration experiments similar to those described earlier.²⁷ The only difference is that now the plateau of the sigmoid curves, i.e. maximum turbidity T_max, obtained for different initial reactant concentrations is sought instead of t_ind. It is found that T_max changes linearly with the concentration of solid particles for both methods. Hence, an analogue of the Beer–Lambert law can be validly applied to our precipitation system even though the light intensity change is caused by solid particles and not dissolved species. In addition, such a behaviour suggests that the kinetics and mechanism of precipitation reactions may be studied by using the entire T–t curves since they provide information about product concentration over time. After achieving the appropriate concentration calibration curves, we estimated the local reactant concentration for the HSC experiment carried out with 40 mM initial reactant concentrations (in stock solution) shown in Fig. 1b. Substituting the gray scale corresponding to the end of the induction period in the HSC calibration curve, it is found that the product concentration is similar to that which would have been produced by homogeneously mixing ∼0.5 mM reactant solutions (instead of 40 mM). This result suggests that reactant solutions barely mix due to the short induction period. Further information about the calibration curves and local concentration estimations are found in the ESI.†

In parallel we have also performed 3D hydrodynamic simulations to investigate the mixing of fluids. To mimic our experimental conditions, interMixingFoam solver of OpenFOAM is used which models the mixing of two miscible incompressible liquids in the presence of a gas phase. The interface calculation is based on the volume of fluid method while mixing is driven by the Navier–Stokes equation. Since neither the precipitation reaction nor the interaction between solid particles and fluid flow are taken into account by the solver, in principle the results are valid until the onset of precipitate formation. Therefore we can consider the simulated results valid within a 0.1–0.2 s interval after impact because the amount of the product is negligible in the beginning of the reaction and the particles are tiny as seen in Fig. 1b. The parameters used for the simulations (e.g., density, viscosity, drop size, etc.) are set in accordance with the experiments and listed in the ESI.† The schematic of the initial stage of the simulations is illustrated in Fig. 2a. A drop of CaCl₂ solution is placed in the air above the underlying pool of Na₂(COO)₂ solution. To aid the visualization of mixing, the relative mixture composition is shown only for the CaCl₂ reactant (Fig. 2b and c1-6). Upon impact the drop sinks and mixes by forming a well-visible convection plume close to the bottom of the reactor. Such a calculated flow field coincides with that seen in experiments performed with a 20 mM reactant concentration where a precipitate is observed at a time corresponding to Fig. 2c6. Simulations are carried out with various density distributions corresponding to different reactant concentrations to investigate how the mixing efficiency relies on such a parameter. It is found – within the experimentally relevant concentration range – that the flow field is essentially independent of the initial density distribution (see Fig. S5, ESI†). The formation of similar flow fields allows us to assume that the change of local reactant concentrations caused by dilution upon mixing is independent of reactant concentration.

Fig. 2 Part a: Schematic representation of the initial stage of the simulations with a CaCl₂ drop (orange) in the air (white) above the Na₂(COO)₂ pool (cyan). Part b: Colour code for the relative concentration of CaCl₂ shown in Part c. Part c: Mixing dynamics at selected times after the impact of the falling drop; reactant concentration is 20 mM (c1–6). Part d: Spatial distribution of the product of the reactant concentrations (P). The cross section is composed of vertical slices taken at the middle and a horizontal slice taken at the bottom of the cuvette. The time corresponds to picture c6.

Although our model does not take the precipitation reaction into account, it can still provide information about the location of precipitate formation. To verify that the flow fields seen in Fig. 2c are the same as those visualized by precipitate particles in Fig. 1b, one may search for positions where the product of the reactant concentrations (P) has a maximum, since this is where the chemical reaction takes place at the highest rate. The spatial distribution of the product quantifying the extent of supersaturation is illustrated in Fig. 2d at an instance corresponding to Fig. 2c6. The precipitate will appear in the reddish and greenish regions which form a 3D pattern resembling a typical plume shape. The side view of the pattern depicts a pair of convection rolls as observed in our experiments (Fig. 1b) which are also known from the work of J. J. Thomson on nonreactive liquids back in the 19th century.^40,41 To investigate the contribution of macroscopic convection in the mixing during the time scale of the HSC experiments, the product of the reactant concentrations was calculated and integrated over the entire cuvette volume for different initial density distributions (see Fig. S6, ESI†). The time evolution of this integrated value showed the same trend independently of reactant concentration. This suggests that microscale mixing advances via diffusion, while macroscale convection plays a role only in shaping the spatial distribution of the precipitate during the time scale of the HSC experiments. Furthermore, since the reactants were used in equal concentrations in the experiments, and simulations revealed that the precipitate appears at a thin contact zone of the two reactant solutions, the local concentration is the half of the initial one because of cross diffusion.

3.2 Scaling laws and comparison of the methods

The aim of our study was to elaborate and validate an experimental method for the kinetic characterization of fast precipitation reactions by determining induction periods and their dependence on reactant concentration. Induction periods determined from the two methods are plotted as a function of reactant concentration in Fig. 3. A power law function²⁸ is fitted to both data series: t_ind/s = (310 ± 73) (c/mM)^−3.1±0.1 with regression coefficient R² = 0.998 (solid line in Fig. 3) and t_ind/s = (6.3 ± 0.3) (c/mM)^−2.9±0.1 with regression coefficient R² = 0.996 (dashed line in Fig. 3) are obtained for the HSC and photometric experiments, respectively. The fitted curves are graphically extrapolated to lead the eyes and provide an easier comparison of the results obtained. In our study, induction periods were determined via two different methods by measuring two different physical properties. Turbidity is measured in the UV-Vis experiments, while image gray scale was used for the evaluation of the HSC experiments. This directly means that, although there is a relation between the two properties measured, a shift in the absolute values is present when comparing the results which leads to fitted curves with different intercepts. Even though the absolute value of the induction periods cannot be directly compared, the exponents of the power laws fitted are equal within experimental error. These results prove that the HSC method is suitable for the kinetic study of fast precipitation reactions. For a successful HSC experiment, the drop must sink into the underlying pool and leave the vicinity of the meniscus because the latter appears black in the recorded images, thus no light intensity change can be detected. Therefore induction periods greater than 10 ms can be determined. Also, t_ind should not exceed ∼1 s otherwise advection becomes less negligible, for which time scale well-stirred photometric measurement becomes available.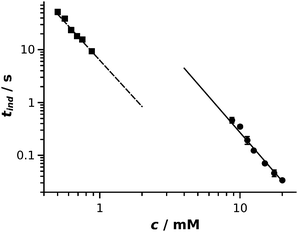

Fig. 3 Log–log representation of induction period as a function of reactant concentration for HSC (circle) and well-stirred photometric (square) experiments. Error bars are smaller than the symbols.

Both methods, either supported with a UV-Vis spectrophotometer or with a HSC, are based on the interaction of solid particles and UV-Vis light. In the experiments, when the two reactants are mixed together, nucleation and crystal growth take place thus the initially homogeneous solution transforms to a very fine colloid dispersion which goes through coarsening via further crystal growth and aggregation. Nucleation and the initial stage of crystal growth cannot be tracked by such visual methods. Also, a dilute solution of nanoparticles with size below ∼40 nm would appear transparent. In the concentration range of our experiments, however, precipitate particles are produced in a sufficiently large amount and the process is fast thus light scattering on solid particles becomes detectable due to the Tyndall effect in the early stage of the reaction, i.e., when the particles reach a size of ∼50–100 nm. The induction period is determined when colloid dispersion evolves thus it provides no direct information about nucleation. However, t_ind can be reproducibly measured and it is considered as a characteristic time for precipitation reactions. The exponent of the fitted power law function is the most important parameter in order to achieve a successful time scale matching between precipitation and coupled transport phenomena since exact particle size–reaction time scaling must be achieved separately for different reactions. In addition, such exponents refer to the mechanism of crystallization, i.e., crystallization takes place via a mono or polynuclear mechanism,^28,31 which directly influences the product properties. Therefore, being able to determine power laws corresponding to precipitation reactions characterised by significantly different time scales is crucial. In this context, the HSC method is complementary to the photometric one since most of the reactions cannot be equivalently followed by the two methods.

4 Conclusion

We have shown that an analogue of the Beer–Lambert law can be established for the concentration dependence of turbidity in well-stirred photometric experiments for slow precipitation reactions which may pave the way to investigating the kinetics and mechanisms of such reactions. An experimental method has also been elaborated to determine induction periods in the case of fast precipitation reactions. The method is validated by investigating the same model reaction on significantly different time scales. The HSC experiment presented is a handy method for the kinetic characterization of fast events (induction periods in the range of 10 ms to 1 s) accompanied by a liquid–solid phase transition; only a few steps have to be performed: (1) force a drop of reactant A to fall into the pool of reactant B; (2) record the gray scale over time at a high time resolution and determine the induction period; and (3) reveal the induction period–reactant concentration relation. The method is illustrated based on the example of calcium oxalate formation which is biologically relevant for the growth of kidney stones. The initial stage of blood coagulation and clarifying-agent-driven flocculation in water treatment can be mentioned as practical applications. Also, we consider our HSC system useful in achieving precise time scale matching between fast reactions and fluid flow relevant in microfluidic reactors (e.g., continuous nanoparticle synthesis).

Conflicts of interest

There are no conflicts to declare.

Acknowledgements

This work was supported by the National Research, Development and Innovation Office (K119795 and PD121010) and GINOP-2.3.2-15-2016-00013 and M-ERA.net MaSNEC projects.

References

1. N. V. Mantzaris, Chem. Eng. Sci., 2005, 60, 4749.
2. C. Tan and H. Zhang, Nat. Commun., 2015, 6, 7873.
3. J. Schlomach, K. Quarch and M. Kind, Chem. Eng. Technol., 2006, 29, 215.
4. D. Wang, Q. Wang and T. Wing, Inorg. Chem., 2011, 50(14), 6482.
5. J. M. García-Ruiz, E. Melero-García and S. T. Hyde, Science, 2009, 323(5912), 362.
6. P. Knoll and O. Steinbock, J. Phys. Chem. C, 2018, 122, 23554.
7. P. Knoll and O. Steinbock, Isr. J. Chem., 2018, 58, 682.
8. L. Zhu, L. Y. Wang, Z. L. Sha, Y. F. Wang, L. B. Yang, X. Y. Zhao and W. Du, Cryst. Growth Des., 2017, 17, 4582.
9. B. Bohner, G. Schuszter, O. Berkesi, D. Horváth and Á. Tóth, Chem. Commun., 2014, 50, 4289.
10. A. D. Bond, R. Boese and G. R. Desiraju, Angew. Chem., Int. Ed., 2007, 46, 618.
11. J. Sibik, M. J. Sargent, M. Franklin and J. A. Zeitler, Mol. Pharmaceutics, 2014, 11, 1326.
12. E. Tóth-Szeles, J. Horváth, G. Holló, R. Szücs, H. Nakanishi and I. Lagzi, Mol. Syst. Des. Eng., 2017, 2, 274.
13. L. M. Barge, S. S. S. Cardoso, J. H. E. Cartwright, G. J. T. Cooper, L. Cronin, A. De Wit, I. J. Doloboff, B. Escribano, R. E. Goldstein, F. Haudin, D. E. H. Jones, A. L. Mackay, J. Maselko, J. J. Pagano, J. Pantaleone, M. J. Russell, C. I. Sainz-Díaz, O. Steinbock, D. A. Stone, Y. Tanimoto and N. L. Thomas, Chem. Rev., 2015, 115, 8652.
14. F. Glaab, J. Rieder, J. M. García-Ruiz, W. Kunz and M. Kellermeier, Phys. Chem. Chem. Phys., 2016, 18, 24850.
15. M. Dayeh, M. Ammar and M. Al-Ghoul, RSC Adv., 2014, 4(104), 60034.
16. A. Adamo, R. L. Beingessner, M. Behnam, J. Chen, T. F. Jamison, K. F. Jensen, J.-C. M. Monbaliu, A. S. Myerson, E. M. Revalor, D. R. Snead, T. Stelzer, N. Weeranoppanant, S. Y. Wong and P. Zhang, Science, 2016, 352(6281), 61.
17. N. Lamborelle, J. F. Simon, A. Luxen and J.-C. M. Monbaliu, Org. Biomol. Chem., 2015, 13, 11602.
18. G. Laffite, C. Leroy, C. Bonhomme, L. Bonhomme-Coury, E. Letavernier, M. Daudon, V. Frochot, J. P. Haymann, S. Rouzière, I. T. Lucas, D. Bazin, F. Babonneaub and A. Abou-Hassan, Lab Chip, 2016, 16, 1157.
19. F. Haudin, V. Brasiliense, J. H. E. Cartwright, F. Brau and A. De Wit, Phys. Chem. Chem. Phys., 2015, 17, 12804.
20. J. H. E. Cartwright, B. Escribano, S. Khokhlov and C. I. Sainz-Díaz, Phys. Chem. Chem. Phys., 2011, 13, 1030.
21. G. Schuszter and A. De Wit, J. Chem. Phys., 2016, 145, 224201.
22. S. Thouvenel-Romans, J. J. Pagano and O. Steinbock, Phys. Chem. Chem. Phys., 2005, 7, 2610.
23. É. Pópity-Tóth, G. Schuszter, D. Horváth and Á. Tóth, J. Chem. Phys., 2018, 148, 184701.
24. E. Rauscher, G. Schuszter, B. Bohner, Á. Tóth and D. Horváth, Phys. Chem. Chem. Phys., 2018, 20, 5766.
25. B. C. Batista and O. Steinbock, J. Phys. Chem. C, 2015, 119(48), 27045.
26. Q. Wang, M. R. Bentley and O. Steinbock, J. Phys. Chem. C, 2017, 121(26), 14120.
27. N. P. Das, B. Müller, Á. Tóth, D. Horváth and G. Schuszter, Phys. Chem. Chem. Phys., 2018, 20, 19768.
28. A. G. Xyla, E. K. Giannimaras and P. G. Koutsoukos, Colloids Surf., 1991, 53, 241.
29. S. Jiang and J. H. ter Horst, Cryst. Growth Des., 2011, 11, 256.
30. C. Brandel and J. H. ter Horst, Faraday Discuss., 2015, 179, 199.
31. J. W. Mullin, Crystallization – IV Ed., Butterworth-Heinemann, Oxford, 2001.
32. O. Pryor, S. Barak, B. Koroglu, E. Ninnemann and S. S. Vasu, Combust. Flame, 2017, 180, 63.
33. R. Zhang, K. Lei, B. Q. Ye, J. Cao and D. Liu, Bioresour. Technol., 2018, 268, 278.
34. H. Shimada, R. Kanai, T. Kondo, K. Yoshino-Saito, A. Uchida, M. Nakamura, J. Ushiba, H. Okano and N. Ogihara, Neurosci. Res. Lett., 2017, 125, 11.
35. S. Rosenkranz, S. Breitung-Faes and A. Kwade, Powder Technol., 2011, 212, 224.
36. W. Feng, Z. L. Jun and Z. Y. Hong, Chin. Sci. Bull., 2008, 53(14), 2139.
37. D. M. Herlach, Crystals, 2015, 5, 355.
38. A. Naillon, P. Joseph and M. Prat, J. Cryst. Growth, 2017, 463, 201.
39. W. Merzkirch, Flow Visualization, Academic Press, 1987.
40. J. J. Thomson and H. F. Newall, Proc. R. Soc. London, 1886, 39, 417.
41. M. Rein, Fluid Dynam. Res., 1993, 12, 61.

---

Footnote

† Electronic supplementary information (ESI) available. See DOI: 10.1039/c9cp01707k

---