Open Access Article
Open Access ArticleCOSMOplex: self-consistent simulation of self-organizing inhomogeneous systems based on COSMO-RS†
Andreas
Klamt
 *ab,
Johannes
Schwöbel
*ab,
Johannes
Schwöbel
 a,
Uwe
Huniar
a,
Uwe
Huniar
 a,
Larissa
Koch
a,
Selman
Terzi
a and
Théophile
Gaudin
ac
a,
Larissa
Koch
a,
Selman
Terzi
a and
Théophile
Gaudin
ac
aCOSMOlogic GmbH & Co KG, Imbacher Weg 46, D-51379 Leverkusen, Germany. E-mail: andreas.KLAMT@3ds.com
bInstitute of Physical and Theoretical Chemistry, Universität Regensburg, Germany
cSchool of Chemistry and Chemical Engineering, Nanjing University, China
First published on 17th April 2019
Abstract
During the past 20 years, the efficient combination of quantum chemical calculations with statistical thermodynamics by the COSMO-RS method has become an important alternative to force-field based simulations for the accurate prediction of free energies of molecules in liquid systems. While it was originally restricted to homogeneous liquids, it later has been extended to the prediction of the free energy of molecules in inhomogeneous systems such as micelles, biomembranes, or liquid interfaces, but these calculations were based on external input about the structure of the inhomogeneous system. Here we report the rigorous extension of COSMO-RS to a self-consistent prediction of the structure and the free energies of molecules in self-organizing inhomogeneous systems. This extends the application range to many new areas, such as the prediction of micellar structures and critical micelle concentrations, finite loading effects in micelles and biomembranes, the free energies and structure of liquid interfaces, microemulsions, and many more related topics, which often are of great practical importance.
Introduction
The formation and properties of self-organizing systems are of tremendous importance in the chemical industry (e.g., enhanced oil recovery), the pharmaceutical industry and biochemistry (e.g., drug delivery formulations, biomembrane properties), and in daily life (e.g. components of washing powders, cosmetic ingredients). The interactions taking place are complex in nature and difficult to study experimentally and to describe mathematically due to the delicate balance of weak attractions in the lipophilic domain of surfactant molecules and much stronger interactions between the hydrophilic domain of surfactant molecules and the polar solvent and within the solvent environment.1,2Several theoretical approaches are used to handle self-organizing systems. Due to the wide application area, the following selection of methods and references is by no means intended to be complete.
The simplest theoretical approaches are quantitative structure–property relationships (QSPR) between molecular structures and specific properties of interest,3e.g. for critical micelle concentrations (CMC).4,5 Group contribution methods were used for the prediction of micellar and microemulsion properties, for example applying the universal functional activity coefficient model (UNIFAC).6,7 Another interesting thermodynamic approach is the integrated free energy model (IFEM) for microemulsions.1 Here, the Gibbs free energy is split up into a balance of different lipophilic and hydrophilic energetic contributions. Thermodynamic activity coefficient and equation of state models were adapted to cover surfactant systems, such as the non-random two-liquid model (NRTL) or the statistical associating fluid theory (SAFT).8,9 Dissipative particle dynamics (DPD) simulations provide mechanistic insight into micellar systems and their phase behaviour.10,11 All these methods have in common that they are based on fitted interaction parameters or require experimental data.
Molecular dynamics (MD) simulations are widely used and considered as predictive to study micellar and biomembrane systems.12–15 On the one hand, they operate mechanistically on an atomistic scale. On the other hand they are computationally demanding and, thus, they have not found extensive use in microemulsion modelling.1
The conductor-like screening model for realistic solvation16–18 (COSMO-RS) is a predictive, generally applicable and efficient computational model to handle fluid phase properties. COSMO-RS is a combination of the dielectric continuum solvation model COSMO19 with an efficient statistical thermodynamic model of pairwise molecular surface interactions, known as the quasi-chemical approximation20 or COSMOSPACE.21 For the quantification of the surface interactions it uses the surface polarization charge densities σ of each solute arising from quantum chemical COSMO calculations.
In several blind prediction challenges and benchmark studies COSMO-RS has been proven to be one of the most accurate tools for the prediction of the free energies of molecules in solution,22–27 and thus for all equilibrium distribution properties, such as partition coefficients, solubilities, vapour pressures and related properties.
Several combinations of COSMO-RS and the methods mentioned above have been used already towards predictions of inhomogeneous systems: first, critical micelle concentrations or micelle:water partition coefficients in combination with MD and DPD simulations;13,28,41–43 second, interfacial tensions, with COSMO-RS calculations fitted to experimental data or combined with DPD simulations;29,30 and third, equivalent alkane carbon numbers (EACN) of microemulsion systems, with a QSPR model using COSMO-RS parameters for non-polar oil/surfactant/water systems.31,32
One of the limitations of COSMO-RS was its inability to handle inhomogeneous, structured liquid systems directly on a mechanistic basis. This was partially overcome by the introduction of the COSMOmic approach,33 which uses external information about the structure of a micelle or biomembrane, usually taken from MD simulations, in order to represent the micelle as a layered liquid of varying composition with respect to the COSMO polarization charge densities σ. COSMOmic then calculates the free energies of solutes in such a layered liquid system by sampling over all relevant conformations, positions and orientations of the solute in this system, resulting in reliable predictions of micelle or membrane to water partition coefficients and free energy profiles of solutes in such systems.
While it is based on MD simulations as an initial step, COSMOmic has been demonstrated to yield at least comparably reliable results for the free energies of neutral solutes in micellar systems to those achievable with MD simulations, at about 0.01 percent of the computational cost.34–36 More recently, COSMOmic has been extended to ionic solutes,37,38 now allowing for the prediction of the biomembrane to water partition coefficients of neutral and ionic species with an accuracy of about 0.7![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) log10 units.
log10 units.
While the COSMOmic approach has been proven to be efficient and reliable with respect to the prediction of free energies of solutes at infinite dilution in micellar systems,41 many applications of eminent practical importance could not be handled by the COSMO-RS model so far, such as the direct prediction of the critical micelle concentration (CMC) of new surfactants and surfactant mixtures,13 or the effects of finite concentration enrichment of solutes in micelles, as well as the predictive simulation of liquid–liquid interfaces and microemulsions. As a COSMOmic calculation ends up with a detailed prediction for the probability distribution of each solute with respect to position, orientation and conformational population, it was tempting since the beginnings of COSMOmic to calculate the distribution of the constituents of a micellar system, i.e. usually surfactants and water, in the same way and thus to yield a self-consistent prediction of the structure of the inhomogeneous system. But the missing point was the inability of COSMOmic to take into account the hard-core repulsion of molecules, i.e. COSMOmic would predict completely unrealistic, high concentrations of atoms in some layers of the simulation box, leaving other layers rather empty.
In this paper, we describe a fundamental way to overcome this problem by introducing a system pressure in each of the layers, similar to molecular dynamics or dissipative particle dynamics simulations. This system pressure is the response of the system to over-occupation, i.e. it is the result of the Pauli or Lennard-Jones repulsion of the molecules in the self-organizing system. We simultaneously converge a pressure function P(z) together with the COSMOmic distribution probabilities of the molecules in the system, leading to a self-consistent prediction of the structures and free energies of molecules in self-organizing systems. Since this method extends the COSMOmic approach beyond micellar systems to a much wider range of complex, self-organizing systems, we will label this new method COSMOplex, further on.
The theory as well as first application examples of COSMOplex for the prediction of properties of biomembranes, micelles, microemulsions, and liquid–liquid interfaces is described in this paper.
Material and methods
In this section, after a short introduction of the concepts of COSMO, COSMO-RS and COSMOmic, the theory of COSMOplex is presented.COSMO
The conductor-like screening model (COSMO)19 is a dielectric continuum solvation model using the limit of an ideal conductor, i.e. with an infinite dielectric constant. The result of such a quantum chemical COSMO calculation contains the self-consistently calculated energy of the molecule in the presence of a perfect conductor, embedding the molecule on the COSMO surface, together with individual COSMO surface segments and their positions, segment areas and conductor screening charge densities on the particular segments.Each chemical compound is represented by an ensemble of the relevant conformations of the compound, i.e. of its relevant local geometry minima. Each of these conformations has to undergo a separate quantum chemical COSMO calculation, generating the surface polarization charge information and the energy EXcCOSMO of conformation c of compound X. The expression “molecule” is used here for each distinct conformation, whereas the expression “compound” is used for all considered conformations of a chemical entity. The approach used to determine the relative weights of the different conformations is described in the COSMOmic subsection.
COSMO-RS
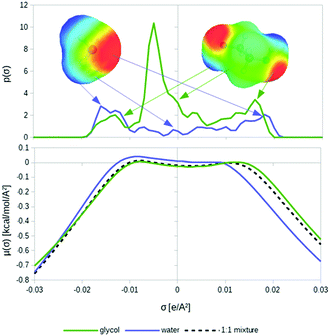
The conductor-like screening model for realistic solvation (COSMO-RS)16–18 starts from quantum chemical COSMO calculations for all involved molecules in the system. COSMO-RS takes the COSMO surface segments and utilizes an efficient statistical thermodynamics algorithm called COSMOSPACE,21 which is equivalent to an exact solution of Guggenheim's quasi-chemical approximation.20 This results in a kind of thermodynamic continuum response function, the so-called σ-potential, comprising the free energies of the different types of surface segments in the ensemble of pairwise interacting surface segments. From the sum of the segment free energies, COSMOSPACE directly yields free energies or chemical potentials of the compounds in a pure or mixed liquid. A schematic illustration of the COSMO-RS method is shown in Fig. 1.The interaction energies of the surface segments are based on the local properties of the two surface segments involved in the contact. In the initial one-descriptor version of COSMO-RS, only the most important of these properties is considered, i.e. the conductor polarization charge density σ. This is an excellent descriptor for the local polarity of the molecular surface at the position of the segment. The short range electrostatic interactions, or more precisely the local deviation of the electrostatic interaction of the two segments compared with the reference state of the conductor-imbedded molecules, is
| ΔEmisfit ≅ acontactcmisfit(σ + σ′)2 | (1) |
| ΔEhb ≅ acontactchb(T)min(0,σσ′ − σhb2) | (2) |
Each molecule X is described by its surface composition histogram with respect to σ, the so-called σ-profile pX(σ), and a pure or mixed liquid system is characterized by its solvent σ-profile
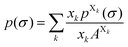 | (3) |
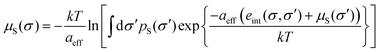 | (4) |
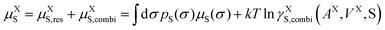 | (5) |
![[r with combining macron]](https://www.rsc.org/images/entities/i_char_0072_0304.gif) s and average molecular surface area
s and average molecular surface area ![[q with combining macron]](https://www.rsc.org/images/entities/i_char_0071_0304.gif) s. Volumes and surface areas are taken from the COSMO cavities of the molecules. μXS is the pseudo-chemical potential, expressing the chemical potential (at a reference mole fraction of 1 mol mol−1).
s. Volumes and surface areas are taken from the COSMO cavities of the molecules. μXS is the pseudo-chemical potential, expressing the chemical potential (at a reference mole fraction of 1 mol mol−1).
It should be noted that in general multiple conformations of a molecule are considered. Knowing the internal energy of each conformation from the initial quantum chemical COSMO calculation and the individual pseudo-chemical potentials from eqn (5), all thermodynamic equilibrium properties of the conformational ensemble are calculated from the conformational partition function.
Meanwhile COSMO-RS has been refined by more advanced variants of eqn (1)–(4), including the influence of other surface descriptors,17e.g., local polarizability and element specific hydrogen bonding and dispersion parameters, in order to improve the accuracy of the surface interaction expressions. But the basic scheme of COSMO-RS is conserved, i.e. the interactions are calculated based on the local surface properties of the surface segments, which can be derived from quantum chemical COSMO calculations.
For the sake of clarity, we describe the concepts of COSMOmic and COSMOplex solely in terms of polarization charge density interactions; the results presented in this paper are obtained by inclusion of the more advanced surface properties.17,18
COSMOmic
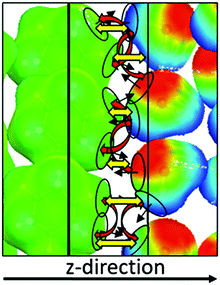
While the original COSMO-RS was applicable only to homogeneous bulk liquids, it has been extended to inhomogeneous, micellar systems33,37 by considering such systems as layered liquids, each layer being considered as homogeneous and described by COSMO-RS. An illustration of the COSMOmic method is shown in Fig. 2.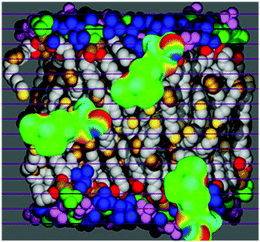 | ||
| Fig. 2 Schematic illustration of COSMOmic: a micelle is considered as a layered liquid. The composition of each liquid is taken from MD simulations. After the calculation of the σ-profiles and σ-potentials of the layers, all positions and orientations of a solute molecule are sampled, calculating the state specific free energy from the local σ-potentials. (Biomembrane snapshot taken from ref. 59). | ||
In COSMOmic, information about the individual composition of each layer has to be derived from external information, usually from snapshots of molecular dynamics simulations of a micellar system M. The distribution of atoms over the layers of a micelle was converted into an atom probability distribution. Multiplication of the individual atom probabilities by the partial σ-profiles of the corresponding atoms of a COSMO calculation leads to a specific σ-profile for each layer, i.e. to a surface polarity distribution pM(σ,z) depending on the coordinate z directed along the outward normal vector of the micelle layers. In the case of spherical or cylindrical systems, z corresponds to the radial direction. Given these layer σ-profiles, we can use the standard COSMO-RS algorithm to calculate the σ-potential μM(σ,z) of each layer.
For the calculation of the chemical potential of a compound X at virtual infinite dilution in such a layered liquid system, a systematic sampling of all possible states, i.e. of conformations, centre positions and orientations of the solute relative to the z-direction, is performed. In practice, the middle of each layer is tested as the centre position, and a grid of vectors on the unit sphere is used for the orientations of the micelle normal relative to the molecule (herein, this grid is defined by a number of nori = 162 orientation vectors). Different choices for the exact definition of the molecular centre have been implemented into COSMOmic. We use the geometric surface centre throughout this paper. For a given state, i.e. conformation, position and orientation of the compound, abbreviated as a cpo state further on, each of the surface segments ν has a coordinate zcpoν with respect to the z-direction of the micellar system. The chemical potential of this surface segment ν is then evaluated by linear interpolation of the two adjacent layer-σ-potentials μM(σν,z). Additional boundary conditions are explained further in Appendix A. Then, in close analogy to eqn (5), all segment chemical potentials of each conformation Xc of a compound X are summed to yield the residual chemical potential of Xc. It should be noted that an electrostatic membrane potential φ(z) simply can be taken into account in the energy of each surface segment by the multiplication of the polarization charge density σ by the membrane potential and the segment area.37
The combinatorial contribution is estimated based on appropriate averages of the surface areas and volumes of the molecules contributing to each layer and from the volume contribution of the solute in each layer. Combining the residual and the combinatorial chemical potentials with the inner energy of the conformation resulting from the quantum chemical COSMO calculation yields the total free energy of the compound for a particular cpo state.
Sampling of all positions, orientations, and conformations thus allows us to calculate the partition function of compound X in the micellar system M, and from that we can derive all thermodynamic equilibrium properties, including the partition coefficients of the solute between the solvent, usually water, and the micellar system. Because most experimental data is available for these systems, COSMOmic has been validated to a large degree based on biomembrane–water partition coefficients,33,36,37 which are of interest for biochemistry and pharmaceutical research. But also for other micelle–water partition systems COSMO-RS yields reliable partition coefficients.15,24–26 No special parameterization of COSMOmic was required beyond the underlying COSMO-RS parameterization, except for the inclusion of ions, for which the membrane potential needed to be derived from fitting of an appropriate functional form with three adjustable parameters.37
COSMOplex: simulation of complex, self-organizing systems based on COSMO-RS
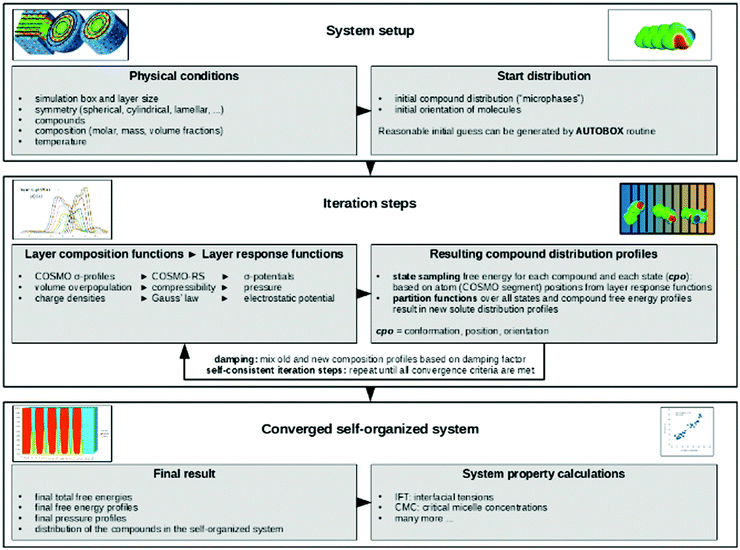
The terminology introduced in the previous chapters sets the framework for COSMOplex. The general workflow is outlined in Fig. 3, and we refer to this figure and the steps indicated therein throughout the explanation of the method.| Vgeo(zi) = Aδ | (6a) |
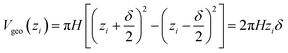 | (6b) |
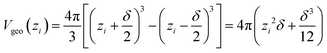 | (6c) |
At a particular temperature T, we consider the box to be filled with Ntot = ∑Nk molecules of nc different compounds. Each compound Xk may be represented by mk conformations.
In our workflow, each conformation XJk (with a conformer index J) is represented by a particular COSMO file, which provides all information about its internal energy EJk in the COSMO reference state, the elements and coordinates of the atoms, and the coordinates, sizes, and screening charges of all segments on the COSMO cavity. The sum of all segment areas is considered as the COSMO surface area AJk. The enclosed volume of the COSMO surface is VJk,COSMO. The total volume is split into atom volumes Vα based on a relative closest distance criterion, so that we have atom volumes available for each atom α. More detail on atom volumes and atom centres is given in Appendix B.
First, we assign the partial σ-profiles of the atoms to the respective layers and generate layer σ-profiles p0sos(σ,zi), in the same way as it was done in COSMOmic. The index zero indicates that this is just the initial guess.
As a second composition function we calculate the expectation values Q0sos(zi) of the layer charge for all layers by summing the product of the polarization charge density and the segment area for all segments in a layer.
As a new ingredient of COSMOplex vs. COSMOmic, the space filling ratio
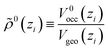 | (7) |
The average molecular surface area and the average molecular volume are also calculated in each layer, see Appendix C.
The combinatorial contribution μcombi, a kind of size correction, may be considered as an additional response function. Since its contribution is small we refer the reader to Appendix F for details.
For each cpo state, the total free energy of the state 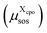 is initialized with the conformational energy of the compound X
is initialized with the conformational energy of the compound X 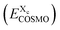 . For the COSMO-RS part of the free energy
. For the COSMO-RS part of the free energy 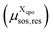 we determine the position of each surface segment and of each atom of a particular compound. Using a linear interpolation between the two neighbouring layers of each segment, we determine the value of the σ-potential of the segment at its position and the corresponding electrostatic potential φ and the respective contributions of each segment
we determine the position of each surface segment and of each atom of a particular compound. Using a linear interpolation between the two neighbouring layers of each segment, we determine the value of the σ-potential of the segment at its position and the corresponding electrostatic potential φ and the respective contributions of each segment 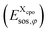 to the total free energy of the state. In addition, we determine the position of each atom. The atom volume is multiplied by the interpolated pressure P of the two nearest layers and this pressure penalty
to the total free energy of the state. In addition, we determine the position of each atom. The atom volume is multiplied by the interpolated pressure P of the two nearest layers and this pressure penalty 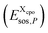 is added to the total free energy of the state. Finally, the combinatorial free energy
is added to the total free energy of the state. Finally, the combinatorial free energy 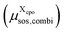 is added, see Appendix F. Hence, the free energy of a particular cpo state is
is added, see Appendix F. Hence, the free energy of a particular cpo state is
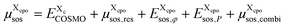 | (8) |
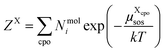 | (9) |
GX = −kT![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) ln(Zk) ln(Zk) | (10) |
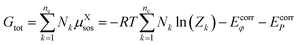 | (11) |
The individual probability to find compound X in state cpo is
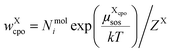 | (12) |
As in every non-linear optimization procedure, the achieved minimum can either be the global minimum, or just a local minimum. Starting from different start conditions, or by using different damping schemes, it should be checked whether the global optimum has been found. According to our findings, the systems converge directly to the global minimum in the majority of cases, if they are set up from a reasonable initial distribution of the molecules, which is facilitated by the AUTOBOX routine.
Directional segment extension (DIRPLEX)
Although the COSMOplex algorithm as described above already yields qualitatively and in many cases also quantitatively plausible results, it is necessary to introduce a further extension of the COSMOplex algorithm which concerns the directionality of the surface segments. Since in a bulk, homogeneous and isotropic solvent no direction is preferred, the orientation of surface segments does not require special attention, although even in such systems two segments need to have opposite orientations in order to form an interacting segment pair. But in COSMOplex we consider an anisotropic liquid, with a specially preferred direction, defined as the z-direction of the SOS further on. Thus, it may be that some segment types preferably point in the positive z-direction, and others preferably point in lateral or opposite directions. As an example, we may consider the interface of water with a non-polar solvent, e.g. cyclohexane, as illustrated in Fig. 4. If the alkane phase is in the region of low z-values and water at high z-values, then the layer accommodating the relatively sharp interface of the liquids will mainly have nonpolar surface segments with a positive z-normal direction, while the polar water segments will have an excess of negative segment normal directions. Standard COSMO-RS thermodynamics for the segments in such a layer would allow for large numbers of contacts between the polar water surface segments and between the nonpolar alkane segments, but geometry prohibits such contacts. This constraint can be implemented into COSMO-RS by considering the segment normal direction as an additional segment property. For the purpose of COSMOplex it is sufficient to split each segment ν into two subsegments in the following way: if the scalar product of the segment normal vector with the z-direction (nν,z) is positive, the portion nν,z is added to a z+-sub-ensemble of surface segments, and the portion (1 − nν,z) is added to the z0-sub-ensemble. If nν,z is negative, the portion |nν,z| is added to a z−-sub-ensemble of surface segments, and the portion (1 + nν,z) is added to the z0-sub-ensemble. Then we solve the COSMOSPACE equations with the additional boundary condition that surface segments from the z+-sub-ensemble may only interact with surface segments of the z−-sub-ensemble and vice versa, while segments from the orthogonal z0-sub-ensemble can still freely interact with each other. It should be noted that the COSMOSPACE equations for the coupled z+- and z−-sub-ensembles do only converge if the amount of segment surface is exactly identical in both sub-ensembles. In order to achieve this in every layer, we solve a system of linear equations yielding the minimum transfer of z+- and z−-segments from the neighbouring layers which is necessary to yield identical amounts of z+- and z−-areas in each layer. The acronym DIRPLEX will be used in the following sections for this directional segment extension.Basically, segment directionality should already have been taken into account in the COSMOmic method, but apparently COSMOmic worked well without this extension. The reason is that in COSMOmic we mostly studied soft, surfactant-rich interfaces, at which apparently the segment pairing is mainly controlled by the segment polarity, and less by directionality. In the results section we compare COSMOplex with and without the DIRPLEX extension for a phospholipid biomembrane and for the cyclohexane–water interface. Larger differences are only found in the latter case. In general, DIRPLEX causes an increase of the computation time by roughly a factor of three.
Software
Quantum chemical density functional theory (DFT) calculations are performed for each of the molecules, i.e. for the solute and solvent molecules under consideration. The COSMOconf software44 in combination with the quantum chemistry software package TURBOMOLE45 was used to generate the COSMO files of the relevant conformations for the compounds considered in this paper. The BP86 density functional46,47 in combination with the TZVP basis set48 was used for the COSMO calculations. COSMOconf was slightly modified to the needs of COSMOplex, in order to keep geometrically diverse conformations with very similar σ-profiles in the set, while these are filtered out with standard COSMOconf settings, because they are irrelevant in homogeneous liquids. The BP_TZVP_2019 parameterization of COSMOtherm49 was used for the COSMO-RS calculations within COSMOplex in this article.Results and discussion
In this section, we describe a range of different application examples. All applications are considered as proof of principle, and therefore it should not be expected that the optimal performance of COSMOplex has yet been achieved.Self-organization of a phospholipid bilayer and phospholipid–water partition coefficients
As a first example, we apply COSMOplex to the self-organization of a biomembrane. The phospholipid 1,2-dimyristoyl-sn-glycero-3-phosphocholine (DMPC) was the most important system studied by COSMOmic.33,37 Four COSMOplex simulations were started from an AUTOBOX generated input: one calculation with the extended DIRPLEX routine, one with an optional self-consistent electrostatic potential switched on, one with both options, and one standard calculation with none of these options.Fig. 5 shows the volume distribution profiles for DMPC and water, respectively, resulting from the four COSMOplex simulations. The distribution resulting from the MD simulations,50 as used in COSMOmic, is shown for comparison. As can be seen, all distributions are in reasonable agreement with each other, but the COSMOplex distributions are generally a bit sharper than the distribution derived from the MD simulations. Most likely this is a result of the geometry scatter in MD, i.e. the fact that the geometry and symmetry of the DMPC double layer in each snap shot deviate a bit from the idealized flat and reflection symmetry arrangement. This already caused some uncertainty in the position of the reference plane, and some stretching or compression. Within the COSMOplex generated models, the use of the DIRPLEX extension causes some broadening of the profiles, while the use of the self-consistent electrostatic potential has negligible effect. Fig. 5 also shows the self-consistent electrostatic potentials arising from the two last options, in comparison to the empirically fitted potential, more in detail, fitted to experimental DMPC–water partition coefficients of ions.37 Given the fact that most reported DMPC MD simulations yield values between 1.0 and 1.3 V in the membrane centre,37,51 the difference between the COSMOplex result of 0.1 V and the “true” experimental value of 0.3 V must be considered as an encouraging result. Comparing the COSMOplex potentials with the membrane potential generated by the fit to ion partition coefficients, it is apparent that the latter has its strongest increase in the region of the zwitterionic groups (z ∼ 17 Å), while the COSMOplex potentials rise at z ∼ 12 Å and thus seem to arise from the ester groups, which are located in that region of the membrane. More detailed analysis will be presented in forthcoming papers.
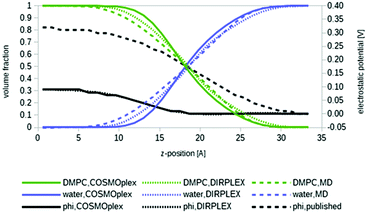 | ||
| Fig. 5 Volume fractions of the phospholipid DMPC (green lines) and water (blue lines) in a simulated biomembrane system. The centre of the bilayer is at the left end of the diagram. Bare COSMOplex is marked by continuous lines, COSMOplex with DIRPLEX by dotted lines, and the MD composition50 by dashed lines. The continuous and dotted black lines show the two particular self-consistent electrostatic potentials, the fitted, pseudo-experimental potential37 is given for reference (dashed black line). | ||
In all cases we also calculated the DMPC–water partition coefficients for the 207 neutral solutes considered by Endo et al.52 The statistics for the different models is given in Table 1. The MD-based COSMOmic model is slightly better than the COSMOplex models. Within the COSMOplex models the DIRPLEX model without electrostatics seems to be slightly worse than the other three models. Nevertheless, all differences in the performance for the partition coefficient models are very small, and we may conclude that COSMOplex-based models are essentially as good as the COSMOmic models, which required CPU intensive MD simulations as an input.
| Model | φ | Mean dev. | RMSD* | Slope | Shift | r 2 | RMSD |
|---|---|---|---|---|---|---|---|
| MD based | Fitted | −0.72 | 0.86 | 1.24 | −1.56 | 0.78 | 0.81 |
| COSMOplex | Off | −0.15 | 0.90 | 1.15 | −0.61 | 0.75 | 0.88 |
| COSMOplex | Self-consistent | −0.21 | 0.88 | 1.16 | −0.70 | 0.76 | 0.86 |
| DIRPLEX | Off | −1.23 | 0.94 | 1.05 | −1.45 | 0.71 | 0.94 |
| DIRPLEX | Self-consistent | −1.24 | 0.89 | 1.11 | −1.68 | 0.75 | 0.88 |
Prediction of critical micelle concentrations
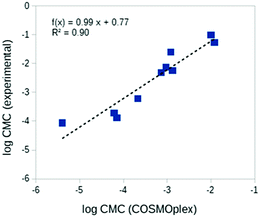
The prediction of critical micelle concentrations (CMCs) is of special interest in many areas of formulation science.13 Here we consider the prediction of the CMCs of ten diverse neutral surfactants. For each surfactant a spherical aqueous micelle model was built with AUTOBOX based on the surfactant geometry, and a COSMOplex calculation with a self-consistent electrostatic field was started. As shown in Table 2 and Fig. 6, the trends in the CMC are reasonably well predicted by COSMOplex. Initial simulations for ionic surfactants also converged nicely and showed reasonable results (details not shown). These systems will be studied in more detail in a forthcoming paper.![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) CMC in [mol l−1] units) of ten diverse non-ionic surfactants
CMC in [mol l−1] units) of ten diverse non-ionic surfactants
| Surfactant | Abbreviation | log10![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) CMC (COSMOplex) CMC (COSMOplex) |
log10![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) CMC (experimental)58 CMC (experimental)58 |
|---|---|---|---|
| Triethylene glycol monohexyl ether | C6E3 | −2.00 | −1.00 |
| Dimethyl nonylamine oxide | C9C2NO | −1.92 | −1.27 |
| Octyl β-D-glucoside | C8BG1 | −2.92 | −1.60 |
| Triethylene glycol monooctyl ether | C8E3 | −3.03 | −2.12 |
| Octyl α-glyceryl ether | C8BGLYE | −2.88 | −2.24 |
| Octyl glycol ether | C8E1 | −3.14 | −2.31 |
| Triethylene glycol monodecyl ether | C10E3 | −3.67 | −3.22 |
| Dodecyl β-D-glucoside | C12BG1 | −4.21 | −3.72 |
| Octoxynol-2 | C8(C6H4)E2 | −4.15 | −3.88 |
| Hexaethylene glycol monododecyl ether | C12E6 | −5.40 | −4.06 |
Microemulsion systems
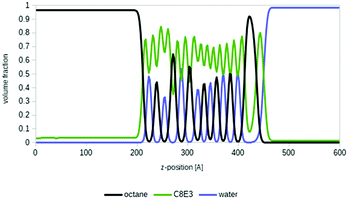
Microemulsions are of special interest for many areas of formulation science and for the important field of enhanced oil recovery.7 Deeper insights into microemulsion systems and the physical–chemical properties involved are provided elsewhere, for example on the definition of Winsor types, fish tail points and fish diagrams, or equivalent alkane carbon numbers.2,7,53 In short, a typical microemulsion system is composed of a less polar compound (usually called oil), a surfactant and water. After shaking this mixture in a test tube, three phases show up: an oil-rich phase at the top, an aqueous phase at the bottom, and a micellar, surfactant-rich phase in the middle.As a proof of principle, we applied COSMOplex to a typical microemulsion system, i.e. n-octane, a surfactant C8E3, and water at 288 K. We initialized the system as a three-zone system of oil (35 vol%), surfactant (30 vol%) and water (35 vol%). Experimentally, this system is expected to form an oil-rich phase, a microemulsion phase and a water rich phase under these conditions.54 And indeed, after initial fluctuations it really formed three phases with surfactant saturated oil and water phases, and a middle region in which the oil, surfactant and water self-organize into multiple micellar layers (see Fig. 7). This means that with COSMOplex – without any special pre-conditioning – we were able to investigate the self-organization of such complicated systems in silico with simulation times in the range of a few hours on a single CPU.
Even though the quantitative agreement with experimental microemulsion phase diagrams is not yet perfect, COSMOplex may become an important tool for the systematic investigation of microemulsion formation. In forthcoming publications, the prediction of more sophisticated fish diagrams53 by COSMOplex will be described in detail. These are calculated by temperature and concentration grids at the areas of phase transitions between a single phase, two phase systems and three phase systems.
It should be noted that curvatures of micellar systems are not directly implemented in COSMOplex, beyond the three base geometries (sphere, cylinder and disc). System properties of a curvature could be possibly derived by derivatives of the micelle radius and accounting for the varying micelle:water interface areas and corresponding free energies. As an alternative, a linear combination of properties derived from different geometries could be used, where the pre-factors of this linear combination could be related to a comparison of the particular geometry dependent free energies. Also, the critical packing parameter could be a useful guide in the initial choice of the micellar shape.55 This is, however, a matter for future investigations.
Interfacial tensions
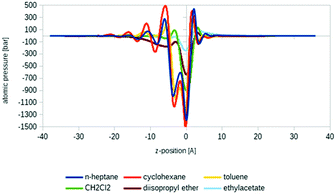
Another promising application area of COSMOplex is the prediction of the self-organization of molecules at a liquid–liquid interface and of the resulting interfacial tension (IFT). As introduced in the context of MD simulations,56 the IFT can be simply calculated as the z-integral of the lateral pressure.The initialization of a rectangular simulation box with mirror boundary conditions is performed by the AUTOBOX routine. In Fig. 8 three typical interfacial pressure profiles are shown. The profiles have been base-line corrected. In Fig. 9 we show the results for the IFT prediction of 40 aqueous systems taken from the paper of Andersson et al.29 Since negative predictions must result from numerical noise, we replaced them by zero. The results, which take into account the segment directionality (DIRPLEX), are in good agreement with experimental interfacial tensions (see Fig. 9). It should be noted that no parameters have been adjusted to fit the COSMOplex results to the experimental data. As explained in the DIRPLEX section, results without the DIRPLEX extension underestimate the experimental interfacial tensions by a factor of almost two. The use of the self-consistent electrostatic potential has almost no influence on the interfacial tension prediction.
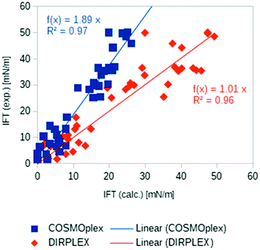 | ||
| Fig. 9 Experimental29 and predicted interfacial tensions for 40 aqueous systems: COSMOplex predictions without DIRPLEX extensions are in blue, with DIRPLEX in red. For the compound list and data see Table S1 in the ESI.† | ||
Conclusions and outlook
The COSMO-RS method was originally developed for homogenous, bulk liquids. The COSMOmic method extended the application of COSMO-RS to the simulation of solutes in micellar systems. However, it was limited to infinite dilution and required computationally expensive molecular dynamics input to describe the structure of the system. By the introduction of a layer specific pressure, the applicability of the method – now named COSMOplex – has been extended to the self-consistent simulation of a wide range of self-organizing molecular systems.First applications to micelle formation, microemulsion systems, biomembrane–water partitioning, and liquid–liquid interfacial tension predictions yield promising results in good agreement with experimental data. All simulations only took between 10 minutes and 24 hours on a single laptop CPU. Thus, the simulations are three to four orders of magnitude less CPU demanding than comparable molecular dynamics simulations. No adjustment of empirical parameters was required. All interactions are directly derived from the surface segment interactions by the COSMO-RS method, supplemented by parameter-free expressions for the pressure and the long-range electrostatic interactions.
Overall, COSMOplex enables many simulation applications of self-organizing systems at significantly lower computational costs and – at the same time – potentially achieving better agreement with experiments due to its sound quantum chemical and statistical thermodynamic fundamentals. These potential applications include – to mention just a few examples – the direct physical prediction of complex so-called fish diagrams for microemulsion systems, microemulsion systems formed by hydrotropes,60 the temperature or salt concentration dependence of surfactant properties, or even the fast self-consistent generation of biomembrane systems, for example to investigate the effect of penetration enhancers in human skin.61
Furthermore, COSMOplex has still considerable potential for tuning its performance. Even though the method is already capable of treating the electrostatic potential of self-organizing systems self-consistently, the COSMOplex application examples studied in this article are restricted to non-ionic surfactants and neutral solutes. Ionic surfactants and ionic solutes will be considered in a forthcoming paper. Extensions to gas–liquid interfaces and solid–liquid interfaces, confined liquids, and liquid crystals should be possible with minor effort and will be considered soon. By the implementation of logarithmically scaling layer widths, COSMOplex should be extendable to the simulation of macroscopic distances, e.g. for the complete simulation of the volume between the anode and cathode of an electrochemical cell. As a distant future goal, the simulation of 3D-inhomogeneous systems seems to be possible, optimistically enabling a completely new way of simulating water and drug molecules in enzyme pockets.
Conflicts of interest
The authors declare the following competing financial interests: Andreas Klamt is chief executive officer and all other authors are active or former employees of COSMOlogic GmbH&CoKG. COSMOlogic commercially distributes the software used in this paper.Appendix
Appendix A: boundary conditions in COSMOplex
Currently the following boundary conditions are supported by COSMOplex:(1) Mirror boundary conditions for rectangular boxes: if a coordinate is outside the box, it is transformed into the box by reflection. This assumes mirror symmetry perpetuation of the system outside the box. By reflection boundary conditions, most systems, which usually are simulated with periodic boundary conditions in MD simulations, can be reduced to half of the simulation volume, saving simulation time and memory.
(2) Pseudo-mirror boundary conditions for cylindrical and spherical simulation boxes: in spherical and cylindrical systems coordinates cannot escape at the inner boundary. But at the outer boundary a molecule, while centered in one of the outer layers, may have segments and atoms sticking out of the simulated system. In this case we transform them back into the system in the same way as we do with mirror boundaries for rectangular boxes, i.e. a coordinate z > zmax is transformed to 2·zmax − z. In order to be physically correct this boundary condition requires that the system does not show major changes any more at the outer boundary.
(3) Periodic boundary conditions for rectangular boxes: if the z-coordinate of an atom or segment exceeds the outer box limit zmax, it is translated back into the simulation volume by subtraction of one box length, i.e. by zmax − zmin. Analogously, coordinates escaping the box on the other side are translated by addition of a box length.
If not stated otherwise, all COSMOplex calculations in this paper are performed using the first boundary condition for rectangular boxes and the second one for spherical and cylindrical systems. In classic COSMOmic calculations, for negative values of z, which may appear in lamellar micelle geometries, a mirror boundary condition is applied, and for values of z larger than the outer boundary of the simulated box the σ-potential is assumed to be the same as in the pure solvent containing the micelle, i.e. in most cases pure water.
Appendix B: details of atomic volume assignment
The geometric centre position of the associated volume of an atom α is introduced as zαvol. This slightly deviates from the atom position zα which usually is defined by the position of the nucleus of the atom.In a next step, we define rescaled volumes for the molecules and atoms. The rescaled molecular volume Vk of a compound is defined as the liquid volume at room temperature, i.e. molecular weight divided by liquid density. The liquid density can either be given as experimental input data, or it can be estimated within the COSMOtherm software.49 All atom volumes are rescaled by the ratio of Vk and Vk,COSMO, where the latter is the thermodynamic average of the COSMO volumes of the conformations according to their Boltzmann population in the pure liquid k.
Next, we adjust either the size of the simulation box or the number of molecules in the box in order to achieve equality of the box volume and the sum of the molecular volumes of all molecules in the system. It should be noted that fractional numbers for the counts of molecules are allowed in COSMOplex.
Appendix C: calculation of the number of molecules per layer and of the average molecular surface area and volume in each layer
The average molecular size parameters, i.e. the average molecular volume![[r with combining macron]](https://www.rsc.org/images/entities/i_char_0072_0304.gif) sos(zi) and average molecular surface area
sos(zi) and average molecular surface area ![[q with combining macron]](https://www.rsc.org/images/entities/i_char_0071_0304.gif) sos(zi), are calculated as well. These are required for the calculation of the combinatorial free energy term in eqn (5), i.e. for the combinatorial response function of the layered liquid continuum. For this purpose, each molecule in each state is assigned to a layer i according to the amount of surface area residing in layer i divided by the total surface area of the molecule. Summation over all molecules and their state probabilities yields the number of molecules per layer Nmoli. Multiplying the fraction of surface in layer i by the molecular volume yields the average volume
sos(zi), are calculated as well. These are required for the calculation of the combinatorial free energy term in eqn (5), i.e. for the combinatorial response function of the layered liquid continuum. For this purpose, each molecule in each state is assigned to a layer i according to the amount of surface area residing in layer i divided by the total surface area of the molecule. Summation over all molecules and their state probabilities yields the number of molecules per layer Nmoli. Multiplying the fraction of surface in layer i by the molecular volume yields the average volume ![[r with combining macron]](https://www.rsc.org/images/entities/i_char_0072_0304.gif) sos(zi), and multiplying the fraction by the molecular area yields the average surface area
sos(zi), and multiplying the fraction by the molecular area yields the average surface area ![[q with combining macron]](https://www.rsc.org/images/entities/i_char_0071_0304.gif) sos(zi).
sos(zi).
Appendix D: calculation of the electrostatic potential from layer charges
The electrostatic potential φsos(zi) arising from the net charges in the layers is calculated, taking into account the geometry of the simulation box and the electronic polarizability, i.e. the infinite frequency dielectric constant ε∞ = n2, of the layers. The latter is calculated from pure compound refractive indices and averaged by using particular atom volume probabilities in the layers. The pure compound refractive indices can either be given as an experimental input, or they are calculated from an increment scheme.The reduction of the electric field resulting from the re-orientational polarizability should already be taken into account by the self-consistent organization of the molecules, since they feel the electrostatic potential.
In the planar geometry (rectangular box), the change of the electric field ΔE(zi) within a layer i is given by the volume charge density, i.e. the layer charge Qsos(zi) divided by the layer volume, multiplied by the layer width δ. Hence, we have for the electric field at the interface between layer i and i − 1, i.e. at zi − δ/2,
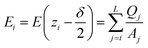 | (D1) |
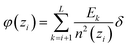 | (D2) |
In the spherical geometry the electric field at a radius z is the same as the electric field of a point charge at the centre which has the value of all included charge Qinc(zi). Outer charge does not contribute. Hence, we can easily get the electrostatic potential by summing up the small changes of the electric field ΔE(zi) reduced by n2(zi), starting at 0 and ending up at the outer shell, at which the field should have dropped to zero, because the total charge in the simulated sphere must be zero.
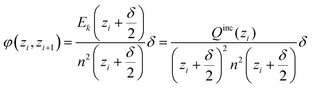 | (D3) |
In the cylindrical geometry the electric field at a radius z is the same as the electric field E(z) of a line charge at the centre which has the value of all included charge. In close analogy to the spherical case we get (with H being the height of the simulated cylinder)
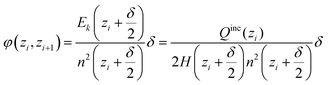 | (D4) |
Appendix E: pressure as a response to volume occupation
The new continuum response function considered in COSMOplex is the pressure function P(zi). The pressure response in a layer zi is calculated via the space filling ratio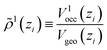 | (E1) |
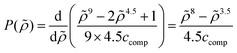 | (E2) |
Appendix F: combinatorial contribution
The combinatorial contribution to the free energy of a molecule X in layer i is calculated utilizing the surface area and volume of molecule X and the average molecular volume and surface area in layer i, as described in Appendix C. For each state (cpo) of molecules X the combinatorial contribution is assigned according to the fraction of surface residing in layer i.Appendix G: total free energy corrections for the Coulomb energy and the compression energy
In variational, self-consistent field quantum chemical algorithms, the total energy of the system usually is calculated as a sum of the expectation values of the energies of the electrons. But this has to be corrected by adding half of the Coulomb energy, because otherwise the electrostatic interaction of each electron is double counted. In other words, the electrostatic energy included in the expectation values has to be replaced by the correct value of the Coulomb energy. The same correction is required in COSMOplex for the Coulomb energy, i.e. the total Coulomb energy has to be reduced by a factor 1/2 (Ecorrφ). The correction is also required for the compression energy, because the compression energy included in the partition functions of the molecules reflects the interaction of each atom volume with the final, self-consistent pressure, while the compression related energy (EcorrP) has a different value given by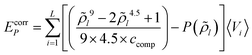 | (G1) |
Acknowledgements
We thank Steven Abbott, Jean-Marie Aubry and Maximilian Hahn for valuable discussions and feedback during the development of COSMOplex.References
- A. Boza Troncoso and E. Acosta, Integrated free energy model (IFEM) for microemulsions, J. Colloid Interface Sci., 2016, 466, 400–412 CrossRef CAS PubMed.
- R. Nagarajan and E. Ruckenstein, Molecular theory of microemulsions, Langmuir, 2000, 16, 6400–6415 CrossRef CAS.
- J. Hu, X. Zhang and Z. Wang, A review on progress in QSPR studies for surfactants, Int. J. Mol. Sci., 2010, 11, 1020–1047 CrossRef CAS PubMed.
- P. D. Huibers, V. S. Lobanov, A. R. Katritzky, D. O. Shah and M. Karelson, Prediction of critical micelle concentration using a quantitative structure–property relationship approach. 1. Nonionic surfactants, Langmuir, 1996, 12, 1462–1470 CrossRef CAS.
- P. D. T. Huibers, V. S. Lobanov, A. R. Katritzky, D. O. Shah and M. Karelson, Prediction of critical micelle concentration using a quantitative structure-property relationship approach, J. Colloid Interface Sci., 1997, 187, 113–120 CrossRef CAS PubMed.
- H. Cheng, G. M. Kontogeorgis and E. H. Stenby, Prediction of micelle formation for aqueous polyoxyethylene alcohol solutions with the UNIFAC model, Ind. Eng. Chem. Res., 2002, 41, 892–898 CrossRef CAS.
- A. Boza Troncoso and E. Acosta, The UNIFAC model and the partition of alkyl and alkylphenol ethoxylate surfactants in the excess phases of middle phase microemulsions, Fluid Phase Equilib., 2015, 397, 117–125 CrossRef CAS.
- C.-C. Chen, Molecular thermodynamic model for Gibbs energy of mixing of nonionic surfactant solutions, AIChE J., 1996, 42, 3231–3240 CrossRef CAS.
- X.-S. Li, J.-F. Lu and Y.-G. Li, Study on ionic surfactant solutions by SAFT equation incorporated with MSA, Fluid Phase Equilib., 2000, 168, 107–123 CrossRef CAS.
- E. Ryjkina, H. Kuhn, H. Rehage, F. Müller and J. Peggau, Molecular dynamic computer simulations of phase behavior of non-ionic surfactants, Angew. Chem., Int. Ed., 2002, 41, 983–986 CrossRef CAS PubMed.
- A. Vishnyakov, M.-T. Lee and A. V. Neimark, Prediction of the critical micelle concentration of nonionic surfactants by dissipative particle dynamics simulations, J. Phys. Chem. Lett., 2013, 4, 797–802 CrossRef CAS PubMed.
- S. A. Sanders and A. Z. Panagiotopoulos, Micellization behavior of coarse grained surfactant models, J. Chem. Phys., 2010, 132, 114902 CrossRef PubMed.
- S. Jakobtorweihen, D. Yordanova and I. Smirnova, Predicting critical micelle concentrations with molecular dynamics simulations and COSMOmic, Chem. Ing. Tech., 2017, 89, 1288–1296 CrossRef CAS.
- D. Lopes, S. Jakobtorweihen, C. Nunes, B. Sarmento and S. Reis, Shedding light on the puzzle of drug-membrane interactions: experimental techniques and molecular dynamics simulations, Prog. Lipid Res., 2017, 65, 24–44 CrossRef CAS PubMed.
- M. Lundborg, A. Narangifard, C. L. Wennberg, E. Lindahl, B. Daneholt and L. Norlén, Human skin barrier structure and function analyzed by cryo-EM and molecular dynamics simulation, J. Struct. Biol., 2018, 203, 149–161 CrossRef CAS PubMed.
- A. Klamt, Conductor-like screening model for real solvents: a new approach to the quantitative calculation of solvation phenomena, J. Phys. Chem., 1995, 99, 2224–2235 CrossRef CAS.
- A. Klamt, V. Jonas, T. Bürger and J. C. Lohrenz, Refinement and parametrization of COSMO-RS, J. Phys. Chem. A, 1998, 102, 5074–5085 CrossRef CAS.
- A. Klamt, COSMO-RS From Quantum Chemistry to Fluid Phase Thermodynamics and Drug Design, Elsevier, Amsterdam, The Netherlands, Boston, MA, USA, 2005 Search PubMed.
- A. Klamt and G. Schüürmann, COSMO: a new approach to dielectric screening in solvents with explicit expressions for the screening energy and its gradient, J. Chem. Soc., Perkin Trans. 2, 1993, 799–805 RSC.
- E. A. Guggenheim, Mixtures, Clarendon Press, Oxford, 1952 Search PubMed.
- A. Klamt, G. J. P. Krooshof and R. Taylor, COSMOSPACE: alternative to conventional activity-coefficient models, AIChE J., 2002, 48, 2332–2349 CrossRef CAS.
- C. C. Bannan, K. H. Burley, M. Chiu, M. R. Shirts, M. K. Gilson and D. L. Mobley, Blind prediction of cyclohexane-water distribution coefficients from the SAMPL5 challenge, J. Comput.-Aided Mol. Des., 2016, 30, 927–944 CrossRef CAS PubMed.
- A. Klamt, F. Eckert, J. Reinisch and K. Wichmann, Prediction of cyclohexane-water distribution coefficients with COSMO-RS on the SAMPL5 data set, J. Comput.-Aided Mol. Des., 2016, 30, 959–967 CrossRef CAS PubMed.
- J. Reinisch, A. Klamt and M. Diedenhofen, Prediction of free energies of hydration with COSMO-RS on the SAMPL3 data set, J. Comput.-Aided Mol. Des., 2012, 26, 669–673 CrossRef CAS PubMed.
- J. Zhang, B. Tuguldur and D. van der Spoel, Force field benchmark of organic liquids. 2. Gibbs energy of solvation, J. Chem. Inf. Model., 2015, 55, 1192–1201 CrossRef CAS PubMed.
- J. Zhang, B. Tuguldur and D. van der Spoel, Correction to force field benchmark of organic liquids. 2. Gibbs energy of solvation, J. Chem. Inf. Model., 2016, 56, 819–820 CrossRef CAS PubMed.
- A. Klamt, B. Mennucci, J. Tomasi, V. Barone, C. Curutchet, M. Orozco and F. J. Luque, On the performance of continuum solvation methods. A comment on “Universal approaches to solvation modeling”, Acc. Chem. Res., 2009, 42, 489–492 CrossRef CAS PubMed.
- R. Oviedo-Roa, J. M. Martínez-Magadán, A. Muñoz-Colunga, R. Gómez-Balderas, M. Pons-Jiménez and L. S. Zamudio-Rivera, Critical micelle concentration of an ammonium salt through DPD simulations using COSMO-RS-based interaction parameters, AIChE J., 2013, 59, 4413–4423 CrossRef CAS.
- M. P. Andersson, M. V. Bennetzen, A. Klamt and S. L. S. Stipp, First-principles prediction of liquid/liquid interfacial tension, J. Chem. Theory Comput., 2014, 10, 3401–3408 CrossRef CAS PubMed.
- H. Alasiri and W. G. Chapman, Dissipative particle dynamics (DPD) study of the interfacial tension for alkane/water systems by using COSMO-RS to calculate interaction parameters, J. Mol. Liq., 2017, 246, 131–139 CrossRef CAS.
- T. Lukowicz, A. Benazzouz, V. Nardello-Rataj and J.-M. Aubry, Rationalization and prediction of the equivalent alkane carbon number (EACN) of polar hydrocarbon oils with COSMO-RS σ-moments, Langmuir, 2015, 31, 11220–11226 CrossRef CAS PubMed.
- T. Lukowicz, E. Illous, V. Nardello-Rataj and J.-M. Aubry, Prediction of the equivalent alkane carbon number (EACN) of aprotic polar oils with COSMO-RS sigma-moments, Colloids Surf., A, 2018, 536, 53–59 CrossRef CAS.
- A. Klamt, U. Huniar, S. Spycher and J. Keldenich, COSMOmic: a mechanistic approach to the calculation of membrane-water partition coefficients and internal distributions within membranes and micelles, J. Phys. Chem. B, 2008, 112, 12148–12157 CrossRef CAS PubMed.
- M. Paloncýová, R. DeVane, B. Murch, K. Berka and M. Otyepka, Amphiphilic drug-like molecules accumulate in a membrane below the head group region, J. Phys. Chem. B, 2014, 118, 1030–1039 CrossRef PubMed.
- E. Ritter, D. Yordanova, T. Gerlach, I. Smirnova and S. Jakobtorweihen, Molecular dynamics simulations of various micelles to predict micelle water partition equilibria with COSMOmic: influence of micelle size and structure, Fluid Phase Equilib., 2016, 422, 43–55 CrossRef CAS.
- S. Jakobtorweihen, A. C. Zuniga, T. Ingram, T. Gerlach, F. J. Keil and I. Smirnova, Predicting solute partitioning in lipid bilayers: free energies and partition coefficients from molecular dynamics simulations and COSMOmic, J. Chem. Phys., 2014, 141, 045102 CrossRef CAS PubMed.
- K. Bittermann, S. Spycher, S. Endo, L. Pohler, U. Huniar, K.-U. Goss and A. Klamt, Prediction of phospholipid-water partition coefficients of ionic organic chemicals using the mechanistic model COSMOmic, J. Phys. Chem. B, 2014, 118, 14833–14842 CrossRef CAS PubMed.
- A. Klamt, COSMO-RS for aqueous solvation and interfaces, Fluid Phase Equilib., 2016, 407, 152–158 CrossRef CAS.
- A. Klamt, J. Reinisch, F. Eckert, A. Hellweg and M. Diedenhofen, Polarization charge densities provide a predictive quantification of hydrogen bond energies, Phys. Chem. Chem. Phys., 2012, 14, 955–963 RSC.
- A. Klamt, J. Reinisch, F. Eckert, J. Graton and J.-Y. Le Questel, Interpretation of experimental hydrogen-bond enthalpies and entropies from COSMO polarisation charge densities, Phys. Chem. Chem. Phys., 2013, 15, 7147–7154 RSC.
- T. Ingram, S. Storm, L. Kloss, T. Mehling, S. Jakobtorweihen and I. Smirnova, Prediction of micelle/water and liposome/water partition coefficients based on molecular dynamics simulations, COSMO-RS, and COSMOmic, Langmuir, 2013, 29, 3527–3537 CrossRef CAS PubMed.
- L. Mokrushina, M. Buggert, I. Smirnova, W. Arlt and R. Schomäcker, COSMO-RS and UNIFAC in prediction of micelle/water partition coefficients, Ind. Eng. Chem. Res., 2007, 46, 6501–6509 CrossRef CAS.
- M. Buggert, C. Cadena, L. Mokrushina, I. Smirnova, E. J. Maginn and W. Arlt, COSMO-RS calculations of partition coefficients: different tools for conformation search, Chem. Eng. Technol., 2009, 32, 977–986 CrossRef CAS.
- COSMOconf 4.3, COSMOlogic GmbH & Co. KG, Leverkusen, Germany, 2018, http://www.cosmologic.de Search PubMed.
- TURBOMOLE V7. 3, University of Karlsruhe and Forschungszentrum Karlsruhe GmbH, 1989-2007, TURBOMOLE GmbH, since 2007, Karlsruhe, Germany, 2018; available from http://www.turbomole.com.
- A. D. Becke, Density-functional exchange-energy approximation with correct asymptotic behavior, Phys. Rev. A: At., Mol., Opt. Phys., 1988, 38, 3098–3100 CrossRef CAS.
- J. P. Perdew, Density-functional approximation for the correlation energy of the inhomogeneous electron gas, Phys. Rev. B: Condens. Matter Mater. Phys., 1986, 33, 8822–8824 CrossRef.
- A. Schäfer, C. Huber and R. Ahlrichs, Fully optimized contracted Gaussian basis sets of triple zeta valence quality for atoms Li to Kr, J. Chem. Phys., 1994, 100, 5829 CrossRef.
- COSMOtherm, Release 19, COSMOlogic GmbH & Co. KG, Leverkusen, Germany, 2019, http://www.cosmologic.de Search PubMed.
- S. Jakobtorweihen, T. Ingram and I. Smirnova, Combination of COSMOmic and molecular dynamics simulations for the calculation of membrane-water partition coefficients, J. Comput. Chem., 2013, 34, 1332–1340 CrossRef CAS PubMed.
- L. Wang, Measurements and implications of the membrane dipole potential, Annu. Rev. Biochem., 2012, 81, 615–635 CrossRef CAS PubMed.
- S. Endo, B. I. Escher and K.-U. Goss, Capacities of membrane lipids to accumulate neutral organic chemicals, Environ. Sci. Technol., 2011, 45, 5912–5921 CrossRef CAS PubMed.
- S. Queste, J. L. Salager, R. Strey and J. M. Aubry, The EACN scale for oil classification revisited thanks to fish diagrams, J. Colloid Interface Sci., 2007, 312, 98–107 CrossRef CAS PubMed.
- A. Benazzouz, L. Moity, C. Pierlot, V. Molinier and J.-M. Aubry, Hansen approach versus COSMO-RS for predicting the solubility of an organic UV filter in cosmetic solvents, Colloids Surf., A, 2014, 458, 101–109 CrossRef CAS.
- M. J. Rosen and J. T. Kunjappu, Surfactants and Interfacial Phenomena, Wiley, Hoboken, NJ, USA, 4th edn, 2012 Search PubMed.
- Y. Zhang, S. E. Feller, B. R. Brooks and R. W. Pastor, Computer simulation of liquid/liquid interfaces. I. Theory and application to octane/water, J. Chem. Phys., 1995, 103, 10252–10266 CrossRef CAS.
- CRC Handbook of Tables for Applied Engineering Science, ed. R. E. Bolz and G. L. Tuve, CRC Press, Boca Raton, Florida, 2nd edn, 2000 Search PubMed.
- P. Mukerjee and J. Mysels, Critical micelle concentrations of aqueous surfactant systems. Prepared under contract for the Office of Standard Reference Data, National Bureau of Standards of NSRDS-NBS 36, Washington, DC, J. Pharm. Sci., 1972, 61, 319 CrossRef.
- D. P. Tieleman, private communication.
- M. Hahn, S. Krickl, T. Buchecker, G. Jost, D. Touraud, P. Bauduin, A. Pfitzner, A. Klamt and W. Kunz, Ab-initio prediction of structuring/mesoscale inhomogeneities in surfactant-free microemulsions and hydrogen-bonding-free microemulsions, Phys. Chem. Chem. Phys. 10.1039/C8CP07544A.
- J. A. H. Schwöbel and A. Klamt, Mechanistic skin penetration model by the COSMOperm method: Routes of permeation, vehicle effects and skin variations in the healthy and compromised skin, Comput. Toxicol., 2019, 11, 50–64 CrossRef.
Footnote |
| † Electronic supplementary information (ESI) available: A description of the AUTOBOX algorithm used for the preparation of COSMOplex input distributions and experimental reference values for different systems. See DOI: 10.1039/c9cp01169b |
| This journal is © the Owner Societies 2019 |