Open Access Article
Open Access ArticleCreative Commons Attribution 3.0 Unported Licence
Hybrid QSPR models for the prediction of the free energy of solvation of organic solute/solvent pairs†
Tohid N.
Borhani
 a,
Salvador
García-Muñoz
a,
Salvador
García-Muñoz
 b,
Carla
Vanesa Luciani
b,
Amparo
Galindo
b,
Carla
Vanesa Luciani
b,
Amparo
Galindo
 a and
Claire S.
Adjiman
a and
Claire S.
Adjiman
 *a
*a
aCentre for Process Systems Engineering, Department of Chemical Engineering, Imperial College London, London SW7 2AZ, UK. E-mail: c.adjiman@imperial.ac.uk; Tel: +44 (0)0207 594 6638
bLilly Research Laboratories, Indianapolis, IN 46082, USA
First published on 17th June 2019
Abstract
Due to the importance of the Gibbs free energy of solvation in understanding many physicochemical phenomena, including lipophilicity, phase equilibria and liquid-phase reaction equilibrium and kinetics, there is a need for predictive models that can be applied across large sets of solvents and solutes. In this paper, we propose two quantitative structure property relationships (QSPRs) to predict the Gibbs free energy of solvation, developed using partial least squares (PLS) and multivariate linear regression (MLR) methods for 295 solutes in 210 solvents with total number of data points of 1777. Unlike other QSPR models, the proposed models are not restricted to a specific solvent or solute. Furthermore, while most QSPR models include either experimental or quantum mechanical descriptors, the proposed models combine both, using experimental descriptors to represent the solvent and quantum mechanical descriptors to represent the solute. Up to twelve experimental descriptors and nine quantum mechanical descriptors are considered in the proposed models. Extensive internal and external validation is undertaken to assess model accuracy in predicting the Gibbs free energy of solvation for a large number of solute/solvent pairs. The best MLR model, which includes three solute descriptors and two solvent properties, yields a coefficient of determination (R2) of 0.88 and a root mean squared error (RMSE) of 0.59 kcal mol−1 for the training set. The best PLS model includes six latent variables, and has an R2 value of 0.91 and a RMSE of 0.52 kcal mol−1. The proposed models are compared to selected results based on continuum solvation quantum chemistry calculations. They enable the fast prediction of the Gibbs free energy of solvation of a wide range of solutes in different solvents.
Introduction
The Gibbs free energy of solvation is a fundamental thermodynamic property relevant in chemical, biological, pharmacological and environmental processes due to its relation to a variety of physical properties such as Henry's law constants, infinite dilution activity coefficients, solubility, and distribution of species in demixed solvents. In solution chemistry, the Gibbs free energy of solvation influences reaction equilibrium constants and reaction rates.1 Consequently, it has been the focus of many studies, from the creation of extensive databases2–5 to the development of predictive methods and their assessment (e.g., Klamt,6 Lin and Hsieh,7 Nicholls et al.,8 and Fingerhut et al.9).The Gibbs free energy of solvation of a solute i in a solvent j is defined as the difference between the free energy of solute i in solvent j at temperature T and pressure P and its free energy in the gas phase at the same temperature and pressure, where care needs to be taken in defining the standard states in the gas and liquid phases.10 Here, we focus on the Gibbs free energy of solvation at infinite dilution, ΔGsij(T,P), which corresponds to the limit of one molecule of i (i.e., infinite dilution), as is most commonly reported in the literature,11 and which can be calculated as a residual chemical potential or in terms of the liquid-phase fugacity coefficient.12 Note that in the remainder of this paper, the term “infinite dilution” is sometimes omitted when referring to the free energy of solvation, but this is always implied.
Given the central role of ΔGsij in understanding solvation phenomena, the need often arises to obtain the Gibbs free energy of solvation of compounds for which no experimental data are available, simply because measurements have not yet been carried out or because the compound of interest has not been synthesized, is transient in nature (e.g., reaction intermediates and transition states) or difficult or dangerous to handle. As a result, considerable effort has been devoted to the development of reliable predictive models. Existing methods to predicting solvation free energies can be classified into three main categories: (i) quantum mechanical (QM) methods (explicit, implicit, hybrid); (ii) classical methods (molecular simulations, equations of state and activity coefficient models); and (iii) empirical methods (quantitative structure property relations (QSPR)/group contribution method (GCM), linear solvation energy relationships (LSER)/linear free energy relationships (LFER)/theoretical linear solvation energy relationships (TLSER)). While it is beyond the scope of this article to review the literature on free energy of solvation prediction, we highlight a few key contributions in which the predictive accuracy of available methods has been investigated for a range of solute/solvent systems.
Continuum solvation (or implicit) QM models incorporate a detailed treatment of the electronic structure of the solute and make it possible to account, via a bulk electrostatic term, for the polarization and conformational changes that can arise in a solute due to the presence of a field induced by the solvent dielectric. Given the ab initio nature of at least part of the calculation, continuum solvation models are applicable to a wide variety of solutes, including neutral and ionic compounds, and even transient species such as reaction intermediates and transition states. Among implicit QM methods, the polarizable continuum model (PCM),7,13 the solvation models (SM),11,14–17 and the conductor-like screening model for realistic solvation (COSMO-RS)4,7,18 and related approaches9,19 have been used extensively for the prediction of free energies of solvation.
The SM series of methods consists in continuum (implicit) solvation models that have been parameterized based on an extensive set of experimental data of free energies of solvation.15 The most recent version of the SM models, SMD,11 was reported to have a mean unsigned error (MUE) of 0.6–1.0 kcal mol−1 in the free energy of solvation based on a study of 2346 solute/solvent pairs involving 318 neutral solutes and 91 solvents. Zanith and Pliego20 have recently investigated the predictive capabilities of SMD and its precursor SM8 for 77 data points corresponding to the Gibbs free energy of solvation of a number of solutes in methanol, DMSO (dimethyl sulfoxide), and acetonitrile, three common solvents. They reported a root mean squared error (RMSE) of 0.53 kcal mol−1 in acetonitrile, 0.83 kcal mol−1 in methanol and 1.22 kcal mol−1 in DMSO for SMD and 0.69 kcal mol−1 in acetonitrile, 0.71 kcal mol−1 in methanol and 1.05 kcal mol−1 in DMSO for SM8. It is worth noting that not all the data considered in the comparison had been included in the parameterization of SMD; in particular, no data in methanol had been used by Marenich et al.11 in its development.
Several studies of the prediction of Gibbs free energies of solvation with COSMO-RS have also been carried out. Klamt and Diedenhofen21 reported an RMSE of 1.56 kcal mol−1 for the prediction of the free energies of hydration of 23 compounds, while Reinisch et al.22 predicted the free energies of hydration of 36 components including chlorinated alkanes, biphenyls and dioxins. They obtained an overall RMSE of 1.05 kcal mol−1. Reinisch and Klamt23 investigated 47 complex multifunctional compounds and reported an overall RMSE of 1.46 kcal mol−1 (and 1.18 kcal mol−1 when removing the dominant outlier). In a broader study, Klamt et al.24 predicted the free energies of solvation for the SM8 test set of 2346 solute/solvent pairs, reporting a MUE of 0.48 kcal mol−1. Klamt and Diedenhofen25 proposed an alternative approach, direct COSMO-RS (DCOSMO-RS), and evaluated it for the same data set, obtaining an overall MUE of 0.7 kcal mol−1. In addition, Fingerhut et al.9 investigated the predictive capabilities of COSMO-SAC 2010![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 26 and COSMO-SAC-dsp27 for over 29
26 and COSMO-SAC-dsp27 for over 29![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 000 infinite dilution activity coefficients, reporting mean absolute relative deviations of 96% and 85% for the two methods, respectively. While the metrics of model performance considered in these various studies differ, it appears that an average error of approximately 1 kcal mol−1 or less can be expected in the calculation of the Gibbs free energy of solvation when using continuum solvation QM models.
000 infinite dilution activity coefficients, reporting mean absolute relative deviations of 96% and 85% for the two methods, respectively. While the metrics of model performance considered in these various studies differ, it appears that an average error of approximately 1 kcal mol−1 or less can be expected in the calculation of the Gibbs free energy of solvation when using continuum solvation QM models.
There are several approximations that arise when developing or applying continuum solvation models.28 These vary from model to model but may include: the arbitrary partitioning of the free energy of solvation; the use of a simplified representation of the solvent that makes it difficult to account for specific interactions; the reliance on the user to identify specific conformations of the solute as input, making it difficult to account reliably for the multiple solute conformations that occur in solution. Overcoming these limitations within a QM framework often requires the use of explicit methods,29 where a finite number of solvent molecules are modelled explicitly; this approach is associated with a significant increase in computational cost. As a less demanding strategy, hybrid QM/MM methods have attracted considerable attention recently; the reader is referred to Wood et al.,30 and König et al.31,32 for further information on these methods.
Many authors have studied the use of classical molecular simulation methods for the prediction of free energies of solvation. With molecular simulation methods, the computational cost of treating the solvent molecules explicitly is more tractable than when using an explicit QM representation of the system. The accuracy of these calculations is however reliant on the availability of an accurate force field for the system of interest. The accuracy that can be achieved has been explored in a few systematic studies. Thus, McDonald et al.33 applied Monte Carlo simulations/free energy perturbation (FEP) to obtain absolute Gibbs free energies of solvation in chloroform for 16 organic molecules, reporting an average error in predicted free energies of solvation of 0.8 kcal mol−1. Monte Carlo simulations have also been carried out by Duffy and Jorgensen34 for more than 200 organic solutes in aqueous solution, using the OPLS-AA force field augmented with CM1P partial charges. They also derived descriptors such as solute-water Coulomb and Lennard-Jones interaction energies, solvent-accessible surface area and numbers of donor and acceptor hydrogen bonds, and correlated these to Gibbs free energies of solvation in hexadecane, octanol and water. The RMSEs for the predicted Gibbs free energies of solvation of 68 solutes in hexadecane, 85 solutes in octanol and 85 solutes in water were 0.43, 0.64, and 0.87 kcal mol−1, respectively. Gonçalves and Stassen35 used a molecular dynamics approach that combines an explicit model of the solution with an implicit solvation model to compute the Gibbs free energies of solvation of different small molecules in three solvents. They reported a mean unsigned error of 0.50 kcal mol−1 for 23 solutes in chloroform, 0.49 kcal mol−1 for 21 solutes in carbon tetrachloride and 0.78 kcal mol−1 for 17 solutes in benzene. Mobley et al.36 computed the Gibbs free energies of hydration of 504 small organic molecules using an all-atom force field in explicit water, obtained a RMSE of 1.24 kcal mol−1. Shivakumar et al.37 used molecular dynamics free energy perturbation simulations with explicit water molecules to compute the absolute hydration free energies of a set of 239 small molecule, finding a high coefficient of determination (R2 = 0.94) and a mean unsigned error of 1.10 kcal mol−1. The FreeSolv database,4,38 which contains, in version 0.5 (Duarte Ramos Matos et al.4), experimental hydration free energy values for 643 small neutral molecules, has been used to assess the suitability of the alchemical method MBAR39 to predict hydration free energies, finding a RMSE of 1.4 kcal mol−1. In principle, molecular simulation methods can provide a more accurate representation of solvation than continuum solvation QM models, because specific interactions are considered and sufficiently large numbers of molecules are used to enable an explicit statistical mechanical treatment of the mixture thermodynamics. However, the force fields employed may have limited transferability and often do not incorporate a treatment of polarizability, which may be an important contribution to the Gibbs free energy of solvation. It is also challenging to model certain solutes of interest such as transition states. Furthermore, the computational cost of these methods can often be much greater than that of continuum solvation QM calculations.
A further alternative for the calculation of the Gibbs free energy of solvation is the class of group contribution (GC) models, which consists of GC equations of state (e.g., SAFT-γ Mie12,40,41) and GC activity coefficient models (e.g., UNIFAC,42 modified UNIFAC43). These models can be used to predict solvation properties provided the relevant group parameters have been parameterized. Computations with such models are extremely fast and are applicable over the entire composition range. As a result, model accuracy has largely been evaluated based on entire phase diagrams rather than based on infinite dilution properties, and there are few extensive studies of the prediction error in Gibbs free energies of solvation. Voutsas and Tassios44 evaluated several versions of UNIFAC using 600 data points for infinite dilution activity coefficients at various temperatures and found that the best performance was achieved with the modified UNIFAC of Gmehling et al.,43 with average absolute relative errors (AARE) ranging between 3% and 23.6% depending on the class of compounds. In their comprehensive study, Fingerhut et al.9 also investigated the predictive capability of original UNIFAC42 and modified UNIFAC (Dortmund).43 They found better overall performance than with the COSMO-based approaches studied, with AAREs in the infinite dilution activity coefficients of 73% and 58% for UNIFAC and modified UNIFAC, respectively. While GC methods are computationally inexpensive, their applicability is limited by the need to obtain group–group interaction parameters from experimental data and by the inability to model transient species such as transition states.
Finally, data-driven methods have also received attention due to their simplicity and ease of application.45 In QSPR approaches, the relationship between molecular properties (or descriptors) and the Gibbs free energy of solvation is expressed in the form of a linear or nonlinear expression46 of the following general form:
| Property = f(solvent or/and solute parameters/descriptors). |
There are two main types of QSPR models, namely theory- and experiment-based. Theory-based QSPR models can be developed using molecular descriptors such as topological indices, geometric, quantum mechanical, and thermodynamic quantities.47,48 The importance of QM descriptors in chemometric studies and their applications have been reviewed and discussed by several authors.49–52 Certain group contribution methods (GCMs), in which the equations do not have any physical basis (in contrast to the equation of state/activity coefficient methods described earlier), can also be classed as theory-based QSPR methods, by postulating that any property can be expressed as a function of some predefined structural features such as atoms, bonds, chemically relevant groups, and larger fragments of the molecules.53 Well-known experiment-based QSPR models are the linear solvation energy relationships (LSER models) in which the descriptors are physical properties, such as solvatochromic parameters and Hildebrand solubility parameters, and are usually obtained from experimental measurements. This can limit the predictive capability of the approach, although it has been shown that the relevant properties in LSER can sometimes be derived from GCMs.54,55 Furthermore, a theoretical version of linear solvation energy relationships, TLSER, in which theoretical quantum mechanical descriptors replace empirical ones has been presented.46
Different statistical and regression methods (linear and non-linear approaches), such as multivariate linear regression (MLR), partial least squares (PLS), principal component regression (PCR), genetic programming (GP), and artificial neural network (ANN) can be used to derive QSPR/LSER models.56,57 In addition, several algorithms such as genetic algorithm (GA), stepwise forward selection, and particle swarm optimization (PSO) can be employed in these studies to reduce the number of descriptors.58
There have been a number of attempts to develop the empirical models for the prediction of Gibbs free energies of solvation. The vast majority of the studies to date have been focused on developing models for a range of solutes in a given solvent (usually water) or for a given solute in a range of solvents. Models that are applicable to a single solvent are by far the most common. For example, using water as a solvent, Michielan et al.59 combined autocorrelation molecular electrostatic potential (auto MEP) descriptors with a response surface analysis (RSA) to develop their model. They used 271 organic molecules as solutes and divided the dataset into a training set of 248 data points and a testing set of 23 data points. For the training set, their model was found to have a determination coefficient of 0.99 and a RMSE equal to 0.069 kcal mol−1. For the test set (23 data points) the determination coefficient found was 0.92. Bernazzani et al.60 used a recursive neural network (RNN) to predict the Gibbs free energy of hydration of 339 solutes from 16 different chemical classes. They obtained an absolute residual of about 0.24 kcal mol−1 and a standard deviation of 0.43 kcal mol−1. Delgado and Jaña61 focused on octanol as the solvent, and modelled the Gibbs free energy of solvation of 147 components using a QSPR approach. They used the MLR method to develop their model based on three descriptors and obtained a determination coefficient of 0.93 and with a standard deviation of 0.57 kcal mol−1.
In what is perhaps the broadest QSPR study so far, Katritzky et al.53,62 derived QSPR models of solubility for different solutes and solvents, and then related the solubility to the free energy of solvation. Their first approach was based on calculations of the Ostwald solubility of a series of solutes in a single solvent, for 69 different solvents, therefore obtaining 69 solvent-specific equations (MLR models). The number of solutes included in the regression for any given solvent varied from 14 to 226. Since the solvent was constant in each model, only solutes descriptors were used in each MLR model. The authors calculated the natural logarithm of the Ostwald solubility coefficient, ln![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) L, and then related this to the Gibbs free energy of solvation. The standard deviations for the 69 models ranged from 0.06 to 0.80 kcal mol−1. In their second paper,62 new models were developed to predict ln
L, and then related this to the Gibbs free energy of solvation. The standard deviations for the 69 models ranged from 0.06 to 0.80 kcal mol−1. In their second paper,62 new models were developed to predict ln![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) L (and subsequently the Gibbs free energy of solvation) for a single solute in a series of solvents. Eighty solutes were found to have experimental data across a sufficiently large range of solvents (14 or more solvents) to enable model regression and thus 80 MLR equations were derived. Since the solute was constant in each model, only solvent descriptors were used in this case. The standard deviations for the 80 models ranged from 0.02 kcal mol−1 to 0.60 kcal mol−1.
L (and subsequently the Gibbs free energy of solvation) for a single solute in a series of solvents. Eighty solutes were found to have experimental data across a sufficiently large range of solvents (14 or more solvents) to enable model regression and thus 80 MLR equations were derived. Since the solute was constant in each model, only solvent descriptors were used in this case. The standard deviations for the 80 models ranged from 0.02 kcal mol−1 to 0.60 kcal mol−1.
The systematic studies reported here and the corresponding performance indicators are summarized in Table 1. Although a range of data sets were used to derive error metrics and the scope of the various methods differs, QSPR approaches appear promising in terms of their predictive capability and relatively low computational cost. In principle, theory-based QSPR approaches can be applied to a wide range of compounds since they rely on the calculation of molecular descriptors at the quantum mechanical level. However, the QSPR methods proposed to date are limited by the imposition of a fixed solvent or a fixed solute. In the current study, we propose a new methodology to construct QSPR models that can be used to predict the free energy of solvation for any solute/solvent pair for which the relevant descriptors are available. The methodology is a hybrid between theory-based and experiment-based QSPR methods. The effects of both solute and solvent on the Gibbs free energy of solvation for the pair are accounted for by adopting several quantum-mechanical descriptors for the solute and several experimental descriptors for the solvent, and combining these in an additive way. The use of quantum mechanical descriptors for the solute thus makes it possible to model a very wide range of solutes, including those for which no experimental data are available. On the other hand, experimental descriptors (bulk thermodynamic properties) are chosen for the solvents, recognising that the range of solvents that are typically of interest is smaller than that for solutes and that experimental properties account for condensed phase behaviour in a way that is not achievable with QM descriptors. Correlation analysis is first applied to identify relationships between the descriptors. QSPR models are then developed using the PLS and MLR methods. Validation techniques are applied to check the validity and reliability of the presented models. The results are compared to experimental data and to the results of other methods from literature.
| Method | Source | Solutes | Solvents | Data points | Error measure | Error (kcal mol−1 or %) |
|---|---|---|---|---|---|---|
| SMD | Marenich et al.11 | 318 | 91 (including water) | 2346 | MUE | 0.6–1 |
| SMD | Zanith and Pliego20 | 51 | methanol, DMSO, acetonitrile | 77 | RMSE | 0.53–1.22 |
| COSMO-RS | Klamt et al.24 | 318 | 91 (including water) | 2346 | MUE | 0.48 |
| COSMO-RS | Klamt and Diedenhofen21 | 23 | Water | 23 | RMSE | 1.56 |
| COSMO-RS | Reinisch et al.22 | 36 | Water | 36 | RMSE | 1.05 |
| DCOSMO-RS | Klamt and Diedenhofen25 | 318 | 91 (including water) | 2346 | MUE | 0.7 |
| COSMO-SAC 2010 | Fingerhut et al.9 | — | — | >29![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 000 000 |
AARE%* | 96% |
| COSMO-SAC-dsp | Fingerhut et al.9 | — | — | >29![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 000 000 |
AARE%* | 85% |
| Monte Carlo simulations/free energy perturbation | McDonald et al.33 | 16 | Chloroform | 16 | MUE | 0.8 |
| Monte Carlo simulations | Duffy and Jorgensen34 | 68–85 | 3 | 238 | RMSE | 0.43–0.87 |
| Molecular dynamics simulations with implicit solvation | Gonçalves and Stassen35 | 17–23 | 3 | RMSE | 0.49–0.78 | |
| Alchemical molecular dynamics | Mobley et al.36 | 504 | Water | 504 | RMSE | 1.24 |
| Molecular dynamics free energy perturbation | Shivakumar et al.37 | 239 | Water | 239 | MUE | 1.10 |
| MBAR | Duarte Ramos Matos et al.4 | 643 | Water | 643 | RMSE | 1.4 |
| Modified UNIFAC (Dortmund) | Voutsas and Tassios44 | — | — | 600 | AARE%* | 3–23.6% |
| UNIFAC | Fingerhut et al.9 | — | — | >29![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 000 000 |
AARE%* | 73% |
| Modified UNIFAC (Dortmund) | Fingerhut et al.9 | — | — | >29![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 000 000 |
AARE%* | 58% |
| QSPR | Michielan et al.59 | 248 (test set: 23) | Water | 248 | RMSE | 0.069 |
| Recursive neural net | Bernazzani et al.60 | 339 (test set: 60) | Water | 339 | MUE (test set) | 0.24 |
| QSPR | Delgado and Jaña61 | 147 | Octanol | 147 | SD | 0.57 |
| QSPR | Katritzky et al.53 | 69 | 14–226 | 3208 | SD | 0.06–0.80 |
| QSPR | Katritzky et al.62 | 80 | 14–82 | 2409 | SD | 0.02–0.61 |
The remainder of the paper is organised as follows. First, the methodology adopted in this study is described, including the datasets, resources and methods used to obtain the solvent and solute descriptors are discussed. The analysis and modelling methods (PLS and MLR) used in the study are also introduced briefly. In the next section, the results of the PLS and MLR methods are presented and analysed based on the use of different validation methods. Subsequently, selected model predictions are compared with those of other methods reported in the literature to provide a broader basis for analysis. The findings of this study are summarised in the final section.
Methodology
The methodology typically used in QSPR/QSAR studies consists of the following steps: the collection or measurement of property data points (here, the free energy of solvation), the collection or computation of descriptor data, the analysis of the data to ensure its suitability (e.g., the application of methods such as correlation analysis), the training and development of the model and finally, its validation.Datasets
In order to develop QSPR models to predict a given property, two types of data are required: data for the property to be modelled (here, the Gibbs free energy of solvation) and descriptor values for a range of compounds.(i) The first category consists of self Gibbs free energies of solvation, i.e., the Gibbs free energy of solvation of a solute dissolved in itself, for example, ΔGsbenzene,benzene, the Gibbs free energy of solvation of benzene in benzene. An initial data set consisting of 254 points was collected from Marcus63 and Marenich et al.11
(ii) The second category consists of Gibbs free energies of solvation where the solute and solvent are different compounds. A total of 2149 initial data points were collected from Marenich et al.,11 who presented 2072 data points for 310 neutral solutes in 90 organic solvents, and from Zanith and Pliego,20 who presented 77 data points for different solutes in methanol, DMSO, and acetonitrile.
Duplicate data points were removed. The Gibbs free energies of solvation of hydrogen, ammonia, any inorganic materials other than water, and racemic components were removed from the database. Gibbs free energies of solvation for water as a solute were included but Gibbs free energies of hydration were not included in the database as aqueous solutions exhibit unusual behaviour as a result of the extremely high dielectric constant of water and its unique hydrogen-bonding structure. Moreover, solutes contain bromine (Br) and iodine (I) atoms were discarded due to the low number of solutes containing these atoms. Principal component analysis (PCA) was applied to the remaining data points to detect and remove outliers. This resulted in a set of 1777 Gibbs free energy of solvation values to be used in the development of the models in this study. The overall dataset contains 295 solutes and 210 solvents. The list of solutes and solvents in the database is presented in ESI,† Table S1, where all free energies of solvation are reported in kcal mol−1.
Solvent descriptors. In this study, twelve experimental descriptors, or properties, were selected to represent the solvents. The properties were selected from a longer list based on the availability of extensive data sets, their ease of calculation/prediction, their common use in other models of solvent effects (e.g., SMD,11 the solvatochromic equation64), and finally by giving preference to well-defined bulk thermodynamic properties. The use of bulk thermodynamic properties brings two advantages relative to QM descriptors obtained from isolated-molecule calculations: first, they take into account solvent–solvent interactions, which play an important role in solvation phenomena; second, they make it easier to account for the variation in the properties of the solvent with thermodynamic conditions, i.e., temperature, pressure and composition, and could thus be used to extend the scope of the model in the future. In this work, we take advantage of the fact that many solvents have been well studied in the literature and choose to collect experimental values of the thermodynamic properties, rather than computing them from predictive models.65
The selected experimental solvent descriptors are listed in Table 2. Experimental values for the selected properties for all 210 solvents in the database were collected from different sources such as DETHERM,2 ChemSpider,66 DIPPR,67 PubChem,68 National Institute of Standards and Technology,69 the Minnesota solvent descriptor database,70 and other sources.63,71–73
| Property | Symbol | Units |
|---|---|---|
| Boiling point at 1 atm | T b | K |
| Molecular weight | M w | g mol−1 |
| Relative permittivity at 298 K and 1 atm | ε r | — |
| Surface tension at 298 K and 1 atm | σ | mN m−1 |
| Refractive index at 298 K and 1 atm | n D | — |
| Enthalpy of vaporization at the normal boiling point | ΔHv | kJ mol−1 |
| Molar volume at 298 K and 1 atm | V m | m3 kmol−1 |
| Octanol–water partition coefficient at 298 K and 1 atm and infinite dilution | log![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) P P |
— |
| Critical temperature | T c | K |
| Critical pressure | P c | MPa |
| Critical volume | V c | m3 kmol−1 |
| Dipole moment at 298 K and 1 atm | μ j | Debye |
Solute descriptors. QM descriptors are used for the solutes in this study. One of the advantages of these descriptors in the context of the solute is that they are calculated using only the theoretical gas phase structure of the molecule, and therefore they can be obtained for compounds that have never been synthesized before or whose properties cannot be measured, with the caveat that a specific molecular conformation must be computed/chosen and that it is difficult to account for entropic and temperature effects. There are numerous types of QM descriptors that can be used, based on atomic charges, molecular orbitals, frontier orbital densities, superdelocalizabilities, atom–atom polarizability, molecular polarizability, dipole moment and polarity indices, energy, atomic orbital electron populations, overlap populations, vectors of lone pair densities, partitioning of energy data into one-centre and two-centre terms, and free valence of atoms.74 QM descriptors have been used in QSPR/QSAR studies extensively75,76 and have typically been calculated using semi-empirical or density functional theory (DFT) methods.51 DFT descriptors have been found to offer a good balance between computational cost and accuracy.77,78 In particular, the B3LYP functional79,80 has been reported to be suitable for the calculation of molecular properties and descriptors81 and is adopted here.
Previous QSPR and LSER studies of free energy of solvation, solubility, octanol/water partition coefficient and other related properties have led to a better understanding of the descriptors that should be considered. In their review, Karelson et al.51 identify the most commonly used classes of descriptors as those relating to charges, highest occupied molecular orbital (HOMO) and lowest unoccupied molecular orbital (LUMO) energies, orbital electron densities, superdelocalizabilities, atom–atom polarizabilities, molecular polarizabilities, dipole moments and polarity indices, and energies. Wilson and Famini82 and Famini and Wilson46 investigated the relationship between some QM descriptors and empirical LSER methods83–85 in order to propose a theoretical linear solvation energy relationship (TLSER) in which QM descriptors replace empirical ones. They used the most negative atomic partial charge in the molecule or electrostatic basicity (q−), the most positive partial charge on a hydrogen atom in the molecule or electrostatic acidity (q+), the molecular van der Waals volume (Vmc),86 the polarizability (π1), which is obtained by dividing the polarization volume by the molecular volume,87 the covalent acidity (εα), defined as the energy difference between the HOMO of water and the LUMO of the solute, and the covalent basicity (εβ), defined as the energy difference between the LUMO of water and the HOMO of the solute. The relevance of these descriptors was later confirmed by Abraham et al.88
On the basis of these previous studies, the nine QM descriptors listed in Table 3 were chosen in our work. DFT calculations were carried out at the B3LYP/6-31G(d,p) level of theory using Gaussian 09![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 89 for all 295 solutes: the structures were optimized starting from 3D molecular structures obtained from PubChem68 and ChemSpider66 and frequency calculations were performed to obtain the entropy.
89 for all 295 solutes: the structures were optimized starting from 3D molecular structures obtained from PubChem68 and ChemSpider66 and frequency calculations were performed to obtain the entropy.
| Property | Symbol | Units |
|---|---|---|
| a As calculated using the approach of Famini and Wilson.46 | ||
| Electronic basicitya | q − | — |
| Electronic aciditya | q + | — |
| Energy of the HOMO | ε H | a.u. |
| Energy of the LUMO | ε L | a.u. |
| Molecular van der Waals volume | V mc | Å3 |
| Electronic energy | E | a.u. |
| Isotropic polarizability | π | Bohr3 |
| Ideal gas entropy at 298 K | S | cal mol−1 K−1 |
| Dipole moment | μ i | Debye |
![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 317 entries in the matrix. The solvent properties can be found in the data sources listed in the Solvent Descriptors section. Values of the Gibbs free energies of solvation are collected in ESI,† Table S1. The computed solute descriptors are listed in ESI,† Table S2.
317 entries in the matrix. The solvent properties can be found in the data sources listed in the Solvent Descriptors section. Values of the Gibbs free energies of solvation are collected in ESI,† Table S1. The computed solute descriptors are listed in ESI,† Table S2.
Model development
Two types of models were developed: a linear PLS model, in which all descriptors play a role, and an MLR model, which may be nonlinear or linear, in which a trade-off is struck between the number of descriptors and the performance and validity of the model. This latter model is less demanding to use as it requires fewer descriptors to be computed and measured.In order to develop the models, 80% of the solute/solvent pairs (ntrain = 1421) were selected for training from the 1777 pairs in the database and the remaining pairs (ntest = 356) were set aside for testing the model. The dataset was split such that the maximum, minimum, and mean unsigned errors, and the standard deviation of the unsigned errors were consistent across the training and testing data sets. Furthermore, when sufficient data were available, representative solutes and solvents from each chemical family in the database were included in the training and testing sets. For example, the training set contains 1,4-dichlorobenzene in heptane and 1,4-dioxane in isopropanol, while the test set contains 1,4-dichlorobenzene in cyclohexane and 1,4-dioxane in ethanol. The numbers of data points in the training and test sets for different types of solute–solvent pairs are presented in ESI,† Table S6.
The partitioning of solute/solvent pairs into the training or testing set is shown in ESI,† Table S1. The same partitioning was used to develop the PLS and MLR models.
| X = TPT + Ex | (1) |
| Y = UQT + Ey | (2) |
| T = XW* | (3) |
| ΔGs,0ij = aTxi + bTxj | (4) |
A genetic algorithm (GA) was used for the selection of the best descriptors (feature selection) and functional form, by optimising with respect to the RQK fitness function.47,74 a constrained multi-criteria fitness function based on leave-one-out cross validation variance (QLoo2) and four simultaneous constraints.92 This ensures that the final model is valid and has good predictive capability, with limited correlation between the descriptors.
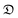 , that the subset of
, that the subset of 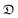 that contains the testing points is denoted by
that contains the testing points is denoted by 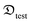 , that the experimental and predicted Gibbs free energies of solvation for solute i in solvent j are denoted by ΔGs,expij and ΔGs,predij, respectively.
, that the experimental and predicted Gibbs free energies of solvation for solute i in solvent j are denoted by ΔGs,expij and ΔGs,predij, respectively.
In order to validate the PLS model, the following criteria and statistical parameters are computed:93
• the determination coefficients for X (RX2) and Y (RY2);
• the cross-validation coefficient (Q2), which shows the predictivity of the PLS model;
• the variable importance in the projection score (VIP), which summarises the influence of individual X variables on the Y variance;94
• the root mean square error (RMSE), given by:
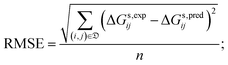 | (5) |
• the percentage average absolute relative error (AARE%):
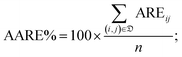 | (6) |
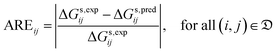 | (7) |
• the mean unsigned error (MUE), which is also known as average absolute error (AAE):
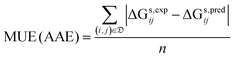 | (8) |
• the mean signed error (MSE):
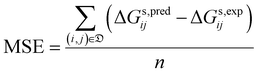 | (9) |
For MLR models, internal and external validation tests are used. Thus, in addition to the tests described for the PLS model, the following are applied:
• the bootstrapping test, in which a high average QBoot2 indicates model robustness and internal ability in prediction (internal);
• y-scrambling, to assess robustness and chance correlation95 (internal);
• leave-one-out cross-validation (LOOCV), which indicates the stability of the model96 and requires a value of QLoo2 greater than 0.5 (internal);
• the external cross-validation coefficient, QExt2, defined as:
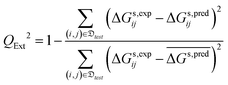 | (10) |
Several statistical tests are also applied to the descriptors in the MLR model, as follows:
• the t-test or t-ratio, to assess the significance of a descriptor in the regression model;
• the standard error for selected descriptors in the MLR model;
• the F-ratio (Fisher Value) to check the significance of independent variables on the dependent variable. Larger F-ratios indicate higher significance.
• the Prob(t) value, which is the probability of obtaining the estimated value of the parameter if the actual parameter value is zero, and for which values close to zero are desirable.
Results and discussion
A correlation analysis was first carried out on the set of Gibbs free energies of solvation for 1777 solute/solvent pairs. This was followed by the derivation and analysis of two hybrid models for the prediction of free energies of solvation, that combine experimental descriptors for the solvents and QM descriptors for the solutes: a PLS model and a MLR model.Correlation analysis results
A correlation analysis was performed for all descriptors. We highlight the key findings here, while the full correlation matrix can be found in ESI,† Table S3. Among the (experimental) solvent descriptors, the normal boiling point is found to have a high degree of correlation with the molecular weight, critical temperature and enthalpy of vaporization, with absolute correlation coefficients of 0.53 to 0.87. The critical properties exhibit some degree of correlation with the molecular weight, as expected.65 The octanol–water partition coefficient is found to correlate to some extent with critical pressure, the dipole moment of the solvent, its relative permittivity and its heat of vaporization. The surface tension and refractive index are found to be strongly correlated, with a coefficient of 0.77. Finally, there is a correlation between the relative permittivity and the dipole moment (0.65); this dependence has been used previously to relate these two properties.54 Overall, however, many of the solvent descriptors reveal weak correlations with each other.In terms of solute descriptors, the molecular van der Waals volume is found to have a very high degree of correlation (greater than 0.9) with polarizability and entropy and a correlation coefficient of 0.79 is found between entropy and polarizability, indicating that these three descriptors are correlated.
Interestingly, the Gibbs free energies of solvation correlate most strongly with solute properties. In decreasing order of strength, there is a negative correlation with polarizability, molecular van der Waals volume, entropy and, to a lesser extent, εH. Weak positive correlations are observed for εL and E. The solvent properties correlate only weakly with the Gibbs free energy of solvation, with the dipole moment and octanol–water partition coefficient showing the largest absolute correlation coefficients of about 0.3. The relative permittivity/Gibbs free energy of solvation pair has a correlation coefficient of only −0.15.
PLS model results
Using the 1421 points in the training set, the statistics of PLS models with up to six latent variables (LVs) are reported in Table 4. Beyond six latent variables, the changes in the determination coefficient (R2) and cross-validation coefficient (Q2) are not significant and all LVs from LV #7 onwards have eigenvalues less than one. The graph of captured variance for each variable (Fig. 1) also indicates that six latent variables are appropriate. According to the figure, LV #5 and LV #6 play a considerable role in explaining the variance in several descriptors, such as the critical temperature of the solvent and LUMO energy for the solute, and show proper variance per variable. Therefore, these two latent variables are included in the PLS model. We note that the variance of some solvent properties (specifically the critical volume and the molar volume) remains poorly characterised even when six latent variables are included.| LV # | Eigenvalue | R X 2 (%) | R Xc 2 (%) | R Y 2 (%) | R Yc (%) | Q 2 (%) | Q c 2 (%) |
|---|---|---|---|---|---|---|---|
| 1 | 2.61 | 13.17 | 13.17 | 76.34 | 76.34 | 75.98 | 75.98 |
| 2 | 1.44 | 10.22 | 23.39 | 8.08 | 84.43 | 8.03 | 84.01 |
| 3 | 1.51 | 10.15 | 33.54 | 3.77 | 88.19 | 3.97 | 87.97 |
| 4 | 1.50 | 10.74 | 44.28 | 1.56 | 89.76 | 1.56 | 89.53 |
| 5 | 2.12 | 14.99 | 59.27 | 0.56 | 90.32 | 0.72 | 90.26 |
| 6 | 1.36 | 7.84 | 67.11 | 0.43 | 90.75 | 0.40 | 90.66 |
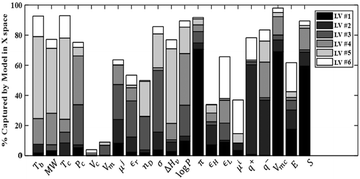 | ||
| Fig. 1 Percentage of the variance in the descriptors captured by each variable, for the first six latent variables. The reader is referred to Tables 2 and 3 for the definitions of the variables shown here. | ||
As can be seen in Table 4, the six selected components have high eigenvalues. The six latent variables selected explain 67.11% of the variance of the descriptors and 90.75% of the variance of the free energy of solvation. It should be noted that Qc2 is equal to 90.66%, which is considerably higher than the 50% recommended as a good predictivity parameter.74 The scores and loadings matrix for the PLS model are shown in Table S4 of ESI.† An Excel implementation of the model is provided as ESI.†
When applying this model to the 356 solute/solvent pairs in the test set, the determination coefficient between the experimental and predicted ΔGsij is found to be 88.10%. The results of the error analysis for the PLS model are presented in Table 5. As can be seen, the RMSEs across all data sets are of the order of 0.5 kcal mol−1. The AARE% for the test set is slightly less than that for the training set, and indicates that the PLS model can be used to predict the Gibbs free energy of solvation to within approximately 9–10%. The RMSE of 0.55 kcal mol−1 for the testing set is very encouraging.
| Whole data set | Training set | Testing set | |
|---|---|---|---|
| Number of data points | 1777 | 1421 | 356 |
| RMSE (kcal mol−1) | 0.52 | 0.52 | 0.55 |
| MUE (kcal mol−1) | 0.43 | 0.43 | 0.44 |
| AARE% | 10.0 | 10.18 | 9.33 |
The values of the Gibbs free energy of solvation predicted by the PLS model are compared with the experimental data in Fig. 2, which includes the training and test sets. The training and test sets can be seen to be distributed throughout the range of Gibbs free energy of solvation values and visual inspection indicates that the external testing of the model (prediction of the testing set) yields similar outcomes to the training set, as expected based on model statistics.
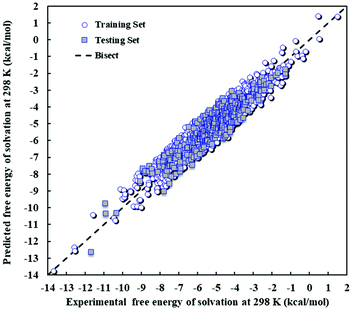 | ||
| Fig. 2 Scatter plot of predicted against experimental Gibbs free energy of solvation at 298 K and 1 atm for the PLS model. | ||
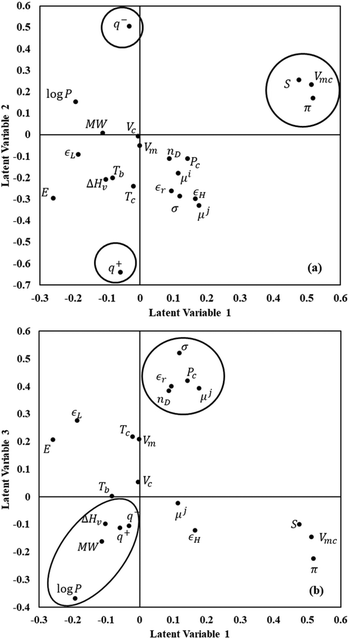
The contributions of the descriptors to the first three latent variables are shown in Fig. 3 using a loading plot with the most important variables highlighted with circles/ovals. Component 1 is dominated by solute variables that include the molecular van der Waals volume (Vmc), the polarizability (π), and entropy (S). These were found to be highly correlated in the initial analysis of the data set, and it is thus not surprising that they are found to contribute in similar ways. Component 2 is dominated by different solute descriptors, namely the electrostatic basicity (q−) and the electrostatic acidity (q+). Component 3 is dominated by several solvent descriptors such as molecular weight, octanol–water partition coefficient, and heat of vaporization, as well as surface tension (σ) and relative permittivity (εr).
The VIP plot presented in Fig. 4 for the PLS model reveals that the polarizability, molecular van der Waals volume, and entropy of the solute are most important in the model, in order of decreasing relevance. As far as solvent properties are concerned, the dipole moment, octanol–water partition coefficient and surface tension appear to carry the greatest weight. On the other hand, the heat of vaporization and molar volume of the solvent appear to be of limited importance in the model. While the VIP analysis is consistent with the findings of the correlation analysis presented at the beginning of the Results and discussion section, the lack of importance of the solvent heat of vaporization and molar volume is surprising given the frequent use, in LSERs such as the solvatochromic equation,83 of the Hildebrand solubility parameter or cohesive energy density, which depends on the heat of vaporization and, inversely, on the molar volume.
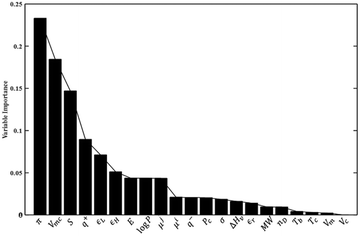 | ||
| Fig. 4 Variable importance in the projection (VIP) scores for the PLS model. The reader is referred to Tables 2 and 3 for the definition of the variables shown here. | ||
MLR model results
Following the development of the PLS model, the same training and testing sets were used to develop an MLR model, which involves fewer descriptors and can thus be simpler to use. As mentioned before, a genetic algorithm was used for feature selection, i.e., to identify a small set of descriptors. It was found that for more than five descriptors, the precision of the MLR model did not significantly improve and therefore the following model was selected:ΔGs,0ij = −0.4404 − 0.0446π + 10.9051εL − 8.1461q+ − 0.0216ΔHv + 0.3348![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) log log![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) P P | (11) |
The proposed model thus depends on three solute descriptors, polarizability (π), LUMO energy (εL), and electrostatic acidity (q+) and two solvent descriptors, the heat of vaporization (ΔHv) and the octanol–water partition coefficient (log![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) P).
P).
The statistics of this MLR model are presented in Table 6: the values of the determination coefficients (R2) for the training and testing sets are high, around 0.88, which shows a strong correlative capacity for the model. The R2 values for both sets are similar, and this is a positive attribute of the proposed model. In addition, the Radj2 values indicate an acceptable agreement between correlation and variation within the ΔGsij dataset. Further tests of the model's validity yield consistently positive results. Leave-one-out cross validation (QLoo2) along with the four RQK constraints reveals good internal robustness and predictive ability of the model. Considering that a large data set was used, and that the differences between QBoot2, QLoo2, QExt2 and R2 are small, it can be concluded that the model can be used to predict ΔGsij with good accuracy. In addition, based on several hundreds of y-scrambling runs, the intercept values of the y-scrambling technique were found to yield low values of a(R2) and a(Q2), of around 0.5, which provides further validation of the model. External validation and the large value of the F ratio also confirm that the MLR model is statistically sound. The MLR model has large value of F ratio.
| Whole data set | Training set | Testing set | |
|---|---|---|---|
| Number of data points | 1777 | 1421 | 356 |
| R 2 | 88.05 | 88.01 | 88.15 |
| R adj 2 | 88.04 | 88.01 | 88.12 |
| ΔQ | 0.000 | — | — |
| ΔK | 0.058 | — | — |
| R N | 0.001 | — | — |
| R P | 0.067 | — | — |
| Q Loo 2 | — | 87.99 | — |
| Q Boot 2 | — | 88.76 | — |
| Q Ext 2 | — | — | 96.29 |
| a(R2) | 0.517 | — | — |
| a(Q2) | 0.515 | — | — |
| F ratio | 2655 | — | — |
In order to compare the performance of the MLR and PLS models, the error analysis for the MLR model is presented in Table 7. The MUE values for all sets are very similar to each other, and to the values obtained with the PLS model, despite the much smaller set of descriptors used. The RMSE values obtained show a small deterioration (of 0.07 kcal mol−1) for the training set, relative to the PLS model but the same performance for the testing set. The spread of values is narrow and below 0.60 kcal mol−1, which suggests that the proposed model has both a good predictive ability (low value of RMSE) and a good generalization performance (similar values of RMSE across sets). Similar observations can be made based on the AARE% values. The correlation matrix for the descriptors in the MLR model is presented in Table 8.
| Whole data set | Training set | Testing set | |
|---|---|---|---|
| Number of data points | 1777 | 1421 | 356 |
| RMSE (kcal mol−1) | 0.58 | 0.59 | 0.55 |
| MUE (kcal mol−1) | 0.44 | 0.45 | 0.42 |
| AARE% | 10.32 | 11.50 | 9.02 |
| ΔHv (kJ mol−1) | log![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) P (−) P (−) |
π (Bohr3) | ε L (a.u.) | q + (−) | |
|---|---|---|---|---|---|
| ΔHv (kJ mol−1) | 1 | ||||
log![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) P (−) P (−) |
0.51 | 1 | |||
| π (Bohr3) | 0.05 | 0.10 | 1 | ||
| ε L (a.u.) | 0.03 | −0.04 | −0.23 | 1 | |
| q + (−) | −0.04 | −0.13 | −0.23 | 0.40 | 1 |
The descriptors of the MLR model are presented in Table 9 along with their standard error, t-test and Prob(t) values. A larger value of the t-test indicates the greater importance of the corresponding descriptor in the regression model. All Prob(t) values are found to be zero, as is desirable. The extensive suite of validation techniques applied to the model highlights that the proposed model is statistically valid and can be utilized to estimate ΔGsij for a wide range of solute i/solvent j pairs. The predicted values of Gibbs free energy of solvation are shown against experimental values in Fig. 5 for both the training and test sets. As can be seen in this figure, there is an appropriate distribution of errors for the training and test data. A visual comparison of Fig. 2 and 5 suggests that the maximum absolute deviation obtained with the MLR model is greater than that obtained with the PLS model, and this contributes to the slightly higher values of RMSE and AARE% in the MLR model.
| Descriptor | Standard error | t-test | Prob(t) |
|---|---|---|---|
| ΔHv (kJ mol−1) | 0.0010 | −18.23 | 0.0000 |
log![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) P (−) P (−) |
0.0081 | 40.25 | 0.0000 |
| π (Bohr3) | 0.0005 | −85.25 | 0.0000 |
| ε L (a.u.) | 0.3296 | 33.34 | 0.0000 |
| q + (−) | 0.1895 | −44.58 | 0.0000 |
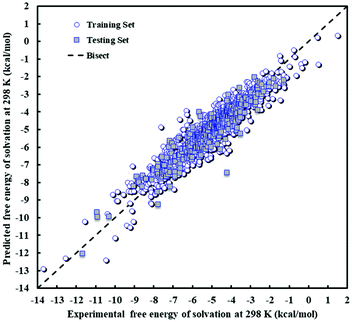 | ||
| Fig. 5 Scatter plot of predicted against experimental free energy of solvation at 298 K and 1 atm for the MLR model. | ||
The MLR model exhibits large errors for a small number of solute–solvent pairs. The solvent exhibiting the largest number of data points with an error greater than 1 kcal mol−1 is octanol, which is well-represented in both training and test sets. The largest error is found for p-hydroxybenzoic acid (ethylparaben)–octanol at 3.46 kcal mol−1, against an average error of 0.44 kcal mol−1. Other solutes or solvents with a large error do not follow any pattern. For instance, for butanone in mixed xylenes, an error of 3.20 kcal mol−1 is observed. For all other ketones in mixed xylenes, a mean unsigned error of 0.31 kcal mol−1 is observed. Of these data points, only butanone in mixed xylenes appears in the test set, indicating poor predictive capability in this instance. Such a deviation is not observed for other pairs containing mixed xylenes, regardless of whether the data are in the training or test set. For butanone, the only other large error is observed for a data point in the training set (butanone–tetrahydrothiophenedioxide), with an error of 2.09 kcal mol−1. This compares to an average error for butanone as a solute of 0.30 kcal mol−1 and for tetrahydrothiophenedioxide as a solvent of 0.28 kcal mol−1. Given the lack of systematic error, it is likely that the few large deviations observed are an inherent limitation of a model which contains very few parameters.
Comparison with other methods
Selected Gibbs free energy of solvation values obtained with the models proposed in our study are compared with other studies in the literature. As mentioned in the Introduction, there are no other QSPR models that can be applied to such a varied set of solute/solvent pairs. Thus, the most relevant model for comparison is the SM series of models developed at Minnesota, including the SMD model.11 The overall MUE of the SMD model for neutral solutes was reported11 to vary from 0.64 to 0.79 kcal mol−1, depending on the level of theory used for the electronic structure calculations, compared to the values of 0.43 and 0.44 kcal mol−1 reported here for the PLS and MLR models respectively. However, the SMD model was developed to be applicable to a broader range of solutes, including charged solutes, and the overall MUE values for SMD are based on a larger set of 2346 data points (compared to the 1777 data points used in the current study), which makes a thorough comparison difficult.For a more detailed comparison, we use the study of Zanith and Pliego20 who presented calculations for 77 Gibbs free energies of solvation of different solutes in methanol, DMSO, and acetonitrile. They used the SMD/X3LYP/6-31G(d) and SM8/B3LYP/6-31G(d) methods to predict the Gibbs free energies of solvation. Of the 77 data points, only 33 data points passed the outlier detection test when building the database used in the current study. All 33 points have been used in the training set to develop the MLR and PLS models, although we have found similar results when testing different training sets that did not include all 33 points. The results of these 33 data points are compared with the SMD and SM8 calculations presented by Zanith and Pliego20 in Table 10.
| Solute/solvent | Gibbs free energy of solvation at 298 K and 1 atm (kcal mol−1) | ||||
|---|---|---|---|---|---|
| EXP. | MLR | PLS | SMD/X3LYP/6-31G(d) | SM8/B3LYP/6-31G(d) | |
| p-Cresol/acetonitrile | −8.08 | −7.75 | −8.09 | −7.08 | −6.59 |
| m-Toluidine/acetonitrile | −8.04 | −7.46 | −7.77 | −7.16 | −7.39 |
| o-Cresol/acetonitrile | −7.92 | −7.69 | −7.95 | −6.95 | −6.55 |
| m-Cresol/acetonitrile | −7.90 | −7.73 | −8.01 | −7.31 | −6.69 |
| o-Toluidine/acetonitrile | −7.85 | −7.42 | −7.69 | −7.11 | −7.20 |
| p-Cresol/methanol | −7.84 | −7.20 | −8.78 | −6.13 | −7.48 |
| m-Toluidine/methanol | −7.75 | −7.68 | −8.46 | −6.35 | −6.97 |
| o-Cresol/methanol | −7.72 | −8.46 | −8.64 | −5.61 | −7.16 |
| m-Cresol/methanol | −7.68 | −8.50 | −8.70 | −6.10 | −7.58 |
| o-Toluidine/methanol | −7.54 | −8.19 | −8.38 | −6.26 | −6.76 |
| Gama-picoline/acetonitrile | −5.75 | −5.78 | −5.85 | −5.81 | −6.62 |
| 1-Propanol/DMSO | −5.68 | −4.88 | −5.03 | −3.45 | −4.05 |
| Gama-picoline/methanol | −5.60 | −6.55 | −6.54 | −5.03 | −6.28 |
| o-Xylene/acetonitrile | −5.43 | −6.37 | −6.34 | −4.89 | −5.09 |
| Ethylbenzene/acetonitrile | −5.36 | −6.22 | −6.17 | −4.94 | −5.03 |
| 1-Butanol/methanol | −5.31 | −5.50 | −6.09 | −6.03 | −6.45 |
| m-Xylene/acetonitrile | −5.28 | −5.20 | −6.49 | −4.76 | −5.11 |
| p-Xylene/acetonitrile | −5.27 | −5.44 | −6.51 | −4.96 | −5.08 |
| Butanol/acetonitrile | −5.20 | −5.30 | −5.40 | −4.68 | −4.65 |
| 2-Propanol/DMSO | −5.14 | −4.88 | −5.01 | −4.52 | −5.33 |
| 1-Propanol/methanol | −4.75 | −4.89 | −5.42 | −5.39 | −5.96 |
| 1-Propanol/acetonitrile | −4.65 | −4.49 | −4.73 | −4.38 | −4.15 |
| 2-Propanol/methanol | −4.53 | −5.21 | −5.40 | −5.21 | −5.39 |
| Ethanol/methanol | −4.41 | −4.62 | −4.76 | −5.04 | −5.57 |
| 2-Propanol/acetonitrile | −4.39 | −4.44 | −4.71 | −3.98 | −3.76 |
| Benzene/acetonitrile | −4.25 | −3.95 | −4.62 | −4.66 | −4.47 |
| Dichloromethane/DMSO | −4.10 | −4.10 | −4.98 | −4.11 | −2.49 |
| Benzene/DMSO | −3.96 | −5.23 | −4.93 | −2.92 | −3.91 |
| Acetone/DMSO | −3.76 | −4.35 | −4.61 | −4.29 | −5.11 |
| Tetrahydrofuran/DMSO | −3.64 | −3.97 | −3.67 | −3.00 | −4.36 |
| Dimethylether/methanol | −2.31 | −2.87 | −3.01 | −1.80 | −2.28 |
| n-Pentane/acetonitrile | −2.08 | −3.64 | −3.43 | −2.17 | −2.38 |
| 1,1-Difluorethane/methanol | −1.90 | −2.58 | −2.45 | −2.60 | −3.28 |
| RMSE (kcal mol−1) | 0.59 | 0.71 | 1.11 | 1.08 | |
| MUE (kcal mol−1) | 0.46 | 0.59 | 0.83 | 0.79 | |
| MSE (kcal mol−1) | −0.22 | −0.52 | 0.61 | 0.27 | |
| AARE% | 10.77 | 13.13 | 15.36 | 16.21 | |
As can be seen in Table 10, the MLR method presented in this work yields the best results for these 33 data points. This model has the lowest RMSE, MUE, MSE and AARE% values. In addition, the PLS model shows better performance than the SMD/X3LYP/6-31G(d) and SM8/B3LYP/6-31G(d) models. While the MLR model has poorer statistics than the PLS model overall (cf.Tables 4 and 6), it performs better for this small set of compounds. The MLR model may thus be preferred for certain applications, especially as it requires fewer descriptors. One should also note that methanol was not included as a solvent in the training set used to develop the SMD and SM8 models by Marenich et al.,11 which explains the larger errors found for those systems with the SMD and SM8 models. Excluding methanol, the RMSE obtained for the MLR, PLS, SMD, and SM8 models are 0.47, 0.53, 0.60, 0.69 kcal mol−1, respectively. Finally, we note that this comparison does not explore the full capabilities of the SMD models in terms of levels of theory or range of solutes.
To date and to the best of our knowledge no similar QSPR based study for such a wide range of solutes in solvents has been reported, and a comparison between the current study and the most recent previous QSPR works is presented in Table 11. In many, but not all, cases, the use of a different model per solute or a different model per solvent leads to slightly improved performance. However, our more comprehensive models display comparable performance to that of the more specific models, with a significant increase in applicability.
| Studies | R 2 or R | Error | Method | Dataset size |
|---|---|---|---|---|
| Katritzky et al.53 | R all 2 = 0.8370 to 0.998 for 69 equations | squared standard errors: 0.1 to 0.02 kcal mol−1 for 69 equations | MLR | 500 solutes in 69 solvents |
| Katritzky et al.62 | R all 2 = 0.604 to 0.996 for 80 equations | squared standard errors: 0.368 to 0.0006 kcal mol−1 for 80 equations | MLR | 80 solutes in 15 to 82 solvents |
| Michielan et al.59 | R train = 0.9900 | RMSE = 0.069 kcal mol−1 | RSA | 271 solutes in water as solvent |
| R test = 0.9200 | ||||
| Delgado and Jaña61 | R all 2 = 0.9300 | Standard deviation = 0.57 kcal mol−1 | MLR | 147 solutes in octanol as solvent |
| Bernazzani et al.60 | R train = 0.9990 | MUE = 0.24 kcal mol−1 | RNN | 339 solutes in water |
| R test = 0.9820 | Standard deviation = 0.43 kcal mol−1 | |||
| Current study (MLR) | R train 2 = 0.8801 | RMSE = 0.58 kcal mol−1 | GA-MLR | 1777 solute/solvent pairs |
| R test 2 = 0.8815 | MUE = 0.44 kcal mol−1 | |||
| Current study (PLS) | R train 2 = 0.9075 | RMSE = 0.52 kcal mol−1 | PLS | 1777 solute/solvent pairs |
| R test 2 = 0.8810 | MUE = 0.43 kcal mol−1 |
Conclusions
We have presented MLR and PLS models for the prediction of the Gibbs free energy of solvation of a wide range of neutral organic solutes in organic solvents. The dataset used to develop the models contains 1777 free energies of solvation, derived from a set of 295 neutral organic solutes and 210 organic solvents. The models are hybrid in nature, combining QM descriptors for the solutes with bulk thermodynamic properties for the solvents. This differs from standard practice in QSPR model development, in which only QM descriptors are typically used and either the solvent or the solute is held constant. The experimental descriptors selected in our work provide a good description of the bulk properties of the solvent, while the QM descriptors ensure the applicability of the model to a broad range of compounds including short-lived intermediates and transition states. A thorough statistical analysis of both models has been carried out, including external validation; MUEs over the entire dataset of 0.44 kcal mol−1 and 0.43 kcal mol−1 were obtained for the MLR and PLS models, respectively.Detailed comparisons with other models are difficult to carry out given the different training sets used but a comparison of MUEs or RMSEs across the training and testing sets of different models provides a useful indicator. The average performance obtained with the proposed models is comparable to that obtained with models developed for specific solvents or solutes. The proposed models also compare favourably to the average performance of the SMD model, although we note that the SMD model is broader in scope since it extends to charged solutes, which have not been considered in the present study. The two models proposed display similar performance statistics. The PLS model appears to be slightly better overall, but relies on more descriptors than the MLR model, making it more difficult to apply for solvents which have been less well studied experimentally.
Due to the interpolative nature of the proposed models, they should only be applied to the calculation of the Gibbs free energy of solvation of neutral organic solutes in organic solvents (i.e., they should not be applied to charged solutes or aqueous solutions). Nevertheless, the applicability of both models could be extended to novel solvents by predicting the relevant solvent properties using group contribution methods40,42,54,97,98 or other structure–property relations, rather than relying on experimental solvent properties. There is also scope to increase the accuracy of the models by developing nonlinear versions of the PLS and MLR models. In both models, it is assumed that solvent and solute have an additive effect on the overall Gibbs free energy of solvation. This is in effect a first-order representation of solvation. This approximation may be lifted by incorporating second-order terms that depend on both solute and solvent in the models – for instance, the product or ratio of a solvent descriptor and a solute descriptor – enabling a better representation of the available data.
Data statement
Data underlying this article and not available in the references cited are available in ESI.†Nomenclature
| AAE | Average absolute error |
| ARE | Absolute relative error |
| AARE% | Average absolute relative error |
| ANN | Artificial neural network |
| GCM | Group contribution method |
| MLR | Multivariate linear regression |
| MSE | Mean signed error |
| MUE | Mean unsigned error |
| PLS | Partial least square or projection to latent structures |
| GA | Genetic algorithm |
| QSPR | Quantitative structure–property relationship |
| Q 2 | Cross validation coefficient |
| Q Loo 2 | Leave-one-out cross validation coefficient |
| Q Boot 2 | Bootstrapping validation coefficient |
| Q Ext 2 | External validation coefficient |
| R 2 | Squared correlation coefficient |
| RMSE | Root mean square error |
| VIF | Variance inflation factors |
| VIP | Variables importance in the projection |
| ΔGsij | Free energy of solvation of solute i in solvent j |
Conflicts of interest
There are no conflicts to declare.Acknowledgements
Financial support from Eli Lilly via the Lilly Research Award Program (LRAP) and from the UK Engineering and Physical Sciences Research Council (EPSRC) of the UK via a Leadership Fellowship (EP/J003840/1) is gratefully acknowledged. Access to computational resources and support from the High Performance Computing Cluster at Imperial College London are gratefully acknowledged. We wish to acknowledge the use of the EPSRC funded National Chemical Database Service hosted by the Royal Society of Chemistry.Notes and references
- A. Jalan, R. W. Ashcraft, R. H. West and W. H. Green, Annu. Rep. Prog. Chem., Sect. A: Inorg. Chem., 2010, 106, 211–258 RSC.
- U. Westhaus, T. Dröge and R. Sass, Fluid Phase Equilib., 1999, 158–160, 429–435 CrossRef CAS.
- A. V. Marenich, C. P. Kelly, J. D. Thompson, G. D. Hawkins, C. C. Chambers, D. J. Giesen, P. Winget, C. J. Cramer and D. G. Truhlar, Minnesota Solvation Database – Version 2012, University of Minnesota, Minneapolis, 2012, https://comp.chem.umn.edu/mnsol/ Search PubMed.
- G. Duarte Ramos Matos, D. Y. Kyu, H. H. Loeffler, J. D. Chodera, M. R. Shirts and D. L. Mobley, J. Chem. Eng. Data, 2017, 62, 1559–1569 CrossRef PubMed.
- Dortmund Data Bank, 2018.
- A. Klamt, Wiley Interdiscip. Rev.: Comput. Mol. Sci., 2011, 1, 699–709 CAS.
- S.-T. Lin and C.-M. Hsieh, J. Chem. Phys., 2006, 125, 124103 CrossRef PubMed.
- A. Nicholls, D. L. Mobley, J. P. Guthrie, J. D. Chodera, C. I. Bayly, M. D. Cooper and V. S. Pande, J. Med. Chem., 2008, 51, 769–779 CrossRef CAS PubMed.
- R. Fingerhut, W.-L. Chen, A. Schedemann, W. Cordes, J. Rarey, C.-M. Hsieh, J. Vrabec and S.-T. Lin, Ind. Eng. Chem. Res., 2017, 56, 9868–9884 CrossRef CAS.
- C. J. Cramer, Essentials of computational chemistry: theories and models, John Wiley & Sons, 2004 Search PubMed.
- A. V. Marenich, C. J. Cramer and D. G. Truhlar, J. Phys. Chem. B, 2009, 113, 6378–6396 CrossRef CAS PubMed.
- P. Hutacharoen, S. Dufal, V. Papaioannou, R. M. Shanker, C. S. Adjiman, G. Jackson and A. Galindo, Ind. Eng. Chem. Res., 2017, 56, 10856–10876 CrossRef CAS.
- J. Tomasi, B. Mennucci and E. Cancès, J. Mol. Struct. THEOCHEM, 1999, 464, 211–226 CrossRef CAS.
- C. J. Cramer and D. G. Truhlar, J. Am. Chem. Soc., 1991, 113, 8305–8311 CrossRef CAS.
- C. J. Cramer and D. G. Truhlar, Trends and Perspectives in Modern Computational Science, 2006, vol. 6, pp. 112–140 Search PubMed.
- C. J. Cramer and D. G. Truhlar, Acc. Chem. Res., 2008, 41, 760–768 CrossRef CAS PubMed.
- A. V. Marenich, C. J. Cramer and D. G. Truhlar, J. Chem. Theory Comput., 2013, 9, 609–620 CrossRef CAS PubMed.
- A. Klamt, V. Jonas, T. Bürger and J. C. W. Lohrenz, J. Phys. Chem. A, 1998, 102, 5074–5085 CrossRef CAS.
- S.-T. Lin and S. I. Sandler, Ind. Eng. Chem. Res., 2002, 41, 899–913 CrossRef CAS.
- C. C. Zanith and J. R. Pliego, J. Comput.-Aided Mol. Des., 2015, 29, 217–224 CrossRef CAS PubMed.
- A. Klamt and M. Diedenhofen, J. Comput.-Aided Mol. Des., 2010, 24, 357–360 CrossRef CAS PubMed.
- J. Reinisch, A. Klamt and M. Diedenhofen, J. Comput.-Aided Mol. Des., 2012, 26, 669–673 CrossRef CAS PubMed.
- J. Reinisch and A. Klamt, J. Comput.-Aided Mol. Des., 2014, 28, 169–173 CrossRef CAS PubMed.
- A. Klamt, B. Mennucci, J. Tomasi, V. Barone, C. Curutchet, M. Orozco and F. J. Luque, Acc. Chem. Res., 2009, 42, 489–492 CrossRef CAS PubMed.
- A. Klamt and M. Diedenhofen, J. Phys. Chem. A, 2015, 119, 5439–5445 CrossRef CAS PubMed.
- C.-M. Hsieh, S. I. Sandler and S.-T. Lin, Fluid Phase Equilib., 2010, 297, 90–97 CrossRef CAS.
- C.-M. Hsieh, S.-T. Lin and J. Vrabec, Fluid Phase Equilib., 2014, 367, 109–116 CrossRef CAS.
- F. Javier Luque, C. Curutchet, J. Munoz-Muriedas, A. Bidon-Chanal, I. Soteras, A. Morreale, J. L. Gelpi and M. Orozco, Phys. Chem. Chem. Phys., 2003, 5, 3827–3836 RSC.
- C. W. Kehoe, C. J. Fennell and K. A. Dill, J. Comput.-Aided Mol. Des., 2012, 26, 563–568 CrossRef CAS PubMed.
- R. H. Wood, E. M. Yezdimer, S. Sakane, J. A. Barriocanal and D. J. Doren, J. Chem. Phys., 1999, 110, 1329–1337 CrossRef CAS.
- G. König, F. C. Pickard, Y. Mei and B. R. Brooks, J. Comput.-Aided Mol. Des., 2014, 28, 245–257 CrossRef PubMed.
- G. König, Y. Mei, F. C. Pickard, A. C. Simmonett, B. T. Miller, J. M. Herbert, H. L. Woodcock, B. R. Brooks and Y. Shao, J. Chem. Theory Comput., 2016, 12, 332–344 CrossRef PubMed.
- N. A. McDonald, H. A. Carlson and W. L. Jorgensen, J. Phys. Org. Chem., 1997, 10, 563–576 CrossRef CAS.
- E. M. Duffy and W. L. Jorgensen, J. Am. Chem. Soc., 2000, 122, 2878–2888 CrossRef CAS.
- P. F. B. Gonçalves and H. Stassen, J. Comput. Chem., 2003, 24, 1758–1765 CrossRef PubMed.
- D. L. Mobley, C. I. Bayly, M. D. Cooper, M. R. Shirts and K. A. Dill, J. Chem. Theory Comput., 2009, 5, 350–358 CrossRef CAS PubMed.
- D. Shivakumar, J. Williams, Y. Wu, W. Damm, J. Shelley and W. Sherman, J. Chem. Theory Comput., 2010, 6, 1509–1519 CrossRef CAS PubMed.
- D. L. Mobley and J. P. Guthrie, J. Comput.-Aided Mol. Des., 2014, 28, 711–720 CrossRef CAS PubMed.
- M. R. Shirts and J. D. Chodera, J. Chem. Phys., 2008, 129, 124105 CrossRef PubMed.
- V. Papaioannou, T. Lafitte, C. Avendaño, C. S. Adjiman, G. Jackson, E. A. Müller and A. Galindo, J. Chem. Phys., 2014, 140, 054107 CrossRef PubMed.
- S. Dufal, V. Papaioannou, M. Sadeqzadeh, T. Pogiatzis, A. Chremos, C. S. Adjiman, G. Jackson and A. Galindo, J. Chem. Eng. Data, 2014, 59, 3272–3288 CrossRef CAS.
- A. Fredenslund, R. L. Jones and J. M. Prausnitz, AIChE J., 1975, 21, 1086–1099 CrossRef CAS.
- J. Gmehling, J. Li and M. Schiller, Ind. Eng. Chem. Res., 1993, 32, 178–193 CrossRef CAS.
- E. C. Voutsas and D. P. Tassios, Ind. Eng. Chem. Res., 1996, 35, 1438–1445 CrossRef CAS.
- H. Choi, H. Kang and H. Park, J. Cheminf., 2013, 5, 8 CAS.
- G. R. Famini and L. Y. Wilson, J. Phys. Org. Chem., 1999, 12, 645–653 CrossRef CAS.
- T. N. G. Borhani, M. Bagheri and Z. A. Manan, Fluid Phase Equilib., 2013, 360, 423–434 CrossRef CAS.
- T. N. G. Borhani, M. Saniedanesh, M. Bagheri and J. S. Lim, Water Res., 2016, 98, 344–353 CrossRef CAS PubMed.
- A. H. Lowrey, C. J. Cramer, J. J. Urban and G. R. Famini, Comput. Chem., 1995, 19, 209–215 CrossRef CAS.
- C. J. Cramer, G. R. Famini and A. H. Lowrey, Acc. Chem. Res., 1993, 26, 599–605 CrossRef CAS.
- M. Karelson, V. S. Lobanov and A. R. Katritzky, Chem. Rev., 1996, 96, 1027–1044 CrossRef CAS PubMed.
- A. R. Katritzky, M. Kuanar, S. Slavov, C. D. Hall, M. Karelson, I. Kahn and D. A. Dobchev, Chem. Rev., 2010, 110, 5714–5789 CrossRef CAS PubMed.
- A. R. Katritzky, A. A. Oliferenko, P. V. Oliferenko, R. Petrukhin, D. B. Tatham, U. Maran, A. Lomaka and W. E. Acree, J. Chem. Inf. Comput. Sci., 2003, 43, 1794–1805 CrossRef CAS PubMed.
- T. J. Sheldon, C. S. Adjiman and J. L. Cordiner, Fluid Phase Equilib., 2005, 231, 27–37 CrossRef CAS.
- M. Folić, C. S. Adjiman and E. N. Pistikopoulos, AIChE J., 2007, 53, 1240–1256 CrossRef.
- M. Dehmer, K. Varmuza, D. Bonchev and F. Emmert-Streib, Statistical Modelling of Molecular Descriptors in QSAR/QSPR, Wiley, 2012 Search PubMed.
- K. Roy, S. Kar and R. N. Das, A Primer on QSAR/QSPR Modeling: Fundamental Concepts, Springer International Publishing, 2015 Search PubMed.
- T. N. G. Borhani, A. Afzali and M. Bagheri, Process Saf. Environ. Prot., 2016, 103(pt A), 115–125 CrossRef CAS.
- L. Michielan, M. Bacilieri, C. Kaseda and S. Moro, Bioorg. Med. Chem., 2008, 16, 5733–5742 CrossRef CAS PubMed.
- L. Bernazzani, C. Duce, A. Micheli, V. Mollica and M. R. Tiné, J. Chem. Eng. Data, 2010, 55, 5425–5428 CrossRef CAS.
- E. J. Delgado and G. A. Jaña, Int. J. Mol. Sci., 2009, 10, 1031–1044 CrossRef CAS PubMed.
- A. R. Katritzky, A. A. Oliferenko, P. V. Oliferenko, R. Petrukhin, D. B. Tatham, U. Maran, A. Lomaka and W. E. Acree, J. Chem. Inf. Comput. Sci., 2003, 43, 1806–1814 CrossRef CAS PubMed.
- Y. Marcus, The properties of solvents, Wiley, 1998 Search PubMed.
- R. W. Taft, N. J. Pienta, M. J. Kamlet and E. M. Arnett, J. Org. Chem., 1981, 46, 661–667 CrossRef CAS.
- B. E. Poling, J. M. Prausnitz and J. P. O'Connell, The Properties of Gases and Liquids, McGraw-Hill Education, 2000 Search PubMed.
- E. Moine, R. Privat, B. Sirjean and J.-N. Jaubert, J. Phys. Chem. Ref. Data, 2017, 46, 033102 CrossRef.
- R. Rowley, W. Wilding, J. Oscarson, Y. Yang, N. Zundel, T. Daubert and R. Danner, Design Institute for Physical Properties, AIChE, New York, 2003 Search PubMed.
- S. Kim, P. A. Thiessen, E. E. Bolton, J. Chen, G. Fu, A. Gindulyte, L. Han, J. He, S. He, B. A. Shoemaker, J. Wang, B. Yu, J. Zhang and S. H. Bryant, Nucleic Acids Res., 2016, 44, D1202–D1213 CrossRef CAS PubMed.
- P. J. Linstrom and W. G. Mallard, NIST Chemistry WebBook, NIST Standard Reference Database Number 69, National Institute of Standards and Technology, Gaithersburg MD, 20899, https://doi.org/10.18434/T4D303 (retrieved May 3, 2019) Search PubMed.
- P. Winget, D. M. Dolney, D. J. Giesen, C. J. Cramer and D. G. Truhlar, Department of Chemistry and Supercomputer Institute, University of Minnesota, Minneapolis, MN, 1999, p. 55455 Search PubMed.
- W. M. Haynes, CRC Handbook of Chemistry and Physics, CRC Press, 96th edn, 2015 Search PubMed.
- G. Wypych, Knovel Solvents – A Properties Database, ChemTec Publishing, 2012 Search PubMed.
- C. L. Yaws, Yaws' Handbook of Thermodynamic and Physical Properties of Chemical Compounds, Knovel, 2003 Search PubMed.
- R. Todeschini and V. Consonni, Molecular descriptors for chemoinformatics, Wiley-VCH, 2009 Search PubMed.
- S. Riahi, M. R. Ganjali, P. Norouzi and F. Jafari, Sens. Actuators, B, 2008, 132, 13–19 CrossRef CAS.
- S. Van Damme and P. Bultinck, J. Mol. Struct. THEOCHEM, 2010, 943, 83–89 CrossRef CAS.
- P. P. Singh, H. K. Srivastava and F. A. Pasha, Bioorg. Med. Chem., 2004, 12, 171–177 CrossRef CAS PubMed.
- E. Eroğlu, H. Türkmen, S. Güler, S. Palaz and O. Oltulu, Int. J. Mol. Sci., 2007, 8, 145 CrossRef.
- A. D. Becke, Phys. Rev. A: At., Mol., Opt. Phys., 1988, 38, 3098 CrossRef CAS.
- P. J. Stephens, F. J. Devlin, C. F. Chabalowski and M. J. Frisch, J. Phys. Chem., 1994, 98, 11623–11627 CrossRef CAS.
- X.-L. Zeng, H.-J. Wang and Y. Wang, Chemosphere, 2012, 86, 619–625 CrossRef CAS PubMed.
- L. Y. Wilson and G. R. Famini, J. Med. Chem., 1991, 34, 1668–1674 CrossRef CAS PubMed.
- M. J. Kamlet, J. L. M. Abboud, M. H. Abraham and R. W. Taft, J. Org. Chem., 1983, 48, 2877–2887 CrossRef CAS.
- R. W. Taft, M. H. Abraham, G. R. Famini, R. M. Doherty, J.-L. M. Abboud and M. J. Kamlet, J. Pharm. Sci., 1985, 74, 807–814 CrossRef CAS PubMed.
- M. H. Abraham, G. S. Whiting, R. Fuchs and E. J. Chambers, J. Chem. Soc., Perkin Trans. 2, 1990, 291–300 RSC.
- A. J. Hopfinger, J. Am. Chem. Soc., 1980, 102, 7196–7206 CrossRef CAS.
- H. A. Kurtz, J. J. Stewart and K. M. Dieter, J. Comput. Chem., 1990, 11, 82–87 CrossRef CAS.
- M. H. Abraham, A. Ibrahim and A. M. Zissimos, J. Chromatogr. A, 2004, 1037, 29–47 CrossRef CAS PubMed.
- M. J. Frisch, G. W. Trucks, H. B. Schlegel, G. E. Scuseria, M. A. Robb, J. R. Cheeseman, G. Scalmani, V. Barone, B. Mennucci, G. A. Petersson, H. Nakatsuji, M. L. Caricato, X. Li, H. P. Hratchian, A. F. Izmaylov, J. Bloino, G. Zheng, J. L. Sonnenberg, M. Hada, M. Ehara, K. Toyota, R. Fukuda, J. Hasegawa, M. Ishida, T. Nakajima, Y. Honda, O. Kitao, H. Nakai, T. Vreven, J. A. Montgomery, Jr., J. E. Peralta, F. Ogliaro, M. Bearpark, J. J. Heyd, E. Brothers, K. N. Kudin, V. N. Staroverov, R. Kobayashi, J. Normand, K. Raghavachari, A. Rendell, J. C. Burant, S. S. Iyengar, J. Tomasi, M. Cossi, N. Rega, J. M. Millam, M. Klene, J. E. Knox, J. B. Cross, V. Bakken, C. Adamo, J. Jaramillo, R. Gomperts, R. E. Stratmann, O. Yazyev, A. J. Austin, R. Cammi, C. Pomelli, J. W. Ochterski, R. L. Martin, K. Morokuma, V. G. Zakrzewski, G. A. Voth, P. Salvador, J. J. Dannenberg, S. Dapprich, A. D. Daniels, Ö. Farkas, J. B. Foresman, J. V. Ortiz, J. Cioslowski and D. J. Fox, Wallingford, CT, 2009.
- E. Buncel and R. A. Stairs, Solvent Effects in Chemistry, John Wiley & Sons, Inc., 2015 Search PubMed.
- H. Wold, in Multivariate Analysis-III, ed. P. R. Krishnaiah, Academic Press, 1973, pp. 383–407 Search PubMed.
- M. Bagheri, T. N. G. Borhani and G. Zahedi, Energy Convers. Manage., 2012, 58, 185–196 CrossRef CAS.
- B. Chen, T. Zhang, T. Bond and Y. Gan, J. Hazard. Mater., 2015, 299, 260–279 CrossRef CAS PubMed.
- M. Farrés, S. Platikanov, S. Tsakovski and R. Tauler, J. Chemom., 2015, 29, 528–536 CrossRef.
- P. Gramatica, QSAR Comb. Sci., 2007, 26, 694–701 CrossRef CAS.
- A. Golbraikh and A. Tropsha, J. Mol. Graphics Modell., 2002, 20, 269–276 CrossRef CAS PubMed.
- L. Constantinou and R. Gani, AIChE J., 1994, 40, 1697–1710 CrossRef CAS.
- J. Marrero and R. Gani, Fluid Phase Equilib., 2001, 183–184, 183–208 CrossRef CAS.
Footnote |
| † Electronic supplementary information (ESI) available. See DOI: 10.1039/c8cp07562j |
| This journal is © the Owner Societies 2019 |