Transmembrane domain dimerization induces cholesterol rafts in curved lipid bilayers

Abstract

Are the dimerization of transmembrane (TM) domains and the reorganization of the lipid bilayer two independent events? Does one event induce or interfere with the other? In this work, we have performed well-tempered metadynamics simulations to calculate the free energy cost to bend a model ternary lipid bilayer in the presence of a TM peptide in its dimer form. We have compared this result with the free energy cost needed to bend a bilayer-only system. Additionally, we have calculated the free energy cost to form a model TM peptide dimer quantitatively describing how lipids reorganize themselves in response to the increase of the membrane curvature and to the lipid–peptide interactions. Our results indicate that the formation of the peptide dimer inside the bilayer increases the cost of the membrane bending due to the spontaneous clustering of cholesterol molecules.

---

Lipid bilayers are a key element in most cellular events, their curvature being a ubiquitous biological feature. In addition, many cellular functions and structures require membrane deformation and/or lipid reorganization. For example, bending of the plasma membrane occurs in tubulation, cellular fission and fusion.¹ In particular, the overall shape of the bilayer and its lipid distribution are conditioned by the membrane interactions with proteins, leading to an intricate molecular mechanism crucial for many biological functions. Although our knowledge of protein association mechanisms in solutions (3D) is rapidly increasing, there is a clear need for further research to understand how these processes are mediated through cell membranes (2D).

The motif glycine-XXX-glycine (X is any amino acid) has been intensively studied and is considered a primary factor for successful association of many single-pass transmembrane (TM) dimer proteins² (i.e., those that span the membrane bilayer with a single TM helix). A significant example is the onion-like structure of the mitochondrial cristae where the dimerization of the ATP20 subunit in the F1–F0 ATPase is diminished by the mutation of its G-XXX-G motif.^3–5 Despite its common occurrence (this motif is present in more than 2300 TM proteins) the fundamental physical rules that determine the strength of its dimerization are yet not well understood.

It was postulated that the presence of peptides inside the membrane could influence its shape and that the shape of the membrane itself could modify the dimerization pathway of intrinsic membrane proteins. By measuring membrane fluctuations in giant unilamellar vesicles Usery and collaborators demonstrated that TM peptides increased the rigidity of membranes containing cholesterol.¹ Besides, they highlight the counterintuitive observation that less energy is needed to bend bilayers with “nonraft” low cholesterol content.

The study of lipids’, cholesterol's and TM peptides’ energetic effects on the bending of the bilayer has been difficult due to the lack of a closed form collective variable, essential for energy calculations using standard methods such as umbrella sampling^6,7 or metadynamics.⁸ The recent discovery of an effective formulation that captures the key characteristics of the membrane bending process has opened the possibility to understand phenomena that initially appeared to be contrary to common sense.⁹

In this study, we have used a model tripartite membrane with cholesterol (DPPC : DOPC : CHOL at concentrations 0.58 : 0.12 : 0.3) and the C-terminal of the TM protein subunit g. This is a supernumerary subunit loosely bound to the mitochondrial ATP synthase, not present in the monomeric form of the yeast enzyme and not involved in ATP synthesis.³ The peptides have a hydrophobic core containing the G-XXX-G motif and charged residues at the ends that prefer the aqueous membrane interface.

We have studied the dimerization process of the subunit g C-terminal TM domain inside a lipid bilayer, identifying the optimal helix–helix distance and angle. With our in-house collective variable (Ψ) that induces curvature in the bilayer,⁹ we quantitatively show that the free energy cost to bend a three component bilayer is increased by the presence of the subunit g TM dimer domain. Moreover, we report that the TM dimer reshapes local cholesterol concentrations as the membrane bends inducing the formation of a cholesterol raft domain. We hypothesize that the dynamic connection of the bending/dimerization mechanisms is a fundamental attribute during the collective reorganization.

1 Subunit g

We have studied the intermembrane space that includes the C-terminal part of subunit g, which was constructed geometrically following an α-helix structure at atomic resolution and then converted to MARTINI¹⁰ coarse-grained (see Fig. 1). The 26 amino acid sequence used here corresponds to Homo sapiens (H.s.) (NP_006467): LVATEVLMWFYVGEIIGKRGIIGYDV, as reported by Bustos and Velours.³

Fig. 1 Geometric construction of one α-helix of subunit g in the atomistic (left) and the coarse-grained (right) representation.

The C-terminal domain includes the well-known conserved putative G-XXX-G motif (G101–G105 numbers correspond to the complete yeast protein), defined by two glycine residues separated by any three amino acids along the helix structure. This G-XXX-G pattern has shown to function as a scaffold during TM helix–helix association¹¹ and G-XXX-G-mediated interactions have been suggested to be crucial in the glycophorin A transmittance (GpA-TM) segment for structural and functional purposes.¹² Moreover, among the large number of organisms where subunit g has been identified (see Table 1) the number of fully conserved amino acids is low and they are all located in the C-terminal region. Between these amino acids are the two glycines of the G-XXX-G motif (G101 and G105 highlighted in bold in Table 1 together with the other conserved residue Tyr112 which marks the end of the intermembrane space).

Table 1 Subunit g in different organisms and residue conservation

Species	UniProt	Sequence G101-Y112
Bostaurus (B.t.)	AAB31108	⋯GEIMGKRGIIGY⋯
Homo sapiens (H.s.)	NP_006467	⋯GEIIGKRGIIGY⋯
Mus musculus (M.m.)	NP_038823	⋯GEIIGKRGIVGY⋯
Mus musculus (M.m.2)	BAB25507	⋯GEIIGKRGIVGY⋯
Drosophila melanogaster (D.m.)	AAF53041	⋯GECIGKRHIVGY⋯
Drosophila melanogaster (D.m.2)	AAF52549	⋯GEVIGRRHLVGY⋯
Caenorhabditis elegans (C.e.)	NP_509152	⋯GEMIGRRYIFGY⋯
Caenorhabditis elegans (C.e.2)	NP_492352	⋯GEMIGRRYIFGY⋯
Candida glabrata (C.a.)	XP_448330	⋯GEIIGRRKFIGY⋯
Kluyveromyces lactis (K.l.)	XP_452979	⋯GEIIGRRKVVGY⋯
Debaryomyces hansenii (D.h.)	XP_460026	⋯GEIIGRRSVFGY⋯
Neurospora crassa (N.c.)	XP_324824	⋯GEMIGRMKLIGY⋯
Saccharomyces pombe (S.p.)	NP_593034	⋯GQMVGRRKITPY⋯
Saccharomyces cerevisiae (S.c.)	NP_015345	⋯GEIIGRRKLVGY⋯

---

2 Bilayer bending

To calculate the free energy, we have used our in-house collective variable to induce bending in lipid bilayers,⁹ defined as Ψ (see eqn (1)). Conceptually, Ψ is a dimensionless reaction coordinate that controls a normalized density at the geometric center of the bilayer.

In eqn (1), the sum ranges over the centers of mass of all lipid molecules (N = 1024). Variables d_x, d_y and d_z are the components of the 3D distance between the center of mass of each lipid molecule and the center of mass of the bilayer. N₀ is the average equilibrium value of the summation in the numerator, obtained from an unbiased simulation of an intact membrane (N₀ = 991.771). We have used previously this collective variable to study the free energy cost needed to bend a lipid bilayer in the presence of a Bin/Amphiphysin/Rvs (BAR) domain adsorbed on the surface.⁹ The case in this work is rather different as the subunit g C-terminal domain is TM.

Given that Ψ is a function of the lipid distribution in the plane of the bilayer (d_x and d_y) it is sensitive to composition fluctuations. The introduction of the normal component of the distance (d_z) allows the membrane for further displacements to satisfy the collective variable requirements under biased dynamics. The curvature is a collective response of the many body system and its shape emerges as a result of multiple interactions. Additionally, different bilayers with characteristic bending moduli k_c, surface tension σ and height h exhibit different free energy landscapes in the Ψ space.⁹

We have shown in previous work that the needed free energy to bend an identical ternary bilayer (DPCP : DOPC : CHOL at concentrations 0.58 : 0.12 : 0.3) increases monotonically with the curvature⁹ in the absence of TM peptides (see the black curve in Fig. 2). Fig. 2 shows the free energy cost needed to bend the bilayer up to Ψ ∼ −0.5, with and without the TM helices embedded in it (always in their dimer form). Interestingly, the addition of TM peptide dimers changes the overall free energy profile, giving rise to three distinctive regimes (see the red curve in Fig. 2), namely −0.3 < Ψ < 0, −0.4 < Ψ < −0.3 and Ψ < −0.4. For −0.3 < Ψ < 0 the cost to bend the bilayer increases almost linearly. At Ψ ∼ −0.3 and Ψ ∼ −0.4 the slope changes and the bilayer switches regimes.

Fig. 2 Three component bilayer (DPPC/DOPC/CHOL) free energy calculations during bending, with and without subunit g helices in their dimer form. The Ψ collective variable takes values in the range [−0.5, 0]. Snapshots show subunit g helices’ (green and purple) instantaneous position and orientation together with the curvature induced in the bilayer at different Ψ values. For clarity, water molecules are not shown. Error bars are standard errors calculated by splitting well-tempered metadynamics runs into nine independent blocks. See the ESI† for convergence details.

Importantly, in these metadynamics simulations no restrictions were imposed on the peptides, but only on the bilayer through collective variable Ψ. Hence, subunit g helices were free to move inside the bilayer where they were inserted. It is observed that the free energy needed to bend the bilayer in the presence of the TM dimer is systematically higher than the one needed to bend the bilayer only system.

Although widely used for protein–lipid molecular modeling,^13–19 MARTINI does not account for hydrogen bonds or salt bridges. However, it has been repeatedly demonstrated that its parametrization is able to capture most of the basic characteristics of many biological systems.^10,20–24

3 Cholesterol spontaneously aggregates in raft-like domains

Cholesterol being a major component of the plasma membrane in mammalian cells, it has been pointed out that proteins play an important role in determining the cholesterol distribution which in general is not uniform.²⁵ Even under the coarse-grained parametrization, cholesterol properties are quite different from those of polar lipids and those with large headgroups;²⁶ then, it is to be expected that proteins will interact to a different extent with cholesterol and phospholipids.

To understand the free energy landscape we have analyzed self-species coordination as a function of the membrane curvature (for technical details and the physical meaning of self-coordination numbers see the ESI†). We have observed that the presence of the TM peptides in their dimer form imposes a change in the cholesterol distribution, which in a collective response to the increasing curvature forms a large raft-like domain at the apical zone of the bilayer.

Fig. 3A shows cholesterol coordination numbers as a function of the bilayer curvature (from Ψ = 0 for a flat bilayer to Ψ = −0.8 for the highest curvature). Fig. 3A demonstrates that as the membrane bends the aggregation of cholesterol molecules increases. On the other hand, DOPC lipids remain mostly dispersed along the bilayer (see Fig. 3B).

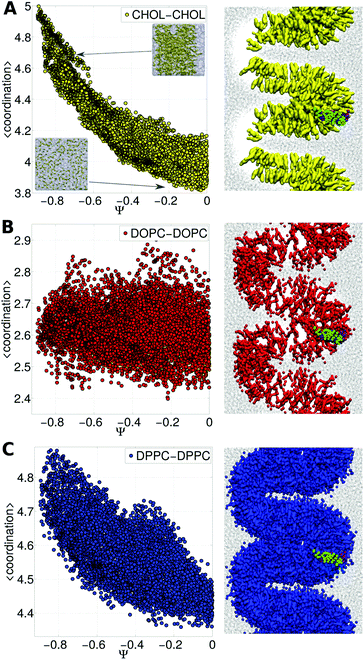Fig. 3 Lipid distribution and membrane bending. Self-coordination numbers were calculated for each species (DPPC, DOPC and CHOL) in the ternary membrane in the presence of the TM peptide dimer as a function of Ψ (the curvature increases as Ψ is more negative, see Fig. 2). Panel A: CHOL, panel B: DOPC and panel C: DPPC. On the right, side views of the corresponding molecule distributions are shown for extreme bending (Ψ ∼ −0.75) in the presence of the subunit g helical domain in its dimer form. In all three cases water molecules are shown as black dots.

Consequently, the reason for the different free energy regimes (see Fig. 2) is the degree to which cholesterol aggregates, as reflected in self-coordination plots in Fig. 3A. Even more interesting is the indirect effect on DPPC lipids (the most abundant species), which fill the empty spaces left by cholesterol molecules, revealing the aggregation rate of change at Ψ ∼ −0.3 and Ψ ∼ −0.4 (see Fig. 3C). From the thermodynamic (and biological) point of view this result suggests that the bilayer reorganizes to bend while the interactions between lipid molecules and the TM dimer modulate the Ψ space, forcing cholesterol to aggregate and making the free energy increase. This is an indication of the capability of Ψ to couple bilayer bending and composition fluctuations.

Therefore, the cholesterol raft formation has major consequences for the total energetic cost needed to bend the bilayer with the TM dimer. Making cholesterol molecules gather around the vicinity of the dimerized helices adds to the free energy and explains the reported excess of ΔG ∼ 1000 kJ mol⁻¹ (400k_BT) (see Fig. 2). This value is in good agreement with calculations made for complex membrane associated events, such as dividing a single spherical phospholipid bilayer into two smaller vesicles (≃350k_BT)²⁷ or the generation of membrane curvature by fusion or fission catalyzed by specialized proteins (≃450k_BT).²⁸

Moreover, as reported by Hatta and collaborators,²⁹ the needed free energy for a single pair of cholesterol molecules to form a dimer in a 1-palmitoyl-2-oleoyl-phosphatidylcholine (POPC) lipid bilayer is ≃3.5 kJ mol⁻¹ at 310.15 K. Roughly extrapolating this value to the ∼300 cholesterol molecules included in the bilayer used here (neglecting any cross-linked effects and the different lipid composition) gives the additional free energy cost of ∼1000 kJ mol⁻¹. The local aggregation of cholesterol molecules by the subunit g TM dimer has crucial importance in nanoscopic domains and membrane raft studies. Lipid nanodomains have decisive biological functions in cell membranes and much effort has been made to characterize their size, distribution, composition and lifetime.³⁰

Furthermore, the shape of the bilayer conditions the location of the helices; as observed again in Fig. 3, the subunit g helical dimer keeps itself in the region of maximum curvature (apical region). This result is an indication of close protein–lipid interactions dynamically equalizing the bilayer reorganization process due to the hydrophobic mismatch between the protein and the membrane.³¹ Accordingly, it has been shown experimentally and through simulations that some proteins induce cholesterol-enriched or cholesterol-depleted shells, which modify the interactions between proteins themselves.³²

4 Free energy calculations for TM peptide dimerization

By repeating the same simulations for the bilayer with the TM peptides now in their monomeric form, we have observed that no cholesterol aggregation takes place no matter the amount of induced curvature (see Fig. S4 in the ESI†). From this result the importance of peptide–peptide interactions appears to be crucial for cholesterol clustering. As observed in Fig. 3 and in ESI† Fig. S4, the composition fluctuations in the bilayer are very different if the peptides have or have not dimerized (or even if they are not present, see Fig. S6 in the ESI†). Specifically, cholesterol molecules form a raft-like cluster only when the TM peptides have formed a stable dimer. Then, if (as predicted experimentally³) there is an optimum orientation of the peptides when they bind together, the free energy surface along some collective variables should exhibit a local minimum to reflect their most stable relative position and orientation.

Consequently, we have studied the dimerization process of the TM peptides using the helix–helix angle θ (defined as the angle between two vectors passing along each helix) and the distance d (measured between helices’ centers of mass) as collective variables. We have calculated the free energy necessary to dimerize this peptide inserted in a flat bilayer. Fig. 4 plots dimerization free energy costs along collective variables θ and d. We have found that the minimum free energy for d is located at ∼0.75 nm with an optimum angle of θ ∼ −0.35 rad, in good agreement with previous experimental and computational results.^3,33–35

Fig. 4 Free energy cost for subunit g dimerization in a flat bilayer. Panels A and B are free energy profiles projected along the helix–helix distance (d) and angle (θ). Subunit g helices are shown in surface representations in green and purple. Panel C is the free energy surface along both collective variables (d) and (θ). In panel D snapshots from well tempered metadynamics are shown together with subunit g helices highlighted in the vdW representation in green/purple. Shown as the transparent surface is the 1024 ternary DPPC/DOPC/CHOL bilayer (blue/red/yellow). Error bars are standard errors calculated by splitting well-tempered metadynamics runs into nine independent blocks. For clarity, water molecules are not shown.

The existence of the free energy minimum indicates that once the peptide dimer is formed at θ ∼ −0.35 rad and d ∼ 0.75 nm, it will remain in that configuration, unless it is perturbed. In agreement with this behavior we have observed that TM helices dimerize spontaneously in a flat bilayer under unbiased conditions. We suggest that the presence of the dimer is mandatory for cholesterol clustering and that one of the reasons is geometrical. Cholesterol being the shortest of the molecules in the bilayer (∼3 nm, for MARTINI) and the intermembrane space of the peptides (GEIIGKRGIIGY, which includes the G-XXX-G motif) having a length of ∼1.3 nm, for a stable TM dimer it is more favorable in free energy terms to be surrounded by cholesterol than by DPPC or DOPC.

Moreover, the size of the cholesterol cluster is determined by the free energy trade-off between the cost to pull cholesterol molecules together (∼3.5 kJ mol⁻¹ per pair²⁹) and the cost for the peptides to stabilize (∼5 kJ mol⁻¹ in the d space and ∼15 kJ mol⁻¹ in the θ space, see Fig. 4). Protein–cholesterol affinities are of major relevance and have already been related to allosteric signal pathways,³⁶ activity control of neurotransmitter receptors for acetylcholine³⁷ and amyloid β-peptide aggregates.³⁸

5 Conclusions

By exploring the phase space in Ψ, we have found that the free energy cost to bend the bilayer with a TM helical dimer embedded in it is considerably higher (∼1000 kJ mol⁻¹ = 400k_BT) than the free energy for the bilayer only system. This effect is due to the property of TM dimers to locally promote cholesterol molecules to aggregate as the bilayer increases its curvature. We have also observed that the dimer form of the TM peptides is mandatory for the process of cholesterol clustering.

We have observed that TM peptide dimerization and bilayer bending events are closely connected and that the underlying phenomena are correctly captured by collective variable Ψ in combination with the MARTINI model. Our results contribute to the understanding of protein–lipid complexities by dynamically describing subunit g helices’ interactions with a model bilayer. Characterizing coupled effects in many-body systems such as large membranes with protein domains is a step forward in elucidating how membranes modulate signaling pathways.

6 Materials and methods

The estimations of the Free Energy Surfaces (FES) for membrane bending and for the dimerization of the TM peptide were computed using well-tempered metadynamics.^8,39,40 This technique has been systematically used in recent years to explore and quantify free energy surfaces of complex systems⁴¹ and has achieved good results in describing complicated biomolecular events.^42–44 However, like in other methods that estimate the free energy (i.e. umbrella sampling^6,7), a major part of the success relies on the proper choice of the collective variables,^8,39,45 therefore, a considerable amount of effort must be made to identify the collective variables that better project the multidimensional FES.⁴⁶ This scenario is characteristic of many biological systems where configurations of interest (generally, low energy states) are separated by large energy barriers and therefore are difficult to study by standard computational means.⁴⁷ For this reason enhanced sampling methods have been widely used.^48–51

All simulations were modeled under the MARTINI force-field¹⁰ using the polarizable water model,⁵² which continues to be successfully used.^13,53,54 The MARTINI implementation groups between 4 and 6 non-hydrogen atoms into a single particle which interacts according to a parametrization that has been shown to correctly reproduce experimental data. A water layer was added above and below each 1024 lipid bilayer, fulfilling the ample water condition⁵⁵ for MARTINI (>15 coarse-grained water molecules per lipid, which corresponds to 60 atomistic water molecules per lipid). Complete systems consist of 1024 lipids, ∼16 000 water molecules and 2 peptides of 26 residues each.

Molecular dynamics simulations were performed with GROMACS-5.1.4^56–58 patched with Plumed 2.3.1.⁵⁹ The calculation of Ψ was implemented in Plumed by compiling it with the matheval library, which is able to parse and evaluate symbolic mathematical expressions, such as the hyperbolic tangent used here as a switching function (for technical details on the implementation of Ψ, see Masone and collaborators⁹).

All simulations were run in the semi-isotropic NPT ensemble at T = 303.15 K^60–62 using the V-rescale thermostat⁶³ with a coupling constant of 1 ps and maintaining the pressure at 1.0 bar using the Berendsen barostat⁶⁴ with a 5 ps coupling constant and the compressibility set to 3 × 10⁻⁴ bar⁻¹. A time step of 20 fs was set in all cases. Long-range electrostatic interactions were computed with the 4th order Particle-Mesh-Ewald method (PME).⁶⁵ This simulation scheme lets the membrane reach a tensionless equilibrium state after a reasonably long period of equilibration.⁶⁶

Free energies for bending the lipid bilayer in the absence of the peptides were taken from our previous work⁹ which used umbrella sampling molecular dynamics. Details on umbrella sampling calculations in model lipid bilayers are provided in the indicated references.^9,67

All membranes were minimized and equilibrated for 100 ns to generate properly relaxed initial configurations. Metadynamics convergence was assessed by calculating the free energy landscape for each collective variable in consecutive trajectory blocks of 100 ns (see ESI†). For proper convergence, metadynamic simulations ran for more than 1 μs in all cases.

Like other collective variables,^68–70 the definition of Ψ includes the system-dependent parameter N₀, which is a function of the lipid composition and the system size and must be calculated for each case. Besides, when applying Ψ to multicomponent lipid bilayers (as in this study) it becomes necessary to generalize the definition of the collective variable to account for different lipid species with different lengths. Namely, the center of mass of the whole bilayer becomes a useless reference point to calculate 3D distances. Instead, distances for each lipid type must be calculated from the center of mass of that specific lipid species. In this way, curvature can be induced in any kind of heterogeneous bilayer. For technical details on this issue see Masone and collaborators.⁹

Subunit g helices and membrane figures were created using Visual Molecular Dynamics (VMD)⁷¹ and the academic version of Maestro Molecular Modeling Environment.⁷² Bilayer systems were prepared using the CHARMM-GUI web server.⁷³

Conflicts of interest

There are no conflicts to declare.

Acknowledgements

This work was supported by grants from MinCyT (Iniciativa de Proyectos Acelerados de Cálculo) IPAC 2016 (SACT 017-00721036) and IPAC 2017 (2017-75-APN-SECACT#MCT), CONICET (PIP-13CO01), SeCTyP-UNCuyo (J051) and the Roemmers Foundation. Supercomputing time granted by the Sistema Nacional de Computación de Alto Desempeño (SNCAD-MinCyT) in clusters Mendieta (CCAD-UNC), Eulogia (CCAD-UNC), Piluso (UNR), Coyote (CIMEC) and Pirayú (CIMEC) is gratefully acknowledged as well as GPU hardware granted by the NVIDIA Corporation.

References

1. R. D. Usery, T. A. Enoki, S. P. Wickramasinghe, V. P. Nguyen, D. G. Ackerman, D. V. Greathouse, R. E. Koeppe, F. N. Barrera and G. W. Feigenson, Biophys. J., 2018, 114, 2152–2164.
2. A. Prakash, L. Janosi and M. Doxastakis, Biophys. J., 2011, 101, 1949–1958.
3. D. M. Bustos and J. Velours, J. Biol. Chem., 2005, 280, 29004–29010.
4. P. Paumard, J. Vaillier, B. Coulary, J. Schaeffer, V. Soubannier, D. M. Mueller, D. Brethes, J.-P. di Rago and J. Velours, EMBO J., 2001, 21, 221–230.
5. G. Arselin, J. Vaillier, B. Salin, J. Schaeffer, M.-F. Giraud, A. Dautant, D. Brethes and J. Velours, J. Biol. Chem., 2004, 279, 40392–40399.
6. G. Torrie and J. Valleau, J. Comput. Phys., 1977, 23, 187–199.
7. B. Roux, Comput. Phys. Commun., 1995, 91, 275–282.
8. A. Laio and M. Parrinello, Proc. Natl. Acad. Sci. U. S. A., 2002, 99, 12562–12566.
9. D. Masone, M. Uhart and D. M. Bustos, J. Chem. Theory Comput., 2018, 14, 2240–2245.
10. S. J. Marrink, H. J. Risselada, S. Yefimov, D. P. Tieleman and A. H. de Vries, J. Phys. Chem. B, 2007, 111, 7812–7824.
11. W. P. Russ and D. M. Engelman, J. Mol. Biol., 2000, 296, 911–919.
12. R. A. Melnyk, S. Kim, A. R. Curran, D. M. Engelman, J. U. Bowie and C. M. Deber, J. Biol. Chem., 2004, 279, 16591–16597.
13. F. A. Herzog, L. Braun, I. Schoen and V. Vogel, J. Chem. Theory Comput., 2016, 12, 2446–2458.
14. F. J. van Eerden, T. van den Berg, P. W. J. M. Frederix, D. H. de Jong, X. Periole and S. J. Marrink, J. Phys. Chem. B, 2016, 3237–3249.
15. L. Monticelli, et al. , J. Chem. Theory Comput., 2008, 4, 819–834.
16. P. J. Bond, D. L. Parton, J. F. Clark and M. S. Sansom, Biophys. J., 2008, 95, 3802–3815.
17. B. A. Hall, A. P. Chetwynd and M. S. Sansom, Biophys. J., 2011, 100, 1940–1948.
18. M. Javanainen, H. Martinez-Seara and I. Vattulainen, PLoS One, 2017, 12, e0187936.
19. D. H. de Jong, G. Singh, W. D. Bennett, C. Arnarez, T. A. Wassenaar, L. V. Schafer, X. Periole, D. P. Tieleman and S. J. Marrink, J. Chem. Theory Comput., 2012, 9, 687–697.
20. S. J. Marrink and A. E. Mark, J. Am. Chem. Soc., 2003, 125, 11144–11145.
21. S. J. Marrink, A. H. de Vries and D. P. Tieleman, Biochim. Biophys. Acta, Biomembr., 2009, 1788, 149–168.
22. M. Baaden and S. J. Marrink, Curr. Opin. Struct. Biol., 2013, 23, 878–886.
23. J. J. Uusitalo, H. I. Ingolfsson, P. Akhshi, D. P. Tieleman and S. J. Marrink, J. Chem. Theory Comput., 2015, 11, 3932–3945.
24. J. J. Uusitalo, H. I. Ingolfsson, S. J. Marrink and I. Faustino, Biophys. J., 2018, 114, 437a.
25. R. M. Epand, Biochim. Biophys. Acta, Biomembr., 2008, 1778, 1576–1582.
26. T. A. Wassenaar, H. I. Ingolfsson, R. A. Bockmann, D. P. Tieleman and S. J. Marrink, J. Chem. Theory Comput., 2015, 11, 2144–2155.
27. R. Nossal and J. Zimmerberg, Curr. Biol., 2002, 12, R770–R772.
28. F. Campelo, G. Fabrikant, H. T. McMahon and M. M. Kozlov, FEBS Lett., 2010, 584, 1830–1839.
29. Y. Andoh, K. Oono, S. Okazaki and I. Hatta, J. Chem. Phys., 2012, 136, 155104.
30. E. L. Elson, E. Fried, J. E. Dolbow and G. M. Genin, Annu. Rev. Biophys., 2010, 39, 207–226.
31. D. L. Parton, J. W. Klingelhoefer and M. S. Sansom, Biophys. J., 2011, 101, 691–699.
32. F. J.-M. de Meyer, J. M. Rodgers, T. F. Willems and B. Smit, Biophys. J., 2010, 99, 3629–3638.
33. N. Sajot, N. Garnier and M. Genest, Theor. Chem. Acc., 1999, 101, 67–72.
34. N. Garnier, S. Crouzy and M. Genest, J. Biomol. Struct. Dyn., 2003, 21, 179–199.
35. A. Prakash, L. Janosi and M. Doxastakis, Biophys. J., 2011, 101, 1949–1958.
36. G. Jaipuria, A. Leonov, K. Giller, S. K. Vasa, u. Jaremko, M. Jaremko, R. Linser, S. Becker and M. Zweckstetter, Nat. Commun., 2017, 8, 14893.
37. J. Fantini, C. Di Scala, L. S. Evans, P. T. F. Williamson and F. J. Barrantes, Sci. Rep., 2016, 6, 21907.
38. N. A. Avdulov, S. V. Chochina, U. Igbavboa, C. S. Warden, A. V. Vassiliev and W. G. Wood, J. Neurochem., 1997, 69, 1746–1752.
39. A. Laio and F. L. Gervasio, Rep. Prog. Phys., 2008, 71, 126601.
40. A. Barducci, G. Bussi and M. Parrinello, Phys. Rev. Lett., 2008, 100, 020603.
41. P. Tiwary and M. Parrinello, J. Phys. Chem. B, 2015, 119, 736–742.
42. V. Limongelli, L. Marinelli, S. Cosconati, C. La Motta, S. Sartini, L. Mugnaini, F. Da Settimo, E. Novellino and M. Parrinello, Proc. Natl. Acad. Sci. U. S. A., 2012, 109, 1467–1472.
43. V. Limongelli, M. Bonomi and M. Parrinello, Proc. Natl. Acad. Sci. U. S. A., 2013, 110, 6358–6363.
44. O. Valsson, P. Tiwary and M. Parrinello, Annu. Rev. Phys. Chem., 2016, 67, 159–184.
45. D. Masone and S. Grosdidier, Comput. Biol. Chem., 2014, 49, 1–6.
46. G. Saladino, L. Gauthier, M. Bianciotto and F. L. Gervasio, J. Chem. Theory Comput., 2012, 8, 1165–1170.
47. G. A. Tribello, M. Ceriotti and M. Parrinello, Proc. Natl. Acad. Sci. U. S. A., 2010, 107, 17509–17514.
48. J. S. van Duijneveldt and D. Frenkel, J. Chem. Phys., 1992, 96, 4655–4668.
49. D. Moroni, P. R. ten Wolde and P. G. Bolhuis, Phys. Rev. Lett., 2005, 94, 235703.
50. M. Salvalaglio, C. Perego, F. Giberti, M. Mazzotti and M. Parrinello, Proc. Natl. Acad. Sci. U. S. A., 2014, 112, E6–E14.
51. P. M. Piaggi, O. Valsson and M. Parrinello, Phys. Rev. Lett., 2017, 119, 015701.
52. S. Yesylevskyy, S.-J. Marrink and A. E. Mark, Biophys. J., 2009, 97, 40–49.
53. C. Arnarez, S. J. Marrink and X. Periole, Chem. Sci., 2016, 7, 4435–4443.
54. M. Lelimousin, V. Limongelli and M. S. P. Sansom, J. Am. Chem. Soc., 2016, 138, 10611–10622.
55. H. I. Ingolfsson, M. N. Melo, F. J. van Eerden, C. Arnarez, C. A. Lopez, T. A. Wassenaar, X. Periole, A. H. de Vries, D. P. Tieleman and S. J. Marrink, J. Am. Chem. Soc., 2014, 136, 14554–14559.
56. D. Van Der Spoel, E. Lindahl, B. Hess, G. Groenhof, A. E. Mark and H. J. C. Berendsen, J. Comput. Chem., 2005, 26, 1701–1718.
57. S. Pronk, S. Pall, R. Schulz, P. Larsson, P. Bjelkmar, R. Apostolov, M. R. Shirts, J. C. Smith, P. M. Kasson, D. van der Spoel, B. Hess and E. Lindahl, Bioinformatics, 2013, 29, 845–854.
58. M. J. Abraham, T. Murtola, R. Schulz, S. Pall, J. C. Smith, B. Hess and E. Lindahl, SoftwareX, 2015, 1-2, 19–25.
59. G. Tribello, M. Bonomi, D. Branduardi, C. Camilloni and G. Bussi, Comput. Phys. Commun., 2014, 185, 604–613.
60. S. Jo, J. B. Lim, J. B. Klauda and W. Im, Biophys. J., 2009, 97, 50–58.
61. H. Rui, K. I. Lee, R. W. Pastor and W. Im, Biophys. J., 2011, 100, 602–610.
62. S. Jo, T. Kim and W. Im, PLoS One, 2007, 2, e880.
63. G. Bussi, D. Donadio and M. Parrinello, J. Chem. Phys., 2007, 126, 014101.
64. H. J. C. Berendsen, J. P. M. Postma, W. F. van Gunsteren, A. DiNola and J. R. Haak, J. Chem. Phys., 1984, 81, 3684.
65. U. Essmann, L. Perera, M. L. Berkowitz, T. Darden, H. Lee and L. G. Pedersen, J. Chem. Phys., 1995, 103, 8577–8593.
66. J. M. Rodgers and B. Smit, J. Chem. Theory Comput., 2012, 8, 404–417.
67. R. D. Porasso, N. M. Ale, F. Ciocco Aloia, D. Masone, M. G. Del Popolo, A. Ben Altabef, A. Gomez-Zavaglia, S. B. Diaz and J. A. Vila, RSC Adv., 2015, 5, 43537–43546.
68. T. V. Tolpekina, W. K. den Otter and W. J. Briels, J. Chem. Phys., 2004, 121, 12060.
69. T. V. Tolpekina, W. K. den Otter and W. J. Briels, J. Chem. Phys., 2004, 121, 8014.
70. J. Wohlert, W. K. den Otter, O. Edholm and W. J. Briels, J. Chem. Phys., 2006, 124, 154905.
71. W. Humphrey, A. Dalke and K. Schulten, J. Mol. Graphics, 1996, 14, 33–38.
72. Schrodinger LLC, Schrodinger, LLC, New York, NY, 2014.
73. S. Jo, T. Kim, V. G. Iyer and W. Im, J. Comput. Chem., 2008, 29, 1859–1865.

---

Footnote

† Electronic supplementary information (ESI) available: Convergence details for metadynamics simulations; cholesterol raft formation plots as the bilayer bends; mathematical details on coordination number calculations; plots of the curved bilayer with TM peptides in their monomeric form with no cholesterol raft and plots of the curved bilayer without TM peptides with no cholesterol raft. See DOI: 10.1039/c8cp06783j

---