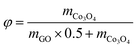Spin glass like transition and the exchange bias effect in Co₃O₄ nanoparticles anchored onto graphene sheets

Abstract

We have synthesized Co₃O₄ nanoparticles having 40 nm average size, which are anchored on reduced graphene oxide. X-ray diffraction, FESEM, TEM and Raman spectroscopy are performed for the characterization. The temperature dependence of field cooled (FC) and zero field cooled (ZFC) magnetization curves exhibits antiferromagnetic (AFM) transition around ∼30 K, as observed for bulk Co₃O₄. The exchange bias effect is observed below ∼30 K. A significant change in the exchange bias effect is noted around ∼8 K, which is close to a spin-glass-like transition. The spin-glass-like phase has been confirmed by the memory effects observed by different experimental protocols. The possible origin of exchange bias is discussed in the manuscript.

---

1. Introduction

Over the past few decades, synthesis and characterization of magnetic metal oxide nanoparticles has been the subject of intense research due to their technological applications in diverse fields such as magnetic storage,¹ magnetic recording,² and magnetic sensors³ and in different areas of medical science like MRI and drug delivery.⁴ Magnetic nanoparticles display different characteristic features, which are noticeably different from their bulk counterpart.⁵ For example, magnetic metal oxide nanoparticles having a significantly different magnetic anisotropy of core and shell structure may show the exchange bias effect (EB). The exchange bias effect typically appears due to the pinning mechanism at the interface between two magnetic components with significantly different anisotropy.⁶ The displacement of the magnetic hysteresis loop is the typical manifestation of the EB effect. Numerous reports of the EB phenomenon in AFM metal oxide nanoparticles like NiO,^7,8 CuO,⁹ γ-Fe₂O₃, Fe₃O₄,^10,11 Cr₂O₃⁷ and Co₃O₄^12,13 are found in recent years. These establish the evidence of distinguishable surface magnetic anisotropy from that of the core. The nature of surface magnetic anisotropy is proposed to be different in different cases. For example, for NiO^7,8 and γ-Fe₂O₃,¹⁰ a frustrated magnetic shell has been suggested, whereas a spin glass component has been suggested in the shell of γ-Fe₂O₃¹⁴ and Fe₃O₄¹⁵ nanoparticles. The presence of a weak ferromagnetic (FM) component has been suggested at the surface of AFM CuO nanoparticles.⁹ Recently, a disordered glassy magnetic phase at the particle surface has been proposed in La_1/3Sr_2/3FeO₃.¹⁶

Recently, graphene, one-atom-thick with sp²-hybridized carbon structure and two-dimensional single sheet morphology, has triggered tremendous research interest owing to its remarkable electrical, optical and mechanical properties.^17,18 Functionalized graphene sheets are realized by converting a fraction of the sp² graphenic carbons to sp³ carbons, which covalently bind with polymers,¹⁹ chemicals²⁰ and nanostructures.^21,22 Of these, graphene–magnetic nanoparticle composites are gaining great attention owing to their multifunctional and unified properties.

Here, we report the EB effect observed in magnetic Co₃O₄ nanoparticles which are anchored on reduced graphene oxide (rGO). Integration of nanoparticles (NPs) and graphene into nanocomposites has recently become a field of intense research^19–22 due to their new and/or enhanced functionalities that cannot be achieved by either component alone, and therefore holds great promise for a wide variety of applications in catalysis, optoelectronic materials, MRI, drug delivery, etc.²³ This composite is analogous to those magnetic nanoparticles embedded in non-magnetic metals where it has been proposed that the RKKY interaction is suppressed by the magnetostatic dipole interactions for particles larger than ∼1 nm.²⁴ The conductivity mechanism of 2D graphene is distinctly different from that of a metal.²⁵ In addition to the dipole–dipole interaction between the Co₃O₄ nanoparticles, the possible magnetic interaction mediated through semi-metallic graphene may show a synergistic effect. To observe the graphene mediated interaction a diluted magnetic system has been chosen where 5% volume fraction of Co₃O₄ is anchored on the reduced graphene oxide (rGO) sheet.

2. Experimental

2.1. Synthesis of Co₃O₄ nanoparticles

Co₃O₄ nanoparticles are synthesized by the sol–gel citrate precursor technique. 3.722 g of cobalt acetate tetrahydrate (Co(CH₃COO)₂·4H₂O) powder is dissolved in 15 ml of diluted nitric acid to form cobalt nitrate solution. A suitable amount of citric acid is added to the solution and stirred for 6 hours at 343 K to ensure the formation of metal citrates. The amount of citric acid is chosen to ensure that all the metal ions form metal citrates by considering that only two of the citrate ions take part in chemical bonding with metal ions.^26,27 The solution is gently and slowly evaporated for a long time to obtain dried citrate precursor powder. The precursor powder is then ground and heated at 773 K for 3 h in air to form well-crystallized oxides. During this process a number of gases, viz. CO and CO₂, organic products, water vapour, etc., evolve as a result of decomposition of mainly citrates.²⁶

2.2. Synthesis of the Co₃O₄@rGO composite

The Co₃O₄ nanoparticles are used in the synthesis of the Co₃O₄@rGO nanocomposite with 5% volume fraction of Co₃O₄. GO is typically synthesized following modified Hummers’ method. 0.1 g of as-prepared GO powder is then sonicated in 50 ml of ethanol for 1 hour. Then, 0.2804 g of Co₃O₄ nanopowder and 50 ml of deionised water are added to the GO solution and stirred for 30 min to get a homogeneous mixture. After that the temperature of the mixture solution is increased to 100 °C and 5 ml of Hydrazine Hydrate solution (80%) is added dropwise to reduce GO to rGO. Stirring at 100 °C is continued for about 12 hours which is followed by centrifugation and washing by ethanol and distilled water. This step is repeated several times. Then the collected precipitate is dried at 60 °C for 6 hours and the desired 5% Co₃O₄@rGO composite is formed. Calculation of the volume fraction of Co₃O₄ in the composite requires the reduction yield of GO to rGO. The yield of rGO by hydrothermal reduction of GO has been estimated to be around 50%. The weight fraction of Co₃O₄ in the nanocomposite can be determined by the following equation:
where m_GO and m_Co3O4 represent the mass of GO and Co₃O₄, respectively. The weight fraction of Co₃O₄ is transformed into the volume fraction by using the densities of rGO (2.26 g per c.c) and Co₃O₄ (6.11 g per c.c). Here the density of rGO is assumed to be close to that of natural graphite.

2.3. Characterization

Samples are characterized at room temperature by using an X-ray diffractometer (model: Bruker D8 Advance) using Cu K_α radiation of wavelength 1.5406 Å. The morphology of the nanoparticles is studied by field emission scanning electron microscopy (FE-SEM) (model: JSM-7610F, JEOL) and tunneling electron microcopy (TEM) (model: JEM-2100F, JEOL). Raman spectroscopy is studied using a SPEX-1403 laser Raman spectrometer with excitation by a 514.5 nm argon laser line in the back-scattering geometry. Magnetization is measured in the temperature range 2–300 K, in a commercial SQUID magnetometer (Quantum Design, MPMS-5).

3. Results and discussion

3.1. Structure and morphology: XRD, FESEM, TEM studies

The X-ray diffraction patterns (XRD) measured at room temperature in the 2θ range of 10°–80° for the Co₃O₄@rGO nanocomposite are illustrated in Fig. 1. All lines are unambiguously indexed for different (hkl) planes (JCPDS No. 43-1003) corresponding to cubic spinel structured Co₃O₄. No characteristic peak for rGO is observed in the XRD pattern of Co₃O₄/rGO composites. The signature of rGO has been confirmed from Raman spectroscopy studies as discussed later. The particle size (D) and microstrain (ε) of Co₃O₄ nanoparticles are estimated by using Williamson and Hall's²⁸ modified Scherrer's formula given by

β cos θ = 0.89λ/D + 2ε sin θ, (1)

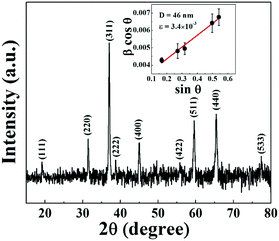Fig. 1 X-ray diffraction pattern of the Co₃O₄@rGO composite. The inset shows the Williamson–Hall plot.

Taking under consideration the prominent XRD peaks having uniquely defined FWHM a linear fit of β cos θ versus sin θ plot is shown in the inset of Fig. 1. The average particle size and the microstrain of Co₃O₄ nanoparticles are estimated to be 46 nm and 3.4 × 10⁻³, respectively. The morphology and size of Co₃O₄ nanopaticles are investigated from FESEM and TEM images. Fig. 2a displays the rGO sheet acting like a substrate on which Co₃O₄ nanoparticles are dispersed. The size distribution of the well anchored nanoparticles follows Gaussian distribution (inset of Fig. 2b) with the maximum number of particles in the range 30–35 nm. The TEM image of Co₃O₄ implanted on the rGO sheet as shown in Fig. 2c indicates the morphology of the particles having a maximum number of particles of size ∼25–35 nm. The interplanar spacing as in Fig. 2d is found to be 0.243 nm which can be assigned to Co₃O₄(311) planes. Selected area electron diffraction (SAED) patterns are depicted in Fig. 2e, where rings correspond to different diffraction planes as observed in the XRD pattern.

Fig. 2 (a, b) FESEM and (c–e) TEM images of the Co₃O₄@rGO composite. The inset of (b) indicates the size distribution of Co₃O₄ nanoparticles following Lorentz distribution shown by a continuous fitted line. The interplanar spacing between the (311) diffraction planes of Co₃O₄ is depicted in (d). Panel (e) indicates the SAED of Co₃O₄ showing different planes.

3.2. Spectroscopic characterization: Raman spectroscopy

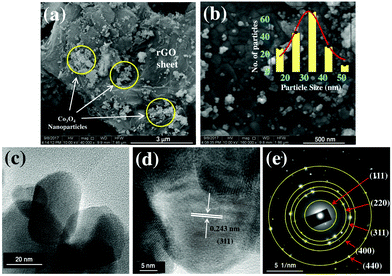
Spectroscopic characterization of the Co₃O₄/rGO nanocomposite has been performed by Raman spectroscopy. Raman active carbonaceous materials are expected to show two characteristic main peaks, the so-called D- and G-band, at around 1350 cm⁻¹ and 1600 cm⁻¹. Fig. 3 shows a broad D band (∼1353 cm⁻¹), a comparatively sharp G band (∼1587 cm⁻¹) along with all the fundamental Raman vibration of Co₃O₄ at 474 cm⁻¹ corresponding to E_g mode, and the bands at 191, 512, and 608 cm⁻¹ corresponding to F_2g mode.²⁹ The D band is due to the defects as well as disordered atomic arrangement caused by the sp³ carbon atom and its intensity is directly proportional to the amount of defects or disorders present in the sample. The intensity of the G-band is proportional to the amount of ordered graphitic (sp²) carbon contained in the sample.^30,31Fig. 3 illustrates that the ratio of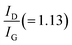 which is a measure of disorder is significantly larger compared to that (1.00) of rGO as reported by Sarkar et al.³² This may refer to the enhancement of the defects induced in the graphene sheet due to the anchoring of Co₃O₄ on the rGO sheet.

Fig. 3 Raman spectroscopy of the Co₃O₄@rGO composite. The inset shows I_D/I_G of rGO alone.

3.3. Magnetic properties

3.3.1. Temperature dependence of dc magnetization. The magnetic properties of the Co₃O₄/rGO nanocomposite are probed by dc magnetization studies. The temperature dependent magnetization under the zero field cooled (ZFC) and field cooled (FC) protocol is shown in Fig. 4. For the ZFC curve, the sample is initially cooled from 300 K to 2 K in the absence of magnetic field and the magnetization measurement is performed in the heating cycle at 100 Oe field. For the FC measurements, the sample is cooled under the same field and magnetization is measured during heating from 2 K to 300 K. Both FC and ZFC magnetization exhibit a peak at the same temperature which is a characteristic of an antiferromagnet (AFM). The AFM transition temperature T_N is defined by the peak in the ∂(χT)/∂T versus T plot.¹³Fig. 5 depicts χ_pT versus T and ∂(χ_pT)/∂T versus T plots, where χ_p = χ − χ₀ is the paramagnetic susceptibility and temperature-independent contribution χ₀ = 7.08 × 10⁻⁶ emu g⁻¹ Oe⁻¹ is discussed later. The plot yields a peak at T_N = 30 K which is the same as reported by Dutta et al.¹³ Here AFM transition around 30 K is exhibited as a diffused peak in the M–T curve measured in both FC and ZFC modes. As found in the literature,³³ the peak position and its sharpness are significantly affected by the particle size and its distribution as well. Here the characteristic of the diffused peak around AFM transition temperature may be the manifestation of the particle size distribution.

Fig. 4 Thermal variation of FC and ZFC magnetization of the Co₃O₄@rGO composite measured in 100 Oe. The inset highlights the low temperature regime of ZFC magnetization measured at 20 Oe, 100 Oe, 1 T and 5 T as discussed in the text.

Fig. 5 Plots of χ_pT versus T and ∂(χ_pT)/∂T versus T for the Co₃O₄@rGO composite where χ_p = χ − χ₀ with χ₀ = 7.08 × 10⁻⁶ emu g⁻¹ Oe⁻¹ (see text). The peak in the ∂(χ_pT)/∂T versus T plot defines the Néel temperature T_N.

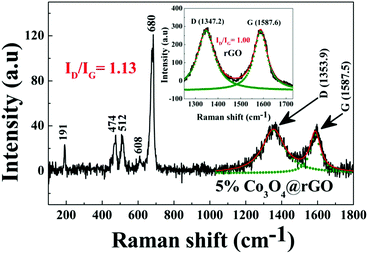
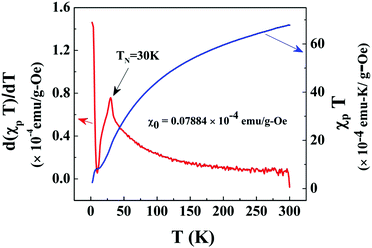
After exhibiting the AFM peak at T_N, FC magnetization increases sharply with lowering of temperature till 2 K, whereas the sharp increase of ZFC magnetization with decreasing temperature is followed by a peak around 5 K (T_sg) as shown in the inset of Fig. 4. This sharp increase of FC and ZFC may indicate the presence of a ferromagnetic (FM) component. This FM component may be ascribed to the uncompensated (UC) spins at the surface of the AFM core of Co₃O₄ nanoparticles which are dispersed on the rGO sheet. To characterize the peak (T_sg) in ZFC magnetization, the M–T measurement has been performed at different magnetic fields of ∼20 Oe, 100 Oe, 1 kOe and 5 kOe as shown in the inset of Fig. 4. ZFC magnetization performed at 20 Oe exhibits a peak at a slightly higher temperature compared to that of at 100 Oe, whereas it does not exhibit any peak down to 2 K for 5 kOe and 1 kOe measuring field. Such a strong dependence of ZFC peak position on the magnetic field designates the presence of a metastable state. This metastable state may be assigned to the re-entrant spin glass (SG) phase as discussed later in Section 3.3.2.

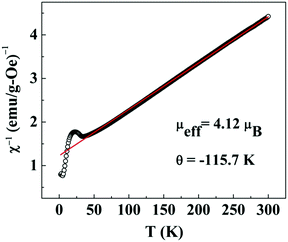
In the high temperature region, i.e. T ≫ T_N, the plot of χ⁻¹versus T (Fig. 6) is fitted with the modified Curie–Weiss law χ = χ₀ + C/(T − θ), where C = Nμ_eff²/3k_BT and 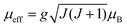, θ is the Curie–Weiss temperature and χ₀ is the temperature-independent contribution. The best fitted line as shown in Fig. 6 evaluates μ_eff = 4.12μ_B, θ = −115.7 K and χ₀ = 7.08 × 10⁻⁶ emu g⁻¹ Oe⁻¹. Co₃O₄ exhibits a normal spinel structure with the occupation of 8 Co²⁺ tetrahedral ions and 16 Co³⁺ octahedral ions per unit cell. Its magnetic moment arises due to Co²⁺ ions only, since Co³⁺ ions have no permanent magnetic moment as a consequence of the splitting of 3d levels in the octahedral crystal field and 3d⁶ electrons are paired in t_2g levels. The value of μ_eff = 4.12μ_B is larger than the spin only μ_eff = 3.87μ_B with S = 3/2. This mismatch may be due to spin–orbit coupling contribution. The large negative value of θ predicts the antiferromagnetic exchange interaction between Co²⁺ ions.

Fig. 6 χ ⁻¹ versus T plot for the Co₃O₄@rGO composite. The solid lines represent linear fit to the Curie–Weiss law.

3.3.2. ZFC relaxation dynamics and the memory effect: characterization of spin glass phase. The slow relaxation dynamics and memory effects in magnetization in the ZFC protocol are the ascertaining signatures of the spin glass system. The investigation of memory effects in superspin-glass nanoparticles as well as in spin-glass systems is carried out through different experimental protocols.^34,35 Memory effects observed in the relaxation dynamics are summarized in Fig. 7. Fig. 7a displays isothermal magnetic relaxation at 4 K measured in 100 Oe after zero-field cooling from 300 K, which is well above T_N. Initially, isothermal relaxation has been recorded for time t₁ = 3600 s. At the end of t₁, the magnetic field is switched off, the temperature is lowered down to 2.5 K and the relaxation is recorded in zero-field for t₂ = 3600 s. Finally, the temperature is restored to 4 K and the relaxation is further measured in 100 Oe for t₃ = 3600 s. Fig. 7b displays magnetic relaxation at 4 K in 100 Oe after zero-field cooling from 300 K. Initially, the measurement has been carried out for t₁ at 4 K. After time t₁, the sample is cooled down to 2.5 K and the relaxation is recorded for t₂. Finally, the sample is heated back to 4 K and the relaxation is further recorded for t₃. In this experiment, the relaxation is measured in 100 Oe throughout.

Fig. 7 Magnetic relaxation at 4 K and 100 Oe for t₁ and t₃ after cooling down from 300 K in ZFC mode with an intermediate measurement time t₂ at 2.5 K in (a) zero field and (b) 100 Oe field. The insets indicate that the sample regains its previous magnetization in both modes of relaxation after time t₂. Both insets show the relaxation at 4 K. The solid line represents the best fit curve which follows the stretched exponential function as discussed in the text.

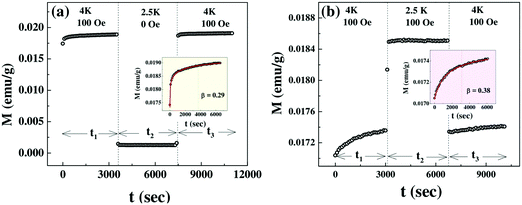
Both plots clearly depict the return of magnetization to nearly the same value after the temporary halt at the lower temperature of 2.5 K. This is a clear confirmation of the memory effect. To further elucidate this effect the magnetization obtained during the aging periods t₁ and t₃ is plotted sequentially in the inset of Fig. 7a and b, leaving out the intermittent time evolution for t₂. Both plots display that the magnetization within the time period t₃ appears as a perfect continuation to the curve measured during t₁. Thus the system recollects its initial configuration as it returns to the initial temperature in both cases.

The time evolution of magnetization resulting from slow relaxation is shown in the inset of Fig. 7a and b. It can be approximated by the stretched exponential function³⁶

M(t) = M₀ + M_g[1 − exp(−(t/t₀))^β]

where M₀ and M_g are involved with the ferromagnetic and glassy components, respectively. t₀ is the time constant and the dispersion parameter β indicates the distribution of relaxation dynamics. For single energy barrier β = 1, while for the system with distribution of energy barriers the value of β lies in the range of 0 < β < 1. Here, the best fit reveals M₀ = 0.0162 emu g⁻¹ and β = 0.29 and 0.38 as shown in the inset of Fig. 7a and b, respectively. The non-zero value of M₀ points to the existence of the FM component^37,38 involved in the relaxation dynamics and the value of β indicates the distribution of anisotropy barriers, as typically found in SG systems.

The ZFC relaxation experiment (Fig. 8) under the same protocol has been repeated at 16 K which is much above the temperature T_sg with 12 K as an intermediate temperature. The absence of the memory phenomenon as clearly demonstrated in the inset of Fig. 8 is expected as it is far above the spin glass transition temperature T_sg.

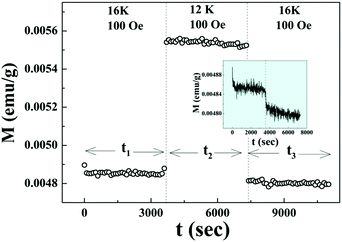Fig. 8 Magnetic relaxation at 16 K and 100 Oe for t₁ and t₃ after cooling down from 300 K in ZFC mode with an intermediate measurement time t₂ in zero field quench at 12 K.

There have been several reports^39,40 on the magnetic properties of bare Co₃O₄ nanoparticles exhibiting superparamagnetic block state exhibiting memory effects in the FC protocol. But the aging and memory effects in the ZFC protocol which confirm the spin glass behavior of Co₃O₄ nanoparticles are rarely found in the literature. Here, the magnetic properties of Co₃O₄ anchored onto the graphene sheet differ remarkably from that of bare Co₃O₄ nanoparticles, which indicates that graphene is a potential substrate for AFM nanoparticles to exhibit their intrinsic magnetic properties.

3.3.3. Exchange bias effect. In order to investigate the possible occurrence of the exchange bias effect, the sample is cooled down to 2 K from 300 K in FC mode with cooling field H_cool = ±1 T and the hysteresis loops are recorded between ±5 T magnetic field. It exhibits an identical shift of the magnetic hysteresis loop toward negative as well as positive magnetic fields with respect to M–H measured in ZFC mode as shown in the inset of Fig. 9. This is a typical manifestation of an exchange bias effect. 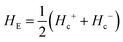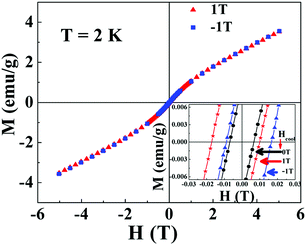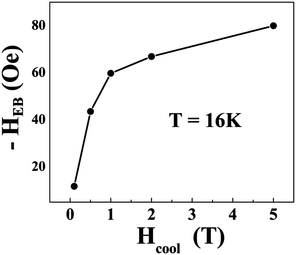The shift along the field-axis defined as the exchange bias field (H_E) and the coercive field (H_c) have been estimated as and 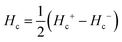respectively, where H_c⁺ (H_c⁻) represents the positive (negative) coercive field. Fig. 10 represents isothermal hysteresis loops at some representative temperatures measured in FC mode under H_cool = 1 T. The thermal variation of the exchange bias field (H_E) and the coercive field (H_c) is shown in Fig. 11. The exchange bias field increases rapidly below T_N with lowering of temperature and remains almost constant in the temperature range 12 ≤ T ≤ 25 K. Below 8 K, as illustrated in the plot, H_E becomes significantly small. This decrease of H_E might be involved with the spin-glass phase as revealed from the memory effect. Unlike other exchange bias systems,⁴¹ the nature of thermal variation of coercive field H_c is different from that of H_E. The coercive field drastically decreases with the increase of temperature from 2 K and becomes almost temperature independent in the temperature range 12 ≤ T ≤ 300 K. This kind of different trends of H_E and H_c has also been reported recently by S. Ye et al.⁴² The explanation of the different trends of H_E and H_c requires more involved experiment as well theoretical understanding. The cooling field (H_cool) dependence of the EB effect at 16 K is investigated here. A systematic variation of H_E as a function of H_cool is depicted in Fig. 12. In the case of a small cooling field, H_E increases sharply with H_cool. With the further increase of H_cool till 5 T, the exchange bias field increases very slowly. The rapid increase of H_E with H_cool is attributed to the alignment of pinned FM spins toward the direction of H_cool. When all the pinned spins are aligned, the increase of H_cool cannot contribute more to the increase of H_E.

Fig. 9 Magnetic hysteresis loops measured at 2 K after cooling the sample under H_cool = ±1 T. The inset highlights the symmetrical shift of the central part of the M–H loop with respect to M–H measured in ZFC mode.

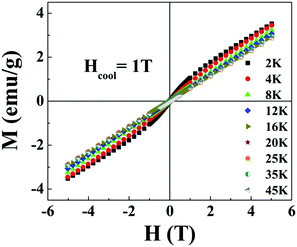Fig. 10 Magnetic hysteresis loops measured at different temperatures T where 2 ≤ T ≤ 45 K after cooling the sample under H_cool = 1 T.

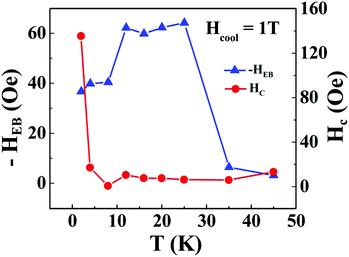Fig. 11 Thermal variation of exchange bias field (H_E) and coercivity (H_C) of the Co₃O₄@rGO composite measured under cooling field H_cool = 1 T.

Fig. 12 Cooling field (H_cool) dependence of H_E measured at 16 K for the Co₃O₄@rGO composite.

4. Summary and conclusions

Co₃O₄ nanoparticles synthesized by the sol–gel citrate precursor technique have been used for the production of the Co₃O₄@rGO nanocomposite having 5% volume fraction of Co₃O₄. Structural and morphological characterization performed by X-ray diffraction, FESEM and TEM reveals the dispersion of cubical spinel structured Co₃O₄ nanoparticles of ∼40 nm average size on the graphene sheet. Spectroscopic characterization performed by Raman spectroscopy illustrates the enhancement of the defects induced in the graphene sheet which ascertains the anchoring of Co₃O₄ on the rGO sheet. The temperature dependence of both field cooled (FC) and zero field cooled (ZFC) magnetization curves exhibits antiferromagnetic (AFM) transition around ∼30 K. The exchange bias field (∼65 Oe) remains almost constant in the temperature range 12 ≤ T ≤ 25 K, which might be attributed to the AFM core and uncompensated (UC) surface spins, as typically observed for the magnetic nanoparticles.⁴¹ Interestingly, this nanocomposite undergoes SG phase transition around 5 K which is indicated by the manifestation of a peak in the ZFC magnetization vs temperature plot. The relaxation dynamics of magnetization satisfying a stretched exponential form supports SG phase. This glassy magnetic phase below 5 K has also been established by relaxation memory studies performed in the ZFC protocol which is commonly accepted as an experimental fingerprint for SG behavior. The significant change of the exchange bias field near the SG transition indicates that the SG phase is involved in the observed exchange bias effect. The unusual observation of re-entrant spin glass in Co₃O₄ nanoparticles is rare and it might have occurred due to graphene mediated exchange interactions. This needs to be confirmed by further experimental and theoretical studies.

Conflicts of interest

There are no conflicts to declare.

Acknowledgements

The authors would like to thank DST, Govt. of India, for developing instrumental facilities like Advance X-ray powder diffractometer (Bruker D8) and FE-SEM (JEOL, JSM-7610F) under FIST programme at Jadavpur University. The authors would like to acknowledge SINP, Kolkata, for providing the instrumental facilities like SQUID vibrating sample magnetometer (Quantum Design). S. Sarkar, A. Mondal and N. Giri wish to thank DST for the INSPIRE fellowship scheme.

References

1. N. A. Frey, S. Peng, K. Cheng and S. Sun, Magnetic nanoparticles: synthesis, functionalization, and applications in bioimaging and magnetic energy storage, Chem. Soc. Rev., 2009, 38, 2532–2542.
2. A. Moser, K. Takano, D. T. Margulies, M. Albrecht, Y. Sonobe, Y. Ikeda, S. Sun and E. E. Fullerton, Magnetic recording: advancing into the future, J. Phys. D: Appl. Phys., 2002, 35, R157–R167.
3. S. Laurent, D. Forge, M. Port, A. Roch, C. Robic, L. Vander Elst and R. N. Muller, Magnetic Iron Oxide Nanoparticles: Synthesis, Stabilization, Vectorization, Physicochemical Characterizations, and Biological Applications, Chem. Rev., 2008, 108(6), 2064–2110.
4. B. Chertok, B. A. Moffat, A. E. David, F. Yu, C. Bergemann, B. D. Ross and V. C. Yang, Iron Oxide Nanoparticles as a Drug Delivery Vehicle for MRI Monitored Magnetic Targeting of Brain Tumors, Biomaterials, 2008, 29(4), 487–496.
5. E. Erdem, Electron beam curing of CoFe₂O₄ nanoparticles, Hybrid Mater., 2014, 1, 62–70.
6. J. Nogués and I. K. Schuller, Exchange bias, J. Magn. Magn. Mater., 1999, 192, 203–232.
7. Sk. Sabyasachi, S. Majumdar and S. Giri, Nanocrystallite interface effect and exchange bias phenomenology in Cr₂O₃ and NiO nanoparticles, Solid State Commun., 2011, 151, 1515–1519.
8. M. P. Proenca, C. T. Sousa, A. M. Pereira, P. B. Tavares, J. Ventura, M. Vazquez and J. P. Araujo, Size and surface effects on the magnetic properties of NiO nanoparticles, Phys. Chem. Chem. Phys., 2011, 13, 9561–9567.
9. A. Punnoose, H. Magnone, M. S. Seehra and J. Bonevich, Bulk to nanoscale magnetism and exchange bias in CuO nanoparticles, Phys. Rev. B: Condens. Matter Mater. Phys., 2001, 64, 174420.
10. T. N. Shendruk, R. D. Desautels, B. W. Southern and J. Van. Lierop, The effect of surface spin disorder on the magnetism of γ-Fe₂O₃ nanoparticle dispersions, Nanotechnology, 2007, 18, 455704.
11. G. Salazar-Alvarez, J. Qin, V. Sepelák, I. Bergmann, M. Vasilakaki, K. N. Trohidou, J. D. Ardisson, W. A. A. Macedo, M. Mikhaylova, M. Muhammed, M. D. Baró and J. Nogués, Cubic versus Spherical Magnetic Nanoparticles: The Role of Surface Anisotropy, J. Am. Chem. Soc., 2008, 130, 13234–13239.
12. M. J. Benitez, O. Petracic, E. L. Salabas, F. Radu, H. Tüysüz, F. Schüth and H. Zabel, Evidence for Core–Shell Magnetic Behavior in Antiferromagnetic Co₃O₄ Nanowires, Phys. Rev. Lett., 2008, 101, 097206.
13. P. Dutta, M. S. Seehra, S. Thota and J. Kumar, A comparative study of the magnetic properties of bulk and nanocrystalline Co₃O₄, J. Phys.: Condens. Matter, 2008, 20, 015218.
14. H. Wang, T. Zhu, K. Zhao, W. N. Wang, C. S. Wang, Y. J. Wang and W. S. Zhan, Surface spin glass and exchange bias in Fe₃O₄ nanoparticles compacted under high pressure, Phys. Rev. B: Condens. Matter Mater. Phys., 2004, 70, 092409.
15. B. Martínez, X. Obradors, Ll. Balcells, A. Rouanet and C. Monty, Low Temperature Surface Spin-Glass Transition in γ-Fe₂O₃ Nanoparticles, Phys. Rev. Lett., 1998, 80, 181–184.
16. Sk. Sabyasachi, M. Patra, S. Majumdar and S. Giri, Glassy magnetic phase driven by short-range charge and magnetic ordering in nanocrystalline La_1/3Sr_2/3FeO_3−δ: Magnetization, Mössbauer, and polarized neutron studies, Phys. Rev. B: Condens. Matter Mater. Phys., 2012, 86, 104416.
17. K. S. Novoselov, Nobel Lecture: Graphene: Materials in the Flatland, Rev. Mod. Phys., 2011, 83, 837–849.
18. A. K. Geim, Nobel Lecture: Random walk to graphene, Rev. Mod. Phys., 2011, 83, 851–862.
19. T. Ramanathan, A. A. Abdala, S. Stankovich, D. A. Dikin, M. Herrera-Alonso, R. D. Piner, D. H. Adamson, H. C. Schniepp, X. Chen, R. S. Ruoff, S. T. Nguyen, I. A. Aksay, R. K. Prud'Homme and L. C. Brinson, Functionalized Graphene Sheets for Polymer Nanocomposites, Nat. Nanotechnol., 2008, 3, 327–331.
20. S. Stankovich, D. A. Dikin, G. H. B. Dommett, K. M. Kohlhaas, E. J. Zimney, E. A. Stach, R. D. Piner, S. T. Nguyen and R. S. Ruoff, Graphene-Based Composite Materials, Nature, 2006, 442, 282–286.
21. Y. Si and E. T. Samulski, Exfoliated Graphene Separated by Platinum Nanoparticles, Chem. Mater., 2008, 20, 6792–6797.
22. X. Wang, S. Tabakman and H. Dai, Atomic Layer Deposition of Metal Oxides on Pristine and Functionalized Graphene, J. Am. Chem. Soc., 2008, 130, 8152–8153.
23. K. Jasuja, J. Linn, S. Melton and V. Berry, Microwave-Reduced Uncapped Metal Nanoparticles on Graphene: Tuning Catalytic, Electrical, and Raman Properties, J. Phys. Chem. Lett., 2010, 1, 1853.
24. R. Skomoski, RKKY interactions between nanomagnets of arbitrary shape, Europhys. Lett., 1999, 48, 455–460.
25. A. H. Castro Neto, F. Guinea, N. M. R. Peres, K. S. Novoselov and A. K. Geim, The electronic properties of graphene, Rev. Mod. Phys, 2009, 81, 109–162.
26. S. Prasad and N. S. Gajbhiye, Magnetic studies of nanosized nickel ferrite particles synthesized by the citrate precursor technique, J. Alloys Compd., 1998, 265, 87–92.
27. R. N. Panda, J. C. Shih and T. S. Chin, Magnetic properties of nano-crystalline Gd- or Pr-substituted CoFe₂O₄ synthesized by the citrate precursor technique, J. Magn. Magn. Mater., 2003, 257, 79–86.
28. G. K. Williamson and W. H. Hall, X-ray line broadening from filed aluminium and wolfram, Acta Metall., 1953, 1, 22–31.
29. V. Hadjiev, M. Iliev and I. Vergilov, The Raman spectra of Co₃O₄, J. Phys. C: Solid State Phys., 1988, 21, L199–L201.
30. R. Genc, M. O. Alas, E. Harputlu, S. Repp, N. Kremer, M. Castellano, S. G. Colak, K. Ocakoglu and E. Erdem, High-Capacitance Hybrid Supercapacitor Based on Multi-Colored Fluorescent Carbon-Dots, Sci. Rep., 2017, 7, 11222.
31. A. Bateni, E. Erdem, S. Repp, S. Acar, I. Kokal, W. Häßler, S. Weber and M. Somer, Electron paramagnetic resonance and Raman spectroscopy studies on carbon-doped MgB₂ superconductor nanomaterials, J. Appl. Phys., 2015, 117, 153905.
32. S. Sarkar, A. Mondal, K. Dey and R. Ray, Defect driven tailoring of colossal dielectricity of Reduced Graphene Oxide, Mater. Res. Bull., 2016, 74, 465–471.
33. S. R. Gawali, A. C. Gandhi, S. S. Gaikwad, J. Pant, T. Chan, C.-L. Cheng, Y.-R. Ma and S. Yun Wu, Role of cobalt cations in short range antiferromagnetic Co₃O₄ nanoparticles: a thermal treatment approach to affecting phonon and magnetic properties, Sci. Rep., 2018, 8, 249.
34. M. Sasaki, P. E. Jönsson, H. Takayama and H. Mamiya, Aging and memory effects in superparamagnets and superspin glasses, Phys. Rev. B: Condens. Matter Mater. Phys., 2005, 71, 104405.
35. Y. Sun, M. B. Salamon, K. Garnier and R. S. Averback, Memory Effects in an Interacting Magnetic Nanoparticle System, Phys. Rev. Lett., 2003, 91, 167206.
36. M. Ulrich, J. García-Otero, J. Rivas and A. Bunde, Slow relaxation in ferromagnetic nanoparticles: indication of spin-glass behavior, Phys. Rev. B: Condens. Matter Mater. Phys., 2003, 67, 024416.
37. S. Biswas, Sk. Sabyasachi, A. Bhaumik and R. Ray, Magnetic Memory Effects in Fe/γ-Fe2O₃ Nanostructures, IEEE Trans. Magn., 2014, 50(3), 2301107.
38. S. Sarkar, A. Mondal, K. Dey and R. Ray, Magnetic memory in nanocrystalline α-Fe₂O₃ embedded in reduced graphene oxide, RSC Adv., 2015, 5, 81260–81265.
39. T. Mousavand, T. Naka, K. Sato, S. Ohara, M. Umetsu, S. Takami, T. Nakane, A. Matsushita and T. Adschiri, Crystal size and magnetic field effects in Co₃O₄ antiferromagnetic nanocrystals, Phys. Rev. B: Condens. Matter Mater. Phys., 2009, 79, 144411.
40. V. Bisht and K. P. Rajeev, Unusual superparamagnetic behavior of Co₃O₄ nanoparticles, arXiv:1008.5245v2 [cond-mat.mes-hall] 2 Sep 2010.
41. S. Giri, M. Patra and S. Majumdar, Exchange bias effect in alloys and compounds, J. Phys.: Condens. Mater., 2011, 23, 073201.
42. S. Ye, S. P. Pati, Y. Shiokawa, M. Al-Mahdawi, T. Nozaki and M. Sahashi, Observation of perpendicular exchange bias in an Ir-doped Fe₂O₃/Co ultrathin film system, Phys. Chem. Chem. Phys., 2017, 19, 8188–8193.

---