Aromaticity, Coulomb repulsion, π delocalization or strain: who is who in endohedral metallofullerene stability?†
Yang
Wang
 *abc,
Sergio
Díaz-Tendero
*abc,
Sergio
Díaz-Tendero
 bcd,
Manuel
Alcamí
bcd,
Manuel
Alcamí
 bce and
Fernando
Martín
*bdef
bce and
Fernando
Martín
*bdef
aSchool of Chemistry and Chemical Engineering, Yangzhou University, Yangzhou, Jiangsu 225002, China. E-mail: yangwang@yzu.edu.cn
bDepartamento de Química, Módulo 13, Universidad Autónoma de Madrid, 28049 Madrid, Spain. E-mail: fernando.martin@uam.es
cInstitute for Advanced Research in Chemical Sciences (IAdChem), Universidad Autónoma de Madrid, 28049 Madrid, Spain
dCondensed Matter Physics Center (IFIMAC), Universidad Autónoma de Madrid, 28049 Madrid, Spain
eInstituto Madrileño de Estudios Avanzados en Nanociencia (IMDEA-Nanociencia), Cantoblanco, 28049 Madrid, Spain
fDonostia International Physics Center (DIPC), Paseo Manuel de Lardizabal 4, 20018 Donostia-San Sebastián, Spain
First published on 23rd November 2018
Abstract
Endohedral metallofullerenes (EMFs) synthetized in the laboratory are known to often violate the isolated pentagon and pentagon adjacency penalty rules that successfully describe the relative stability of pristine fullerene isomers. To explain these anomalies, several models have been proposed. In this work, we have systematically investigated the performance of the widely used IPSI (inverse pentagon separation index), ALA (additive local aromaticity) and CSI (charge stabilization index) models in predicting the relative stability of a large number of EMF isomers with cages ranging from C28 to C104 and charge states of 4− and 6−. By explicitly comparing with existing experiments and quantum chemistry calculations, we show that the predictive power of the ALA and CSI models is similarly good, with CSI being slightly superior though computationally much less involved. IPSI's performance is generally worse though still acceptable in a wide range of cage sizes, except for the higher charge states in the C62 to C82 size interval. From our analysis, we conclude that neither Coulomb electronic repulsion (IPSI) nor aromaticity (ALA) are the sole parameters governing the relative stability of EMF isomers. Electron delocalization in the π shell in combination with minimum strain (CSI) provides a more realistic description of the relative stabilities observed experimentally, as the former can compensate an unfavorable Coulomb repulsion and account for stabilizing binding effects that do not necessarily translate into aromaticity.
1 Introduction
Endohedral metallofullerenes (EMFs)1,2 have received a great deal of attention in recent years due to their exclusive characteristics among carbon-based compounds.3 In EMFs, the encapsulated species, usually a metal atom or a molecule, or a cluster containing one or several metal atoms, transfers electrons to the fullerene cage, which is thus negatively charged and acquires electronic and magnetic properties that are nonexistent in pristine neutral fullerenes. As a consequence, EMFs are considered good candidates for potential new applications in different fields of science,4–8 as for example organic photovoltaics and biomedicine. In the latter case, they have been proposed as possible antitumor9 and antimicrobial10 drugs, as contrast agents in magnetic resonance5 and X-ray imaging,11 and as radiotracers and radiopharmaceuticals.12Most EMFs are synthesized in the lab in very hot environments, e.g., through arc-discharges,13 combustion14,15 or radio-frequencies.16,17 In such environments, cages are formed through carbon-clustering processes18 at temperatures typically higher than 4000 K19 and thus the final products usually correspond to the global minima of the potential energy surface. In this way, carbon cages with sizes ranging from C2820 to C13021 have been produced in very diverse isomeric forms. Negatively charged fullerene cages can also be synthesized by directly attaching electrons to pristine neutral fullerenes, either in the gas phase22–24 or in solution.25,26
Spectroscopic measurements1,2 and quantum chemistry calculations27,28 have shown that the cage structures of synthesized EMFs often violate the well established isolated pentagon (IPR)29 and pentagon adjacency penalty (PAPR)30,31 rules. These rules state that pentagonal rings (hereafter called “pentagons”) tend to separate from each other to minimize strain in the fullerene cage, which is the dominant effect that controls the relative isomer stability of pristine neutral fullerenes. Therefore, it is clear that, to understand the frequent appearance of non-IPR or PAPR-violating isomers in synthesized EMFs, apart from strain, one should take into account other factors. With this aim, many different models have been proposed in the literature.32–38
In this work, we leave apart models designed for specific EMFs and will focus on those developed to predict the most stable structures of negatively charged fullerene isomers in a wide range of cage sizes and charge states. It has been found that the relative isomer stability of EMFs generally coincides with that of the pristine fullerene anions in the appropriate charge states.1,27 Such “general” models, however, stand on quite different physical grounds. Relying on the assumption that negative charges mainly concentrate on the pentagonal rings of the EMF cage, Poblet et al.35,36 have suggested that the larger the separation between the pentagons, the larger the stability. This simple electrostatic picture has been quantified by means of the inverse pentagon separation index (IPSI), which is calculated from the equilibrium geometry of a charged fullerene cage. In contrast, Solà et al.37,38 have found that the relative isomer stability of fullerene anions is mainly governed by the total aromaticity of the carbon cage. They proposed the additive local aromaticity (ALA) index to successfully predict the most stable hosting cages of a variety of EMFs in different charge states. In practice, the ALA is evaluated on the basis of the harmonic oscillator model of aromaticity (HOMA)39 index of each ring, which can be readily calculated using the equilibrium geometry of the cage. At variance with these approaches, more recently,40,41 we have proposed that the relative stability of EMF isomers results from the interplay between the stabilizing effect of π delocalization and the destabilizing effect of σ strain. Both effects have been taken into account through the charge stabilization index (CSI), which is exclusively based on simple topological arguments, namely the carbon–carbon connectivity in the fullerene cage, which does not require the knowledge of the actual EMF geometry. The CSI model has successfully predicted the cage structures of many charged fullerenes and EMFs observed in experiments or determined from elaborate quantum chemistry calculations.
Although the IPSI, ALA and CSI models are now well established and can be routinely applied to predict the lowest-energy structures of EMFs by using available computational tools (e.g., semiempirical quantum chemistry42–44 or density functional tight-binding45 methods), we do not know yet how good they are in providing the correct stability hierarchy within a large set of EMF isomers. As these models rely on very different assumptions, this is a critical point to determine which one provides a better representation of the physical reality.46 Another important point worth exploring is the performance of the CSI model against the IPSI and ALA models, since the former, not requiring any geometry optimization, is more affordable than the other two, thus permitting exploration of the large sets of EMF isomers.
In this work, we present a systematic application of the IPSI, ALA and CSI models to a large number of EMF isomers with cages ranging from C28 to C104 and charge states of 4− and 6−. By explicitly comparing with existing experimental results and quantum chemistry calculations performed for the occasion, we show that the predictive power of the ALA and CSI models is, in general, very good in the whole range of sizes investigated, with CSI being superior in some cases. The IPSI model exhibits a similar good predictive power except for the highest charge state in the C62 to C82 size interval, where errors can be up to three times larger than for the other two methods. Our analysis shows that Coulomb repulsion and aromaticity are two partial manifestations of π delocalization occurring in the fullerene cage, and that other effects resulting from this delocalization not included in the IPSI and ALA models may be crucial in determining the stability of the EMFs in some cases. These are correctly described by the CSI model.
The paper is organized as follows. In Section 2, we briefly describe the three methods, the basic equations on which they are based and the mathematical algorithm used to calculate the corresponding prediction error. In Section 3, we present the results of this comparative study and in Section 4, we summarize the main conclusions of our work.
2 Theoretical methods
We start by briefly describing the basic assumptions and mathematical formulae for the IPSI, ALA and CSI models.2.1 IPSI
The IPSI35,36 for a given cage isomer of fullerene anions is calculated as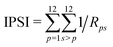 | (1) |
2.2 ALA
The ALA index is defined as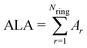 | (2) |
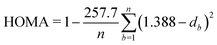 | (3) |
2.3 CSI
The charge stabilization index (CSI)40 of a given negatively charged fullerene isomer i with charge q and size 2n is defined as| CSIqi ≡ Xqi + 0.2NAPPi, | (4) |
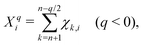 | (5) |
2.4 Electronic structure calculations and geometry optimizations
All initial geometries of fullerene isomers were generated by the CaGe program.49 The conventional labeling50 of isomers with their highest possible symmetries was determined using the FullFun software package,41 on the basis of the database in the Fullerene program.51All energy calculations and geometry optimizations (no symmetry constraint imposed) were performed at the self-consistent charge density functional tight-binding (SCC-DFTB)45 level, using the DFTB+ (version 1.2) code.52 As demonstrated in previous work,40,48,53,54 the SCC-DFTB method describes reasonably well the relative isomer energies of both neutral and charged fullerenes: it predicts correctly the experimental cage structures in EMFs as the lowest-energy isomers, and also gives similar results to those obtained from DFT calculations (B3LYP using 6-31G(d) or 6-31+G(d) basis sets).48
Due to the large computational effort required, we have only considered singlet spin multiplicity in all calculations. To validate this assumption, we have compared the energies of singlet and triplet states for a considerable number of isomers of C2nq with 2n = 68–104 and q = 4−, 6−, at the B3LYP/6-31G(d) level using the Gaussian 09 package.55 It turns out48 that for all the considered systems of C2n6−, the singlet state is more stable than the triplet one. This is also true for most C2n4− fullerene cages, except for a very few cases where the triplet state has slightly (typically 2–3 kcal mol−1) lower energy. Therefore, we believe that the spin multiplicity does not play an important role here.
2.5 Prediction error
In order to compare the performance of the IPSI, ALA and CSI models in predicting the relative stability of fullerene anions, we introduce the quantity PE (prediction error), which measures how much the isomer energy ordering predicted by a given model deviates from that resulting from the SCC-DFTB calculations. The prediction error is evaluated as follows: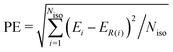 | (6) |
3 Results
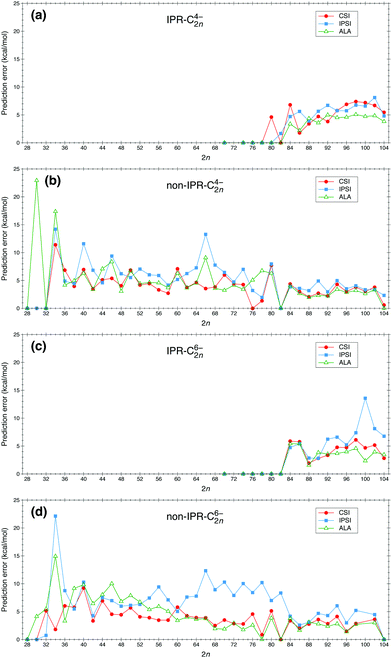
We have applied the IPSI, ALA and CSI models to study the relative stability of fullerene anions C2nq with 2n = 28–104 and q = 4−, 6−. The prediction errors, evaluated as defined in eqn (6), are shown in Fig. 1. For the sake of clarity and the requirement that the ISPI indicator needs to be applied separately to IPR and non-IPR isomers, we show the results corresponding to IPR and non-IPR isomers in separate panels. Fig. 1 shows that, with very few exceptions, prediction errors for the ALA and CSI models are of the order of 5 kcal mol−1 in the whole size range. This is quite remarkable in the case of the CSI calculations, in view of the simplicity of the model. Notably, ALA performs significantly worse than CSI for C304−, C664−, C764−, C784−, C346− and C466−. Typical prediction errors for IPSI are slightly larger than for ALA and CSI, and significantly larger, up to 10 kcal mol−1 or more, for C664−, C1006− and C346−, and all fullerenes with q = −6 in the C626−–C826− size interval. Thus, the problem with IPSI seems to be more severe for medium-sized fullerenes with the highest charge. This means that, for these systems, charge distribution is not the dominant effect at play. The good performance of the ALA and CSI models in these particular cases indicates that stability is mainly the consequence of the π electronic structure, which is well described by both models at different levels of approximation (HOMA versus Hückel). This observation is in line with the connections between electron delocalization, bond length and aromaticity, as recently revealed56,57 within the context of quantum theory of atoms in molecules.58,59One may notice in Fig. 1a and c that the ALA predictions are slightly better than the CSI ones for the larger IPR cages (2n ≥ 94). This is due to the fact that in the latter model, the π and strain energies are estimated in a simple and thus rather approximate manner (based solely on the atomic connectivity), while the ALA indicator is evaluated using the actual molecular geometry (optimized by quantum chemistry calculations). In view of this, we have applied the improved CSI model recently reported in ref. 41 to the IPR cages (C2nq with 2n = 70–104 and q = − 4, −6) by including a structural motif model60 to account for the relative strain energy of IPR isomers. As shown in Fig. S1 of the ESI,† the overall performance of the improved CSI model is better than that of the original CSI model, and becomes comparable with, and in some cases even better than, that of the ALA model.
Originally, the IPSI model was introduced to predict the relative isomer stability of fullerenes containing the same number of APPs.35 For the sake of simplicity, however, this distinction has not been made in Fig. 1. To prove that the above conclusion does not change when we only compare fullerene isomers containing the same number of APPs, we have also evaluated the ALA and CSI indicators for NAPP = 1, 2 and 3 separately and compared the corresponding prediction errors with those of IPSI. The results for C2n6− (2n = 66–82) with NAPP = 1, 2 and 3 are respectively shown in Fig. S2–S4 of the ESI.† For isomers with NAPP = λ (λ being 1, 2 and 3), the energy window of 30 kcal mol−1 has been defined by choosing Emin as the lowest energy among all isomers with λ APPs. This more refined analysis leads essentially to the same conclusion as that obtained from Fig. 1: IPSI leads in general to a significantly larger prediction error than the CSI and ALA indicators.
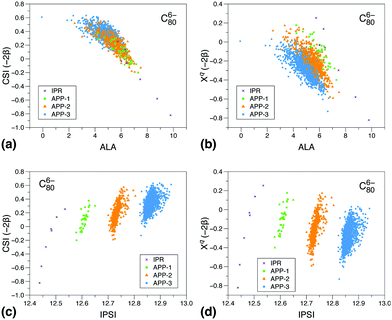
To gain a deeper insight into the reasons for the different performances of the three models, we show correlations of the CSI index and its π contribution, Xqi, with the ALA and IPSI indexes Fig. 2 and 3. We have chosen to show such diagrams for a case in which all three models work reasonably well, C806−, and a case in which CSI is clearly superior to the other two models, C346−. We have considered all isomers containing at most three APPs. As can be seen, for C806− (panel a), there is a very good correlation between CSI and ALA results irrespective of the number of APPs contained in the isomer. Correlation between the π contribution of CSI and ALA is also reasonable (panel b), although here we rather see a correlation line per group of isomers according to the number of APPs. The latter behavior is the consequence of the absence of strain in the Xqi index. This comparison shows that both π delocalization and strain are reasonably described by ALA and CSI, which is the reason why the corresponding prediction errors are very similar. In contrast, similar plots comparing CSI and IPSI (panels c and d) show that correlations are only observed between groups of isomers, irrespective of whether strain is included or not in the CSI model. This suggests that Coulomb repulsion due to the charge distribution resulting from π delocalization is not the only effect that controls the relative isomer stability in this case. As a consequence, the IPSI prediction error is larger than for ALA and CSI, although still acceptable. The result also helps to understand why the IPSI model needs to be applied separately to IPR and non-IPR isomers.35
 | ||
| Fig. 3 Idem Fig. 2 for all isomers of C346− with at most 17 APPs. | ||
Similar plots for C346− shown in Fig. 3 show no apparent correlations between CSI or its π component and the other two models. In this case, the CSI prediction error is less than 2 kcal mol−1, while that for ALA and IPSI is 15 kcal mol−1 and 22 kcal mol−1, respectively. So, again Coulomb repulsion and also total aromaticity resulting from π delocalization are not the key parameters responsible for the relative stability of C346− isomers. Both are partial aspects of π delocalization, which is a subtle effect that has other manifestations. Delocalization does not always imply aromaticity, or at least, not only aromaticity.61 Also, in order to lead to the largest possible stabilization, delocalization does not always place the charges in the most distant places in a molecule, as stabilization due to π delocalization can compensate the increase in Coulomb repulsion. In contrast with ALA and IPSI, CSI reasonably accounts for all aspects of π delocalization and its consequences, because, as described above and in ref. 40 and 41, the π contribution Xqi is mathematically equivalent to solving the Hückel equations for a π delocalized system. As is well known, although Hückel theory is not as accurate as standard quantum chemistry methods, it is still able to provide a very reasonable description of the relative energies of frontier orbitals in π delocalized systems,40,41,62,63 which are the relevant orbitals at play in negatively charged fullerenes. Even more importantly, Hückel theory allows one to easily and unambiguously compute the relative π stabilization energy, as this is the only energy considered in the model. The present results show that, in those cases where several effects due to π delocalization are at play, the CSI index provides a more equilibrated description of all these effects than the other two models.
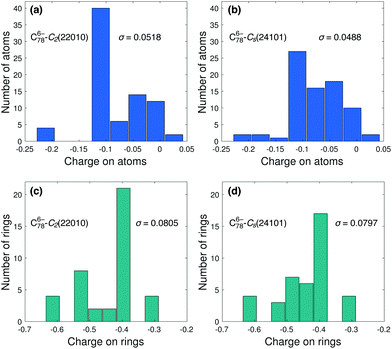
To better illustrate that neither Coulomb repulsion nor aromaticity are the only factors determining the relative stability of fullerene anion isomers, we analyze in more detail the cases of non-IPR C786− and C304−, for which the IPSI and ALA prediction errors are, respectively, much larger than those resulting from CSI (see Fig. 1b and d). We first consider two isomers of C786−, both having two APPs. The IPSI model predicts that isomer Cs(24![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 101) is the most stable one among all isomers with NAPP = 2, while the CSI model assigns the lowest-energy isomer to C2(22
101) is the most stable one among all isomers with NAPP = 2, while the CSI model assigns the lowest-energy isomer to C2(22![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 010) (see Table 1). In fact, SCC-DFTB calculations show that the former isomer is considerably higher in energy (by 48.8 kcal mol−1) than the latter, which contradicts the prediction by ISPI based on Coulomb repulsion arguments. Fig. 4a and b show the calculated charge distribution for both isomers. As can be seen, the charge is more evenly distributed in the Cs(24
010) (see Table 1). In fact, SCC-DFTB calculations show that the former isomer is considerably higher in energy (by 48.8 kcal mol−1) than the latter, which contradicts the prediction by ISPI based on Coulomb repulsion arguments. Fig. 4a and b show the calculated charge distribution for both isomers. As can be seen, the charge is more evenly distributed in the Cs(24![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 101) cage than in the C2(22
101) cage than in the C2(22![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 010) one, with a standard deviation of 0.0488 and 0.0518 for the former and the latter, respectively. The charge distribution on rings also shows a similar trend (see Fig. 4c and d). Consequently, one would expect34 less Coulomb repulsion in Cs(24
010) one, with a standard deviation of 0.0488 and 0.0518 for the former and the latter, respectively. The charge distribution on rings also shows a similar trend (see Fig. 4c and d). Consequently, one would expect34 less Coulomb repulsion in Cs(24![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 101) than in C2(22
101) than in C2(22![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 010), however, as mentioned above, the former structure is not the most stable one. Therefore, IPSI provides a reasonable estimate of the relative importance of Coulomb repulsion in both isomers, but clearly this is not the only criterion that explains their relative stability. In other words, a minimum Coulomb repulsion does not always correspond to maximum stability.
010), however, as mentioned above, the former structure is not the most stable one. Therefore, IPSI provides a reasonable estimate of the relative importance of Coulomb repulsion in both isomers, but clearly this is not the only criterion that explains their relative stability. In other words, a minimum Coulomb repulsion does not always correspond to maximum stability.
![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 010) and Cs(24
010) and Cs(24![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 101), both having two APPs
101), both having two APPs
| Isomer of C786− | E rel | IPSI | CSI |
|---|---|---|---|
C
2(22![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 010) 010) |
0.0 | 12.880 | −0.248 |
C
s(24![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 101) 101) |
48.8 | 12.867 | 0.144 |
We now consider the two isomers of C304− presented in Table 2. SCC-DFTB calculations indicate that isomer C2v(3) is considerably more stable (by 22.9 kcal mol−1) than C2v(2), as correctly predicted by the CSI model. The ALA index, however, predicts the opposite. In fact, Table 2 shows that the less stable isomer C2v(2) is much more aromatic (ALA index being less negative) than isomer C2v(3). Therefore, the present result clearly demonstrates that higher aromaticity does not necessarily imply higher stability of the fullerene anion.
| Isomer of C304− | E rel | ALA | CSI |
|---|---|---|---|
| C 2v(3) | 0.0 | −19.593 | 2.922 |
| C 2v(2) | 22.9 | −17.958 | 3.320 |
4 Conclusions
In this work, we have systematically analyzed the performance of the widely used IPSI, ALA and CSI models in predicting the relative stability of endohedral metallofullerene isomers. The three models link stability to different physical properties: minimum electronic repulsion (IPSI), maximum aromaticity (ALA), and maximum π delocalization in combination with minimum strain (CSI). We have shown that, with few exceptions, the performance of ALA and CSI is similarly good, with CSI being slightly superior though computationally much less involved, as it only requires the knowledge of the fullerene cage topology without the need for elaborate quantum-chemical geometry optimizations. IPSI's performance is generally worse but still acceptable in a wide range of cage sizes; however, for medium-sized fullerene cages containing six extra electrons, the corresponding prediction errors are significantly large.From our analysis, we conclude that neither Coulomb electronic repulsion nor aromaticity are the sole concepts governing the relative stability of endohedral metallofullerene isomers. Electron delocalization in the π shell, which is a more general concept than aromaticity, in combination with minimum strain provides a more realistic description of the relative stabilities observed experimentally.40,48 Indeed, in some cases, π delocalization of the additional cage electrons compensates an unfavorable Coulomb repulsion thus leading to a larger stability. Similarly, π electron delocalization does not necessarily translate into aromaticity, as the latter is only a partial aspect of the former.
Conflicts of interest
There are no conflicts to declare.Acknowledgements
This work has been supported by the MINECO projects FIS2016-77889-R and CTQ2016-76061-P, the ‘Severo Ochoa’ Programme for Centres of Excellence in R&D (SEV-2016-0686) and the ‘María de Maeztu’ Programme for Units of Excellence in R&D (MDM-2014-0377). We also acknowledge the generous allocation of computer time at the Centro de Computación Científica of the Universidad Autónoma de Madrid CCC-UAM. Y. W. acknowledges the Thousand Talents Plan for Young Professionals of China.Notes and references
- A. A. Popov, S. Yang and L. Dunsch, Chem. Rev., 2013, 113, 5989–6113 CrossRef CAS
.
- X. Lu, L. Feng, T. Akasaka and S. Nagase, Chem. Soc. Rev., 2012, 41, 7723–7760 RSC
.
- T. Akasaka and X. Lu, Chem. Rec., 2012, 12, 256–269 CrossRef CAS
.
- H. C. Dorn and P. P. Fatouros, Nanosci. Nanotechnol. Lett., 2010, 2, 65–72 CrossRef CAS
.
- P. Anilkumar, F. Lu, L. Cao, P. G. Luo, J.-H. Liu, S. Sahu, K. N. Tackett II, Y. Wang and Y.-P. Sun, Curr. Med. Chem., 2011, 18, 2045–2059 CrossRef CAS
.
- Z. Chen, R. Mao and Y. Liu, Curr. Drug Metab., 2012, 13, 1035–1045 CrossRef CAS
.
- M. Rudolf, S. Wolfrum, D. M. Guldi, L. Feng, T. Tsuchiya, T. Akasaka and L. Echegoyen, Chem. – Eur. J., 2012, 18, 5136–5148 CrossRef CAS
.
- R. B. Ross, C. M. Cardona, D. M. Guldi, S. G. Sankaranarayanan, M. O. Reese, N. Kopidakis, J. Peet, B. Walker, G. C. Bazan, E. Van Keuren, B. C. Holloway and M. Drees, Nat. Mater., 2009, 8, 208–212 CrossRef CAS
.
- J. Meng, X. Liang, X. Chen and Y. Zhao, Integr. Biol., 2013, 5, 43–47 RSC
.
- D. M. McCluskey, T. N. Smith, P. K. Madasu, C. E. Coumbe, M. A. Mackey, P. A. Fulmer, J. H. Wynne, S. Stevenson and J. P. Phillips, ACS Appl. Mater. Interfaces, 2009, 1, 882–887 CrossRef CAS PubMed
.
- E. B. Iezzi, J. C. Duchamp, K. R. Fletcher, T. E. Glass and H. C. Dorn, Nano Lett., 2002, 2, 1187–1190 CrossRef CAS
.
- D. W. Cagle, S. J. Kennel, S. Mirzadeh, J. M. Alford and L. J. Wilson, Proc. Natl. Acad. Sci. U. S. A., 1999, 96, 5182–5187 CrossRef CAS
.
- S. Farhat and C. D. Scott, J. Nanosci. Nanotechnol., 2006, 6, 1189–1210 CrossRef CAS
.
- H. Murayama, S. Tomonoh, J. M. Alford and M. E. Karpuk, Fullerenes, Nanotubes, Carbon Nanostruct., 2005, 12, 1–9 CrossRef
.
- H. Takehara, M. Fujiwara, M. Arikawa, M. D. Diener and J. M. Alford, Carbon, 2005, 43, 311–319 CrossRef CAS
.
- G. Peters and M. Jansen, Angew. Chem., Int. Ed., 1992, 31, 223–224 CrossRef
.
- M. Jansen, G. Peters and N. Wagner, Z. Anorg. Allg. Chem., 1995, 621, 689–693 CrossRef CAS
.
- S. Irle, G. Zheng, Z. Wang and K. Morokuma, J. Phys. Chem. B, 2006, 110, 14531–14545 CrossRef CAS
.
- K. R. Hearne, S. A. Nixon and D. Whittaker, J. Phys. D, 1972, 5, 710 CrossRef CAS
.
- P. W. Dunk, N. K. Kaiser, M. Mulet-Gas, A. Rodríguez-Fortea, J. M. Poblet, H. Shinohara, C. L. Hendrickson, A. G. Marshall and H. W. Kroto, J. Am. Chem. Soc., 2012, 134, 9380–9389 CrossRef CAS
.
- C. Pan, L. Bao, X. Yu, H. Fang, Y. Xie, T. Akasaka and X. Lu, ACS Nano, 2018, 12, 2065–2069 CrossRef CAS
.
-
Y. Wang, M. Alcamí and F. Martín, Clusters and Fullerenes, in Handbook of Nanophysics, ed. K. D. Sattler, Taylor & Francis Publisher (CRC Press), London, 2010, vol. 2, ch. 25, pp. 1–23 Search PubMed
.
- O. T. Ehrler, J. M. Weber, F. Furche and M. M. Kappes, Phys. Rev. Lett., 2003, 91, 113006 CrossRef PubMed
.
- S. Tomita, J. U. Andersen, H. Cederquist, B. Concina, O. Echt, J. S. Forster, K. Hansen, B. A. Huber, P. Hvelplund, J. Jensen, B. Liu, B. Manil, L. Maunoury, S. Brøndsted Nielsen, J. Rangama, H. T. Schmidt and H. Zettergren, J. Chem. Phys., 2006, 124, 024310 CrossRef CAS
.
- X.-B. Wang, H.-K. Woo, X. Huang, M. M. Kappes and L.-S. Wang, Phys. Rev. Lett., 2006, 96, 143002 CrossRef
.
- L. Echegoyen and L. E. Echegoyen, Acc. Chem. Res., 1998, 31, 593–601 CrossRef CAS
.
- A. A. Popov and L. Dunsch, J. Am. Chem. Soc., 2007, 129, 11835–11849 CrossRef CAS PubMed
.
- M. Mulet-Gas, L. Abella, P. W. Dunk, A. Rodriguez-Fortea, H. W. Kroto and J. M. Poblet, Chem. Sci., 2015, 6, 675–686 RSC
.
- H. W. Kroto, Nature, 1987, 329, 529–531 CrossRef CAS
.
- E. Campbell, P. Fowler, D. Mitchell and F. Zerbetto, Chem. Phys. Lett., 1996, 250, 544–548 CrossRef CAS
.
- E. Albertazzi, C. Domene, P. W. Fowler, T. Heine, G. Seifert, C. Van Alsenoy and F. Zerbetto, Phys. Chem. Chem. Phys., 1999, 1, 2913–2918 RSC
.
- J. M. Campanera, C. Bo and J. M. Poblet, Angew. Chem., Int. Ed., 2005, 44, 7230–7233 CrossRef CAS PubMed
.
- R. Valencia, A. Rodríguez-Fortea and J. M. Poblet, J. Phys. Chem. A, 2008, 112, 4550–4555 CrossRef CAS PubMed
.
- H. Zettergren, M. Alcamí and F. Martín, ChemPhysChem, 2008, 9, 861–866 CrossRef CAS PubMed
.
- A. Rodríguez-Fortea, N. Alegret, A. L. Balch and J. M. Poblet, Nat. Chem., 2010, 2, 955–961 CrossRef PubMed
.
- N. Alegret, M. Mulet-Gas, X. Aparicio-Anglès, A. Rodríguez-Fortea and J. M. Poblet, C. R. Chim, 2012, 15, 152–158 CrossRef CAS
.
- M. Garcia-Borràs, S. Osuna, M. Swart, J. M. Luis and M. Solà, Angew. Chem., Int. Ed., 2013, 52, 9275–9278 CrossRef PubMed
.
- M. Garcia-Borràs, S. Osuna, J. M. Luis, M. Swart and M. Solà, Chem. Soc. Rev., 2014, 43, 5089–5105 RSC
.
- J. Kruszewski and T. Krygowski, Tetrahedron Lett., 1972, 13, 3839–3842 CrossRef
.
- Y. Wang, S. Díaz-Tendero, M. Alcamí and F. Martín, Nat. Chem., 2015, 7, 927–934 CrossRef CAS PubMed
.
- Y. Wang, S. Díaz-Tendero, M. Alcamí and F. Martín, J. Chem. Theory Comput., 2018, 14, 1791–1810 CrossRef CAS
.
- M. J. S. Dewar, E. G. Zoebisch, E. F. Healy and J. J. P. Stewart, J. Am. Chem. Soc., 1985, 107, 3902–3909 CrossRef CAS
.
- J. J. P. Stewart, J. Comput. Chem., 1989, 10, 209–220 CrossRef CAS
.
- J. J. P. Stewart, J. Comput. Chem., 1989, 10, 221–264 CrossRef CAS
.
- M. Elstner, D. Porezag, G. Jungnickel, J. Elsner, M. Haugk, T. Frauenheim, S. Suhai and G. Seifert, Phys. Rev. B: Condens. Matter Mater. Phys., 1998, 58, 7260–7268 CrossRef CAS
.
- A. Rodríguez-Fortea and J. M. Poblet, Faraday Discuss., 2014, 173, 201–213 Search PubMed
.
- P. W. Fowler and D. E. Manolopoulos, Nature, 1992, 355, 428–430 CrossRef CAS
.
- Y. Wang, S. Díaz-Tendero, F. Martín and M. Alcamí, J. Am. Chem. Soc., 2016, 138, 1551–1560 CrossRef CAS PubMed
.
- G. Brinkmann, O. D. Friedrichs, S. Lisken, A. Peeters and N. V. Cleemput, MATCH, 2010, 63, 533–552 CAS
.
-
P. Fowler and D. E. Manolopoulos, An Atlas of Fullerenes, Clarendon Press, Oxford, UK, 1995 Search PubMed
.
- P. Schwerdtfeger, L. Wirz and J. Avery, J. Comput. Chem., 2013, 34, 1508–1526 CrossRef CAS PubMed
.
- B. Aradi, B. Hourahine and T. Frauenheim, J. Phys. Chem. A, 2007, 111, 5678–5684 CrossRef CAS
.
- G. Zheng, S. Irle and K. Morokuma, Chem. Phys. Lett., 2005, 412, 210–216 CrossRef CAS
.
- Y. Wang, H. Zettergren, P. Rousseau, T. Chen, M. Gatchell, M. H. Stockett, A. Domaracka, L. Adoui, B. A. Huber, H. Cederquist, M. Alcamí and F. Martín, Phys. Rev. A: At., Mol., Opt. Phys., 2014, 89, 062708 CrossRef
.
-
M. J. Frisch, G. W. Trucks, H. B. Schlegel, G. E. Scuseria, M. A. Robb, J. R. Cheeseman, G. Scalmani, V. Barone, B. Mennucci, G. A. Petersson, H. Nakatsuji, M. Caricato, X. Li, H. P. Hratchian, A. F. Izmaylov, J. Bloino, G. Zheng, J. L. Sonnenberg, M. Hada, M. Ehara, K. Toyota, R. Fukuda, J. Hasegawa, M. Ishida, T. Nakajima, Y. Honda, O. Kitao, H. Nakai, T. Vreven, J. A. Montgomery, Jr., J. E. Peralta, F. Ogliaro, M. Bearpark, J. J. Heyd, E. Brothers, K. N. Kudin, V. N. Staroverov, T. Keith, R. Kobayashi, J. Normand, K. Raghavachari, A. Rendell, J. C. Burant, S. S. Iyengar, J. Tomasi, M. Cossi, N. Rega, J. M. Millam, M. Klene, J. E. Knox, J. B. Cross, V. Bakken, C. Adamo, J. Jaramillo, R. Gomperts, R. E. Stratmann, O. Yazyev, A. J. Austin, R. Cammi, C. Pomelli, J. W. Ochterski, R. L. Martin, K. Morokuma, V. G. Zakrzewski, G. A. Voth, P. Salvador, J. J. Dannenberg, S. Dapprich, A. D. Daniels, O. Farkas, J. B. Foresman, J. V. Ortiz, J. Cioslowski and D. J. Fox, Gaussian 09, Revision C.01, Gaussian, Inc., Wallingford CT, 2010 Search PubMed
.
-
M. Rafat and P. L. A. Popelier, in The quantum theory of atoms in molecules: from solid state to DNA and drug design, ed. C. F. Matta and R. J. Boyed, Wiley-VCH, Weinheim, 2007, pp. 121–141 Search PubMed
.
- Z. Badri and C. Foroutan-Nejad, Phys. Chem. Chem. Phys., 2016, 18, 11693–11699 RSC
.
-
R. F. W. Bader, Atoms in Molecules: A Quantum Theory, Oxford University Press, Oxford, 1990 Search PubMed
.
- R. F. W. Bader, Chem. Rev., 1991, 91, 893–928 CrossRef CAS
.
- Y. Wang, S. Diaz-Tendero, M. Alcami and F. Martin, Phys. Chem. Chem. Phys., 2017, 19, 19646–19655 RSC
.
- I. Fernández, C. A. Dyker, A. DeHope, B. Donnadieu, G. Frenking and G. Bertrand, J. Am. Chem. Soc., 2009, 131, 11875–11881 CrossRef
.
- Y. Wang, S. Díaz-Tendero, M. Alcamí and F. Martín, J. Am. Chem. Soc., 2017, 139, 1609–1617 CrossRef CAS
.
- P. Pla, Y. Wang and M. Alcamí, Chem. Commun., 2018, 54, 4156–4159 RSC
.
Footnote |
| † Electronic supplementary information (ESI) available: Fig. S1–S4. See DOI: 10.1039/c8cp06707d |
| This journal is © the Owner Societies 2019 |