Coexistence of piezoelectricity and magnetism in two-dimensional vanadium dichalcogenides

Abstract

Akin to three dimensional (3D) multiferroics, two dimensional (2D) piezoelectric materials with intrinsic magnetic properties are promising applications in nanoscale spintronic devices. In this study, 2D magnetic transition metal dichalcogenides (VS₂, VSe₂, and Janus-VSSe) have been investigated by the first principles method for their structural, magnetic, electronic, and piezoelectric properties. H type Janus-VSSe has been shown to be more stable than the T type, and dynamically stable through phonon frequency analysis. Our calculations show that H type Janus-VSSe is not only a magnetic semiconductor but also exhibits appreciable in-plane and vertical piezoelectricity. Additionally, H type VS₂ and VSe₂ also show high in-plane piezoelectricity. The calculated values of in-plane piezoelectricity for these magnetic materials are higher than traditional 3D piezoelectric materials such as α-quartz. The coexistence of magnetism and piezoelectricity in H type VS₂, Janus-VSSe, and VSe₂ makes them promising piezoelectric materials in nanoscale spin devices.

---

1. Introduction

In recent years, significant attention has been directed towards the study of layered two-dimensional (2D) materials such as graphene, black phosphorus,¹ MXenes,^2–5 and transition metal dichalcogenides (TMDs) due to their potential applications in spin electronics,⁶ semiconductors,⁷ and sensors.⁸ Among these 2D materials, TMDs show remarkable optical and electronic properties, and are promising materials for electronic devices.^9–13 Particularly, free standing monolayer MoS₂ has been shown to have piezoelectricity by Zhang et al.¹⁴ In-plane piezoelectric d₁₁ coefficients of 2D materials such as CrSe₂ and CrTe₂ are typically greater than 5 pm V⁻¹, which is a typical value for applications.¹¹ Interestingly, through density functional theory calculations, Dong et al. showed that Janus-MoSSe has a large in-plane and vertical piezoelectricity due to the structural breaking-symmetry.¹⁵ Also, a variant of Janus MoSSe has been synthesized with all top-layer S atoms replaced by Se.¹⁶ This indicates that inducing structural breaking-symmetry by Janus phase to enhance piezoelectric coefficients is executable. Thus, TMDs including Janus structures are promising piezoelectric materials.

2D piezoelectric materials with intrinsic tunable magnetic properties can have extended applications in spin electronic devices similar to 3D multiferroics. In the case of 3D materials, multiferroics have magnetic ordering with simultaneous ferroelectric properties.¹⁷ The magneto–electric coupling makes them promising materials in sensors and spin electronic devices with atomic-level scales. More importantly, the properties of 2D piezoelectric magnetic materials can be tuned easily through epitaxial strain or magnetic field. As a result, there is a growing need to investigate the piezoelectricity and magnetic properties of 2D materials.

Until now, a few types of 2D magnetic materials have been studied, such as VS₂, Cr₂Ge₂Te₆, CrI₃, Cr or Mn-based MXene, and transition metal doped MXene.^18–22 For example, Gong et al. showed that Cr₂Ge₂Te₆ is an intrinsic ferromagnetic 2D material.²⁰ Previous work from our group also showed that Cr-based double metal MXenes can be antiferromagnetic or ferromagnetic depending on their terminations and compounds.^2,3 2D vanadium dichalcogenides such as VS₂ and VSe₂ have also been experimentally demonstrated to be magnetic by Guo et al. and studied theoretically by Ma et al.^19,23 From a structural standpoint, theoretical results have shown that 2D VS₂ and VSe₂ energetically prefer to be H type rather than T type.¹⁹ However, until now, VS₂ and VSe₂ have been synthesized in the T type.^23,24 Through harmonic approximation, Liu et al. showed that bulk VS₂ prefers to exhibit the T type at room temperature, whereas monolayer VS₂ prefers to exhibit the H type below or at room temperature.¹⁸

Due to the inversion symmetry along the z-direction, piezoelectricity of H type TMDs has been restricted in the xy-plane along the armchair direction.¹⁵ In order to possess piezoelectricity along the vertical direction, breaking-symmetry along the z-direction is necessary. Interestingly, H type Janus-TMDs have the required breaking-symmetry along z-directions, which explains their large piezoelectricity along the vertical direction.¹⁵ Hence, theoretical study on the piezoelectricity of Janus-VSSe can generate insights and promote the application of TMDs in spin electronics. In fact, experimental studies have shown that Janus phase of TMDs is an effective approach to tune the physical and chemical properties of TMDs.^16,25 For example, Janus phase with different compounds on its two sides has distinct features and promising applications due to its structural breaking-symmetry, which has been extensively implemented on nano-particles and some 2D materials.^26,27 Calculations and experimental results have indicated that Janus 2D materials can be synthesized and their piezoelectricity is quite distinct from pure TMDs.

Taking all these factors into account, the structural and magnetic properties of VS₂, VSe₂ and Janus-VSSe in T and H types are investigated through density functional theory (DFT) in this study. The band structures of H type VS₂, VSe₂ and Janus-VSSe are analyzed, and used to calculate their piezoelectricity and elasticity. The corresponding values of piezoelectricity (d₁₁) in the xy-plane along the armchair direction for H type VS₂, VSe₂ and Janus-VSSe are calculated to be 2.34, 2.30, and 2.97 pm V⁻¹, respectively. Finally, the piezoelectricity along the vertical direction of multilayer Janus-VSSe is studied. The value of e₃₃ is calculated to be 0.49 C m⁻², corresponding to a d₃₃ of 4.92 pm V⁻¹.

2. Calculation methods and models

DFT was used for all ionic relaxations integrated in the Vienna Ab initio simulation package (VASP).^28–30 Piezoelectricity was calculated using density functional perturbation theory (DFPT).³¹ The generalized gradient approximation (GGA-PBE) functional was utilized to determine the exchange–correlation energy.³² Projector augmented wave (PAW) potentials were used in all calculations.³³ The kinetic energy cutoff was set to 500 eV. The vacuum layer thickness along the z-axis was chosen to be larger than 15 Å to minimize the interactions between two nearest layers. The ionic relaxation was performed until the force on each atom was less than 0.01 eV Å⁻¹. The Monkhorst–Pack method was chosen to set the k-point meshes.³⁴ The k-point grid spacing in each direction of reciprocal space was within 0.03 Å⁻¹.

3. Results and discussion

3.1. Structural and magnetic properties of monolayer vanadium dichalcogenides

Analysis of the T and H types of monolayer VS₂, Janus-VSSe, and VSe₂, shows that H type is more energetically preferred than T type for all the compounds, in accordance with previous theoretical results.¹⁹ From first principles calculations, Zhang et al. also showed that H type for monolayer VS₂ is energetically favorable as compared to T type at room temperature.¹⁸ These results validate the calculation methods used in this study. Furthermore, H type Janus-VSSe is energetically more preferable than a mixture of VS₂ and VSe₂ (VS₂/2 + VSe₂/2). This result indicates that Janus-VSSe can be synthesized experimentally and the thermodynamic aspects are favorable.

The lattice parameters of T type VS₂ and VSe₂ are 3.18 and 3.33 Å, respectively, which are in good agreement with the experimental results of 3.22 and 3.35 Å.^35,36 The lattice parameters of H types are similar to the corresponding T types. For T and H type Janus-VSSe, the lattice parameters are 3.26 and 3.25 Å, respectively, which are larger than VS₂ but smaller than VSe₂. The bond lengths of V–S (L_V–S) in VS₂ and Janus-VSSe are 2.34 and 2.36 Å, respectively, while the bond length of V–Se (L_V–Se) is about 2.50 Å, which is larger than that of L_V–S.

The magnetic moment of V atoms in T type VS₂ and VSe₂ are 0.54 and 0.68 μ_B, respectively, in accordance with earlier experimental and theoretical results.³⁵ The magnetic moments of V atoms in H types are higher than those of T types (∼1.0 μ_B) and a similar trend is obtained for Janus-VSSe. Note that the calculation results by the PBE functional here are similar to that of the GGA+U method conducted by Popov and coworkers.³⁷ This is mainly due to the localization and correlations of 3d electrons in the V atoms are weaker than other 3d elements such as Mn, Co, Fe, and Ni. For the ground states of all 2D vanadium dichalcogenides, the spin directions of V atoms are in-plane along the x-axis. When a spin up channel is fixed along the z axis (out-of-plane), the energy of all 2D vanadium dichalcogenides increases with an order of 10⁻³ eV.

Due to inversion symmetry in T type, no piezoelectric properties can be expected. As a result, H type VS₂, VSe₂, and Janus-VSSe are investigated for piezoelectricity in this study. The lattice parameters, bond lengths and magnetic moments of the constituent V, S, and Se atoms are summarized in Table 1.

Table 1 Energy (E), lattice parameter (a), bond length of V–S (L_V–S), bond length of V–Se (L_V–Se) and magnetic moment (M) of V, S, and Se atoms

	H-VS2	T-VS2	H-VSSe	T-VSSe	H-VSe2	T-VSe2
E (eV)	−39.49	−39.40	−37.78	−37.69	−36.06	−35.97
a (Å)	3.18	3.18	3.25	3.26	3.33	3.33
L V–S (Å)	2.36	2.35	2.36	2.34	—	—
L V–Se (Å)	—	—	2.51	2.50	2.50	2.49
M V (μB)	1.02	0.54	1.02	0.67	1.08	0.68
M S (μB)	−0.05	−0.03	−0.02	−0.02	—	—
M Se (μB)	—	—	−0.08	−0.05	−0.07	−0.05

---

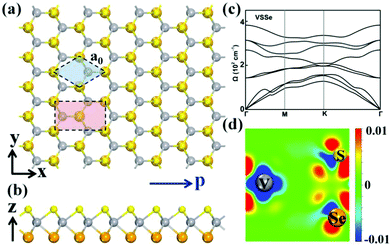
Since, energetically favorable configurations obtained through ionic relaxations based on DFT may not be stable in their equilibrium positions, the stability of H type Janus-VSSe is further probed by phonon dispersions. The corresponding top and side views of H type Janus-VSSe are shown in Fig. 1(a and b). As shown in Fig. 1(c), all phonon frequencies of H type Janus-VSSe are positive, indicating that H type Janus-VSSe is dynamically stable. The highest phonon frequencies are around 400 cm⁻¹, which is close to VS₂ and VSe₂.³⁸

Fig. 1 (a) Top view of H type Janus-VSSe. (b) Side view of H type Janus-VSSe. (c) Phonon branches of two-dimensional single-layer H type Janus-VSSe. Phonon dispersions are presented along the Γ–K–M–Γ directions of the Brillouin zone. (d) Charge density difference of H type Janus-VSSe.

Since the electronegativity of S is larger than that of Se, there are more electrons assembling near S. As show in Table 2, for H type VS₂, there are 6.90 electrons on S atoms, as compared to 6.81 electrons on Se atoms in H type VSe₂. For H type Janus-VSSe, there are also more electrons on S atoms as compared to Se atoms, as shown in Fig. 1(d). This induces an asymmetry of Janus-VSSe along the vertical direction, thereby significantly influencing the piezoelectricity.

Table 2 Valence electrons (e) of V, S, and Se atoms in H type VS₂, VSSe, and VSe₂

	H-VS2	H-VSSe	H-VSe2
e V	3.20	3.28	3.37
e S	6.90	6.96	—
e Se	—	6.75	6.81

---

Piezoelectric materials also can act as semiconductors, so the band structures of H type VS₂, Janus-VSSe, and VSe₂ structures were calculated using the Heyd–Scuseria–Ernzerhof (HSE06) hybrid functional, which has been shown to be effective in studying semiconductors.³⁹ The calculation results show that H type VS₂, Janus-VSSe, and VSe₂ are semiconductors with band gaps of 0.43, 0.91 and 0.88 eV, respectively (Fig. 2). Specifically, H type VS₂ and VSSe are indirect semiconductors, while H type VSe₂ is a direct semiconductor.

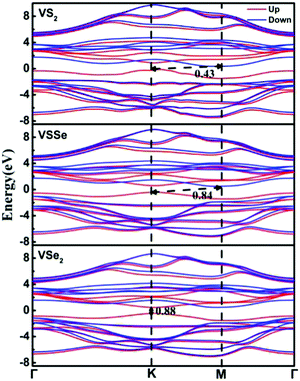Fig. 2 Band structures of H type VS₂, Janus-VSSe, and VSe₂. The red and blue lines represent the spin-up and spin-down bands.

3.2. In-plane and vertical piezoelectric coefficients of vanadium dichalcogenides

The first-order partial derivative was used to characterize the linear piezoelectric effect of single layer 2D vanadium dichalcogenides, as shown in the following equations:

e_ijk = əP_i/əε_j = əε_jk/əE_i (1)

d_ijk = əP_i/əσ_jk = əσ_jk/əE_i (2)

where, P_i is the surface polarization, ε_jk is the strain tensor, E_i the macroscopic electric field, and σ_jk is the stress. e_ijk and d_ijk are third-rank piezoelectric tensors. i, j, and k ∈ (1, 2, and 3), in which 1 and 2 refer to armchair and zigzag directions in the atomic layer plane (Fig. 1(a)), respectively, while 3 refers to the vertical direction of the 2D atomic layer. Using the Voigt notation, e_ijk and d_ijk can be represented as e_il and d_il, respectively, where l ∈ (1, 2, 4, 5, and 6).^11,15,40C_ij represents the elastic tensors, and then e_il and d_il have the following relationship:

e_ik = d_ijC_jk (3)

For 2D materials, C_ij and e_ij are multiplied by the length of the z-axis. For nonmagnetic single TMDs, earlier studies have shown that e₁₁ = −e₁₂ and e₂₆ = −e₁₁, which is caused by their 3m point-group symmetry.⁴⁰ However, spin directions may lead to the absence of such symmetry in magnetic TMDs.

An orthorhombic unit cell was used for the calculation of piezoelectricity, as shown in Fig. 1(a). The calculated values of e₁₁ for H type VS₂, VSSe, and VSe₂ are 311.46, 282.87 and 322.83 pC m⁻¹, respectively. The corresponding values of d₁₁ for H type VS₂, VSSe, and VSe₂ are 2.34, 2.30, and 2.97 pm V⁻¹, respectively. These results are comparable with earlier reported values for other transition metal dichalcogenides such as WS₂ obtained from DFT calculations.^11,15,40 The values of d₁₁ for these H type VS₂, VSSe, and VSe₂ are higher than α-quartz (d₁₁ = 2.27 pm V⁻¹), which is a common 3D piezoelectric material.⁴¹ This indicates that H type VS₂, Janus-VSSe, and VSe₂ show potential in atomic in-plane piezoelectric devices.

Due to the inversion symmetry along the z-direction, e₃₁ and d₃₁ of monolayer H type VS₂ and VSe₂ are zero, and their piezoelectric polarizations are restricted in the xy-plane along the armchair direction. However, for the H type Janus-VSSe monolayer, e₃₁ is obtained as 76.95 pC m⁻¹. Such a non-zero value is attributed to the structural breaking-symmetry along the z-direction. Thus, extensile strain can cause both vertical and in-plane piezoelectric polarizations in Janus-VSSe monolayers. All the obtained piezoelectric coefficients are summarized in Table 3.

Table 3 Piezoelectric coefficients e₁₁ and e₂₆ of single layer H type VS₂, Janus-VSSe, and VSe₂

	e 11 (pC m^−1)	e 31 (pC m^−1)	C 11 (N m^−1)	C 12 (N m^−1)	d 11 (pm V^−1)
H type VS2	311.46	0	102.46	31.20	2.34
H type VSSe	282.87	76.95	93.10	28.71	2.30
H type VSe2	322.83	0	84.12	26.65	2.97

---

Additionally, the polarization along the x-axis (arm-chair direction) and magnetic moment were calculated under different extensile strains. The strain was realized by stretching or compressing the optimized orthorhombic unit cell along the x axis by ±1 and ±0.5% with y-axis. As shown in Fig. 3, the polarizations for VS₂ and VSSe increased linearly with extensile strain, while a non-linear variation is observed for VSe₂ under ±1% strain. Similarly, the magnetic moment of Cr atoms also increased monotonically with extensile strain. The bond lengths of V–V, V–S, and V–Se increase with extensile strain, weakening the covalence interaction between V and nearby atoms. This leads to an increase in the number of unpaired electrons for V atoms, which results in the enhanced magnetic moment of V atoms. The inverse piezoelectric effect means that application of an electric field will lead to a deformation or strain of these materials along the corresponding direction. The induced deformation or strain will also cause the variation of magnetic moment. As a result, the magnetic moment can be varied by an electric field, which is a kind of magnetoelectric effect. Such a characteristic will promote the applications of two-dimensional vanadium dichalcogenides in spin electronic nano-devices.

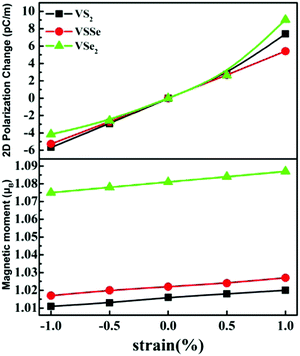Fig. 3 Polarization along the x-axis (top panel) and the magnetic moment of V atoms (down panel) for monolayer VS₂, VSSe, and VSe₂ with uniaxial strain along the x-axis.

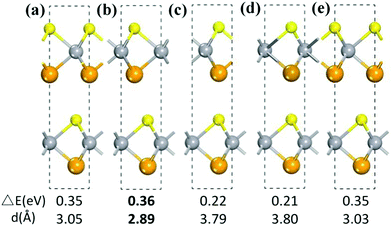
Since Janus-VSSe possesses vertical piezoelectricity, a multilayer Janus-VSSe comprising of stacked monolayers can yield a large vertical piezoelectricity. Five different stacking models (Fig. 4) with high symmetry were considered to ascertain the energetically favorable configuration. The second model as shown in Fig. 4(b) was found to be the most stable stacking models with 2.89 Å interlayer distance and 0.36 eV binding energy. For this structure, the value of e₃₃ is 0.49 C m⁻², corresponding to a d₃₃ of 4.92 pm V⁻¹. The vertical piezoelectricity value for H type Janus-VSSe is close to Janus-MoSSe and AlN.¹⁵ This suggests that H type Janus-VSSe is applicable to piezoelectric devices while maintaining its magnetic properties.

Fig. 4 Five high-symmetry stacking structures of multilayer Janus-VSSe. For (a), (b), and (c), the two Janus-VSSe monolayers are antiparallel orientated. S and Se atoms in up layers are settled on V-top site (a), on hollow site (b), and S-top site (c). For (d) and (e) the two Janus-VSSe monolayers are parallel orientated. S and Se atoms in up layers are settled on S-top site (d), and on V-top site (e).

Although the in-plane piezoelectric coefficients of H type VS₂, Janus-VSSe, and VSe₂ and the vertical piezoelectric coefficients of multilayer Janus-VSSe are smaller than other transition metal dichalcogenides, having a similar magnetic property makes them interesting 2D materials for applications in nanoscale devices.

4. Conclusions

The electronic and magnetic properties of H type VS₂, Janus-VSSe, and VSe₂ were studied by the first principles method. The results showed that H type was more energetically preferred for Janus-VSSe, VS₂, and VSe₂, as compared to T type. H type Janus-VSSe was also shown to be dynamically stable through phonon frequency analysis. All the H types were magnetic semiconductors with the band gap range of 0.4 to 1.0 eV. The corresponding values of d₁₁ (along armchair direction) obtained for VS₂, Janus-VSSe, and VSe₂ were 2.34, 2.30, and 2.97 pm V⁻¹, respectively, which are higher than traditional 3D piezoelectric material such as α-quartz (d₁₁ = 2.27 pm V⁻¹). Vertical piezoelectricity was observed along the z-direction of Janus-VSSe due to the structural breaking-symmetry. Piezoelectricity of the multilayer Janus-VSSe e₃₃ was 0.49 C m⁻², corresponding to a d₃₃ of 4.92 pm V⁻¹. H type VS₂, VSSe, and VSe₂ have shown to be promising 2D materials due to their unique piezoelectric and magnetic properties for applications in nanoscale spin electronic devices.

Conflicts of interest

There are no conflicts to declare.

Acknowledgements

We acknowledge the financial support by the National Natural Science Foundation of China (Grant No. 51502154, 51472255, and 21401116), the NSF of Ningbo (2017A610037), the program for Ningbo Municipal Science and Technology Innovative Research Team (2015B11002), the Visiting Scholar Program from the China Scholarship Council, and special funds for the Construction Teacher of Quzhou University (Grant No. XNZQN201501).

References

1. T. Sasaki, K. Kondo, Y. Akahama, S. Nakano and T. Taniguchi, Jpn. J. Appl. Phys., 2017, 56, 05FB06.
2. J. Yang, X. Zhou, X. Luo, S. Zhang and L. Chen, Appl. Phys. Lett., 2016, 109, 203109.
3. J. Yang, X. Luo, X. Zhou, S. Zhang, J. Liu, Y. Xie, L. Lv and L. Chen, Comput. Mater. Sci., 2017, 139, 313–319.
4. J. Yang, A. Wang, S. Zhang, H. Wu and L. Chen, Comput. Mater. Sci., 2018, 153, 303–308.
5. J. Yang, S. Zhang, A. Wang, R. Wang, C.-K. Wang, G.-P. Zhang and L. Chen, Nanoscale, 2018, 10, 19492–19497.
6. J. H. Yang, X. P. Luo, S. Z. Zhang and L. Chen, Phys. Chem. Chem. Phys., 2016, 18, 12914–12919.
7. Y. Y. Liu, P. Stradins and S. H. Wei, Sci. Adv., 2016, 2, 1600069.
8. S. Cui, H. Pu, S. A. Wells, Z. Wen, S. Mao, J. Chang, M. C. Hersam and J. Chen, Nat. Commun., 2015, 6, 8632.
9. K. F. Mak, C. Lee, J. Hone, J. Shan and T. F. Heinz, Phys. Rev. Lett., 2010, 105, 136805.
10. X. Zhang, X. F. Qiao, W. Shi, J. B. Wu, D. S. Jiang and P. H. Tan, Chem. Soc. Rev., 2015, 44, 2757–2785.
11. M. N. Blonsky, H. L. Zhuang, A. K. Singh and R. G. Hennig, ACS Nano, 2015, 9, 9885–9891.
12. Y. X. Zhen, M. Yang, H. Zhang, G. S. Fu, J. L. Wang, S. F. Wang and R. N. Wang, Sci. Bull., 2017, 62, 1530–1537.
13. Q. Li, Y. H. Zhao, C. Y. Ling, S. J. Yuan, Q. Chen and J. L. Wang, Angew. Chem., Int. Ed., 2017, 56, 10501–10505.
14. H. Zhu, Y. Wang, J. Xiao, M. Liu, S. Xiong, Z. J. Wong, Z. Ye, Y. Ye, X. Yin and X. Zhang, Nat. Nanotechnol., 2014, 10, 151–155.
15. L. Dong, J. Lou and V. B. Shenoy, ACS Nano, 2017, 11, 8242–8248.
16. A.-Y. Lu1, H. Zhu, J. Xiao, C.-P. Chuu, Y. Han, M.-H. Chiu, C.-C. Cheng, C.-W. Yang, K.-H. Wei, Y. Yang, Y. Wang, D. Sokaras, D. Nordlund, P. Yang, D. A. Muller, M.-Y. Chou, X. Zhang and L.-J. Li, Nat. Nanotechnol., 2017, 8, 744–749.
17. R. Ramesh and N. A. Spaldin, Nat. Mater., 2007, 6, 21–29.
18. H. Zhang, L.-M. Liu and W.-M. Lau, J. Mater. Chem. A, 2013, 1, 10821.
19. Y. Ma, Y. Dai, M. Guo, C. Niu, Y. Zhu and B. Huang, ACS Nano, 2012, 6, 1695–1701.
20. C. Gong, L. Li, Z. Li, H. Ji, A. Stern, Y. Xia, T. Cao, W. Bao, C. Wang, Y. Wang, Z. Q. Qiu, R. J. Cava, S. G. Louie, J. Xia and X. Zhang, Nature, 2017, 546, 265–269.
21. B. Huang, G. Clark, E. Navarro-Moratalla, D. R. Klein, R. Cheng, K. L. Seyler, D. Zhong, E. Schmidgall, M. A. McGuire, D. H. Cobden, W. Yao, D. Xiao, P. Jarillo-Herrero and X. Xu, Nature, 2017, 546, 270–273.
22. L. Dong, H. Kumar, B. Anasori, Y. Gogotsi and V. B. Shenoy, J. Phys. Chem. Lett., 2017, 8, 422–428.
23. Y. Guo, H. Deng, X. Sun, X. Li, J. Zhao, J. Wu, W. Chu, S. Zhang, H. Pan, X. Zheng, X. Wu, C. Jin, C. Wu and Y. Xie, Adv. Mater., 2017, 29, 1700715.
24. Z. Zhang, J. Niu, P. Yang, Y. Gong, Q. Ji, J. Shi, Q. Fang, S. Jiang, H. Li, X. Zhou, L. Gu, X. Wu and Y. Zhang, Adv. Mater., 2017, 29, 1702359.
25. Z. Zheng, C. T. Nottbohm, A. Turchanin, H. Muzik, A. Beyer, M. Heilemann, M. Sauer and A. Goelzhaeuser, Angew. Chem., Int. Ed., 2010, 49, 8493–8497.
26. P.-G. de Gennes, Angew. Chem., Int. Ed., 1992, 31, 842–845.
27. M. Lattuada and T. A. Hatton, Nano Today, 2011, 6, 286–308.
28. G. Kresse and J. Hafner, Phys. Rev. B: Condens. Matter Mater. Phys., 1994, 49, 14251–14269.
29. G. Kresse and J. Furthmuller, Phys. Rev. B: Condens. Matter Mater. Phys., 1996, 54, 11169–11186.
30. G. Kresse and J. Furthmuller, Comput. Mater. Sci., 1996, 6, 15–50.
31. S. Baroni, P. Giannozzi and A. Testa, Phys. Rev. Lett., 1987, 58, 1861–1864.
32. J. P. Perdew, K. Burke and M. Ernzerhof, Phys. Rev. Lett., 1997, 78, 1396.
33. G. Kresse and D. Joubert, Phys. Rev. B: Condens. Matter Mater. Phys., 1999, 59, 1758–1775.
34. H. J. Monkhorst and J. D. Pack, Phys. Rev. B: Solid State, 1976, 13, 5188–5192.
35. D. Gao, Q. Xue, X. Mao, W. Wang, Q. Xu and D. Xue, J. Mater. Chem. C, 2013, 1, 5909.
36. J. A. Wilson and A. D. Yoffe, Adv. Phys., 1969, 18, 193–335.
37. Z. I. Popov, N. S. Mikhaleva, M. A. Visotin, A. A. Kuzubov, S. Entani, H. Naramoto, S. Sakai, P. B. Sorokinae and P. V. Avramov, Phys. Chem. Chem. Phys., 2016, 18, 33047–33052.
38. C. Ataca, H. Sahin and S. Ciraci, J. Phys. Chem. C, 2012, 116, 8983–8999.
39. J. Heyd, G. E. Scuseria and M. Ernzerhof, J. Chem. Phys., 2003, 118, 8207–8215.
40. K.-A. N. Duerloo, M. T. Ong and E. J. Reed, J. Phys. Chem. Lett., 2012, 3, 2871–2876.
41. V. E. Bottom, J. Appl. Phys., 1970, 41, 3941–3944.

---