Tailoring Fano lineshapes using plasmonic nanobars for highly sensitive sensing and directional emission†
Guozhou
Li
,
Hongjin
Hu
and
Lijun
Wu
 *
*
Guangdong Provincial Key Laboratory of Nanophotonic Functional Materials and Devices, School of Information and Optoelectronic Science and Engineering, South China Normal University, Guangzhou 510006, China. E-mail: ljwu@scnu.edu.cn
First published on 23rd November 2018
Abstract
Plasmonic oligomers are one class of the most promising nanoclusters for generating Fano resonances. This study reveals that a nanobar-based heptamer concurrently sustains triple polarization-dependent Fano resonances, in sharp contrast to traditional nanodisk or nanosphere-based counterparts. Benefiting from the enhanced near field and reduced spectral linewidth, the gold heptamer exhibits a high refractive index sensitivity (940 nm per RIU) together with a figure of merit (FoM) value as large as 20.9, which outperforms that of most other gold oligomers. On the other hand, it is found that the spectral positions of hybridized eigenmodes depend strongly on the spatial configurations of the constituent nanobars. As a proof of concept, we design a simple heterodimer comprising a nanocross and a nanobar, where plasmonic modes with opposite radiative decay characteristics are excellently overlapped both spectrally and spatially by elaborate tailoring. Double strong Fano resonances appear on opposite sides of the spectrum as expected. More interestingly, the radiation main lobes all point to one direction at these two Fano resonances due to the spatial charge distributions and mode interferences with the maximal directivity ratio (DR) as high as 22.4, in a similar manner to the radio frequency (RF) Yagi–Uda antenna. Furthermore, the emission directions can also be easily switched by adjusting the orientations of the individual nanobar in the heterodimer. Our study demonstrates that the nanobar-based oligomers with tailored Fano lineshapes could serve as versatile and delicate platforms for the label-free biochemical sensing and directional transmission of optical information at the nanometre scale.
1. Introduction
Noble metals such as gold and silver nanostructures have intriguing optical properties enabled by the collective oscillation of the conduction electrons at the metal–dielectric interface, known as localized surface plasmon resonances.1 In closely spaced plasmonic oligomers, plasmon coupling can give rise to a new set of hybridized collective plasmonic modes, accompanied by the generation of the so-called “hot spots”.2 Plasmonic Fano resonances originating from destructive interferences between bright superradiant and dark subradiant modes in metallic nanostructures have gained considerable attention in recent years.3–16 Owing to the sharp and asymmetric profiles in combination with strong near field confinement and enhancement, plasmonic Fano resonances have shown a variety of applications including plasmonic rulers,17–19 waveguides,20,21 biosensors22–24 and spectral sorting,25 just to name a few.Compared with a single Fano resonance, two or more Fano resonances are preferable and desirable since the lineshape can be modulated at several spectral positions with many promising applications.15,17,24 Liu et al. proposed and fabricated a multilayer plasmon nanostructure composed of a dipole antenna and two quadrupole antennas, which sustains two dark quadrupole modes with frequency detuning.17 They showed that such a nanostructure can generate two Fano resonances and function as three-dimensional plasmon rulers. Li et al. designed a plasmonic heptamer cluster consisting of coupled nanocrosses to demonstrate double Fano resonances, where electric and magnetic modes can be tailored independently due to different physical origins.15 Recently, Wang et al. reported a self-reference refractive index sensor based on double Fano resonances in a metallic grating.24 This plasmonic sensor can be applied to reducing the influence of power fluctuations and temperature variations.
Due to the strong coupling between adjacent particles, the oligomer clusters often possess a bright superradiant mode and several possible dark subradiant modes, providing an excellent plasmonic platform for producing multiple Fano resonances.26–31 However, the oligomer nanoclusters reported in previous studies are mainly composed of nanodisks or nanospheres, where the variability and tunability of the structures are more limited than those with nanobars. In this context, a more robust and flexible solution for Fano resonance systems is proposed to engineer them from metallic nanobars that can not only support highly tunable fundamental and higher-order plasmonic modes, but also can be attempted to construct different types of plasmonic artificial atoms or molecules. Hence, the oligomer nanoclusters composed of nanobars are highly suitable for Fano lineshape tailoring. Furthermore, the assembly of anisotropic nanobars into appropriate plasmonic metamolecules could spawn very important and fascinating functionalities empowered by Fano resonances at the nanoscale.
In this article, we propose a heptamer oligomer consisting of nanobars with high degree of flexibility, which sustains triple polarization-dependent Fano resonances simultaneously in the near-infrared region. The underlying physical mechanisms responsible for the generation of triple Fano resonances are elucidated explicitly by spatially decomposing the complex structure into different subgroups and mapping the electric field and charge distributions. The heptamer oligomer exhibits high sensitivity together with narrow linewidths. On the other hand, we find that the spectral positions of hybridized eigenmodes rely on the spatial distributions of the nanobars. As an example, we design a hybrid oligomer comprising a nanocross and a nanobar, where the plasmonic modes with opposite radiative decay characteristics are overlapped spectrally and spatially by optimizing the geometrical parameters. As a result, double Fano resonances are obtained on both sides of the spectrum, and the highly directional emissions are achieved by taking advantage of the mode interference at these two Fano resonances. Moreover, the emission directions of the optical nanoantenna can be well controlled by changing the orientations of the single nanobar due to the high symmetry of the nanocross. Our study herein provides further understanding of the remarkable optical properties in plasmonic oligomers, and has far-reaching implications for developing nanophotonic devices with Fano resonance-assisted superior performance.
2. Results and discussion
2.1 Triple Fano resonances in the nanobar-based heptamer
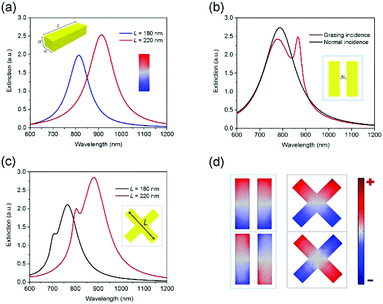
As an elementary building block in plasmonic nanostructures, the nanobar has a high degree of tunability by changing the length-to-width aspect ratio, which is indispensable to the optimization of optical properties. In general, a gold nanobar supports two kinds of plasmonic modes with different orientations: transversal and longitudinal surface plasmon modes. Throughout this article, only the longitudinal plasmon mode of the single nanobar is excited in the spectral range of interest when the polarization is along the major axis. We use full-wave simulations to analyze the optical properties of plasmonic oligomers. The calculations are implemented with a three-dimensional finite element method (FEM, COMSOL Multiphysics). The gold nanobar with the length L = 180 nm, the width W = 50 nm, and the thickness H = 40 nm exhibits a prominent dipolar plasmon response under normal incident excitation (see Fig. 1(a)). The resonant positions of the nanobar are red shifted by as much as 100 nm (from 815 nm to 915 nm) by increasing the bar length L (from 180 nm to 220 nm). When two identical nanobars are combined, the formed configurations are referred to as the side-by-side (SS) dimer and nanocross, respectively. The two nanobars with an interparticle separation G = 30 nm for the SS dimer are placed in parallel to enable strong near field coupling, whereas the ones in the nanocross are perpendicular to each other (see the inset of Fig. 1(b and c)). The effect of spatial arrangement of the nanobars on the optical properties of these new systems is investigated in the following.According to plasmon hybridization theory, strong near field interactions between the plasmonic nanoparticles can give rise to new hybridized eigenmodes in the total system. For the SS dimer, the dipole moment vectors of the two hybridized modes are parallel and antiparallel, corresponding to a higher energy antibonding dipole–dipole mode and a lower energy bonding dipole–dipole mode, respectively. Consequently, the antibonding dipole–dipole mode has an increased effective dipole moment compared to a single nanobar, resulting in a broad superradiant envelope centered at around 785 nm with high radiative losses as shown by the dark line in Fig. 1(b). However for the bonding dipole–dipole mode, the net dipole moment approaches zero, and hence is inaccessible to the external continuum. An additional peak is clearly distinguished in the red part of the spectrum at around 870 nm under grazing incidence from the side due to phase retardation (red line in Fig. 1(b)). The dipolar and quadrupolar nature of these modes can be unambiguously deduced from their respective surface charge distributions as shown in the left panel of Fig. 1(d). For the case of the nanocross, the two identical nanobars intersect and pass through one another vertically. This system also supports a superradiant dipolar mode and a subradiant quadrupolar mode (see Fig. 1(c) and the right panel of Fig. 1(d)). It is observed that the peak wavelength of the quadrupolar mode is located in the higher energy side of the dipolar mode. This is often common in single nanoparticles such as the nanobar and nanosphere.2 For example, the higher-order modes usually have a higher energy than the dipolar mode, whereas the opposite is true for the SS dimer under the same nanobar geometry parameters (see Fig. 1(b)). The capacitive coupling through coulomb interactions between adjacent nanobars for the SS dimer dominates the charge distributions and the relative positions of the hybridized modes, whereas the conductive coupling takes effect in the nanocross.32,33 In addition, the nanocross with four-fold rotational symmetry (D4h point group) sustains the polarization-independent optical response at normal incidence (not shown). The plasmon response of the nanocross can be flexibly tuned over a wide spectral region by scaling the arm length L. When L is gradually increased from 180 nm to 220 nm, the position of the dipole (quadrupole) mode of the nanocross shifts from 760 nm (700 nm) to 880 nm (800 nm) (see Fig. 1(c)) along with a spectral broadening. The extinction spectra of the nanocross can also be adjusted by varying the width W or the thickness H (Fig. S1, ESI†). Overall, the spectral position of the dipole and quadrupole modes is mainly determined by the aspect ratio (L/W or L/H).
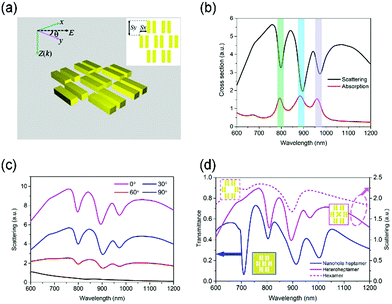
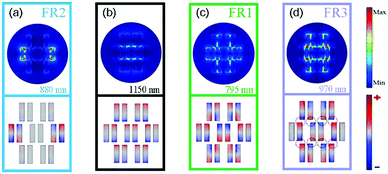
Drawing inspiration from the well-known disk shaped heptamer26,34 and the compelling analogy to the molecular structures of aromatic molecules in organic chemistry, such as benzene molecules and naphthalene molecules, a plasmonic heptamer oligomer consisting of a SS dimer surrounded by six SS dimers is proposed and designed, where the distance Sx between adjacent dimers in the horizontal direction (x-axis) is 105 nm and the distance Sy in the vertical direction (y-axis) is 210 nm (see Fig. 2(a)). In the plasmonic artificial molecule, the left and right halves are bonded by a SS dimer, just like the two rings of a naphthalene molecule are fused together by two carbon atoms. The black line in Fig. 2(b) represents the scattering spectrum of the heptamer oligomer under y-polarized illumination. Three pronounced Fano resonances appear, and the second Fano resonance (FR2) at around 880 nm is very close to the spectral position of the aforementioned quadrupole mode in the single SS dimer. The subradiant quadrupole mode of the SS dimers on the leftmost and rightmost sides is efficiently excited, and the energy is primarily concentrated in the nanobar gap regions as depicted by the near field enhancement and surface charge distributions (see Fig. 3(a)). In the tail of spectrum, all of the electric dipoles oscillate in-phase just like a single dipole, corresponding to the bright superradiant mode of the entire system (see the lower panel of Fig. 3(b)). Therefore, this subradiant quadrupole mode inherited from the SS dimer spectrally overlaps with the superradiant bright mode, and their destructive interference results in the creation of FR2. In the case of the first Fano resonance (FR1) at 795 nm, the giant near field enhancement is confined into the gap locations of the upper and lower four SS dimers (see Fig. 3(c)). The surface charge profiles further demonstrate the quadrupolar characteristics akin to the subradiant mode of FR2. Besides that, the middle three SS dimers also play a key role in the generation of FR1. Specifically, the surface charge of the central SS dimer oscillates out-of-phase with the leftmost and rightmost SS dimers, leading to the suppression of radiative damping in this subgroup (see Fig. 3(c)).14 It implies that the heptamer oligomer can be decomposed into two subgroups: a SS trimer and a SS quadrumer.30 The joint contribution of the two subgroups is responsible for generating the collective subradiant mode, thus giving rise to FR1. Owing to the repulsive interaction between two subgroups, the spectral position of FR1 is located at the higher energy side of FR2 (the distance between dips is 100 nm). As for the third Fano resonance (FR3) at around 970 nm, the surface charge distributions are similar to those of FR1 (see Fig. 3(d)). But the field enhancement in the gaps between the two subgroups is stronger, which is due to the additional dipole moments. Upon a closer examination, we discover that the surface charge oscillations are out of phase between the region one (marked with red circles in Fig. 3(d)) and two (marked with black circles in Fig. 3(d)). The combined effects reduce the radiative losses, resulting in FR3. The spectral position of FR3 is located at the lower energy side of FR2 due to the attractive interaction between two subgroups (the distance between dips is 80 nm), in sharp contrast to FR1. Overall, three Fano resonances are simultaneously introduced and densely distributed in the same spectral region, which is greatly conducive to the improvement of the sensing capability as demonstrated later.
Fig. 2(c) presents the scattering spectra of the nanobar heptamer under different excitation polarizations. We only plot several representative cases. At the vertical polarization θ = 0°, all of the Fano resonances are most efficiently excited. The contrast ratios of the Fano resonances in the scattering spectra gradually decrease with an increase in the polarization angle, and no Fano resonance appears in the spectrum at θ = 90°. This is understandable since the dipole moment direction is along the minor axis of the nanobar under such circumstances. These results indicate that the Fano resonances of the nanobar-based heptamer are highly polarization-dependent, which holds promise for single molecule sensing.35 The nanobar-based heptamer has some advantages over the counterparts consisting of seven nanospheres or nanodisks in terms of Fano resonances. In this well-known heptamer, the dipolar plasmon of the central nanodisk hybridizes with the plasmons of the ringlike hexamer, leading to the formation of the subradiant and superradiant modes.26 Such a Fano resonance hence is only observable in the presence of the central nanoparticle. In contrast, there still remains one Fano resonance at around 880 nm (FR2) even though the central SS dimer is absent from the nanobar-based heptamer (magenta dashed line in Fig. 2(d)). As we have analyzed above, FR1 and FR3 are relevant to the central SS dimer, and the SS dimers on both sides govern the occurrence of FR2. Moreover, these three Fano resonances are still pronounced and robust even when the central SS dimer is replaced by a nanocross (magenta line in Fig. 2(d)). According to the Babinet's principle,36,37 these three Fano resonances can also be observed in the transmittance spectrum as shown by the blue line in Fig. 2(d). This also confirms the correctness and reliability of the results. Besides, there is a sharp lattice resonance at around 700 nm due to the diffraction effect because the lattice constant (700 nm) is longer than the illuminating wavelength. Overall, the preceding results manifest that the nanobar-based oligomers possess more abundant spectral information and better versatility in comparison with the nanosphere or nanodisk oligomers.
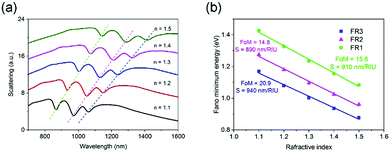
One of the most fascinating applications for Fano resonances might be in refractive index sensing, which partially relies on plasmon lineshape engineering. The capability of the plasmonic sensor is generally quantified by the so-called figure of merit (FoM), which is typically defined as the resonance energy per unit refractive index change (S = ΔE/Δn) divided by the resonance linewidth Δλ,37 namely FoM = (ΔE/Δn)/Δλ. The linewidth Δλ is defined as the energy difference between the Fano dip and its closest peak.23,24,38–40 Three Fano resonances exhibit pronounced red-shifts upon increasing the refractive index of the embedding medium (see Fig. 4(a)). As shown in Fig. 4(b), the FoMs (sensitivity S) have the values of 15.6 (810 nm per RIU), 14.8 (890 nm per RIU) and 20.9 (940 nm per RIU) at FR1, FR2 and FR3, respectively. As a consequence of the strong attractive coupling between two subgroups at FR3, more spatial regions with enhanced electric fields are exposed to the environment and are accessible by the surrounding medium (see the upper panel of Fig. 3(d)). Therefore, the refractive index sensitivity is the highest at FR3. More importantly, due to the presence of three Fano resonances concurrently in a short wavelength range of 700–1100 nm, the spectral lineshapes of the individual Fano resonances are all modulated. This can be easy to see by the contrasting black line in Fig. 2(b) and the magenta dashed line in Fig. 2(d). More specifically, the spectral distance from the dip to the left (right) peak for the single Fano resonance (FR2) in the hexamer is 110 nm (70 nm). When a central SS dimer is introduced to form a heptamer, another two Fano resonances (namely, FR1 and FR3) appear on both sides of FR2. The interval between FR2 and FR1 (FR3) in the heptamer is only 100 nm (80 nm). Accordingly, FR2 is squeezed along with the diminishing linewidth of 50 nm, and the linewidths of FR1 and FR3 are only 40 nm and 30 nm, respectively. The average linewidths related to FR1, FR2 and FR3 are eventually 52 nm, 60 nm, and 45 nm, respectively. The resultant FoMs thus have a maximal value of 20.9 at FR3. Their performances have a significant improvement (about two-fold) compared with that of most other reported single Fano resonances for gold oligomers, which is generally as low as 10 in the optical regime (Table S1, ESI†).23,29,38–40 It can be improved in silver oligomers due to the lower imaginary part of its dielectric constant. For example, a FoM of ∼50 has been achieved in an Ag dimer.41 The fabrication of an aligned nanoparticle dimer is possible by self-assembly approaches.42 The gap distance can also be down to a sub-nanometer precision (<5 nm).43,44 Nevertheless, the fabrication of nanoparticle dimers with gaps as small as 2 nm is costly and low throughput. Moreover, this tiny gap is also unsuitable for the biomacromolecule detection. Besides, silver is susceptible to oxidation under ambient conditions, resulting in performance instability and even deterioration. In our case, we exploit more stable gold nanoparticles as the material, and the sensor possesses three Fano resonances in the same oligomer, which allows for both miniaturization and multiwavelength detection. Thereby, our proposed nanobar-based gold heptamer is a promising candidate for the high-sensitivity multispectral sensor at the nanoscale.
2.2 Double Fano resonances in the nanobar-based heterodimer
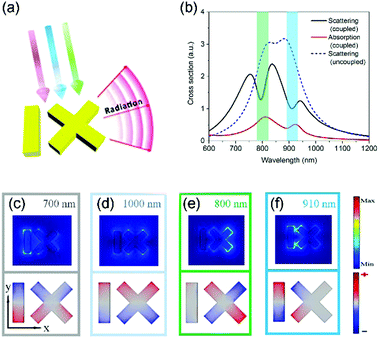
Plasmonic nano-optical antennas could enable an efficient conversion between the highly localized near field and propagating far-field electromagnetic waves.45–51 Among these efforts, the directional transmission and manipulation of optical signals is of particular interest and lies at the heart of the photonic integrated circuits (PICs). To this end, we design horn nanoantennas with high directionality using the plasmonic nanobars. The above analysis and results already indicate that the spatial arrangement of the constituent nanobars profoundly affects the eigenfrequencies of the SS dimer and nanocross. For the identical nanobar parameters, the mode overlap between the SS dimer and nanocross is poor (see the red line in Fig. 1(b) and the dark line in Fig. 1(c)). To achieve an excellent spectral overlap between the radiant and subradiant states, we adjust the length L of the nanobars. It is found that the modes with opposite radiative decay characteristics are spectrally overlapped very well at both ends of the spectrum as the lengths of the nanobars (L = 220 nm) in the nanocross are longer than that (L = 180 nm) in the SS dimer (see the red line in Fig. 1(b) and the red line in Fig. 1(c)). Further, the nanocross can share one nanobar with the SS dimer, indicating that the oligomer becomes simpler and compact as shown in Fig. 5(a).For the uncoupled case, the subradiant modes are not excited due to the negligible near field interaction between the nanobar and nanocross, and the spectrum traces a sum of their individual dipolar resonances as shown by the blue dashed line in Fig. 5(b). When the nanocross and nanobar are brought into close proximity with a gap distance d = 30 nm and impinged by the y-polarized light, two clear Fano resonances are observed in the scattering spectrum at around 800 nm and 910 nm, respectively (see the black line in Fig. 5(b)). The spectral lineshape is modulated by the double Fano resonances and changes drastically from two peaks to two dips. In order to gain deeper insight, the electric field and surface charge distributions are plotted to clarify the optical properties of the heterodimer. Away from the Fano resonances, at the wavelengths corresponding to Fig. 5(c and d), the charge distributions are associated with the both tails of the superradiant mode characterized by in-phase dipolar excitation of the plasmonic structure constituents. As expected from classical dipolar resonances, there is a π phase difference between the charge distributions at 700 nm and 1000 nm. The first Fano resonance at around 800 nm can be attributed to the subradiant quadrupole mode (denoted by Q1) of the nanocross itself. We can observe very strong field enhancement in the nanocross, and the field enhancement in the nanobar is very weak (see the upper panel in Fig. 5(e)). The surface charge distributions further reveal the nature of the quadrupole mode from the nanocross (see the lower panel of Fig. 5(e)). The second resonance is distinct from the first one. The electric dipole at the left half of nanocross oscillates out-of-phase with that in the nanobar, corresponding to another quadrupole mode (denoted by Q2) of the oligomer, which is similar to the SS dimer in nature (see Fig. 5(f)). The dipole moment at the right half of the nanocross is very weak. Besides that, it is found that the absorption peak is slightly red-shifted compared with the scattering minimum of the Fano resonance (see Fig. 5(b)). Due to intrinsic ohmic losses, frequency detuning between the absorption and scattering extrema is ubiquitous in plasmonic nanostructures.52,53
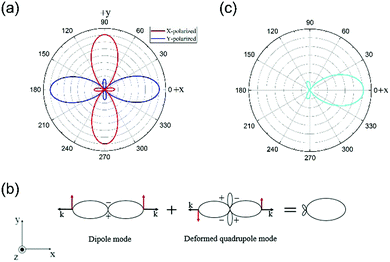
The far-field emission properties of metallic nanoparticles are less investigated compared with the near field response. In general, the radiation in a direction that is perpendicular to the charge oscillations (dipole moments) is the strongest, and the radiation in a parallel direction is zero. For some relatively complicated nanoparticles such as the nanocross, the charge oscillations of the higher-order modes are polarization-dependent so that we cannot straightforwardly obtain the far-field emission pattern of the weak higher-order mode (i.e. quadrupole). Thanks to the high symmetry of the nanocross (point group D4h), we can extract the veiled far-field response of the higher-order mode from multistep excitation processes. The red and blue lines in Fig. 6(a) are the radiation patterns obtained with x-polarized and y-polarized glancing incidence at 800 nm, respectively. There is two big lobes in a direction perpendicular to the polarization, and two low lobes oriented parallel to the polarization. These four small lobes constitute far-field emission profiles of the subradiant quadrupole mode Q1 of the nanocross, whereas these big lobes are primarily ascribed to the polarization-driven charge oscillations in the nanocross. Namely, for these big lobes, the directions of the charge oscillation match well with the excitation polarization, leading to the enhanced radiation. It is noteworthy that the radiation phase difference between two big lobes in opposite propagation directions is out-of-phase due to the inherent antisymmetric charge distributions of the quadrupole mode with respect to the polarization (see the lower right of Fig. 1(d)). In contrast, the radiation phase difference between two big lobes of the superradiant dipole mode in opposite propagation directions is an integral multiple of 2π due to the symmetric charge distributions of the dipole with respect to the polarization (see the upper right of Fig. 1(d)).
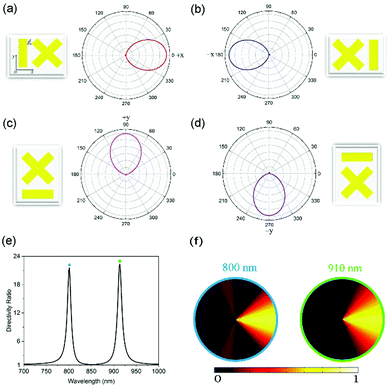
Through rational design of the plasmonic nanostructures, the tailored spectral lineshape can influence the far-field radiation distributions at the resonance frequencies.45,51,54 The first Fano resonance is switched on under y-polarized normal incidence when an adjacent nanobar is introduced so as to allow for the mode coupling and interaction. For the heterodimer, the charge distribution plots in the lower panel of Fig. 5(c and e) clearly illustrate that the radiation of the superradiant mode is out-of-phase (in-phase) with that of the deformed quadrupole mode Q1 on the left (right). The destructive interference between the superradiant and subradiant modes makes the big lobes on the left vanish almost completely at the first Fano resonance (see Fig. 6(b)). Only the right big lobes of the superradiant mode are preserved and enhanced together with two low side lobes descending from the quadrupole mode Q1 of a single nanocross as shown in Fig. 6(c). For the second Fano resonance (910 nm), the quadrupole mode Q2 is entirely located on one side of the superradiant dipole mode as illustrated by the charge distributions in the lower panel of Fig. 5(f). The destructive interference between the superradiant and subradiant modes on the left results in one directional radiation at the second resonance wavelength.45,55 The angular emission pattern in the xy plane is plotted in Fig. 7(a), where a high unidirectional emission is observed with main lobes of the radiation patterns pointing to the right, in much the same way as radio frequency (RF) Yagi–Uda antennas.47,50,56 The parts with the radiant (subradiant) mode act as the director (reflector) of the antenna structure. Based on this principle, the emission direction can turn to the left when the nanobar is located on the right of the nanocross as shown in Fig. 7(b). In order to realize more azimuthal emission, we change the single nanobar orientations so that the emission directions are regulated on purpose (see Fig. 7(c and d)). It is expected that the same design concepts can be easily extended to telecommunication wavelengths.
The unique characteristic described above can be exploited for nanoscale directional transmission of on-chip optical information. To evaluate the directivity of the heterodimer nanoantenna, a directivity ratio (DR) is defined as:
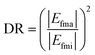 | (1) |
![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 0.9) between the two are commensurable (see Fig. 7(f)). Consequently, two independent Fano resonance wavelengths can be used to encode the public key and ciphertext in the asymmetric encryption communication systems,57 respectively, realizing the on-chip secure and unidirectional transmission of optical information. It is also important to note that these plasmonic horn antennas are quite simple and illuminated simply by a bulk incident wave, rather than a deep-subwavelength sized dipole excitation source (e.g., quantum dots (QDs) or nitrogen-vacancy (NV) centers in diamond nanocrystals) with a specific orientation or a high-energy electron beam at the subnanoscale utilized by previous studies.45,46,50,51 In the latter two cases, they either require accurate positioning and alignment or extremely high spatial resolution (∼10 nm) and harsh operating conditions, which are very challenging and complicated. Instead, our proposed schemes are much more easily carried out and cost-effective.
0.9) between the two are commensurable (see Fig. 7(f)). Consequently, two independent Fano resonance wavelengths can be used to encode the public key and ciphertext in the asymmetric encryption communication systems,57 respectively, realizing the on-chip secure and unidirectional transmission of optical information. It is also important to note that these plasmonic horn antennas are quite simple and illuminated simply by a bulk incident wave, rather than a deep-subwavelength sized dipole excitation source (e.g., quantum dots (QDs) or nitrogen-vacancy (NV) centers in diamond nanocrystals) with a specific orientation or a high-energy electron beam at the subnanoscale utilized by previous studies.45,46,50,51 In the latter two cases, they either require accurate positioning and alignment or extremely high spatial resolution (∼10 nm) and harsh operating conditions, which are very challenging and complicated. Instead, our proposed schemes are much more easily carried out and cost-effective.
3. Conclusions
In summary, the gold nanobar is introduced as a useful and flexible “scissor” for tailoring the spectral lineshape of plasmonic resonances. The two mutual parallel and orthogonal nanobars can form the SS dimer and nanocross, respectively. These two subsystems have different plasmonic coupling mechanisms. By inspecting the near field and surface charge distributions, it is found that the polarization-dependent triple Fano resonances emanate from the coupling between different subgroups in the nanobar-based heptamer comprising the SS dimers. A good sensing performance with a maximal value of FoM up to 20.9 is attained, making the heptamer oligomer valuable platforms for label-free biochemical sensing. The spatial arrangement of the nanobars has also a great impact on the spectral location of the hybridized eigenstates. With this insight, a simple hybrid oligomer built from a nanocross and a nanobar is designed such that the plasmonic modes with opposite radiative decay characteristics are overlapped spectrally and spatially, leading to double Fano resonances located in both flanks of the spectrum as predicted. In analogy to the well-established Yagi–Uda antennas, the coupled oligomer can function as an ultracompact and highly directional on-chip antenna. Regardless of the low side lobes, the radiation main lobes all point to one direction at these two Fano resonances. The inherent symmetric (antisymmetric) charge distributions of the dipole (quadrupole) mode with respect to the polarization and mode interaction result in one directional radiation at the first Fano resonance. The coupling and interference between superradiant and subradiant modes in the specific space result in the unidirectional radiation at the second Fano resonance. The emission of light can be easily and flexibly switched to the desired directions. In particular, our suggested optical nanoantenna schemes have a unique advantage over other existing relevant technologies using nanometric emitters. We expect that such a systematical study and design strategy on the nanobar-based oligomer will inspire and facilitate future works involving Fano resonances, and provide guidelines for the development of a wide range of on-demand nanophotonic devices with extremely compact architectures and unprecedented optical properties.Conflicts of interest
The authors declare no competing financial interests.Acknowledgements
This work was supported by the National Natural Science Foundation of China (Grant No. 61675070, Grant No. 61378082, and Grant No. 11704133).Notes and references
- S. A. Maier, Plasmonics: Fundamentals and Applications, Spinger, New York, 2007 Search PubMed.
- S. Zhang, G. Li, Y. Chen, X. Zhu, S. Liu, D. Y. Lei and H. Duan, ACS Nano, 2016, 10, 11105–11114 CrossRef CAS PubMed.
- C. Yan and O. J. Martin, ACS Nano, 2014, 8, 11860–11868 CrossRef CAS PubMed.
- F. Hao, Y. Sonnefraud, P. Van Dorpe, S. A. Maier, N. J. Halas and P. Nordlander, Nano Lett., 2008, 8, 3983–3988 CrossRef CAS.
- S. Mukherjee, H. Sobhani, J. B. Lassiter, R. Bardhan, P. Nordlander and N. J. Halas, Nano Lett., 2010, 10, 2694–2701 CrossRef CAS PubMed.
- H.-J. Hu, F.-W. Zhang, G.-Z. Li, J.-Y. Chen, Q. Li and L.-J. Wu, Photonics Res., 2018, 6, 204 CrossRef.
- Q. Zhang, J. J. Xiao, X. M. Zhang, Y. Yao and H. Liu, Opt. Express, 2013, 21, 6601–6608 CrossRef CAS.
- L. V. Brown, H. Sobhani, J. B. Lassiter, P. Nordlander and N. J. Halas, ACS Nano, 2010, 4, 819–832 CrossRef CAS.
- K. C. Woo, L. Shao, H. Chen, Y. Liang, J. Wang and H. Q. Lin, ACS Nano, 2011, 5, 5976–5986 CrossRef CAS.
- G. Bachelier, I. Russier-Antoine, E. Benichou, C. Jonin, N. Del Fatti, F. Vallee and P. F. Brevet, Phys. Rev. Lett., 2008, 101, 197401 CrossRef CAS PubMed.
- S. Zhang, K. Bao, N. J. Halas, H. Xu and P. Nordlander, Nano Lett., 2011, 11, 1657–1663 CrossRef CAS PubMed.
- H. Chen, L. Shao, T. Ming, K. C. Woo, Y. C. Man, J. Wang and H. Q. Lin, ACS Nano, 2011, 5, 6754–6763 CrossRef CAS PubMed.
- R. Adato, A. Artar, S. Erramilli and H. Altug, Nano Lett., 2013, 13, 2584–2591 CrossRef CAS PubMed.
- G. Li, Q. Li, L. Xu and L. Wu, Plasmonics, 2015, 10, 1401–1407 CrossRef CAS.
- G.-Z. Li, Q. Li and L.-J. Wu, Nanoscale, 2015, 7, 19914–19920 RSC.
- S. Liu, Z. Yang, R. Liu and X. Li, ACS Nano, 2012, 6, 6260–6271 CrossRef CAS PubMed.
- N. Liu, M. Hentschel, T. Weiss, A. P. Alivisatos and H. Giessen, Science, 2011, 332, 1407–1410 CrossRef CAS.
- L. Shao, C. Fang, H. Chen, Y. C. Man, J. Wang and H.-Q. Lin, Nano Lett., 2012, 12, 1424–1430 CrossRef CAS PubMed.
- B. Gallinet, T. Siegfried, H. Sigg, P. Nordlander and O. Martin, Nano Lett., 2013, 13, 497–503 CrossRef CAS PubMed.
- N. Liu, S. Mukherjee, K. Bao, L. V. Brown, J. Dorfmueller, P. Nordlander and N. J. Halas, Nano Lett., 2012, 12, 364–369 CrossRef CAS PubMed.
- N. Liu, S. Mukherjee, K. Bao, Y. Li, L. V. Brown, P. Nordlander and N. J. Halas, ACS Nano, 2012, 6, 5482–5488 CrossRef CAS PubMed.
- N. Verellen, P. Van Dorpe, C. Huang, K. Lodewijks, G. A. E. Vandenbosch, L. Lagae and V. V. Moshchalkov, Nano Lett., 2011, 11, 391–397 CrossRef CAS.
- J. B. Lassiter, H. Sobhani, J. A. Fan, J. Kundu, F. Capasso, P. Nordlander and N. J. Halas, Nano Lett., 2010, 10, 3184–3189 CrossRef CAS.
- Y. Wang, C. Sun, H. Li, Q. Gong and J. Chen, Nanoscale, 2017, 9, 11085–11092 RSC.
- Y. Chen, J. Chu and X. Xu, ACS Photonics, 2016, 3, 1689–1697 CrossRef CAS.
- M. Hentschel, M. Saliba, R. Vogelgesang, H. Giessen, A. P. Alivisatos and N. Liu, Nano Lett., 2010, 10, 2721–2726 CrossRef CAS PubMed.
- H. L. Liu, E. S. P. Leong, Z. L. Wang, G. Y. Si, L. J. Zheng, Y. J. Liu and C. Soci, Adv. Opt. Mater., 2013, 1, 978–983 CrossRef.
- A. Lovera, B. Gallinet, P. Nordlander and O. J. Martin, ACS Nano, 2013, 7, 4527–4536 CrossRef CAS.
- J. A. Fan, K. Bao, C. Wu, J. Bao, R. Bardhan, N. J. Halas, V. N. Manoharan, G. Shvets, P. Nordlander and F. Capasso, Nano Lett., 2010, 10, 4680–4685 CrossRef CAS.
- M. Rahmani, D. Y. Lei, V. Giannini, B. Lukiyanchuk, M. Ranjbar, T. Y. Liew, M. Hong and S. A. Maier, Nano Lett., 2012, 12, 2101–2106 CrossRef CAS.
- B. Hopkins, D. S. Filonov, A. E. Miroshnichenko, F. Monticone, A. Alu and Y. S. Kivshar, ACS Photonics, 2015, 2, 724–729 CrossRef CAS.
- N. Liu, S. Kaiser and H. Giessen, Adv. Mater., 2008, 20, 4521–4525 CrossRef CAS.
- N. Liu, H. Guo, L. Fu, S. Kaiser, H. Schweizer and H. Giessen, Nat. Mater., 2008, 7, 31 CrossRef CAS PubMed.
- J. A. Fan, C. Wu, K. Bao, J. Bao, R. Bardhan, N. J. Halas, V. N. Manoharan, P. Nordlander, G. Shvets and F. Capasso, Science, 2010, 328, 1135–1138 CrossRef CAS.
- H. Deng, X. Chen, Y. Xu and A. E. Miroshnichenko, Nanoscale, 2015, 7, 20405–20413 RSC.
- T. Zentgraf, T. P. Meyrath, A. Seidel, S. Kaiser and H. Giessen, Phys. Rev. B: Condens. Matter Mater. Phys., 2007, 76, 3407 CrossRef.
- H. U. Yang, R. L. Olmon, K. S. Deryckx, X. G. Xu, H. A. Bechtel, Y. Xu, B. A. Lail and M. B. Raschke, ACS Photonics, 2014, 1, 894–899 CrossRef CAS.
- X. Wei, M. Altissimo, T. J. Davis and P. Mulvaney, Nanoscale, 2014, 6, 5372–5377 RSC.
- Y. Zhan, D. Y. Lei, X. Li and S. A. Maier, Nanoscale, 2014, 6, 4705–4715 RSC.
- Y. Bao, Z. Hu, Z. Li, X. Zhu and Z. Fang, Small, 2015, 11, 2177–2181 CrossRef CAS PubMed.
- S. Zhang and H. Xu, Nanoscale, 2016, 8, 13722–13729 RSC.
- S. F. Tan, L. Wu, J. K. W. Yang, P. Bai, M. Bosman and C. A. Nijhuis, Science, 2014, 343, 1496–1499 CrossRef CAS.
- D. S. Kim, J. Heo, S. H. Ahn, S. W. Han, W. S. Yun and Z. H. Kim, Nano Lett., 2009, 9, 3619–3625 CrossRef CAS.
- M. Pellarin, J. Ramade, J. M. Rye, C. Bonnet, M. Broyer, M.-A. Lebeault, J. Lerme, S. Marguet, J. R. G. Navarro and E. Cottancin, ACS Nano, 2016, 10, 11266–11279 CrossRef CAS.
- A. Artar, A. A. Yanik and H. Altug, Nano Lett., 2011, 11, 3694–3700 CrossRef CAS.
- T. Coenen, E. J. Vesseur, A. Polman and A. F. Koenderink, Nano Lett., 2011, 11, 3779–3784 CrossRef CAS.
- T. Kosako, H. F. Hofmann and Y. Kadoya, Nat. Photonics, 2010, 4, 312–315 CrossRef CAS.
- I. S. Maksymov, I. Staude, A. E. Miroshnichenko and Y. S. Kivshar, Nanophotonics, 2012, 1, 65–81 Search PubMed.
- C. Sun, H. Li, Q. Gong and J. Chen, Adv. Opt. Mater., 2017, 5, 1700510 CrossRef.
- D. Dregely, R. Taubert, J. Dorfmüller, R. Vogelgesang, K. Kern and H. Giessen, Nat. Commun., 2011, 2, 267 CrossRef.
- I. M. Hancu, A. G. Curto, M. Castro-López, M. Kuttge and N. F. van Hulst, Nano Lett., 2013, 14, 166–171 CrossRef PubMed.
- J. Zuloaga and P. Nordlander, Nano Lett., 2011, 11, 1280–1283 CrossRef CAS PubMed.
- B. Gallinet and O. J. F. Martin, Opt. Express, 2011, 19, 22167 CrossRef PubMed.
- R. Guo, M. Decker, F. Setzpfandt, I. Staude, D. N. Neshev and Y. S. Kivshar, Nano Lett., 2015, 15, 3324–3328 CrossRef CAS PubMed.
- X. Zhang, Q. Xu, Q. Li, Y. Xu, J. Gu, Z. Tian, C. Ouyang, Y. Liu, S. Zhang, X. Zhang, J. Han and W. Zhang, Sci. Adv., 2016, 2, e1501142 CrossRef PubMed.
- G. Lerose, Nat. Photonics, 2010, 4, 1–2 CrossRef.
- W. Diffie and M. E. Hellman, IEEE Trans. Inf. Theory, 1976, 22, 644–654 CrossRef.
Footnote |
| † Electronic supplementary information (ESI) available. See DOI: 10.1039/c8cp05779f |
| This journal is © the Owner Societies 2019 |