The shielding effect of metal complexes on the binding affinities of ligands to metalloproteins†
Deliang
Chen
 *a,
Yibao
Li
a,
Wei
Guo
a,
Yongdong
Li
a,
Tor
Savidge
bc,
Xun
Li
*a and
Xiaolin
Fan
a
*a,
Yibao
Li
a,
Wei
Guo
a,
Yongdong
Li
a,
Tor
Savidge
bc,
Xun
Li
*a and
Xiaolin
Fan
a
aJiangxi Key Laboratory of Organo-Pharmaceutical Chemistry, Chemistry and Chemical Engineering College, Gannan Normal University, Ganzhou, Jiangxi 341000, P. R. China. E-mail: deliang2211@hotmail.com; 18365412618@163.com
bDepartment of Pathology & Immunology, Baylor College of Medicine, Houston, TX 77030, USA
cTexas Children's Microbiome Center, Texas Childrens Hospital, Houston, TX 77030, USA
First published on 30th November 2018
Abstract
Metal ions are important regulatory cofactors in a wide variety of proteins. Conventional wisdom suggests that stronger metal–ligand interactions have a larger effect on the ligand binding affinity. However, some experimental data do not support this conventional wisdom. In this study, we used a theoretical derivation approach to explore the effect of metal–ligand interactions on ligand binding affinities. Both theoretical derivation and experimental data indicate that metal–ligand interactions weaken the original interactions of the metal ions, which reduce the contributions of the metal–ligand interactions to the ligand binding affinities. The shielding effect is so large that some strong metal–ligand interactions contribute little to the ligand binding affinities. The binding free energies contributed by metal–ligand interactions have a limited relationship with the strengths of the interactions. Considering that the shielding effect of metal complexes is essential for accurately modelling metal–ligand interactions, our findings challenge the conventional wisdom and represent a significant advance for the design of drugs targeted for metalloproteins and for exploring the enormous catalytic power of metalloproteins.
Introduction
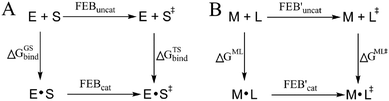
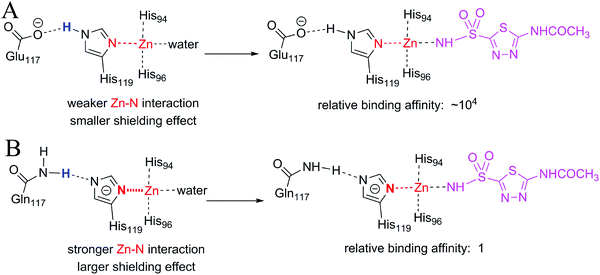
More than one-third of known proteins contain a metal ion center that regulates some part of biological activity.1,2 Protein metal centers are known to stabilize the structures of proteins,3–5 and catalyze many reactions in biological systems.6–10 Metalloproteins have been implicated in many diseases and are important targets for effective drug design.11–16 The interactions between metal ions and inhibitors are essential for the activity of inhibitors targeted for metalloproteins.17–19 Moreover, the catalytic powers of the metal ions in metalloenzymes have inextricable relationship with the interactions between the metal ions and substrates. As shown in Fig. 1A, the catalytic power of an enzyme (E), which is the difference in free energy barrier (FEB) between the reference solution reaction and the enzymatic reaction (FEBuncat − FEBcat), equals the difference in binding free energy between the ground state (GS) and transition state (TS) of the substrate (ΔGGSbind − ΔGTSbind). Similarly, as shown in Fig. 1B, the catalytic power contributed by a metal–substrate interaction (FEB′uncat − FEB′cat) equals the difference between the binding free energy contributed by the metal–ligand interaction in the GS (ΔGML) and the binding free energy contributed by the metal–ligand interaction in the TS (ΔGML≠). Thus, understanding how the interactions between metal ions and ligands (or substrates) affect the binding free energies of the ligands (or substrates) is important for drug design and enzyme catalysis.Many scoring functions, e.g. MpSDock,20 GOLD,21,22 Glide,22,23 X-score,22,24 ChemScore,25,26 AutoDock,27–30 CHARMM,31,32 have been developed to model protein–ligand interactions, which also include metal–ligand interactions.17,33 Although various scoring functions model metal–ligand interactions differently, they make the general assumption that the contribution of metal–ligand interactions to the ligand binding affinities depends on the strengths of the interactions. It is widely accepted that the strengths of the interactions between metal ions and ligands determine the effects of the interactions on binding affinities. This assumption is supported by many experimental data.34–36 However, many other experimental data indicate that the metal–ligand interaction strengths have little relationship with the effects on binding affinities. For example, it has been reported that the binding affinity of acetazolamide to carbonic anhydrase II (CAII) decreases by approximately 104-fold after the mutation of Glu117 of wild-type CAII to Gln117. The mutation of Glu117 in CAII to Gln117 causes no discrete structural changes (PDB: 1ZSB).37 The only difference between the E117Q CAII complex and the wild-type CAII complex is residue 117 (Fig. 2), which has no interaction with acetazolamide. Thus, the mutation has little effect on the interaction between acetazolamide and CAII. Many widely used scoring functions, including X-score, GOLD and ChemScore have been used to calculate the binding free energy of acetazolamide to E117Q CAII; however, none have been able to determine why acetazolamide has an extremely low binding affinity to E117Q CAII.24 Thus, the effect of metal–ligand interactions on ligand-binding affinities cannot be simply determined from the interaction strengths. How metal–ligand interactions affect binding affinities remain elusive. For various metalloproteins, the effect may be quite different. Thus, it is challengeable to make a general rule for determining the effect metal–ligand interactions on ligand binding affinities. In this study, we used a theoretical approach to explore this phenomenon. We then validated the general rule with experimental data. We found that newly formed metal–ligand interactions weaken the original interactions of metal ions, which then considerably reduce the contributions of the metal–ligand interactions to the ligand binding affinities. The binding free energies contributed by metal–ligand interactions have little relationship with the strengths of the metal–ligand interactions.
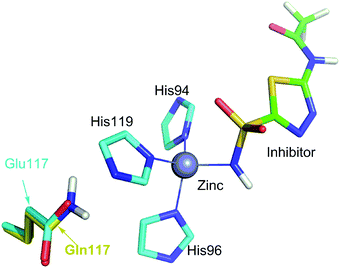 | ||
| Fig. 2 Comparison of the binding site of wild-type carbonic anhydrase II (CAII) binding with acetazolamide with the binding site of E117Q CAII binding with acetazolamide. The interactions of acetazolamide with CAII and with E117Q CAII are not shown because interactions between acetazolamide and wild-type CAII are the same to the interactions between acetazolamide and E117Q CAII.37 The only difference is residue 117, which is Glu for wild-type CAII or Gln for E117Q CAII. | ||
Results and discussion
Theoretical derivation for exploring the effect of metal–ligand interactions on ligand binding affinities
In this study, the term “ligand” refers to small molecules that bind to metal complexes; the term “coordinating atom” refers to atoms that bind to metal ions. Coordinating atoms may come from ligands (including water molecules) or proteins. In the following theoretical derivation, we explore the difference between actual binding free energies contributed by metal–ligand interactions and the binding free energies calculated from the interaction strengths.| MLn−1 + L → MLn ΔGn | (1) |
Because the M–L bonds in MLn are usually identical, the binding free energy calculated from the M–L strength in MLn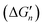 equals the total binding free energy change of M with n coordinating atoms (ΔGtot) divided by n.
equals the total binding free energy change of M with n coordinating atoms (ΔGtot) divided by n.
| M + nL → MLn ΔGtot | (2) |
 | (3) |
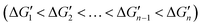 . This relationship indicates that the original interactions of a metal complex are weakened upon binding of the metal complex with an additional coordinating atom. Both reported computational and experimental data show that the metal–coordinating atom distances in metal complexes increase with increasing CNs,40,41 supporting that the M–L strength in MLn becomes weaker as n increases. Thus, in the binding of MLn−1 with L (eqn (1)), the original interactions, which are the M–L interactions in MLn−1, reduce the contribution of the newly formed M–L interaction to the ligand binding affinity. The extent of this shielding effect determines whether the binding free energy contributed by the metal–ligand interaction can be calculated accurately from the strength of the metal–ligand interactions.
. This relationship indicates that the original interactions of a metal complex are weakened upon binding of the metal complex with an additional coordinating atom. Both reported computational and experimental data show that the metal–coordinating atom distances in metal complexes increase with increasing CNs,40,41 supporting that the M–L strength in MLn becomes weaker as n increases. Thus, in the binding of MLn−1 with L (eqn (1)), the original interactions, which are the M–L interactions in MLn−1, reduce the contribution of the newly formed M–L interaction to the ligand binding affinity. The extent of this shielding effect determines whether the binding free energy contributed by the metal–ligand interaction can be calculated accurately from the strength of the metal–ligand interactions.
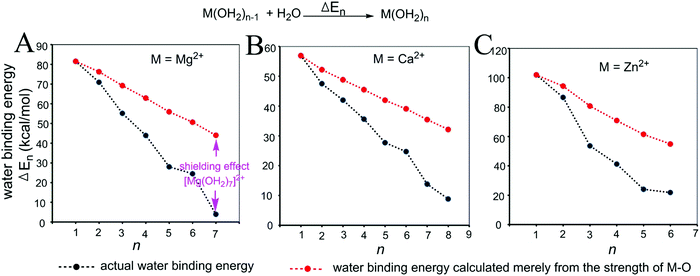 | ||
| Fig. 3 Relationships between the actual stepwise water binding energies (black) and the stepwise water binding energies calculated based on the M–O strengths (red) for metal ions Mg2+ (A), Ca2+ (B) and Zn2+ (C). The calculations are described in the Methods and the data are provided in Table S1 (ESI†). | ||
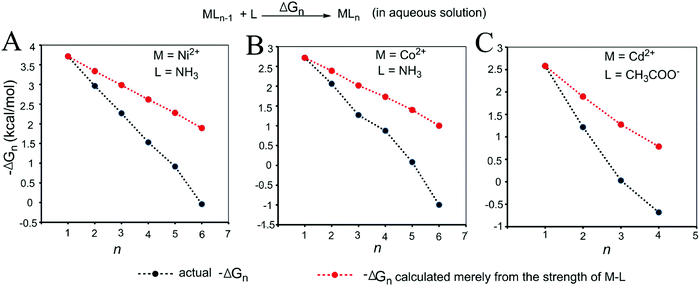 | ||
| Fig. 4 Relationships between the actual stepwise free energy changes for the formation of metal–ligand complexes in aqueous solution (black) and the corresponding stepwise free energy changes calculated based on the M–L strengths (red). (A) M = Ni2+, L = NH3; (B) M = Co2+, L = NH3; and (C) M = Cd2+, L = COO−. The calculations are shown in the Methods and the data are provided in Table S2 (ESI†). | ||
As shown in Fig. 3 and 4, regardless of the method of expressing the stepwise bonding power of metal complexes (e.g., using enthalpy change, or free energy change; with or without displacing a metal-bound water molecule), the shielding effect always exists and affects the bonding powers of metal complexes in a similar manner. Based on eqn (3), we derived the general relationship between the actual metal–ligand binding free energy for the binding of MLn−1 with L and the corresponding binding free energy calculated from the interaction strength (Fig. 5, see Fig. S1 for the derivation, ESI†). Fig. 5 shows that the actual binding free energies are quite different from their corresponding binding free energies calculated from the interaction strengths. First, for a metal complex with OCN, the actual binding free energy is zero or unfavorable (see the black dot at OCN + 1); however, the binding free energy estimated from the M–L interaction strength is quite favourable (see the red dot at OCN + 1). Second, the binding free energy contributed by a metal–ligand interaction does not depend on the strength of the interaction (relating to red dots), but instead depends on the stability of the metal ion (relating to black dots). Only the interactions of hypo-coordinated metal ions contribute to the binding affinities.
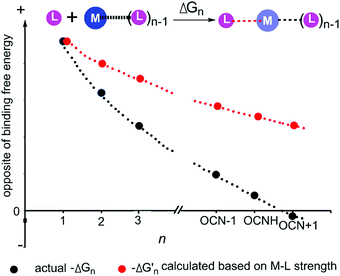 | ||
Fig. 5 General relationships between the actual and calculated binding free energies for the binding of MLn−1 with L. OCN: optimal coordination number. The actual binding free energy for the binding of MLn−1 with L is represented by ΔGn and the corresponding calculated binding free energy is represented by 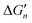 . . 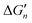 is calculated from the stepwise actual free energy changes (ΔG0, ΔG0,…, ΔGn) using eqn (3). The relationship between ΔGn and is calculated from the stepwise actual free energy changes (ΔG0, ΔG0,…, ΔGn) using eqn (3). The relationship between ΔGn and 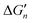 applies to any metal–coordinating atom interaction without displacement of the original coordinating atoms. It also applies to the metal–coordinating atom interaction that displaces a metal-bound water. However, the metal–coordinating atom interaction must be stronger than the metal–water interaction; otherwise, all binding free energies are unfavorable. applies to any metal–coordinating atom interaction without displacement of the original coordinating atoms. It also applies to the metal–coordinating atom interaction that displaces a metal-bound water. However, the metal–coordinating atom interaction must be stronger than the metal–water interaction; otherwise, all binding free energies are unfavorable. | ||
Fig. 5 shows the general trend of bonding power and the general shielding effect of metal complexes. This trend applies to both the metal–ligand interactions that do not change the geometries of the metal complexes and to the metal–ligand interactions that change the geometries of the metal complexes. The water bindings of the metal complexes shown in Fig. 3 change the geometries of the metal complexes. In the calculation of the stepwise water binding energies, the metal complexes are in their optimized geometries (most stable geometries) so that unfavorable interactions in the metal complexes (e.g., charge–charge repulsive interactions between coordinating atoms) are minimal. The trend of the actual stepwise water binding energies shown in Fig. 3 indicate that the general trend of bonding power shown in Fig. 5 applies to metal–ligand interactions that change the geometries of the metal complexes. The formation of metal–ligand complexes in aqueous solution shown in Fig. 4 may not change the geometries of the metal complexes because the newly formed metal–ligand interactions may just substitute for the original metal–water interactions. The actual stepwise free energy changes shown in Fig. 4 indicate that the general trend of bonding power shown in Fig. 5 applies to metal–ligand interactions that do not change the geometries of the metal complexes.
This general trend can be theoretically explained. For metal–ligand interactions that do not change the geometries of the metal complexes, a favorable metal–ligand interaction is the main factor affecting the bonding powers of the metal complex. Because of charge transfer,40,42–44 positive charge densities of metal ions decrease with increasing CNs. Thus, favorable metal–ligand interactions decrease with increasing CNs, indicating that the general trend applies to the metal–ligand interactions that do not change the geometries of the metal complexes. For metal–ligand interactions that change the geometries of the metal complexes, both the favorable metal–ligand interactions and the unfavorable interactions between coordinating atoms affect the bonding power of the metal complexes. The unfavorable interactions increase with increasing CNs because the numbers of unfavorable interactions and the strengths of the unfavorable interactions increase with increasing CNs. Both decreasing favorable interactions and increasing unfavorable interactions decrease the bonding power. Thus, the general trend also applies to the metal–ligand interactions that change the geometries of the metal complexes.
Because the bonding power trend for metal complexes shown in Fig. 5 is typical, the shielding effect shown in Fig. 5 is also typical. For a metal–ligand interaction, the newly formed metal–ligand interaction decreases the positive charge density of the metal ion, which then weakens the original interactions of the metal ion. The interactions of the coordinating atoms with larger negatively charged densities are weakened more and have a larger shielding effect. Therefore, stronger original interactions have a larger shielding effect than the weaker original interactions.
Optimal coordination numbers for the metal complexes in metalloproteins
To validate the large shielding effect of the metal complexes in metalloproteins, it is important to determine their OCNs. The metal complexes in metalloproteins usually contain more than one type of coordinating atom. The CN of a metal complex is the sum of coordinating atoms in the complex. For convenience, M(L)n also represents metal complexes that contain different types of coordinating atoms. Theoretically, whether the metal ion in a metal complex is sufficiently coordinated or hypo-coordinated can be determined from the free energy change of its binding with a coordinating atom. However, it is challenging to obtain thermodynamic data for metal complexes in metalloproteins via experimental methods. Thus, we determined whether or not the metal ion in a metal complex is sufficiently coordinated based on whether or not the metal complex can bind with water spontaneously. For example, if the metal complex M(L)n(OH2) exists in metalloproteins, the binding of M(L)n with water must be spontaneous and the M in M(L)n or in M(L)m (m < n) is hypo-coordinated. Additionally, if M(L)n(OH2)x (x > 1) is not found in the database that contains a larger number of M complexes, it is most likely that the binding of M(L)n(OH2) with water is unfavorable. In this case, we consider the M in M(L)n(OH2) to be a sufficiently coordinated metal ion. The binding of M(L)n(OH2) to an additional coordinating atom is not favorable in terms of Gibbs free energy and the CN of M(L)n(OH2) is considered to be the OCN for the metal complexes M(L)n(OH2), M(L)n and M(L)m (m < n). Note that the database must contain a larger number of the M complexes. It is possible that some metal-bound water molecules were not observed in the crystal structures. In addition, some metal complexes in metalloproteins do not have enough space for binding with water. Thus, we can determine whether the binding of M(L)n(OH2) with water is unfavourable only when a larger number of M complexes are examined.Using this approach we analysed how the coordinating atom microenvironment affects the water binding properties of metal complexes. Water-bound zinc complexes are used as a prototypic example of how this approach can be used to predict OCNs. The PDBbind database45 was used to explore the OCNs of zinc ions in metalloproteins and more than 2900 zinc complexes are examined. We classified the coordinating atoms into two groups: N/S and O coordinating atoms. This classification is based on the two following reasons: (1) almost all coordinating atoms found in the PDBbind database are N, S and O, and (2) N and S (N/S) coordinating atoms are generally softer than O atoms based on the Pearson's hard and soft acids and bases concept.46 The details for exploring the OCNs for the zinc ions in metalloproteins are demonstrated in Fig. S2 (ESI†). The relation between the OCNs and the types of coordinating atoms in zinc complexes is summarized in Table 1.
| Coordinating atoms | OCN | Coordinating atoms | OCN |
|---|---|---|---|
| 4N/S | 4 | 2N/S | 6 |
| 3N/S + O− | 5 | 1N/S | 6 |
| 3N/S without O− | 6 | 0N/S | 6 |
Based on the relation between the OCNs and the types of coordinating atoms, we found that the OCNs of zinc complexes ranging from 4 to 6, depend on the types of coordinating atoms. Zinc complexes binding with 4 N/S coordinating atoms are sufficiently coordinated and cannot bind to additional water molecules. Decreasing the N/S coordinating atoms increases the OCNs of the zinc complexes, indicating that an N or S coordinating atom stabilizes Zn2+ more than an oxygen atom. For zinc complexes containing three N/S coordinating atoms, the OCN is five if the zinc ions bind at least one negatively charged oxygen atom (e.g. the oxygen atom from carboxyl group); otherwise, the OCN is six. Thus, negatively charged oxygen atoms from carboxyl groups stabilize Zn2+ more than neutral oxygen atoms, which suggests that enhancing the charge density of a coordinating atom in a hypo-coordinated metal zinc complex stabilizes the Zn2+ more.
Experimental validation for the shielding effect of metal–ligand interactions on the ligand binding affinity
Because both protein–ligand interactions and metal–ligand interactions affect the binding affinities of ligands, it is challenging to design experiments to obtain the binding free energies contributed by metal–ligand interactions. Thus, we searched the PDBbind database45 for ligands that have the same interactions with a metalloprotein but possess distinct metal–ligand interactions. Then we systematically analyzed how differences in the ligand binding affinities are influenced by variations in the metal–ligand interactions.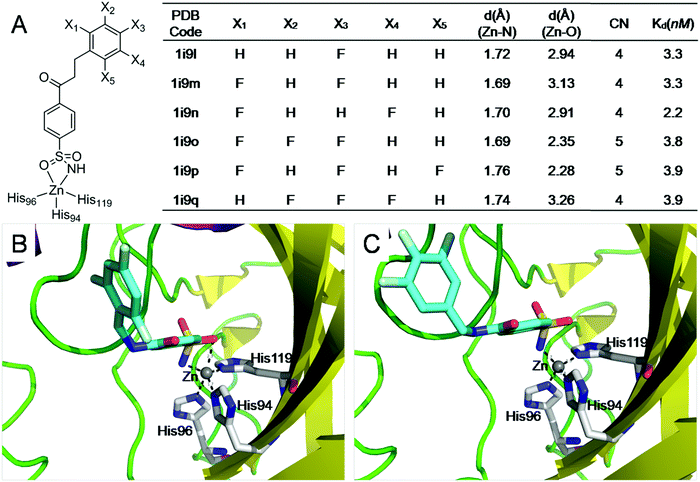 | ||
| Fig. 6 The electrostatic interactions of ligands with sufficiently coordinated metal ions provide minimal little contribution to the ligand binding affinities. (A) Structures and binding affinities of the six structurally similar inhibitors binding to carbonic anhydrase II47 (F131V). (B) The interactions of a 5-coordinated zinc complex (pdb: lI9P); (C) the interactions of a 4-coordinated zinc complex (pdb: lI9Q). The 5-coordinated zinc complex has one more Zn–O interaction than the 4-coordinated zinc complex. However, the Zn–O interaction has little contribution to ligand binding affinity. | ||
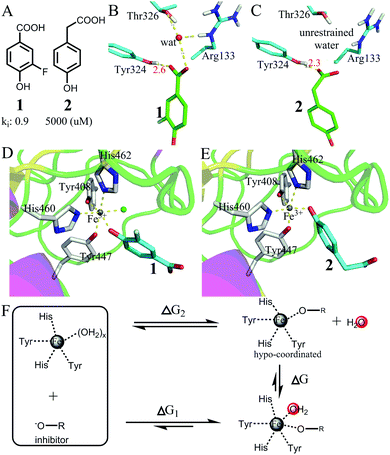 | ||
| Fig. 7 Favorable binding free energy contributed by the interactions of hypo-coordinated metal ions. (A) The structures of two inhibitors 1 and 2 and their binding affinities to protocatechuate 3,4-dioxygenase49 (PDB codes: 3PCF for the complex of 1 and 3PCG for the complex of 2). (B and C) Comparison of the interactions of the carboxyl groups in 1 and 2. Both carboxyl groups have strong interactions with Tyr324. The carboxyl group of 1 interacts with a restrained water molecule, whereas the carboxyl group of 2 interacts with bulk water. (D and E) Comparison of the interactions of the metal ions (Fe3+): both inhibitors interact with Fe3+ with a phenol oxygen atom. However, the metal ion in (D) binds one more water molecule than the metal ion in (E). (F) The thermodynamic cycle showing that the binding of the 5-coordinated Fe ion with a water molecule is largely favourable in terms of Gibbs free energy. | ||
Fig. 7D and E show the two metal ions interacting with 1 and 2. The crystal structures show that the metal ion in (D) binds one more water molecule than the metal ion in (E). The reason for the absence of a metal-bound water molecule in (E) is that the metal-complex does not have enough space for binding with water (Fig. S4, ESI†). Thus, the large difference in binding affinity between the two inhibitors mainly arises from the difference in breaking metal–water coordination interactions as shown in Fig. 7F. The thermodynamic cycle indicates that the difference in the binding free energy between the two inhibitors (ΔG1 − ΔG2 = −5.1 kcal mol−1) approximately equals the binding free energy of the 5-coordinated Fe ion with a water molecule from bulk water. Because the OCN for Fe3+ is 6 and because the 5-coordinated Fe ion is hypo-coordinated (Fig. S5, ESI†), the binding of a hypo-coordinated ion with a coordinating atom may be largely favourable in terms of Gibbs free energy.
We further validated the large binding free energy contributed by the interactions of hypo-coordinated metal ions through exploring the binding of protocatechuate 3,4-dioxygenase with inhibitors 3, 4, and 550,51 (Fig. 8). By analysing the interactions of the carboxyl groups, we found that the free energies contributed by the interactions of the carboxyl groups of the three inhibitors are almost the same (similar to the interactions shown in Fig. S3, ESI†). Also 3, 4, and 5 interact with iron ions similarly by using two oxygen atoms on the benzene ring (note: inhibitors 1 and 2 use only one oxygen atom). Thus, all three inhibitors have very similar interactions with protocatechuate 3,4-dioxygenase and Fe3+. The difference in binding affinity is mainly due to the binding of water to the 5-coordinated iron. The iron ions in 3PCJ and 3PCK are different from the iron in 3PCN in that the iron ions in 3PCJ and 3PCK bind one more water molecule. The iron in 3PCN does not bind with water because its complex does not have enough space for water binding (Fig. S6, ESI†). Because the inhibitors in 3PCJ and 3PCK (3 and 4) are much more potent than the inhibitor (5) in 3PCN, the binding of a 5-coordinated Fe ion with a water molecule from bulk water is largely favourable in terms of Gibbs free energy. The results further support that the binding of an hypo-coordinated ion with a coordinating atom may be largely favourable in terms of Gibbs free energy.
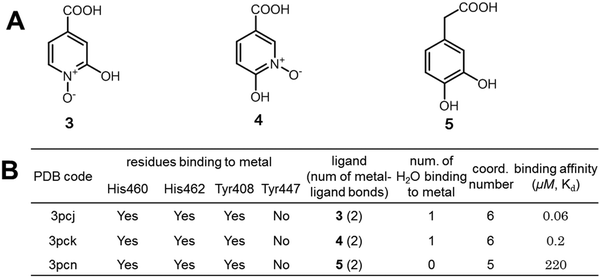 | ||
| Fig. 8 Further validation of the largely favorable binding free energies contributed by the interactions of hypo-coordinated metal ions. (A) The structures of three structurally similar inhibitors of protocatechuate 3,4-dioxygenase; (B) interactions of the metal ions in the enzyme–inhibitor complexes and the binding affinities of inhibitors.49–51 Ligands 3 and 4 have much larger binding affinities than ligand 5 because the iron ions of 3PCJ and 3PCK bind a water molecule but the iron ion of 3PCN does not. | ||
In both wild-type CAII and E117Q CAII, residue 117 interacts with His119 via a hydrogen atom (colored blue in Fig. 9), which requires either residue 117 or His119 to be negatively charged (Fig. S7, ESI†). Which residue should be negatively charged depends on the relative stability of CAII. As demonstrated in Fig. S7 (ESI†), wild-type CAII is more stable when Glu117 is negatively charged than when His119 is negatively charged; however, mutated CAII is more stable when His119 is negatively charged. Thus, the zinc ion in E117Q CAII is less positively charged than the zinc ion in wild-type CAII. It is expected that the metal–ligand interaction for wild-type CAII is stronger than the metal–ligand interaction for E117Q CAII. However, the metal–water interaction in the ligand-free wild-type CAII, which is broken upon the binding of the ligand, is also stronger than the metal–water interaction for the ligand-free E117Q CAII, regardless of the fact that the zinc-bound water molecules are in their neutral states or deprotonated states (Fig. S8, ESI†). Thus, the large difference in binding affinity between the wild-type and E117Q CAIIs cannot be explained merely by the difference in the metal–ligand interaction strength. The large difference in binding affinity has a relation with the large shielding effect due to the strong interaction between Zn2+ and the negatively charged histidine 119 in E117Q CAII (see the change of the red N–Zn bond in Fig. 9B). Thus, stronger original interactions in metal complexes have larger shielding effects, further reducing the contribution of metal–ligand interactions to the ligand binding affinities. In addition, it is important to consider original interactions of metal ions for accurately quantifying the effect of metal–ligand interactions on the ligand binding affinities. Given that the original interactions of the metal complexes have large shielding effects on the ligand-binding affinities, the effects of metal–ligand interactions on the ligand-binding affinities cannot be simply determined from the interaction strengths.
In this example, the binding of the ligand to the metal ion displaces a metal-bound water molecule. In this case, the requirement for stronger original interactions to have a larger shielding effect is that the metal–ligand interactions must be stronger than the metal–water interactions, which is shown in Fig. 5.
Considering shielding effects is essential for modelling metal–ligand interactions accurately
It is widely accepted that stronger metal–ligand interactions have larger contributions to ligand binding affinities. This conventional wisdom is correct if the formation of metal–ligand interactions does not accompany a change in other interactions. However, the formation of metal–ligand interactions must weaken the original interactions of the metal complexes. The contribution of metal–ligand interactions to ligand binding affinities may be completely negated by the weakening of the original interactions. As a result, there is no linear relationship between the strengths of metal–ligand interactions and the contributions of the interactions to ligand binding affinities. Thus, in molecular modelling, it is essential to consider the shielding effects of metal complexes by considering all interactions of the metal ions before and after ligand–binding. It is also essential to consider the original interactions that are broken during the metal–ligand binding processes because the newly formed metal–ligand interactions may substitute for one or more original interactions of the metal complexes. Both shielding effects and the breaking of original interactions are considered by including all interactions of the metal ions before and after ligand–binding. All the interactions of metal ions affect the stabilities of the metal ions as represented with black dots in Fig. 5. Thus, both the stabilities of the metal ions before and after binding are important for determining the effect of metal–ligand interactions on ligand binding affinities. For the binding of inhibitors 1–5 (Fig. 7 and 8) to protocatechuate 3,4-dioxygenase, the stabilities of the metal ions before binding are the same, thus, the difference in binding affinity of the five inhibitors depends on the stabilities of the metal ions after binding. Ligands 1, 3 and 4, which bind to a 6-coordinated iron complex, have significantly stronger binding affinities compared to ligands 2 and 5, which bind a 5-coordinated iron complex. Therefore, enhancing the stability of the metal ions after binding enhances binding affinities of ligands. The stability of the metal ions can be increased by binding them to coordinating atoms, irrespective of whether the coordinating atoms are from ligands, proteins, or water. Moreover, total numbers of metal–ligand coordination bonds play a minor role in regulating binding affinities. For example, inhibitor 1 with one metal–ligand bond is about 245 fold more potent than 5 with two metal–ligand bonds. Therefore, the stabilities of metal ions before and after binding are important for the effect of the metal–ligand interactions on the binding free energies.Understanding how metal–ligand interactions affect ligand binding affinities has important ramifications in the design of potent metal-bound ligands. It is therefore vital for developing reliable scoring functions. It is impossible to develop accurate scoring functions without correctly modelling metal–ligand interactions. Given that the catalytic power of a metalloenzyme is the difference in binding free energy between the substrate in the TS and the substrate in the GS (Fig. 1), this study also provided a novel approach for exploring the enormous catalytic power of the metal ions in metalloenzymes.
Important role of theoretical derivation
The formation of metal–ligand interactions always weakens the original interactions of the metal complexes. Thus, the metal–ligand binding process is complex and is not readily interpretable using existing experimental data. For example, it is impossible to obtain a general rule for explaining the effect of the metal–ligand interactions shown in Fig. 6–9 on the ligand binding affinities only based on the strengths of the interactions. Thus, theoretical derivation plays an irreplaceable role in revealing the effect of metal–ligand interactions on ligand binding affinities. Many biological processes are highly complex, and we have used theoretical derivations to explore some complicated biological problems that are not readily interpretable using existing experimental data.48,52 We believe more complicated biological problems can be understood via theoretical derivations.Conclusion
We demonstrate that the original interactions in the metal complexes of metalloproteins largely reduce the contribution of metal–ligand interactions to the ligand binding affinities. The contributions of the metal–ligand interactions to the ligand binding affinities do not depend on the strengths of the metal–ligand interactions, but depend on the relative thermodynamic stabilities of the metal ions in their metal complexes. The relative stability of the metal ion in a metal complex depends on its CN and its OCN, which in turn depends on the properties of the metal ion and the coordinating atoms. Correctly understanding how the metal–ligand interactions affect the ligand binding affinities is essential for designing potent metal-bound ligands and for establishing potent scoring functions. We also expect that this study will facilitate our understanding of the fundamental basis for the catalysis of metalloproteins.Methods
Method for calculating the water binding energies in Fig. 3. The stepwise water binding energies in Fig. 3 (ΔEn, black dots) represents the water binding energy of M(OH2)n−1 as shown in following process:| M(OH2)n−1 + H2O → M(OH2)n | (M1) |
The ΔEn data were obtained from a ref. 40, in which the density functional method B3LYP was used to calculate the stepwise water binding energies.
The stepwise water binding energy calculated merely based on the M–O strength of the metal complex M(OH2)n (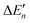 in Fig. 3) equals the total water binding energies of the metal M with n water molecules (ΔEtot) divided by n.
in Fig. 3) equals the total water binding energies of the metal M with n water molecules (ΔEtot) divided by n.
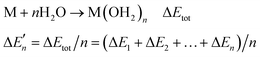 | (M2) |
The calculation of the 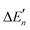 values for Zn2+ is illustrated in Text S1 (ESI†). The actual stepwise water binding energies and the stepwise water binding energies calculated based on the M–O strengths for Mg2+, Ca2+, and Zn2+ are provided in Table S1 (ESI†).
values for Zn2+ is illustrated in Text S1 (ESI†). The actual stepwise water binding energies and the stepwise water binding energies calculated based on the M–O strengths for Mg2+, Ca2+, and Zn2+ are provided in Table S1 (ESI†).
Methods for calculating free energy changes for the formation of metal–ligand complexes in aqueous solution in Fig. 4. The actual stepwise free energy change for the formation of a metal–ligand complex (MLn) in aqueous solution (ΔGn for MLn−1 + L → MLn, black dots in Fig. 4) are calculated from the stepwise association constants (Kn) based on the formula ΔGn = −2.303RT![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) log
log![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) Kn. Here, R equals 0.0019872 kcal mol−1 K−1 and T equals 298 K. The stepwise association constants are obtained from a ref. 53.
Kn. Here, R equals 0.0019872 kcal mol−1 K−1 and T equals 298 K. The stepwise association constants are obtained from a ref. 53.
The stepwise free energy changes calculated merely based on M–L interaction strength (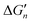 , red dots in Fig. 4) for the metal complex MLn equals the total binding free energy of the metal M with nLs (ΔGtot) divided by n.
, red dots in Fig. 4) for the metal complex MLn equals the total binding free energy of the metal M with nLs (ΔGtot) divided by n.
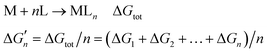 | (M3) |
The calculation of the 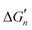 values for metal complexes [Ni(NH3)n]2+ is illustrated in Text S2 (ESI†). The actual stepwise free energy changes for the formation of metal–ligand complexes in aqueous solution and the corresponding stepwise free energy changes calculated based on the M–L strengths for M = Ni2+, L = NH3; M = Co2+, L = NH3; and M = Cd2+, L = CH3COO− are provided in Table S2 (ESI†).
values for metal complexes [Ni(NH3)n]2+ is illustrated in Text S2 (ESI†). The actual stepwise free energy changes for the formation of metal–ligand complexes in aqueous solution and the corresponding stepwise free energy changes calculated based on the M–L strengths for M = Ni2+, L = NH3; M = Co2+, L = NH3; and M = Cd2+, L = CH3COO− are provided in Table S2 (ESI†).
Method for obtaining the optimal coordination numbers of the metal complexes in metalloproteins. The optimal coordination numbers of the metal complexes in metalloproteins are obtained by analysing the metal complexes in a database that contains a larger number of the metal complex. The details are in Fig. S2 (ESI†).
Database analysis
The binding sites of the protein–ligand complexes were analyzed from the “refined” PDBbind database.45 PDBbind is a comprehensive listing of experimentally measured binding affinity data (Kd, Ki, and IC50) for protein–ligand complexes deposited in the Protein Data Bank (PDB). Data entries with a structural resolution greater than 2.5 Å were excluded. A cut off distance of 2.8 Å was applied to metal–ligating atom interactions, but all metal complexes within 7 Å of ligands were recorded to include sufficient water-bound complexes in the analysis.Solvent accessible surface area (SASA)
SASA is calculated using the ‘rolling ball’ algorithm developed by Sharke & Rupley.54 The radii of solvent (water) is set at 1.4 Å. All water molecules are removed from the crystal structure before calculation.Conflicts of interest
There are no conflicts to declare.Acknowledgements
This work is supported by grants from the National Natural Science Foundation of China (21473041, 21763002), the Jiangxi Natural Science Foundation (20171BAB204014) and the National Institute of Health (NIAID U01AI124290-01 and R01-AI10091401). The authors would like to thank Enago (http://www.enago.cn) for the English language review.References
- C. Andreini, I. Bertini and A. Rosato, Metalloproteomes: a bioinformatic approach, Acc. Chem. Res., 2009, 42, 1471–1479 CrossRef CAS PubMed.
- C. Andreini, G. Cavallaro, S. Lorenzini and A. Rosato, MetalPDB: a database of metal sites in biological macromolecular structures, Nucleic Acids Res., 2013, 41, D312–D319 CrossRef CAS PubMed.
- C. G. Frankaer, P. Sonderby, M. B. Bang, R. V. Mateiu, M. Groenning, J. Bukrinski and P. Harris, Insulin fibrillation: the influence and coordination of Zn(2), J. Struct. Biol., 2017, 199, 27–38 CrossRef CAS PubMed.
- M. Lee, J. I. Kim, S. Na and K. Eom, Metal ions affect the formation and stability of amyloid beta aggregates at multiple length scales, Phys. Chem. Chem. Phys., 2018, 20, 8951–8961 RSC.
- J. Perales-Calvo, A. Lezamiz and S. Garcia-Manyes, The Mechanochemistry of a Structural Zinc Finger, J. Phys. Chem. Lett., 2015, 6, 3335–3340 CrossRef CAS PubMed.
- J. W. Slater and H. S. Shafaat, Nickel-Substituted Rubredoxin as a Minimal Enzyme Model for Hydrogenase, J. Phys. Chem. Lett., 2015, 6, 3731–3736 CrossRef CAS PubMed.
- H. M. Key, P. Dydio, D. S. Clark and J. F. Hartwig, Abiological catalysis by artificial haem proteins containing noble metals in place of iron, Nature, 2016, 534, 534–537 CrossRef CAS PubMed.
- B. Hermann, M. Kern, L. La Pietra, J. Simon and O. Einsle, The octahaem MccA is a haem c-copper sulfite reductase, Nature, 2015, 520, 706–709 CrossRef CAS PubMed.
- T. J. Paul, A. Barman, M. Ozbil, R. P. Bora, T. Zhang, G. Sharma, Z. Hoffmann and R. Prabhakar, Mechanisms of peptide hydrolysis by aspartyl and metalloproteases, Phys. Chem. Chem. Phys., 2016, 18, 24790–24801 RSC.
- K. Oohora, H. Meichin, L. Zhao, M. W. Wolf, A. Nakayama, J. Y. Hasegawa, N. Lehnert and T. Hayashi, Catalytic Cyclopropanation by Myoglobin Reconstituted with Iron Porphycene: Acceleration of Catalysis due to Rapid Formation of the Carbene Species, J. Am. Chem. Soc., 2017, 139, 17265–17268 CrossRef CAS PubMed.
- M. Fujimoto, Y. Takagi, T. Aoki, M. Hayase, T. Marumo, M. Gomi, M. Nishimura, H. Kataoka, N. Hashimoto and K. Nozaki, Tissue inhibitor of metalloproteinases protect blood–brain barrier disruption in focal cerebral ischemia, J. Cereb. Blood Flow Metab., 2008, 28, 1674–1685 CrossRef CAS PubMed.
- A. Kofla-Dlubacz, M. Matusiewicz, M. Krzystek-Korpacka and B. Iwanczak, Correlation of MMP-3 and MMP-9 with Crohn's disease activity in children, Dig. Dis. Sci., 2012, 57, 706–712 CrossRef CAS PubMed.
- H. Liu, Y. Kato, S. A. Erzinger, G. M. Kiriakova, Y. Qian, D. Palmieri, P. S. Steeg and J. E. Price, The role of MMP-1 in breast cancer growth and metastasis to the brain in a xenograft model, BMC Cancer, 2012, 12, 583 CrossRef CAS PubMed.
- S. Skagseth, S. Akhter, M. H. Paulsen, Z. Muhammad, S. Lauksund, O. Samuelsen, H. S. Leiros and A. Bayer, Metallo-beta-lactamase inhibitors by bioisosteric replacement: preparation, activity and binding, Eur. J. Med. Chem., 2017, 135, 159–173 CrossRef CAS PubMed.
- V. Sladek, J. Kona and H. Tokiwa, In silico analysis of interaction pattern switching in ligand receptor binding in Golgi alpha-mannosidase II induced by the protonated states of inhibitors, Phys. Chem. Chem. Phys., 2017, 19, 12527–12537 RSC.
- A. Allam, L. Maigre, R. Alves de Sousa, E. Dumont, J. Vergalli, J. M. Pages and I. Artaud, New amphiphilic neamine conjugates bearing a metal binding motif active against MDR E. aerogenes Gram-negative bacteria, Eur. J. Med. Chem., 2017, 127, 748–756 CrossRef CAS PubMed.
- T. Singh, O. A. Adekoya and B. Jayaram, Understanding the binding of inhibitors of matrix metalloproteinases by molecular docking, quantum mechanical calculations, molecular dynamics simulations, and a MMGBSA/MMBappl study, Mol. Biosyst., 2015, 11, 1041–1051 RSC.
- M. R. Nechay, C. E. Valdez and A. N. Alexandrova, Computational treatment of metalloproteins, J. Phys. Chem. B, 2015, 119, 5945–5956 CrossRef CAS PubMed.
- H. Guo, N. Rao, Q. Xu and H. Guo, Origin of tight binding of a near-perfect transition-state analogue by cytidine deaminase: implications for enzyme catalysis, J. Am. Chem. Soc., 2005, 127, 3191–3197 CrossRef CAS PubMed.
- F. Bai, S. Liao, J. Gu, H. Jiang, X. Wang and H. Li, An accurate metalloprotein-specific scoring function and molecular docking program devised by a dynamic sampling and iteration optimization strategy, J. Chem. Inf. Model., 2015, 55, 833–847 CrossRef CAS PubMed.
- M. L. Verdonk, J. C. Cole, M. J. Hartshorn, C. W. Murray and R. D. Taylor, Improved protein–ligand docking using GOLD, Proteins, 2003, 52, 609–623 CrossRef CAS PubMed.
- S. S. Lodhi, R. Farmer, A. K. Singh, Y. K. Jaiswal and G. Wadhwa, 3D structure generation, virtual screening and docking of human Ras-associated binding (Rab3A) protein involved in tumourigenesis, Mol. Biol. Rep., 2014, 41, 3951–3959 CrossRef CAS PubMed.
- R. A. Friesner, R. B. Murphy, M. P. Repasky, L. L. Frye, J. R. Greenwood, T. A. Halgren, P. C. Sanschagrin and D. T. Mainz, Extra precision glide: docking and scoring incorporating a model of hydrophobic enclosure for protein–ligand complexes, J. Med. Chem., 2006, 49, 6177–6196 CrossRef CAS PubMed.
- R. Wang, Y. Lu, X. Fang and S. Wang, An extensive test of 14 scoring functions using the PDBbind refined set of 800 protein–ligand complexes, J. Chem. Inf. Comput. Sci., 2004, 44, 2114–2125 CrossRef CAS PubMed.
- E. Ortega-Carrasco, A. Lledos and J. D. Marechal, Assessing protein–ligand docking for the binding of organometallic compounds to proteins, J. Comput. Chem., 2014, 35, 192–198 CrossRef CAS PubMed.
- M. D. Eldridge, C. W. Murray, T. R. Auton, G. V. Paolini and R. P. Mee, Empirical scoring functions: I. The development of a fast empirical scoring function to estimate the binding affinity of ligands in receptor complexes, J. Comput. – Aided Mol. Des., 1997, 11, 425–445 CrossRef CAS PubMed.
- H. Li, K. S. Leung, M. H. Wong and P. J. Ballester, Improving AutoDock Vina Using Random Forest: The Growing Accuracy of Binding Affinity Prediction by the Effective Exploitation of Larger Data Sets, Mol. Inf., 2015, 34, 115–126 CrossRef CAS PubMed.
- D. S. Goodsell, G. M. Morris and A. J. Olson, Automated docking of flexible ligands: applications of AutoDock, J. Mol. Recognit., 1996, 9, 1–5 CrossRef CAS PubMed.
- G. M. Morris, D. S. Goodsell, R. Huey and A. J. Olson, Distributed automated docking of flexible ligands to proteins: parallel applications of AutoDock 2.4, J. Comput. – Aided Mol. Des., 1996, 10, 293–304 CrossRef CAS PubMed.
- M. R. Koebel, G. Schmadeke, R. G. Posner and S. Sirimulla, AutoDock VinaXB: implementation of XBSF, new empirical halogen bond scoring function, into AutoDock Vina, J. Cheminf., 2016, 8, 27 Search PubMed.
- A. Grosdidier, V. Zoete and O. Michielin, Fast docking using the CHARMM force field with EADock DSS, J. Comput. Chem., 2011, 32, 2149–2159 CrossRef CAS PubMed.
- B. R. Brooks, C. L. Brooks, 3rd, A. D. Mackerell, Jr., L. Nilsson, R. J. Petrella, B. Roux, Y. Won, G. Archontis, C. Bartels, S. Boresch, A. Caflisch, L. Caves, Q. Cui, A. R. Dinner, M. Feig, S. Fischer, J. Gao, M. Hodoscek, W. Im, K. Kuczera, T. Lazaridis, J. Ma, V. Ovchinnikov, E. Paci, R. W. Pastor, C. B. Post, J. Z. Pu, M. Schaefer, B. Tidor, R. M. Venable, H. L. Woodcock, X. Wu, W. Yang, D. M. York and M. Karplus, Charmm: the biomolecular simulation program, J. Comput. Chem., 2009, 30, 1545–1614 CrossRef CAS PubMed.
- N. S. Pagadala, K. Syed and J. Tuszynski, Software for molecular docking: a review, Biophys. Rev., 2017, 9, 91–102 CrossRef CAS PubMed.
- P. Shi, Y. Zhang, Y. Li and L. Bian, Probing the interaction of l-captopril with metallo-beta-lactamase CcrA by fluorescence spectra and molecular dynamic simulation, Luminescence, 2018, 33, 954–961 CrossRef CAS PubMed.
- K. C. Hsu, Y. F. Chen and J. M. Yang, GemAffinity: a scoring function for predicting binding affinity and virtual screening, Int. J. Data Min. Bioinf., 2012, 6, 27–41 CrossRef.
- Z. Zheng and K. M. Merz, Jr., Ligand Identification Scoring Algorithm (LISA), J. Chem. Inf. Model., 2011, 51, 1296–1306 CrossRef CAS PubMed.
- C. C. Huang, C. A. Lesburg, L. L. Kiefer, C. A. Fierke and D. W. Christianson, Reversal of the hydrogen bond to zinc ligand histidine-119 dramatically diminishes catalysis and enhances metal equilibration kinetics in carbonic anhydrase II, Biochemistry, 1996, 35, 3439–3446 CrossRef CAS PubMed.
- M. Zhao, M. A. Iron, P. Staszewski, N. E. Schultz, R. Valero and D. G. Truhlar, Valence-Bond Order (VBO): A New Approach to Modeling Reactive Potential Energy Surfaces for Complex Systems, Materials, and Nanoparticles, J. Chem. Theory Comput., 2009, 5, 594–604 CrossRef CAS PubMed.
- T. Dudev and C. Lim, Competition among metal ions for protein binding sites: determinants of metal ion selectivity in proteins, Chem. Rev., 2014, 114, 538–556 CrossRef CAS PubMed.
- M. Pavlov, P. E. M. Siegbahn and M. Sandstrom, Hydration of Beryllium, Magnesium, Calcium, and Zinc Ions Using Density Functional Theory, J. Phys. Chem. A, 1998, 102, 219–228 CrossRef CAS.
- O. Carugo, K. Djinovic and M. Rizzi, Comparison of the Co-ordinative Behaviour of Calcium(II) and Magnesium(II) from Crystallographic Data, J. Chem. Soc., Dalton Trans., 1993, 2127–2135 RSC.
- P. V. Maye and M. Mezei, Calculation of the free energy of solvation of the Li+ and Na+ ions in water and chloroform, THEOCHEM, 1996, 362, 317–324 CrossRef CAS.
- A. Rondi, Y. Rodriguez, T. Feurer and A. Cannizzo, Solvation-driven charge transfer and localization in metal complexes, Acc. Chem. Res., 2015, 48, 1432–1440 CrossRef CAS PubMed.
- D. Chaturvedi, V. Gupta, P. Tandon, A. Sharma, C. Baraldi and M. C. Gamberini, Intermolecular charge transfer and vibrational analysis of hydrogen bonding in acetazolamide, Spectrochim. Acta, Part A, 2012, 99, 150–159 CrossRef CAS PubMed.
- R. Wang, X. Fang, Y. Lu, C. Y. Yang and S. Wang, The PDBbind database: methodologies and updates, J. Med. Chem., 2005, 48, 4111–4119 CrossRef CAS PubMed.
- P. W. Ayers, R. G. Parr and R. G. Pearson, Elucidating the hard/soft acid/base principle: a perspective based on half-reactions, J. Chem. Phys., 2006, 124, 194107 CrossRef PubMed.
- C. Y. Kim, P. P. Chandra, A. Jain and D. W. Christianson, Fluoroaromatic-fluoroaromatic interactions between inhibitors bound in the crystal lattice of human carbonic anhydrase II, J. Am. Chem. Soc., 2001, 123, 9620–9627 CrossRef CAS PubMed.
- D. Chen, Y. Li, M. Zhao, W. Tan, X. Li, T. Savidge, W. Guo and X. Fan, Effective lead optimization targeting the displacement of bridging receptor–ligand water molecules, Phys. Chem. Chem. Phys., 2018, 20, 24399–24407 RSC.
- A. M. Orville, N. Elango, J. D. Lipscomb and D. H. Ohlendorf, Structures of competitive inhibitor complexes of protocatechuate 3,4-dioxygenase: multiple exogenous ligand binding orientations within the active site, Biochemistry, 1997, 36, 10039–51100 CrossRef CAS PubMed.
- A. M. Orville, J. D. Lipscomb and D. H. Ohlendorf, Crystal structures of substrate and substrate analog complexes of protocatechuate 3,4-dioxygenase: endogenous Fe3+ ligand displacement in response to substrate binding, Biochemistry, 1997, 36, 10052–10066 CrossRef CAS PubMed.
- T. E. Elgren, A. M. Orville, K. A. Kelly, J. D. Lipscomb, D. H. Ohlendorf and L. Que Jr., Crystal structure and resonance Raman studies of protocatechuate 3,4-dioxygenase complexed with 3,4-dihydroxyphenylacetate, Biochemistry, 1997, 36, 11504–11513 CrossRef CAS PubMed.
- D. Chen, N. Oezguen, P. Urvil, C. Ferguson, S. M. Dann and T. C. Savidge, Regulation of protein–ligand binding affinity by hydrogen bond pairing, Sci. Adv., 2016, 2, e1501240 CrossRef PubMed.
- A. E. Martell and R. M. Smith, Critical stability constants, Plenum Press, New York, 1976, pp. 1–6 Search PubMed.
- A. Shrake and J. A. Rupley, Environment and exposure to solvent of protein atoms. Lysozyme and insulin, J. Mol. Biol., 1973, 79, 351–371 CrossRef CAS PubMed.
Footnote |
| † Electronic supplementary information (ESI) available. See DOI: 10.1039/c8cp06555a |
| This journal is © the Owner Societies 2019 |