Exploring the ultrafast dynamics of a diarylethene derivative using sub-10 fs laser pulses

Abstract

A diarylethene derivative, 1,2-bis(2,4-dimethyl-5-phenyl-3-thienyl)perfluorocyclopentene (DMP), is a photoswitch molecule utilizing a reversible aromatic ring-opening reaction. The quantum yield of the ring-opening reaction is however remarkably low. We investigate the origin of this behaviour by means of ultrafast transient absorption spectroscopy utilizing sub-10 fs pulses, which is an invaluable tool for simultaneously studying both the electronic and the vibrational molecular dynamics. Namely, a noncollinear optical parametric amplifier (NOPA) generating sub-10 fs pulses in the spectral range 605–750 nm is employed. The transient absorption signal is modulated by several vibrational modes, which are compared with experimental and computational Raman spectra and then assigned to the ground or excited electronic state. We observe that the most pronounced vibrational mode – the ethylenic stretching mode at a frequency of 1501 cm⁻¹ – exhibits instantaneous frequency and amplitude modulation. The observed modulations occur due to weak coupling with another 1431 cm⁻¹ stretching mode mediated by a vibrational mode of low frequency, i.e. around 60 cm⁻¹. Fast internal conversion S₁ → S₀ originates in a relaxation through a conical intersection (found by density-functional theory computations), facilitated by the two aforementioned stretching modes.

---

Introduction

Photochromic molecules are compounds able to undergo a light-triggered reversible transformation between two forms characterized by distinct absorption spectra. Among them fluorinated diarylethene derivatives bearing heterocyclic aryl groups developed by Irie et al.¹ are prominent due to their high thermal and optical stability and high fatigue resistance combined with versatile functional properties. Thanks to these unique features diarylethenes are the subject of intense studies as materials having potential applications in a variety of fields – from molecular electronics² to super-resolution imaging,³ biological markers,^4,5 and bioactivity controls.⁶

Light-driven electrocyclic reactions in diarylethenes are known to follow the Woodward–Hoffman rules that imply conrotatory movement of atomic orbitals as the photochemical reaction proceeds in the excited state. Typically, the open-ring isomer absorbs UV light while the closed-ring form has its absorption band in both UV and visible due to the formation of an extended π-electron system. This implies that UV irradiation of the open ring isomer leads to formation of a photostationary state (PSS) in which both isomers are present in photochemical equilibrium. For diarylethenes to become efficient photoswitches, it is essential to maximize the molar absorption coefficient of the closed-ring form. For this purpose a diarylethene derivative called 2-bis(2,4-dimethyl-5-phenyl-3-thienyl) perfluorocyclopentene (DMP) was synthesized (see Fig. 1).⁷ The substitution of hydrogens in the 5′ position in 1,2-bis(2,4-dimethylthiophene-3-yl)perfluorocyclopentene with phenyl groups has indeed led to nearly doubling the molar absorption coefficient of the closed-ring isomer and to a bathochromic shift of the absorption maximum from 534 to 562 nm.⁷ Those promising properties of DMP have led to further studies.^8–11

Fig. 1 Chemical structure of DMP and its photochemical reactions.

The content of the closed-ring isomer in the PSS in DMP was found to be about 70% when 310 nm was used as an excitation wavelength.⁸ Furthermore, the open ring isomer in the ground state typically exists in two conformations that interconvert to each other at room temperature. One conformer has aromatic groups in a mirror (C_s) symmetry (anti-parallel (AP)) while the other possesses C₂ (parallel (P)) symmetry. Only the AP conformer undergoes a cyclization reaction resulting in the decrease of the quantum yield of the ring closure reaction. In diarylethene derivatives, including DMP, bearing large adjacent aromatic rings, the interconversion is expected to be slow enough to capture the fraction of the AP and P conformers in NMR experiments.¹²

DMP is characterized by a high quantum yield of the ring closure reaction (0.46) and a very low quantum yield of cycloreversion (0.015).⁸ Such a drastic difference in the reaction quantum yields was observed also for DMP's close cousin – dithienylethene – and explained using a computational approach involving spin–flip time-dependent density functional theory (SF TD-DFT) by Morokuma et al.¹³ The authors have shown that three isomers of 1,2-dithenylethene called normal (N), inverse (I), and mixed (M) with different positions of the sulfur atom in the thienyl ring exhibit distinct quantum yields of ring closure and opening reactions. For the N-type 1,2-dithienylethene, having the sulphur atom in the same position as in the thienyl ring of DMP, the excitation of the open- and closed-ring isomers leads to the same conical intersection which favours the closed-ring product.¹³ In the case of the I isomer the open-ring photoproduct is preferred, while for the M type isomer the quantum yield of both photoproducts is similar. In other studies, Sumi and co-workers have shown experimentally that the quantum yield of cycloreversion is wavelength-dependent¹⁴ which was attributed to the energy barrier on the excited state potential surface.

Elucidating the fate of diarylethene derivatives in excited states is crucial for the effective development of new compounds possessing efficient photochemical quantum yields towards specific photoproducts. Since these reactions typically occur on the picosecond timescale, ultrafast spectroscopy provides a necessary tool to study electronic dynamics on excited state potential energy surfaces. To gain information on molecular motions occurring after the electronic excitation it is essential to employ a spectroscopic technique sensitive to molecular vibrations in which rate constants related to nuclear motions are not blurred by electronic relaxation. So far, several time-resolved studies with picosecond and femtosecond timescale resolution on diarylethenes have been performed.^{8–11,15–28} However, most of them do not reveal the vibrational dynamics accompanying the electronic decay as the applied laser pulses are too long (∼100 fs) to observe the modulation of temporal decay by molecular vibrations. The notable exceptions in which the vibrational dynamics of diarylethenes has been studied include studies by Jean-Ruel et al. employing femtosecond electron crystallography²¹ and the one by Pontercorvo et al. where femtosecond stimulated Raman scattering was applied.²⁵ The present work is the first study of both electronic and vibrational dynamics.

The ring opening reaction in DMP has been studied by Miyasaka et al.⁸ by means of transient absorption (TA) spectroscopy in femtosecond and picosecond time regimes. They observed a significant enhancement of the cycloreversion quantum yield for 532 nm picosecond laser excitation while no significant increase was observed when a femtosecond laser was used for excitation. This enhancement was explained by step-wise two-photon excitation to the higher excited states that activated an efficient cycloreversion pathway. The authors found that the excited state of the closed isomer of DMP decays to the ground with a time constant of 7.4 ps in competition with the very low-yield cycloreversion reaction.

In the present work, we have studied electronic and vibrational relaxation of DMP in the PSS by means of TA spectroscopy using two sets of femtosecond laser systems of sub-10 fs and <150 fs temporal resolution. The sub-10 fs set-up served as a tool to determine molecular vibrations accompanying the electronic decay while the <150 fs allowed us to obtain accurate electronic decay time constants. The application of sub-10 fs laser pulses to transient absorption spectroscopy allows study of the dynamics of molecular vibrations whose vibrational period is shorter than temporal resolution of the pump–probe experiment. The vibrational wave-packets in both the ground and the excited state are prepared by a broadband electronic excitation.²⁹ The applied methodology offers a few advantages over more frequently employed time-resolved vibrational spectroscopies utilizing infrared absorption and Raman scattering. These advantages include the opportunity for simultaneous study of electronic dynamics and molecular vibrations coupled to the electronic transitions. Our homemade NOPA set-up has been already successfully applied to resolve fundamental processes in a variety of molecular systems.^30–36 Complementary to the time-resolved experiment employing sub-10 fs pulses we utilized another femtosecond laser system with ∼150 fs resolution to cover pump–probe delays longer than 13 ps that were beyond the range of the NOPA set-up.

The application of sub-10 fs laser pulses allowed us to identify molecular vibrations in the ground and the excited electronic state of DMP. The FFT of the TA signal ΔA allowed determination of several vibrational modes. The most pronounced vibrational modes at 1501 and 1431 cm⁻¹ involve motions of the C–C atoms within the central ring that contribute to the internal conversion S₁ → S₀ through a conical intersection (CI). Furthermore, an analysis using a gated-window FFT allows exploration of potential vibrational coupling between 1431 and 1501 cm⁻¹ modes mediated by a low-frequency vibrational mode of a frequency of ca. 60 cm⁻¹ that may have an impact on the mechanism of internal conversion. The supplementary computations allowed locating the CI between S₁ and S₀ states, which can be a pathway of relaxation to the closed-form S₀ state.

Experimental

A homemade NOPA set-up has been employed to perform femtosecond pump–probe TA experiments with 10 fs temporal resolution (set-up I). The details of this experimental set-up are described elsewhere.³⁷ Briefly, the pump and seed for the homemade NOPA part are provided by a commercial laser system consisting of a femtosecond Ti:sapphire oscillator (Mai Tai, Spectra-Physics, 80 MHz, 800 nm, pulse duration <100 fs) pumped by a diode laser (Millennia Pro, Spectra Physics, 532 nm, 5 W) and an amplifier (Spitfire ACE, Spectra-Physics, 5 kHz, output power: 1 W).

The output from the NOPA is separated into two beams and used as a pump and probe in the TA measurements. The full width at half maximum (the pulse duration) of the intensity profile of the NOPA system was measured to be ∼10 fs by the second-harmonic generation autocorrelation method. The pulse energies and corresponding laser intensities of the pump and probe beams were adjusted to be ∼40 nJ and ∼5 nJ, respectively. The spectrum of the pump and probe beams ranges from 1.65 eV (750 nm) to 2.05 eV (605 nm). In the TA experiments, the probe beam after the sample is directed into a polychromator and is detected by a 128-channel lock-in amplifier.²⁹ The spectral resolution defined by a single-channel detector size is a range of 1.5 nm.

The compound 2-bis(2,4-dimethyl-5-phenyl-3-thienyl)perfluorocyclopentene of reagent grade 99.32% (HPLC grade) has been purchased from Yamada Chemical Co. and used without further purification. The sample of DMP in the PSS for TA measurements was prepared by dissolving DMP powder in hexane followed by irradiation of the solution using a xenon lamp (Hamamatsu L11034) equipped with a short pass UV filter (cut off wavelength: 330 nm). The irradiation was continued until no further spectral changes were detected. After the irradiation, the equilibrium absorbance of the generated PSS was 2.2 at 560 nm in a 0.5 mm quartz cell.

The TA measurements were performed using a cell of 0.5 mm pathlength. The sample was not circulated during the measurements since there were no observable spectral changes in the stationary UV-vis spectrum. Spectra were recorded for several hours of sample irradiation using femtosecond pulse radiation from the NOPA. The TA signals using the NOPA set-up with sub-10 fs resolution were recorded in two time ranges: from −200 to 1800 fs with a 0.2 fs step and from −1 ps to 13 ps with a 1.4 ps step. Two-colour experiments using another TA set-up with ∼150 fs described below were recorded from −20 ps to 100 ps with a varying time step.

Two-colour transient absorption measurements have been performed using another femtosecond laser set-up (set-up II). In this set-up a Ti:sapphire oscillator (Tsunami, Spectra-Physics, 82 MHz, 800 nm, pulse duration <100 fs) is pumped by a diode laser (Millennia Pro, Spectra Physics, 532 nm, 5 W) and amplified in a regenerative amplifier (Spitfire ACE, Spectra-Physics, 1 kHz, output power: 4 W). The output from the amplifier has been used to pump two optical parametric amplifiers (OPA) (Topas Prime, Light Conversion), the first of which has been used to generate the pump beam, while the second produced the probe beam. The pump and probe pulse energies were adjusted to be ∼40 nJ, and ∼5 nJ, respectively. The pump–probe measurements have been performed in a 0.5 mm cell.

The quantum chemical calculations have been performed using Gaussian 09 rev. D³⁸ (TD-B3LYP for excited-state computations) after validating the method's performance on the IR spectrum. The CIOpt program combined with Gaussian 09 was used for finding the conical intersection.³⁹ The Natural Transition Orbital (NTO) method was used to visualize the character of the electronic excitation.⁴⁰

Results and discussion

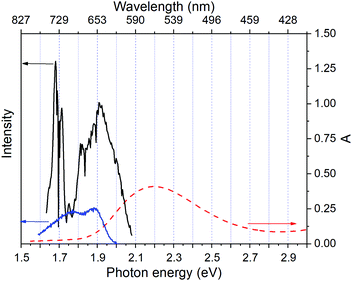
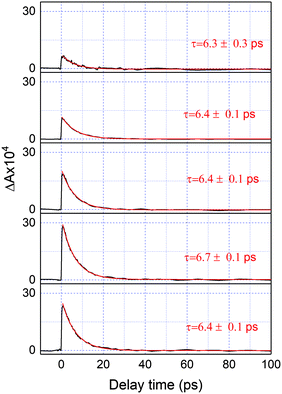
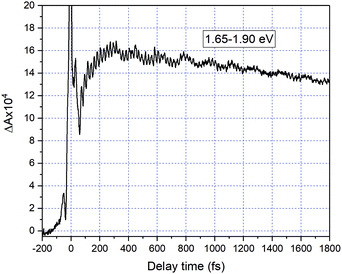
Fig. 2 shows a comparison of the electronic absorption spectra of DMP in the open ring form with the PSS attained by the irradiation of a hexane solution of DMP in the open ring form by a UV photodiode at 300 nm and the fluorescence spectrum of the PSS upon excitation at 550 nm. As the open-ring isomer of DMP does not possess absorption bands in the spectral range below 2.10 eV (590.4 nm) where NOPA and PSS spectra overlap, only the closed-ring isomer of DMP contributes to the measured transient absorption signal. The two-dimensional spectrum of the transient absorption signal (2D ΔA) is presented in Fig. 3 and the corresponding time-resolved difference absorption spectra are shown in Fig. 4. The spectra exhibit positive ΔA signals below 1.94 eV (639.1 nm) and negative ΔA signals in the spectral range 1.94–2.05 eV (604.8–639.1 nm). The negative contribution is dominated by the ground state bleaching since molar absorption coefficients of the ground state of DMP are large in this spectral range. Below 1.94 eV (639.1 nm) the ΔA signals become positive as the excited state absorption (ESA) from the lowest electronic excited state to the higher excited state (S₁ → S_n) dominates over the ground state bleaching. Several real-time traces of ΔA signals are presented in Fig. 5. In the measured spectral range, fluorescence occurs (see Fig. 2) which suggests that stimulated emission can contribute to the measured ΔA signal. The intensity of the recorded fluorescence in the stationary measurement was very low indicating the fluorescence quantum yield is below 10⁻⁵. The lack of apparent SE around time zero indicates strong intramolecular reorganization within the time-resolution leading to a substantial decrease of the SE cross-section and/or a rapid transition to a “dark” state. In consequence, the contribution from the stimulated emission is likely dominated by the ESA and ground state bleaching in relevant spectral ranges. To be able to precisely determine the time constants associated with the decay of ΔA signals, we employed a femtosecond transient absorption set-up equipped with a longer delay line than NOPA (setup I). The used setup has the additional advantage of an improved signal-to-noise ratio of ΔA thanks to the use of a single-channel detector (unlike in NOPA, where ΔA is divided into 128 channels). The obtained real-time time traces of ΔA for pump pulses at 2.05 eV (605 nm) and several probe pulses are presented in Fig. 6. These time traces exhibit a single-exponential decay function. In the measured spectral range, the probe wavelength dependence is negligibly small. For example, the time constants are ranging from 6.4 ± 0.1 ps at 717 nm (1.73 eV) to 6.3 ± 0.1 ps at 1.90 eV (623 nm). The essentially absent probe wavelength dependence indicates that the contribution from spectral shifting due to vibration cooling to the ΔA signals is minor. Moreover, as the quantum yield of cycloreversion is very low (0.015), and considering that there are no apparent ΔA signals for the longest delay times that could arise from the open-ring photoproduct, we conclude that the observed dynamics of the ΔA signal is mainly due to internal conversion from the excited state S₁ to the ground state.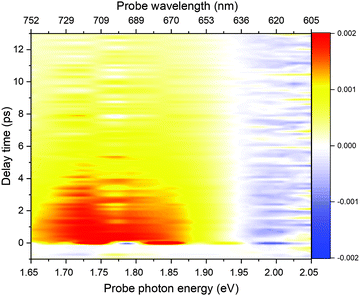

Fig. 2 The absorption spectra of the PSS of DMP attained by the irradiation of a hexane solution of the open ring isomer using a UV photodiode at 300 nm (dashed red line), the fluorescence spectrum of the PSS upon excitation at 550 nm (solid blue line) and the laser spectrum of the NOPA (solid black line).

Fig. 3 Two-dimensional difference absorption spectrum plotted against pump–probe delay time ranging from −200 fs to 12 ps in the probe range 1.66–2.05 eV.

Fig. 4 Time-resolved difference absorption spectra for delay times in the range 200 fs to 12 ps.

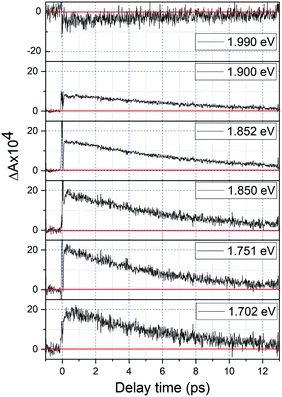Fig. 5 The real-time traces of transient absorption signal at 1.70, 1.75, 1.80, 1.85, 1.90, and 1.99 eV obtained using the homemade NOPA – setup I.

Fig. 6 The real-time traces of the transient absorption signal of DMP excited at 605 nm (2.05 eV) and probed at 1.70 eV (728 nm), 1.75 eV (708 nm), 1.80 eV (687 nm), 1.85 (669 nm), and 1.90 eV (653 nm) obtained in two colour pump–probe experiments using set-up II. The red curves represent fits using a single exponential function.

Despite the fact that the vibrational cooling is not manifested as a time constant when real-time traces in Fig. 6 are fitted using more than one exponential component it is obvious that the molecule must “cool down” vibrationally since no radiative process seems to occur and no high energy species is being formed.⁴¹ The vibrational cooling rate can be obtained by the application of window-gated FFT to ΔA signals obtained using 10 fs laser pulses. This analysis results in vibrational cooling rates of 800 ± 200 fs. The details of this method and the implications of obtained vibrational cooling rates on the mechanism of internal conversion will be discussed in the subsequent paragraphs. The obtained 6.4 ps time constant is consistent with 7.4 ps obtained by Miyasaka and co-workers.⁸ This slight disagreement may result from the fact that in our experiments the polarizations of the pump and probe were parallel to each other while in the case of Miyasaka et al. they were set at the magic angle. It is also important to mention that Miyasaka et al. used a 15 ps, 532 nm laser in their experiment.

In their seminal work, Robb and co-workers proposed a general scheme of electronic energy dissipation of the normal type of diarylethenes using complete active space self-consistent field (CASSCF) and molecular mechanics-valence bond (MMVB) methods.⁴² In this scheme upon excitation the closed-ring isomer of a DAE derivative molecule must overcome a barrier to reach a CI leading to the open ring isomer. As this CI is not easily accessible due to the existence of an energy barrier, the quantum yield of the ring opening reaction is low. On the other hand, due to a favourable shape of the potential energy surface (PES) upon excitation of an open ring isomer of normal type DAE the ring closure reaction goes smoothly resulting in high values of quantum yields of ring closure reactions. Since the energies of excited states and the detailed shape of the PES may strongly depend on substituents,^43,44 we performed our own TD-DFT computations (see Table 1). Upon broadband excitation using the NOPA set-up in the spectral range 590–800 nm (1.65–2.10 eV) the only achievable excited electronic state is the lowest singlet S₁. Our computations, therefore, contradict the previously proposed scheme for DMP in which after the vertical excitation to the Franck–Condon state of 1B symmetry the molecule relaxes through the CI to the dark state of 2A symmetry in about 100 fs. This disagreement is not surprising, as the old model was based on the excitation of cyclohexadiene (CHD) – a relatively small molecule – and therefore treatable with sophisticated computational methods. As CHD constitutes a chromophore in many larger molecules, the results of quantum chemical calculations for this molecule are often employed to interpret experimental data of larger molecules such as diarylethenes that are beyond the reach of more advanced quantum chemical methods. However, in case of diarylethenes, it has been shown that the presence of the heteroatoms in the central ring, as well as their position, has a critical impact on the electronic structure, the location of conical intersections and the related quantum yields of ring opening and closure reactions.¹³ Unlike in the case of CHD, our TD-DFT calculations do not predict the presence of a dark electronic state below the S₁ state and therefore they imply that the electronic dissipation process happens only on the PES of S₁. In Fig. S1 of the ESI,† the NTOs⁴⁰ of the excitation highlight the roles that the thiophene rings and the perfluorocyclopentane ring fused with the CHD chromophore play in the S₀ → S₁ excitation which explains why the CHD model is insufficient here.

Table 1 Electronic excitations of the closed-ring isomer of DMP calculated with TD-DFT

Singlet excitation (eV)	Singlet excitation (nm)	Oscillator strength
2.11	588	0.298
3.03	410	0.023
3.48	356	0.162
3.69	336	0.017
3.93	316	0.142
3.95	314	0.237
4.05	306	0.015
4.07	304	0.102
4.13	301	0.001
4.18	297	0.006

---

The short lifetime of the ΔA signal (∼7 ps), the very weak fluorescence and the large Stokes shift observed in both stationary fluorescence (0.30 eV) and in theoretical calculations (0.57 nm) signal that the minimum of the S₁ state is not reached because there exists a more efficient electronic energy dissipation channel via a CI located on the path from the Franck–Condon state to the minimum of the S₁ state. We found such a CI using the TD-DFT method. While TD-DFT, as a single-reference method, is not able to correctly reproduce the topology of the CI and the exact energetics, it is able to find the approximate geometry for which the CI appears. In the case of DMP, a minimal energy CI (MECI) was found for the central-ring C–C bond as large as R_CC = 1.98 Å (while at the FC geometry it reads R_CC = 1.54 Å). From the CI DMP could relax either to its ground state in the closed form or in the open one. The probability of each path is determined by the topology of the PES around the CI. Although it is impossible to accurately describe the PES near the CI with TD-DFT, the small yield of the ring-opening reaction implies that the CI has a sloped character, which promotes photostability.⁴⁵

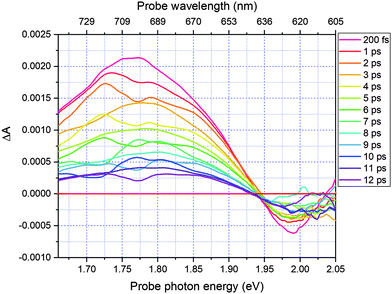
As indicated previously, when the applied pulse durations of both pump and probe pulses are shorter than a vibrational period of molecular vibrations, the temporal amplitude and frequency changes of these vibrations can be probed simultaneously with the electronic relaxation dynamics by the time-resolved absorption measurement. This is manifested by the amplitude–modulation of time dependences of transient difference absorption ΔA(t,λ) represented by δΔA(t,λ) with frequencies corresponding to the molecular vibrational modes in the ground and/or the excited electronic states. The time dependences are named real-time (vibrational) traces showing real-time probed values of vibrational amplitude including the vibrational phase instead of the frequency domain spectrum. It follows that the application of a fast Fourier transform (FFT) to the δΔA(t,λ) signal allows determination of the modulation frequencies and their amplitudes that correspond to frequencies and amplitudes of molecular vibrations. Therefore, we first averaged the real-time traces of transient absorption signal changes δΔA(t,λ) in the spectral range of 1.65–1.90 eV to reduce noise and thereafter calculated the FFT in the delay time range 150–1800 fs. The FFT can correspond to both the ground and the excited state since the lifetime of the excited state is about 6 ps (Fig. 6) and no following intermediate state is involved in the latter case. The resultant mean real-time trace averaged for the probe range of 1.65–1.90 eV is shown in Fig. 7 while the FFT amplitude spectrum of δΔA(t,λ) is presented in Fig. 8. This shows a kind of impulsive Raman spectrum. It does not contain background non-resonant contributions in contrast to coherent anti-Stokes Raman scattering (CARS). The FFT of δΔA(t,λ) has been compared with the stimulated Raman spectrum of DMP in hexane (Fig. 8 – blue line). Several frequencies appearing clearly in both the FFT spectrum and Raman spectrum are listed in Table 2. Additionally, we performed quantum chemical calculations of the Raman spectrum of DMP at the B3LYP/6-31G(d,p) level. The most intense vibrational mode has a peak at 1501 ± 8 cm⁻¹. As the resolution of the FFT calculation is in our case 8 cm⁻¹, 1501 cm⁻¹ is considered to be corresponding to the 1503 cm⁻¹ vibrational mode in the Raman spectrum of DMP and the 1501 cm⁻¹ one in the quantum chemical calculations, which is assigned to a delocalized C=C stretching mode of the extended π-conjugated polyene backbone of the molecule. The other vibrational modes appearing in both the FFT of the δΔA(t,λ) signal and the conventional frequency domain Raman spectrum of DMP in hexane have peaks at 202, 507, 574, 750, 962, 1173, 1330, 1372, 1431, and 1501 cm⁻¹. The modes at 574, 962, 1330, 1372, 1431, and 1501 cm⁻¹ closely match the stimulated Raman spectrum and therefore can be attributed to the ground state in DMP. In contrast, the vibrational modes at 202, 507, 750, and 1173 cm⁻¹ not appearing in the Raman spectrum can be assigned to the electronic excited state in DMP (see Table 2).

Fig. 7 The pump–probe real-time traces averaged in the probe time range 1.65–1.90 eV.

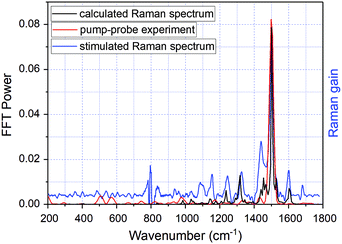Fig. 8 The FFT of δΔA(λ,t) defined as the modulation amplitude of ΔA real-time traces averaged over the time range of 1.65–1.90 eV (red line). The modulation δΔA(λ,t) is obtained by subtracting the exponential fitting curve from the observed ΔA signals. The stimulated Raman spectrum of the closed-ring isomer – black line (measured by Pontercorvo et al.²⁵). The blue line represents the calculated Raman spectrum of DMP at the B3LYP/6-31G(d,p) level. The scaling factor 0.97 was used to fit the experimental stimulated Raman spectrum.

Table 2 The comparison of vibrational frequencies obtained from the pump–probe experiment, the stimulated Raman spectrum, and the computed Raman spectrum

Vibrational frequency, cm^−1
(a) Pump–probe experiment	(b) The stimulated Raman spectrum (experiment)	(c) The computed Raman spectrum (B3LYP/6-31G(d,p) with a scaling factor 0.97). Values in parentheses denote relative Raman intensities
202	—	218 (1)
507	—	508 (1)
574	574	583 (3)
750	—	—
962	962	984 (25)
1173	—	1175 (22)
1330	1326	1318 (173)
1372	1368	1392 (18)
1431	1438	1453 (158)
1501	1500	1501 (1050)

---

Another way to distinguish the signals of the ground state from those of the excited state is to perform the FFT of real time-traces averaged in the limited spectral range 1.65–1.80 eV to avoid a substantial contribution from the ground state absorption in the spectral range 1.80–1.90 eV. As shown in Fig. 9, the FFT power of 1501 cm⁻¹ of time-traces averaged in the range 1.65–1.80 eV is approximately two times smaller in comparison with integration in the range 1.65–1.90 eV. It indicates that the ground state contributes greatly to the observed 1501 cm⁻¹ mode, though there is also a possibility of a contribution from the excited state. For other modes, the FFT power for time-traces averaged in the limited spectral range is similar or larger compared to 1.65–1.90 eV. It suggests that the modes having frequencies that match the stimulated Raman spectrum have large contributions from both the electronic excited and ground states.

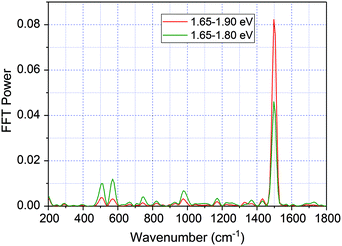Fig. 9 The FFT of δΔA(λ,t) real-time traces averaged in the range 1.65–1.90 eV (red line) and 1.65–1.80 eV (green line).

Besides the information on the vibrational amplitudes and frequencies obtained from the gated FFT in an appropriate temporal window (i.e. 150–1800 fs windows are used in the present case), it is feasible to investigate the instantaneous vibrational amplitude and the frequency changes which provide information on the vibrational couplings between particular modes and instantaneous forces exerted by solvent molecules on solute molecules that determine dephasing times. Importantly, the DMP molecule has two phenyl groups attached to the thienyl groups. These two phenyl groups can rotate and this rotation yields various molecular geometries at room temperature. Because the spectral window of the pump pulse is quite wide in the present pump pulse, it can pump various geometries with different frequencies, which also impact the observed frequency and amplitude modulations.

The dynamics of instantaneous frequency components can be obtained by the spectrogram analysis that involves the application of gating-window FFT to δΔA(t,λ) signals. Care must be taken in this case that the real-time vibrational spectrum is associated with the electronic signal, ΔA(t,λ), and hence the dynamics includes the electronic process. For a simple example, the vibrational phase relaxation is given by the exponential decay rate k_(vib) and the electronic decay rate by k_(el) and then the spectrogram decay rate k_(spec) is given by the sum of the two. Hence the vibrational decay rate is given by k_(spec) − k_(el). For spectrogram calculations, the gating window width should be selected to satisfy both the temporal and frequency resolution required. This means that the gating window width should be short enough to capture gentle instantaneous frequencies and amplitude changes and long enough to provide sufficient periods for accurate FFT calculation.

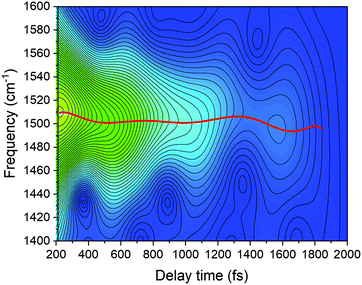
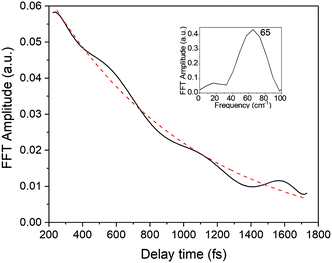
In the present study, we focused on the most intense mode appearing in the FFT amplitude spectrum of the δΔA(t,λ) signal centred at 1501 cm⁻¹. The bands other than 1501 cm⁻¹ feature much lower intensity in comparison to 1501 cm⁻¹. Consequently, the FFT intensity in the spectrogram for delay times longer than 500 fs is too low for reliable discussion about time-dependent frequency and intensity modulations. Another difficulty preventing the analysis using the time-dependent changes for the Fourier-transform Raman bands of the excited state using the spectrogram is the long period times for the low-frequency mode gate window widths (which must be much longer than the periods). Information to be obtained by the analysis of the change of the frequency is very limited due to the small ratio between the full probe delay time span and the gate widths in the case of low-frequency modes and due to the small signal-to-noise ratio. Since 1501 cm⁻¹ is close to the corresponding conventional Raman frequency, it is considered to be due to the ground state wave-packet, though a partial contribution from the electronic excited state cannot be excluded, as there is a significant contribution in the spectral range 1.65–1.80 eV. In Fig. 10, the two-dimensional display of the spectrogram for δΔA(t,λ) signals averaged in the spectral range of 1.65–1.90 eV is shown. For these calculations, a gating window with a FWHM of 800 fs width was applied and a Blackman function was employed to minimize interference among the neighbouring modes in the FFT calculations at the edges of the gating window. The central frequency in the spectrogram at 1501 cm⁻¹ clearly features both frequency and intensity modulations which suggests coupling of the 1501 cm⁻¹ mode to other vibrational mode(s). To identify potential candidates for vibrational modes that may couple with the 1501 cm⁻¹ mode we calculated the FFT of the frequency and amplitude modulation of the 1501 cm⁻¹ mode as shown in Fig. 11 and 12. The FFT spectrum of amplitude modulation has been calculated after the subtraction of single exponential fitting functions from the FFT amplitude decay profile. The FFT calculations performed in such a way result in central peaks of frequency and amplitude modulation at 57 ± 8 cm⁻¹ and 65 ± 8 cm⁻¹, respectively. Both peaks are close to the difference between the 1501 cm⁻¹ mode and the neighbouring mode at 1431 cm⁻¹. The observed modulations appear as results of the mathematical artefact that comes from the interference between 1431 cm⁻¹ and 1501 cm⁻¹ modes, even though the amplitude of 1431 cm⁻¹ is much weaker than that of 1501 cm⁻¹. The impact of the artificial interference between neighbouring modes on the observed amplitude and frequency modulations in the spectrogram can be verified by the simulation that involves the spectrogram calculations for the model signal that contain only two frequencies of interest and maintain their experimental amplitude and phase relationship. In that case, the model signal is calculated according to eqn (1) using the same Blackman function of 800 fs width as in the case of spectrogram calculation from the experimental data.

Fig. 10 The spectrogram calculated for real-time traces of vibrationally modulated δΔA(λ,t) integrated in the probe spectral range of 1.65–1.90 eV. A Hanning window function of 800 fs FWHM was used as a compromise between temporal and frequency resolution. 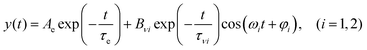The blue line is plotted along the peak of the spectrogram amplitude and it shows the frequency modulation of the frequency centred around 1500 cm⁻¹.

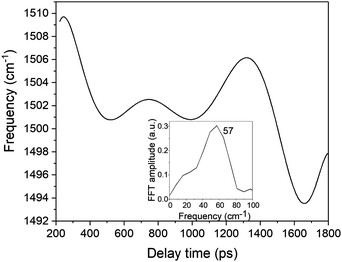Fig. 11 The frequency modulation in the spectrogram peak around 1500 cm⁻¹. The inset shows the FFT of the frequency modulation.

Fig. 12 The amplitude modulation of the spectrogram peak centred around 1500 cm⁻¹ (black line) fitted with a single exponential function (red-dashed line). The inset shows the FFT of the amplitude modulation.

In eqn (1)ω₁ and ω₂ denote the vibrational frequency modes of 1431 cm⁻¹ and 1501 cm⁻¹, τ_e is the electronic decay time (6.4 ps), τ_ν1 and τ_ν2 are the vibrational lifetimes of 1431 cm⁻¹ and 1501 cm⁻¹ modes, and φ₁ and φ₂ are the vibrational phases. A_e is the amplitude of the electronic decay that was set to fit the observed experimental electronic decay, and B_νi are the vibrational amplitudes.

By varying the phases φ_i, lifetimes τ_νi, and the relative amplitudes B_νi of 1501 and 1431 cm⁻¹ frequencies we have obtained the simulated spectrogram which best reproduces the one obtained from the experimental data. From the simulated spectrogram (see Fig. 13a) the dephasing times of 1501 and 1430 cm⁻¹ modes are estimated to be 800 ± 200 fs, respectively, and the phase difference is 0.11 π. The amplitude ratio in eqn (1) in each simulation was set in such a way that the FFT amplitude ratio of the FFT of the simulated signal calculated in the delay time window 150–1800 fs corresponds to the one calculated in the same manner for the experimental data. The error of the dephasing time determination can be estimated to be around 200 fs judging from the spectrograms calculated with different dephasing times. As the dephasing time and FFT amplitudes of 1501 and 1430 cm⁻¹ are much longer than in the case of other vibrational modes observed in the FFT of δΔA(t,λ) and the corresponding FFT amplitudes are the largest across the spectrum, these modes are expected to play an essential role in the vibrational relaxation. The correspondence of both 1501 and 1431 cm⁻¹ frequencies in the FFT of δΔA(t,λ) and the stimulated Raman spectrum of DMP suggests a dominant contribution from the electronic ground state. However, as mentioned previously, these assignments are not unambiguous and the electronic excited state can also participate. According to the DFT computations (see Fig. 14a and b) the 1501 and 1431 cm⁻¹ modes involve stretching of those C–C bonds within the central ring of DMP which do not break during the photochromic reaction with high amplitude and the C–C bond participating in the photochromic reaction with low amplitude. The displacement of carbon atoms involved in the stretching mode is much larger in the case of 1501 cm⁻¹ than that of 1431 cm⁻¹. Apart from the C–C stretching in the central ring, both 1501 and 1431 cm⁻¹ modes contain contributions from H–C–H bending modes of the side methyl groups. Even though the calculations were performed for the ground state, they may give some hint regarding molecular motions involved in the vibrational relaxation within the electronic excited state towards the S₁ → S₀ CI. Such an interpretation can be justified by the occurrence of excited and ground state vibrational modes at common frequencies at 1501 and 1431 cm⁻¹.

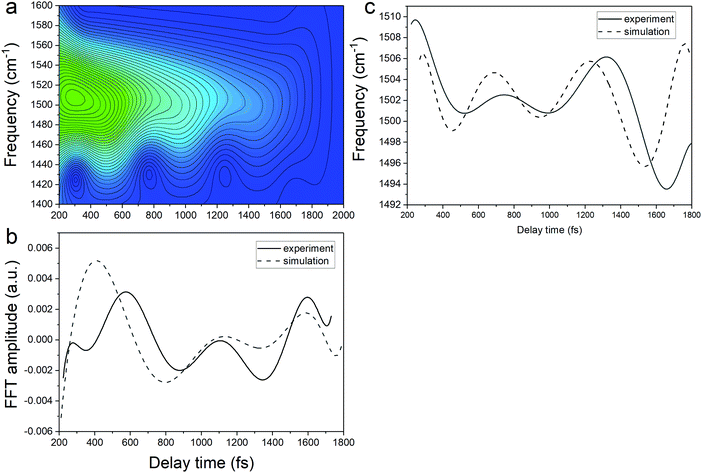Fig. 13 (a) The spectrogram simulated according to eqn (1). (b) The experimental (solid line) and simulated (dashed line) FFT amplitude modulation of the central frequency in the spectrogram. (c) The experimental (solid line) and simulated (dashed line) frequency modulation of the central peak in the spectrogram. The baseline was subtracted.

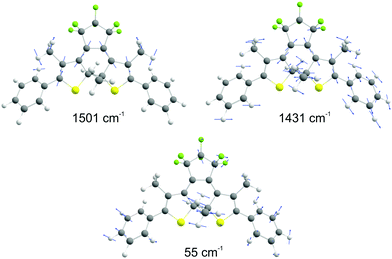Fig. 14 The molecular vibrations of 1501 and 1430 cm⁻¹ according to DFT calculations (B3LYP/6-31G(d,p)). The atom displacement vectors are drawn as blue vectors.

The central frequency of this spectrogram features both the amplitude and the frequency modulations and if we compare the calculated modulations to the experimental ones (Fig. 13b and c) it turns out that experimental and simulated modulations are of the same order of magnitude. Thus, the simulations prove that the mathematical interference has an impact on the observed amplitude and frequency modulations, though there exists a possibility of coupling between the neighbouring modes. We have already observed a similar effect on the instantaneous frequency and amplitude modulations for polythiophene,⁴⁶ and polydiacetylene (PDA).⁴⁷ In polythiophene, we found frequency and amplitude modulations with a frequency of 120–130 cm⁻¹ for the C–C stretching mode of 1343 cm⁻¹. We concluded that the low-frequency bending mode of 120–130 cm⁻¹ mediates in dynamical coupling between the stretching mode of 1343 cm⁻¹ and another stretching mode. In the case of PDA, similarly, the C=C and C–C stretching modes are modulated by a bending mode with a period of 145 fs (230 cm⁻¹). Here in the study of DMP, we observe amplitude and frequency modulations of the 1501 cm⁻¹ mode with a frequency of 57 cm⁻¹ and 65 cm⁻¹, respectively. Typically, frequencies between 50 and 100 cm⁻¹ correspond to vibrational modes that involve large amplitude displacements of a great number of atoms in the molecule, crucial for conformational structure changes. According to our computations, there appears a low-intensity Raman mode at 55 cm⁻¹ for the closed-ring isomer of DMP (Fig. 14c). This mode involves a flattening of the DMP molecule (twisting of phenylthiophene rings) that constitutes one of the criteria for a mode assisting the photochromic reaction in the electronic excited state. Recently, the 55 cm⁻¹ mode has been identified in the theoretical vibrational spectrum of the open ring isomer of DMP calculated by the time-dependent DFT method (TD-DFT) as facilitating a photochromic reaction in DMP in the excited state.⁹ This mode has been selected as the one which may drive the molecule toward the conical intersection, leading to the formation of the open ring photoproduct since both criteria for such a purpose are fulfilled: the large change of C–C distance involved in the ring closure/opening reaction and a torsional movement of the phenyl-thienyl group leading to the flattening of the molecule. Additionally, the frequency of 55 cm⁻¹ corresponds to twice the time constant of the primary step of the ring closure reaction occurring on the excited state potential surface (300 fs) that was determined from the femtosecond transient absorption coefficient. In the case of our computations of the closed-ring isomer, the 55 cm⁻¹ mode involves a torsional motion of the phenyl-thienyl group, but the C–C distance forming a ring does not change. It indicates that in the case of the closed-ring isomer of DMP the low-frequency mode of ∼60 cm⁻¹ cannot steer the molecule towards the reactive regions of the S₁ PES near the CI, leading to the open-ring isomer. Moreover, there exists a possibility of an efficient energy transfer between the low-frequency mode of ∼60 cm⁻¹ and the solvent molecules, which may lead to a weakening of the role of the low-frequency mode in mediating coupling between 1501 cm⁻¹ and 1430 cm⁻¹ modes. Such energy transfer can occur through a coupling of the 60 cm⁻¹ vibration with the librational modes of the solvent occurring at frequencies in the range 50–100 cm⁻¹.^48,49

While the low-frequency mode does not fulfil necessary conditions to drive the closed-ring isomer to the CI that would lead to the opening of the ring, there exists an effective electronic energy dissipation channel that favours the internal conversion to the ground state of the closed-ring isomer. Our DFT computations have shown that there exists a CI at which the C–C bond is as large as R_CC = 1.98 Å. Even though it seems easier for the molecule to relax to its S₁ minimum (where R_CC = 1.59 Å), it is clearly not the case. Therefore the relaxation through the CI must be facilitated by vibrational modes, creating a pathway from FC to the CI. The pivotal molecular movement to establish such a path is expected to involve changes within the central ring, as R_CC increases from 1.54 Å to 1.98 Å. The modes at 1501 and 1431 cm⁻¹ observed in the FFT of the ΔA signal fulfil this condition even though the C–C bond during the vibration changes only slightly compared to the other C–C bonds in the central ring, not directly participating in the photochromic reaction. In the light of these observations, and taking into account the relatively long dephasing times of 1501 and 1431 modes (800 ± 200 fs), we can conclude that both vibrations constitute potential modes that can actively participate in driving the molecule toward the CI and in this way enhancing S₁ → S₀ internal conversion.

Conclusions

We have applied a NOPA generating sub-10 fs pulses in the spectral range 605–750 nm (1.65–2.05 eV) to study real-time vibrational dynamics of a diarylethene derivative – 1,2-bis(2,4-dimethyl-5-phenyl-3-thienyl)perfluorocyclopentene (DMP) – in hexane solution. By comparing the FFT of transient absorption signal change δΔA(t, λ) in the spectral range 653–752 (1.65–1.90 eV) with the stimulated Raman spectrum we concluded that vibrational modes of 574, 962, 1330, 1372, 1431, and 1501 cm⁻¹ have dominant contributions from the ground electronic state while in the case of 202, 507, 750, and 1173 cm⁻¹ modes the electronic excited state dominates. This assignment should be however regarded as tentative since the vibrational spectrum in the excited state is unknown.

The most pronounced of the observed vibrational modes, the ethylenic stretching mode at 1501 cm⁻¹, is characterized by frequency and amplitude modulations explainable in terms of vibrational coupling between 1501 cm⁻¹ and another stretching mode at 1431 cm⁻¹ mediated by a vibrational mode of a frequency around 60 cm⁻¹. The simulated interference of the modes is of the same order of magnitude as the one observed experimentally, which points to a weak coupling. The vibrational mode of a frequency as low as 60 cm⁻¹ was proposed as a molecular vibration which can facilitate the photochromic reaction.⁹ This is not the case in the ring opening reaction of DMP, as the relevant quantum yield is very low (0.015).⁸ What is more, the DFT calculations of molecular vibrations of DMP in the ground state show that the low-frequency mode at 60 cm⁻¹ does not involve a change in C–C bond length, which is a critical criterion for a molecular mode to assist the photochromic reaction. The hypothesis of the limited role played by the ∼60 cm⁻¹ mode in the electronic energy dissipation is supported by a weak coupling between this mode and high-frequency modes of 1501 and 1431 cm⁻¹ concluded from the spectrogram analysis. On the other hand, there exists an efficient electronic energy dissipation pathway leading to the ground state of DMP. Our computations have shown the presence of a minimal energy CI for the central ring C–C bond at R_C–C = 1.98 Å. Its shape is expected to be sloped, which promotes photostability. Two possible candidates for vibrational modes involving the molecular motions able to drive the DMP molecule towards the CI on the S₁ PES are 1501 cm⁻¹ and 1431 cm⁻¹ observed in the FFT of the ΔA signal, as these modes involve major structural changes within the central ring (see Fig. 14a and b) and feature long dephasing times (800 ± 200 fs in both cases).

We have shown that real-time vibrational spectroscopy employing sub-10 fs laser systems is a valuable tool, capable of probing simultaneously the electronic and the vibrational dynamics in molecules. As this method is sensitive to structural changes occurring during photochemical reactions and relaxation processes, it can serve as a complementary technique to femtosecond stimulated Raman scattering (FSRS) and femtosecond time-resolved absorption employing infrared pulses. The elucidation of nuclear motion associated with chemical reactions occurring in electronically excited states is still a challenging task due to the ambiguity of the assignment of vibrational wave-packets to a particular electronic state in the case of resonant excitation. The calculation of vibrational spectra in the ground and the excited state could in principle be supportive to resolve these ambiguities. However, such calculations for excited states are often not yet possible. Other issues include the difficulty of capturing the electronic and vibrational dynamics in the early stages after the excitation i.e. in the temporal window 0–200 fs. The transient signal in this time window is blurred by non-resonant contributions (the coherent artefact effect) mainly resulting from the cross-phase modulation between pump and probe pulses, i.e. the modulation of the refractive index of the sample induced by a strong pump pulse and experienced by a weak probe. This effect is particularly strong for pulse durations as short as 10 fs. Recently, it has been shown that spectroscopic information from the early time window can be obtained by time-resolved emission spectroscopy with high temporal resolution, which does not suffer from the coherent artefact effect.⁵⁰ The role of the vibrational modes 1501 and 1431 cm⁻¹ in the ring-opening reaction of DMP could be further elucidated with the help of this technique.

Conflicts of interest

There are no conflicts to declare.

Acknowledgements

The authors thank Prof. Tullio Scopigno for providing the stimulated Raman spectrum of the closed-ring isomer of DMP and Dr Marian Wolszczak for performing the fluorescence measurements and enlightening discussions. The research was supported by the JSPS Postdoctoral Fellowship Program for Foreign Researchers (No. 12755) and the National Science Centre of Poland (grant no. 2015/19/D/ST4/01813).

References

1. M. Irie, T. Fukaminato, K. Matsuda and S. Kobatake, Photochromism of Diarylethene Molecules and Crystals: Memories, Switches, and Actuators, Chem. Rev., 2014, 114(24), 12174–12277.
2. T. Sendler, K. Luka-Guth, M. Wieser, L. Lokamani, J. Wolf, M. Helm, S. Gemming, J. Kerbusch, E. Scheer, T. Huhn and A. Erbe, Light-Induced Switching of Tunable Single-Molecule Junctions, Adv. Sci., 2015, 2(5), 1500017.
3. B. Roubinet, M. L. Bossi, P. Alt, M. Leutenegger, H. Shojaei, S. Schnorrenberg, S. Nizamov, M. Irie, V. N. Belov and S. W. Hell, Carboxylated Photoswitchable Diarylethenes for Biolabeling and Super-Resolution RESOLFT Microscopy, Angew. Chem., Int. Ed., 2016, 55(49), 15429–15433.
4. Y. Zou, T. Yi, S. Xiao, F. Li, C. Li, X. Gao, J. Wu, M. Yu and C. Huang, Amphiphilic Diarylethene as a Photoswitchable Probe for Imaging Living Cells, J. Am. Chem. Soc., 2008, 130(47), 15750–15751.
5. M. Fernandez-Suarez, Redirecting lipoic acid ligase for cell surface protein labeling with small-molecule probes, Nat. Biotechnol., 2007, 25, 1483–1487.
6. O. Babii, S. Afonin, M. Berditsch, S. Reiβer, P. K. Mykhailiuk, V. S. Kubyshkin, T. Steinbrecher, A. S. Ulrich and I. V. Komarov, Controlling Biological Activity with Light: Diarylethene-Containing Cyclic Peptidomimetics, Angew. Chem., Int. Ed., 2014, 53(13), 3392–3395.
7. M. Irie, K. Sakemura, M. Okinaka and K. Uchida, Photochromism of Dithienylethenes with Electron-Donating Substituents, J. Org. Chem., 1995, 60(25), 8305–8309.
8. Y. Ishibashi, K. Okuno, C. Ota, T. Umesato, T. Katayama, M. Murakami, S. Kobatake, M. Irie and H. Miyasaka, Multiphoton-gated cycloreversion reactions of photochromic diarylethene derivatives with low reaction yields upon one-photon visible excitation, Photochem. Photobiol. Sci., 2010, 9(2), 172–180.
9. H. Jean-Ruel, R. R. Cooney, M. Gao, C. Lu, M. A. Kochman, C. A. Morrison and R. J. D. Miller, Femtosecond Dynamics of the Ring Closing Process of Diarylethene: A Case Study of Electrocyclic Reactions in Photochromic Single Crystals, J. Phys. Chem. A, 2011, 115(45), 13158–13168.
10. C. L. Ward and C. G. Elles, Controlling the Excited-State Reaction Dynamics of a Photochromic Molecular Switch with Sequential Two-Photon Excitation, J. Phys. Chem. Lett., 2012, 3(20), 2995–3000.
11. C. L. Ward and C. G. Elles, Cycloreversion Dynamics of a Photochromic Molecular Switch via One-Photon and Sequential Two-Photon Excitation, J. Phys. Chem. A, 2014, 118(43), 10011–10019.
12. K. Uchida, E. Tsuchida, Y. Aoi, S. Nakamura and M. Irie, Substitution Effect on the Coloration Quantum Yield of a Photochromic Bisbenzothienylethene, Chem. Lett., 1999,(1), 63–64.
13. M. Isegawa and K. Morokuma, Photochemical Ring Opening and Closing of Three Isomers of Diarylethene: Spin–Flip Time-Dependent Density Functional Study, J. Phys. Chem. A, 2015, 119(18), 4191–4199.
14. T. Sumi, Y. Takagi, A. Yagi, M. Morimoto and M. Irie, Photoirradiation wavelength dependence of cycloreversion quantum yields of diarylethenes, Chem. Commun., 2014, 50(30), 3928–3930.
15. J. Ern, A. T. Bens, H. D. Martin, S. Mukamel, S. Tretiak, K. Tsyganenko, K. Kuldova, H. P. Trommsdorff and C. Kryschi, Reaction Dynamics of a Photochromic Fluorescing Dithienylethene, J. Phys. Chem. A, 2001, 105(10), 1741–1749.
16. P. R. Hania, A. Pugzlys, L. N. Lucas, J. J. D. de Jong, B. L. Feringa, J. H. van Esch, H. T. Jonkman and K. Duppen, Ring Closure Dynamics of BTE-Based Photochromic Switches:  Perfluoro- versus Perhydrocyclopentene Derivatives, J. Phys. Chem. A, 2005, 109(42), 9437–9442.
17. P. R. Hania, R. Telesca, L. N. Lucas, A. Pugzlys, J. van Esch, B. L. Feringa, J. G. Snijders and K. Duppen, An Optical and Theoretical Investigation of the Ultrafast Dynamics of a Bisthienylethene-Based Photochromic Switch, J. Phys. Chem. A, 2002, 106(37), 8498–8507.
18. Y. Ishibashi, M. Fujiwara, T. Umesato, H. Saito, S. Kobatake, M. Irie and H. Miyasaka, Cyclization Reaction Dynamics of a Photochromic Diarylethene Derivative as Revealed by Femtosecond to Microsecond Time-Resolved Spectroscopy, J. Phys. Chem. C, 2011, 115(10), 4265–4272.
19. Y. Ishibashi, M. Mukaida, M. Falkenstrom, H. Miyasaka, S. Kobatake and M. Irie, One- and multi-photon cycloreversion reaction dynamics of diarylethene derivative with asymmetrical structure, as revealed by ultrafast laser spectroscopy, Phys. Chem. Chem. Phys., 2009, 11(15), 2640–2648.
20. Y. Ishibashi, T. Umesato, S. Kobatake, M. Irie and H. Miyasaka, Femtosecond Laser Photolysis Studies on Temperature Dependence of Cyclization and Cycloreversion Reactions of a Photochromic Diarylethene Derivative, J. Phys. Chem. C, 2012, 116(7), 4862–4869.
21. H. Jean-Ruel, M. Gao, M. A. Kochman, C. Lu, L. C. Liu, R. R. Cooney, C. A. Morrison and R. J. D. Miller, Ring-Closing Reaction in Diarylethene Captured by Femtosecond Electron Crystallography, J. Phys. Chem. B, 2013, 117(49), 15894–15902.
22. K. Mori, Y. Ishibashi, H. Matsuda, S. Ito, Y. Nagasawa, H. Nakagawa, K. Uchida, S. Yokojima, S. Nakamura, M. Irie and H. Miyasaka, One-Color Reversible Control of Photochromic Reactions in a Diarylethene Derivative: Three-Photon Cyclization and Two-Photon Cycloreversion by a Near-Infrared Femtosecond Laser Pulse at 1.28 μm, J. Am. Chem. Soc., 2011, 133(8), 2621–2625.
23. M. Murakami, H. Miyasaka, T. Okada, S. Kobatake and M. Irie, Dynamics and Mechanisms of the Multiphoton Gated Photochromic Reaction of Diarylethene Derivatives, J. Am. Chem. Soc., 2004, 126(45), 14764–14772.
24. J. C. Owrutsky, H. H. Nelson, A. P. Baronavski, O. K. Kim, G. M. Tsivgoulis, S. L. Gilat and J. M. Lehn, Optical properties and dynamics of a photochromic bisthienylethene in solution and in a polymer film, Chem. Phys. Lett., 1998, 293(5–6), 555–563.
25. E. Pontecorvo, C. Ferrante, C. G. Elles and T. Scopigno, Structural Rearrangement Accompanying the Ultrafast Electrocyclization Reaction of a Photochromic Molecular Switch, J. Phys. Chem. B, 2014, 118(24), 6915–6921.
26. S. Shim, I. Eom, T. Joo, E. Kim and K. S. Kim, Ring Closure Reaction Dynamics of Diarylethene Derivatives in Solution, J. Phys. Chem. A, 2007, 111(37), 8910–8917.
27. S. Shim, T. Joo, S. C. Bae, K. S. Kim and E. Kim, Ring Opening Dynamics of a Photochromic Diarylethene Derivative in Solution, J. Phys. Chem. A, 2003, 107(40), 8106–8110.
28. H. Sotome, T. Nagasaka, K. Une, C. Okui, Y. Ishibashi, K. Kamada, S. Kobatake, M. Irie and H. Miyasaka, Efficient Cycloreversion Reaction of a Diarylethene Derivative in Higher Excited States Attained by Off-Resonant Simultaneous Two-Photon Absorption, J. Phys. Lett., 2017, 8(14), 3272–3276.
29. N. Ishii, E. Tokunaga, S. Adachi, T. Kimura, H. Matsuda and T. Kobayashi, Optical frequency- and vibrational time-resolved two-dimensional spectroscopy by real-time impulsive resonant coherent Raman scattering in polydiacetylene, Phys. Rev. A: At., Mol., Opt. Phys., 2004, 70(2), 023811.
30. J. Du, T. Teramoto, K. Nakata, E. Tokunaga and T. Kobayashi, Real-Time Vibrational Dynamics in Chlorophyll a Studied with a Few-Cycle Pulse Laser, Biophys. J., 2011, 101(4), 995–1003.
31. T. Kobayashi, T. Iiyama, K. Okamura, J. Du and T. Masuda, Ultrafast electronic relaxation and vibrational dynamics in a polyacetylene derivative, Chem. Phys. Lett., 2013, 567, 6–13.
32. T. Kobayashi, T. Saito and H. Ohtani, Real-time spectroscopy of transition states in bacteriorhodopsin during retinal isomerization, Nature, 2001, 414(6863), 531–534.
33. K. Nakata, T. Kobayashi and E. Tokunaga, Electric field-controlled dissociation and association of porphyrin J-aggregates in aqueous solution, Phys. Chem. Chem. Phys., 2011, 13(39), 17756–17767.
34. K. Nakata, E. Tokunaga, J. Du, B. Xue, J. Miyazaki, K. Seto and T. Kobayashi, Sub-10 fs spectroscopy of K-TCNQ crystal for observation of intramolecular vibration modulation in melting of the Peierls dimer, Phys. Rev. B: Condens. Matter Mater. Phys., 2014, 90(8), 085119.
35. A. Shirakawa and T. Kobayashi, Noncollinearly phase-matched femtosecond optical parametric amplification with a 2000 cm−1 bandwidth, Appl. Phys. Lett., 1998, 72(2), 147–149.
36. A. Shirakawa, I. Sakane, M. Takasaka and T. Kobayashi, Sub-5-fs visible pulse generation by pulse-front-matched noncollinear optical parametric amplification, Appl. Phys. Lett., 1999, 74(16), 2268–2270.
37. T. Kobayashi and A. Baltuska, Sub-5 fs pulse generation from a noncollinear optical parametric amplifier, Meas. Sci. Technol., 2002, 13(11), 1671.
38. M. J. Frisch, G. W. Trucks, H. B. Schlegel, G. E. Scuseria, M. A. Robb, J. R. Cheeseman, G. Scalmani, V. Barone, B. Mennucci, G. A. Petersson, H. Nakatsuji, M. Caricato, X. Li, H. P. Hratchian, A. F. Izmaylov, J. Bloino, G. Zheng, J. L. Sonnenberg, M. Hada, M. Ehara, K. Toyota, R. Fukuda, J. Hasegawa, M. Ishida, T. Nakajima, Y. Honda, O. Kitao, H. Nakai, T. Vreven, J. A. Montgomery, J. E. Peralta, F. Ogliaro, M. Bearpark, J. J. Heyd, E. Brothers, K. N. Kudin, V. N. Staroverov, R. Kobayashi, J. Normand, K. Raghavachari, A. Rendell, J. C. Burant, S. S. Iyengar, J. Tomasi, M. Cossi, N. Rega, J. M. Millam, M. Klene, J. E. Knox, J. B. Cross, V. Bakken, C. Adamo, J. Jaramillo, R. Gomperts, R. E. Stratmann, O. Yazyev, A. J. Austin, R. Cammi, C. Pomelli, J. W. Ochterski, R. L. Martin, K. Morokuma, V. G. Zakrzewski, G. A. Voth, P. Salvador, J. J. Dannenberg, S. Dapprich, A. D. Daniels, O. Farkas, J. B. Foresman, J. V. Ortiz, J. Cioslowski and D. J. Fox, Gaussian 09, Revision D, Wallingford CT, 2009.
39. B. G. Levine, J. D. Coe and T. J. Martínez, Optimizing Conical Intersections without Derivative Coupling Vectors:  Application to Multistate Multireference Second-Order Perturbation Theory (MS-CASPT2), J. Phys. Chem. B, 2008, 112(2), 405–413.
40. R. L. Martin, Natural transition orbitals, J. Chem. Phys., 2003, 118(11), 4775–4777.
41. S. A. Kovalenko, R. Schanz, H. Hennig and N. P. Ernsting, Cooling dynamics of an optically excited molecular probe in solution from femtosecond broadband transient absorption spectroscopy, J. Chem. Phys., 2001, 115(7), 3256–3273.
42. M. Boggio-Pasqua, M. Ravaglia, M. J. Bearpark, M. Garavelli and M. A. Robb, Can Diarylethene Photochromism Be Explained by a Reaction Path Alone? A CASSCF Study with Model MMVB Dynamics, J. Phys. Chem. A, 2003, 107(50), 11139–11152.
43. T. Yanai, M. Saitow, X.-G. Xiong, J. Chalupský, Y. Kurashige, S. Guo and S. Sharma, Multistate Complete-Active-Space Second-Order Perturbation Theory Based on Density Matrix Renormalization Group Reference States, J. Chem. Theory Comput., 2017, 13(10), 4829–4840.
44. M. Kim, J.-H. Yun and M. Cho, Light penetration-coupled photoisomerization modeling for photodeformation of diarylethene single crystal: upscaling isomerization to macroscopic deformation, Sci. Rep., 2017, 7(1), 967.
45. K. F. Hall, M. Boggio-Pasqua, M. J. Bearpark and M. A. Robb, Photostability Via Sloped Conical Intersections:  A Computational Study of the Excited States of the Naphthalene Radical Cation, J. Phys. Chem. A, 2006, 110(50), 13591–13599.
46. J. Du and T. Kobayashi, Real-time observation of dynamic coupling between the stretching and bending modes in a polythiophene, Chem. Phys. Lett., 2009, 481(4), 204–208.
47. T. Kobayashi, A. Shirakawa, H. Matsuzawa and H. Nakanishi, Real-time vibrational mode-coupling associated with ultrafast geometrical relaxation in polydiacetylene induced by sub-5-fs pulses, Chem. Phys. Lett., 2000, 321(5), 385–393.
48. T. Hattori, A. Terasaki, T. Kobayashi, T. Wada, A. Yamada and H. Sasabe, Optical-heterodyne-detected induced phase modulation for the study of femtosecond molecular dynamics, J. Chem. Phys., 1991, 95(2), 937–945.
49. K. Kurokawa, T. Hattori and T. Kobayashi, Subpicosecond molecular dynamics studied by degenerate four-wave mixing with incoherent light, Phys. Rev. A: At., Mol., Opt. Phys., 1987, 36(3), 1298–1304.
50. G. Lee, J. Kim, S. Y. Kim, D. E. Kim and T. Joo, Vibrational Spectrum of an Excited State and Huang–Rhys Factors by Coherent Wave Packets in Time-Resolved Fluorescence Spectroscopy, ChemPhysChem, 2017, 18(6), 670–676.

---

Footnote

† Electronic supplementary information (ESI) available. See DOI: 10.1039/c8cp05882b

---