Special features of monolayer characteristics of N-alkanoyl substituted threonine amphiphiles

Abstract

The monolayers of N-alkanoyl substituted threonine amphiphiles, similar to those of other N-alkanoyl-substituted amino acid amphiphiles, point to substantial differences in the main characteristics compared to usual amphiphilic monolayers. π–A measurements of the enantiomeric and racemic forms of N-alkanoyl-substituted threonine monolayers with C16 and C18 chain lengths reveal that, independent of the alkyl chain length, all compression curves are located above the corresponding decompression curves. A theoretical model developed for the kinetics of two-dimensional condensation of Langmuir monolayers can describe this behavior concluding the attachment of monomers to large aggregates. The linear fit of the entropy changes versus temperature (ΔS = f(T)) at the LE/LC phase transition and extrapolation to zero ΔS specifies the critical temperature T_c, above which the monolayer cannot be compressed into the condensed state. The relatively small ΔT_c difference between the enantiomeric and the racemic forms is consistent with the increased strength of van der Waals interactions between the longer alkyl chains reducing the influence of chirality on the thermodynamic parameters. The BAM experiments reveal clearly the absence of inner anisotropy as a specific feature of the domain topology of N-palmitoyl-threonine monolayers. Furthermore, the growth kinetics of the racemic N-palmitoyl-DL-threonine domains reveals a transition from homochiral discrimination and chiral separation within the domain to a state with heterochiral preference. GIXD studies show that at all pressures the enantiomers exhibit three Bragg peaks indicating an oblique lattice structure, whereas the racemates show only two Bragg peaks indicating a NNN tilted orthorhombic structure. Characteristic for the structure of all condensed monolayer phases is the large tilt angle of ∼49°, nearly independent of the lateral pressure. The transition from the oblique lattice structures, as detected for enantiomeric monolayers, to orthorhombic structures of racemic monolayers is clear evidence that the dominant heterochiral interaction in the racemic mixtures leads to the formation of a compound with congruent transition pressure having with ∼20.0 Ų an essentially smaller alkyl chain cross-sectional area than the enantiomers with ∼20.7 Ų.

---

Introduction

The relationship between chirality and intermolecular interaction in amino acids is a fascinating research topic due to their role played in the still unsolved problem of homochiral evolution in nature. In this quest, monolayers of different N-alkanoyl substituted α-amino acid amphiphiles have been used as easy to handle model systems for studying chiral discrimination effects. N-Alkanoyl-substitution in amino acid amphiphiles prevents the possible effects of zwitterion formation, as expected for an amino acid monolayer. The relatively easy preparation of pure enantiomeric forms of N-alkanoyl-substituted amino acid amphiphiles made possible their use as amino acid-type model substances for chiral discrimination studies.^1–5 On the basis of π–A measurements, it was suggested that the head group structure, surface pressure, temperature, and subphase composition essentially influence chiral discrimination. However, as the measurements of π–A isotherms provide only thermodynamic information, the indication of the chirality effect in terms of interaction at the molecular level is restricted.

The development of highly-sensitive imaging techniques, as Brewster angle microscopy (BAM), offered complementary information on the mesoscopic morphology of the condensed phase domains formed in the two-phase coexistence region of Langmuir monolayers. The large variety observed in the domain topology of various amphiphiles has demonstrated that the chemical structure has a strong influence on the domain shapes and their molecular orientation.^6–8 In particular, the chiral amphiphiles represent well-defined model systems that express pronounced chiral discrimination effects in the textural features of Langmuir monolayers. Both homo- and heterochiral preferences for chiral interaction have been discussed.⁹ Large topological differences were observed in the condensed phase domains of several amino acid amphiphiles such as, N-palmitoyl aspartic acid, N-palmitoyl- or N-stearoyl serine methyl ester,¹⁰N-stearoyltyrosine,¹¹N-palmitoyl or N-myristoyl alanine.^12–14

However, even the BAM experiments proved to be insufficient for obtaining general conclusions on the domain topography/molecular structure relationship for a large variety of domain shapes of different N-alkanoyl-substituted α-amino acids.⁶ Therefore, theoretical studies^15,16 and infrared reflection–absorption spectroscopy (IRRAS) have been additionally used to obtain information about the role of alkyl chain ordering in enantiomeric and racemic structures in the monolayers of N-alkanoyl-substituted amino acid amphiphiles.^17–20 It was postulated that H-bond formation via the carboxyl group is crucial for the mutual recognition of the enantiomers among themselves, favoring thus the homochiral interaction.¹⁸ Despite the additional information delivered by IRRAS data, even this method proved to be limited.²⁰ With the development of the grazing incidence X-ray diffraction (GIXD) technique, it became possible to obtain a better characterization of the Langmuir monolayer structures. Yet, information about the lattice structures of N-alkanoyl substituted α-amino acid amphiphiles is rather scarce.

Thus, the present study aimed at a detailed characterization of the monolayers of two N-alkanoyl substituted threonine amphiphiles in their chiral and racemic states. In order to specify the special features of their monolayer characteristics, the compounds have been investigated on mesoscopic and molecular scales. Thus, thermodynamic and morphological results were obtained from Langmuir isotherms and BAM experiments, while grazing incidence X-ray diffraction (GIXD) was employed for defining the monolayer structure at the Angstrom level.

Experimental section

The N-alkanoyl-substituted threonine amphiphiles N-palmitoyl-D-threonine, N-palmitoyl-DL-threonine, N-stearoyl-D-threonine, and N-stearoyl-DL-threonine (Fig. 1) were synthesized by condensation of chiral threonine methylester and palmitoyl/stearoyl chloride in chloroform and aqueous potassium carbonate according to ref. 21. The obtained reaction products were purified by repeated crystallization in methanol. The chemical purity and chiral purity (99%) of the final products were verified by elemental analysis and HPLC. Characterization information of N-palmitoyl-D-threonine is included in the ESI† C16–D.

Fig. 1 Chemical structures of the synthesized N-alkanoyl-substituted threonine amphiphiles.

A heptane/ethanol (9 : 1) (Merck p.a. grade) solvent system was used for spreading the N-alkanoyl-substituted threonine amphiphiles on water with a specific resistance of 18.2 MΩ cm, purified with a Millipore desktop system. The surface pressure–molecular area (π–A) isotherms were measured using a self-made, computer-interfaced film balance coupled with a Brewster angle microscope (BAM1+, NFT, Göttingen, Germany).²² Using the Wilhelmy method with a roughened glass plate, the compression and decompression curves were measured at a compression rate of ≤10 Ų (molecule min)⁻¹ with an accuracy of a surface tension of ±0.1 mN m⁻¹ and a molecular area of ±0.5 Ų.

The lateral resolution of BAM1+ is ∼4 μm. Comprehensive information about the BAM method is given elsewhere (see e.g.ref. 22–24).

The grazing incidence X-ray diffraction patterns were measured using a liquid-surface diffractometer at the undulator beamline BW1 at the HASYLAB (DESY, Hamburg, Germany).²⁵ The thermostated Langmuir film balance is placed in an air-tight container with a Kapton (polyimide film) window under a helium atmosphere. During the experiment, a monochromatic X-ray beam (λ = 1.304 Å) comes into contact with the water surface at a grazing incidence angle α_i = 0.85α_c (where α_c = 0.13° is the critical angle for total reflection of the X-ray beam at the water surface) illuminating an approximately 2 × 50 mm² monolayer surface. A slow lateral movement of the trough is used to avoid sample damage by the strong X-ray beam. The diffracted signal was measured using a linear position-sensitive MYTHEN detector system (PSI, Villigen, Switzerland). The in-plane Q_xy component of the scattering vector was scanned by rotation of the detector around the sample in the x–y plane, and the out-of-plane Q_z component of the scattering vector between 0.0 and 0.75 Å⁻¹ is obtained using the vertical strips of MYTHEN. The Bragg peaks, obtained by integration of the scattering intensity (corrected for polarization, effective area, and Lorentz factor) over a certain Q_z window, and the Bragg rods, obtained by the integration of the scattering intensity over a certain Q_xy window, stipulate the unit cell dimensions (lattice parameters a, b and c, in-plane area A_xy, cross-sectional area A₀ and tilt angle t). The in-plane lattice repeat distances, d, of the ordered structures in the monolayer were calculated from the Bragg peak positions: d = 2π/Q_xy. The in-plane coherence length L_xy, was estimated from the full-width at half-maximum (FWHM) of the Bragg peak using L_xy ∼ 0.9(2π)/FWHM (Q_xy). The thickness of the monolayer was estimated from the FWHM of the Bragg rod using 0.9(2π)/FWHM(Q_z). More details can be found in the literature.^26–29

Results and discussion

Information about the influence of alkyl chain length and chiral discrimination on the thermodynamic characteristics of N-alkanoyl-substituted threonine monolayers are obtained by comparison of the enantiomeric (both enantiomers yield exactly the same isotherms) and racemic forms with C16 and C18 chain lengths. The complete set of experimental π–A curves of the corresponding monolayers, spread on pH 3 water and measured at different temperatures during compression and expansion, are shown in the ESI† (Fig. S1–S4). Selected π–A curves of racemic and enantiomeric N-palmitoyl-threonine monolayers measured at 5 °C (Fig. 2 left) and of racemic and enantiomeric N-stearoyl-threonine monolayers measured at 20 °C (Fig. 2 right) are presented in Fig. 2. The different temperatures are chosen on the basis of the generic behavior of homologs since the characteristic temperatures (see Table 1) are shifted by 15 K.³⁰

Fig. 2 π–A curves of N-palmitoyl-threonine (left) monolayers at 5 °C and N-stearoyl-threonine monolayers at 20 °C spread on pH 3 water. The D-enantiomers (red) and the racemic mixtures (black) are measured during compression (solid) and decompression (dash–dot–dot).

Table 1 Characteristic temperatures of the zero phase transition pressure T₀ (π_t = 0) and of the zero entropy change T_c (ΔS = 0) of N-C16- and N-C18-alkanoyl-threonine monolayers

C16	Enantiomer, D	Racemate, DL	ΔT0	ΔTc
T 0, K	275.2	274.3	0.9
T c, K	291.1	287.1		4

---

C18	Enantiomer, D	Racemate, DL	ΔT0	ΔTc
T 0, K	292.5	289.6	2.9
T c, K	304.2	302.4		1.8

---

Some characteristic features can be clearly observed in the isotherms. Comparing the corresponding isotherms of the C16 and C18 N-alkanoyl-substituted threonine amphiphiles, the usual shift to lower temperatures, as expected for increasing alkyl chain length by two CH₂ entities, can be seen (Fig. S1–S4, ESI†). All π–A curves present the characteristic differences obtained between compression and decompression of the monolayers designated as hysteresis by Stine et al. for other N-alkanoyl-substituted amino acid amphiphiles.^10,11 That means, for any temperature, all compression curves are located above the corresponding decompression curves independent of the alkyl chain length. In ref. 31 it was shown that this behavior can be understood on the basis of dynamic π–A experiments using different compression rates. The results of such experiments, accomplished with N-palmitoyl-D-allo-threonine methylester monolayers at different compression rates are shown in Fig. S5 (ESI†) confirming that the hysteresis increases with increasing compression rate.³¹ According to this result, the slowest compression curve approaches the decompression curve. Thus, the decompression curves (Fig. S1–S4, right, ESI†) can be considered as equilibrium isotherms for both enantiomeric and racemic N-alkanoyl-substituted threonine amphiphiles. Furthermore, the hysteresis depends also on the chirality. It can be clearly seen (Fig. 2) that the hysteresis is larger for the racemic mixture compared to the pure enantiomer. It seems that a larger energy barrier has to be overcome to start the nucleation into the condensed phase. This could indicate that homochiral interactions dominate the nucleation process, and in the racemic mixture a critical molecule density is needed to start homochiral nucleation.

The properties of compression curves can be described on the basis of a theoretical kinetic model developed for the kinetics of two-dimensional condensation of Langmuir monolayers at the air/water interface.³¹ This model accounts for different mechanisms of the monomer aggregation (dimerization, trimerisation, etc.) and different dependencies of the aggregation rate on time. The good agreement between theory and experiment has been found with the consequence that the most preferred reaction to describe the experimental results is the attachment of monomers to large aggregates.³¹

The temperature dependence of the phase transition pressure (π_t), that means the kink point in the π–A isotherm, obtained from the equilibrium decompression isotherms offers information about the thermodynamic characteristics for the transition between the fluid and condensed phases. At the recorded temperatures, an extended horizontal plateau region is observed, which is gradually more inclined and less extended at higher temperatures. Fig. 3 presents the π_t–T relationship of the N-alkanoyl-substituted threonine monolayers on pH 3 water. The slope dπ_t/dT of the linear fit to the experimental data amounts to 1.373 mN (m K)⁻¹ for N-palmitoyl-D-threonine, 1.634 mN (m K)⁻¹ for N-palmitoyl-DL-threonine, 1.768 mN (m K)⁻¹ for N-stearoyl-D-threonine, and 1.245 mN (m K)⁻¹ for N-stearoyl-DL-threonine.

Fig. 3 Temperature dependence of the main phase-transition pressure π_t at the LE/LC phase transition of enantiomeric (red) and racemic (black) N-palmitoyl-threonine monolayers (left) and N-stearoyl-threonine monolayers (right) spread on pH 3 water.

The linearly fitted curves reach zero pressure (π_t = 0 mN m⁻¹) at the following T₀-values: 275.2 K (2 °C) for N-palmitoyl-D-threonine, 274.3 K (1.1 °C) for N-palmitoyl-DL-threonine, 292.5 K (19.3 °C) for N-stearoyl-D-threonine, and 289.6 K (16.4 °C) for N-stearoyl-DL-threonine, respectively. These T₀ values give rise to slight ΔT₀ = 0.9 K differences between the enantiomeric (D) and the racemic (DL) forms of N-palmitoyl-threonine, whereas in the case of N-stearoyl-threonine, these differences are with ΔT₀ = 2.9 K considerably larger.

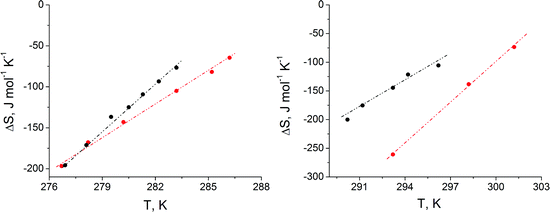
Access to the transition entropy (ΔS), presented in Fig. 4, is obtained by assessment of the temperature dependence of the phase transition pressure (π_t) and the area change (ΔA = A_LC − A_LE, with A_LC the molecular area in the condensed state and A_LE the molecular area in the liquid-expanded state at the phase transition pressure π_t) by using the two-dimensional Clapeyron equation, ΔS = ΔA·dπ_t/dT. It can be seen that the absolute ΔS values increase as the temperature decreases, indicating the increase of the condensed phase ordering at lower temperatures. The linear fit and extrapolation to zero ΔS stipulate the critical temperature T_c, above which the monolayer cannot be compressed into the condensed state. The shorter chain C16-homologue has lower T_c-values than the larger C18-homologue. The ΔT_c difference between the enantiomeric and the racemic forms is again comparatively small, but with ΔT_c = 4 °C for the C16 homologue larger than ΔT_c = 1.8 °C for the C18 homologue. The stronger van der Waals interactions between the longer chains together with increased temperature reduce the influence of chirality on the thermodynamical parameters. The characteristic temperatures of the zero phase transition pressure (π_t = 0) and zero entropy change (ΔS = 0) are listed in Table 1.

Fig. 4 Temperature dependence of the entropy change ΔS at the LE/LC phase transition of enantiomeric (red) and racemic (black) N-palmitoyl-threonine monolayers (left) and N-stearoyl-threonine monolayers (right) spread on pH 3 water.

It is interesting to note that the determined critical temperatures of the monolayers are very different from the main-transition temperatures observed in bulk dispersions. The T_m values of the C18 compounds are 351.6 K (78.4 °C) for the enantiomer and 360.4 K (87.2 °C) for the racemate. This suggests a large structural difference between mono- and bilayers. We show later that the area requirement of the head group network forces the alkyl chains into a strongly tilted state to optimize their van der Waals interactions in the monolayers. In bulk, there is another energetically more favored organization of the molecules: instead of the large tilt, the chains of the opposite monolayers can interdigitate.

The extended two-phase coexistence region of the equilibrium isotherm at ≤5 °C stipulates suitable conditions for studying the domain topology. The mesoscopic topology of monolayers, presented for N-palmitoyl-threonine, demonstrates chiral discrimination: (left) D-enantiomer; (middle) L-enantiomer; (right) 1 : 1 DL-racemate (Fig. 5). Chiral discrimination is observable between the two enantiomeric and racemic compounds. The condensed-phase domains of the enantiomeric monolayers are curved at one end of the domain in sense of the respective chiral form and in the opposite direction of the other enantiomeric form. The domain of the 1 : 1 racemic monolayer shows curvature in opposite directions from a center implying chiral influence within the domain.

Fig. 5 Chiral discrimination in the domain texture of N-palmitoyl-threonine monolayers: (left) D-enantiomer; (middle) L-enantiomer; (right) 1 : 1 DL-racemate. T = 5 °C. Scale bar 100 μm.

Generally, two categories of enantiomer pair mixtures are distinguished: (1) homochirality with a favored interaction between the same enantiomers (E_D–D and E_L–L > E_D–L) and (2) heterochirality with a favored interaction between the different enantiomers (E_D–D and E_L–L < E_D–L), where for strong interactions racemic compounds can be formed. The growth kinetics of the racemic N-palmitoyl-DL-threonine domains provides further useful information (Fig. 6). Starting from the center of a nucleus symmetric structure with opposite curvatures grow within 25 s. The thickness of the domain arms increases considerably, filling the interior of the domain and resulting finally in a round domain without holes in it. As Fig. 7 suggests, the racemic N-palmitoyl-DL-threonine domains grow to a shape which suggests a new mesoscopic state with heterochiral preference without any indication for homochiral discrimination and chiral separation within the domain. This behavior indicates that during the growth kinetics, a transition occurs from preferred homochirality to heterochirality. A similar crossover between homo- and heterochiral discrimination during the growth kinetics of 1-stearoylamine-glycerol domains has been revealed using quantum mechanical methods.³² A comparable change from homo- to heterochiral preference was also observed in the studies of N-palmitoyl-alanine monolayers using infrared reflection–absorption spectroscopic (IRRAS) measurements.²⁷

Fig. 6 Growth kinetics of N-palmitoyl-DL-threonine domains in the two-phase coexistence region at 2 °C during compression from 0.50 to 0.37 nm² per molecule: (from left to right) domain development within 25 s (0, 5, 10 and 25 s). T = 5 °C. Scale bar 100 μm. Symmetric domain structures with opposite curvatures grow from the center of the nucleus.

Fig. 7 Equilibrium state of the racemic N-palmitoyl-DL-threonine domains.

It is interesting to note that the domains developed generally by the amino acid amphiphiles, studied so far, e.g.ref. 10–13, possess no inner anisotropy. This is clearly seen in all examples of the N-palmitoyl-threonine domains presented in Fig. 5–7. Consequently, the azimuthal projection of the alkyl chains of neighboring molecules ought to be parallel to each other within a domain. It should be noted that this disagrees with the concept that the presence of mutual orientation of a pair of chiral molecules leads to a spontaneous curvature.³³ This implies that the absence of mutual intermolecular orientation in amino acid amphiphiles and the concomitant curvature of the domain composed of the enantiomeric amphiphile may be due to competing with the strong hydrogen-bonding interaction between the head groups.^6,32

GIXD studies provide information about the characteristic features of the lattice structure of condensed monolayer phases on the Angstrom scale. So far, information about the lattice structures of N-alkanoyl substituted α-amino acid amphiphiles monolayers is rather rare. Therefore, in the present study, GIXD measurements of N-palmitoyl-threonine monolayers were performed at 2.5 °C and of N-stearoyl-threonine at 10 °C on pH 3 subphase at different lateral pressures.

Fig. 8 and 9 show selected contour plots of equal intensity versus the in-plane component Q_xy and the out-of-plane component Q_z of the scattering vector for N-palmitoyl-threonine monolayers at 2.5 °C and for N-stearoyl-threonine at 10 °C, respectively. In the case of the enantiomers (L- and D-enantiomers yield exactly the same diffraction patterns), both compounds exhibit three Bragg peaks at all pressures. The Bragg peak positions, their full-widths at half-maximum, and all lattice parameters obtained at different surface pressures are listed in the ESI† (Tables S1 and S2).

Fig. 8 Contour plots of equal intensity vs. the in-plane component Q_xy and the out-of-plane component Q_z of the scattering vector of N-palmitoyl-DL-threonine (left) and N-palmitoyl-L-threonine (right) monolayers on pH 3 subphase at 25 mN m⁻¹ and 2.5 °C. The racemate forms a NNN tilted orthorhombic structure (2 out-of-plane diffraction peaks) whereas the enantiomer exhibits an oblique unit cell (3 diffraction peaks).

Fig. 9 Contour plots of equal intensity vs. the in-plane component Q_xy and the out-of-plane component Q_z of the scattering vector of N-stearoyl-DL-threonine (left) and N-stearoyl-L-threonine (right) monolayers on pH 3 subphase at 30 mN m⁻¹ and 10 °C. The racemate forms a NNN tilted orthorhombic structure (2 out-of-plane diffraction peaks) whereas the enantiomer exhibits an oblique unit cell (3 diffraction peaks).

For comparison, Table 2 presents selected lattice data obtained at 10 mN for both the enantiomeric and racemic N-palmitoyl-threonine (2.5 °C) and N-stearoyl-threonine (10 °C) monolayers. Characteristic for the structure of all condensed monolayer phases is the large tilt angle of ∼49°. The enantiomers exhibit an oblique lattice structure. The two Bragg peaks at higher Q_xy and lower Q_z values are quite close to each other indicating that the structure is not much deviated from an orthorhombic one with NNN (next-nearest neighbor) tilted chains. This is a first indication of only a weak influence of chirality on the structure. In the case of the racemates, only two Bragg peaks have been detected for both compounds at all pressures indicating a NNN tilted orthorhombic structure. The transition from the oblique lattice structures, as detected for enantiomeric monolayers, to orthorhombic structures, as usual for racemic monolayers, is clear evidence that the dominant heterochiral interaction in the racemic mixtures leads to the formation of a compound with congruent transition point. Correspondingly, the alkyl chain cross-sectional area with ∼20.0 Ų for the racemates is essentially smaller than that of the enantiomers with ∼20.7 Ų. Generally, such values are typical for a rotator phase indicating free rotation of the alkyl chains.

Table 2 (a): Bragg peak and rod positions and the corresponding full-widths at half-maximum of racemic and enantiomeric N-palmitoyl-threonine (2.5 °C) and N-stearoyl-threonine (10 °C) monolayers at 10 mN m⁻¹. (b): Lattice parameters of racemic and enantiomeric N-palmitoyl-threonine (2.5 °C) and N-stearoyl-threonine (10 °C) monolayers at 10 mN m⁻¹

Compound	Q xy , Å^−1	Q z , Å^−1	Q xy , Å^−1	Q z , Å^−1	Q xy , Å^−1	Q z , Å^−1
(a)
C16-Racemate			1.370	0.59	0.996	1.18
			0.009	0.35	0.024	0.35
C16-Enantiomer	1.402	0.67	1.338	0.45	0.981	1.12
	0.010	0.31	0.008	0.31	0.016	0.31
C18-Racemate			1.367	0.59	1.003	1.18
			0.010	0.33	0.052	0.33
C18-Enantiomer	1.399	0.66	1.337	0.46	0.978	1.12
	0.011	0.30	0.008	0.30	0.031	0.30

---

Compound	a, b, c, Å	α, β, γ, °	d	t, °	A xy , Å^2	A 0, Å^2
(b)
C16-Racemate	4.923	137.4	0.3729	50.0	31.1	20.0
	6.772	111.3	NNN	NNN
C16-Enantiomer	4.922	138.1	0.3934	48.8	31.5	20.7
	6.714	114.4
	7.035	107.4
C18-Racemate	4.941, 6.734	137.0, 111.5	0.3637	49.6	31.0	20.0
			NNN	NNN
C18-Enantiomer	4.928	138.2	0.3946	49.0	31.7	20.8
	6.737	114.3
	7.049	107.5

---

In contrast to usual amphiphilic monolayers, the tilt angle t with respect to the surface normal is for all studied compounds nearly independent of the lateral pressure (Fig. 10).

Fig. 10 Alkyl chain tilt angle of N-alkanoyl-threonine vs. lateral pressure. ● enantiomeric C16, ▲ racemic C16, enantiomeric C18 and racemic C18.

The transition pressure into a non-tilted phase can be calculated by extrapolating towards 1/cos(t) = 1 assuming linear relations between the pressure and molecular area and a constant cross-sectional area in the condensed phase.²⁹ In the case of N-alkanoyl-substituted threonine monolayers, such an extrapolation does not lead to any reasonable pressure values. Obviously, a strong hydrogen bonding network between the head groups prevents the change of the alkyl chain lattice on compression. Such strong head group interactions are the only reasonable explanation for the observed high and almost constant distortion d values contradicting the measured large cross-sectional areas typical for rotator phases.³⁴

Conclusions

The studied N-alkanoyl-substituted threonine amphiphiles indicate considerable differences in the main monolayer characteristics compared to usual amphiphilic monolayers. The π–A isotherms of the enantiomeric and racemic forms with C16 and C18 chain lengths show that at any assigned temperature all compression curves are located above the corresponding decompression curves independent of chain length and chirality. The equilibrium expansion curves have been used for thermodynamic analysis. The critical temperature T_c, above which the monolayer cannot be compressed into the condensed state, as well as the characteristic temperature T₀, below which no liquid-expanded phase state exists, are quite similar for the enantiomeric and racemic forms and depend only strongly on the chain length. Obviously, the stronger van der Waals interactions between the alkyl chains reduce the influence of chirality on the thermodynamic parameters.

The BAM experiments reveal clearly that the domains of N-palmitoyl-threonine monolayers have no inner anisotropy. This special feature is in agreement with the domain topology of other N-alkanoyl substituted amino acid amphiphiles. Consequently, the azimuthal projection of the alkyl chains of neighboring molecules should be parallel to each other within a domain disagreeing with the concept that the presence of mutual orientation of a pair of chiral molecules leads to a spontaneous curvature.³² The absence of mutual intermolecular orientation is attributable to a competition with the strong hydrogen-bonding interaction between the head groups.

Another interesting phenomenon is the observation that the racemic N-palmitoyl-DL-threonine domains start from the center with symmetric structures of opposite curvatures that grow within a short time to a shape which suggests a new mesoscopic state without any indication for homochiral discrimination and chiral separation within the domain. This suggests a transition from homochirality to heterochirality during the growth kinetics. This concept is in perfect agreement with the above discussion of homochiral nucleation even in racemic mixtures.

The present GIXD studies provide clear evidence concerning homochiral or heterochiral preference in the condensed phases of racemic mixtures. The three Bragg peaks of the enantiomers indicate an oblique lattice with strongly tilted chains. The two peaks of the corresponding racemates signify an orthorhombic structure with NNN tilted chains. The transition to the NNN tilted orthorhombic structure is convincing evidence that the heterochiral interactions are dominant in the condensed phase of racemic mixtures leading to the formation of a compound with congruent transition point. The alkyl chain cross-sectional area with ∼20.0 Ų (C16) and ∼19.9 Ų (C18), respectively, for the racemates is essentially smaller than that of the enantiomers with ∼20.8 Ų (C16) and ∼20.6 Ų (C18). However, in all four studied monolayers, the tilt of the alkyl chains is nearly the same because of the larger in-plane areas of the enantiomeric forms. This indicates that the heterochiral interactions in the racemates lead to a tighter in-plane packing nearly independent of the lateral pressure and the alkyl chain length. Strong head group interactions (hydrogen bond network) are the only reasonable explanation for the observed high and almost constant distortion values contradicting the measured large cross-sectional areas typical for rotator phases. In summary, the strong head group interactions between the enantiomers are connected with a larger in-plane area (less tight packing) compared to that of the racemic dimer.

Conflicts of interest

There are no conflicts to declare.

Acknowledgements

We thank HASYLAB at DESY, Hamburg, Germany, for beamtime and excellent support, Dr K. Schinkowski for the preparation of N-alkanoyl-substituted threonine amphiphiles, Irina Berndt for careful Langmuir isotherm experiments and René Genz of the IT division for versatile technical assistance. Open access funding provided by the Max Planck Society.

References

1. E. M. Arnett, N. G. Harvey and P. L. Rose, Acc. Chem. Res., 1989, 22, 131–138.
2. N. G. Harvey, P. L. Rose, D. Mirajovsky and E. M. Arnett, J. Am. Chem. Soc., 1990, 112, 3547–3554.
3. J. G. Heath and E. M. Arnett, J. Am. Chem. Soc., 1992, 114, 4500–4514.
4. P. L. Rose, N. G. Harvey and E. M. Arnett, Adv. Phys. Org. Chem., 1993, 28, 45–138.
5. E. M. Arnett, K. Amarnath, N. G. Harvey and J. Cheng, J. Am. Chem. Soc., 1990, 112, 344–355.
6. N. Nandi and D. Vollhardt, Chem. Rev., 2003, 103, 4033–4075.
7. D. Vollhardt, Encyclopedia of Surface and Colloid Science, Taylor & Francis, New York, 2nd edn, 2006, vol. 5, pp. 4104–4118.
8. N. Nandi and D. Vollhardt, Colloids Surf., A, 2001, 183–185, 67–83; N. Nandi and D. Vollhardt, Colloids Surf., A, 2002, 198–200, 207–221.
9. N. Nandi and D. Vollhardt, J. Phys. Chem. B, 2003, 107, 3464–3475.
10. K. J. Stine, J. Y.-J. Uang and S. D. Dingman, Langmuir, 1993, 9, 2112–2118.
11. K. J. Stine, S. A. Whitt and J. Y.-J. Uang, Chem. Phys. Lipids, 1994, 69, 41–50.
12. S. Akamatsu, O. Bouloussa, K. To and F. Rondelez, Phys. Rev. A: At., Mol., Opt. Phys., 1992, 46, 4504–4507.
13. J. Parazak, Y.-J. Uang, B. Turner and K. J. Stine, Langmuir, 1994, 10, 3787–3793.
14. F. Hoffmann, K. J. Stine and H. Hühnerfuss, J. Phys. Chem. B, 2005, 109, 240–252.
15. D. Andelman, J. Am. Chem. Soc., 1989, 111, 6536–6544.
16. D. Andelman and H. Orlando, J. Am. Chem. Soc., 1993, 115, 12322–12329.
17. A. Gericke and H. Hühnerfuss, Langmuir, 1994, 10, 3782–3786.
18. F. Hoffmann, H. Hühnerfuss and K. J. Stine, Langmuir, 1998, 14, 4525–4534.
19. H. Hühnerfuss, V. Neumann and K. J. Stine, Langmuir, 1996, 12, 2561–2569.
20. H. Hühnerfuss, A. Gericke, V. Neumann and K. J. Stine, Thin Solid Films, 1996, 284, 694–697.
21. F. J. Zeelen and E. Havinga, Recl. Trav. Chim. Pays-Bas, 1958, 77, 267–272.
22. D. Vollhardt, Curr. Opin. Colloid Interface Sci., 2014, 19, 183–197.
23. S. Hénon and J. Meunier, Rev. Sci. Instrum., 1991, 62, 936–939.
24. D. Hönig and D. Möbius, J. Phys. Chem., 1991, 95, 4590–4592.
25. R. Frahm, J. Weigelt, G. Meyer and G. Materlik, Rev. Sci. Instrum., 1995, 66, 1677–1680.
26. J. Als Nielsen, F. Christensen and P. S. Pershan, Phys. Rev. Lett., 1982, 48, 1107–1111.
27. J. Als-Nielsen, D. Jacquemain, K. Kjaer, F. Leveiller, M. Lahav and L. Leiserowitz, Phys. Rep., 1994, 246, 251–313.
28. K. Kjaer, Physica B, 1994, 198, 100–109.
29. D. Vollhardt and G. Brezesinski, in Recent Progress in Colloid and Surface Chemistry with Biological Applications, ed. C. Wang, et al., ACS Symposium Series, American Chemical Society, Washington, DC, 2015, pp. 377–419.
30. I. R. Peterson, V. Brzezinsky, R. M. Kenn and R. Steitz, Langmuir, 1992, 8, 2995–3002.
31. D. Vollhardt and V. B. Fainerman, J. Phys. Chem. B, 2002, 106, 345–351.
32. N. Nandi, K. Thirumoorthy and D. Vollhardt, Langmuir, 2008, 24, 9489–9494.
33. J.-H. Fuhrhop and W. Helfrich, Chem. Rev., 1993, 93, 1565–1582.
34. V. M. Kaganer, H. Möhwald and P. Dutta, Rev. Mod. Phys., 1999, 71, 779–819.

---

Footnote

† Electronic supplementary information (ESI) available. See DOI: 10.1039/c8cp06481d

---