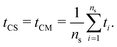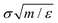Thermo-orientation in fluids of arbitrarily shaped particles
Received
28th September 2018
, Accepted 28th November 2018
First published on 28th November 2018
Abstract
Recent nonequilibrium Molecular Dynamics (NEMD) simulations revealed preferential orientation, induced by a temperature gradient, in fluids of uncharged dumbbell-like particles. The magnitude of this phenomenon, called thermo-orientation, was found to be linear in the applied temperature gradient and to increase with the difference in shape or mass between the two beads of the particles. The underlying mechanism and the microscopic determinants of the phenomenon are not obvious. Here, after examination of the general symmetry requirements for thermo-orientation, we have extended the NEMD simulations to uncharged particles of various shapes and mass distribution, including chiral cases. The numerical results are rationalized by a microscopic model, based on the assumption of local equilibrium. This allows us to correlate the thermo-orientation response of arbitrarily shaped particles to quantities that characterize their shape and mass distribution.
1 Introduction
It is well known that, under a temperature gradient, a multicomponent mixture reaches a steady state of non-uniform composition, because some components accumulate at the cold side, whereas the others migrate in the opposite direction.1 This effect, discovered by C. Ludwig2 and Soret,3 is known as thermal diffusion or Soret effect. Important examples of thermodiffusion can be found in nature and in industrial applications,4e.g. in mass separation of chemicals. A related phenomenon is thermophoresis, i.e. the directed motion of colloids or macromolecules in a solvent induced by a temperature gradient,5,6 which has a large number of applications, e.g. to characterize biomolecular interaction.7 Despite being known for a long time, these phenomena are constantly attracting interest. One reason is that the underlying microscopic mechanism remains controversial.8 Moreover, the development of nanotechnologies poses new questions, which concern the effect of strong temperature gradients,9 the coupling of these to optical and electric fields,10–12 the control of heat transfer at the nanoscale13 and their exploitation for novel applications such as thermal therapy and energy conversion devices.
A new effect was revealed by recent nonequilibrium molecular dynamics (NEMD) simulations, which showed that a temperature gradient can induce a preferred orientation in fluids of dumbbell-like particles (dimers). This new phenomenon was called thermo-orientation.14 The initial study focused on dimers made of beads with different mass or diameter and purely repulsive interactions, described by the repulsive term of the Lennard-Jones potential. The response was reported to be linear in the applied temperature gradient and to be enhanced by an increase of the difference in size or mass between the beads. The physical behaviour observed in simulations was explained in the framework of nonequilibrium thermodynamics. The orientational response was found to be consistent with the Soret effect: as small/heavy particles in mixtures accumulate in the cold region, so the smaller/heavier bead of dimers preferentially points towards the cold source. Moreover, a correlation between the thermo-orientation and the Soret effect was observed: the diameter and mass differences that lead to the stronger separation in binary mixtures also lead to an higher degree of orientation of dimers. Later on, shape poalr dimers with units interacting through the full Lennard-Jones potential were considered and it was found that dispersion interactions do not strongly alter the thermo-orientational behaviour. This was taken as an indication of the key role of geometric factors in the microscopic mechanism.15 Thermo-orientation was reported also in a very recent NEMD study of rod-like particles with non-uniform mass distribution, suspended in a dense fluid of spherical beads,16 whereas no orientation was observed for rod-like particles with uniform mass distribution.17
In the case of particles possessing an electric dipole, the preferential orientation under a temperature gradient is associated with the onset of electric polarization, thus an electric field even in the absence of ions. This effect, called thermo-polarization, was observed by NEMD simulations of water.18–21 It was suggested theoretically that the polarization field can cause an effective interaction between colloidal particles embedded in a polar fluid at different temperatures, as if they were charged electric or magnetic monopoles.22 This prediction was confirmed by NEMD simulations of colloids in an off-center Stockmayer fluid, consisting of particles with a point dipole and a Lennard-Jones center displaced along the direction of the dipole moment.23
The degree of thermo-orientation obtained from NEMD simulations is very small, therefore extremely high temperature gradients are required. This could be the reason for the lack of experimental evidences of thermo-orientation in isotropic fluids. On the contrary, orientation induced by temperature gradients was reported for nematic liquid crystal, where however the effect remains controversial,24,25 and for cholesteric liquid crystals. In the latter case, the coupling with chirality generates special effects, such as the uniform rotation of the internal structure of droplets.26–29
Nonequilibrium thermodynamics provides a framework for the interpretation of the thermo-orientation effect. However, this is done in terms of phenomenological coefficients, which cannot be easily related to microscopic quantities. A first attempt to provide a microscopic interpretation of thermo-orientation was given in ref. 30, where a mean-field theory based on a local equilibrium hypothesis was developed, to explain the thermo-orientational behaviour of dimers comprised of beads of different size. The magnitude of the effect was found to be proportional to the ratio of the diameter of the spheres and to their volume, in agreement with the results of MD simulations reported in ref. 15. Very recently, a mean field theory based on the assumption of local equilibrium was found to provide predictions of the thermo-orientation of a Stockmeyer fluid in very good agreement with NEMD simulations and showed that thermo-orientation and thermo-polarization have the same underlying physical mechanism.23
The present work is aimed at investigating the relationship between thermo-orientation and the structure of the fluid particles. Previous studies focused on dumbbell-like14,15 and rod-like particles.16 Here, we extend the study to particles of different shapes and symmetries. The systems investigated include chiral particles, since there are claims of special effects due to chirality in the presence of temperature gradients.26,31,32 One specific question concerns the possibility of a distinct behaviour of pairs of enantiomers under thermal gradients. NEMD simulations are complemented by a microscopic model of thermo-orientation, which allows us to correlate the orientational response to the geometric characteristics of the particles.
The remainder of the paper is organized as follows. The next section presents general symmetry considerations, then the third section is focused on NEMD simulations: after a short description of methods, the numerical results are reported. In the subsequent section a microscopic model of the thermo-orientation effect is developed and its predictions are compared with the results of NEMD simulations. Finally, we present the conclusions of our study and future outlook.
2 Thermo-orientation and symmetry
Symmetry considerations allow us to determine whether a given particle structure is compatible with the existence of polar order and to identify quantities that are suitable to characterize this order (order parameters). The latter must be invariant with respect to any symmetry operation of the particle and of the phase. A fluid in the presence of a temperature gradient has C∞v symmetry (C∞ axis parallel to the temperature gradient) and is compatible with polar order of particles belonging to polar point groups, i.e. Cn, Cnv and C∞v, Cs.†![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 33 Henceforth, we will denote as polar all particles belonging to these point groups, irrespective of the presence of an electric dipole. In particular, we will speak of shape- and mass-polarity, depending on whether polarity derives from the shape or from the mass distribution of the particle.
33 Henceforth, we will denote as polar all particles belonging to these point groups, irrespective of the presence of an electric dipole. In particular, we will speak of shape- and mass-polarity, depending on whether polarity derives from the shape or from the mass distribution of the particle.
A suitable order parameter is the average value of the cosine of the angle (θ) between the thermo-alignment direction of a particle, identified by the unit vector û, and the temperature gradient. With reference to a laboratory frame having its Z axis along the thermal gradient, the order parameter is denoted as 〈cos![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) θ〉Z, where the subscript indicates that this is a local value at the Z-coordinate. For particles of Cn, Cnv and C∞v symmetry, the vector û is parallel to the Cn (n = 2, 3,…) or C∞ rotation axis. For particles of Cs symmetry û must lie on the reflection plane, whereas in the case of the point group C1 there are no symmetry constraints on the direction of û. In the absence of a temperature gradient all particle orientations are equiprobable and the order parameter vanishes, 〈cos
θ〉Z, where the subscript indicates that this is a local value at the Z-coordinate. For particles of Cn, Cnv and C∞v symmetry, the vector û is parallel to the Cn (n = 2, 3,…) or C∞ rotation axis. For particles of Cs symmetry û must lie on the reflection plane, whereas in the case of the point group C1 there are no symmetry constraints on the direction of û. In the absence of a temperature gradient all particle orientations are equiprobable and the order parameter vanishes, 〈cos![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) θ〉Z = 0. On the contrary, 〈cos
θ〉Z = 0. On the contrary, 〈cos![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) θ〉Z ≠ 0 when a temperature gradient is applied.
θ〉Z ≠ 0 when a temperature gradient is applied.
3 NEMD simulations
3.1 Systems
The systems investigated here are fluids of particles that are made of (rigid) chains of beads. Their structure is shown in Fig. 1. Beads belonging to different particles interact with each other through the soft repulsive Weeks–Chandler–Andersen (WCA) potential:34| | 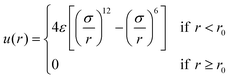 | (1) |
Here ε and σ are an energy and a length parameter, respectively, and r0 = 21/6σ is a cut-off distance. Actually, a modified form of eqn (1) was used to avoid discontinuity in the forces.35 Henceforth, all quantities will be expressed in reduced Lennard-Jones units (see Table 1).
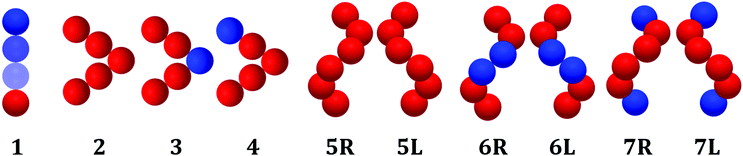 |
| | Fig. 1 The particles investigated in the present work are rigid chains of WCA beads. 1 has C∞v symmetry, 2 and 3 have C2v symmetry and 4 has Cs symmetry. 5–7 are helices of C2 symmetry, right-handed (R) and left-handed (L). Red beads have a reduced mass equal to 1, whereas blue beads are heavier, and in particular: in 1 the mass increases as 1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) : :![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 2 2![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) : :![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 4 4![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) : :![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 8 on moving from the red to the blue end; in 3 and 4 the blue bead has a reduced mass equal to 4, in 6 and 7 the blue beads have a reduced mass equal to 5. 8 on moving from the red to the blue end; in 3 and 4 the blue bead has a reduced mass equal to 4, in 6 and 7 the blue beads have a reduced mass equal to 5. | |
Table 1 Units used throughout this work
| Quantity |
Unit |
| Length |
σ
|
| Temperature |
ε/kB |
| Energy |
ε
|
| Mass |
m
|
| Time |
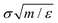
|
Each particle is comprised of ns WCA beads, with reduced length and energy parameters both equal to 1 and mass as specified in Fig. 1. Strong harmonic potentials are used to avoid significant fluctuations of bond lengths, angles and dihedrals.
3.2 Methods
NEMD simulations were conducted using the enhanced heat exchange (eHEX) algorithm,36 which belongs to the so-called Boundary Driven approaches (BD-NEMD).37 In early NEMD algorithms38,39 the system was confined between two parallel walls, perpendicular to the heat flow. However, this has the drawback of unphysical wall effects. Therefore, other algorithms were subsequently developed, combining NEMD simulations with fully periodic boundary conditions, so as to reduce finite size effects.40,41 Among these there are the BD-NEMD methods, where a stationary heat flux is established by withdrawing kinetic energy from one region and supplying kinetic energy to another region. One of these is the heat exchange (HEX)42,43 algorithm, of which eHEX is an extension with improved energy conservation, so that longer simulation time scales are accessible.
Fig. 2 shows a schematic of the simulation box, which includes a hot (Γ1) and a cold (Γ2) reservoir, each of width δ, where the thermal gradient algorithm operates. The remaining parts of the box are free evolution regions. The box contains a constant number of particles, in our simulations N = 384. An orthorhombic box with sides in the ratio (Lx, Ly, Lz) = (1, 1, 3) was used; the width of the reservoirs was given the value δ = 6, but in the simulations of particles 2–4 the value δ = 4 was taken. The equations of motion were integrated using the velocity Verlet algorithm with a time step of Δt = 0.002. The linear momentum of the box was initialized to zero at the beginning and was conserved during the whole simulation. The simulations were carried out using the free software package LAMMPS (version 31Mar17).44
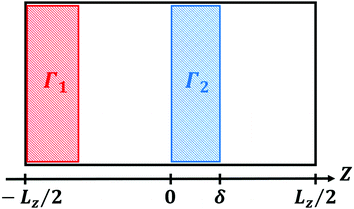 |
| | Fig. 2 Schematic of the simulation box used in BD-NEMD simulations. Γ1 is the hot reservoir, Γ2 is the cold reservoir and the zones outside the reservoirs are free evolution regions. | |
The simulation protocol described in ref. 36 was adopted. First, the system is brought from the initial configuration to the thermodynamic equilibrium state of interest by a sequence of NVE and NVT runs (the latter using a Nosé–Hoover thermostat45,46 with a relaxation time equal to 0.5) for a total length of 106 steps. In the second part of the simulation, starting from an equilibrated state, a spatial temperature profile between the heat reservoirs is generated. In the enhanced heat exchange (eHEX) algorithm kinetic energy is periodically swapped from one region to another of the simulation box by rescaling velocities and the dynamics between velocity rescaling steps is Hamiltonian.36 A first period is needed to achieve the stationary state; in our case, from 5–10 × 106 timesteps were taken, depending on the kind of particles. Subsequently, a production trajectory of 80 × 106 timesteps was collected, which was found to be long enough to allow sufficient sampling of orientations with a limited energy drift (of the order of 1%).
3.3 Results
Fig. 3 – top and bottom show profiles of temperature and number density of particles across the reservoirs, obtained from NEMD simulations of the rod-like particle 1 at different values of the temperature gradient ∇ZT and of the average number density ![[small rho, Greek, macron]](https://www.rsc.org/images/entities/i_char_e0d1.gif) . The number density is defined as ρ = N/Vbox, where N is the number of particles and Vbox is the volume of the simulation box. The figures show that in the region between the reservoirs the temperature exhibits a linear dependence on the Z-coordinate and the same occurs also for the number density, whose gradient is proportional to that of temperature, but opposite in sign. Analogous behaviour of the temperature and number density was obtained for all the systems under examination.
. The number density is defined as ρ = N/Vbox, where N is the number of particles and Vbox is the volume of the simulation box. The figures show that in the region between the reservoirs the temperature exhibits a linear dependence on the Z-coordinate and the same occurs also for the number density, whose gradient is proportional to that of temperature, but opposite in sign. Analogous behaviour of the temperature and number density was obtained for all the systems under examination.
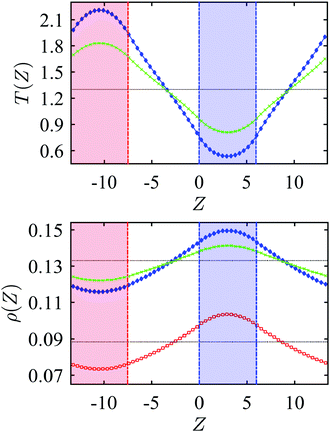 |
| | Fig. 3 Profiles of temperature (top) and of number density ρ (bottom), as a function of the Z-position across the simulation box, for the rod-like particle 1. ∇ZT = −0.09 (green crosses) and ∇ZT = −0.13 (blue diamonds), with mean number density ![[small rho, Greek, macron]](https://www.rsc.org/images/entities/i_char_e0d1.gif) = 0.13 and mean temperature = 0.13 and mean temperature ![[T with combining macron]](https://www.rsc.org/images/entities/i_char_0054_0304.gif) = 1.3; ∇ZT = −0.13, with mean number density = 1.3; ∇ZT = −0.13, with mean number density ![[small rho, Greek, macron]](https://www.rsc.org/images/entities/i_char_e0d1.gif) = 0.09 and mean temperature = 0.09 and mean temperature ![[T with combining macron]](https://www.rsc.org/images/entities/i_char_0054_0304.gif) = 1.3 (red open squares). The black dotted lines indicate the mean temperature (top) and the mean number density (bottom). The colored regions correspond to the hot (red) and the cold (blue) reservoir. = 1.3 (red open squares). The black dotted lines indicate the mean temperature (top) and the mean number density (bottom). The colored regions correspond to the hot (red) and the cold (blue) reservoir. | |
The thermo-orientation effect is quantified by the local mean value of cos![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) θ, where θ is the angle between the unit vector û, which identifies the thermo-alignment axis of particles and the Z-axis of the simulation box, which we have taken anti-parallel to the temperature gradient. For the rod-like particle 1, û is parallel to the C∞ rotation axis (see Fig. 4 – left) and points from the lighter to the heavier bead. Fig. 4 – middle shows the distribution of cos
θ, where θ is the angle between the unit vector û, which identifies the thermo-alignment axis of particles and the Z-axis of the simulation box, which we have taken anti-parallel to the temperature gradient. For the rod-like particle 1, û is parallel to the C∞ rotation axis (see Fig. 4 – left) and points from the lighter to the heavier bead. Fig. 4 – middle shows the distribution of cos![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) θ across the temperature gradient. In the simulation box there are two equivalent free evolution regions between the reservoirs (see Fig. 2); here and in the plots presented in the following only one Z-range is shown and the results displayed are the mean of the data in the two regions of the simulation box. In Fig. 4 – middle we can see that positive values of cos
θ across the temperature gradient. In the simulation box there are two equivalent free evolution regions between the reservoirs (see Fig. 2); here and in the plots presented in the following only one Z-range is shown and the results displayed are the mean of the data in the two regions of the simulation box. In Fig. 4 – middle we can see that positive values of cos![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) θ are more likely than negative ones at any position across the whole temperature range. This means that the rods preferentially orient their heavy end towards the cold reservoir, which is in agreement with the thermo-orientation effect reported for mass polar dimers in ref. 14. Fig. 4-right shows the corresponding profile of mean values, 〈cos
θ are more likely than negative ones at any position across the whole temperature range. This means that the rods preferentially orient their heavy end towards the cold reservoir, which is in agreement with the thermo-orientation effect reported for mass polar dimers in ref. 14. Fig. 4-right shows the corresponding profile of mean values, 〈cos![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) θ〉Z, calculated at different values of the mean number density
θ〉Z, calculated at different values of the mean number density ![[small rho, Greek, macron]](https://www.rsc.org/images/entities/i_char_e0d1.gif) and of the temperature gradient ∇ZT. The order parameter is small, yet different from zero and 2–3 times higher than that obtained for dimers under the same temperature gradient;14 as for dimers, it grows on moving from the hot to the cold reservoir and, for given mean temperature
and of the temperature gradient ∇ZT. The order parameter is small, yet different from zero and 2–3 times higher than that obtained for dimers under the same temperature gradient;14 as for dimers, it grows on moving from the hot to the cold reservoir and, for given mean temperature ![[T with combining macron]](https://www.rsc.org/images/entities/i_char_0054_0304.gif) and temperature gradient ∇ZT, shows an approximately linear increase with the mean density. The 〈cos
and temperature gradient ∇ZT, shows an approximately linear increase with the mean density. The 〈cos![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) θ〉Z profiles scale linearly with the temperature gradient, as in previous studies for dimers and in agreement with the prediction of nonequilibrium thermodynamics.14 The same behaviour was obtained also for the other systems investigated here. Also in line with the study of dimers, the order parameter was found to vanish for rod-like particles made of identical beads having the same mass.
θ〉Z profiles scale linearly with the temperature gradient, as in previous studies for dimers and in agreement with the prediction of nonequilibrium thermodynamics.14 The same behaviour was obtained also for the other systems investigated here. Also in line with the study of dimers, the order parameter was found to vanish for rod-like particles made of identical beads having the same mass.
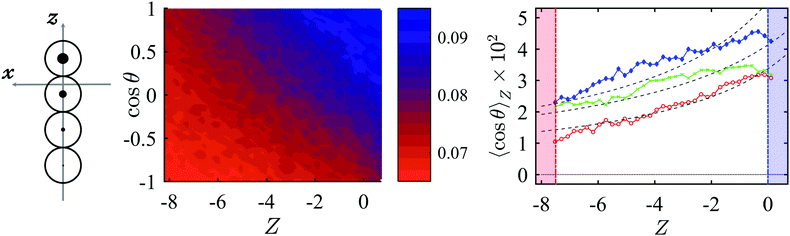 |
| | Fig. 4 (left) Rod-like particle 1 with the body-fixed reference frame (BF), having the origin in the position of the center of mass. The mass of the beads that form the rod increases in the direction of positive z-values. (middle) Distribution of particle orientations as a function of the Z-position across the simulation box, for ∇ZT = −0.13, ![[T with combining macron]](https://www.rsc.org/images/entities/i_char_0054_0304.gif) = 1.3 and = 1.3 and ![[small rho, Greek, macron]](https://www.rsc.org/images/entities/i_char_e0d1.gif) = 0.09. Color coding is based on the local density of particles with given orientation. (right) Profiles of 〈cos = 0.09. Color coding is based on the local density of particles with given orientation. (right) Profiles of 〈cos![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) θ〉Z as a function of the Z-position across the simulation box, obtained from NEMD simulations of particle 1 at θ〉Z as a function of the Z-position across the simulation box, obtained from NEMD simulations of particle 1 at ![[small rho, Greek, macron]](https://www.rsc.org/images/entities/i_char_e0d1.gif) = 0.09 (red open circles) and = 0.09 (red open circles) and ![[small rho, Greek, macron]](https://www.rsc.org/images/entities/i_char_e0d1.gif) = 0.13 (green crosses), both with ∇ZT = −0.13, and for = 0.13 (green crosses), both with ∇ZT = −0.13, and for ![[small rho, Greek, macron]](https://www.rsc.org/images/entities/i_char_e0d1.gif) = 0.13 and ∇ZT = −0.16 (blue diamonds). In all cases the mean temperature is = 0.13 and ∇ZT = −0.16 (blue diamonds). In all cases the mean temperature is ![[T with combining macron]](https://www.rsc.org/images/entities/i_char_0054_0304.gif) = 1.3. The dashed lines are fitting curves to the microscopic model. θ is the angle between the z-axis of the BF and the Z-axis of the simulation box. The colored regions correspond to the hot (red) and cold (blue) reservoir. = 1.3. The dashed lines are fitting curves to the microscopic model. θ is the angle between the z-axis of the BF and the Z-axis of the simulation box. The colored regions correspond to the hot (red) and cold (blue) reservoir. | |
Fig. 5 and 6 show the profile of order parameter obtained for particles 2–4, which have the same shape and interactions, but different mass distribution. Particles 2 and 3 have C2v symmetry, therefore their thermo-alignment axis, if any, must be along the C2 rotation axis. This direction defines the z axis of the body-fixed reference frame, shown on top of Fig. 5. The behaviour of 〈cos![[thin space (1/6-em)]](https://www.rsc.org/images/entities/i_char_2009.gif) θ〉Z displayed in Fig. 5 shows that particles 2, which are made of beads with identical mass, do not exhibit thermo-orientation (black squares). The same result was found for any V-shaped particle made of identical beads with equal mass, irrespective of geometric parameters, such as bend angle and length of the two arms, and of the thermodynamic conditions. This demonstrates that polar symmetry is necessary, but not sufficient for thermo-orientation. Conversely, the 〈cos
θ〉Z displayed in Fig. 5 shows that particles 2, which are made of beads with identical mass, do not exhibit thermo-orientation (black squares). The same result was found for any V-shaped particle made of identical beads with equal mass, irrespective of geometric parameters, such as bend angle and length of the two arms, and of the thermodynamic conditions. This demonstrates that polar symmetry is necessary, but not sufficient for thermo-orientation. Conversely, the 〈cos![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) θ〉Z profiles for particles 3, in which the central bead has a mass different from the other beads, indicate the presence of a preferred orientation (blue diamonds and red open circles in Fig. 5). The magnitude of thermo-orientation is a little smaller than that of the rod-like particles 1, yet clearly different from zero. The order parameter is positive, which means that particles 3 preferentially orient their heavy unit towards the cold region. As for the rod-like particle 1, the value of 〈cos
θ〉Z profiles for particles 3, in which the central bead has a mass different from the other beads, indicate the presence of a preferred orientation (blue diamonds and red open circles in Fig. 5). The magnitude of thermo-orientation is a little smaller than that of the rod-like particles 1, yet clearly different from zero. The order parameter is positive, which means that particles 3 preferentially orient their heavy unit towards the cold region. As for the rod-like particle 1, the value of 〈cos![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) θ〉Z increases on moving from the hot to the cold reservoir and, for given mean temperature and temperature gradient, it increases approximately linearly with the mean density.
θ〉Z increases on moving from the hot to the cold reservoir and, for given mean temperature and temperature gradient, it increases approximately linearly with the mean density.
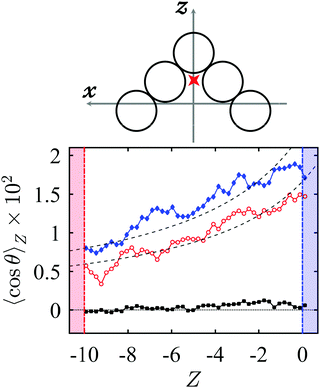 |
| | Fig. 5 (top) V-shaped particle with the body-fixed reference frame (BF) {x, y, z} having its origin in the center of mass. The cartoon shows the case of particle 2, with the red star indicating the position of the center of mass of particle 3. (bottom) Profiles of 〈cos![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) θ〉Z as a function of the Z-position across the simulation box, obtained from NEMD simulations of particles 2 (black squares) and 3 (blue diamonds) at ∇ZT = −0.13, mean temperature θ〉Z as a function of the Z-position across the simulation box, obtained from NEMD simulations of particles 2 (black squares) and 3 (blue diamonds) at ∇ZT = −0.13, mean temperature ![[T with combining macron]](https://www.rsc.org/images/entities/i_char_0054_0304.gif) = 1.3, number density = 1.3, number density ![[small rho, Greek, macron]](https://www.rsc.org/images/entities/i_char_e0d1.gif) = 0.11, and particle 3 at ∇ZT = −0.13, mean temperature = 0.11, and particle 3 at ∇ZT = −0.13, mean temperature ![[T with combining macron]](https://www.rsc.org/images/entities/i_char_0054_0304.gif) = 1.3 and number density = 1.3 and number density ![[small rho, Greek, macron]](https://www.rsc.org/images/entities/i_char_e0d1.gif) = 0.09 (red open circles). θ is the angle between the z-axis of the BF and the Z-axis of the simulation box. The dashed lines are fitting curves to the microscopic model. The colored regions indicate the hot (red) and cold (blue) reservoir. = 0.09 (red open circles). θ is the angle between the z-axis of the BF and the Z-axis of the simulation box. The dashed lines are fitting curves to the microscopic model. The colored regions indicate the hot (red) and cold (blue) reservoir. | |
 |
| | Fig. 6 (top) Particle 4, with the heavy bead shown in gray. The reference frames {x′, y′, z′} and {x, y, z} have the origin in the center of mass; z is parallel to the unit vector û, which identifies the thermo-alignment direction of the particle. (Bottom) Profile of 〈cos![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) θ1〉Z (red crosses), 〈cos θ1〉Z (red crosses), 〈cos![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) θ2〉Z (green open squares) and 〈cos θ2〉Z (green open squares) and 〈cos![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) θ〉Z (blue circles) as a function of the Z-position across the simulation box, obtained from NEMD simulations of particle 4 at ∇ZT = −0.13, mean temperature θ〉Z (blue circles) as a function of the Z-position across the simulation box, obtained from NEMD simulations of particle 4 at ∇ZT = −0.13, mean temperature ![[T with combining macron]](https://www.rsc.org/images/entities/i_char_0054_0304.gif) = 1.3 and number density = 1.3 and number density ![[small rho, Greek, macron]](https://www.rsc.org/images/entities/i_char_e0d1.gif) = 0.09. θ1, θ2 and θ are the angles between the x′-, z′-, z-axis, respectively, and the Z-axis of the simulation box. The dashed line is a fitting curve of the 〈cosθ〉Z profile to the microscopic model. The colored regions indicate the hot (red) and cold (blue) reservoir. = 0.09. θ1, θ2 and θ are the angles between the x′-, z′-, z-axis, respectively, and the Z-axis of the simulation box. The dashed line is a fitting curve of the 〈cosθ〉Z profile to the microscopic model. The colored regions indicate the hot (red) and cold (blue) reservoir. | |
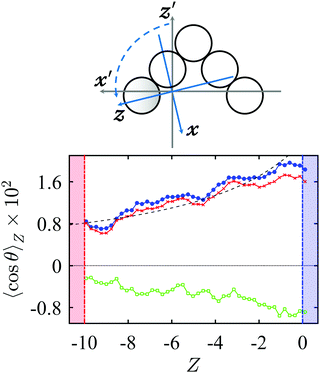
In the V-shaped particles 4, the presence of a bead with different mass at one end breaks the two-fold symmetry; these particles belong to the Cs point group and the thermo-orientation axis, if any, must lie on the reflection plane, but its direction on this plane has to be determined case by case. Fig. 6 shows the profiles of 〈cos![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) θ1〉Z and 〈cos
θ1〉Z and 〈cos![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) θ2〉Z, where θ1 and θ2 are the angles between the Z-axis and the axes (x′, z′) of a body-fixed reference frame, which is defined as shown in the cartoon on top of the figure. From 〈cos
θ2〉Z, where θ1 and θ2 are the angles between the Z-axis and the axes (x′, z′) of a body-fixed reference frame, which is defined as shown in the cartoon on top of the figure. From 〈cos![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) θ1〉Z (red crosses) and 〈cos
θ1〉Z (red crosses) and 〈cos![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) θ2〉Z (green open squares) we can calculate the orientation of the unit vector û, which defines the thermo-alignment direction of the particle, and the average projection of û on the Z-axis, based on the following considerations. Let us call χ the rotation angle from the x′, z′-axes to the x, z-axes of a reference frame (BF), having z‖û. Since û = sin
θ2〉Z (green open squares) we can calculate the orientation of the unit vector û, which defines the thermo-alignment direction of the particle, and the average projection of û on the Z-axis, based on the following considerations. Let us call χ the rotation angle from the x′, z′-axes to the x, z-axes of a reference frame (BF), having z‖û. Since û = sin![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) χ
χ![[x with combining circumflex]](https://www.rsc.org/images/entities/b_char_0078_0302.gif) + cos
+ cos![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) χẑ, we can write:
χẑ, we can write:
| | 〈cos![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) θ〉Z = sin θ〉Z = sin![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) χ〈cos χ〈cos![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) θ1〉Z + cos θ1〉Z + cos![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) χ〈cos χ〈cos![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) θ2〉Z. θ2〉Z. | (2) |
The average
Z-projection of any axis perpendicular to
û will vanish,
i.e.:
| | 0 = cos![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) χ〈cos χ〈cos![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) θ1〉Z − sin θ1〉Z − sin![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) χ〈cos χ〈cos![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) θ2〉Z, θ2〉Z, | (3) |
and from this we can calculate the rotation angle as
χ = arctan(〈cos
![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) θ1
θ1〉
Z)/(〈cos
![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) θ2
θ2〉
Z). Using the values of 〈cos
![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) θ1
θ1〉
Z and 〈cos
![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) θ2
θ2〉
Z shown in
Fig. 6 we obtain
χ ≈ 114°; substituting this value in
eqn (2) we calculate the profile of 〈cos
![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) θ
θ〉
Z that is reported in the same
Fig. 6 (blue circles). The magnitude of thermo-orientation is similar to that of particle
3, and also in this case the positive value of 〈cos
![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) θ
θ〉
Z indicates that particle
4 preferentially orients with its heavy bead pointing towards the cold reservoir.
Finally, Fig. 7 shows the profile of order parameter for the helical particles 5–7, which are chiral and belong to the C2 point group. Thus, the alignment vector û, if any, must be parallel to the two-fold rotation axis. The plot in Fig. 7 shows that thermo-orientation is absent for helices made of identical beads. On the contrary, 〈cos![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) θ〉Z is different from zero for helices having two heavier units in the middle (particles 6) or at the ends (particles 7). The order parameter is practically the same for R and L helices, as shown in Fig. 7 for the two enantiomorphs of particle 6, in agreement with the symmetry considerations presented in Section 2. In the figure we can also see that the order parameter has opposite sign for particles 6 and 7; in view of our definition of the BF, the signs correspond in both case to a preference to point the heavy beads towards the cold reservoir.
θ〉Z is different from zero for helices having two heavier units in the middle (particles 6) or at the ends (particles 7). The order parameter is practically the same for R and L helices, as shown in Fig. 7 for the two enantiomorphs of particle 6, in agreement with the symmetry considerations presented in Section 2. In the figure we can also see that the order parameter has opposite sign for particles 6 and 7; in view of our definition of the BF, the signs correspond in both case to a preference to point the heavy beads towards the cold reservoir.
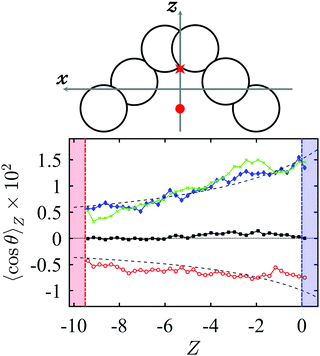 |
| | Fig. 7 (top) Helical particle with the body-fixed reference frame (BF), having its origin in the center of mass. The cartoon shows the case of particle 5, with the red star and circle indicating the position of the center of mass for particles 6 and 7, respectively. (bottom) Profiles of 〈cos![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) θ〉Z as a function of the Z-position across the simulation box, obtained from NEMD simulations of the helical particles 5R (black squares), 6R (blue diamonds), 6L (green crosses) and 7R (red open circles), at ∇ZT = −0.13, mean temperature θ〉Z as a function of the Z-position across the simulation box, obtained from NEMD simulations of the helical particles 5R (black squares), 6R (blue diamonds), 6L (green crosses) and 7R (red open circles), at ∇ZT = −0.13, mean temperature ![[T with combining macron]](https://www.rsc.org/images/entities/i_char_0054_0304.gif) = 1.3 and mean number density = 1.3 and mean number density ![[small rho, Greek, macron]](https://www.rsc.org/images/entities/i_char_e0d1.gif) = 0.09. θ is the angle between the z-axis of the BF and the Z-axis of the simulation box. The colored regions indicate the hot (red) and cold (blue) reservoir. = 0.09. θ is the angle between the z-axis of the BF and the Z-axis of the simulation box. The colored regions indicate the hot (red) and cold (blue) reservoir. | |
Summarizing the results of our simulations, we can say that thermo-orientation appears for particles of any shape, provided that they possess a polar distribution of mass density. As a general rule, particles exhibit a tendency to orient their more (less) dense parts towards the cold (hot) reservoir. Analogous considerations were reported for mass polar rods.16 One can see an analogy with electric polarization, which requires a nonuniform distribution of charge density in molecules. However, thermo-orientation is not directly related to the mass density; in fact, 〈cos![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) θ〉Z depends on the relative values of the mass of the beads of which a particle is made, but does not change if the mass of all the units is changed by the same factor. In agreement with previous studies,14,15 〈cos
θ〉Z depends on the relative values of the mass of the beads of which a particle is made, but does not change if the mass of all the units is changed by the same factor. In agreement with previous studies,14,15 〈cos![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) θ〉Z, for a given particle and given mean temperature and density, is proportional to the temperature gradient and its magnitude increases across the simulation box on moving from the hot to the cold reservoir.
θ〉Z, for a given particle and given mean temperature and density, is proportional to the temperature gradient and its magnitude increases across the simulation box on moving from the hot to the cold reservoir.
4 Microscopic model
4.1 Theoretical outline
In ref. 30 a mean field model was developed to explain the thermo-orientation of dimer particles, made of spherical beads of different diameter. The model relies on the assumption of local equilibrium, as recently proposed for thermophoresis.47–50 The microscopic mechanism was assumed to be essentially the same as in thermophoresis, with the torque exerted on an anisotropic particle due to a Soret force, which pushes the larger bead toward the warmer region. A simple form of the local effective potential experienced by a dimer in a thermal gradient was proposed, where each spherical bead contributes with a term proportional to its surface area:| | ![[scr V, script letter V]](https://www.rsc.org/images/entities/char_e149.gif) = −kBα(T1σ12 + T2σ22). = −kBα(T1σ12 + T2σ22). | (4) |
Here kB is the Boltzmann constant, σi is the diameter of ith bead, Ti is the temperature in the center of the ith bead and α is a parameter, with the dimension of an inverse square length, which accounts for the interaction of the particle with the surrounding environment. A positive (negative) value of α favors exposure of the larger (smaller) bead to the higher temperature.
We have reformulated the model in a more general form, suitable for particles of arbitrary shape and mass distribution. Considering that each point on the particle surface is at a different temperature, depending on its position, we generalise eqn (4) as
| | 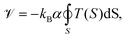 | (5) |
where the integral is over the particle surface and
T(
S) is the local temperature at a point on the surface.
Assuming the temperature gradient ∇ZT to be along the Z-axis of a laboratory frame of reference (LF), the temperature at a point on the particles surface, R′ = (X′,![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) Y′,
Y′,![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) Z′), is a function of its Z′-coordinate. If TZ is the temperature at the position of the center of mass of the particle, R = (X, Y, Z), the temperature at any point on the particle surface can be expressed as
Z′), is a function of its Z′-coordinate. If TZ is the temperature at the position of the center of mass of the particle, R = (X, Y, Z), the temperature at any point on the particle surface can be expressed as
| | | T(Z′) = TZ + (Z′ − Z)∇ZT. | (6) |
Substituting
eqn (6) into
eqn (5) we obtain
| | 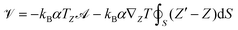 | (7) |
where
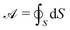
is the surface area of the particle. The second term in
eqn (7) depends on the molecular orientation, and to make explicit this dependence we introduce the BF, with its origin in the center of mass of the particle and the
z-axis parallel to the axis that preferentially aligns to the temperature gradient, see
Fig. 8. A point belonging to the particle surface has the coordinates
r = (
x,
![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) y
y,
![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) z
z) in BF, and we can write
| | (R′ − R) = ![[E with combining low line]](https://www.rsc.org/images/entities/b_char_0045_0332.gif) T·r, T·r, | (8) |
where
![[E with combining low line]](https://www.rsc.org/images/entities/b_char_0045_0332.gif) T
T is the transpose of the matrix for the rotation from LF to BF, defined in terms of the angles
θ, between the
Z and the
z axes, and
φ, describing the rotation around the molecular
z-axis (see
Fig. 8). Thus we obtain:
| | 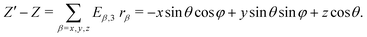 | (9) |
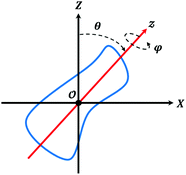 |
| | Fig. 8 Angles used to specify the orientation of a particle with respect to the temperature gradient along the Z axis. | |
Using eqn (6) and (9), the local effective potential experienced by a particle in the (θ, φ) orientation, with the center of mass at the Z-coordinate, can be expressed as
| | 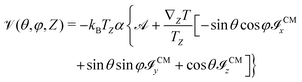 | (10) |
where
![[scr I, script letter I]](https://www.rsc.org/images/entities/char_e143.gif) CMt
CMt (
t =
x,
y,
z) is the surface integral
| | 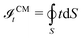 | (11) |
Here the subscript CM is used to stress that the origin of the reference frame coincides with the center of mass of the particle. For a shift of the origin,
r →
r′ =
r −
r0,
eqn (11) transforms as
| | 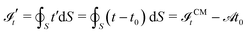 | (12) |
There is a special point, the centroid of the surface (CS) with coordinates
tCS = −
![[scr I, script letter I]](https://www.rsc.org/images/entities/char_e143.gif) t
t/
![[scr A, script letter A]](https://www.rsc.org/images/entities/char_e520.gif)
, such that
![[scr I, script letter I]](https://www.rsc.org/images/entities/char_e143.gif) t
t′ = 0. With reference to this point we can write:
| | ![[scr I, script letter I]](https://www.rsc.org/images/entities/char_e143.gif) CMt = CMt = ![[scr A, script letter A]](https://www.rsc.org/images/entities/char_e520.gif) tCS, tCS, | (13) |
and
eqn (10) can be rewritten as:
| | 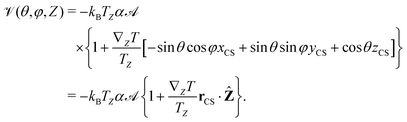 | (14) |
In the last line,
Ẑ is a unit vector parallel to the
Z axis of the Laboratory reference frame and
rCS is a vector from the center of mass to the centroid of the surface of the particle. In
eqn (14) we can distinguish an isotropic contribution and a term that depends on the particle orientation with respect to the temperature gradient. This is responsible for the thermo-orientation. The thermo-alignment axis of the particle is identified by the vector
rCS, which is defined by a geometric criterion. For
α > 0 the effective potential experienced by a particle attains its lowest value when the vector from the CM to the CS is parallel to the temperature gradient,
i.e. when the heavier part of the particle points towards the cold and the lighter part points towards the hot reservoir. This is in qualitative agreement with the results of NEMD simulations, described in the previous Section. One may notice a formal analogy of the second term of
eqn (14) with the interaction potential of an electric dipole with an electric field, with the vector
![[scr A, script letter A]](https://www.rsc.org/images/entities/char_e520.gif) rCS
rCS being here the particle property that couples to the the external field.
Under the assumption of local equilibrium, the local order parameter 〈cos![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) θ〉Z is evaluated by a Boltzmann average over all orientations of a particle with respect to the temperature gradient. Then, we can write:
θ〉Z is evaluated by a Boltzmann average over all orientations of a particle with respect to the temperature gradient. Then, we can write:
| | 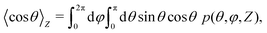 | (15) |
where
p(
θ,
φ,
Z) is the orientational-positional probability density:
| | 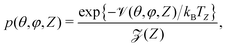 | (16) |
and the local orientational partition function is defined as
| | 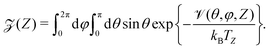 | (17) |
Since the exponent is much smaller than unity (as demonstrated by the low values of the order parameter), the exponential in the integrals can be approximated by the truncated Taylor expansion:
| | 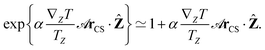 | (18) |
Using this expression in
eqn (15) and (17), we easily obtain:
| | 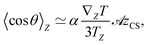 | (19) |
which is a generalization to particles of any shape and mass distribution of the result obtained in
ref. 30 for shape polar dimers. For non-polar particles, both the centroid of the surface and the center of mass coincide with the center of symmetry, then
zCS = 0. Therefore, no thermo-orientation is expected. For particles of
Cn,
Cnv (
n > 1) and
C∞v symmetry, the center of symmetry and the centroid of the surface lie on the
Cn or
C∞ rotation axis, whereas for less symmetric particles there are no symmetry constraints on the position of the centroid of the surface and of the center of mass. It can be easily shown that for the special case of shape polar dimers,
eqn (19) reduces to the expression obtained in
ref. 30.
Central to our model are the definition of centroid of the surface, which is a purely geometric parameter, and its non-coincidence with the center of mass. In a more physical sense, this can be intended as non-coincidence of center of mass and center of interaction in a particle. Such a concept underlies the requirement of shape or mass polarity for the thermo-orientation of dumbbell-like particles,14,15,30 and was exploited in the off-center Stockmeyer model used in ref. 23. The present model allows us to put the concept in quantitative terms, which may be important for our understanding of thermo-orientation, for the optimization of this effect and for the correlation with the results of numerical simulations (or experiments, if any).
4.2 Comparison with NEMD simulations
Fig. 9 shows the particles that we have investigated, with an arrow going from their center of mass (CM) to their centroid of surface (CS). Particles 2 and 5 are not shown because the two points coincide (rCS = 0); in fact these particles do not exhibit thermo-orientation. For particles of C∞v symmetry the vector rCS is parallel to the C∞ axis, whereas for particles of C2 or C2v symmetry it is parallel to the two-fold rotation axis. For particle 4, rCS is found to be tilted by ≈120° with respect to the bisector of the angle between the two arms, which is in good agreement with the value obtained from the simulations (χ ≈ 114°). The particles in Fig. 9 are shown in their preferred orientation in a temperature gradient.
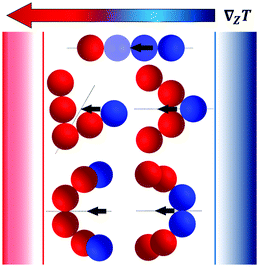 |
| | Fig. 9 Particles that in NEMD simulations show thermo-orientation, in their preferred orientation under a temperature gradient. The black arrow on each particle is parallel to the rCS vector and goes from the center of mass (CM) to the centroid of the surface (CS). The colored regions indicate the hot (red) and cold (blue) reservoir. | |
The profiles of 〈cos![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) θ〉Z obtained from NEMD simulations were fitted to eqn (19), with α as a fitting parameter. The value of zCS, the z-coordinate of the surface centroid in the BF, which has its origin at the center of mass and the centroid on the z-axis, was calculated from the geometry of each particle (see Appendix) and the effective particle surface was evaluated as
θ〉Z obtained from NEMD simulations were fitted to eqn (19), with α as a fitting parameter. The value of zCS, the z-coordinate of the surface centroid in the BF, which has its origin at the center of mass and the centroid on the z-axis, was calculated from the geometry of each particle (see Appendix) and the effective particle surface was evaluated as ![[scr A, script letter A]](https://www.rsc.org/images/entities/char_e520.gif) = nsπ (having assumed the reduced diameter of the beads equal to 1). The values of TZ and ∇ZT were taken from the simulations. The fitting results are shown by the dashed lines in Fig. 4–7 and we can see that the numerical trends are generally well predicted. Some more discrepancy is observed for the rod-like particle 1 at
= nsπ (having assumed the reduced diameter of the beads equal to 1). The values of TZ and ∇ZT were taken from the simulations. The fitting results are shown by the dashed lines in Fig. 4–7 and we can see that the numerical trends are generally well predicted. Some more discrepancy is observed for the rod-like particle 1 at ![[small rho, Greek, macron]](https://www.rsc.org/images/entities/i_char_e0d1.gif) = 0.13, which corresponds to a high mean volume fraction,
= 0.13, which corresponds to a high mean volume fraction, ![[small eta, Greek, macron]](https://www.rsc.org/images/entities/i_char_e0c8.gif) = 0.28.‡ In the investigated temperature range α was found to be scarcely dependent on the mean temperature and temperature gradient, which is an indication that the temperature dependence is reasonably well described by eqn (19). On the contrary, α exhibits a clear dependence on density. Table 2 collects the α values obtained from fitting 〈cos
= 0.28.‡ In the investigated temperature range α was found to be scarcely dependent on the mean temperature and temperature gradient, which is an indication that the temperature dependence is reasonably well described by eqn (19). On the contrary, α exhibits a clear dependence on density. Table 2 collects the α values obtained from fitting 〈cos![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) θ〉Z profiles. We can see that for a given particle α is an increasing function of the mean number density, but also the density gradient has an effect, as shown by the results reported in the Table for the helices 6 and 7. The comparison between particles of different shape shows that, at the same number density, α increases on moving from helices to V-shaped particles and from these to rods. This can be another indication of the limits of the model, due to the simple parameterization of the interaction potential in terms of the particle surface, and to the lack of an explicit account of the effects of density. In fact, the same number density corresponds to significantly different packing fractions for particles 1–7. These shortcomings could be particularly critical for non-convex bodies, as are most of the particles under investigation.
θ〉Z profiles. We can see that for a given particle α is an increasing function of the mean number density, but also the density gradient has an effect, as shown by the results reported in the Table for the helices 6 and 7. The comparison between particles of different shape shows that, at the same number density, α increases on moving from helices to V-shaped particles and from these to rods. This can be another indication of the limits of the model, due to the simple parameterization of the interaction potential in terms of the particle surface, and to the lack of an explicit account of the effects of density. In fact, the same number density corresponds to significantly different packing fractions for particles 1–7. These shortcomings could be particularly critical for non-convex bodies, as are most of the particles under investigation.
Table 2 For the particles showing thermo-orientation: zCS, the position of the centroid of surface in the body-fixed reference frame; ![[small rho, Greek, macron]](https://www.rsc.org/images/entities/i_char_e0d1.gif) , the mean number density and ∇Zρ, the gradient of number density; α, the interaction strength parameter obtained from fitting to eqn (19) of 〈cos
, the mean number density and ∇Zρ, the gradient of number density; α, the interaction strength parameter obtained from fitting to eqn (19) of 〈cos![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) θ〉Z profiles obtained from NEMD simulations (∇ZT = −0.13,
θ〉Z profiles obtained from NEMD simulations (∇ZT = −0.13, ![[T with combining macron]](https://www.rsc.org/images/entities/i_char_0054_0304.gif) = 1.3)
= 1.3)
| Particle |
z
CS
|
![[small rho, Greek, macron]](https://www.rsc.org/images/entities/i_char_e0d1.gif)
|
∇Zρ × 103 |
α × 102 |
|
∇ZT = −0.16.
|
|
1
|
−0.77 |
0.13 |
2.68 |
8.90 |
| 0.13 |
3.25 |
8.98a |
| 0.09 |
2.75 |
5.79 |
|
3
|
−0.37 |
0.11 |
1.76 |
6.35 |
| 0.09 |
1.70 |
4.78 |
|
4
|
−0.50 |
0.11 |
1.65 |
6.60 |
| 0.09 |
1.68 |
4.75 |
|
6R(L) |
−0.37 |
0.09 |
1.62 (1.64) |
4.12 (4.13) |
|
7R(L) |
0.35 |
0.09 |
1.04 (1.07) |
2.64 (2.61) |
A last comment concerns the sign of the interaction strength α. We have obtained positive values, which means that the interaction of a particle with its environment is stabilized by high temperature. Thus, particles tend to orient with the vector rCS parallel to the temperature gradient, which corresponds to the center of mass, i.e. the heavy beads, pointing towards the cold reservoir, as shown in Fig. 9. Our systems interact through a purely repulsive potential, but in simulations of dumbbell-like particles it was found that the thermo-orientation response is not strongly modified by the introduction of dispersion interactions.14,15 On the other hand, it may be worth mentioning that an off-center Stockmeyer fluid in a temperature gradient was found to orient with the center of mass pointing towards the hot reservoir.23
5 Conclusions
In this work, we have extended previous studies of thermo-orientation to fluids of particles of arbitrary shape and mass distribution. We have performed NEMD simulations for particles belonging to polar point groups which, based on symmetry considerations, are candidates for thermo-orientation. These simulations show that symmetry conditions are necessary, but not sufficient for the emergence of this effect. This is nicely illustrated by V-shaped particles with uniform mass density, which do not show thermo-orientation although their symmetry is compatible with this effect. We have examined also (polar) chiral particles and we have found no difference in the thermo-orientation of the two enantiomorphs, which is justified by symmetry considerations.
To rationalize the results of simulations we have generalized a microscopic model based on a local equilibrium hypothesis, which was recently proposed to explain the thermo-orientation of dimer particles made of two spherical beads of different diameter. We obtain a simple expression relating the average orientation of particles to what we can identify as the key property of particles in this context, i.e. the shift (rCS) from the center of mass to the centroid of the surface, which can be interpreted as the center of intermolecular interactions. Specifically, a particle tends to orient rCS parallel to the temperature gradient, which means that its heavier parts point towards the cold side. This model gives a criterion to interpret the thermo-orientation of particles of arbitrary shape, it allows us to predict the direction and strength of the effect and provides a semi-quantitative correlation with the results of numerical simulations.
Conflicts of interest
There are no conflicts to declare.
Appendix: centroid of the surface of a particle made of tangent spheres
For particles made of tangent spheres, the evaluation of the integral ![[scr I, script letter I]](https://www.rsc.org/images/entities/char_e143.gif) CMt (t = x, y, z), defined in eqn (11), is particularly simple since this can be decomposed as the sum of single sphere contributions:
CMt (t = x, y, z), defined in eqn (11), is particularly simple since this can be decomposed as the sum of single sphere contributions:| |  | (20) |
where ns is the number of spheres and ![[scr I, script letter I]](https://www.rsc.org/images/entities/char_e143.gif) CMt,i is the contribution of the ith sphere. In a reference frame with the origin at the center of this sphere,
CMt,i is the contribution of the ith sphere. In a reference frame with the origin at the center of this sphere,  , so using eqn (12) we obtain
, so using eqn (12) we obtain| | ![[scr I, script letter I]](https://www.rsc.org/images/entities/char_e143.gif) CMt,i = πtiσi2, CMt,i = πtiσi2, | (21) |
where σi is the diameter of the ith sphere and ti is a coordinate of the sphere center in a reference frame having its origin at the CM of the particle. Thus we can write| | 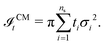 | (22) |
According to eqn (13) the coordinates of the centroid of the surface are given by:
| | 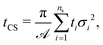 | (23) |
which in general will be different from the coordinates of the center of mass of the particle:
| | 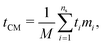 | (24) |
where
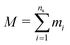
is mass of the particle. However, for identical spheres (
σi =
σ,
mi =
m,
![[scr A, script letter A]](https://www.rsc.org/images/entities/char_e520.gif)
=
nsπ
σ2) we obtain:
| | 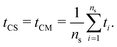 | (25) |
Notes and references
- S. Wiegand, J. Phys.: Condens. Matter, 2004, 16, R357 CrossRef CAS.
- C. Ludwig, Sitzber. Kaiserl. Akad. Wiss. Wien, Math. – Natwiss. Kl., 1856, 20, 539–540 Search PubMed.
- C. Soret, Arch. Sci. Phys. Nat., Genève, 1879, 2, 48–61 Search PubMed.
- W. Köhler, K. I. Morozov, G. Kronkalns, A. Mezulis, S. Kjelstrup and M. Z. Saghir, J. Non-Equilib. Thermodyn., 2016, 41, 348 Search PubMed.
- R. Piazza and A. Parola, J. Phys.: Condens. Matter, 2008, 20, 153102 CrossRef.
- A. Würger, Rep. Prog. Phys., 2010, 73, 126601 CrossRef.
- M. Jerabek-Willemsen, C. Wienken, D. Braun, P. Baaske and S. Duhr, Assay Drug Dev. Technol., 2011, 9, 342–353 CrossRef CAS.
- A. Würger, C. R. Mec., 2013, 341, 438–448 CrossRef.
- P. K. Jain, I. H. El-Sayed and M. A. El-Sayed, Nano Today, 2007, 2, 18–29 CrossRef.
- P. V. Ruijgrok, N. R. Verhart, P. Zijlstra, A. L. Tchebotareva and M. Orrit, Phys. Rev. Lett., 2011, 107, 037401 CrossRef CAS PubMed.
- L. Lin, E. H. Hill, X. Peng and Y. Zheng, Acc. Chem. Res., 2018, 5, 1465–1474 CrossRef.
- L. Shao and M. Käll, Adv. Funct. Mater., 2018, 28, 1706272 CrossRef.
- S. Merabia, S. Shenogin, L. Joly, P. Keblinksi and K. Barrat, Proc. Natl. Acad. Sci. U. S. A., 2009, 106, 15113–15118 CrossRef CAS PubMed.
- F. Romer, F. Bresme, J. Muscatello, D. Bedeaux and J. M. Rubi, Phys. Rev. Lett., 2012, 108, 105901 CrossRef PubMed.
- F. Romer and F. Bresme, Mol. Simul., 2012, 38, 1198–1208 CrossRef CAS.
- J. Olarte-Plata, J. M. Rubi and F. Bresme, Phys. Rev. E, 2018, 97, 052607 CrossRef PubMed.
- Z. Tan, M. Yang and M. Ripoll, Soft Matter, 2017, 13, 7283–7291 RSC.
- J. A. Armstrong and F. Bresme, J. Chem. Phys., 2013, 139, 1–10 CrossRef.
- J. Armstrong, A. Lervik and F. Bresme, J. Phys. Chem. B, 2013, 117, 14817–14826 CrossRef CAS.
- J. Armstrong and F. Bresme, Phys. Rev. E: Stat., Nonlinear, Soft Matter Phys., 2015, 92, 1–5 CrossRef.
- P. Wirnsberger, D. Fijan, A. Šarić, M. Neumann, C. Dellago and D. Frenkel, J. Chem. Phys., 2016, 144, 1–16 CrossRef.
- D. Frenkel, J. Phys. Chem. B, 2016, 50, 5987–5989 CrossRef.
- P. Wirnsberger, C. Dellago, D. Frenkel and A. Reinhardt, Phys. Rev. Lett., 2018, 120, 226001 CrossRef CAS.
- G. W. Stewart, J. Chem. Phys., 1936, 4, 231–236 CrossRef CAS.
- S. Sarman and A. Laaksonen, Phys. Chem. Chem. Phys., 2014, 16, 14741–14749 RSC.
- O. Lehmann, Ann. Phys., 1900, 5, 649–705 CrossRef.
- F. M. Leslie, Proc. R. Soc. London, Ser. A, 1968, 307, 359–372 CrossRef CAS.
- P. Oswald and A. Dequidt, Phys. Rev. Lett., 2008, 100, 217802 CrossRef.
- J. Yoshioka, F. Ito, Y. Suzuki, H. Takahashi, H. Takizawa and Y. Tabe, Soft Matter, 2014, 10, 5869–5877 RSC.
- A. A. Lee, Soft Matter, 2016, 12, 8661–8665 RSC.
- M. Yang, R. Liu, M. Ripoll and K. Chen, Nanoscale, 2014, 6, 13550–13554 RSC.
- P. Mineo, V. Villari, E. Scamporrino and N. Micali, J. Phys. Chem. B, 2015, 119, 12345–12353 CrossRef CAS.
-
F. A. Cotton, Chemical applications of group theory, Wiley, New York, 1990 Search PubMed.
- J. D. Weeks, D. Chandler and H. C. Andersen, J. Chem. Phys., 1971, 54, 5237–5247 CrossRef CAS.
-
M. P. Allen and D. J. Tildesley, Computer simulations of liquids, Oxford University Press, Oxford, 1989 Search PubMed.
- P. Wirnsberger, D. Frenkel and C. Dellago, J. Chem. Phys., 2015, 143, 124104 CrossRef CAS.
-
F. Bresme, A. Lervik and J. Armstrong, in Experimental Thermodynamics, Volume X: Non-equilibrium Thermodynamics with Applications, ed. D. Bedeaux, S. Kjelstrup and J. Sengers, RSC, Cambridge, 2016, ch. 6, pp. 105–133 Search PubMed.
- W. Ashurst and W. Hoove, Phys. Rev. A: At., Mol., Opt. Phys., 1975, 11, 658–678 CrossRef.
- A. Tenenbaum, G. Ciccotti and R. Gallico, Phys. Rev. A: At., Mol., Opt. Phys., 1982, 25, 2778–2787 CrossRef CAS.
- A. Tenenbaum, Phys. Rev. A: At., Mol., Opt. Phys., 1983, 28, 3132–3133 CrossRef CAS.
- T. Ikeshoji and B. Hafskjold, Mol. Phys., 1984, 81, 251–261 CrossRef.
- B. Hafskjold, T. Ikeshoji and S. K. Ratkje, Mol. Phys., 1993, 80, 1389–1412 CrossRef CAS.
- B. Hafskjold and T. Ikeshoji, Mol. Phys., 1994, 81, 251–261 CrossRef.
- S. Plimpton, J. Comput. Phys., 1995, 117, 1–19 CrossRef CAS.
- S. Nosé, J. Chem. Phys., 1984, 81, 511–519 CrossRef.
- W. G. Hoover, Phys. Rev. A: At., Mol., Opt. Phys., 1985, 31, 1695–1697 CrossRef.
- S. Duhr and D. Braun, Proc. Natl. Acad. Sci. U. S. A., 2006, 103, 19678–19682 CrossRef CAS PubMed.
- S. Duhr and D. Braun, Phys. Rev. Lett., 2006, 96, 168301 CrossRef.
- R. D. Astumian, Proc. Natl. Acad. Sci. U. S. A., 2007, 104, 3–4 CrossRef CAS.
- J. M. Sancho, J. Stat. Phys., 2018, 172, 1609–1616 CrossRef CAS.
Footnotes |
| † Particles belonging to these point groups have the following symmetry elements: a mirror plane for Cs; one n-fold rotation axis for Cn plus n additional mirror planes containing the n-fold axis for Cnv (n = ∞ or n integer). |
| ‡ The volume fraction is defined as η = v0ρ, where v0 is the volume of a particle. For our particles, made of ns beads with a reduced diameter equal to 1, v0 = ns(π/6). |
|
| This journal is © the Owner Societies 2019 |
Click here to see how this site uses Cookies. View our privacy policy here.  *
*
![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 33 Henceforth, we will denote as polar all particles belonging to these point groups, irrespective of the presence of an electric dipole. In particular, we will speak of shape- and mass-polarity, depending on whether polarity derives from the shape or from the mass distribution of the particle.
33 Henceforth, we will denote as polar all particles belonging to these point groups, irrespective of the presence of an electric dipole. In particular, we will speak of shape- and mass-polarity, depending on whether polarity derives from the shape or from the mass distribution of the particle.
![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) θ〉Z, where the subscript indicates that this is a local value at the Z-coordinate. For particles of Cn, Cnv and C∞v symmetry, the vector û is parallel to the Cn (n = 2, 3,…) or C∞ rotation axis. For particles of Cs symmetry û must lie on the reflection plane, whereas in the case of the point group C1 there are no symmetry constraints on the direction of û. In the absence of a temperature gradient all particle orientations are equiprobable and the order parameter vanishes, 〈cos
θ〉Z, where the subscript indicates that this is a local value at the Z-coordinate. For particles of Cn, Cnv and C∞v symmetry, the vector û is parallel to the Cn (n = 2, 3,…) or C∞ rotation axis. For particles of Cs symmetry û must lie on the reflection plane, whereas in the case of the point group C1 there are no symmetry constraints on the direction of û. In the absence of a temperature gradient all particle orientations are equiprobable and the order parameter vanishes, 〈cos![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) θ〉Z = 0. On the contrary, 〈cos
θ〉Z = 0. On the contrary, 〈cos![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) θ〉Z ≠ 0 when a temperature gradient is applied.
θ〉Z ≠ 0 when a temperature gradient is applied.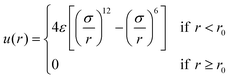

![[small rho, Greek, macron]](https://www.rsc.org/images/entities/i_char_e0d1.gif) . The number density is defined as ρ = N/Vbox, where N is the number of particles and Vbox is the volume of the simulation box. The figures show that in the region between the reservoirs the temperature exhibits a linear dependence on the Z-coordinate and the same occurs also for the number density, whose gradient is proportional to that of temperature, but opposite in sign. Analogous behaviour of the temperature and number density was obtained for all the systems under examination.
. The number density is defined as ρ = N/Vbox, where N is the number of particles and Vbox is the volume of the simulation box. The figures show that in the region between the reservoirs the temperature exhibits a linear dependence on the Z-coordinate and the same occurs also for the number density, whose gradient is proportional to that of temperature, but opposite in sign. Analogous behaviour of the temperature and number density was obtained for all the systems under examination.
![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) θ, where θ is the angle between the unit vector û, which identifies the thermo-alignment axis of particles and the Z-axis of the simulation box, which we have taken anti-parallel to the temperature gradient. For the rod-like particle 1, û is parallel to the C∞ rotation axis (see Fig. 4 – left) and points from the lighter to the heavier bead. Fig. 4 – middle shows the distribution of cos
θ, where θ is the angle between the unit vector û, which identifies the thermo-alignment axis of particles and the Z-axis of the simulation box, which we have taken anti-parallel to the temperature gradient. For the rod-like particle 1, û is parallel to the C∞ rotation axis (see Fig. 4 – left) and points from the lighter to the heavier bead. Fig. 4 – middle shows the distribution of cos![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) θ across the temperature gradient. In the simulation box there are two equivalent free evolution regions between the reservoirs (see Fig. 2); here and in the plots presented in the following only one Z-range is shown and the results displayed are the mean of the data in the two regions of the simulation box. In Fig. 4 – middle we can see that positive values of cos
θ across the temperature gradient. In the simulation box there are two equivalent free evolution regions between the reservoirs (see Fig. 2); here and in the plots presented in the following only one Z-range is shown and the results displayed are the mean of the data in the two regions of the simulation box. In Fig. 4 – middle we can see that positive values of cos![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) θ are more likely than negative ones at any position across the whole temperature range. This means that the rods preferentially orient their heavy end towards the cold reservoir, which is in agreement with the thermo-orientation effect reported for mass polar dimers in ref. 14. Fig. 4-right shows the corresponding profile of mean values, 〈cos
θ are more likely than negative ones at any position across the whole temperature range. This means that the rods preferentially orient their heavy end towards the cold reservoir, which is in agreement with the thermo-orientation effect reported for mass polar dimers in ref. 14. Fig. 4-right shows the corresponding profile of mean values, 〈cos![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) θ〉Z, calculated at different values of the mean number density
θ〉Z, calculated at different values of the mean number density ![[small rho, Greek, macron]](https://www.rsc.org/images/entities/i_char_e0d1.gif) and of the temperature gradient ∇ZT. The order parameter is small, yet different from zero and 2–3 times higher than that obtained for dimers under the same temperature gradient;14 as for dimers, it grows on moving from the hot to the cold reservoir and, for given mean temperature
and of the temperature gradient ∇ZT. The order parameter is small, yet different from zero and 2–3 times higher than that obtained for dimers under the same temperature gradient;14 as for dimers, it grows on moving from the hot to the cold reservoir and, for given mean temperature ![[T with combining macron]](https://www.rsc.org/images/entities/i_char_0054_0304.gif) and temperature gradient ∇ZT, shows an approximately linear increase with the mean density. The 〈cos
and temperature gradient ∇ZT, shows an approximately linear increase with the mean density. The 〈cos![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) θ〉Z profiles scale linearly with the temperature gradient, as in previous studies for dimers and in agreement with the prediction of nonequilibrium thermodynamics.14 The same behaviour was obtained also for the other systems investigated here. Also in line with the study of dimers, the order parameter was found to vanish for rod-like particles made of identical beads having the same mass.
θ〉Z profiles scale linearly with the temperature gradient, as in previous studies for dimers and in agreement with the prediction of nonequilibrium thermodynamics.14 The same behaviour was obtained also for the other systems investigated here. Also in line with the study of dimers, the order parameter was found to vanish for rod-like particles made of identical beads having the same mass.![[thin space (1/6-em)]](https://www.rsc.org/images/entities/i_char_2009.gif) θ〉Z displayed in Fig. 5 shows that particles 2, which are made of beads with identical mass, do not exhibit thermo-orientation (black squares). The same result was found for any V-shaped particle made of identical beads with equal mass, irrespective of geometric parameters, such as bend angle and length of the two arms, and of the thermodynamic conditions. This demonstrates that polar symmetry is necessary, but not sufficient for thermo-orientation. Conversely, the 〈cos
θ〉Z displayed in Fig. 5 shows that particles 2, which are made of beads with identical mass, do not exhibit thermo-orientation (black squares). The same result was found for any V-shaped particle made of identical beads with equal mass, irrespective of geometric parameters, such as bend angle and length of the two arms, and of the thermodynamic conditions. This demonstrates that polar symmetry is necessary, but not sufficient for thermo-orientation. Conversely, the 〈cos![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) θ〉Z profiles for particles 3, in which the central bead has a mass different from the other beads, indicate the presence of a preferred orientation (blue diamonds and red open circles in Fig. 5). The magnitude of thermo-orientation is a little smaller than that of the rod-like particles 1, yet clearly different from zero. The order parameter is positive, which means that particles 3 preferentially orient their heavy unit towards the cold region. As for the rod-like particle 1, the value of 〈cos
θ〉Z profiles for particles 3, in which the central bead has a mass different from the other beads, indicate the presence of a preferred orientation (blue diamonds and red open circles in Fig. 5). The magnitude of thermo-orientation is a little smaller than that of the rod-like particles 1, yet clearly different from zero. The order parameter is positive, which means that particles 3 preferentially orient their heavy unit towards the cold region. As for the rod-like particle 1, the value of 〈cos![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) θ〉Z increases on moving from the hot to the cold reservoir and, for given mean temperature and temperature gradient, it increases approximately linearly with the mean density.
θ〉Z increases on moving from the hot to the cold reservoir and, for given mean temperature and temperature gradient, it increases approximately linearly with the mean density.![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) θ1〉Z and 〈cos
θ1〉Z and 〈cos![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) θ2〉Z, where θ1 and θ2 are the angles between the Z-axis and the axes (x′, z′) of a body-fixed reference frame, which is defined as shown in the cartoon on top of the figure. From 〈cos
θ2〉Z, where θ1 and θ2 are the angles between the Z-axis and the axes (x′, z′) of a body-fixed reference frame, which is defined as shown in the cartoon on top of the figure. From 〈cos![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) θ1〉Z (red crosses) and 〈cos
θ1〉Z (red crosses) and 〈cos![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) θ2〉Z (green open squares) we can calculate the orientation of the unit vector û, which defines the thermo-alignment direction of the particle, and the average projection of û on the Z-axis, based on the following considerations. Let us call χ the rotation angle from the x′, z′-axes to the x, z-axes of a reference frame (BF), having z‖û. Since û = sin
θ2〉Z (green open squares) we can calculate the orientation of the unit vector û, which defines the thermo-alignment direction of the particle, and the average projection of û on the Z-axis, based on the following considerations. Let us call χ the rotation angle from the x′, z′-axes to the x, z-axes of a reference frame (BF), having z‖û. Since û = sin![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) χ
χ![[x with combining circumflex]](https://www.rsc.org/images/entities/b_char_0078_0302.gif) + cos
+ cos![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) χẑ, we can write:
χẑ, we can write:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) θ〉Z = sin
θ〉Z = sin![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) χ〈cos
χ〈cos![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) θ1〉Z + cos
θ1〉Z + cos![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) χ〈cos
χ〈cos![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) θ2〉Z.
θ2〉Z.![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) χ〈cos
χ〈cos![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) θ1〉Z − sin
θ1〉Z − sin![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) χ〈cos
χ〈cos![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) θ2〉Z,
θ2〉Z,![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) θ1〉Z)/(〈cos
θ1〉Z)/(〈cos![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) θ2〉Z). Using the values of 〈cos
θ2〉Z). Using the values of 〈cos![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) θ1〉Z and 〈cos
θ1〉Z and 〈cos![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) θ2〉Z shown in Fig. 6 we obtain χ ≈ 114°; substituting this value in eqn (2) we calculate the profile of 〈cos
θ2〉Z shown in Fig. 6 we obtain χ ≈ 114°; substituting this value in eqn (2) we calculate the profile of 〈cos![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) θ〉Z that is reported in the same Fig. 6 (blue circles). The magnitude of thermo-orientation is similar to that of particle 3, and also in this case the positive value of 〈cos
θ〉Z that is reported in the same Fig. 6 (blue circles). The magnitude of thermo-orientation is similar to that of particle 3, and also in this case the positive value of 〈cos![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) θ〉Z indicates that particle 4 preferentially orients with its heavy bead pointing towards the cold reservoir.
θ〉Z indicates that particle 4 preferentially orients with its heavy bead pointing towards the cold reservoir.
![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) θ〉Z is different from zero for helices having two heavier units in the middle (particles 6) or at the ends (particles 7). The order parameter is practically the same for R and L helices, as shown in Fig. 7 for the two enantiomorphs of particle 6, in agreement with the symmetry considerations presented in Section 2. In the figure we can also see that the order parameter has opposite sign for particles 6 and 7; in view of our definition of the BF, the signs correspond in both case to a preference to point the heavy beads towards the cold reservoir.
θ〉Z is different from zero for helices having two heavier units in the middle (particles 6) or at the ends (particles 7). The order parameter is practically the same for R and L helices, as shown in Fig. 7 for the two enantiomorphs of particle 6, in agreement with the symmetry considerations presented in Section 2. In the figure we can also see that the order parameter has opposite sign for particles 6 and 7; in view of our definition of the BF, the signs correspond in both case to a preference to point the heavy beads towards the cold reservoir.![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) θ〉Z depends on the relative values of the mass of the beads of which a particle is made, but does not change if the mass of all the units is changed by the same factor. In agreement with previous studies,14,15 〈cos
θ〉Z depends on the relative values of the mass of the beads of which a particle is made, but does not change if the mass of all the units is changed by the same factor. In agreement with previous studies,14,15 〈cos![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) θ〉Z, for a given particle and given mean temperature and density, is proportional to the temperature gradient and its magnitude increases across the simulation box on moving from the hot to the cold reservoir.
θ〉Z, for a given particle and given mean temperature and density, is proportional to the temperature gradient and its magnitude increases across the simulation box on moving from the hot to the cold reservoir.![[scr V, script letter V]](https://www.rsc.org/images/entities/char_e149.gif) = −kBα(T1σ12 + T2σ22).
= −kBα(T1σ12 + T2σ22).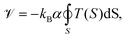
![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) Y′,
Y′,![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) Z′), is a function of its Z′-coordinate. If TZ is the temperature at the position of the center of mass of the particle, R = (X, Y, Z), the temperature at any point on the particle surface can be expressed as
Z′), is a function of its Z′-coordinate. If TZ is the temperature at the position of the center of mass of the particle, R = (X, Y, Z), the temperature at any point on the particle surface can be expressed as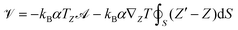
 is the surface area of the particle. The second term in eqn (7) depends on the molecular orientation, and to make explicit this dependence we introduce the BF, with its origin in the center of mass of the particle and the z-axis parallel to the axis that preferentially aligns to the temperature gradient, see Fig. 8. A point belonging to the particle surface has the coordinates r = (x,
is the surface area of the particle. The second term in eqn (7) depends on the molecular orientation, and to make explicit this dependence we introduce the BF, with its origin in the center of mass of the particle and the z-axis parallel to the axis that preferentially aligns to the temperature gradient, see Fig. 8. A point belonging to the particle surface has the coordinates r = (x, ![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) y,
y, ![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) z) in BF, and we can write
z) in BF, and we can write![[E with combining low line]](https://www.rsc.org/images/entities/b_char_0045_0332.gif) T·r,
T·r,![[E with combining low line]](https://www.rsc.org/images/entities/b_char_0045_0332.gif) T is the transpose of the matrix for the rotation from LF to BF, defined in terms of the angles θ, between the Z and the z axes, and φ, describing the rotation around the molecular z-axis (see Fig. 8). Thus we obtain:
T is the transpose of the matrix for the rotation from LF to BF, defined in terms of the angles θ, between the Z and the z axes, and φ, describing the rotation around the molecular z-axis (see Fig. 8). Thus we obtain: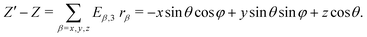

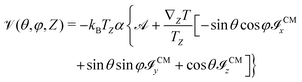
![[scr I, script letter I]](https://www.rsc.org/images/entities/char_e143.gif) CMt (t = x, y, z) is the surface integral
CMt (t = x, y, z) is the surface integral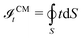
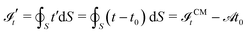
![[scr I, script letter I]](https://www.rsc.org/images/entities/char_e143.gif) t/
t/![[scr A, script letter A]](https://www.rsc.org/images/entities/char_e520.gif) , such that
, such that ![[scr I, script letter I]](https://www.rsc.org/images/entities/char_e143.gif) t′ = 0. With reference to this point we can write:
t′ = 0. With reference to this point we can write:![[scr I, script letter I]](https://www.rsc.org/images/entities/char_e143.gif) CMt =
CMt = ![[scr A, script letter A]](https://www.rsc.org/images/entities/char_e520.gif) tCS,
tCS,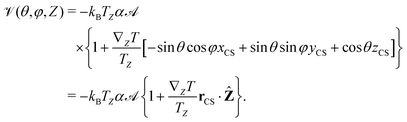
![[scr A, script letter A]](https://www.rsc.org/images/entities/char_e520.gif) rCS being here the particle property that couples to the the external field.
rCS being here the particle property that couples to the the external field.
![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) θ〉Z is evaluated by a Boltzmann average over all orientations of a particle with respect to the temperature gradient. Then, we can write:
θ〉Z is evaluated by a Boltzmann average over all orientations of a particle with respect to the temperature gradient. Then, we can write: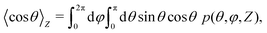
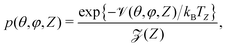
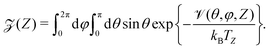
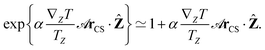
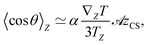
![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) θ〉Z obtained from NEMD simulations were fitted to eqn (19), with α as a fitting parameter. The value of zCS, the z-coordinate of the surface centroid in the BF, which has its origin at the center of mass and the centroid on the z-axis, was calculated from the geometry of each particle (see Appendix) and the effective particle surface was evaluated as
θ〉Z obtained from NEMD simulations were fitted to eqn (19), with α as a fitting parameter. The value of zCS, the z-coordinate of the surface centroid in the BF, which has its origin at the center of mass and the centroid on the z-axis, was calculated from the geometry of each particle (see Appendix) and the effective particle surface was evaluated as ![[scr A, script letter A]](https://www.rsc.org/images/entities/char_e520.gif) = nsπ (having assumed the reduced diameter of the beads equal to 1). The values of TZ and ∇ZT were taken from the simulations. The fitting results are shown by the dashed lines in Fig. 4–7 and we can see that the numerical trends are generally well predicted. Some more discrepancy is observed for the rod-like particle 1 at
= nsπ (having assumed the reduced diameter of the beads equal to 1). The values of TZ and ∇ZT were taken from the simulations. The fitting results are shown by the dashed lines in Fig. 4–7 and we can see that the numerical trends are generally well predicted. Some more discrepancy is observed for the rod-like particle 1 at ![[small rho, Greek, macron]](https://www.rsc.org/images/entities/i_char_e0d1.gif) = 0.13, which corresponds to a high mean volume fraction,
= 0.13, which corresponds to a high mean volume fraction, ![[small eta, Greek, macron]](https://www.rsc.org/images/entities/i_char_e0c8.gif) = 0.28.‡ In the investigated temperature range α was found to be scarcely dependent on the mean temperature and temperature gradient, which is an indication that the temperature dependence is reasonably well described by eqn (19). On the contrary, α exhibits a clear dependence on density. Table 2 collects the α values obtained from fitting 〈cos
= 0.28.‡ In the investigated temperature range α was found to be scarcely dependent on the mean temperature and temperature gradient, which is an indication that the temperature dependence is reasonably well described by eqn (19). On the contrary, α exhibits a clear dependence on density. Table 2 collects the α values obtained from fitting 〈cos![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) θ〉Z profiles. We can see that for a given particle α is an increasing function of the mean number density, but also the density gradient has an effect, as shown by the results reported in the Table for the helices 6 and 7. The comparison between particles of different shape shows that, at the same number density, α increases on moving from helices to V-shaped particles and from these to rods. This can be another indication of the limits of the model, due to the simple parameterization of the interaction potential in terms of the particle surface, and to the lack of an explicit account of the effects of density. In fact, the same number density corresponds to significantly different packing fractions for particles 1–7. These shortcomings could be particularly critical for non-convex bodies, as are most of the particles under investigation.
θ〉Z profiles. We can see that for a given particle α is an increasing function of the mean number density, but also the density gradient has an effect, as shown by the results reported in the Table for the helices 6 and 7. The comparison between particles of different shape shows that, at the same number density, α increases on moving from helices to V-shaped particles and from these to rods. This can be another indication of the limits of the model, due to the simple parameterization of the interaction potential in terms of the particle surface, and to the lack of an explicit account of the effects of density. In fact, the same number density corresponds to significantly different packing fractions for particles 1–7. These shortcomings could be particularly critical for non-convex bodies, as are most of the particles under investigation.![[small rho, Greek, macron]](https://www.rsc.org/images/entities/i_char_e0d1.gif) , the mean number density and ∇Zρ, the gradient of number density; α, the interaction strength parameter obtained from fitting to eqn (19) of 〈cos
, the mean number density and ∇Zρ, the gradient of number density; α, the interaction strength parameter obtained from fitting to eqn (19) of 〈cos![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) θ〉Z profiles obtained from NEMD simulations (∇ZT = −0.13,
θ〉Z profiles obtained from NEMD simulations (∇ZT = −0.13, ![[T with combining macron]](https://www.rsc.org/images/entities/i_char_0054_0304.gif) = 1.3)
= 1.3)
![[scr I, script letter I]](https://www.rsc.org/images/entities/char_e143.gif) CMt (t = x, y, z), defined in eqn (11), is particularly simple since this can be decomposed as the sum of single sphere contributions:
CMt (t = x, y, z), defined in eqn (11), is particularly simple since this can be decomposed as the sum of single sphere contributions:
![[scr I, script letter I]](https://www.rsc.org/images/entities/char_e143.gif) CMt,i is the contribution of the ith sphere. In a reference frame with the origin at the center of this sphere,
CMt,i is the contribution of the ith sphere. In a reference frame with the origin at the center of this sphere,  , so using eqn (12) we obtain
, so using eqn (12) we obtain![[scr I, script letter I]](https://www.rsc.org/images/entities/char_e143.gif) CMt,i = πtiσi2,
CMt,i = πtiσi2,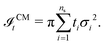
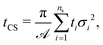
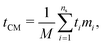
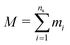 is mass of the particle. However, for identical spheres (σi = σ, mi = m,
is mass of the particle. However, for identical spheres (σi = σ, mi = m, ![[scr A, script letter A]](https://www.rsc.org/images/entities/char_e520.gif) = nsπσ2) we obtain:
= nsπσ2) we obtain: