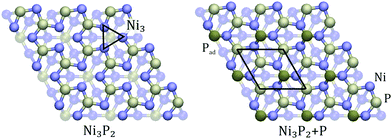Hydrogen adsorption trends on various metal-doped Ni2P surfaces for optimal catalyst design†
Lauri
Partanen
 ,
Mikko
Hakala
,
Mikko
Hakala
 and
Kari
Laasonen
and
Kari
Laasonen
 *
*
Department of Chemistry and Materials Science, Aalto University, P.O. Box 16100, FI-00076 Aalto, Finland. E-mail: kari.laasonen@aalto.fi
First published on 28th November 2018
Abstract
In this study, we looked at the hydrogen evolution reaction on Mg-, Mo-, Fe-, Co-, V-, and Cu-doped Ni3P2 and Ni3P2 + P terminated Ni2P surfaces. The DFT calculated hydrogen adsorption free energy was employed as a predictor of the materials' catalytic HER activity. Our results indicate that doping can substantially improve the catalytic activity of the Ni3P2 terminated surface. In contrast, the Ni3P2 + P terminated one seems to be catalytically active irrespective of the type of doping, including in the absence of doping. Based on our doping energy and adsorption free energy calculations, the most promising dopants are iron and cobalt, whereas copper is less likely to function well as a doping element.
1 Introduction
Due to the broad-ranging detrimental climate effects associated with the burning of fossil fuels, the impending rise in the global population, and the consequent increase in energy demand, the development of cleaner energy sources has become a top priority within the scientific community.1–3 However, the intermittent nature of solar and wind energies means that an efficient storage system is required to realise their potential.1,2 The absence of carbon emissions during conversion, high energy density, long-term storage capability, and flexibility of use both in mobile and stationary applications make hydrogen an appealing energy depository.4 One of the most promising candidates for large-scale hydrogen production is water-splitting through electrolysis, which enables the clean conversion of water into hydrogen and oxygen gases.3,5The hydrogen evolution reaction (HER) occurs at the cathode of a water-splitting cell, while the four-electron oxygen evolution reaction (OER) takes place at the anode. Hydrogen production through reduction (i.e., 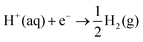 ) is a two-step process where two alternative reaction pathways are typically considered.6 Both pathways start with the Volmer reaction, where hydrogen adsorbs on a surface site symbolised by an asterisk *:
) is a two-step process where two alternative reaction pathways are typically considered.6 Both pathways start with the Volmer reaction, where hydrogen adsorbs on a surface site symbolised by an asterisk *:
| H+(aq) + e− + * → *H. | (1) |
| *H + *H → H2(g) + 2*, | (2) |
| *H + H+(aq) + e− → H2(g) + *. | (3) |
Irrespective of the exact reaction mechanism, efficient catalysts are mandatory for turning the dream of a hydrogen energy economy into reality. While noble metals like Pt are some of the best HER catalysts, their high cost and scarcity hinder large-scale application.3 Thus, recent studies have looked at HER on various non-precious materials like heteroatom-doped nano-carbons,7–10 together with nitrides, oxides, carbides, selenides, and sulfides of transition metals,7 which could replace platinum as the principal HER catalysts.
Compared to the other transition metal compounds, phosphides like MoP, CoP, and Ni2P display HER activities on par with the best transition metal catalyst like MoS2.7,11–13 Generally speaking, phosphides possess advantages either in terms of synthesis routes or catalytic performance over the other classes of transition metal compounds. For example, MoS2 needs to be nanostructured into nanosheets to yield catalytic properties comparable to MoP,7,14 which can show high HER ability even in its bulk state.15 Particularly, nickel phosphide nanostructures like nanosheets and -particles have emerged as promising materials for HER catalysis under acidic conditions.7,11,12,16–18
Chemical doping provides a novel way of enhancing the catalytic activity of many of the non-noble metal catalysts.7 In the case of Ni2P, transition metal dopants such as Mo,19 Al,20 Mn,21 W,22 and Fe23,24 have been experimentally demonstrated to improve the HER activity. On the computational side, in our previous density functional theory (DFT) study of transition metal doping of a MoS2 surface, we showed that the H-adsorption strength in the Volmer step depends on the microscopic structure of the surface and the nature of the dopant.25 A similar result regarding the microscopic nature of the surface was observed in our computational study of aluminium doping on Ni2P.26
In this article, we expand our previous investigation of the impact of Al doping on the HER activity of Ni2P26 to include the dopants Mg, Mo, Fe, Co, V and Cu. As before, we focus on the two most stable Ni2P surface terminations: Ni3P2 and phosphorised Ni3P2 + P.27,28 We utilise the typical hydrogen adsorption free energy (ΔGH) approach for HER activity, which has also been employed in previous Ni–P studies.26,29 In this approach, ΔGH on the electrode surface is used as a descriptor for predicting the catalytic activity with respect to a molecular H2(g) reference.6 In line with Sabatier's principle, a value ΔGH ≈ 0 indicates that the hydrogen neither binds too weakly nor too strongly to the surface, and corresponds to good HER activity.30 As, for example, the choice of DFT functional affects the ΔGH values,26 following Greeley et al.30 we consider sites with |ΔGH| < 0.1 eV as optimal. Our primary goal is to understand how different dopants and doping induced surface structures impact HER activity and to suggest doping schemes that result in improved catalysts.
2 Systems and methods
2.1 Computational details
All our DFT calculations utilised the QUICKSTEP module31 of the publicly available CP2K simulation suite.32 The package employs the hybrid Gaussian/plane wave method where the wave functions are represented in a Gaussian-type basis and an auxiliary plane-wave basis is used for the electronic density. As in our previous Ni2P and MoS2 studies,25,26 the Perdew–Burke–Ernzerhof (PBE) functional33 was used with the Kohn–Sham orbitals expanded in the molecularly-optimised double-valence polarised basis set (MOLOPT-SR-DZVP) and the core electrons represented by the Goedecker–Teter–Hutter pseudopotentials (GTH).34–36 In all calculations, the plane-wave kinetic energy cut-off was set to 700 Ry and the cutoff for the reference grid to 60 Ry. The force convergence criterion of the geometry optimisations was left to its default value of 0.023 eV Å−1. The Poisson equation for the electrostatic potential was solved with periodic boundary conditions.The Ni2P bulk lattice parameters were taken from our previous study,26 where a supercell of 4 × 4 × 4 unit cells was allowed to relax under a 0.1 kbar pressure tolerance. The system relaxed to a nonferromagnetic state with cell parameters a = b = 5.860 Å and c = 3.332 Å. For the calculation of the atomic reference energies of Ni, Mg, Mo, Fe, Co, Cu, and V in the crystalline phase, we employed a supercell of 10 × 10 × 10 units with the PBE lattice parameters taken from the literature.37–40 Our original Ni2P calculation employed the orbital transformation method, whereas in the reference energy calculation the diagonalisation method was used with the Fermi temperature set to 75 K. The effect of increasing this temperature to 300 and 400 K was studied but the impact on the energy/atom was less than 0.02 eV in all cases.
Our surface calculations used the same diagonalisation method with a 75 K electronic smearing but included the Grimme D3(BJ) dispersion corrections.41,42 Of the different surface structures for Ni2P, we focused on the Ni3P2 termination of the (0001) surface because it is the preferred bulk-like termination in the Ni2P stability region.27,43 At around pH = 0, which corresponds to the typical experimental conditions for HER in acid, this surface phase dominates at potentials U > −0.21 V vs. the standard hydrogen electrode.28 Below this region, there is both experimental and computational evidence that the surface becomes enriched by phosphorus.27,28,44–49 Specifically, the Ni3P2 + P termination predominates within the potential region −0.21 V ≥ U ≥ −0.36 V, whereas below this range the pristine Ni3P2 surface becomes passivated by H atoms on the Ni3 hollow sites.28 Hence, both Ni3P2 and Ni3P2 + P surfaces were included in this study.
Based on our previous hydrogen adsorption free energy test calculations on 5, 7, 9, 11, and 13 layer slabs,26 we modelled our two surfaces with a seven layers deep symmetric slab where the atoms at the bottom layer were fixed to their bulk positions. At least a 10 Å wide vacuum layer was used on both sides of the slab. For Ni3P2 + P, the extra phosphorus atom was added to the Ni3 hollow site of the Ni3P2 structure, as depicted in Fig. 1. In both cases, 5 × 5 × 1 Monkhorst–Pack k-points were utilised.
2.2 HER activity model
Our analysis of the H-coverage and differential Gibbs free energies of the H-adsorption followed the self-consistent scheme proposed by Nørskov et al.6 and Skúlason et al.50 According to this scheme, the relevant H coverage at a particular chemical potential μ is determined by the minimum of the total adsorption energy ΔtotGH(n):| ΔtotGH(n) = G(n) − G(0) − nμ | (4) |
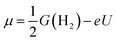 | (5) |
| ΔGH(n) = G(n) − G(n − 1) − μ, | (6) |
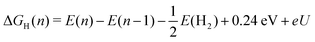 | (7) |
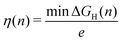 | (8) |
3 Results and discussion
As illustrated in Fig. 2, the Ni3P2 terminated Ni2P surface has alternating Ni3P2 and Ni3P layers.52,53 The dopant atoms were restricted to the top four layers. To identify the different doping schemes, the notation lxdy is used where x is the layer of the dopant atoms (i.e. x ∈ {1, 2, 3, 4}) and y is their number (i.e. y ∈ {1, 2, 3}). In cases where dopants were present in two layers, we employ the simpler notation lx1lx2, where x1 and x2 tell the layers of the two dopant atoms, respectively, since we only investigated cases with one dopant atom per layer.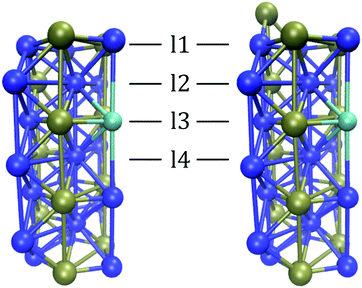 | ||
| Fig. 2 The slab model for the Ni3P2 and Ni3P2 + P terminated Ni2P surface. In the figure, the third layer is doped by a single metal atom which corresponds to an l3d1 doping scheme. | ||
3.1 Doping energies
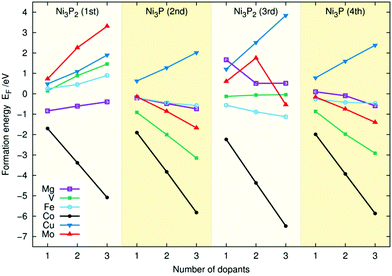 | ||
| Fig. 3 Doping energies (EF) for Mg, V, Fe, Co, Cu, and Mo for the four topmost layers of the Ni3P2 termination of Ni2P. | ||
The large deviations from linear behaviour for Mo and Mg in the third layer are accompanied by radical surface reconstructions. For example, in the double and triple doping for Mg and the triple doping in Mo, one of the P atoms moves away from the third Ni3P2 layer, creating a vacancy and a surface structure that resembles the Ni3P2 + P one. In most cases, the introduction of dopants causes no substantial changes in geometry. For Fe and Co, it results in a slight contraction of the slab with the magnitude generally depending on the number of dopants, and for the other metals a slight expansion. Interestingly, for first layer Mg doping, the Mg atoms lift up from the surface, staying more than 0.6 Å above the corresponding Ni atoms. Similarly, for the triple Mo doping of the first layer, the atoms of the two topmost layers of the Ni2P surface lift up from the surface, while the P atom from the first layer moves down to the second one.
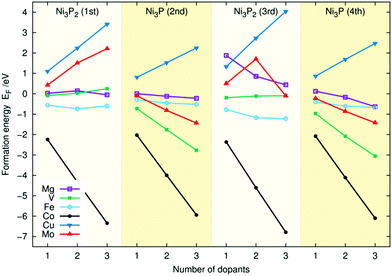 | ||
| Fig. 4 Doping energies (EF) for Mg, V, Fe, Co, Cu, and Mo for the four topmost layers of the Ni3P2 + P termination of Ni2P. | ||
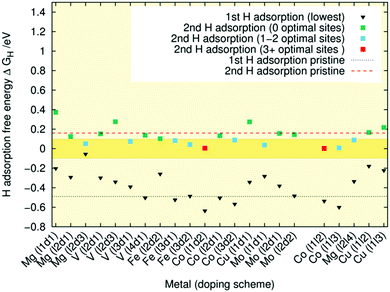
Comparing the linear trends of different dopants in Fig. 3 and 4, one sees that for Mo, V, Co, and Fe the doping energies are higher for the first layer for Ni3P2 termination whereas for Cu, and Mg the energies are lower. Unsurprisingly, in the lower layers, the doping energies are similar. Based on the figures, we predict that Ni2P should be readily dopable by Co, Fe, V, Mg, and Mo. In contrast, for Cu, the doping is clearly energetically unfavourable in all cases, and according to our test calculations inserting two Cu atoms to different layers does not remedy the situation.
3.2 Hydrogen adsorption free energies
Aligned with previous studies on pristine and Al-doped Ni3P2 surfaces,26,28,54 we find a strongly binding Ni3-hollow site together with a number of more weakly binding sites. In most studied surfaces, the first hydrogen is found in the Ni3 deep site with the exception of Mg where it is located on the Ni–Ni bridge of the Ni3 site. In these three bridge configurations, the closer the hydrogen is to the centre of the Ni3 site (or in the case of Mg (l1d1) the Ni2Mg site) the lower the ΔGH-value. In addition to the Mg-doped cases, also the l1d2 Co doping had the hydrogen localise to a Co–Co bridge site for the lowest free energy configuration. As the H also moved towards the Ni-atoms from the centre of the Ni3 site for the l1d1 doping with Cu and Mo, we conclude that the prevalent adsorption pattern of H on the strongly binding Ni3 hollow site is most perturbed by substitutional doping of the first layer, at least in low doping conditions. This is in agreement with the results of Hakala and Laasonen who observed that low Al doping of the surface layer effectively weakened the hollow site's binding energy, resulting in H coordination by just two Ni atoms.26
Recently, Wexler et al.55 were able to show that the effect of nonmetal surface doping of the P atoms surrounding the Ni3 site on a Ni3P2 surface can be explained through a chemical pressure-like effect.56 Consequently, the hollow site Ni–Ni bond length works as a good predictor of the ΔGH value. We also looked at the correlation between these two quantities, but it was not significant in our data, likely because the electronic character of the dopants is more significant at least in the first layer, where the Ni atoms of the hollow site are directly substituted.
The coloured squares in Fig. 5 represent the best, i.e., closest to zero ΔGH values for the second hydrogen adsorption with the H-atom corresponding to the lowest adsorption free energy already on the surface. The colour indicates the number of geometrically different sites that fall into the ideal ΔGH-region. We see that for the Ni3P2 termination, Fe and Co doping seems to be particularly effective with plenty of sites in the optimal region for the tested doping schemes. These findings agree with the experimental results on the activating effects of Fe doping.23,24 In concordance with the predictions of the doping energies of Fig. 3, Cu seems to be rather ineffective as a catalyst while the rest of the studied dopants fall somewhere in between. Looking at the V (l4d1) and Mg (l2l4) cases, one sees that inserting dopants to the fourth layer has minimal impact on the adsorption energies. Unsurprisingly, the doping effects on the adsorption free energies generally increase when one moves from the third layer to the second and first ones.
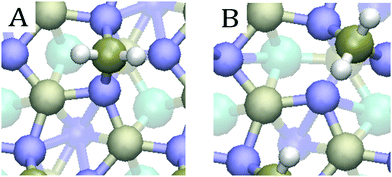
As for the first hydrogen, a number of different adsorption patterns were observed for the second hydrogen. In most cases, the initial hydrogen occupied the hollow Ni3 site whereas the second hydrogen was located on a nearby Ni–P bridge site. This bonding pattern agrees with the findings of Liu and Rodriguez54 for the pristine surface. For Mo- and Mg-doped materials showing ideal sites, both hydrogens were located on bridges. In the l1d2-doped Co, we also encountered an energetically favourable configuration where a hydrogen molecule was formed on top of one of the surface Co atoms. The different bonding patterns are illustrated in Fig. 6 for Co (l1d2).
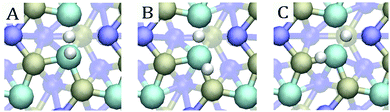 | ||
| Fig. 6 Sample hydrogen adsorption patterns observed in the Co (l1d2) surface: (A) H2 formation, (B) Co–Co and Co–P bridge site hydrogens, and (C) Co2Ni hollow site and Co–P bridge site hydrogens. | ||
Because Hakala and Laasonen26 found that increasing the supercell surface area did not impact the H-adsorption energies, its effect was not investigated in this study. They also tested how changing the PBE functional to RPBE57 and turning off the van der Waals interaction affected the ΔGH values, and found that while the RPBE slightly weakened H binding, the effect of the van der Waals correction was minuscule.26
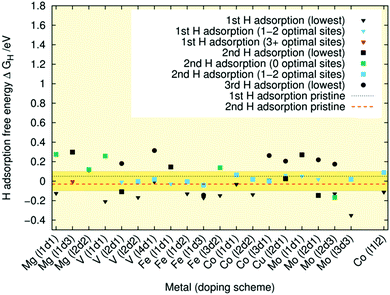
Because the strongly binding Ni3 site is occupied by the P adatom in Ni3P2 + P, for some doping schemes in Fig. 7, the first hydrogen adsorption already results in the best observed ΔGH value as indicated by the coloured triangle. Within the accuracy of the DFT calculations, this agrees with the pristine Ni3P2 + P results indicated by the dashed lines and implies that the surface hydrogen coverage is often lower for this termination.
As expected, doping of the fourth layer in V (l4d1) has virtually no effect on the ΔGH values when compared to the pristine case. Following the trends found in Fig. 5, doping of the Ni atoms in layer 3 generally impacts the adsorption free energies less than doping at the second or first layers, although the effects become large also at the third layer when the number of dopants increases. Most studied systems in Fig. 7 have adsorption energies within the optimal range, indicating that the P adatom leads to surface activation, again in agreement with the pristine case. There does not seem to be a clearly superior candidate for doping material for the Ni3P2 + P termination. Rather, all the systems function roughly on par with the undoped surface within the optimal region.
In terms of the adsorption geometries for the optimal sites, only the first layer l1d3 Mg doping that is accompanied by a surface reconstruction possesses more than 2 geometrically different active sites for the 1st H adsorption within the energetically optimal region. In most cases, the hydrogen is located on top of the P adatom but in some cases, like V (l2d1) also adsorption on the Ni atoms surrounding the P adatom is observed. With 2 hydrogens adsorbed on the surface, typically at least one of them is located on top of the P adatom. Often, such as in Co (l2d2), both hydrogens are on top of the P adatom, but are oriented in symmetrically non-equivalent directions as illustrated in Fig. 8 for Co (l2d2). Similarly to Wexler et al.28 and Hakala et al.,26 we find that the P adatom can adsorb up to three hydrogens. However, in all cases where hydrogen adsorption of three hydrogens was considered, spontaneous H2 formation was also observed during some of the geometry optimisations, underlining the high reactivity of these surfaces.
4 Conclusions
In this study, we have looked at HER on metal-doped Ni3P2 and Ni3P2 + P terminated Ni2P surfaces. The catalytic HER activity of the studied materials was predicted through DFT calculations by using the hydrogen adsorption free energy as a predictor following the self-consistent scheme proposed by Nørskov et al.6 and Skúlason et al.50 Our calculations indicate that doping can substantially improve the catalytic activity of the Ni3P2 terminated Ni2P surface, in agreement with experimental studies. Particularly iron and cobalt emerged as promising dopants. In contrast, the Ni3P2 + P termination seems to be catalytically active irrespective of the type of doping and even in the absence of doping.In addition to the ΔGH values, we also looked at the formation energies of the doped materials to investigate their stability. We predict that the surface should be readily dopable by Co and Fe, for example, whereas for Cu all the energies were unfavourable. Based on our results, the most promising candidates for doping material are iron and cobalt, whereas copper is less likely to function well as a dopant. The rest of the studied metals, V, Mg, and Mo, are predicted to be roughly equal in their applicability.
For the doping geometries, in most cases on Ni3P2 the first hydrogen is adsorbed to the strongly binding Ni3 hollow site, although in some cases it preferred a bridge site on the hollow's edge. In Ni3P2 + P, the Ni3-site is filled by a P adatom. Consequently, for the second hydrogen in the Ni3P2 case and the first, second, and third hydrogen adsorptions in the Ni3P2 + P case, a number of highly active geometrical arrangements were identified with large variations between dopants and doping schemes. In line with previous studies, we find that the P adatom can adsorb up to three hydrogens. However, spontaneous H2 formation was observed during some of the geometry optimisations in all adsorption calculations involving three hydrogens, which underscores the high reactivity of the Ni3P2 + P surfaces.
Conflicts of interest
There are no conflicts to declare.Acknowledgements
The work was supported by the European Union's Horizon 2020 research and innovation programme (CritCat Project, grant agreement no. 686053). We are grateful for the generous computing resources from CSC – IT Center for Scientific Computing including the Grand Challenge project CritCat.References
- N. S. Lewis and D. G. Nocera, Powering the planet: Chemical challenges in solar energy utilization, Proc. Natl. Acad. Sci. U. S. A., 2006, 103, 15729–15735 CrossRef CAS PubMed.
- F. E. Osterloh and B. A. Parkinson, Recent developments in solar water-splitting photocatalysis, MRS Bull., 2011, 36, 17–22 CrossRef CAS.
- Z. W. Seh, J. Kibsgaard, C. F. Dickens, I. Chorkendorff, J. K. Nørskov and T. F. Jaramillo, Combining theory and experiment in electrocatalysis: Insights into materials design, Science, 2017, 355, eaad4998 CrossRef PubMed.
- H. G. Park and J. K. Holt, Recent advances in nanoelectrode architecture for photochemical hydrogen production, Energy Environ. Sci., 2010, 3, 1028–1036 RSC.
- M. G. Walter, E. L. Warren, J. R. McKone, S. W. Boettcher, Q. Mi, E. A. Santori and N. S. Lewis, Solar water splitting cells, Chem. Rev., 2010, 110, 6446–6473 CrossRef CAS PubMed.
- J. K. Nørskov, T. Bligaard, A. Logadottir, J. R. Kitchin, J. G. Chen, S. Pandelov and U. Stimming, Trends in the exchange current for hydrogen evolution, J. Electrochem. Soc., 2005, 152, J23–J26 CrossRef.
- Y. Wang, B. Kong, D. Zhao, H. Wang and C. Selomulya, Strategies for developing transition metal phosphides as heterogeneous electrocatalysts for water splitting, Nano Today, 2017, 15, 26–55 CrossRef CAS.
- W. Cui, Q. Liu, N. Cheng, A. M. Asiri and X. Sun, Activated carbon nanotubes: a highly-active metal-free electrocatalyst for hydrogen evolution reaction, Chem. Commun., 2014, 50, 9340–9342 RSC.
- F. Davodi, M. Tavakkoli, J. Lahtinen and T. Kallio, Straightforward synthesis of nitrogen-doped carbon nanotubes as highly active bifunctional electrocatalysts for full water splitting, J. Catal., 2017, 353, 19–27 CrossRef CAS.
- Y. Zheng, Y. Jiao, Y. Zhu, L. H. Li, Y. Han, Y. Chen, A. Du, M. Jaroniec and S. Z. Qiao, Hydrogen evolution by a metal-free electrocatalyst, Nat. Commun., 2014, 5, 3783 CrossRef PubMed.
- L. Feng and H. Xue, Advances in transition-metal phosphide applications in electrochemical energy storage and catalysis, ChemElectroChem, 2017, 4, 20–34 CrossRef CAS.
- P. Xiao, W. Chen and X. Wang, A review of phosphide-based materials for electrocatalytic hydrogen evolution, Adv. Energy Mater., 2015, 5, 1500985 CrossRef.
- E. Pomerantseva, C. Resini, K. Kovnir and Y. V. Kolen'ko, Emerging nanostructured electrode materials for water electrolysis and rechargeable beyond Li-ion batteries, Adv. Phys.: X, 2017, 2, 211–253 Search PubMed.
- J. Xie, J. Zhang, S. Li, F. Grote, X. Zhang, H. Zhang, R. Wang, Y. Lei, B. Pan and Y. Xie, Controllable disorder engineering in oxygen-incorporated MoS2 ultrathin nanosheets for efficient hydrogen evolution, J. Am. Chem. Soc., 2013, 135, 17881–17888 CrossRef CAS PubMed.
- P. Xiao, M. A. Sk, L. Thia, X. Ge, R. J. Lim, J.-Y. Wang, K. H. Lim and X. Wang, Molybdenum phosphide as an efficient electrocatalyst for the hydrogen evolution reaction, Energy Environ. Sci., 2014, 7, 2624–2629 RSC.
- E. J. Popczun, J. R. McKone, C. G. Read, A. J. Biacchi, A. M. Wiltrout, N. S. Lewis and R. E. Schaak, Nanostructured nickel phosphide as an electrocatalyst for the hydrogen evolution reaction, J. Am. Chem. Soc., 2013, 135, 9267–9270 CrossRef CAS PubMed.
- L. Feng, H. Vrubel, M. Bensimon and X. Hu, Easily-prepared dinickel phosphide (Ni2P) nanoparticles as an efficient and robust electrocatalyst for hydrogen evolution, Phys. Chem. Chem. Phys., 2014, 16, 5917–5921 RSC.
- X. Wang, Y. V. Kolen'ko, X.-Q. Bao, K. Kovnir and L. Liu, One-step synthesis of self-supported nickel phosphide nanosheet array cathodes for efficient electrocatalytic hydrogen generation, Angew. Chem., Int. Ed., 2015, 54, 8188–8192 CrossRef CAS PubMed.
- Y. Sun, L. Hang, Q. Shen, T. Zhang, H. Li, X. Zhang, X. Lyu and Y. Li, Mo doped Ni2P nanowire arrays: an efficient electrocatalyst for the hydrogen evolution reaction with enhanced activity at all pH values, Nanoscale, 2017, 9, 16674–16679 RSC.
- J. L. Lado, X. Wang, E. Paz, E. Carbó-Argibay, N. Guldris, C. Rodríguez-Abreu, L. Liu, K. Kovnir and Y. V. Kolen'ko, Design and synthesis of highly active Al–Ni–P foam electrode for hydrogen evolution reaction, ACS Catal., 2015, 5, 6503–6508 CrossRef CAS.
- Y. Zhang, Y. Liu, M. Ma, X. Ren, Z. Liu, G. Du, A. M. Asiri and X. Sun, A Mn-doped Ni2P nanosheet array: an efficient and durable hydrogen evolution reaction electrocatalyst in alkaline media, Chem. Commun., 2017, 53, 11048–11051 RSC.
- Z. Jin, P. Li, X. Huang, G. Zeng, Y. Jin, B. Zheng and D. Xiao, Three-dimensional amorphous tungsten-doped nickel phosphide microsphere as an efficient electrocatalyst for hydrogen evolution, J. Mater. Chem. A, 2014, 2, 18593–18599 RSC.
- P. Wang, Z. Pu, Y. Li, L. Wu, Z. Tu, M. Jiang, Z. Kou, I. S. Amiinu and S. Mu, Iron-doped nickel phosphide nanosheet arrays: an efficient bifunctional electrocatalyst for water splitting, ACS Appl. Mater. Interfaces, 2017, 9, 26001–26007 CrossRef CAS PubMed.
- Y. Li, H. Zhang, M. Jiang, Q. Zhang, P. He and X. Sun, 3D self-supported Fe-doped Ni2P nanosheet arrays as bifunctional catalysts for overall water splitting, Adv. Funct. Mater., 2017, 27, 1702513 CrossRef.
- M. Hakala, R. Kronberg and K. Laasonen, Hydrogen adsorption on doped MoS2 nanostructures, Sci. Rep., 2017, 7, 15243 CrossRef PubMed.
- M. Hakala and K. Laasonen, Hydrogen adsorption trends on Al-doped Ni2P surfaces for optimal catalyst design, Phys. Chem. Chem. Phys., 2018, 20, 13785–13791 RSC.
- R. B. Wexler, J. M. P. Martirez and A. M. Rappe, Stable phosphorus-enriched (0001) surfaces of nickel phosphides, Chem. Mater., 2016, 28, 5365–5372 CrossRef CAS.
- R. B. Wexler, J. M. P. Martirez and A. M. Rappe, Active role of phosphorus in the hydrogen evolving activity of nickel phosphide (0001) surfaces, ACS Catal., 2017, 7, 7718–7725 CrossRef CAS.
- M. H. Hansen, L.-A. Stern, L. Feng, J. Rossmeisl and X. Hu, Widely available active sites on Ni2P for electrochemical hydrogen evolution – insights from first principles calculations, Phys. Chem. Chem. Phys., 2015, 17, 10823–10829 RSC.
- J. Greeley, T. F. Jaramillo, J. Bonde, I. Chorkendorff and J. K. Nørskov, Computational high-throughput screening of electrocatalytic materials for hydrogen evolution, Nat. Mater., 2006, 5, 909–913 CrossRef CAS PubMed.
- J. VandeVondele, M. Krack, F. Mohamed, M. Parrinello, T. Chassaing and J. Hutter, QUICKSTEP: Fast and accurate density functional calculations using a mixed gaussian and plane waves approach, Comput. Phys. Commun., 2005, 167, 103–128 CrossRef CAS.
- J. Hutter, M. Iannuzzi, F. Schiffmann and J. VandeVondele, cp2k: atomistic simulations of condensed matter systems, Wiley Interdiscip. Rev.: Comput. Mol. Sci., 2014, 4, 15–25 CAS.
- J. P. Perdew, K. Burke and M. Ernzerhof, Generalized gradient approximation made simple, Phys. Rev. Lett., 1996, 77, 3865–3868 CrossRef CAS PubMed.
- S. Goedecker, M. Teter and J. Hutter, Separable dual-space Gaussian pseudopotentials, Phys. Rev. B: Condens. Matter Mater. Phys., 1996, 54, 1703–1710 CrossRef CAS.
- C. Hartwigsen, S. Goedecker and J. Hutter, Relativistic separable dual-space Gaussian pseudopotentials from H to Rn, Phys. Rev. B: Condens. Matter Mater. Phys., 1998, 58, 3641–3662 CrossRef CAS.
- M. Krack, Pseudopotentials for H to Kr optimized for gradient-corrected exchange-correlation functionals, Theor. Chem. Acc., 2005, 114, 145–152 Search PubMed.
- P. Haas, F. Tran and P. Blaha, Calculation of the lattice constant of solids with semilocal functionals, Phys. Rev. B: Condens. Matter Mater. Phys., 2009, 79, 085104 CrossRef.
- A. H. Reshak and M. Jamal, Calculation of the lattice constant of hexagonal compounds with two dimensional search of equation of state and with semilocal functionals a new package (2D-optimize), J. Alloys Compd., 2013, 555, 362–366 CrossRef CAS.
- F. Tran, R. Laskowski, P. Blaha and K. Schwarz, Performance on molecules, surfaces, and solids of the Wu-Cohen GGA exchange-correlation energy functional, Phys. Rev. B: Condens. Matter Mater. Phys., 2007, 75, 115131 CrossRef.
- U. Wedig, M. Jansen, B. Paulus, K. Rosciszewski and P. Sony, Structural and electronic properties of Mg, Zn, and Cd from Hartree-Fock and density functional calculations including hybrid functionals, Phys. Rev. B: Condens. Matter Mater. Phys., 2007, 75, 205123 CrossRef.
- S. Grimme, J. Antony, S. Ehrlich and H. Krieg, A Consistent and accurate ab initio parametrization of density functional dispersion correction (DFT-D) for the 94 elements H–Pu, J. Chem. Phys., 2010, 132, 154104 CrossRef PubMed.
- S. Grimme, S. Ehrlich and L. Goerigk, Effect of the damping function in dispersion corrected density functional theory, J. Comput. Chem., 2011, 32, 1456–1465 CrossRef CAS PubMed.
- Q. Li and X. Hu, First-principles study of Ni2P (0001) surfaces, Phys. Rev. B: Condens. Matter Mater. Phys., 2006, 74, 035414 CrossRef.
- A. B. Hernandez, H. Ariga, S. Takakusagi, K. Kinoshita, S. Suzuki, S. Otani, S. T. Oyama and K. Asakura, Dynamical LEED analysis of Ni2P(0001)-1 × 1: evidence for P-covered surface structure, Chem. Phys. Lett., 2011, 513, 48–52 CrossRef CAS.
- D. Kanama, S. T. Oyama, S. Otani and D. F. Cox, Photoemission and LEED characterization of Ni2P(0001), Surf. Sci., 2004, 552, 8–16 CrossRef CAS.
- M. G. Moula, S. Suzuki, W.-J. Chun, S. Otani, S. T. Oyama and K. Asakura, Surface structures of Ni2P(0001) scanning tunneling microscopy (STM) and low-energy electron diffraction (LEED) characterizations, Surf. Interface Anal., 2006, 38, 1611–1614 CrossRef CAS.
- S. Suzuki, G. M. Moula, T. Miyamoto, Y. Nakagawa, K. Kinosthita, K. Asakura, S. T. Oyama and S. Otani, Scanning tunneling microscopy and photoemission electron microscopy studies on single crystal Ni2P surfaces, J. Nanosci. Nanotechnol., 2009, 9, 195–201 CrossRef CAS PubMed.
- D. Guo, Y. Nakagawa, H. Ariga, S. Suzuki, K. Kinoshita, T. Miyamoto, S. Takakusagi, K. Asakura, S. Otani and S. T. Oyama, STM studies on the reconstruction of the Ni2P(10
![[1 with combining macron]](https://www.rsc.org/images/entities/char_0031_0304.gif) 0) surface, Surf. Sci., 2010, 604, 1347–1352 CrossRef CAS.
0) surface, Surf. Sci., 2010, 604, 1347–1352 CrossRef CAS. - H. Ariga, M. Kawashima, S. Takakusagi and K. Asakura, Density function theoretical investigation on the Ni3PP structure and the hydrogen adsorption property of the Ni2P(0001) surface, Chem. Lett., 2013, 42, 1481–1483 CrossRef CAS.
- E. Skúlason, G. S. Karlberg, J. Rossmeisl, T. Bligaard, J. Greeley, H. Jónsson and J. K. Nørskov, Density functional theory calculations for the hydrogen evolution reaction in an electrochemical double layer on the Pt(111) electrode, Phys. Chem. Chem. Phys., 2007, 9, 3241–3250 RSC.
- J. K. Nørskov, J. Rossmeisl, A. Logadottir, L. Lindqvist, J. R. Kitchin, T. Bligaard and H. Jónsson, Origin of the overpotential for oxygen reduction at a fuel-cell cathode, J. Phys. Chem. B, 2004, 108, 17886–17892 CrossRef.
- P. Liu, J. A. Rodriguez, T. Asakura, J. Gomes and K. Nakamura, Desulfurization reactions on Ni2P(001) and α-Mo2C(001) surfaces: Complex role of P and C sites, J. Phys. Chem. B, 2005, 109, 4575–4583 CrossRef CAS PubMed.
- J. A. Rodriguez, J.-Y. Kim, J. C. Hanson, S. J. Sawhill and M. E. Bussell, Physical and chemical properties of MoP, Ni2P, and MoNiP hydrodesulfurization catalysts: time-resolved X-ray diffraction, density functional, and hydrodesulfurization activity studies, J. Phys. Chem. B, 2003, 107, 6276–6285 CrossRef CAS.
- P. Liu and J. A. Rodriguez, Catalysts for hydrogen evolution from the [NiFe] hydrogenase to the Ni2P(001) surface: The importance of ensemble effect, J. Am. Chem. Soc., 2005, 127, 14871–14878 CrossRef CAS PubMed.
- R. B. Wexler, J. M. P. Martirez and A. M. Rappe, Chemical pressure-driven enhancement of the hydrogen evolving activity of Ni2P from nonmetal surface doping interpreted via machine learning, J. Am. Chem. Soc., 2018, 140, 4678–4683 CrossRef CAS PubMed.
- S. Raaen and R. D. Parks, Mixed valence in CeNi5; effects of dilution and chemical pressure, Solid State Commun., 1983, 48, 199–202 CrossRef CAS.
- B. Hammer, L. B. Hansen and J. K. Nørskov, Improved adsorption energetics within density-functional theory using revised Perdew–Burke–Ernzerhof functionals, Phys. Rev. B: Condens. Matter Mater. Phys., 1999, 59, 7413–7421 CrossRef.
Footnote |
| † Electronic supplementary information (ESI) available. See DOI: 10.1039/c8cp06143b |
| This journal is © the Owner Societies 2019 |