Experimental quantification of electron spectral-diffusion under static DNP conditions†
Krishnendu
Kundu
 ,
Marie Ramirez
Cohen
,
Akiva
Feintuch
,
Daniella
Goldfarb
,
Marie Ramirez
Cohen
,
Akiva
Feintuch
,
Daniella
Goldfarb
 and
Shimon
Vega
*
and
Shimon
Vega
*
Department of Chemical and Biological Physics, Weizmann Institute of Science, Rehovot 7610001, Israel. E-mail: shimon.vega@weizmann.ac.il
First published on 28th November 2018
Abstract
Dynamic Nuclear Polarization (DNP) is an efficient technique for enhancing NMR signals by utilizing the large polarization of electron spins to polarize nuclei. The mechanistic details of the polarization transfer process involve the depolarization of the electrons resulting from microwave (MW) irradiation (saturation), as well as electron–electron cross-relaxation occurring during the DNP experiment. Recently, electron–electron double resonance (ELDOR) experiments have been performed under DNP conditions to map the depolarization profile along the EPR spectrum as a consequence of spectral diffusion. A phenomenological model referred to as the eSD model was developed earlier to describe the spectral diffusion process and thus reproduce the experimental results of electron depolarization. This model has recently been supported by quantum mechanical calculations on a small dipolar coupled electron spin system, experiencing dipolar interaction based cross-relaxation. In the present study, we performed a series of ELDOR measurements on a solid glassy solution of TEMPOL radicals in an effort to substantiate the eSD model and test its predictability in terms of electron depolarization profiles, in the steady-state and under non-equilibrium conditions. The crucial empirical parameter in this model is ΛeSD, which reflects the polarization exchange rate among the electron spins. Here, we explore further the physical basis of this parameter by analyzing the ELDOR spectra measured in the temperature range of 3–20 K and radical concentrations of 20–40 mM. Simulations using the eSD model were carried out to determine the dependence of ΛeSD on temperature and concentration. We found that for the samples studied, ΛeSD is temperature independent. It, however, increases with a power of ∼2.6 of the concentration of TEMPOL, which is proportional to the average electron–electron dipolar interaction strength in the sample.
1. Introduction
Over the years, Nuclear Magnetic Resonance (NMR) has become one of the predominant spectroscopic tools for structure determination and imaging. Despite being a very useful technique, NMR is limited by its inherently low sensitivity due to the relatively small nuclear Zeeman energies, compared to the ambient thermal energy. Dynamic Nuclear Polarization (DNP) is a process where NMR polarizations are enhanced far beyond their ambient Boltzmann values. This is accomplished by a transfer of polarization from unpaired electron spins to the nuclei in the sample during microwave (MW) irradiation. During the last two decades, it has become one of the predominant spectroscopic tools for enhancing the sensitivity of NMR and MRI,1,2 in particular for studies in biology3 and materials science.4,5In solid solutions of free radicals, the DNP mechanism strongly depends on the EPR spectral width and concentration of the radicals used as polarizers. The commonly recognized DNP mechanisms, the solid effect6,7 (SE), the cross effect6,8–13 (CE) and thermal mixing14–18 (TM), all play a role in nuclear enhancement. The SE is responsible for the nuclear enhancement that is induced by MW excitation of electron-nuclear zero-quantum and double-quantum transitions. The CE also transfers electron polarization to nuclear polarization, but this time it is mediated by a dipolar interaction between neighboring electrons. In the TM description, the NMR enhancement is rationalized by a spin thermodynamic process14 between the spin heat baths19 of the multi-electron system and of the nuclei.20–28 When the polarizers are nitroxyl radicals with an in-homogeneously broadened EPR spectrum, the dominant DNP mechanisms are the SE and CE. Furthermore, the deviations from the TM predicted EPR line shape29,30 under DNP conditions at 95 GHz indicate that the contribution of the TM mechanism is negligible.31,32
Recently we made a distinction between the direct and the indirect CE mechanism. During a direct CE experiment one directly irradiates a pair of electron spins with a resonance frequency difference equal to the nuclear Larmor frequency (the CE conditions). During an indirect CE (iCE) enhancement process, the electron polarizations of a pair are affected by a redistribution mechanism of the electron depolarization throughout the full EPR spectrum, due to spectral diffusion.31 In solutions with radical concentrations above 10 mM, the MW irradiation initially burns a hole that then spreads throughout the EPR spectrum. Its lineshape reaches a steady state that is determined mainly by (i) the strength of the electron–electron dipolar interactions,33,34 (ii) the associated electron–electron cross relaxation, (iii) the electron spin–lattice relaxation and (iv) the strength of the applied MW amplitude.35–38 The polarization of the core and local nuclei39 coupled to the electrons is then enhanced by the iCE process that transfers the polarization difference of coupled electron spins fulfilling the CE conditions,40,41 to their nearby nuclei. In the next DNP stage, the enhanced polarizations of the local nuclei are transferred to the bulk nuclei by spin diffusion,42 governed by the nuclear dipolar interactions and longitudinal relaxation. Accordingly, once the depolarization profile within the EPR line shape is known and analyzed in terms of polarization gradients, it can be used to directly calculate the DNP lineshape, namely the DNP enhancement as a function of the MW irradiation frequency.
The EPR lineshape, under conditions of MW irradiation typically used in DNP experiments, can be determined by a set of electron–electron double resonance (ELDOR) experiments.43,44 To analyze and extract the polarization gradients within the EPR spectrum, we introduced a mathematical model referred to as the electron spectral diffusion (eSD) model. This model is based on a set of coupled rate equations for the electron polarizations of the frequency bins composing the EPR spectrum. The rate constants, representing the electron spectral diffusion responsible for the electron depolarization during MW irradiation, are defined by a single eSD parameter ΛeSD. This single parameter, together with the spin relaxation rates, has been sufficient for reconstructing ELDOR frequency profiles31,45 and from them EPR and DNP spectra.46 In our recent theoretical study,47 we discussed the dependence of ΛeSD on the electron–electron dipolar interactions in the system, and in the present study, we experimentally address the question of how it depends in practice on the temperature and the radical concentration, which is directly related to the average dipolar interaction between the electron spins.
We report on ELDOR experiments carried out on samples of TEMPOL at different concentrations, where the CE is highly efficient, namely in the range of 20–40 mM in a 50![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 50 (v/v%) DMSO/H2O amorphous glassy solvent at different temperatures. The eSD model is then used to analyze the ELDOR spectra and to extract the concentration and temperature dependence of ΛeSD. Additionally, we compare experimental temporal evolutions of the polarizations after MW irradiation with simulations relying on the values of ΛeSD. This comparison also reveals that to successfully reproduce the experimental data, it is necessary to introduce time-dependent SE parameters to the eSD model.
50 (v/v%) DMSO/H2O amorphous glassy solvent at different temperatures. The eSD model is then used to analyze the ELDOR spectra and to extract the concentration and temperature dependence of ΛeSD. Additionally, we compare experimental temporal evolutions of the polarizations after MW irradiation with simulations relying on the values of ΛeSD. This comparison also reveals that to successfully reproduce the experimental data, it is necessary to introduce time-dependent SE parameters to the eSD model.
2. Experimental and simulation procedures
2.1 Sample preparation
TEMPOL and DMSO were purchased from Sigma-Aldrich and solutions with various concentrations of TEMPOL, 20, 25, 30, 35 and 40 mM, were prepared with a 50/50 (v/v%) mixture of water and dimethyl sulfoxide (DMSO).Measurements were carried out on three sets of samples referred to as I, II and III. Sample sets I and II were measured on our pulse EPR spectrometer (95 GHz).48 They were placed in a 0.9 mm outer diameter (OD) quartz capillary, containing about 2–4 μl, then degassed, and immediately frozen in liquid nitrogen. These samples were then introduced cold into the precooled cryostat of the spectrometer. In this spectrometer, cooling is done with a liquid helium flow cryostat. On sample set I, a series of ELDOR measurements was performed with different detection frequencies covering the full EPR line. From these ELDOR spectra, 2D-ELDOR maps were constructed. For these measurements, the superior SNR of the pulse EPR spectrometer was of importance and enabled obtaining reasonable ELDOR data, even when detecting at the edges of the EPR spectrum. Sample set II was used to test the reproducibility and estimate the uncertainties of the measurements. To test a broad range of temperatures and concentrations, we added the third set of samples, set III, which were measured using our hybrid pulsed-EPR-NMR spectrometer49 (henceforth called the DNP spectrometer). These measurements allowed experiments at 3 K, not possible for the EPR spectrometer. Synchronization between the EPR and NMR parts of this spectrometer enables the application of independent and simultaneous RF and MW irradiation pulse schemes. Similar to the EPR spectrometer, it operates at a magnetic field of 3.4 T, corresponding to a 1H-Larmor frequency of 144 MHz and an electron-Larmor frequency of approximately 95 GHz. Both spectrometers have a very similar design in terms of their microwave bridge, with two channels for applying two different MW frequencies during single measurements. For measurements on the DNP spectrometer, a series of samples at different concentrations were placed in a glass sample holder containing about 20 μl of the required solution, degassed, and sealed. The samples, placed in the probe head, were then cooled to cryogenic temperatures, by inserting the probe head into a cryogen-free variable temperature system from Cryogenic Limited, UK. The DNP setup does not support inserting precooled samples.
2.2 EPR and ELDOR measurements
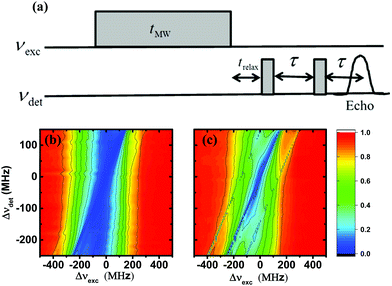
For all ELDOR measurements, the EPR signals were detected using a two-pulse echo detection sequence49 α–τ–α–echo, with pulse durations of 400 ns and a delay, τ, of 1 μs, using a 180° phase cycle on the first pulse. The equal lengths of the pulses are dictated by the low power available in the DNP spectrometer, and were optimized to obtain maximal echo intensity.49 As is also common in pulse EPR spectroscopy, the signal intensity was obtained by an integration window positioned around the half width of the echo peak. The ELDOR pulse sequence is shown in Fig. 1a. Experiments were conducted by applying a long MW excitation pulse at a frequency νexc for a duration of tMW, followed by a delay trelax = 10 μs, and then an EPR echo detection sequence applied at a detection frequency νdet. The length of tMW, required to achieve a steady-state ELDOR spectrum, depends on the value of T1e. In the case of the EPR spectrometer, it was set at 20 ms which was sufficient at all temperatures. For the experiments on the DNP spectrometer, tMW was equal to 40 ms at 20 K and 10 K and to 100 ms at 5 K and 3 K. For each ELDOR experiment, νdet was kept fixed and νexc varied from 94.3 to 95.3 GHz, which is the active range of the spectrometer. In the EPR spectrometer, a series of ELDOR experiments were performed with different νdet. The ELDOR spectra were normalized with respect to the thermal equilibrium EPR signal at each νdet value, which was the intensity of the signal obtained after MW irradiation at a frequency νexc′, situated far outside the EPR spectrum. Such irradiation should not have any direct or indirect effect on the detected electron polarizations. The MW amplitude, ν1, was 640 kHz for the DNP and 500 kHz for the EPR spectrometer. These values were determined by nutation experiments performed at 94.8 GHz, the frequency of the maximum of the EPR spectrum. For the DNP spectrometer, we assumed that due to the low Q of the MW setup, this ν1 value is constant over the frequency range used in the ELDOR experiments. In the EPR spectrometer, a low-Q MW cavity was used, with a center frequency of 94.8 GHz, to minimize the variation in ν1 over the same frequency range.The temporal behavior of the electron depolarization during MW irradiation was measured by recording EPR echo signals after various values of tMW. We also recorded the time-domain behavior of the electron polarization, following a short MW pulse of 100 μs, for monitoring the influence of the spectral diffusion process during the return of the EPR spectrum to its thermal equilibrium line shape.
2.3 Spin–lattice relaxation measurements
Spin–lattice relaxation times were measured, using a saturation recovery sequence which included a long MW pulse with a duration of 50–100 ms, followed by a variable delay and echo detection. The results were fitted using either a single exponent or, when required, using a double exponential function with the slow component considered as the true spin–lattice relaxation time.2.4 Simulations of ELDOR profiles
We used the eSD model to calculate ELDOR spectra for different values of ΛeSD and fit them to the experimental ELDOR spectra.31 The eSD model is based on approximating the EPR spectrum by a set of N discrete bins, with average electron polarizations Pe,j with j = 1…N and an average bin frequency of ωj. The time-evolution under MW irradiation of the bin polarizations Pe,j is described by the following rate equation: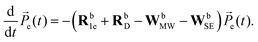 | (1) |
![[P with combining right harpoon above (vector)]](https://www.rsc.org/images/entities/i_char_0050_20d1.gif) e(t) of polarizations is defined by
e(t) of polarizations is defined by ![[P with combining right harpoon above (vector)]](https://www.rsc.org/images/entities/i_char_0050_20d1.gif) e(t) = [1,Pe,1,Pe,2…Pe,N]. The first element in the vector will be given an index, Pe,0 = 1, and is necessary for the spin–lattice relaxation, as will be described. The rate matrices, Rb1e and RbD, describe the action of the electron spin–lattice relaxation and the spectral diffusion, respectively, while the rate matrices, WbMW and WbSE, describe the effect of MW irradiation on the allowed and “forbidden” EPR transitions respectively. For completeness, we reintroduce the necessary expressions defining the matrix elements of these rate matrices:31
e(t) = [1,Pe,1,Pe,2…Pe,N]. The first element in the vector will be given an index, Pe,0 = 1, and is necessary for the spin–lattice relaxation, as will be described. The rate matrices, Rb1e and RbD, describe the action of the electron spin–lattice relaxation and the spectral diffusion, respectively, while the rate matrices, WbMW and WbSE, describe the effect of MW irradiation on the allowed and “forbidden” EPR transitions respectively. For completeness, we reintroduce the necessary expressions defining the matrix elements of these rate matrices:31
The spin–lattice relaxation of the jth bin is described by the equation:
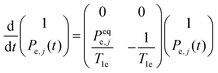 | (2a) |
The non-zero elements of the electron spin–lattice relaxation rate matrix, Rb1e, are therefore given by:
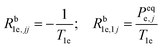 | (2b) |
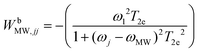 | (3) |
The electron–electron cross relaxation mechanism for any two bins, j and j′, with polarizations Pe,j(t) and Pe,j′(t), respectively, is described by the equation:
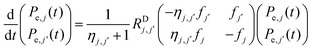 | (4a) |
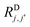 , are defined by
, are defined by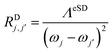 | (4b) |
| ηj,j′ = exp(−(ωj − ωj′)/kBT) | (4c) |
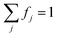 . The role of the ηj,j′ values is to assure that, at thermal equilibrium, each pair of polarizations Pe,j(t) and Pe,j′(t) maintain their Boltzmann ratio. The matrix elements of RbD will be a sum of the rate matrixes between pairs of bins, as described in detail elsewhere.31
. The role of the ηj,j′ values is to assure that, at thermal equilibrium, each pair of polarizations Pe,j(t) and Pe,j′(t) maintain their Boltzmann ratio. The matrix elements of RbD will be a sum of the rate matrixes between pairs of bins, as described in detail elsewhere.31
The last rate matrix WbSE in eqn (1) represents electron depolarization due to the SE-DNP process. This is represented by an effective MW irradiation in the ZQ or DQ transitions, and again has only diagonal elements, given by:
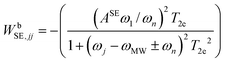 | (5) |
Solving eqn (1) for a set of parameters results in a polarization profile determining the values of Pe,j as a function of their bin resonance frequencies ωj. These profiles enable us to calculate the EPR spectra during MW irradiation, by taking the values of fj into account:
| EEPRsim(ωj,t;ωMW) = fjPe,j(t) | (6) |
For consistency, from here on, we will present all frequencies in units of Hertz as Δνj = ωj/2π − νe and ΔνMW = ωMW/2π − νe, with νe = 94.8 GHz, and νn = ωn/2π. The parameters necessary for fitting the data are: T1e the electron spin–lattice relaxation, ΛeSD the spectral diffusion parameter, ν1 the MW irradiation intensity, νn the nuclear Larmor frequency, ASE the SE depolarization parameter and T2e the electron spin–spin relaxation. Before the data analysis we determined experimentally the shape of the EPR spectrum of the TEMPOL radical and its fj values, the values of T1e and ν1, set νn equal to the proton Larmor frequency and chose a value for ΔνMW. We also measured phase memory times, TM, which represent only a lower limit for T2e. Thus using these values, the remaining parameters ΛeSD, T2e and ASE are determined by a fitting procedure. The first parameter determines the overall depolarization profiles of the ELDOR spectra, the second defines the off-resonance excitation efficiency of the MW irradiation and the third is responsible for the spectral features induced by the SE-DNP process.
Using this rate equation we can now simulate ELDOR spectra with the following procedure: at first, after fixing the value for the widths of the frequency bins we define all bin frequencies ωj in units of Hertz and with respect to νe = 94.8 GHz: Δνj = (ωj − 2πνe)/2π. For each chosen set of parameters {ΛeSD,ASE(tMW),T2e} and MW irradiation at a specific bin frequency, Δνexc,j, we can calculate a normalized steady state EPR spectrum of the form
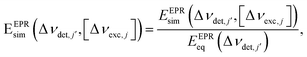 | (7) |
In all calculations discussed here, the bin-width was set equal to Δνb = 2 MHz. This value was chosen because it is of the order of the average (e–e) dipolar interaction strength in the samples with the highest radical concentration. From our earlier calculations (not shown here), it follows that varying Δνb between 2 and 0.5 MHz does not affect the best-fit values for ΛeSD. Thus, to minimize the dimension of ![[P with combining right harpoon above (vector)]](https://www.rsc.org/images/entities/i_char_0050_20d1.gif) e(t) in eqn (1), we choose a bin size of 2 MHz. During the calculations, the Δνexc,j and Δνdet,j frequencies were always set at the center frequencies of one of the bins which, in turn, were fixed with respect to the EPR spectrum. This restriction is of course not valid for the experimental Δνexc and Δνdet values. To compare the simulated and experimental ELDOR results, the detection frequencies Δνdet,j during the calculations were set to be as close as possible to the experimental Δνdet values, by choosing Δνdet − Δνb/2 < Δνdet,j < Δνdet + Δνb/2, and the same rule follows for Δνexc.
e(t) in eqn (1), we choose a bin size of 2 MHz. During the calculations, the Δνexc,j and Δνdet,j frequencies were always set at the center frequencies of one of the bins which, in turn, were fixed with respect to the EPR spectrum. This restriction is of course not valid for the experimental Δνexc and Δνdet values. To compare the simulated and experimental ELDOR results, the detection frequencies Δνdet,j during the calculations were set to be as close as possible to the experimental Δνdet values, by choosing Δνdet − Δνb/2 < Δνdet,j < Δνdet + Δνb/2, and the same rule follows for Δνexc.
3. Results
3.1 Relaxation time measurements
The T1e values of all sample sets, I, II and III studied in this work (see Section 2.1), are listed in Table 1. We note that in contrast to recently published results52–54 related to the anisotropy of T1e, in all our samples the experimental values of T1e (the slow component of the bi-exponential analysis of the spin–lattice experiments) were found to be only slightly dependent on the position of the detection frequency along the EPR line. In the ESI,† Fig S1, we show saturation recovery curves of sample III40, of set III at 40 mM, recorded at Δνdet = −200, −100, 0 and 100 MHz. These curves show that the variation of T1e is less than 10–20% along all the EPR line. The reported results, showing a frequency dependence of T1e, were obtained from the sample at much higher temperatures than our samples52,53 (>80 K), or at lower radical concentrations.54 Under both these conditions, the spectral diffusion mechanism among radicals at different orientations is expected not to be very effective. Contrary to that, in our cases, the relatively high radical concentrations and the rather efficient cross relaxation are expected to quench the anisotropy in the experimentally determined T1e.| Sample set | Temp. (K) | Conc. (mM) | T 1e (ms) | Sample set | Temp. (K) | Conc. (mM) | T 1e (ms) | Sample set | Temp. (K) | Conc. (mM) | T 1e (ms) |
|---|---|---|---|---|---|---|---|---|---|---|---|
| I | 20 | 20 | 5.3 | III | 5 | 25 | 5.5 | III | 10 | 35 | 48 |
| I | 20 | 40 | 5.3 | III | 5 | 30 | 5.6 | III | 10 | 40 | 47 |
| II | 10 | 20 | 41.3 | III | 5 | 35 | 5.3 | III | 20 | 20 | 280 |
| II | 10 | 40 | 28.3 | III | 5 | 40 | 5.1 | III | 20 | 25 | 290 |
| II | 20 | 20 | 5.4 | III | 10 | 20 | 63 | III | 20 | 30 | 278 |
| II | 20 | 40 | 5.3 | III | 10 | 25 | 57 | III | 20 | 35 | 280 |
| III | 5 | 20 | 5.5 | III | 10 | 30 | 56 | III | 20 | 40 | 260 |
| Temperature | 5 K | 10 K | 20 K |
|---|---|---|---|
| T m (20 mM) | 0.53 μs | 0.49 μs | 0.46 μs |
| T m (40 mM) | 0.35 ![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) μs μs |
0.33 μs | 0.28 μs |
3.2 Steady-state ELDOR spectra and their analysis
Fig. 1 shows a contour plot of the steady-state 2D-ELDOR spectra of the 20 mM and 40 mM samples from set I, which we will name I40 and I20, respectively, measured on the EPR spectrometer at 20 K. The data were collected as described in Section 2.2, by performing a series of ELDOR measurements for different detection frequencies with a spectral resolution of 10 MHz on both axes. The axes of the plot are defined as Δνdet = νdet − νe, Δνexc = νexc − νe with νe = 94.8 GHz. The intensity of the 2D plot EELDORexp(Δνexc,[Δνdet]) is normalized as described in Section 2.2 and is given by: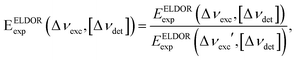 | (8) |
![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) ms which is much longer than the electron spin relaxation times of the two samples, T1e{I20, 20 K} = 5.4 ms and T1e{I40, 20 K} = 5.3
ms which is much longer than the electron spin relaxation times of the two samples, T1e{I20, 20 K} = 5.4 ms and T1e{I40, 20 K} = 5.3![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) ms (see Table 1). The differences between the spectra of the 40 and 20 mM samples are clear, while for I20 the 1H SE lines are resolved (see arrows in Fig. 1b), for I40 they are buried within the broad ELDOR hole. As there is no difference between the T1e values of these samples, it is clear that the difference is a result of a difference between their spectral diffusion parameters ΛeSD.
ms (see Table 1). The differences between the spectra of the 40 and 20 mM samples are clear, while for I20 the 1H SE lines are resolved (see arrows in Fig. 1b), for I40 they are buried within the broad ELDOR hole. As there is no difference between the T1e values of these samples, it is clear that the difference is a result of a difference between their spectral diffusion parameters ΛeSD.
To test the reproducibility of these ELDOR profiles, we prepared an additional pair of samples with 40 mM and 20 mM radical concentrations, samples II40 and II20 respectively, and measured their ELDOR spectra. For these samples, we chose only three detection frequencies, Δνdet = −100, ![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 0,
0, ![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) and 100
and 100 ![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) MHz. A comparison of the detection frequency Δνdet = 0
MHz. A comparison of the detection frequency Δνdet = 0 ![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) MHz is shown in the ESI,† Fig. S2. While samples I40 and II40 give very similar ELDOR spectra, some differences are noted between samples I20 and II20.
MHz is shown in the ESI,† Fig. S2. While samples I40 and II40 give very similar ELDOR spectra, some differences are noted between samples I20 and II20.
All the steady-state ELDOR data collected were analyzed by the simulation procedure described in Section 2.3, resulting in the best fit values for ASE and ΛeSD. In practice, we first determined the values of the proton ASE by reproducing the ELDOR spectra at frequencies outside the EPR spectrum. Manual eye inspection resulted in ASE = 4 MHz for all samples and at both temperatures. During the determination of ASE, the value for T2e was set at 10 μs for all cases. This T2e value determines also the off-resonance excitation efficiency of the MW irradiation and in particular, the shape of the ELDOR profiles after a short irradiation time, and is not necessarily equal to the phase-memory time Tm. The values of all ΛeSD extracted from these best-fit simulations are given in Table 3, showing that the ΛeSD values are basically the same for both sample sets within the uncertainty in the fitting parameters, and are generally temperature independent.
| I20, 20 K | I40, 20 K | II20, 10 K | II20, 20 K | II40, 10 K | II40, 20 K | |
|---|---|---|---|---|---|---|
| Λ eSD (μs−3) | 500 | 2500 | 400 ± 50 | 400 ± 50 | 2500 ± 250 | 2500 ± 250 |
Fig. 2 shows the fitting of the ELDOR spectra of the II40 (a–c) and II20 (d–f) samples at 20 K (black) and 10 K (red) and at three detection frequencies, Δνdet = −100,![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 0,
0, ![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) and 100
and 100 ![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) MHz. We would like to emphasize that for all the fittings we have done in this work, the ΛeSD values were independent of the detection frequency, i.e. we assume ΛeSD is isotropic. This assumption is based on the understanding that the spectral diffusion is a result of a cross-relaxation process which we assume is isotropic. We notice that in particular at 20 K, we observe in the ELDOR spectra a broadening around Δνdet that originates from the 14N-SE depolarization. In the present simulations, these depolarization effects are not taken into account during the analysis and therefore the fit was based on reproducing the total width of the spectrum, relying less on the central part. The positions of the 14N-SE depolarizations and their effect on the ELDOR profiles determined by the hyperfine interaction with 14N will be treated in a separate publication.
MHz. We would like to emphasize that for all the fittings we have done in this work, the ΛeSD values were independent of the detection frequency, i.e. we assume ΛeSD is isotropic. This assumption is based on the understanding that the spectral diffusion is a result of a cross-relaxation process which we assume is isotropic. We notice that in particular at 20 K, we observe in the ELDOR spectra a broadening around Δνdet that originates from the 14N-SE depolarization. In the present simulations, these depolarization effects are not taken into account during the analysis and therefore the fit was based on reproducing the total width of the spectrum, relying less on the central part. The positions of the 14N-SE depolarizations and their effect on the ELDOR profiles determined by the hyperfine interaction with 14N will be treated in a separate publication.
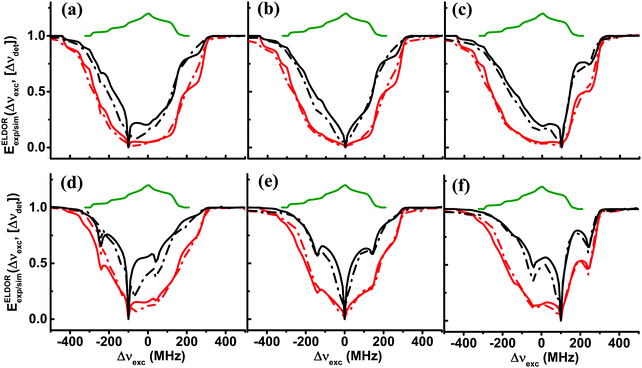 | ||
| Fig. 2 The experimental (dotted lines) and simulated (solid lines) steady state ELDOR spectra EELDORexp/sim(Δνexc,[Δνdet]) are shown for sample II40 in (a–c), and for sample II20 in (d–f), for two temperatures, 10 K (red) and 20 K (black). The detection frequencies are Δνdet = −100 MHz in (a and d); Δνdet = 0 in (b and e); and Δνdet = 100 MHz in (c and f). In each case, the solid lines are the simulated spectra EELDORsim(Δνexc,[Δνdet]) using the eSD model with the parameters listed in Table 1. The thermal equilibrium EPR spectrum is shown in green. | ||
The estimated error of the best-fit ΛeSD parameters was determined on the basis of the least squares fitting while keeping the parameters T2e and ASE fixed. To show this, we plot in Fig. S3 in the ESI† the sums of the squares of the differences for all Δνexc,j, between the simulated and experimental ELDOR profiles of the II20 and II40 samples at 20 K, as a function of ΛeSD for the fixed values Δνdet = −100, 0, ![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) and 100
and 100 ![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) MHz. A similar procedure was performed for these samples at 10 K. The ΛeSD values for each sample and temperature were set equal to the average of the best fit values for each Δνdet value, plus/minus their maximum deviations from this average value. These deviations are added to the ΛeSD values in Table 3.
MHz. A similar procedure was performed for these samples at 10 K. The ΛeSD values for each sample and temperature were set equal to the average of the best fit values for each Δνdet value, plus/minus their maximum deviations from this average value. These deviations are added to the ΛeSD values in Table 3.
In Fig. 3a and b, we show a reconstruction of the steady-state EPR spectra of sample I40 and sample I20, respectively, as a function of Δνdet and for the fixed values Δνexc = −200, ![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) −100,
−100, ![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 0,
0, ![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) and 100
and 100 ![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) MHz, derived from the 2D plot in Fig. 1. These spectra are obtained by extracting slices of the 2D plots, EELDORexp(Δνexc,[Δνdet]), of constant excitation frequency and varying detection frequency, EEPRexp(Δνdet,[Δνexc]), and then multiplying them with the EPR lineshape function, EEPReq(Δνdet), of TEMPOL recorded with low concentration at thermal equilibrium.55 Finally, these EPR spectra are presented by setting the maxima of EEPReq(Δνdet) to unity. This way of presenting the data gives a better perspective on the effect of spectral diffusion when burning a hole. We can, of course, look also at the simulated EPR spectra, EEPRsim(Δνdet,[Δνexc]), of the samples using the ΛeSD parameters given in Table 3, as shown in Fig. 3c and d. As expected, we see in the simulated ELDOR spectra that the eSD model shows narrower MW excitation profiles around Δνdet than their corresponding experimental profiles, because 14N-SE effects are not taken into account.
MHz, derived from the 2D plot in Fig. 1. These spectra are obtained by extracting slices of the 2D plots, EELDORexp(Δνexc,[Δνdet]), of constant excitation frequency and varying detection frequency, EEPRexp(Δνdet,[Δνexc]), and then multiplying them with the EPR lineshape function, EEPReq(Δνdet), of TEMPOL recorded with low concentration at thermal equilibrium.55 Finally, these EPR spectra are presented by setting the maxima of EEPReq(Δνdet) to unity. This way of presenting the data gives a better perspective on the effect of spectral diffusion when burning a hole. We can, of course, look also at the simulated EPR spectra, EEPRsim(Δνdet,[Δνexc]), of the samples using the ΛeSD parameters given in Table 3, as shown in Fig. 3c and d. As expected, we see in the simulated ELDOR spectra that the eSD model shows narrower MW excitation profiles around Δνdet than their corresponding experimental profiles, because 14N-SE effects are not taken into account.
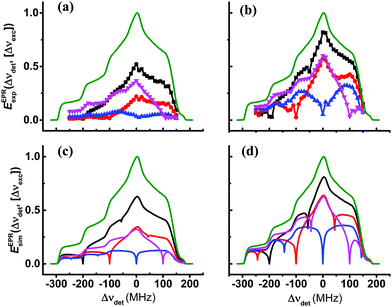 | ||
| Fig. 3 Experimental and simulated steady-state EPR spectra EEPRexp/sim(Δνdet,[Δνexc]) derived from EELDORexp/sim(Δνexc,[Δνdet]) × EEPReq(Δνdet) obtained after a MW irradiation period tMW = 20 ms of sample I40 in (a and c), and of sample I20 in (b and d). The experimental spectra in (a and b) are extracted from the 2D-ELDOR spectra shown in Fig. 1 at Δνexc = −200 MHz (black), Δνexc = −100 MHz (red), Δνexc = 0 MHz (blue) and Δνexc = 100 MHz (magenta). The spectra in (c and d) are colored accordingly. The EPR spectrum at thermal equilibrium, EEPReq(Δdet), is shown in green. The simulated EPR spectra obtained using the eSD model with parameters as in Table 3 are shown in (c and d). | ||
Looking at the results in Table 3, we see that an increase of the radical concentration by a factor of 2 causes an increase of ΛeSD by a factor of 6. This increase manifests itself as a profound expansion of the depolarization area when comparing the EPR spectra of I20 and I40. Another observation is that the ΛeSD parameter stays constant when the temperature of the samples is varied between 10 and 20 K, while T1e varies by a factor of 6–8 (see Table 1).
3.3 The time dependence of the electron depolarization
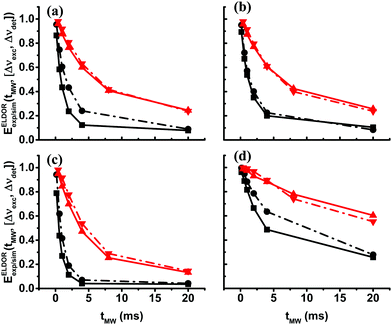
After reproducing the experimental results of the steady-state ELDOR profiles of the 40 mM and 20 mM samples with the eSD model, in this section, we show the temporal evolution of the electron depolarization by recording the ELDOR spectra of samples II40 and II20 at 10 K, after MW irradiation periods of different durations, tMW. The purpose of these measurements is to further substantiate the eSD model and to show that the non-steady-state spectra can be reproduced by using the single ΛeSD values derived from the steady-state spectra. In Fig. 4 the temporal dependences of the experimental ELDOR spectra, EELDORexp(Δνexc,[tMW,Δνdet]), are shown for two different detection frequencies, Δνdet = 0, 100 MHz, along with the simulation using the values T2e and ΛeSD, determined from the simulation of the ELDOR spectra under steady-state conditions. These profiles show clearly the effect of the 1H-SE process on the electron polarizations, in the form of narrow holes for tMW values less than 1 ms. To properly fit these 1H-SE contributions, it was necessary to change the value of ASE as a function of tMW. To demonstrate why we should expect a tMW dependence of ASE, we present in the SI spin dynamics calculations on a small spin system composed of 9 coupled electrons and a nucleus, rationalizing the source of this dependence. The dependence on tMW of the ASE values used in the simulation is given in Fig. 4c and f, for samples II40 and II20 respectively, both showing a decrease in ASE for longer tMW. For simplicity, the values of ASE were changed in discrete steps of 1 MHz. This still enabled reasonable fitting of the data, however, resulted in the step-like result in Fig. 4f. To show also the resemblance between the time constants characterizing the evolution of the experimental and simulated time dependent ELDOR profiles, we plot in Fig. 5 EELDORexp/sim(tMW,[Δνexc,Δνdet]) values for four different pairs of frequencies, Δνdet and Δνexc, as mentioned in the figure caption. Fitting the resulting tMW dependent functions to single exponential functions yield time constants τdep varying between 1 ms and 10 ms. The maximum deviation between simulations and experiments is found to be less than 10%. For a summary of all these τdep values, see Tables S1 and S2 in the ESI.†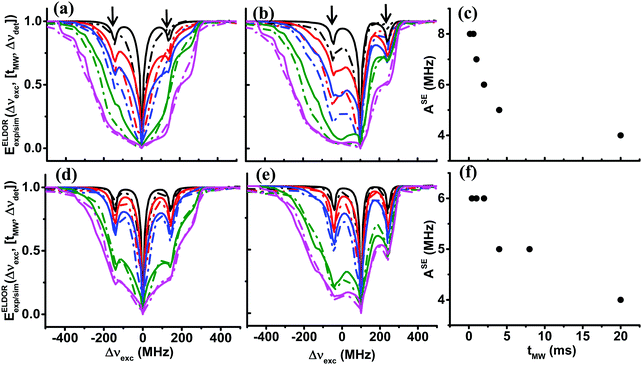 | ||
| Fig. 4 Experimental (dotted lines) and simulated (solid lines) ELDOR spectra, EELDORexp/sim(Δνexc,[tMW,Δνdet]), of sample II40 at 10 K, are shown for 5 different values of tMW with detection frequencies Δνdet = 0 MHz in (a), Δνdet = 100 MHz in (b), and of sample II20 also for 5 values of tMW, with detection frequencies Δνdet = 0 MHz in (d) and Δνdet = 100 MHz in (e). In (a and b) spectra are plotted for tMW = 0.15, 0.6, 1, 4, 20 ms and in (d and e) for tMW = 0.4, 1, 2, 8, 20 ms, in black, red, blue, green and magenta, respectively. The simulated solid lines are obtained using the eSD model with parameters listed in Table 1. The tMW dependent values of ASE used during the simulations are plotted for sample II40 in (c) and for sample II20 in (f). The frequency positions of the 1H-SE features in the spectra are marked with arrows. | ||
The τdep values are a complex function of the eSD parameter ΛeSD, the MW amplitude ω1 and the T1e value and of course, the values of Δνdet and Δνexc. If the electron depolarization would have been determined solely by the spectral diffusion mechanism, we would have expected the τdep times to be about inversely proportional to ΛeSD. Inspection of the τdep values of sample II40 and sample II20, with the ratio between their ΛeSD values equal to ∼6, reveals that the ratio between the τdep values at equal Δνdet and Δνexc with different T1e values varies between 3.5 and 5.5.
To verify further the validity of the eSD model, we also followed the temporal evolution of the electron polarizations back to equilibrium after the MW irradiation, on sample II20 at 10 K. The pulse sequence used for the evaluation consists of MW irradiation of fixed duration tMW, followed by a varying time delay trelax before the echo detection pulses. Here we chose a short MW irradiation time tMW = 100 μs, preventing any significant cross-relaxation induced spectral diffusion effect during this pulse. Normalized EPR spectra EEPRexp(trelax,Δνdet,[Δνexc]) were constructed by performing a large set of ELDOR experiments within the range of −200 MHz < Δνdet < 100 MHz as a function of trelax. The results are shown in Fig. 6a together with the thermal equilibrium EPR spectrum.
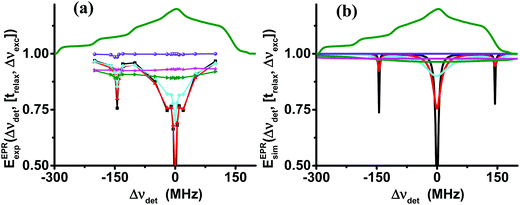 | ||
| Fig. 6 Experimental (a) and simulated (b) EPR spectra, EEPRexp/sim(Δνdet,[trelax,Δνexc]), of sample II20 at 10 K, obtained after a short MW pulse of tMW = 100 μs and an increasing delay time, trelax, shown in black (0.01 ms), red (0.2 ms), cyan (0.7 ms), green (5 ms), magenta (20 ms) and violet (200 ms). The simulated spectra in (b) are derived using the eSD model with parameters tabulated in Table 3. In (a) the 14N-SE depleted signals are marked with arrows. | ||
The narrow hole in the spectrum created by the short MW irradiation broadens due to the spectral diffusion, and after 5 ms the normalized EPR spectrum reaches a flat profile that shows that the unnormalized EPR spectrum itself has reached the same shape as the thermal equilibrium EPR spectrum, but with a smaller overall intensity. This intensity grows to its equilibrium value with a time constant T1e, that is the same for all Δνdet values. In addition to the hole at Δνexc = 0, we observe the effect of SE processes of 1H and 14N. In Fig. 6b we show the simulated normalized EPR spectra using again the value of ΛeSD derived from the ELDOR analysis. The broadening of the initial hole and the equilibration of the intensity over the whole spectrum are clearly reproduced by the simulation in Fig. 6b. However, a comparison between the experimental and simulated spectra shows a significant deviation. The sharp features in the experiment are missing in the simulation and the level of equilibration is much closer to 1 than in Fig. 6a. The reason for this difference is the fact that the 14N-SE depolarization process is not taken into account in the calculations. A preliminary simulation taking the 14N-SE process into account is shown in Fig. S4 (ESI†). The evolution of EEPRexp/sim(trelax,[ΔνdetΔνexc]) at detection frequencies that are not in the initial hole, burnt by the MW irradiation, during the initial 5 ms is shown in Fig. S4 (ESI†) for both samples. The initial decay can be fitted by single exponentials with a decay constant, τdecay. The time constants of these fitting procedures are summarized in Tables S3 and S4 (ESI†), which show that their experimental and simulated values agree within 10%. As this decay process is a direct consequence of spectral diffusion effects, this agreement of experiments and simulations is another indication that the model describes properly the spectral diffusion process.
The experiments and their analysis in this section have shown that, for each sample, a single ΛeSD value can explain the steady state ELDOR spectra, as well as the time behavior of the electron polarizations during and after MW irradiation. This shows that this empirical parameter indeed represents the dipolar interaction driven spectral diffusion mechanism. In the next section, we discuss in which manner ΛeSD depends on the average electron–electron dipolar interaction in our samples.
4. Temperature and radical concentration dependence of ΛeSD
In the above discussion, the eSD process was investigated on samples with two different TEMPOL concentrations, 20 mM and 40 mM, and at two temperatures, 10 K and 20 K. The eSD analysis showed that the ΛeSD value changes with radical concentration and not with temperature. Realizing that the average electron–electron dipolar interaction is proportional to the concentration, it is of interest to determine the concentration dependence of ΛeSD. To do so we prepared a new set of samples, IIIc, with different concentrations c = 20, 25, 30, 35, and 40 mM. Steady-state ELDOR experiments on all these new samples were conducted at temperatures 5, 10 and 20 K and on sample III40, also at 3 K. This time the data were recorded on the DNP spectrometer enabling data collection at 3 K. Except for the difference in the freezing procedure, described in the Experimental section, the experimental parameters were the same as for experiments on the EPR spectrometer reported above. The 20-to-40 mM range of concentrations was chosen because at lower values the spectral diffusion process is rather inactive. Above this range, the EPR spectrum is fully depolarized after a very short MW irradiation period. Typical ELDOR profiles for Δνdet = 0 MHz of samples III40 and III20 are shown in Fig. 7a and b. Additional profiles can be found in Fig. S5 in the ESI.† All profiles were analyzed as described above and the results are summarized in Table 4.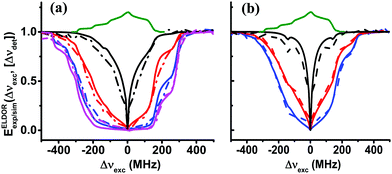 | ||
| Fig. 7 Experimental (dotted lines) and simulated (solid lines) steady-state ELDOR spectra EELDORexp/sim(Δνexc,[Δνdet]) of sample III40 in (a) and sample III20 in (b), with Δνdet = 0 MHz obtained at different temperatures are shown in magenta (3 K), blue (5 K), red (10 K) and black (20 K). The simulated spectra are derived using the eSD model with parameters tabulated in Table 3. | ||
| Sample | III20 | III25 | III30 | III35 | III40 |
|---|---|---|---|---|---|
| A SE/2π (MHz) | 1.5 | 1.5 | 2 | 2 | 2 |
| Λ eSD | 100 ± 20 μs−3 | 200 ± 20 μs−3 | 250 ± 25 μs−3 | 400 ± 25 μs−3 | 600 ± 50 μs−3 |
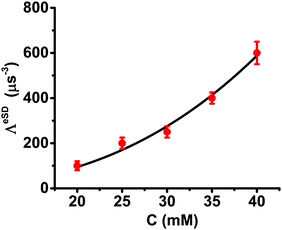
For all concentrations c, the value of ΛeSD was found to be temperature independent. The ASE parameter under the steady state conditions needed to be varied from 2 to 1.5 MHz to reproduce the depolarization for Δνexc values outside the EPR spectral range. The errors associated with ΛeSD were evaluated in the same way as described in the previous section. The relevant least square analysis for the data of the III20, III25 and III30 samples at 10 K is shown in Fig. S6 (ESI†). Another observation is the similarity between the T1e temperature dependence for all samples, as shown in Table 1. We can, therefore, conclude that changes in the ELDOR profiles as a function of temperature for a particular concentration are all a result of the temperature dependence of T1e. The dependence of ΛeSD in μs−3 units on concentration in mM units is plotted in Fig. 8. The points in this figure can be analyzed by fitting them to a simple exponential function:
ΛeSD(c) = λc![[small script l]](https://www.rsc.org/images/entities/char_e146.gif) , , | (9) |
![[small script l]](https://www.rsc.org/images/entities/char_e146.gif) = 2.6. An important consequence of this result is that we can express the change in ΛeSD as a result of a change in c from c1 to c2 as:
= 2.6. An important consequence of this result is that we can express the change in ΛeSD as a result of a change in c from c1 to c2 as: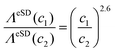 | (10) |
![[D with combining macron]](https://www.rsc.org/images/entities/i_char_0044_0304.gif) , between the radicals in the solid solutions should be proportional to the concentration, a similar dependence of ΛeSD on
, between the radicals in the solid solutions should be proportional to the concentration, a similar dependence of ΛeSD on ![[D with combining macron]](https://www.rsc.org/images/entities/i_char_0044_0304.gif) is expected. A similar dependence was already suggested in ref. 47, where we determined ΛeSD values from calculations on small electron spin systems. There we were able to describe the time domain and steady-state electron depolarisation profiles by introducing the zero quantum electron–electron cross-relaxation mechanism driven by electron flip–flip processes, governed by fluctuations of the zero-quantum
is expected. A similar dependence was already suggested in ref. 47, where we determined ΛeSD values from calculations on small electron spin systems. There we were able to describe the time domain and steady-state electron depolarisation profiles by introducing the zero quantum electron–electron cross-relaxation mechanism driven by electron flip–flip processes, governed by fluctuations of the zero-quantum ![[D with combining macron]](https://www.rsc.org/images/entities/i_char_0044_0304.gif) (S+iS−j + S−iS+j) terms.35,38,56 An effort in analyzing a set of calculated EPR spectra by using the eSD model resulted in the following relationship between the ΛeSD values for different
(S+iS−j + S−iS+j) terms.35,38,56 An effort in analyzing a set of calculated EPR spectra by using the eSD model resulted in the following relationship between the ΛeSD values for different ![[D with combining macron]](https://www.rsc.org/images/entities/i_char_0044_0304.gif) values; ΛeSD(D1)/ΛeSD(D2) = (D1/D2)3.1. This is explicitly shown in the ESI,† Section S3. Thus the experimental concentration dependence presented here suggests that the zero quantum electron–electron cross-relaxation should indeed be an important source of the spectral diffusion process.
values; ΛeSD(D1)/ΛeSD(D2) = (D1/D2)3.1. This is explicitly shown in the ESI,† Section S3. Thus the experimental concentration dependence presented here suggests that the zero quantum electron–electron cross-relaxation should indeed be an important source of the spectral diffusion process.
The temperature independence of ΛeSD may be related to the weak temperature dependence of the phase memory time (Tm), here observed for samples III20 and III40 and presented in Table 2. While the contribution of the dipolar flip–flop process on Tm57–59 is expected to decrease its value at high concentration,38,60 its temperature dependent influence is negligible. Similarly, the dipolar induced cross relaxation increases ΛeSD with concentration and leaves it unchanged as a function of temperature. Naively, we can say that the weak temperature dependence of Tm is a consequence of the temperature-independent cross-relaxation process rate in this range, which also approximately justifies the temperature independent behavior of ΛeSD obtained by ELDOR simulations.
We are aware of the fact that the ΛeSD(c) values of the present samples, measured on the DNP spectrometer, are about four times smaller than what was obtained from the samples measured on the EPR spectrometer. Together with this, we observe that the T1e values for each concentration measured using the DNP spectrometer are about 1.2 times longer than those measured using the EPR spectrometer. Whether these two differences are correlated is not clear at the moment. Changes in the distribution of the radicals caused by the sample preparation methods for the two spectrometers could be an origin for the differences in ΛeSD and T1e values. The “EPR” samples are frozen quickly by insertion into liquid nitrogen where, in the case of “DNP”, they are rather cooled slowly. Other differences may arise from the different B1 distributions in the samples, knowing that the EPR spectrometer exhibits a better B1 homogeneity at the position of the sample than the DNP spectrometer. We expect, however, that all these effects will not affect the concentration and temperature dependence of ΛeSD.
Conclusions
We have succeeded in using the eSD model to fit a series of ELDOR spectra obtained from frozen solutions with different concentrations of TEMPOL radicals at different temperatures. The time-domain analysis substantiated the physical meaning of the parameter ΛeSD as truly a rate constant for a spectral diffusion process. The temperature and concentration dependence studies show that it is insensitive to changes in temperature but concentration-dependent according to ΛeSD(c) ∝ c2.6. Comparing these results with model calculations on dipolar coupled electron spin systems can suggest that the spectral diffusion mechanism is at least partially governed by zero quantum cross-relaxation processes, which together with the static dipolar interaction, do not necessarily result in the standard TM model. Finally, we also showed that SE depolarization features in the ELDOR spectra, after the onset of the MW irradiation, can be accounted for by the effective ZQ and DQ rate matrices of the eSD model, only when the ASE parameter is allowed to be dependent on the duration of the MW field tMW.Conflicts of interest
There is no conflicts to declare.Acknowledgements
This work is supported by a grant of the Binational Science Foundation (Grant #2014149) and was made possible in part by the historic generosity of the Harold Perlman Family (D. G.). D. G. holds the Erich Klieger Professorial Chair in Chemical Physics.References
- J. G. Krummenacker, V. P. Denysenkov, M. Terekhov, L. M. Schreiber and T. F. Prisner, DNP in MRI: An in-bore approach at 1.5 T, J. Magn. Reson., 2011, 215, 94–99 CrossRef PubMed.
- K. Golman, R. i. Zandt, M. Lerche, R. Pehrson and J. H. Ardenkjaer-Larsen, Metabolic Imaging by Hyperpolarized 13C Magnetic Resonance Imaging for In vivo Tumor Diagnosis, Cancer Res., 2006, 66, 10855–10860 CrossRef CAS PubMed.
- A. B. Barnes, G. De Paëpe, P. C. A. Van Der Wel, K. N. Hu, C. G. Joo, V. S. Bajaj, M. L. Mak-Jurkauskas, J. R. Sirigiri, J. Herzfeld, R. J. Temkin and R. G. Griffin, High-field dynamic nuclear polarization for solid and solution biological NMR, Appl. Magn. Reson., 2008, 34, 237–263 CrossRef CAS PubMed.
- R. G. Griffin and T. F. Prisner, High Field Dynamic Nuclear Polarization-The Renaissance, Phys. Chem. Chem. Phys., 2010, 12, 5737–5740 RSC.
- P. Berruyer, M. Lelli, M. P. Conley, D. L. Silverio, C. M. Widdifield, G. Siddiqi, D. Gajan, A. Lesage, C. Copéret and L. Emsley, Three-dimensional structure determination of surface sites, J. Am. Chem. Soc., 2017, 139, 849–855 CrossRef CAS PubMed.
- C. D. Jeffries, Dynamic orientation of nuclei by forbidden transitions in paramagnetic resonance, Phys. Rev., 1960, 117, 1056–1069 CrossRef CAS.
- T. J. Schmugge and C. D. Jeffries, High dynamic polarization of protons, Phys. Rev., 1965, 138, A1785–A1801 CrossRef.
- A. V. Kessenikh, V. I. Lushchikov, A. A. Manenkov and Y. V. Taran, Proton Polarization In Irradiated Polyethylenes, Phys. Solid State, 1963, 5, 321–329 Search PubMed.
- C. F. Hwang and D. A. Hill, New effect in dynamic polarization, Phys. Rev. Lett., 1967, 18, 110–112 CrossRef CAS.
- C. F. Hwang and D. A. Hill, Phenomenological Model for the New Effect in Dynamic Polarisation, Phys. Rev. Lett., 1967, 19, 1011–1014 CrossRef CAS.
- A. V. Kessenikh, A. A. Manenkov and G. I. Pyatnitskii, On Explanation of Experimental Data on Dynamic Polarization of Protons in Irradiate Polyethylenes, Phys. Solid State, 1964, 6, 641–643 Search PubMed.
- D. S. Wollan, Dynamic nuclear polarization with an inhomogeneously broadened ESR line. I. Theory, Phys. Rev. B: Solid State, 1976, 13, 3671–3685 CrossRef CAS.
- D. S. Wollan, Dynamic nuclear polarization with an inhomogeneously broadened ESR line. II. Experiment, Phys. Rev. B: Solid State, 1976, 13, 3686–3696 CrossRef CAS.
- B. N. Provotorov, Magnetic resonance saturation in crystals, J. Exp. Theor. Phys., 1962, 14, 1126–1131 Search PubMed.
- M. Borghini, Spin-temperature model of nuclear dynamic polarization using free radicals, Phys. Rev. Lett., 1968, 20, 419–421 CrossRef CAS.
- A. Abragam and M. Goldman, Principles of dynamic nuclear polarisation, Rep. Prog. Phys., 1978, 41, 395–467 CrossRef CAS.
- A. Abragam and M. Borghini, Dynamic Polarization of Nuclear Targets, Prog. Low Temp. Phys., 1964, 4, 384–449 CAS.
- M. Goldman, Spin temperature and magnetic resonance in solids, London, 1970 Search PubMed.
- A. G. Redfield, Nuclear Magnetic Resonance Saturation and Rotary Saturation in Solids, Phys. Rev., 1955, 98, 1787–1809 CrossRef CAS.
- A. Karabanov, G. Kwiatkowski, C. Perotto, D. Wisniewski, J. McMaster, I. Lesanovsky and W. Kockenberger, Dynamic nuclear polarisation by thermal mixing: quantum theory and macroscopic simulations, Phys. Chem. Chem. Phys., 2016, 18, 30093–30104 RSC.
- F. Caracciolo, M. Filibian, P. Carretta, A. Rosso and A. De Luca, Evidences of spin-temperature in Dynamic Nuclear Polarization: an exact computation of the EPR spectrum, Phys. Chem. Chem. Phys., 2016, 18, 25655–25662 RSC.
- A. De Luca and A. Rosso, Dynamic Nuclear Polarization and the Paradox of Quantum Thermalization, Phys. Rev. Lett., 2015, 115, 1–5 CrossRef PubMed.
- W. T. Wenckebach, Dynamic nuclear polarization via thermal mixing: Beyond the high temperature approximation, J. Magn. Reson., 2017, 277, 68–78 CrossRef CAS PubMed.
- V. A. Atsarkin and A. V. Kessenikh, Dynamic Nuclear Polarization in Solids: The Birth and Development of the Many-Particle Concept, Appl. Magn. Reson., 2012, 43, 7–19 CrossRef.
- V. A. Atsarkin and F. S. Dzheparov, Spin Dynamics and Establishing of Internal Quasi-Equilibrium in Dilute Paramagnetic Solids, Z. Phys. Chem., 2017, 231, 545–560 CAS.
- D. Guarin, S. Marhabaie, A. Rosso, D. Abergel, G. Bodenhausen, K. L. Ivanov and D. Kurzbach, Characterizing Thermal Mixing DNP via Cross-Talk between Spin Reservoirs, J. Phys. Chem. Lett., 2017, 8, 5531–5536 CrossRef CAS PubMed.
- V. A. Atsarkin, Experimental Investigation of the Manifestations of the Spin-spin Interaction Reservoir in a System of EPR Lines Connected with Cross Relaxation, J. Exp. Theor. Phys., 1971, 32, 421–425 Search PubMed.
- S. Jannin, A. Comment and J. J. van der Klink, Dynamic Nuclear Polarization by Thermal Mixing Under Partial Saturation, Appl. Magn. Reson., 2012, 43, 59–68 CrossRef CAS.
- V. A. Atsarkin and M. I. Rodak, Temperature of Spin-Spin Interactions in Electron Spin Resonance, Phys.-Usp., 1972, 15, 251–265 CrossRef.
- V. A. Atsarkin, Verification of the Spin-spin Temperature Concept in Experiments on Saturation of Electron Paramagnetic Resonance, J. Exp. Theor. Phys., 1970, 31, 1012–1018 Search PubMed.
- Y. Hovav, I. Kaminker, D. Shimon, A. Feintuch, D. Goldfarb and S. Vega, The electron depolarization during dynamic nuclear polarization: measurements and simulations, Phys. Chem. Chem. Phys., 2015, 17, 226–244 RSC.
- J. Granwehr and W. Köckenberger, Multidimensional low-power pulse EPR under DNP conditions, Appl. Magn. Reson., 2008, 34, 355–378 CrossRef CAS.
- L. L. Buishvili, M. D. Zviadadze and G. R. Khutsishvili, Role of Spectral Diffusion and Dipole-dipole Reserviour in the Saturation of an Inhomogeneously Broadened Line, J. Exp. Theor. Phys., 1969, 29, 159–164 Search PubMed.
- V. A. Skrebnev, The Role of Reservoirs of Dipole–Dipole Interactions in Cross-Relaxation, Phys. Status Solidi, 1973, 60, 51–57 CrossRef CAS.
- M. K. Bowman and J. R. Norris, Cross relaxation of free radicals in partially ordered solids, J. Phys. Chem., 1982, 86, 3385–3390 CrossRef CAS.
- N. Bloembergen, S. Shapiro, P. S. Pershan and J. O. Artman, Cross-relaxation in spin systems, Phys. Rev., 1959, 114, 445–459 CrossRef CAS.
- V. G. Kustarev, Contribution to spin-spin cross relaxation theory, 1977, vol. 44, pp. 802–807 Search PubMed.
- K. M. Salikov and Y. D. Tsvetkov, in Time domain electron spin rsonance, ed. L. Kevan and R. Schwartz, New York, 1979, pp. 231–277 Search PubMed.
- Y. Hovav, A. Feintuch and S. Vega, Dynamic nuclear polarization assisted spin diffusion for the solid effect case, J. Chem. Phys., 2011, 134, 074509 CrossRef PubMed.
- A. S. Lilly Thankamony, J. J. Wittmann, M. Kaushik and B. Corzilius, Dynamic nuclear polarization for sensitivity enhancement in modern solid-state NMR, Prog. Nucl. Magn. Reson. Spectrosc., 2017, 102–103, 120–195 CrossRef CAS PubMed.
- T. V. Can, Q. Z. Ni and R. G. Griffin, Mechanisms of dynamic nuclear polarization in insulating solids, J. Magn. Reson., 2015, 253, 23–35 CrossRef CAS PubMed.
- C. Ramanathan, Dynamic nuclear polarization and spin-diffusion in non-conducting solids, Appl. Magn. Reson., 2008, 34, 409–421 CrossRef CAS.
- P. Schosseler, T. Wacker and A. Schweiger, Pulsed ELDOR detected NMR, Chem. Phys. Lett., 1994, 224, 319–324 CrossRef CAS.
- J. S. Hyde, R. C. Sneed and G. H. Rist, Frequency-swept electron-electron double resonance: DPPH in liquid and frozen solution, J. Chem. Phys., 1969, 51, 1404–1416 CrossRef CAS.
- A. Leavesley, D. Shimon, T. A. Siaw, A. Feintuch, D. Goldfarb, S. Vega, I. Kaminker and S. Han, Effect of electron spectral diffusion on static dynamic nuclear polarization at 7 Tesla, Phys. Chem. Chem. Phys., 2017, 19, 3596–3605 RSC.
- Y. Hovav, D. Shimon, I. Kaminker, A. Feintuch, D. Goldfarb and S. Vega, Effects of the electron polarization on dynamic nuclear polarization in solids, Phys. Chem. Chem. Phys., 2015, 17, 6053–6065 RSC.
- K. Kundu, A. Feintuch and S. Vega, Electron–Electron Cross-Relaxation and Spectral Diffusion during Dynamic Nuclear Polarization Experiments on Solids, J. Phys. Chem. Lett., 2018, 9, 1793–1802 CrossRef CAS PubMed.
- D. Goldfarb, Y. Lipkin, A. Potapov, Y. Gorodetsky, B. Epel, A. M. Raitsimring, M. Radoul and I. Kaminker, HYSCORE and DEER with an upgraded 95 GHz pulse EPR spectrometer, J. Magn. Reson., 2008, 194, 8–15 CrossRef CAS PubMed.
- A. Feintuch, D. Shimon, Y. Hovav, D. Banerjee, I. Kaminker, Y. Lipkin, K. Zibzener, B. Epel, S. Vega and D. Goldfarb, A Dynamic Nuclear Polarization spectrometer at 95 GHz/144 MHz with EPR and NMR excitation and detection capabilities, J. Magn. Reson., 2011, 209, 136–141 CrossRef CAS PubMed.
- J. Jeener, Superoperators in Magnetic Resonance, Academic Press, Inc., 1982, vol. 10 Search PubMed.
- M. H. Levitt and L. Di Bari, Steady state in magnetic resonance pulse experiments, Phys. Rev. Lett., 1992, 69, 3124–3127 CrossRef PubMed.
- M.-A. Geiger, A. Jagtap, M. Kaushik, H. Sun, D. Stöppler, S. Sigurdsson, B. Corzilius and H. Oschkinat, Efficiency of water-soluble nitroxide biradicals for dynamic nuclear polarization in rotating solids at 9.4 T: bcTol-M and cyolyl-TOTAPOL as new polarizing agents, Chem. – Eur. J., 2018, 24, 13485–13494 CrossRef CAS PubMed.
- M.-A. Geiger, M. Orwick-Rydmark, K. Märker, W. T. Franks, D. Akhmetzyanov, D. Stöppler, M. Zinke, E. Specker, M. Nazaré, A. Diehl, B.-J. van Rossum, F. Aussenac, T. Prisner, Ü. Akbey and H. Oschkinat, Temperature dependence of cross-effect dynamic nuclear polarization in rotating solids: advantages of elevated temperatures, Phys. Chem. Chem. Phys., 2016, 18, 30696–30704 RSC.
- E. M. M. Weber, H. Vezin, J. G. Kempf, G. Bodenhausen, D. Abergl and D. Kurzbach, Anisotropic longitudinal electronic relaxation affects DNP at cryogenic temperatures, Phys. Chem. Chem. Phys., 2017, 19, 16087–16094 RSC.
- D. Shimon, Y. Hovav, A. Feintuch, D. Goldfarb and S. Vega, Dynamic nuclear polarization in the solid state: a transition between the cross effect and the solid effect, Phys. Chem. Chem. Phys., 2012, 14, 5729–5743 RSC.
- D. P. Lin, D. F. Feng, F. Q. H. Ngo and L. Kevan, Electron-electron double resonance study of magnetic energy transfer between trapped electrons and radicals in organic glasses: Relation between dipolar cross relaxation times and dipolar interaction distances, J. Chem. Phys., 1976, 65, 3994–4000 CrossRef CAS.
- M. Romanelli and L. Kevan, Evaluation and interpretation of electron spin∼echo decay part I: Rigid samples, Concepts Magn. Reson., 1997, 9, 403–430 CrossRef CAS.
- A. D. Milov, K. M. Salikhov and Y. D. Tsvetkov, Effect of Spin Dipole-Dipole Interaction on Phase Relaxation in Magnetically Dilute Solid Bodies, Zh. Eksp. Teor. Fiz., 1972, 63, 2329–2335 CAS.
- J. Klauder and P. Anderson, Spectral Diffusion Decay in Spin Resonance Experiments, Phys. Rev., 1962, 125, 912–932 CrossRef CAS.
- D. T. Edwards, S. Takahashi, M. S. Sherwin and S. Han, Distance measurements across randomly distributed nitroxide probes from the temperature dependence of the electron spin phase memory time at 240 GHz, J. Magn. Reson., 2012, 223, 198–206 CrossRef CAS PubMed.
Footnote |
| † Electronic supplementary information (ESI) available. See DOI: 10.1039/c8cp05930f |
| This journal is © the Owner Societies 2019 |