Shell model extension to the valence force field: application to single-layer black phosphorus
Nicholas W.
Hackney
,
Damien
Tristant
,
Andrew
Cupo
 ,
Colin
Daniels
,
Colin
Daniels
 and
Vincent
Meunier
and
Vincent
Meunier
 *
*
Department of Physics, Applied Physics, and Astronomy, Rensselaer Polytechnic Institute, Troy, NY 12180, USA. E-mail: meuniv@rpi.edu
First published on 21st November 2018
Abstract
We propose an extension of the traditional valence force field model to allow for the effect of electronic polarization to be included in the inter-atomic potential. Using density functional theory as a reference, this model is parameterized for the specific case of single-layer black phosphorus by fitting the phonon dispersion relation over the entire Brillouin zone. The model is designed to account for the effect of induced dipole interaction on the long-wavelength (|![[q with combining right harpoon above (vector)]](https://www.rsc.org/images/entities/i_char_0071_20d1.gif) | → 0) modes for the case of homopolar covalent crystals. We demonstrate that the near Γ-point frequencies of the IR-active modes are substantially damped by the inclusion of the induced dipole interaction, in agreement with experiment. The fitting procedure outlined here allows for this model to be adapted to other materials, including but not limited to two-dimensional crystals.
| → 0) modes for the case of homopolar covalent crystals. We demonstrate that the near Γ-point frequencies of the IR-active modes are substantially damped by the inclusion of the induced dipole interaction, in agreement with experiment. The fitting procedure outlined here allows for this model to be adapted to other materials, including but not limited to two-dimensional crystals.
1 Introduction
Despite the broad availability and popularity of more descriptive and predictive modern theoretical and computational methods such as density functional theory (DFT), force fields for molecular dynamics remain of considerable relevance as they can be used to perform large-scale calculations and simulations that would be too computationally expensive (in terms of processing time and memory requirement) for DFT Born–Oppenheimer dynamics.1 Force fields have proven remarkably useful and have therefore become nearly ubiquitous in computational condensed matter physics,2–4 computational chemistry,5 and computational biology.6 The valence force field (VFF) is one example and has been used to study the thermomechanical properties of graphene and the electronic properties of GaAs,7,8 for instance. In addition, the importance of dynamical properties of low-dimensional materials is ubiquitous in many areas of research and applications relying on light–matter interactions. In this context, models capable of faithfully accounting for optical phonon modes are projected to play a key role in advancing nanoscience. However, because this potential only includes information about interactions related to the formation of atomic bonds, it fails to account for the effects of electronic polarization.9 These effects become important in the study of the lattice vibrations of ionic and homopolar covalent crystals (e.g., black phosphorus, wurtzite, diamond, scheelite, etc.), where the induced dipole interactions arising from the lattice vibrations themselves have an important effect on the long-wavelength (|![[q with combining right harpoon above (vector)]](https://www.rsc.org/images/entities/i_char_0071_20d1.gif) | → 0) vibrational modes.10 In this paper, we develop an extension to the VFF model to allow for the effect of electronic polarization to be accounted for. This extension is based off of the shell model proposed by Dick and Overhauser.11 It is designed to capture both the success of the VFF model at reproducing the mechanical properties of materials12,13 and the ability of the shell model at describing the effects of electronic polarization,10 and to combine them into one cohesive model. Here, we introduce the theoretical model and employ the non-linear Nelder–Mead method14 to determine a good set of numerical parameters by fitting the prediction of the model with those made using DFT. We focus on single-layer black phosphorus (SLBP), as it is a prototypical example of a homopolar crystal for which VFF fails at reproducing some specific vibrations.9 In particular, we demonstrate the resulting model's ability to improve the description of the long-wavelength phonon behavior in comparison to the pure VFF case. These improvements are indicative of the model's successful ability to describe both the atomic interactions mediated by covalent bonds and the interactions that arise from the induced dipoles that occur in vibrating crystals.
| → 0) vibrational modes.10 In this paper, we develop an extension to the VFF model to allow for the effect of electronic polarization to be accounted for. This extension is based off of the shell model proposed by Dick and Overhauser.11 It is designed to capture both the success of the VFF model at reproducing the mechanical properties of materials12,13 and the ability of the shell model at describing the effects of electronic polarization,10 and to combine them into one cohesive model. Here, we introduce the theoretical model and employ the non-linear Nelder–Mead method14 to determine a good set of numerical parameters by fitting the prediction of the model with those made using DFT. We focus on single-layer black phosphorus (SLBP), as it is a prototypical example of a homopolar crystal for which VFF fails at reproducing some specific vibrations.9 In particular, we demonstrate the resulting model's ability to improve the description of the long-wavelength phonon behavior in comparison to the pure VFF case. These improvements are indicative of the model's successful ability to describe both the atomic interactions mediated by covalent bonds and the interactions that arise from the induced dipoles that occur in vibrating crystals.
2 Model
The shell model, which is analogous to the Drude oscillator, is a phenomenological theory for describing polarization effects in molecular systems. It does so by placing charged massless shells around each atomic core in the system; these shells are then assumed to interact with each other and with the atomic cores as if they were attached via springs.10,11 While the notion that atoms are surrounded by virtual charged shells interacting via springs may seem a crude approximation, the approach has proven to be an effective method of heuristically describing the effects of electronic polarization while keeping the number of free parameters reasonably small.10 Note that since we intend merely to adapt the shell model for use alongside the more common VFF model, we will not provide details for the atomic–atomic interactions between the cores present in the original formulation of the shell model and assume that we can write our new total potential function in the form:| Φ = ϕ(VFF) + ϕ(shell), | (1) |
VFFs are a general class of simple empirical models for describing the inter-atomic forces of a given structure or molecule. They do so by describing the atomic potential in terms of simple quadratic functions of bond length and bond angle. From these potentials, a complete description of the molecular forces can be obtained and used to carry out molecular dynamic simulations. An example of such a VFF model is provided here for the specific case of SLBP:12
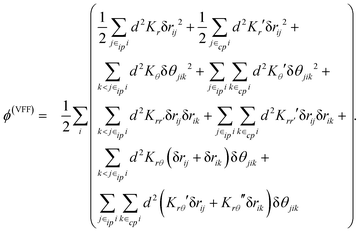 | (2) |
| K r | K r ′ | K θ | K θ ′ | K rr′ | K rr′′ | K rθ | K rθ ′ | K rθ ′′ | |
|---|---|---|---|---|---|---|---|---|---|
| Ref. 12 | 11.17 | 10.3064 | 1.18 | 0.9259 | −0.6763 | 1.2449 | 0.58 | 1.932 | 0.797 |
| This work | 10.60 | 10.45 | 0.86 | 0.63 | −0.77 | 1.36 | 0.61 | 2.02 | 0.94 |
Because all of the shell–shell and the shell–core terms are presumed to vary according to a harmonic potential, it is easy to write down ϕ(shell) in a general form as follows:
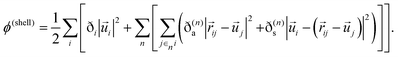 | (3) |
Here the inter-atomic bond vectors are denoted by ![[r with combining right harpoon above (vector)]](https://www.rsc.org/images/entities/i_char_0072_20d1.gif) and the displacement vectors of the shells from their equilibrium position around their cores are denoted by
and the displacement vectors of the shells from their equilibrium position around their cores are denoted by ![[u with combining right harpoon above (vector)]](https://www.rsc.org/images/entities/i_char_0075_20d1.gif) . The n-index represents groups of nth nearest neighbors. The force constant of the springs are represented by the ɀ coefficients, where the “s” and “a” subscripts denote that they belong to shell–shell terms and shell–other atom core terms, respectively. The i-index subscript denotes that the particular atom belongs to a shell–self-atom core term. The sum over i covers all atoms in the supercell while the sum over j∈ni runs over all elements j in the set of nth nearest neighbors of i. Lastly, the sum over n runs over groups of nth nearest neighbors of atom i.
. The n-index represents groups of nth nearest neighbors. The force constant of the springs are represented by the ɀ coefficients, where the “s” and “a” subscripts denote that they belong to shell–shell terms and shell–other atom core terms, respectively. The i-index subscript denotes that the particular atom belongs to a shell–self-atom core term. The sum over i covers all atoms in the supercell while the sum over j∈ni runs over all elements j in the set of nth nearest neighbors of i. Lastly, the sum over n runs over groups of nth nearest neighbors of atom i.
From this expression for the potential due to the shell terms, we obtain the force on an atom i from the shell around atom j by:
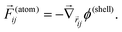 | (4) |
Similarly, we can take the force on the shell around atom i due to the shell around atom j to be:
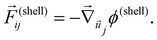 | (5) |
The atom–atom forces are all taken care of by the valence force field part of the potential and we do not need to elaborate on them here, as they have been described in detail elsewhere.12
Now that we have formulated the potential and specified how to find the forces, it is possible to use this new model to perform molecular dynamics simulations provided that one has a good set of VFF and shell force constants. While VFF force constants are widely available in the literature for a large range of materials,12,13 the shell model parameters will need to be found via fitting. In the rest of this work, we will focus on SLBP and use results from DFT as reference for the fitting procedure. The DFT phonon dispersion for SLBP used as a reference to parameterize the VFF is in qualitative agreement with the partial phonon dispersion of bulk BP obtained from inelastic neutron scattering experiments.16,17 In any case, rigorous parameterizations of force fields using only first-principles data constitutes an active area of research.18–22
For the sake of comparison, before we begin fitting the VFF + shell model to the DFT data, we optimize the VFF model by itself to ensure that we find a set of parameters for SLBP that is similar to the literature values.12 The resulting set of parameters are given, along with the literature values, in Table 1. We can see that this optimization does indeed yield a similar set of parameters to those reported by Midtvedt and Croy. Small differences can be explained by the use of a different reference for the fitting procedure and the fact that fitting is performed over the entire Brillouin zone (BZ).
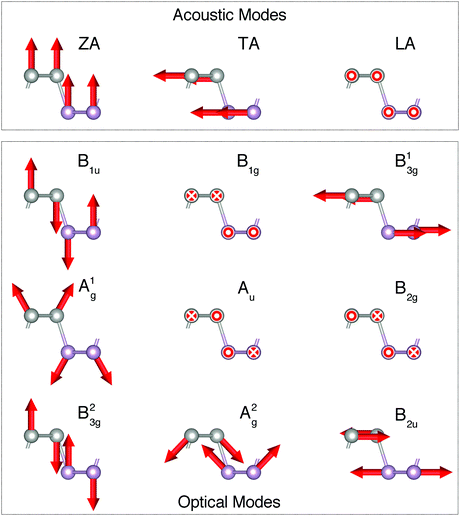
3 Single-layer black phosphorous and the failure of VFF
BP consists of weakly interacting AB-stacked puckered layers, each with inequivalent armchair and zigzag directions. It has an orthorhombic lattice and, in the few-layer configuration, it belongs to the Pmna space group for an odd number of layers and to Pbcm for an even number of layers. In both cases, as well as in bulk, BP belongs to the D2h point group. With knowledge of the space group symmetry it is possible to assign symmetry to each vibrational mode, as shown in Fig. 1. BP's electronic band gap is direct irrespective of the number of layers and increases with decreasing number of layers due to quantum confinement and a change in screening.23 In particular, the band gap of the pristine material is predicted to vary from 0.4 eV in the bulk up to 2.0 eV in the single-layer,24 and can be strongly modified by encapsulation due to a strong screening effect.25 Furthermore, the ambipolar mobility along the armchair direction can reach a value26 of 55![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 000 cm2 V−1 s−1, and is only 3.6 times smaller than the largest value ever measured (graphene).27 Understanding and optimizing such a desirable property requires a description of the crystal vibrations as scattering by phonons is known to contribute significantly to the reduction of carrier mobility. Accurate calculations of the phonon band structure and related properties from first-principles DFT can be time consuming, whereas ultrafast simulations can be performed with classical potentials. As mentioned earlier, a VFF potential has already been optimized for SLBP; however, it is based on experimental Raman and infrared frequencies (which only includes the Γ-point) and, because it neglects the description of polarization, the infrared modes are not described very well.12 Therefore we suggest to optimize the potential using a completely first-principles DFT phonon band structure including all high-symmetry directions, and to add non-local terms to the potential which include electronic polarization effects with the goal of improving the description of the infrared active modes, thus illustrating the usefulness of the model presented.
000 cm2 V−1 s−1, and is only 3.6 times smaller than the largest value ever measured (graphene).27 Understanding and optimizing such a desirable property requires a description of the crystal vibrations as scattering by phonons is known to contribute significantly to the reduction of carrier mobility. Accurate calculations of the phonon band structure and related properties from first-principles DFT can be time consuming, whereas ultrafast simulations can be performed with classical potentials. As mentioned earlier, a VFF potential has already been optimized for SLBP; however, it is based on experimental Raman and infrared frequencies (which only includes the Γ-point) and, because it neglects the description of polarization, the infrared modes are not described very well.12 Therefore we suggest to optimize the potential using a completely first-principles DFT phonon band structure including all high-symmetry directions, and to add non-local terms to the potential which include electronic polarization effects with the goal of improving the description of the infrared active modes, thus illustrating the usefulness of the model presented.
4 Computational details
Before moving to the fitting procedure, we first provide technical details on how the DFT calculations were performed. In order to obtain the first-principles vibrational data for free-standing SLBP, we used the Vienna Ab initio Simulation Package (VASP).28–31 The ion cores were modeled using the projector augmented wave (PAW) pseudo-potentials.32 For these calculations a plane-wave energy cutoff of 500 eV and a Gaussian smearing of 0.005 eV were used to yield well converged total energies and forces. In order to ensure that there were no unwanted interactions with the periodic images of our structure in the ẑ-direction, we added a 12 Å vacuum region. To include van der Waals (vdW) corrections in our calculations, we used the optB86b-vdW scheme.33,34 In fact, this functional improves the match with experiment as SLBP has a puckered structure, which suggests that non-covalent interactions take place between non-bonded atoms. For the sake of comparison, we have compared local, semilocal and non-local exchange–correlation (xc) functionals. The particular choice of (xc) functional is based of the study of thermodynamic and vibrational properties of freestanding and supported (on Au(111)) monolayer BP.35 In contrast to predictions made using other (xc) functionals, calculations performed with the optB86b-vdW scheme are in agreement with existing experimental evidence.36 During relaxation, all of the atoms were relaxed to a force cutoff of 10−4 eV Å−1 and the k-point sampling that we used was based off of a Γ-point centered grid. The primitive cells were optimized on a (10 × 15 × 1) k-point grid.The Phonopy code37 was used for the harmonic phonon calculations. For the DFT phonon dispersion relation we chose an (8 × 8 × 1) supercell to ensure that the forces, which were calculated using VASP, were well converged. For the VFF and VFF + shell calculations we used a (7 × 7 × 1) supercell. Prior to the VFF and VFF + shell force calculation, the atomic positions of the initial structure were relaxed with the lattice vectors (a = 4.51 Å and b = 3.30 Å)35 held constant to ensure that the k-path remained the same length. This is important as the residual cannot be properly calculated during the parameter optimization if the DFT and VFF or VFF + shell frequency data have a different k-space domain.
5 Fitting procedure
In this section we set out to demonstrate that the proposed shell extension to the VFF model resolves issues noted for SLBP. Initially, we randomly select a starting set of parameters, β, for the first through eighth nearest neighbor groups. As there are two terms per nth nearest neighbor group (a shell–shell term and a shell–core term) plus an additional term for the atom to “self-shell” interaction, the procedure requires, in principle, a total of 17 parameters to describe these eight terms. Terms beyond the eighth nearest neighbor group were left out as their contributions are increasingly negligible and the results are not significantly changed by their inclusion. Once a random set of parameters is chosen, the phonon dispersion is calculated using the proposed model. After this is done, a residual function is defined as follows: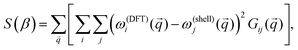 | (6) |
![[q with combining right harpoon above (vector)]](https://www.rsc.org/images/entities/i_char_0071_20d1.gif) ) is the frequency of the ith normal mode at the phonon wave vector
) is the frequency of the ith normal mode at the phonon wave vector ![[q with combining right harpoon above (vector)]](https://www.rsc.org/images/entities/i_char_0071_20d1.gif) . It is important to note that the sum over
. It is important to note that the sum over ![[q with combining right harpoon above (vector)]](https://www.rsc.org/images/entities/i_char_0071_20d1.gif) is actually an integral (crystal momentum being a continuous variable spanning the entire first BZ), however for our purposes here it is sufficient to use a discretized sum over the
is actually an integral (crystal momentum being a continuous variable spanning the entire first BZ), however for our purposes here it is sufficient to use a discretized sum over the ![[q with combining right harpoon above (vector)]](https://www.rsc.org/images/entities/i_char_0071_20d1.gif) -path. Gij(
-path. Gij(![[q with combining right harpoon above (vector)]](https://www.rsc.org/images/entities/i_char_0071_20d1.gif) ) is a weighting function defined to be:
) is a weighting function defined to be: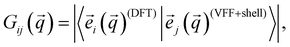 | (7) |
![[e with combining right harpoon above (vector)]](https://www.rsc.org/images/entities/i_char_0065_20d1.gif) i(
i(![[q with combining right harpoon above (vector)]](https://www.rsc.org/images/entities/i_char_0071_20d1.gif) ) represents the normalized eigenvector of the ith normal mode at phonon wave vector
) represents the normalized eigenvector of the ith normal mode at phonon wave vector ![[q with combining right harpoon above (vector)]](https://www.rsc.org/images/entities/i_char_0071_20d1.gif) . This optimization procedure was carried out several times, with different random initial parameters, to ensure that the results were indeed consistent and not highly dependent on the randomly selected initial parameter set.
. This optimization procedure was carried out several times, with different random initial parameters, to ensure that the results were indeed consistent and not highly dependent on the randomly selected initial parameter set.
We will now explain why we introduce the weighting function in the form provided above. Care must be taken to ensure that only bands belonging to the corresponding normal mode are compared to one another. While it is straightforward to do this for bands at high-symmetry points (provided that there is no accidental degeneracy), it becomes considerably more complicated as one moves along the ![[q with combining right harpoon above (vector)]](https://www.rsc.org/images/entities/i_char_0071_20d1.gif) -path from one symmetry point to another. This is because the accepted method for labeling bands is to order them by frequency,38 and this can introduce singular critical points that are not required by symmetry. A singular critical point is a point along the band where one or more component of
-path from one symmetry point to another. This is because the accepted method for labeling bands is to order them by frequency,38 and this can introduce singular critical points that are not required by symmetry. A singular critical point is a point along the band where one or more component of 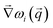 changes sign discontinuously. These unnecessary critical points are called accidental degeneracies (as opposed to essential degeneracies, which are required by symmetry) and are not manifestations of underlying physics, but are instead a result of the method of band labeling. As a result, if care is not taken to correct the appearance of accidental degeneracies then bands belonging to different normal modes may get compared during optimization. In addition, bands can be initially ordered incorrectly, especially when the force field parameters are far from their optimal values. These two effects often lead to a numerical frustration of the minimization that prevents the optimization algorithm from converging to a physically significant minimum, as the residual will have been calculated by comparing bands that do not belong to the same normal mode. The weighting term is included in the residual function to alleviate this situation, as the eigenvectors of two distinct normal modes (at a given
changes sign discontinuously. These unnecessary critical points are called accidental degeneracies (as opposed to essential degeneracies, which are required by symmetry) and are not manifestations of underlying physics, but are instead a result of the method of band labeling. As a result, if care is not taken to correct the appearance of accidental degeneracies then bands belonging to different normal modes may get compared during optimization. In addition, bands can be initially ordered incorrectly, especially when the force field parameters are far from their optimal values. These two effects often lead to a numerical frustration of the minimization that prevents the optimization algorithm from converging to a physically significant minimum, as the residual will have been calculated by comparing bands that do not belong to the same normal mode. The weighting term is included in the residual function to alleviate this situation, as the eigenvectors of two distinct normal modes (at a given ![[q with combining right harpoon above (vector)]](https://www.rsc.org/images/entities/i_char_0071_20d1.gif) -point and computed by the two different methods) are orthonormal to each other when the procedure is close to convergence. Numerically, the introduction of the weighting function makes it convenient to just take the difference between all bands and then multiply them by the magnitude of the inner product of the eigenvectors to filter out the incorrect pairs.
-point and computed by the two different methods) are orthonormal to each other when the procedure is close to convergence. Numerically, the introduction of the weighting function makes it convenient to just take the difference between all bands and then multiply them by the magnitude of the inner product of the eigenvectors to filter out the incorrect pairs.
The residual function S can then be minimized with respect to β in order to obtain a complete set of good force parameters for a given material. We used the non-linear Nelder–Mead algorithm to carry out this minimization as it does not require derivatives of the residual function to be taken with respect to the parameters, which in our case would be difficult.14
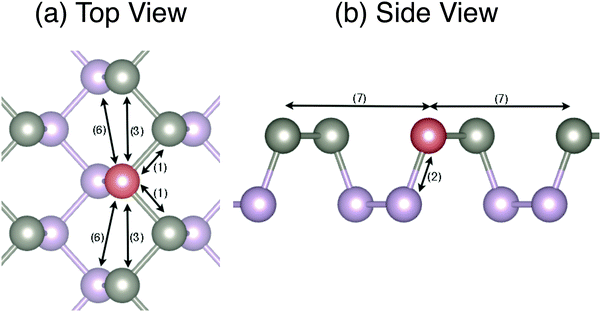
In the specific case of SLBP, we found that the fourth, fifth, and eighth nearest neighbor terms introduced non-physical instabilities into the structure that were manifested as imaginary frequencies in the phonon dispersions, and they were therefore neglected. This leaves us with only the first, second, third, sixth and seventh nearest neighbor terms in the shell portion of the potential (11 shell parameters). The atomic relations that these terms refer to are depicted in Fig. 2. For the initial optimization of the shell force constants we used the VFF and corresponding force constants outlined by Midtvedt and Croy for SLBP.12 The initial force constants are given in Table 1.
Once the initial shell parameter optimization is complete, with the VFF parameters held constant, the entire potential is reoptimized with all 20 parameters (9 VFF + 11 shell). The final set of force constants is given in Table 2.
| K r | K r ′ | K θ | K θ ′ | K rr′ | K rr′′ | K rθ | K rθ ′ | K rθ ′′ |
| 10.4079 | 8.8248 | 0.8489 | 0.8113 | 0.0322 | 0.9197 | 0.2593 | 1.3175 | 0.4056 |
| ɀ i | ɀ a | ɀ s | ɀ a′ | ɀ s′ | ɀ (2)a | ɀ (2)s | ɀ (6)a | ɀ (6)s | ɀ (5)a | ɀ (5)s |
| −1.108 | −0.852 | 0.1957 | −10.2613 | −0.014 | 0.0624 | 11.6562 | 0.1005 | 0.1075 | 0.0584 | 0.1451 |
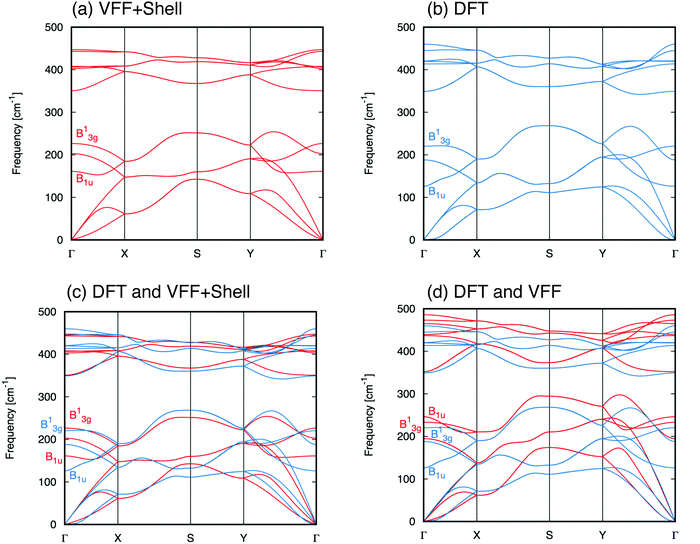
Once this final set of optimized parameters is found, we can use it with the proposed model to calculate the phonon dispersion relation. A plot of the resulting spectrum along with the DFT result is shown in Fig. 3.
In order to get a better understanding of how the inclusion of the electronic polarization via the shell model extension affects the normal modes of lattice vibrations for SLBP, we have superimposed the phonon dispersion plots obtained with our VFF + shell model over the DFT result and displayed it alongside a similar comparison between the plain VFF and DFT dispersions. These juxtaposed plots are displayed in Fig. 3 and the Γ-point frequencies of each normal mode, as calculated with each of these three different models, are given in Table 3.
| Mode | DFT | VFF | VFF + shell |
|---|---|---|---|
| B1u | 126.1 | 246.1 | 162.6 |
| B1g | 188.0 | 194.7 | 209.1 |
| B13g | 220.4 | 233.2 | 230.1 |
| A1g | 349.1 | 352.0 | 348.9 |
| Au | 413.7 | 439.5 | 407.5 |
| B2g | 419.7 | 437.0 | 410.5 |
| B23g | 420.6 | 465.1 | 412.0 |
| A2g | 445.1 | 473.3 | 443.2 |
| B2u | 460.0 | 485.9 | 452.1 |
From these comparisons it is clear that, aside from a general improvement of fit, the apparent “twisting” of the B1u and B13g modes in the VFF-only result was resolved and the overall behavior of the high-frequency modes are greatly improved by the shell model extension. Note that the B1u mode, which suffered a long-wavelength (|![[q with combining right harpoon above (vector)]](https://www.rsc.org/images/entities/i_char_0071_20d1.gif) | → 0) damping of ∼83 cm−1 from the addition of the shell extension to the VFF model, is an IR-active mode.9,39 This observation is important as it is understood9,10,12 that IR-active modes are highly sensitive to the effects of electronic polarization in the near Γ-point region of k-space and their behavior cannot be accurately described without taking these interactions into account.
| → 0) damping of ∼83 cm−1 from the addition of the shell extension to the VFF model, is an IR-active mode.9,39 This observation is important as it is understood9,10,12 that IR-active modes are highly sensitive to the effects of electronic polarization in the near Γ-point region of k-space and their behavior cannot be accurately described without taking these interactions into account.
6 Conclusion
We proposed an extension to the traditional VFF model, based on the historical shell model, to allow for the effects of electronic polarization to be accounted for in the study of lattice vibrations using classical methods. We showed how the developed model can be fitted to reproduce information for a specific material (in our case we chose to fit it to SLBP). This allowed us to calculate the phonon dispersion relation using the new model and compare it and the VFF-only result to the phonon dispersion found using DFT. We highlighted the importance of the effects of electronic polarization in accurately describing the long-wavelength behavior of the IR-active modes, as well as the high-frequency modes of homopolar covalent crystals. This enhancement is important as it allows for an improved use of classical methods in the study of the lattice vibrations of low-dimensional covalent crystals.Conflicts of interest
There are no conflicts to declare.Acknowledgements
Part of this work was performed using supercomputing resources provided by the Center for Computational Innovations (CCI) at Rensselaer Polytechnic Institute. DT acknowledges support from the Office of Naval Research. AC was supported by NSF Grant EFRI 2-DARE (EFRI-1542707).References
- T. P. Senftle, S. Hong, M. M. Islam, S. B. Kylasa, Y. Zheng, Y. K. Shin, C. Junkermeier, R. Engel-Herbert, M. J. Janik, H. M. Aktulga, T. Verstraelen, A. Grama and A. C. T. van Duin, npj Comput. Mater., 2016, 2, 15011 CrossRef CAS.
- D. W. Brenner and B. J. Garrison, Phys. Rev. B: Condens. Matter Mater. Phys., 1986, 34, 1304 CrossRef CAS.
- C. Pryor, J. Kim, L. W. Wang, A. J. Williamson and A. Zunger, J. Appl. Phys., 1998, 83, 2548–2554 CrossRef CAS.
- S. Bose, W. J. Fan and D. H. Zhang, presented in part at the 2017 Conference on Lasers and Electro-Optics Pacific Rim (CLEO-PR), Singapore, 2017 Search PubMed.
- S. C. Kohale, S. Pratihar and W. L. Hase, J. Phys. Chem. Lett., 2018, 9, 1554–1560 CrossRef CAS PubMed.
- E. Boulanger, L. Huang, C. Rupakheti, A. D. MacKerell Jr and B. Roux, J. Chem. Theory Comput., 2018, 14, 3121–3131 CrossRef CAS PubMed.
- A. Lajevardipour, M. Neek-Amal and F. Peeters, J. Phys.: Condens. Matter, 2012, 24, 175303 CrossRef CAS PubMed.
- C. Delerue and M. Lannoo, Phys. Rev. B: Condens. Matter Mater. Phys., 1988, 38, 3966 CrossRef CAS.
- C. Kaneta, H. Katayama-Yoshida and A. Morita, J. Phys. Soc. Jpn., 1986, 55, 1213–1223 CrossRef CAS.
- G. Venkataraman, L. Feldkamp and V. Sahni, Dynamics of perfect crystals, MIT Press, Cambridge, 1975 Search PubMed.
- B. G. Dick Jr and A. W. Overhauser, Phys. Rev., 1958, 112, 90 CrossRef.
- D. Midtvedt and A. Croy, Phys. Chem. Chem. Phys., 2016, 18, 23312–23319 RSC.
- V. Perebeinos and J. Tersoff, Phys. Rev. B: Condens. Matter Mater. Phys., 2009, 79, 241409 CrossRef.
- J. A. Nelder and R. Mead, Comput. J., 1965, 7, 308–313 CrossRef.
- J. Wan, Y.-W. Tan, J.-W. Jiang, T. Chang and X. Guo, arXiv:1808.01714v1, 2018.
- Y. Fujii, Y. Akahama, S. Endo, S. Narita, Y. Yamada and G. Shirane, Solid State Commun., 1982, 44, 579–582 CrossRef CAS.
- Y. Yamada, Y. Fujii, Y. Akahama, S. Endo, S. Narita, J. Axe and D. McWhan, Phys. Rev. B: Condens. Matter Mater. Phys., 1984, 30, 2410 CrossRef CAS.
- F. Ercolessi and J. B. Adams, EPL, 1994, 26, 583 CrossRef CAS.
- S. Izvekov, M. Parrinello, C. J. Burnham and G. A. Voth, J. Chem. Phys., 2004, 120, 10896–10913 CrossRef CAS PubMed.
- P. Brommer and F. Gähler, Modell. Simul. Mater. Sci. Eng., 2007, 15, 295 CrossRef CAS.
- H. Sheng, M. Kramer, A. Cadien, T. Fujita and M. Chen, Phys. Rev. B: Condens. Matter Mater. Phys., 2011, 83, 134118 CrossRef.
- L. Vanduyfhuys, S. Vandenbrande, J. Wieme, M. Waroquier, T. Verstraelen and V. Van Speybroeck, J. Comput. Chem., 2018, 39, 999–1011 CrossRef CAS PubMed.
- H. Liu, A. T. Neal, Z. Zhu, Z. Luo, X. Xu, D. Tomanek and P. D. Ye, ACS Nano, 2014, 8, 4033–4041 CrossRef CAS PubMed.
- L. Liang, J. Wang, W. Lin, B. G. Sumpter, V. Meunier and M. Pan, Nano Lett., 2014, 14, 6400–6406 CrossRef CAS PubMed.
- D. Y. Qiu, F. H. da Jornada and S. G. Louie, Nano Lett., 2017, 17, 4706–4712 CrossRef CAS PubMed.
- J. Yang, S. Tran, J. Wu, S. Che, P. Stepanov, T. Taniguchi, K. Watanabe, H. Baek, D. Smirnov, R. Chen and C. N. Lau, Nano Lett., 2017, 18, 229–234 CrossRef PubMed.
- K. Bolotin, K. Sikes, Z. Jiang, M. Klima, G. Fudenberg, J. Hone, P. Kim and H. Stormer, Solid State Commun., 2008, 146, 351–355 CrossRef CAS.
- G. Kresse and J. Hafner, Phys. Rev. B: Condens. Matter Mater. Phys., 1993, 47, 558–561 CrossRef CAS.
- G. Kresse and J. Hafner, Phys. Rev. B: Condens. Matter Mater. Phys., 1994, 49, 14251–14269 CrossRef CAS.
- G. Kresse and J. Furthmüller, Phys. Rev. B: Condens. Matter Mater. Phys., 1996, 54, 11169–11186 CrossRef CAS.
- G. Kresse and J. Furthmüller, Comput. Mater. Sci., 1996, 6, 15–50 CrossRef CAS.
- P. E. Blöchl, Phys. Rev. B: Condens. Matter Mater. Phys., 1994, 50, 17953–17979 CrossRef.
- J. Klimes, D. R. Bowler and A. Michaelides, J. Phys.: Condens. Matter, 2009, 22, 022201 CrossRef PubMed.
- J. Klimes, D. R. Bowler and A. Michaelides, Phys. Rev. B: Condens. Matter Mater. Phys., 2011, 83, 195131 CrossRef.
- D. Tristant, A. Cupo and V. Meunier, 2D Mater., 2018, 5, 035044 CrossRef.
- J. L. Zhang, S. Zhao, C. Han, Z. Wang, S. Zhong, S. Sun, R. Guo, X. Zhou, C. D. Gu and K. D. Yuan, et al. , Nano Lett., 2016, 16, 4903–4908 CrossRef CAS PubMed.
- A. Togo and I. Tanaka, Scr. Mater., 2015, 108, 1–5 CrossRef CAS.
- J. C. Phillips, Phys. Rev., 1956, 104, 1263–1277 CrossRef CAS.
- Y. Aierken, D. Cakir, C. Sevik and F. M. Peeters, Phys. Rev. B: Condens. Matter Mater. Phys., 2015, 92, 081408 CrossRef.
| This journal is © the Owner Societies 2019 |