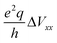14N NQR spectroscopy reveals the proton position in N–H⋯N bonds: a case study with proton sponges
Alan
Gregorovič
 *a,
Tomaž
Apih
a,
Veselko
Žagar
a and
Janez
Seliger
ab
*a,
Tomaž
Apih
a,
Veselko
Žagar
a and
Janez
Seliger
ab
aInstitute “Jožef Stefan”, Jamova 39, 1000 Ljubljana, Slovenia. E-mail: alan.gregorovic@ijs.si
bFaculty of Mathematics and Physics, University of Ljubljana, Jadranska 19, 1000 Ljubljana, Slovenia
First published on 27th November 2018
Abstract
The position of protons in hydrogen bonds is often uncertain to some degree, as the technique most often used for structure determination, X-ray diffraction, is sensitive to electron density, which is not particularly abundant around protons. In hydrogen bonds, protons introduce an additional problem: the potential for proton motion is inherently anharmonic and thus requires the consideration of nuclear quantum effects (NQEs). Here, we demonstrate that 14N NQR spectroscopy is able to rather accurately determine proton positions in N–H⋯N bonds, in certain cases with an accuracy comparable to that of X-ray and neutron diffraction at room temperature. We first derive, using ab initio calculations considering also the NQEs, a relation between the proton distance from the bond midpoint and the difference between the quadrupole coupling constants for the two nitrogen sites. The found relation is linear with a proportionality constant of 0.108 Å MHz−1 for tertiary amine nitrogens. Then, we validate our theoretical calculations experimentally, using several 1,8-bis(dimethylamino)naphthalene (DMAN) complexes.
Introduction
Hydrogen bonds are ubiquitous in organic molecules and their crystals and, because they are stronger than van der Waals interactions, they often substantially influence material properties. The position of heavy atoms in the bond (N, O, F) is usually well known, however, the position of protons is known to a lesser extent, with an accuracy changing from one system to another. This inaccuracy is a characteristic of the principal technique for structure determination in solids: X-ray diffraction. Namely, X-ray diffraction is sensitive to electron density, which is low around protons, but more importantly, this electron density deviates significantly from spherical symmetry.1 Advanced refinement techniques, like difference Fourier maps2 and Hirshfeld atom refinement,3 provide better results, but they also require higher quality experimental data or include extensive calculations. Protons in hydrogen bonds introduce a further problem for X-ray diffraction. The small proton mass makes hydrogen motion inherently quantum mechanical in nature, and effects such as zero-point motion and tunneling, commonly referred to as nuclear quantum effects (NQEs), become important.4–8 When protons move in a harmonic potential, NQEs are rather easily taken into account by augmenting the atomic displacement parameters. However, the potential for proton motion in hydrogen bonds is very often anharmonic, in many cases even of a double well type, e.g. when the donor and acceptor atoms have similar proton affinities.5 In such situations, the anisotropy of the atomic displacement is large and non-symmetric, and in general, difficult to properly account for, especially because protons make only a small contribution to the X-ray intensity.The first alternative to X-ray diffraction is neutron diffraction, which provides accurate hydrogen bond geometries, since neutrons are scattered by nuclei. However, the availability of appropriate infrastructure is limited and thus the method is used less often.
One of the more successful other techniques for structure determination, especially for organic molecules, is Nuclear Magnetic Resonance (NMR). This technique is not ideal to study hydrogen bonds in solids but it is nevertheless often used.9–15 Here, the main issues are: crowded 1H NMR spectra,16 substitution of the hydrogen bond proton with 2H modifies bond geometry, and 17O and 15N have a very low natural abundance,17–19 while 14N has broad spectral lines, due to its large nuclear quadrupole moment. Quadrupole nuclei, like 2H, 14N and 17O, can be also observed indirectly, e.g. with various double resonance techniques,20 providing the nuclear quadrupole resonance (NQR) frequencies rather than chemical shifts, but the sensitivity of such experiments is almost always low. Other nuclei not part of the hydrogen bond, mainly 13C and sometimes 35Cl, are also used, but their NMR/NQR parameters may not easily be related to the hydrogen bond geometry. Nevertheless, the hydrogen bond geometry is an important parameter used in many ab initio studies so that research in this field is still intense.
In this paper, we show how 14N NQR spectroscopy is used to determine the proton position in intramolecular N–H⋯N hydrogen bonds. The motivation for this work is the following: The hydrogen bond proton is known to have a large impact on the electric field gradient (EFG) tensors at the position of the donor and acceptor atoms.21 In the N–H⋯N bond, the nitrogen EFG is roughly a superposition of two contributions due to two types of nitrogen valence electrons. The first contribution comes from the nitrogen lone pair, which is part of the hydrogen bond, and its orbital is strongly influenced by the hydrogen bond proton. A proton closer to the nitrogen atom decreases this contribution, whereas a more distant proton increases it. The second contribution to the EFG comes from the electrons that do not participate in the hydrogen bond. The orbitals of these electrons are mainly defined by the functional groups attached to the nitrogen atoms and unaffected by the position of the hydrogen bond proton. This contribution can then be considered as constant across some similar samples. Thus, by measuring the EFG at both nitrogen sites, which can easy be carried out with NQR spectroscopy, one should obtain some quantitative information on the proton position within the N–H⋯N bond.
We have analyzed this dependence theoretically, using ab initio calculations and vibrational analysis, as well as experimentally, with 14N NQR spectroscopy and published crystallographic data. We find that the accuracy of the method presented here is better than that of X-ray diffraction in certain cases, especially at room temperature. Compared to neutron diffraction, the advantage of 14N NQR spectroscopy is the possibility to use samples as synthesized, most importantly avoiding the preparation of single crystals.
This is not the first use of 14N NQR spectroscopy for N–H⋯N bond studies with an interest in proton transfer, however, the focus in the previous studies20–22 was on molecular conformations associated with proton dynamics, rather than on proton position.
The compounds used in this study are a selection of 1,8-bis(dimethylamino)naphthalene (DMAN) salts, also known as proton sponges.23,24 These compounds are suitable model compounds, as accurate crystal structures are available for many of them, whereas the proton is known to exhibit shifts in a wide range.25–31
Theoretical part
DMAN salt geometry
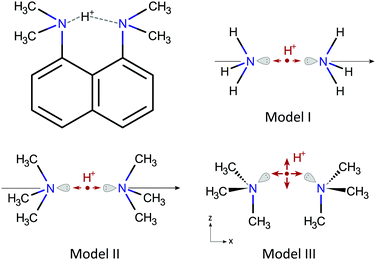
DMAN salts, or complexes, consist of a DMAN-H+ cation and an anion usually of organic origin. The DMAN-H+ cation, shown in Fig. 1, contains an intramolecular N–H⋯N bond, which is incorporated in a rather rigid (naphthalene) skeleton of an almost C2v symmetry. The skeleton geometry changes only slightly from one salt to another; all N–N distances are between 2.56 and 2.64 Å, which makes the N–H⋯N bond of a short, strong type,32 with a characteristic low barrier potential. In a hypothetically isolated cation, the proton would occupy a central position, given the C2v symmetry, between the two nitrogen sites at some distance from the N–N axis since the bond is not linear. In the presence of anions, however, the symmetry of the bond is lifted by interaction with the anion and the proton shifts towards either nitrogen site by a variable amount, while its distance to the N–N axis and the N–H⋯N defined plane remain practically unaffected. The hydrogen bond in DMAN-H+ is relatively isolated, thus, the observed proton displacements are mainly due to the presence of the nearest anion, which is located above the N–H⋯N bond, with its most electronegative part, usually an oxygen ion, almost in the N–H⋯N plane.The models
To better understand the relation between the proton displacement and the nitrogen EFG tensors in a N–H⋯N bond, we devised three models for isolated DMAN-H+ cations progressively increasing in complexity, as shown in Fig. 1.Model I is a simple and popular model for linear N–H⋯N bonds33–35 and it contains two ammonium molecules oriented head to head on a C3v symmetry axis; the hydrogen bond proton is here located between the two nitrogen atoms. Within the model, the proton motion is constrained to the symmetry axis. This model has been studied from several points of view by different authors, and here, it should give us some additional insights related to NQR parameters. Nevertheless, this model is not very suitable to describe N–H⋯N bonds in molecules from the NQR perspective, as nitrogen in molecules is often bound to at least one carbon, which is known to appreciably modify 14N NQR parameters.
Model II is an evolution of Model I, where the hydrogen atoms have been replaced by methyl groups, thus obtaining two trimethylamine molecules oriented head to head. The symmetry of the model is preserved and the hydrogen bond proton is still confined to the symmetry axis. Model II should give us qualitatively similar results to Model I, but quantitatively relevant results for the DMAN-H+ cation.
Model III is a non-linear version of Model II, which is obtained by rotating the two trimethylamine molecules around the nitrogen atom into a configuration similar to the DMAN-H+ ion, which contains a pair of nearly parallel N–C bonds. The symmetry of Model III is Cs. The single mirror plane is defined by the two nitrogen atoms and the two, here parallel, N–C bonds. The symmetry of the model without the proton is C2v, as for the naphthalene skeleton in proton sponges. The N–H⋯N bond in Model III is non-linear and the proton motion is still restricted, but now to the symmetry plane.
The geometry of all models is defined by the N–N distance rNN with the proton coordinates x and z relative to the N–N midpoint, with x running along the N–N direction and z perpendicular to it. For linear N–H⋯N models (Model I and II), z = 0 at all times. The anion itself is not included explicitly in any model, but instead, its influence on the proton is modeled by the inclusion of an anion-specific perturbation potential. More complicated models for proton sponge cations have been treated by other authors, e.g. by Horbatenko et al.,36 but none of these studies included NQR parameters. Here, we decided to keep our models as simple as possible, thus enabling us to extract some general properties.
Ab initio calculations
The first set of calculations involved using ab initio calculations for each model to obtain two quantities as a function of the model geometry (rNN, x, z): (i) the cation potential energy surface (PES) E+e and (ii) the EFG at both nitrogen sites VLμν and VRμν, for the left and right nitrogen site, respectively. The geometries of the ammonium and trimethylamine molecules were not altered during these calculations and were fixed to their optimized geometries.All ab initio calculations were carried out at the MP2/6-311++G** level with the Firefly quantum chemical package,37 which is partially based on the GAMESS program.38
Vibrational analysis
In the second set of calculations, we considered the NQEs in the presence of anions. We first invoked the adiabatic approximation (by freezing rNN) to find the proton ground state wavefunction ψ0 in a cation–anion complex by solving the Schrödinger equation for an anion modified potential for proton motion, U = E+e + δU, where δU is the anion contribution. Here, δU = Exx had a simple form, which considered only an effective electric field Ex pointing in the direction of the coordinate x. The Schrödinger equation was solved for each value of rNN and Ex separately. Finally, the found ψ0 was used to calculate the expectation values of proton coordinates 〈x〉 and 〈z〉, and nitrogen EFG tensors 〈VLμν〉 and 〈VRμν〉. The presence of different anions was simulated by using different Ex, and in a similar way, the slightly different DMAN-H+ geometries were simulated with several rNN. Note, 〈x〉, 〈z〉 (〈z〉 = 0 for Models I and II) and rNN define here the experimentally observed hydrogen bond geometry while 〈VLμν〉 and 〈VRμν〉 define quantities measured by NQR spectroscopy. Within these calculations, the influence of Ex on either VLμν or VRμν is completely neglected, thus the anions do not directly contribute to the nitrogen EFG tensors.The vibrational analysis was carried out with a matrix formalism in the program Mathematica. The proton wavefunctions were expanded on base functions of a harmonic oscillator. The numerically determined potentials were fitted with a polynomial function of coordinates x and z, with a 4th order for x and 2nd order for z. These functions were then used to determine the potential matrix elements. The proton wavefunction expansion coefficients were finally determined by solving the Schrödinger equation.
Experimental part
Samples
The polycrystalline DMAN complexes selected for the study are listed in Table 1. The complexes were prepared by the crystallization of a methanol solution of stoichiometric amounts of DMAN and the corresponding organic acid at room temperature. Only the 1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1 complex DMAN–chloranilic acid was left to crystallize at 4 °C. A complex was assumed to be successfully obtained when sharp 14N NQR lines at frequencies different from DMAN were observed and the proton spin–lattice relaxation time T1 was a single component. The sharp NQR lines confirm the crystalline character of the substance, whereas the shifts of the NQR frequencies from the DMAN values confirm that the complex is formed. The single component proton T1 is a sign that a single substance is present. Samples 1–7, with known crystallographic structures,27–39 were also confirmed using powder X-ray diffraction. All reagents were purchased from Sigma-Aldrich.
1 complex DMAN–chloranilic acid was left to crystallize at 4 °C. A complex was assumed to be successfully obtained when sharp 14N NQR lines at frequencies different from DMAN were observed and the proton spin–lattice relaxation time T1 was a single component. The sharp NQR lines confirm the crystalline character of the substance, whereas the shifts of the NQR frequencies from the DMAN values confirm that the complex is formed. The single component proton T1 is a sign that a single substance is present. Samples 1–7, with known crystallographic structures,27–39 were also confirmed using powder X-ray diffraction. All reagents were purchased from Sigma-Aldrich.
| DMAN complex | Method/temp. | r NN [Å] | x [Å] | z [Å] | N–H | N⋯H | N–H⋯N | |||
|---|---|---|---|---|---|---|---|---|---|---|
| C Q [kHz] | η | C Q [kHz] | η | ΔCQ [kHz] | ||||||
| a Structure in ref. 28. b Structure in ref. 27. c Structure in ref. 39. | ||||||||||
| 1 | DMAN![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) : :![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) benzoic acid (1 benzoic acid (1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) : :![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 2) 2) |
X-raya/300 K | 2.594 | 0.021 | 0.214 | 3550 | 0.132 | 3533 | 0.113 | 17 |
| 2 | DMAN![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) : :![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 2-iodobenzoic acid (1 2-iodobenzoic acid (1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) : :![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 2) 2) |
X-raya/300 K | 2.571 | 0.235 | 0.218 | 3950 | 0.138 | 3180 | 0.126 | 770 |
| Neutr.a/300 K | 2.575 | 0.079 | 0.267 | |||||||
| 3 | DMAN![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) : :![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 4-iodobenzoic acid (1 4-iodobenzoic acid (1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) : :![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 2) 2) |
X-raya/200 K | 2.602 | 0.272 | 0.266 | 4673 | 0.107 | 2473 | 0.202 | 2200 |
| Neutr.b/200 K | 2.602 | 0.236 | 0.279 | |||||||
| 4 | DMAN![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) : :![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 2-fluorobenzoic acid (1 2-fluorobenzoic acid (1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) : :![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 2) 2) |
X-raya/200 K | 2.589 | 0.039 | 0.228 | 3707 | 0.119 | 3380 | 0.124 | 327 |
| Neutr.b/200 K | 2.595 | 0.016 | 0.273 | |||||||
| 5 | DMAN![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) : :![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 4-hydroxybenzoic acid (1 4-hydroxybenzoic acid (1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) : :![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 2) 2) |
X-rayc/100 K | 2.566 | 0.051 | 0.209 | 3740 | 0.102 | 3420 | 0.099 | 320 |
| 6 | DMAN![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) : :![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 2,3-dihydroxybenzoic acid (1 2,3-dihydroxybenzoic acid (1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) : :![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1) 1) |
X-rayb/200 K | 2.593 | 0.189 | 0.229 | 4213 | 0.095 | 2893 | 0.138 | 1320 |
| Neutr.b/200 K | 2.599 | 0.160 | 0.274 | |||||||
| 7 | DMAN![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) : :![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) chloranilic acid (1 chloranilic acid (1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) : :![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1) 1) |
X-rayb/100 K | 2.610 | 0.299 | 0.245 | 4693 | 0.077 | 2420 | 0.124 | 2273 |
| Neutr.b/200 K | 2.621 | 0.228 | 0.271 | |||||||
| 8 | DMAN![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) : :![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) malonic acid (1 malonic acid (1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) : :![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1) 1) |
NQR/300 K | 0.171 | 4353 | 0.096 | 2820 | 0.177 | 1533 | ||
| 9 | DMAN![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) : :![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 3,5-dinitrobenzoic acid (1 3,5-dinitrobenzoic acid (1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) : :![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 2) 2) |
NQR/300 K | 0.086 | 3940 | 0.107 | 3180 | 0.113 | 760 | ||
| 10 | DMAN![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) : :![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 5-chloro-2-hydroxybenzoic acid (1 5-chloro-2-hydroxybenzoic acid (1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) : :![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 2) 2) |
NQR/300 K | 0.249 | 4593 | 0.070 | 2393 | 0.125 | 2200 | ||
NQR spectroscopy
14N NQR frequencies were determined with the technique of cross-relaxation spectroscopy.40 Here, 14N NQR levels are observed indirectly by their influence on 1H relaxation of the whole sample. The found frequencies were then paired and used to determine the quadrupole coupling constant CQ and the EFG asymmetry parameter η, where CQ is linearly proportional to the largest EFG principal value.All measurements were carried out with a homebuilt instrument, where the sample is repeatedly moved from high to low field with a pneumatic unit. The 1H Larmor frequency in a high field was 32 MHz.
Results
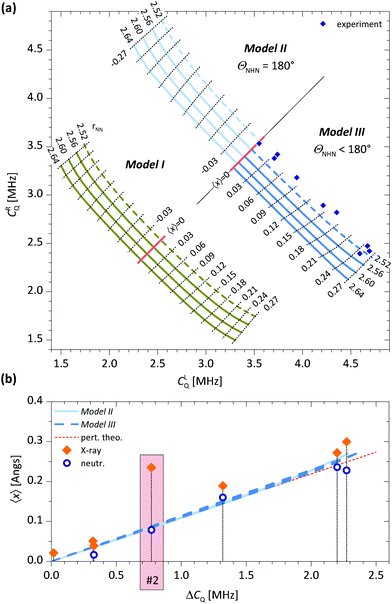
The DMAN salts used in this study, their known hydrogen bond parameters and the 14N EFG parameters determined here are summarized in Table 1. The geometry of the hydrogen bond (x and z relative to the N–N midpoint) was derived from the parameters rNN, rN–H and rN⋯H reported in other studies. The EFG tensor is specified with two parameters: CQ and η. For Models I and II, the symmetry implies η = 0 and CQ = e2q〈Vxx〉/h. For Model III, the symmetry implies η ≠ 0 and the largest EFG tensor principal component is no longer along the x direction but rather approximately along the direction of the nitrogen lone pair. The results of our ab initio calculations and vibrational analysis are shown in Fig. 2.In Fig. 2a we first present the inter-dependencies between the quadrupole coupling constants for the left and right nitrogen atom, CLQ and CRQ for a range of Ex and a selection of rNN. The values for Ex (not shown) were chosen so that |〈x〉| ≤ 0.27 Å, where the limiting cases roughly correspond to the largest experimentally observed proton displacements. Similarly, rNN was chosen from the range of experimentally found rNN.
Qualitatively, the behavior is similar for all three models. When Ex = 0, which corresponds to an isolated cation, 〈x〉 = 0 and the two quadrupole coupling constants are equal, CLQ = CRQ ≡ C0Q. For all three models, C0Q is linearly dependent on rNN, decreasing when rNN increases. This behavior cannot be expected a priori as C0Q depends on the balance between two opposing contributions. When rNN increases, the proton, now further away from both nitrogen sites, becomes less efficient in attracting the two lone pairs, at the same time, however, the repulsion between the two lone pairs also diminishes and allows them to move further away from their nitrogen sites, i.e. closer to the proton. This rNN dependence is also the reason for smaller C0Q values for Model III compared to Model II, as the proton path between the two nitrogen sites in Model III is longer than rNN. The C0Q values in Model I are significantly smaller than those in Models II and III. This is expected and is due to differences in functional groups attached to the nitrogen atoms. In addition, for Model I, we expect a small C0Q based on symmetry alone. The environment around the nitrogen atom is here rather symmetric as there are four hydrogen atoms directly bound to a nitrogen atom, which are arranged in a nearly tetrahedral structure. In a perfect tetrahedral environment, like in the ammonium cation, the symmetry would imply CQ = 0.
The application of Ex induces a shift of the proton in the direction of Ex, thus 〈x〉 ≠ 0, with the magnitude of 〈x〉 increasing with field strength. At the same time, CLQ increases while CRQ decreases, or vice versa, all of which is as expected. A rather unexpected but interesting observation is, however, that CLQ + CRQ for a specific rNN is practically independent of Ex and thus 〈x〉. This relation can be very useful, for example, to determine C0Q ≈ ½(CLQ + CRQ) from a measurement at any Ex, i.e. from any cation–anion complex. Determining C0Q by other means would be rather difficult, especially due to its rNN dependence. Another feature observed in Fig. 2a is the almost equidistant contour lines for 〈x〉. This can be used to determine 〈x〉 empirically, e.g. by a comparison with a suitable reference.
To assess the usefulness of these ab initio calculations, we show our experimentally determined CLQ and CRQ values for all samples in Fig. 2a. The experimental points are within a reasonable range of theoretical values (Models II and III) for 〈x〉, but the predicted rNN values are unrealistically short. This disagreement can be ascribed to a mismatch in functional groups attached to the nitrogen, which affect its C0Q. A simple approach to compensate for an inexact C0Q is to introduce ΔCQ = CLQ − CRQ, which is roughly C0Q independent, as functional groups shift both CLQ and CRQ by the same amount.
In Fig. 2b, we show a plot of 〈x〉 as a function of ΔCQ for Models II and III. The observed relation between 〈x〉 and ΔCQ is linear and, rather unexpectedly, also practically independent of rNN. In addition, there is an almost negligible difference between data for Model II and III, in both cases 〈x〉/ΔCQ = 0.108 Å MHz−1. Also shown in Fig. 2b are our NQR experimental data and the experimentally determined x, found with X-ray and/or neutron diffraction, for samples 1–7. The neutron diffraction data agree very well with the theoretical predictions for all samples. This is rather impressive, as no fitting parameters have been used. The situation for X-ray diffraction data is somewhat different however. For samples 1 and 3–7, the data agree well with the theoretical predictions. For sample 2, however, we observe a large discrepancy. The structure for this sample has been investigated by two separate X-ray studies, both finding a similar proton position, which is obviously different from the neutron diffraction one.41,42 The authors attribute this discrepancy to a difficult refinement of the X-ray structure due to a large amount of noise caused by the large iodine atom.
The theoretical lines presented in Fig. 2b were also used to predict 〈x〉 for samples 8–10 with yet undetermined structures. These results are also shown in Table 1.
The ratio 〈x〉/ΔCQ is practically equal for Models II and III, however, we find a different value for Model I, 〈x〉/ΔCQ = 0.135 Å MHz−1, which is ∼25% larger than for Models II and III. This points to the conclusion that functional groups not only determine C0Q but also influence 〈x〉/ΔCQ as well. This raises the question, how accurate is the predicted 〈x〉 in the DMAN-H+ case when using 〈x〉/ΔCQ determined for Model III, as there is a mismatch in one functional group. We have not pursued an investigation in this direction, however, based on very similar NQR parameters for all tertiary amines, 4.5 < CQ < 5.5 MHz and a generally small η, we are quite confident in claiming that the relation 〈x〉/ΔCQ = 0.108 Å MHz−1, as determined here, is a good approximation for DMAN complexes and also for all other tertiary amines forming similar N–H⋯N bonds. With similar arguments, we anticipate that 〈x〉/ΔCQ for primary and secondary amines should be in the range of 0.108–0.135 Å MHz−1.
In contrast to 〈x〉, 〈z〉 cannot be determined reliably with NQR measurements. First of all, the variations of 〈z〉 are very small between the salts chosen here (see Table 1), and second, the influence of 〈z〉 on CQ is also small, in fact, smaller than the typical NQR experimental error.
Discussion
We expected a linear relation between 〈x〉 and ΔCQ but across a much smaller range, e.g. for ΔCQ/C0Q < 0.1, which is a typical value for 1st order perturbation theory. Instead, we found it to be accurate across a substantially larger range, up to ΔCQ/C0Q ≲ 0.7. Intrigued by this result and in order to assess whether this is just a coincidence, we analysed our models in some more depth.The instantaneous EFG tensor for linear models (Models I and II) can be expanded in a series with respect to the proton coordinate x. For Vxx, which is here the only independent component, we can write
| Vxx(x) = V(0)xx + V(1)xxx + V(2)xxx2 +…+ V(n)xxxn | (1) |
| 〈ΔVxx〉 = 2V(1)xx〈x〉 + 2V(3)xx〈x3〉 + 2V(5)xx〈x5〉 +… | (2) |
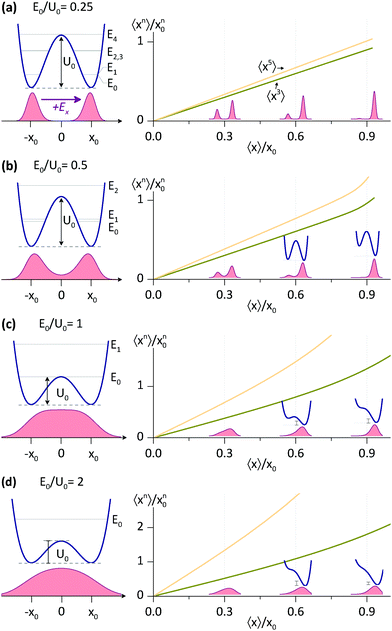
Next, we analysed the 〈xn〉 interdependence for some potentials relevant to this study, the asymmetric double well potentials of the form
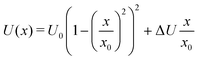 | (3) |
For E0/U0 = 0.25, a potential with a relatively high barrier, we find a direct proportionality between 〈x3〉, 〈x5〉 and 〈x〉, which is accurate for 〈x〉 up to ∼x0. In fact, all 〈xn〉 with odd n are linearly proportional to 〈x〉, although the breakdown for larger n occurs at smaller 〈x〉. For shallower potentials, i.e. with larger E0/U0, the linear relation is still a good approximation at small 〈x〉, the breakdown, however, occurs at progressively smaller 〈x〉. But, even for E0/U0 = 2, the shallowest potential considered, the linearity between 〈x3〉 and 〈x〉 is accurate almost up to 〈x〉 ∼ x0.
The behavior described in Fig. 3 is not limited to the potentials used here (eqn (3)), but rather to all asymmetric potentials whose symmetric part has an energy level structure suitable for a two level approximation. Let us consider an arbitrary symmetric potential, with energy levels E0, E1, E2…, where E1 − E0 ≪ E2 − E1. For this potential, and in general for symmetric potentials, the ground state wavefunction, ψ+, is symmetric, whereas the wavefunction for the first excited state, ψ−, is antisymmetric. Adding an antisymmetric term to this potential (e.g. of size ΔU) mixes the ground state wavefunctions. For ΔU < E2 − E0, but not necessarily ΔU < E1 − E0, we can use 1st order degenerate perturbation theory to find the new ground state wavefunction ψ0′ = cos(½ϕ)ψ+ + sin(½ϕ)ψ−, where ϕ is a mixing angle dependent on ΔU. The expectation values for ψ0′, which we are interested in, have one very striking property, which is straightforward to derive using the symmetry of ψ±. The expectation values for all antisymmetric operators are exactly proportional to sin(ϕ) and thus, proportional to each other. For example, 〈x〉 = sin![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) (ϕ)〈ψ+|
(ϕ)〈ψ+|![[x with combining circumflex]](https://www.rsc.org/images/entities/i_char_0078_0302.gif) |ψ−〉 while 〈x3〉 = sin
|ψ−〉 while 〈x3〉 = sin![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) (ϕ)〈ψ+|
(ϕ)〈ψ+|![[x with combining circumflex]](https://www.rsc.org/images/entities/i_char_0078_0302.gif) 3|ψ−〉. This proportionality is effective as long as ΔU < E2 − E0, which applies to all cases in Fig. 3 at not too large 〈x〉.
3|ψ−〉. This proportionality is effective as long as ΔU < E2 − E0, which applies to all cases in Fig. 3 at not too large 〈x〉.
Thus, using the found linearities between 〈xn〉 and 〈x〉, one can rewrite eqn (2) as
| 〈ΔVxx〉 ≈ 2Ṽ(1)xx〈x〉 | (4) |
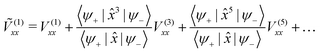 | (5) |
Some useful numerical parameters that we find for Model II with rNN = 2.56 Å are: U0 = 2.21 kcal mol−1 and E0 = 1.77 kcal mol−1 so that E0/U0 = 0.80, whereas at the other end, for rNN = 2.64 Å, we find: U0 = 4.29 kcal mol−1 and E0 = 2.53 kcal mol−1 so that E0/U0 = 0.56. Thus, the cases presented in Fig. 3 that are relevant to this study are primarily (b) and (c). At the moment, it is difficult to find appropriate barrier values for the DMAN-H+ ion, as there are no reliable measurements, whereas calculations yield different numbers, according to the theory level used.36 Nevertheless, the 〈x〉/ΔCQ ratio found here seems to be independent of barrier height, so that knowing which case in Fig. 3 represents the DMAN-H+ ion is rather irrelevant.
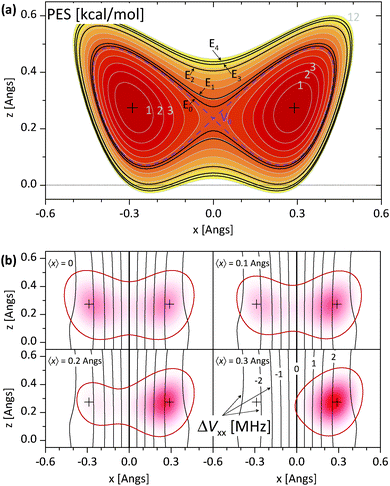
The above discussion is not directly applicable to Model III, i.e. to nonlinear N–H⋯N bonds, and understanding the 〈Vμν〉 dependence on 〈x〉 and 〈z〉 for Model III is less straightforward than it is for Models I and II. In Fig. 4a, we show the PES and the associated energy level structure for Model III with rNN = 2.64 Å. Here, the presence of two low lying levels with nearly equal energies followed by a larger gap can be clearly seen and it justifies the application of the two level approximation. More complications are related to the EFG tensor. The instantaneous nitrogen EFG tensor now depends on two coordinates, x and z. The average values 〈Vμν〉 thus in principle depend on 〈x〉, 〈x2〉, 〈x3〉,…, 〈z〉, 〈z2〉, 〈z3〉…, as well as on mixed terms like 〈xz〉. However, upon inspecting Vμν for Model III in the region of interest, that is, in places with a non-negligible proton ground state density, we find that the major Vμν components are only weakly dependent on z. In Fig. 4b, we show the instantaneous ΔVxx = VLxx − VRxx, whose average mainly determines ΔCQ. Additionally, in Fig. 4b, we also show the proton ground state density and 〈x〉 for four different asymmetric potentials that are derived from the symmetric potential in Fig. 4a by adding an Exx term. In these ΔVxx plots, the weak z dependence in the region of interest can be clearly seen. Thus, it seems permissible to expand ΔVxx only with respect to x even for Model III and afterwards use the same reasoning that led to eqn (4) for linear N–H⋯N models.
There are a few more points that need some attention. In our analysis, we assumed that the anion influences our models only by modifying the PES, through δU, here Ex, but not by affecting Vμν directly. This is an approximation that substantially reduces the computational time, as otherwise, we would have to make ab initio calculations for each instance of δU separately. To assess the plausibility of this approximation, we made an additional set of calculations, only for a few cases, by adding Ex to our ab initio calculations. The values change, but the change is small, on the order of a few percent. In another set of calculations, we added a point charge to our models instead of Ex, in an effort to more closely represent the anion. By moving the point charge around, we obtained different δU. Again, the values change, this time by a slightly larger amount, but not large enough to justify the extra computational time. This last set of calculations also offered the possibility to inspect the influence of the point charge (the anion) on the PES. We found that the uniform field approximation with Ex is acceptable in the region of interest, i.e. between the two minima. Nevertheless, the inclusion of any antisymmetric terms (with respect to x) in δU would not affect the dependencies presented in Fig. 3.
Our analysis completely neglects N–N vibrations. This simplification was necessary, as for our models, the PES attains a minimum at very large rNN; for example, rNN = 2.68 Å for Model I and rNN = 2.88 Å for Model II. Nevertheless, we made an attempt to estimate the influence of N–N vibrations on 〈Vxx〉 and 〈x〉 by using a Gaussian wavefunction for these vibrations, with an average of rNN = 2.6 Å and a root mean square of 0.1 Å. We find a practically negligible difference between these averaged values and the non-averaged values for rNN = 2.6 Å. We should emphasize here that although it is tempting to directly average the lines presented in Fig. 2a and b, this is not the correct procedure. One must average quantities at the same δU, rather than the same 〈x〉.
Conclusions
We have theoretically and experimentally investigated the intramolecular N–H⋯N hydrogen bond in DMAN complexes from the 14N NQR perspective. The aim was to obtain quantitative information on proton displacement from the bond midpoint, which happens in the presence of various anions. Using ab initio calculations and vibrational analysis, we found that there is a very simple linear relation between the proton 〈x〉 and the difference between the quadrupole coupling constants of the two 14N nuclei (ΔCQ). The ratio is 〈x〉/ΔCQ = 0.108 Å MHz−1 for tertiary amines and is rather insensitive to the exact geometry of the N–H⋯N bond, i.e. the N–N distance and the NHN angle. Unfortunately, 14N NQR spectroscopy is also insensitive to displacements in the direction perpendicular to N–N, so that the proton 〈z〉 cannot be determined. The theoretical predictions were also verified experimentally for several DMAN complexes, by comparing the X-ray and/or neutron diffraction proton positions with the predictions from the 14N NQR measurements performed here. The agreement is excellent, especially in view of the fact that no fitting parameters have been used. The relation found here is not limited to DMAN complexes, but can also be used in other systems with intramolecular N–H⋯N bonds if the potential for proton motion satisfies certain conditions.Conflicts of interest
There are no conflicts to declare.References
- P. Müller, R. Herbst-Irmer, A. Spek, T. Schneider and M. Sawaya, Crystal Structure Refinement: A Crystallographer's Guide to Shelxl, Oxford University Press, New York, 2006, vol. 8, ch. 3 Search PubMed.
- A. Parkin, S. M. Harte, A. E. Goetab and C. C. Wilson, New J. Chem., 2004, 28, 718 RSC.
- M. Woinska, S. Grabowsky, P. M. Dominiak, K. Wozniak and D. Jayatilaka, Sci. Adv., 2016, 2, e1600192 CrossRef PubMed.
- X.-Z. Li, B. Walker and A. Michaelides, PNAS, 2011, 108, 6369 CrossRef CAS.
- D. V. Moreno, S. A. González and A. Reyes, J. Chem. Phys., 2011, 134, 024115 CrossRef PubMed.
- R. H. McKenzie, C. Bekker, B. Athokpam and S. G. Ramesh, J. Chem. Phys., 2014, 140, 174508 CrossRef PubMed.
- D. M. Wilkins, D. E. Manolopoulos, S. Pipolo, D. Laage and J. T. Hynes, J. Phys. Chem. Lett., 2017, 8, 2602 CrossRef CAS PubMed.
- T. E. Markland and M. Ceriotti, Nat. Rev. Chem., 2018, 2, 0109 CrossRef CAS.
- E. Brunner and U. Stemberg, Prog. Nucl. Magn. Reson. Spectrosc., 1998, 32, 21–57 CrossRef CAS.
- R. K. Harris, P. Y. Ghi, R. B. Hammond, C.-Y. Ma and K. J. Roberts, Chem. Commun., 2003, 2834 RSC.
- A. E. Aliev and K. D. M. Harris, Supramolecular Assembly via Hydrogen Bonds I, Structure and Bonding, Springer, Berlin, Heidelberg, 2004, vol. 108, pp. 1–53 Search PubMed.
- J. R. Yates, S. E. Dobbins, C. J. Pickard, F. Mauri, P. Y. Ghi and R. K. Harris, Phys. Chem. Chem. Phys., 2005, 7, 1402 RSC.
- M. Baias, C. M. Widdifield, J.-N. Dumez, H. P. G. Thompson, T. G. Cooper, E. Salager, S. Bassil, R. S. Stein, A. Lesage, G. M. Day and L. Emsley, Phys. Chem. Chem. Phys., 2013, 15, 8069 RSC.
- C. M. Widdifield, H. Robson and P. Hodgkinson, Chem. Commun., 2016, 52, 6685 RSC.
- M. G. Siskos, M. I. Choudhary and I. P. Gerothanassis, Molecules, 2017, 22, 415 CrossRef PubMed.
- T. Emmler, S. Gieschler, H. H. Limbach and G. Buntkowsky, J. Mol. Struct., 2004, 700, 29–38 CrossRef CAS.
- H. Benedict, H.-H. Limbach, M. Wehlan, W.-P. Fehlhammer, N. S. Golubev and R. Janoschek, J. Am. Chem. Soc., 1998, 120, 2939–2950 CrossRef CAS.
- A. Brinkmann and A. P. M. Kentgens, J. Am. Chem. Soc., 2006, 128, 14758–14759 CrossRef CAS PubMed.
- Z. J. Li, Y. Abramov, J. Bordner, J. Leonard, A. Medek and A. V. Trask, J. Am. Chem. Soc., 2006, 128, 8199–8210 CrossRef CAS PubMed.
- J. Seliger and V. Žagar, J. Phys. Chem. A, 2011, 115, 11652 CrossRef CAS PubMed.
- J. Seliger and V. Žagar, Phys. Chem. Chem. Phys., 2014, 16, 18141–18147 RSC.
- J. Seliger and V. Žagar, J. Phys. Chem. C, 2013, 117, 20193–20200 CrossRef CAS.
- H. A. Staab and T. Saupe, Angew. Chem., Int. Ed. Engl., 1988, 27, 865 CrossRef.
- A. Llamas-Saiz, C. Foces-Foces and J. Elguero, J. Mol. Struct., 1994, 328, 297 CrossRef CAS.
- P. R. Mallinson, G. T. Smith, C. C. Wilson, E. Grech and K. Wozniak, J. Am. Chem. Soc., 2003, 125, 4259 CrossRef CAS PubMed.
- A. Parkin, K. Wozniak and C. C. Wilson, Cryst. Growth Des., 2007, 7, 1393 CrossRef CAS.
- A. O. F. Jones, A. A. Kallay, H. Lloyd, G. J. McIntyre, C. C. Wilson and L. H. Thomas, Cryst. Growth Des., 2016, 16, 2123 CrossRef CAS.
- L. H. Thomas, A. O. F. Jones, A. A. Kallay, G. J. McIntyre and C. C. Wilson, Cryst. Growth Des., 2016, 16, 2112 CrossRef CAS.
- C. Lopez, R. M. Claramunt, A. L. Llamas-Saiz, C. Foces-Foces, J. Elguero, I. Sobrados, F. A. Parilla and H.-H. Limbach, New J. Chem., 1996, 20, 523 CAS.
- C. Lopez, P. Lorente, R. M. Claramunt, J. Marin, C. Foces-Foces, A. L. Llamas-Saiz, J. Elguero and H.-H. Limbach, Ber. Bunsen-Ges. Phys. Chem., 1998, 102, 414 CrossRef CAS.
- R. Anulewicz, I. Wawer, T. M. Krygowski, F. Männle and H.-H. Limbach, J. Am. Chem. Soc., 1997, 119, 12223 CrossRef CAS.
- C. L. Perrin and J. B. Nielson, Annu. Rev. Phys. Chem., 1997, 48, 511 CrossRef CAS PubMed.
- S. Ikuta, J. Chem. Phys., 1987, 87, 1900 CrossRef CAS.
- J. A. Platts and K. E. Laiding, J. Phys. Chem., 1995, 99, 6497 CrossRef.
- T. Asada, H. Haraguchi and K. Kitaura, J. Phys. Chem. A, 2001, 105, 7423 CrossRef CAS.
- Y. Horbatenko and S. F. Vyboishchikov, ChemPhysChem, 2011, 12, 1118 CrossRef CAS PubMed.
- A. A. Granovsky, Firefly Version 8.1, available at http://classic.chem.msu.su/gran/firefly/index.html Search PubMed.
- M. W. Schmidt, K. K. Baldridge, J. A. Boatz, S. T. Elbert, M. S. Gordon, J. H. Jensen, S. Koseki, N. Matsunaga, K. A. Nguyen, S. Su, T. L. Windus, M. Dupuis and J. A. Montgomery, J. Comput. Chem., 1993, 14, 1347 CrossRef CAS.
- L. K. Saunders, H. Nowell, H. C. E. Spencer, L. E. Hatcher, H. J. Shepherd, L. H. Thomas, C. L. Jones, S. J. Teat, P. R. Raithby and C. C. Wilson, CrystEngComm, 2018, 20, 3074 RSC.
- D. Stephenson and J. A. S. Smith, Proc. R. Soc. London, Ser. A, 1988, 416, 149 CrossRef CAS.
- A. A. Kallay, PhD thesis, University of Glasgow, 2011.
- L. K. Saunders, PhD thesis, University of Bath, 2016.
| This journal is © the Owner Societies 2019 |