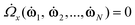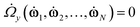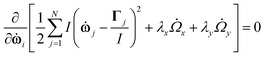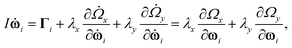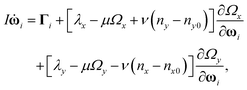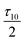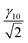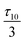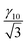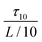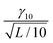Shear flow simulations of smectic liquid crystals based on the Gay–Berne fluid and the soft sphere string-fluid
Received
9th August 2018
, Accepted 26th November 2018
First published on 26th November 2018
Abstract
We have studied the shear flow of the smectic A phase of three coarse grained liquid crystal model systems, namely two versions of the Gay–Berne fluid and the soft sphere string-fluid. At low shear rates, the orientation where the smectic layers are parallel to the shear plane and the orientation parallel to the vorticity plane are both stable in all the systems. In one of the Gay–Berne fluids, there is a transition from the orientation parallel to the shear plane to the orientation parallel to the vorticity plane. At higher shear rates, a nonequilibrium nematic phase is obtained in all the systems in the same way as in linear alkanes under shear. If the initial configuration is an equilibrium smectic A phase or a nematic phase with the molecules parallel to the streamlines, the orientation parallel to the shear plane is attained at low shear rates in the Gay–Berne fluids. In order to analyze the stability of the different orientations, the torque acting on the liquid crystal is calculated. It consists of an elastic torque caused by deformations due to the shape of the simulation cell and the periodic boundary conditions and a shear-induced torque. The elastic torque stabilizes both the orientation parallel to the shear plane and the orientation parallel to the vorticity plane because the liquid crystal is deformed if it is turned away from these orientations. The shear-induced torque, on the other hand, always turns the liquid crystal to the orientation parallel to the vorticity plane where the viscosity and the irreversible energy dissipation rate are minimal. Since the latter torque is proportional to the square of the shear rate, rather high shear rates are required for it to overwhelm the elastic torque. However, the elastic torque decreases with the system size so that it is likely that the shear-induced torque will dominate in large systems and that the orientation parallel to the vorticity plane will be attained at low or even zero shear rate.
1. Introduction
Shear flow of nematic liquid crystals has been thoroughly studied theoretically, experimentally and by molecular dynamics simulation of molecular model systems both in the Newtonian and non-Newtonian regimes.1–5 Consequently, the rheological properties of these liquid crystals are reasonably well understood by now. There are also many elasto-hydrodynamic calculations6–9 and experimental studies10–18 available on the behavior of smectic A liquid crystals under shear. These experimental works deal with, among other things, thermotropic liquid crystals such as 4′-n-octyl-4-cyanobiphenyl,10–14 polymeric liquid crystals15–17 and amphiphilic liquid crystals.18 A common feature of these studies is the presence of a transition from an orientation where the smectic layers are parallel to the shear plane to an orientation where they are parallel to the vorticity plane. There is also an undulation instability accompanying this transition, which has also been found in elasto-hydrodynamic calculations.7,8 However, considerably fewer molecular dynamics simulation studies have been undertaken on the shear flow of smectic A liquid crystals despite their scientific and technological importance in display devices and as lubricants19–21 among other things. So far, a thorough study has been carried out by Guo et al.22–25 on a model where the molecules were composed of Lennard-Jones interaction sites linked by FENE (finitely extensible nonlinear elastic) chain potentials.26,27 This model system forms a smectic A phase but no nematic phase and it is useful for modelling lyotropic liquid crystals composed of amphiphilic molecules. The shear flow was induced by using the Müller–Plathe method.28 Among other things, they examined the above-mentioned transition and they also found the undulation instability.
The purpose of the present work is to examine the shear flow of smectic A phases of two other liquid crystal model systems, namely the Gay–Berne fluid29–34 and the soft sphere string-fluid.35,36 They form nematic and smectic A liquid crystal phases so they are simple models for thermotropic liquid crystals, such as, for example, 4′-n-octyl-4-cyanobiphenyl. However, the mechanisms of the formation of the smectic A phase are different in the two cases. Hard ellipsoids or Lennard-Jones ellipsoids like those in the Gay–Berne fluid, on one hand, do not normally form a smectic A phase because the molecules are streamlined, whereby they easily move from one layer to the neighboring layer, so that the layer structure disintegrates. However, if the side-by-side attraction is strong enough, the layers are stabilized and a smectic A phase arises. On the other hand, since there is no attraction between the molecules in the soft sphere string-fluid, the formation of liquid crystal phases is a purely entropic effect. We intend to drive the shear flow by applying the SLLOD equations of motion37 together with the Lees–Edwards sliding brick boundary conditions.
The first question that we want to answer is whether the smectic layer structure is stable at all or whether it is destroyed by the shear field. If the structure is stable, the next question is whether the smectic layers orient parallel to the shear plane or parallel to the vorticity plane and if there is a transition between these orientations. Then, if there is such a transition, it would be interesting to be able to determine the shear rate at which this transition takes place. These questions are considerably more difficult to answer by molecular dynamics simulation for a smectic liquid crystal than for a nematic liquid crystal because the rotation of the director is hindered by the periodic boundary conditions and the shape of the simulation cell. The reason for this is that the smectic layer structure is elastically deformed and the number of smectic layers varies when the director reorients in a rectangular simulation cell, whereby strong elastic torques arise.
Finally, we are going to determine whether the smectic liquid crystal attains the orientation where the viscosity and thereby the irreversible energy dissipation rate is minimal. This seems to be the case for nematic liquid crystals under a velocity or temperature gradient.38 However, this could very well be fortuitous but, according to a recently proven variational principle, the irreversible energy dissipation rate is minimal in the linear regime of a nonequilibrium steady state,39 so it could also be due to a more fundamental principle.
The article is organized as follows: in Section 2, the basic theory and methods are reviewed, in Section 3, the model systems are described, in Section 4, some technical details are given, in Section 5, the results of the shear flow simulations are presented and discussed, in Section 6, the orientation phenomena are explained and finally in Section 7, there is a conclusion.
2. Basic theory and method
2.1 Order parameter and director
In order to describe the transport properties of a liquid crystal, we must first define the order parameter and the director. In an axially symmetric system such as a nematic or a smectic A liquid crystal, the order parameter, S, is given by the largest eigenvalue of the order tensor,| | 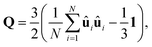 | (1) |
where N is the number of molecules, {ûi; 1 ≤ i ≤ N} is the unit vector parallel to the axis of revolution of molecule i and 1 is the unit second rank tensor. When the molecules are perfectly aligned in the same direction, the order parameter is equal to unity, and when the orientation is completely random, it is equal to zero. The eigenvector corresponding to the order parameter is defined as the director, n, and it is a measure of the average orientation of the molecules in the system. The director angular velocity is defined as Ω = n × ṅ.
2.2 The SLLOD equations of motion for shear flow
Since we simulate shear flow, we have applied the SLLOD equations of motion,37 which take the following form in linear space at constant density:| | 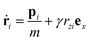 | (2a) |
and| | | ṗi = Fi − γpziex − αpi, | (2b) |
where ri and pi are the position and peculiar momentum, i.e. the momentum relative to the streaming velocity, of molecule i, m is the molecular mass, γ = ∂ux/∂z is the shear rate, i.e. there is a streaming velocity ux in the x-direction varying linearly in the z-direction, ex is the unit vector in the x-direction, Fi is the force exerted on molecule i by the other molecules and α is a Gaussian thermostatting multiplier given by the constraint that the linear peculiar kinetic energy is a constant of motion,| | 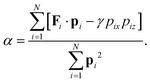 | (2c) |
Note that it is assumed that the velocity profile is linear, i.e. that the flow is laminar, when this thermostat is applied. This does not cause any problems at low shear rates but at high shear rates, fluctuations could be suppressed and at very high shear rates, non-ergodic string phases arise where the molecules are aligned along the streamlines and the irreversible energy dissipation rate and thereby the viscosity go to zero. However, in the present work, the shear rates are very low, so that this thermostat does not affect the results. In order to be on the safe side, we have performed some simulations where we use the ordinary Newtonian equations of motion together with the Lees–Edwards sliding brick boundary conditions and we only thermostat the translational kinetic energy in the vorticity direction, so that the velocity profile is not affected,| | 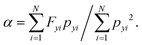 | (2d) |
The results of these simulations were exactly the same as those of the simulations with the SLLOD equations together with the thermostat (2c).
In the following discussion, the xy-plane is defined as the shear plane and the xz-plane is defined as the vorticity plane, see Fig. 1. Due to symmetry, two stable orientations of the smectic layer planes are allowed: parallel to the shear plane or parallel to the vorticity plane.
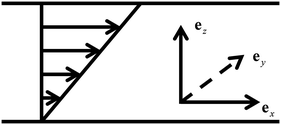 |
| | Fig. 1 The geometry of planar Couette flow or shear flow: there is a streaming velocity in the x-direction varying linearly in the z-direction, u = γzex, where γ = ∂ux/∂z is the velocity gradient and (ex, ey, ez) are the basis vectors in the x-, y- and z-directions, and the xy-plane is defined as the shear plane and the zx-plane is defined as the vorticity plane. | |
A problem when smectic liquid crystals are studied by molecular dynamics simulation is that their structural properties are system size dependent and affected by the shape of the simulation cell. For example, it is easy to realize that the height of the simulation cell must be equal to an integer multiple of the equilibrium layer spacing in order to allow the formation of a smectic phase. This can be achieved by keeping the pressure constant independently in different directions, for example, in the direction of the director and perpendicular to this direction. This case can be handled by various versions of the SLLOD equations of motion, see Appendix 1.
The shear rate dependent viscosity becomes
| | 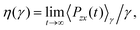 | (3) |
where 〈
Pzx(
t)〉
γ is the
zx component of the pressure tensor obtained from the Irving and Kirkwood definition,
40| | 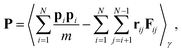 | (4) |
where
rij =
rj −
ri and
Fij is the force exerted on molecule
i by molecule
j and the subscript
γ denotes that the averages are evaluated in a nonequilibrium ensemble at a shear rate of
γ.
2.3 The Euler equations in angular space
Since the molecules in this work are rigid rods, the Euler equations are applied in angular space,| | 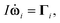 | (5) |
where I is the moment of inertia around the axes perpendicular to the axis of revolution, ωi is the angular velocity of molecule i and Γi is the torque exerted on molecule i by the other molecules. The relation between the angular velocity and the rate of change of the symmetry axis of the molecule, {dûi/dt; 1 ≤ i ≤ N}, is expressed in terms of quaternions.41
In order to determine whether a torque is exerted on the director by the shear field or by elastic deformations caused by the periodic boundary conditions, it is convenient to fix the director in a certain orientation. This can be achieved by augmenting eqn (5) by two Gaussian constraint torques:3,5
| | 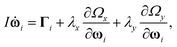 | (6) |
where
Ωx and
Ωy are the
x- and
y-components of the director angular velocity and
λx and
λy are two Gaussian constraint multipliers, the values of which are determined by the requirement that the director angular acceleration is zero. Then, if the director angular velocity is zero at time zero, the director will remain fixed for all subsequent times. We will be interested in the special case where the director is constrained to be perpendicular to the streamlines. Then, the torque density
![[capital Gamma, Greek, circumflex]](https://www.rsc.org/images/entities/i_char_e132.gif) x
x in the direction of the streamlines is given by
| | ![[capital Gamma, Greek, circumflex]](https://www.rsc.org/images/entities/i_char_e132.gif) x = 〈λx〉γ/V = 2Pax, x = 〈λx〉γ/V = 2Pax, | (7) |
where
V is the volume of the system and
Pax is the
x-component of the antisymmetric pressure.
The constraint algorithm (6) has previously been applied to fix the director of nematic and cholesteric liquid crystals under velocity or temperature gradients. Then, it was found that these gradients always exert a torque turning the director towards the preferred orientation, when it is constrained to an orientation away from this orientation. The derivation of the algorithm is given in ref. 42 and in Appendix 2 and the practical implementation is outlined in ref. 43 and in Appendix 3.
2.4 Torques affecting the orientation of shearing smectic liquid crystals
The orientation of a smectic liquid crystal undergoing shear flow is determined by the torques exerted on it. Since a smectic liquid crystal state is a state between the liquid state and the solid state, it can be subjected to shear-induced torques and elastic torques.
The origin of the elastic torque is the fact that the number of smectic layers and the layer spacing change with the angle between the director and the velocity gradient when the director rotates because the periodic boundary conditions must be satisfied. This changing layer spacing is an elastic deformation giving rise to an elastic strain field and consequently elastic free energy minima and maxima at certain director orientations. Moreover, the elastic free energy and thus the torque change discontinuously when a new smectic layer enters or disappears. The elastic torque, ![[capital Gamma, Greek, circumflex]](https://www.rsc.org/images/entities/i_char_e132.gif) xel, is formally defined as the derivative of the elastic free energy, Eel, with respect to the angle between the director and the velocity gradient, θ,
xel, is formally defined as the derivative of the elastic free energy, Eel, with respect to the angle between the director and the velocity gradient, θ,
| | ![[capital Gamma, Greek, circumflex]](https://www.rsc.org/images/entities/i_char_e132.gif) xel = ∂Eel/∂θ. xel = ∂Eel/∂θ. | (8) |
The shear-induced torque arises because there is a velocity gradient, so that the streaming velocity is different at different parts of a non-spherical molecule. Consequently, different parts of the molecule are affected by slightly different viscous forces, whereby a torque arises. It is always present in shearing liquids irrespective of the system size and in every kind of liquid no matter whether it is isotropic or a liquid crystal. Shear induced torques give rise to shear-induced rotation and shear-induced alignment among other things. When the director is perpendicular to the streamlines in a smectic liquid crystal, the shear-induced torque, ![[capital Gamma, Greek, circumflex]](https://www.rsc.org/images/entities/i_char_e132.gif) xshear, must remain unchanged when the shear rate changes sign, i.e. γ → −γ, be zero when θ is equal to an integer multiple of 90 degrees and be a periodic function of θ due to symmetry. This means that it can be expanded in a series of even powers of γ and a Fourier series of sine functions of even multiples of θ,
xshear, must remain unchanged when the shear rate changes sign, i.e. γ → −γ, be zero when θ is equal to an integer multiple of 90 degrees and be a periodic function of θ due to symmetry. This means that it can be expanded in a series of even powers of γ and a Fourier series of sine functions of even multiples of θ,
| | ![[capital Gamma, Greek, circumflex]](https://www.rsc.org/images/entities/i_char_e132.gif) xshear ∼ γ2 xshear ∼ γ2![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) sin sin![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 2θ + higher order terms. 2θ + higher order terms. | (9) |
The presence of the elastic energy minima means that the director can attain an orientation between the orientations parallel to the shear plane and parallel to the vorticity plane even though the shear induced torque turns the director toward the last mentioned orientation. Note also that the orientation parallel to the shear plane is stabilized by elastic torques since the layer spacing must change from the equilibrium layer spacing if the director is turned away from this orientation.
2.5 Quantitative estimation of elastic torques and shear-induced torques
If the constraint eqn (6) is used to fix the director in a given orientation at a given shear rate, the constraint torque will be equal to the sum of the elastic torque and the shear-induced torque. However, the elastic torque can be obtained as the torque at zero shear rate, so that the shear-induced torque can be estimated by subtracting the former torque. Unfortunately, the elastic strain may change the structure of the system in such a way that the shear-induced torque will be different from that of an unstrained system. Consequently, the difference between the torques with and without the shear field is not necessarily equal to shear-induced torque in a system without elastic strains.
There is, however, a somewhat surprising way of circumventing this problem in the special case where the square of the number of smectic layers, L, when these layers are parallel to one of the faces of a cubic simulation cell, is equal to the sum of the squares of two other integers, i.e. L2 = m2 + l2. Then, it is easy to show that the layer spacing is the same as the equilibrium layer spacing when cos![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) θ = m/L or cos
θ = m/L or cos![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) θ = l/L, where θ is the angle between the director and the normal of one of the faces of the simulation cell, m is the number of layers intersecting the x-axis and l is the number of layers intersecting the y-axis, see Fig. 2a and b. Consequently, there are two skew director orientations where there are no elastic deformations. This also means that the constraint torques needed to fix the director in these orientations to a large extent are free from elastic contributions and thus they should be better estimates of the shear-induced torque in the absence of elastic deformations.
θ = l/L, where θ is the angle between the director and the normal of one of the faces of the simulation cell, m is the number of layers intersecting the x-axis and l is the number of layers intersecting the y-axis, see Fig. 2a and b. Consequently, there are two skew director orientations where there are no elastic deformations. This also means that the constraint torques needed to fix the director in these orientations to a large extent are free from elastic contributions and thus they should be better estimates of the shear-induced torque in the absence of elastic deformations.
 |
| | Fig. 2 (a) An instantaneous picture of a configuration of the soft sphere string-fluid at equilibrium, where the director is parallel to the velocity gradient and thus perpendicular to one of the faces of the simulation cell. The picture was produced by using the visualization tool OVITO.44 (b) An instantaneous picture of a configuration of the soft sphere string-fluid, where the director is oriented at a Pythagorean angle of 53.1 degrees relative to the velocity gradient. Note that 8 and 6 smectic layers intersect the horizontal and vertical faces of the simulation cell respectively, and that 62 + 82 = 102, i.e. the square of the number of layers when they are parallel to one of the faces of the simulation cell, see figure (a). The picture was produced by using the visualization tool OVITO.44 | |
3. Model systems
3.1 The Gay–Berne fluid
The ordinary Gay–Berne fluid29 does not display any smectic A phase because the ellipsoids constituting this system are in general not able to form stable layers. Therefore, we use a special version where the side-by-side attraction of the molecules has been enhanced in order to stabilise the smectic layers:30–34| | 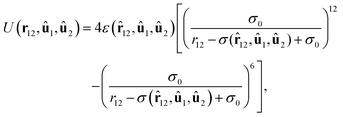 | (10) |
where r12 is the distance vector from the centre of mass of molecule 1 to the centre of mass of molecule 2, ![[r with combining circumflex]](https://www.rsc.org/images/entities/b_char_0072_0302.gif) 12 is the unit vector in the direction of r12 and r12 is the length of r12. The parameter σ0 is the length of the axis perpendicular to the axis of revolution, i.e. the minor axis of a prolate ellipsoid. The strength and range parameters are given by
12 is the unit vector in the direction of r12 and r12 is the length of r12. The parameter σ0 is the length of the axis perpendicular to the axis of revolution, i.e. the minor axis of a prolate ellipsoid. The strength and range parameters are given by| | 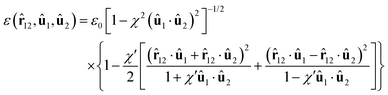 | (11a) |
and| | 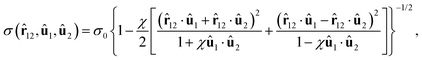 | (11b) |
where ε0 is the depth of the potential minimum where ![[r with combining circumflex]](https://www.rsc.org/images/entities/b_char_0072_0302.gif) 12, û1 and û2 are perpendicular to each other, i.e. the cross configuration, χ = (κ2 − 1)/(κ2 + 1), κ is the ratio between the axis of revolution and the axis perpendicular to this axis, i.e. the length-to-width ratio of prolate ellipsoids, χ′ = (κ′ − 1)/(κ′ + 1) and κ′ is the ratio of the potential energy minima of the side-by-side and end-to-end configurations. The parameter κ has been given the value 4.4 and we have used two values of the parameter κ′, namely 20 (I) and 201/2 ≈ 4.472 (II). These values of κ′ enhance the attraction in the side-by-side configuration, thereby stabilising the smectic layers. The first parameterisation has been comprehensively studied by Bates and Luckhurst30–32 and the second one has been applied by the present authors.3,33,34 The moments of inertia around the axes perpendicular to the axis of revolution have been given the value mσ02, where m is the molecular mass.
12, û1 and û2 are perpendicular to each other, i.e. the cross configuration, χ = (κ2 − 1)/(κ2 + 1), κ is the ratio between the axis of revolution and the axis perpendicular to this axis, i.e. the length-to-width ratio of prolate ellipsoids, χ′ = (κ′ − 1)/(κ′ + 1) and κ′ is the ratio of the potential energy minima of the side-by-side and end-to-end configurations. The parameter κ has been given the value 4.4 and we have used two values of the parameter κ′, namely 20 (I) and 201/2 ≈ 4.472 (II). These values of κ′ enhance the attraction in the side-by-side configuration, thereby stabilising the smectic layers. The first parameterisation has been comprehensively studied by Bates and Luckhurst30–32 and the second one has been applied by the present authors.3,33,34 The moments of inertia around the axes perpendicular to the axis of revolution have been given the value mσ02, where m is the molecular mass.
3.2 The soft sphere string-fluid
We used a soft sphere string-fluid where the molecules are composed of linear rigid strings consisting of 11 soft spheres interacting according to a purely repulsive potential,| | 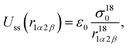 | (12) |
where r1α2β is the scalar distance between sphere α of molecule 1 and sphere β of molecule 2. The scalar distance between two adjacent interaction sites in the molecule is equal to σ0/2, giving a length-to-width ratio of 6![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1. A similar system has been studied by Paolini et al.35 and by Cinacchi et al.36 The mass of the molecule is equal to m and the moment of inertia has been set equal to 5mσ02/2. This value was obtained by assuming that the mass of each sphere is concentrated at its centre of symmetry and equal to m/11. Note, however, that other realistic mass distributions are possible.
1. A similar system has been studied by Paolini et al.35 and by Cinacchi et al.36 The mass of the molecule is equal to m and the moment of inertia has been set equal to 5mσ02/2. This value was obtained by assuming that the mass of each sphere is concentrated at its centre of symmetry and equal to m/11. Note, however, that other realistic mass distributions are possible.
4. Technical details
The numerical results in this work are expressed in length, energy, mass and time units of σ0, ε0, m, and τ = σ0(m/ε0)1/2, respectively. Then, the units of the density, temperature, pressure and torque density, shear rate and viscosity are σ0−3, ε0/kB, ε0/σ03, τ−1 and ε0τ/σ03, respectively. This means that the reduced density, temperature, pressure, torque density, shear rate and viscosity are given by n* = nσ03, T* = kBT/ε0, P* = Pσ03/ε0, ![[capital Gamma, Greek, circumflex]](https://www.rsc.org/images/entities/i_char_e132.gif) * =
* = ![[capital Gamma, Greek, circumflex]](https://www.rsc.org/images/entities/i_char_e132.gif) σ03/ε0, γ* = γτ and η* = ησ03/ε0τ, respectively.
σ03/ε0, γ* = γτ and η* = ησ03/ε0τ, respectively.
In Gay–Berne system I, we simulated 38![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 988 ellipsoids forming 15 smectic layers. These numbers of particles and layers were also used in Gay–Berne system II when the torque density was calculated, and 65
988 ellipsoids forming 15 smectic layers. These numbers of particles and layers were also used in Gay–Berne system II when the torque density was calculated, and 65![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 536 ellipsoids forming 18 layers were used when the viscosity was evaluated. In the case of the soft sphere strings, 12
536 ellipsoids forming 18 layers were used when the viscosity was evaluated. In the case of the soft sphere strings, 12![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 800 strings with a total of 140
800 strings with a total of 140![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 800 soft spheres were employed giving eight smectic layers when the viscosity was evaluated and 25
800 soft spheres were employed giving eight smectic layers when the viscosity was evaluated and 25![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 000 strings with a total of 275
000 strings with a total of 275![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 000 spheres forming 10 layers were used when the torque density was obtained. The above parameters are shown in Table 1. The reason why we wanted 15 and 10 layers when the torque density was evaluated was that these two numbers are Pythagorean numbers, allowing two skew orientations of the smectic layer planes where the layer spacing is equal to the equilibrium layer spacing, see Section 2.5.
000 spheres forming 10 layers were used when the torque density was obtained. The above parameters are shown in Table 1. The reason why we wanted 15 and 10 layers when the torque density was evaluated was that these two numbers are Pythagorean numbers, allowing two skew orientations of the smectic layer planes where the layer spacing is equal to the equilibrium layer spacing, see Section 2.5.
Table 1 The interaction potential, the number of particles, N, the number of smectic layers, L, the reduced temperature, T*, the reduced density, n*, the reduced internal potential energy per particle, U*/N and the properties calculated for the different systems
| System |
Interaction potential |
N
|
L
|
T*
|
n* |
U*/N
|
Property |
| I |
Gay–Berne, κ′ = 20 |
38![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 988 988 |
15 |
1.40 |
0.201 |
−3.43 |
η and Γ |
| II |
Gay–Berne, κ′ = 201/2 |
65![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 536 536 |
18 |
0.95 |
0.166 |
−4.15 |
η
|
| II |
Gay–Berne, κ′ = 201/2 |
38![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 988 988 |
15 |
0.95 |
0.166 |
−4.15 |
Γ
|
| III |
Soft sphere string |
12![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 800 800 |
8 |
1.00 |
0.108 |
+2.29 |
η
|
| III |
Soft sphere string |
25![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 000 000 |
10 |
1.00 |
0.108 |
+2.29 |
Γ
|
The equilibrium layer spacing was found by performing a constant pressure simulation where the pressures parallel and perpendicular to the layer normal are kept constant independent of each other by applying the equations of motion (A1) and (A3). The number of particles in the systems was adjusted in such a way that the sides of the simulation cell are equal to each other and equal to an integer multiple of the equilibrium layer spacing. Thus, a cubic simulation cell was obtained that does not favour the orientation parallel to the shear plane over the one parallel to the vorticity plane or vice versa.
The equations of motion were integrated by a fourth order predictor–corrector method with a time step of 0.001τ. The cut-off radius beyond which the forces and the torques were set equal to zero was 5.5σ0 in the Gay–Berne fluids and 2.0σ0 for the soft spheres in the soft sphere string-fluid.
5. Results and discussion
5.1 Gay–Berne fluid I
The first system that we studied was Gay–Berne fluid I at a density of 0.201σ0−3 and a temperature of 1.40ε0/kB, where there is a stable smectic A phase at equilibrium. The equilibrium layer spacing was found to be 3.6σ0, i.e. shorter than the molecular length of 4.4σ0, so that the smectic layers interpenetrate to some extent. This is possible because the ellipsoidal molecules taper off at the ends.
We began by performing shear flow simulations at constant density by using the SLLOD equations of motion (2) with the smectic layers parallel to the vorticity plane. Then, when we started at a low shear rate of 0.001τ−1, we found that the viscosity was constant and equal to about 1.43ε0τ/σ03 up to a shear rate of 0.05τ−1, see Table 2a and Fig. 3. At shear rates above 0.05τ−1, the viscosity decreases up to a shear rate of about 0.20τ−1 even though the smectic structure remains intact and the layers remain parallel to the vorticity plane. Then, if we decrease the shear rates again, the same states with the same orientations and viscosities are recovered. Above a shear rate of 0.20τ−1, there is a gradual transition to a nonequilibrium nematic liquid crystal with the director more or less parallel to the streamlines. This phase is similar to the nonequilibrium nematic phase arising when linear alkanes are sheared at high rates giving rise to shear thinning.45,46 However, these shear rates are rather high, so it is hard to achieve them in an experimental situation, making comparisons difficult. Therefore, the discussion of this transition has been omitted. Note also that this phase is not a non-ergodic string-phase where the irreversible energy dissipation rate and thereby the viscosity go to zero caused by high shear rates when the SLLOD equations are applied. The viscosity is still finite and the equipartition principle is not violated.
Table 2 (a) The reduced viscosity, η*, and the order parameter, S, as functions of the reduced shear rate, γ*, for Gay–Berne fluid I when the smectic layers are parallel to the vorticity plane. (b) The reduced viscosity, η*, the order parameter, S, and the angle between the director and the layer normal, ϑ, as functions of the reduced shear rate, γ*, for Gay–Berne fluid I when the smectic layers are parallel to the shear plane
| (a) |
|
γ* |
η* |
S
|
| 0.001 |
1.493 ± 0.047 |
0.908 |
| 0.010 |
1.432 ± 0.015 |
0.908 |
| 0.020 |
1.438 ± 0.008 |
0.908 |
| 0.025 |
1.437 ± 0.003 |
0.907 |
| 0.050 |
1.447 ± 0.008 |
0.892 |
| 0.060 |
1.409 ± 0.004 |
0.890 |
| 0.100 |
1.319 ± 0.001 |
0.903 |
| 0.150 |
1.233 ± 0.001 |
0.898 |
| 0.200 |
1.193 ± 0.000 |
0.896 |
| (b) |
|
γ*
|
η*
|
S
|
ϑ
|
| 0.001 |
5.33 ± 0.25 |
0.908 |
0.66 |
| 0.002 |
5.45 ± 0.11 |
0.908 |
1.35 |
| 0.005 |
5.40 ± 0.03 |
0.908 |
3.30 |
| 0.008 |
5.34 ± 0.03 |
0.908 |
5.12 |
| 0.010 |
5.31 ± 0.02 |
0.908 |
6.29 |
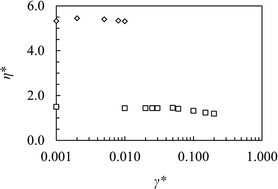 |
| | Fig. 3 The reduced viscosity, η*, of Gay–Berne fluid I as a function of the reduced shear rate, γ*, in the orientations parallel to the shear plane (diamonds) and parallel to the vorticity plane (squares). The orientation parallel to the shear plane turns over to the orientation parallel to the vorticity plane when γ* reaches 0.01, and when γ* is equal to 0.20, the smectic phase is gradually transformed to a nonequilibrium nematic phase. | |
On the other hand, if we start the simulations with a configuration where the smectic layers are parallel to the shear plane, the viscosity will remain constant and equal to approximately 5.4ε0τ/σ03 up to a shear rate of 0.01τ−1 if we start at the same low shear rate of 0.001τ−1 as above, see Table 2b and Fig. 3 and 4. The angle between the director and the normal of the shear plane, ϑ, is approximately proportional to the shear rate i.e. ϑ ≈ 650 × γτ (degrees), see Fig. 5, so that a nonequilibrium smectic C phase is formed. When the shear rate is increased above 0.01τ−1, the smectic layers turn over and become parallel to the vorticity plane. This transition was also observed in ref. 22–25 and it has been found in experiments too.10–18 It is interesting to note that this transition, in contrast to the transition to a nematic liquid crystal at high shear rates, does not seem to be reversible. If the shear rate is lowered again below 0.01τ−1, the orientation parallel to the vorticity plane persists down to very low shear rates, i.e. 0.0001τ−1 or lower. Thus, the system seems to select the orientation where the irreversible energy dissipation rate is minimal in the same way as nematic liquid crystals and in accordance with the variational principle of ref. 39. However, the question still remains why this transition takes place at a rather high shear rate rather than at zero shear rate.
 |
| | Fig. 4 An instantaneous picture of a configuration of the smectic A phase of Gay–Berne fluid I subject to a shear rate of 0.005τ−1 where the smectic layers are parallel to the shear plane. The streamlines are directed in the horizontal direction and the velocity gradient points in the vertical direction. The picture was produced by using the visualization tool OVITO.44 | |
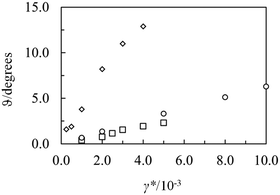 |
| | Fig. 5 The angle between the director and the velocity gradient, ϑ, as a function of the reduced shear rate, γ*, for Gay–Berne fluid I (circles), Gay–Berne fluid II (squares) and the soft sphere string-fluid (diamonds). | |
We finally note that if these simulations are repeated under constant pressure with the pressure equal to the equilibrium pressure, essentially the same results are obtained.
5.2 Gay–Berne fluid II
The second system that we studied was Gay–Berne fluid II. In this system, there is a transition from the isotropic phase to the nematic phase at a temperature of 1.30ε0/kB and a transition to a smectic A phase at a temperature of 1.00ε0/kB when the density is equal to 0.166σ0−3. We selected a temperature equal to 0.95ε0/kB in the smectic A region. The equilibrium layer spacing is equal to 4.1σ0, i.e. less than the molecular length of 4.4σ0 so the smectic layers interpenetrate to some extent in this case too.
When simulations at constant density were performed by using the SLLOD equations of motion (2) with the smectic layers parallel to the vorticity plane in the start configuration, the viscosity stayed constant and was equal to approximately 0.67ε0τ/σ03 up to a shear rate of approximately 0.05τ−1, see Table 3a and Fig. 6. Thus, the viscosity is considerably lower than in Gay–Berne fluid I due to the lower density. At higher shear rates, there is a gradual transition to a nonequilibrium nematic phase just as in Gay–Berne fluid I.
Table 3 (a) The reduced viscosity, η*, and the order parameter, S, as functions of the reduced shear rate, γ*, for Gay–Berne fluid II when the smectic layers are parallel to the vorticity plane. (b) The reduced viscosity, η*, the order parameter, S, and the angle between the director and the layer normal, ϑ, as functions of the reduced shear rate, γ*, for Gay–Berne fluid II when the smectic layers are parallel to the shear plane
| (a) |
|
γ*
|
η*
|
S
|
| 0.002 |
0.72 ± 0.03 |
0.829 |
| 0.005 |
0.68 ± 0.01 |
0.830 |
| 0.010 |
0.674 ± 0.005 |
0.836 |
| 0.020 |
0.68 ± 0.01 |
0.832 |
| 0.030 |
0.6728 ± 0.0001 |
0.835 |
| 0.040 |
0.673 ± 0.0015 |
0.835 |
| 0.050 |
0.6 ± 0.1 |
0.7 ± 0.1 |
| (b) |
|
γ*
|
η*
|
S
|
ϑ
|
| 0.001 |
1.88 ± 0.09 |
0.837 |
0.38 |
| 0.002 |
1.86 ± 0.04 |
0.837 |
0.76 |
| 0.003 |
1.87 ± 0.03 |
0.837 |
1.15 |
| 0.004 |
1.88 ± 0.02 |
0.837 |
1.54 |
| 0.005 |
1.87 ± 0.01 |
0.837 |
1.93 |
| 0.006 |
1.87 ± 0.01 |
0.837 |
2.31 |
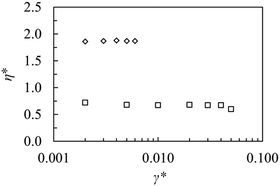 |
| | Fig. 6 The reduced viscosity, η*, of Gay–Berne fluid II as a function of the reduced shear rate, γ*, in the orientations parallel to the shear plane (diamonds) and parallel to the vorticity plane (squares). In the orientation parallel to the shear plane, the smectic phase is gradually transformed to a nematic phase when γ* reaches 0.006 and in the orientation parallel to the vorticity, this transition takes place when γ* is equal to about 0.05. | |
When simulations at constant density were performed with the smectic layers parallel to the shear plane, it was found that the viscosity remains more or less constant and equal to about 1.9ε0τ/σ03 up to a shear rate of 0.006τ−1, see Table 3b and Fig. 6. There is a small shear rate dependent angle between the director and the smectic layer normal, ϑ ≈ 400 × ![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) γτ (degrees), see Fig. 5, so that a nonequilibrium smectic C phase arises. In contrast to Gay–Berne fluid I and to the system studied in ref. 22–25, there is no transition to the orientation parallel to the vorticity plane. At higher shear rates, the smectic layer structure breaks down and there is a gradual transition to a nonequilibrium nematic phase.
γτ (degrees), see Fig. 5, so that a nonequilibrium smectic C phase arises. In contrast to Gay–Berne fluid I and to the system studied in ref. 22–25, there is no transition to the orientation parallel to the vorticity plane. At higher shear rates, the smectic layer structure breaks down and there is a gradual transition to a nonequilibrium nematic phase.
If these simulations are repeated under constant pressure at a pressure equal to the equilibrium pressure with the orientation parallel to the vorticity plane, there is a transition to an isotropic phase with a lower density equal to about 0.14σ0−3 even at shear rates less than 0.001τ−1. The orientation parallel to the shear plane is stable up to a shear rate of 0.004τ−1, and then there is a transition to the isotropic phase. The reason for this could be that the pressure of the isotropic phase is almost the same as that of the smectic phase.
Finally, we note that if the start configuration of Gay–Berne fluids I and II is a smectic or nematic phase with the director parallel to the streamlines, this structure turns over to the orientation parallel to the vorticity plane if the shear rate is higher than approximately 0.005τ−1 but at lower shear rates, the orientation parallel to the shear plane is attained despite the fact that the viscosity is higher in this orientation.
5.3 The soft sphere string-fluid
In order to examine the influence of the shape of the molecules on the flow properties of the smectic A phase, we also studied a version of the soft sphere string-fluid. At a temperature of 1.00ε0/kB, there is a transition from the isotropic phase to the nematic phase at a density of 0.092σ0−3, and when the density is raised to 0.10125σ0−3, there is a transition from the nematic phase to the smectic A phase. We studied the smectic A phase at a density of 0.108σ0−3 where the equilibrium layer spacing is equal to about 6.14σ0, i.e. somewhat wider than the molecular length, so that the layers do not interpenetrate.
If we perform a simulation at constant density with the smectic layers parallel to the vorticity plane, this configuration will be stable up to a shear rate of 0.04τ−1. The viscosity displays a more or less constant value of 1.2ε0τ/σ03 throughout this interval, see Table 4a and Fig. 7. In the shear rate interval of 0.04–0.08τ−1, there is a gradual transition to a nonequilibrium nematic phase.
Table 4 (a) The reduced viscosity, η*, and the order parameter, S, as functions of the reduced shear rate, γ*, for the soft sphere string-fluid when the smectic layers are parallel to the vorticity plane. (b) The reduced viscosity, η*, the order parameter, S, and the angle between the director and the layer normal, ϑ, as functions of the reduced shear rate, γ*, for the soft sphere string-fluid when the smectic layers are parallel to the shear plane
| (a) |
|
γ*
|
η*
|
S
|
| 0.001 |
1.21 ± 0.05 |
0.936 |
| 0.002 |
1.18 ± 0.02 |
0.936 |
| 0.003 |
1.20 ± 0.01 |
0.935 |
| 0.005 |
1.19 ± 0.02 |
0.935 |
| 0.010 |
1.18 ± 0.01 |
0.936 |
| 0.020 |
1.17 ± 0.01 |
0.934 |
| 0.030 |
1.15 ± 0.01 |
0.931 |
| 0.040 |
1.17 ± 0.04 |
0.92 |
| (b) |
|
γ*
|
η*
|
S
|
ϑ
|
| 0.00025 |
4.6 ± 0.2 |
0.934 |
1.6 ± 0.1 |
| 0.0005 |
4.6 ± 0.1 |
0.932 |
1.9 |
| 0.0010 |
4.6 ± 0.2 |
0.934 |
3.8 ± 0.2 |
| 0.0020 |
4.7 ± 0.1 |
0.931 |
8.2 ± 0.5 |
| 0.0025 |
4.82 ± 0.02 |
0.928 |
8.2 |
| 0.0030 |
5.1 ± 0.1 |
0.926 |
11.0 ± 0.1 |
| 0.0040 |
5.2 ± 0.1 |
0.922 |
12.9 ± 0.1 |
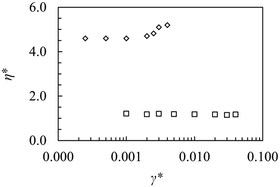 |
| | Fig. 7 The reduced viscosity, η*, of the soft sphere string-fluid as a function of the reduced shear rate, γ*, in the orientations parallel to the shear plane (diamonds) and parallel to the vorticity plane (squares). In the orientation parallel to the shear plane, the smectic phase is gradually transformed to a nematic phase when γ* reaches 0.004 and in the orientation parallel to the vorticity plane, this transition takes place when γ* is equal to 0.04. | |
When the smectic layers are parallel to the shear plane, the viscosity varies between 4.5 and 5.3ε0τ/σ03 at shear rates between 0.00025 and 0.004τ−1, see Table 4b and Fig. 7. The smectic layers are stable even though the angle between the director and the layer normal increases with the shear rate, ϑ ≈ 4000 × ![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) γτ (degrees), see Fig. 5, so that in this case too, the smectic A phase is transformed to a nonequilibrium smectic C phase. Note that the angle is considerably larger than that for the Gay–Berne fluids possibly because the smectic layers do not interpenetrate. At a shear rate of about 0.0045τ−1, there is a gradual transition to a nonequilibrium nematic liquid crystal. There is no transition to the orientation parallel to the vorticity plane in this case either and thus this system too behaves differently to that studied by Guo et al. in ref. 22–25. The behaviour at constant pressure is more or less the same as that at constant volume. If the soft spheres are replaced by attractive Lennard-Jones spheres, the system behaves qualitatively in the same way, at least at some state points.
γτ (degrees), see Fig. 5, so that in this case too, the smectic A phase is transformed to a nonequilibrium smectic C phase. Note that the angle is considerably larger than that for the Gay–Berne fluids possibly because the smectic layers do not interpenetrate. At a shear rate of about 0.0045τ−1, there is a gradual transition to a nonequilibrium nematic liquid crystal. There is no transition to the orientation parallel to the vorticity plane in this case either and thus this system too behaves differently to that studied by Guo et al. in ref. 22–25. The behaviour at constant pressure is more or less the same as that at constant volume. If the soft spheres are replaced by attractive Lennard-Jones spheres, the system behaves qualitatively in the same way, at least at some state points.
6. Stable orientations and transitions – elastic torques vs. shear-induced torques
6.1 Estimation of elastic torques and shear-induced torques
In order to find the stable director orientation relative to the velocity gradient, the torque exerted on the director in the direction of the streamlines was evaluated by using the Gaussian constraint algorithm (6) to fix the director in the plane perpendicular to the streamlines at a given angle relative to the velocity gradient, see Fig. 1. As explained in Section 2.4, this torque is equal to the sum of the shear-induced torque and the elastic torque due to deformations caused by the shape of the simulation cell and the periodic boundary conditions. The elastic torque can be obtained as the torque at zero shear rate and the shear-induced torque can be obtained as the difference between the torque at a finite shear rate and the torque at zero shear rate, at least in principle. In Fig. 8a, the torques at zero shear rate and at a shear rate of 0.005τ−1 are shown as functions of the angle between the director and the velocity gradient for Gay–Berne fluid I. Here, we can see that the torques are very large at zero shear rate, so that the elastic torques are strong and they do not change very much with the shear rate. This indicates that this shear rate does not distort the structure to any great extent. Finally, note that the elastic torques can be negative or positive because they are the derivatives with respect to the angle between the director and the velocity gradient of the elastic free energy, which is an oscillatory function of this angle.
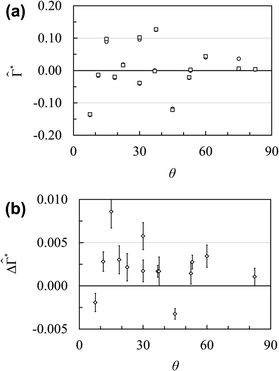 |
| | Fig. 8 (a) The torque density exerted on the director ![[capital Gamma, Greek, circumflex]](https://www.rsc.org/images/entities/i_char_e132.gif) * = (Γ/V)/ε0σ0−3 as a function of the angle θ between the director and the velocity gradient for Gay–Berne fluid I. The squares and the circles depict the torque densities at the shear rates of zero and 0.005τ−1, respectively. The error is of the size of the symbols or less. (b) The difference between the torque densities exerted on the director when the shear rate is equal to 0.005τ−1 and when the shear rate is equal to zero, Δ * = (Γ/V)/ε0σ0−3 as a function of the angle θ between the director and the velocity gradient for Gay–Berne fluid I. The squares and the circles depict the torque densities at the shear rates of zero and 0.005τ−1, respectively. The error is of the size of the symbols or less. (b) The difference between the torque densities exerted on the director when the shear rate is equal to 0.005τ−1 and when the shear rate is equal to zero, Δ![[capital Gamma, Greek, circumflex]](https://www.rsc.org/images/entities/i_char_e132.gif) * = * = ![[capital Gamma, Greek, circumflex]](https://www.rsc.org/images/entities/i_char_e132.gif) *(γ = 0.005τ−1) − *(γ = 0.005τ−1) − ![[capital Gamma, Greek, circumflex]](https://www.rsc.org/images/entities/i_char_e132.gif) *(γ = 0), as a function of the angle θ between the director and the velocity gradient. In principle, this difference is equal to the torque exerted by the shear field alone. *(γ = 0), as a function of the angle θ between the director and the velocity gradient. In principle, this difference is equal to the torque exerted by the shear field alone. | |
In Fig. 8b, we display the differences between the torques at a shear rate of 0.005τ−1 and at zero shear rate as a function of the angle between the director and the velocity gradient. These differences could be accurate estimates of the shear-induced torques. Their sign is such that they turn the smectic layers towards the orientation parallel to the vorticity plane but, unfortunately, there are two exceptions at 7.5 and 45 degrees and the errors are rather large. One reason for this is that the difference between the torques at a finite shear rate and zero shear rate is 10 to 50 times smaller than the torques themselves, so that we have a difference between two almost equally large torques. Thus, these estimates of the shear-induced torques are unreliable.
In order to obtain more accurate estimates of the shear-induced torques, we calculated the torques at the Pythagorean angles of 36.1 and 53.9 degrees between the director and the velocity gradient in the plane perpendicular to the streamlines using 15 smectic layers for Gay–Berne fluid I and II and 10 layers for the soft ellipsoid string-fluid, see Section 2.5. In these orientations, the layer spacing is equal to the equilibrium layer spacing, so that the elastic torque is zero or at least very small, and therefore the torque will be equal to the shear-induced torque. The most reliable results were obtained for Gay–Berne fluid I and the soft sphere string-fluid since the torques are comparatively large due to the rather high density, whereas it was more difficult to obtain the torques for Gay–Berne fluid II because they are smaller due to the lower density. The results are shown in Fig. 9a, b and in Table 5a–c. It is apparent that the torques are more or less zero at zero shear rate and proportional to the square of the shear rate in accordance with symmetry restrictions. The sign of these torques is such that they turn the layer planes to the orientation parallel to the vorticity plane where the viscosity and thereby the irreversible energy dissipation rate are minimal. Thus, the shear field affects the smectic liquid crystal consistently with the variational principle of ref. 39. The quadratic shear rate dependence is also a strong indication that the elastic contribution is absent or at least very small because the elastic torques are nonzero at zero shear rate and rather constant, independent of the shear rate, see Fig. 8a.
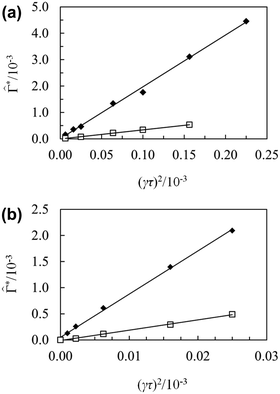 |
| | Fig. 9 (a) The shear-induced torque density ![[capital Gamma, Greek, circumflex]](https://www.rsc.org/images/entities/i_char_e132.gif) * = (Γ/V)/ε0σ0−3 as a function of the square of the shear rate γ for Gay–Berne fluid I. The filled diamonds depict * = (Γ/V)/ε0σ0−3 as a function of the square of the shear rate γ for Gay–Berne fluid I. The filled diamonds depict ![[capital Gamma, Greek, circumflex]](https://www.rsc.org/images/entities/i_char_e132.gif) * at an angle θ of 36.9 degrees, or cos * at an angle θ of 36.9 degrees, or cos![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) θ = 0.80, between the velocity gradient and the director and the open squares depict θ = 0.80, between the velocity gradient and the director and the open squares depict ![[capital Gamma, Greek, circumflex]](https://www.rsc.org/images/entities/i_char_e132.gif) * at an angle θ of 53.1 degrees or cos θ = 0.60. (b) As in (a), but the system is the soft sphere string-fluid. * at an angle θ of 53.1 degrees or cos θ = 0.60. (b) As in (a), but the system is the soft sphere string-fluid. | |
Table 5 (a) The reduced torque density in the direction of the streamlines, ![[capital Gamma, Greek, circumflex]](https://www.rsc.org/images/entities/i_char_e132.gif) * = (Γ/V)/ε0σ0−3, when the director is confined to the plane perpendicular to the streamlines, as a function of the reduced shear rate, γ*, when the angle between the director and the velocity gradient is equal to the Pythagorean angles θ, of 36.9 and 53.1 degrees in Gay–Berne fluid I. (b) As in (a) but the system is Gay–Berne fluid II. (c) As in (a) but the system is the soft sphere string-fluid
* = (Γ/V)/ε0σ0−3, when the director is confined to the plane perpendicular to the streamlines, as a function of the reduced shear rate, γ*, when the angle between the director and the velocity gradient is equal to the Pythagorean angles θ, of 36.9 and 53.1 degrees in Gay–Berne fluid I. (b) As in (a) but the system is Gay–Berne fluid II. (c) As in (a) but the system is the soft sphere string-fluid
| (a) |
|
γ*
|
![[capital Gamma, Greek, circumflex]](https://www.rsc.org/images/entities/i_char_e132.gif) */10−3 (θ = 36.9°) */10−3 (θ = 36.9°) |
![[capital Gamma, Greek, circumflex]](https://www.rsc.org/images/entities/i_char_e132.gif) */10−3 (θ = 53.1°) */10−3 (θ = 53.1°) |
| 0.0025 |
0.16 ± 0.03 |
|
| 0.0040 |
0.36 ± 0.05 |
0.04 ± 0.01 |
| 0.0050 |
0.46 ± 0.09 |
0.07 ± 0.02 |
| 0.0080 |
1.3 ± 0.1 |
0.23 ± 0.01 |
| 0.0100 |
2.12 ± 0.05 |
0.34 ± 0.03 |
| 0.0125 |
3.12 ± 0.07 |
0.49 ± 0.09 |
| 0.0150 |
4.4 ± 0.2 |
|
| (b) |
|
γ*
|
![[capital Gamma, Greek, circumflex]](https://www.rsc.org/images/entities/i_char_e132.gif) */10−3 (θ = 36.9°) */10−3 (θ = 36.9°) |
![[capital Gamma, Greek, circumflex]](https://www.rsc.org/images/entities/i_char_e132.gif) */10−3 (θ = 53.1°) */10−3 (θ = 53.1°) |
| 0.005 |
0.08 ± 0.02 |
0.020 ± 0.005 |
| 0.010 |
0.32 ± 0.03 |
0.087 ± 0.005 |
| (c) |
|
γ* |
![[capital Gamma, Greek, circumflex]](https://www.rsc.org/images/entities/char_e132.gif) */10−3 (θ = 36.9°) */10−3 (θ = 36.9°) |
![[capital Gamma, Greek, circumflex]](https://www.rsc.org/images/entities/char_e132.gif) */10−3 (θ = 53.1°) */10−3 (θ = 53.1°) |
| 0.0010 |
0.13 ± 0.02 |
|
| 0.0015 |
0.26 ± 0.02 |
0.03 ± 0.01 |
| 0.0025 |
0.54 ± 0.03 |
0.11 ± 0.01 |
| 0.0040 |
1.37 ± 0.02 |
0.29 ± 0.05 |
| 0.0050 |
2.06 ± 0.02 |
0.49 ± 0.02 |
The relation between the shear rate and the shear-induced torque can be regarded as a cross coupling coefficient or transport coefficient. This is a material property of the system in the same way as, for example, the viscosity or the heat conductivity. It is highly likely that the cross coupling coefficient is only weakly system size dependent. Therefore, this is a useful quantity that can be obtained from simulations of microscopic systems and be used in macroscopic elasto-hydrodynamic calculations.
6.2 Apparent stability of the orientation parallel to the shear plane
Having established that the torque is composed of a shear-induced torque and an elastic torque, it is possible to explain various orientation phenomena: The stability of the orientation parallel to the shear plane at low shear rates despite the higher viscosity is probably due to a strong elastic torque overwhelming the shear-induced torque. The elastic torque stabilises orientations where the smectic layer planes are parallel to one of the faces of the simulation cell since the equilibrium layer spacing must change if the smectic liquid crystal is turned away from this orientation. Nevertheless, when the shear rate increases, the shear-induced torque increases and it will eventually overwhelm the elastic torque, so that the layer planes turn over and become parallel to the vorticity plane, at least in Gay–Berne fluid I. However, the maximal elastic strain and thereby the elastic torque decrease with the system size and are approximately inversely proportional to the number of layers, if we assume linear elasticity. Thus, the shear rate needed to overwhelm the elastic torque is inversely proportional to the square root of the number of layers since the shear-induced torque is proportional to the square of the shear rate, see Table 6. Therefore, it is highly likely that the transition will take place in Gay–Berne fluid II and in the soft sphere string-fluid too in a larger system. If the system is large enough, it is even possible that the orientation parallel to the vorticity plane will be attained directly when the shear rate is different from zero. This also means that the stability of the orientation parallel to the shear plane at low shear rates is not a counterexample of the variational principle of ref. 39.
Table 6 The maximal elastic torque caused by the periodic boundary conditions and the shape of the simulation cell and the shear rate needed to induce this torque as a function of the number of smectic layers in the simulation. It is assumed that the elastic torque is linearly proportional to the maximal strain, which in turn is inversely proportional to the number of layers. The maximal torque for ten layers is denoted by τ10 and the corresponding shear rate is denoted by γ10. Note that even if the relation between the torque and the strain is nonlinear, the torque and thereby the shear rate needed to overwhelm it will decrease in larger systems
| Number of layers |
Elastic torque |
Shear rate |
| 10 |
τ
10
|
γ
10
|
| 20 |
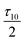
|
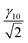
|
| 30 |
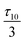
|
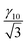
|
|
L
|
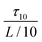
|
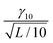
|
The transition between the orientation parallel to the shear plane and the orientation parallel to the vorticity plane has also been observed in macroscopic experimental measurements.10–18 However, the mechanism is different in these cases because some other torque than the elastic torque caused by the periodic boundary conditions must be at work, such as, for example, surface torques, or anchoring torques etc., and they are much smaller than the torques caused by the periodic boundary conditions or the shape of the simulation cell. Thus, the appearance of this transition in the microscopic simulations does not necessarily prove that it will take place in a macroscopic system.
6.3 Spontaneous alignment parallel to the shear plane
Another contradictory result that can be explained is the fact that Gay–Berne fluids I and II align parallel to the shear plane, where the viscosity is maximal, at low shear rates when the simulation is started from a configuration where the director is parallel to the streamlines. This can be understood by realising that the velocity field in a shear flow is a superposition of an irrotational elongational flow field exerting a torque turning the director towards the 45 degree orientation and a rotational flow field exerting a torque rotating the director if the director is confined to the vorticity plane, see Fig. 10. Then, if there is a strong coupling to the rotational part of the shear field, the director will be rotated in the clockwise direction. In a flow unstable nematic phase, the rotation will continue forever, see ref. 34, but in a small smectic liquid crystal system, the rotation will stop when the smectic layers are parallel to the shear plane due to strong elastic torques since the equilibrium layer spacing is attained. However, if the director is slightly skewed relative to the velocity gradient, there is still a shear-induced torque in the direction of the streamlines and in large systems, the elastic torque decreases, so that the shear-induced torque will finally dominate and eventually turn the layers to the orientation parallel to the vorticity plane. Thus, it is likely that the orientation parallel to the vorticity plane will be attained directly even at lower shear rates in larger systems.
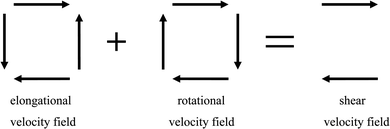 |
| | Fig. 10 The velocity field of a shear flow is the sum of the irrotational elongational flow and the purely rotational flow. The elongational flow exerts a torque turning the director towards the 45 degree orientations relative to the streamlines whereas the rotational flow exerts a torque rotating the director in the clockwise direction. | |
6.4 The undulation instability
In many experimental measurements10–18 and in the simulations,22–25 the transition between the orientations parallel to the shear plane and parallel to the vorticity plane is accompanied by an undulation instability but this instability is absent in our simulations of the Gay–Berne fluid and the soft sphere string-fluid. A plausible reason for this is that the molecular models that we examine are rigid rods. In the case of the Gay–Berne fluid, the smectic layer structure is stabilized by strong attractive forces between the molecules in the side-by-side orientation, making the layers very stiff. The formation of a smectic phase in the soft-sphere string-fluid is due to anisotropic volume exclusion, i.e. a purely entropic effect. The density is rather high, so that the layers become stiffer in this case too. The result is that the undulations are damped and larger systems are required to observe the undulation instability.
Since the side of the simulation cell in the present work is equal to about 15 molecular lengths, corresponding to about 300 Å assuming a molecular length of 20 Å, whereas the gap width in the experimental studies is considerably larger, i.e. at least 3 900 Å in ref. 12 and 1 mm in ref. 14, it cannot be ruled out that the undulation instability will appear if the system size is increased.
On the other hand, the molecules in ref. 22–25 consist of flexible FENE-chains. They are more flexible than the Gay–Berne ellipsoids and the soft sphere strings and for that reason, they are not able to form nematic liquid crystals. The smectic phase forms because the molecules display one A-end and one B-end where the A–A interactions and B–B interactions are attractive, whereas the A–B interaction is repulsive. Thus, the smectic phase is formed by attractive forces between the layers rather than by volume exclusion or attractions within the layers. This probably means that the smectic layers become more flexible, so that the undulation instability can appear in smaller systems.
7. Conclusion
We have studied planar Couette flow or shear flow of the smectic A phase of three molecular model systems: two versions of the Gay–Berne fluid where the length-to-width-ratio is equal to 4.4![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1 and the potential well depth ratio of the side-by-side and end-to-end configuration is equal to 20 (I) and 201/2 ≈ 4.472 (II), respectively, and the soft sphere string-fluid consisting of linear rigid strings of 11 spheres separated by a sphere radius giving a length-to-width-ratio of 6
1 and the potential well depth ratio of the side-by-side and end-to-end configuration is equal to 20 (I) and 201/2 ≈ 4.472 (II), respectively, and the soft sphere string-fluid consisting of linear rigid strings of 11 spheres separated by a sphere radius giving a length-to-width-ratio of 6![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1.
1.
There are two orientations of the smectic layers relative to the shear field allowed by symmetry: parallel to the shear plane and parallel to the vorticity plane. When the density is constant, both these orientations are at least metastable at low shear rates in all the systems. The orientation parallel to the vorticity plane persists to higher shear rates than the orientation parallel to the shear plane. At high shear rates, there is a transition to a nonequilibrium nematic phase with the director almost parallel to the stream lines.
In Gay–Berne fluid I, the configuration parallel to the shear plane changes to the configuration parallel to the vorticity plane at an intermediate shear rate of about 0.01τ−1, but this transition is not reversible and it does not take place in the other two systems.
Moreover, in the two Gay–Berne fluids, the orientation parallel to the shear plane is attained at low shear rates if the initial phase is a nematic or smectic phase with the director parallel to the streamlines.
In order to perform a proper analysis of these orientation phenomena, the torque exerted on the director in the direction of the streamlines was calculated by using a Gaussian constraint algorithm. Then, it was found that this torque consisted of an elastic torque caused by the shape of the simulation cell and the periodic boundary conditions on one hand and a shear-induced torque on the other hand. The functional dependence of the shear-induced torque on the shear rate and the angle between the velocity gradient and the director is in fact a cross coupling coefficient and a material property in the same way as the viscosity or heat conductivity.
The orientations parallel to the faces of the simulation cell are stabilised because the equilibrium layer spacing is attained so that an elastic restoring torque arises because of the accompanying deformations if the director is turned away from these orientations. However, it was also found that the shear-induced torque turned the smectic layers to the orientation parallel to the vorticity plane, where the viscosity and thereby the irreversible energy dissipation rate are minimal. This is consistent with a recently proven theorem stating that the irreversible energy dissipation rate is minimal in the linear regime of a nonequilbrium steady state. It was also found that the shear-induced torque was proportional to the square of the shear rate in accordance with symmetry restrictions. Thus, the shear-induced torque will overwhelm the elastic torque when the shear rate is high enough and turn the smectic layer planes to the orientation parallel to the vorticity plane. Also, the maximal elastic torque is approximately inversely proportional to the number of smectic layers, whereas it is reasonable to assume that the shear-induced torque is less system size dependent. Therefore, it is very likely that the transition from the shear plane to the vorticity plane will take place in Gay–Berne fluid II and in the soft sphere string-fluid in a larger system and that the shear rate at the transition point will be lower or even zero in larger systems. For this reason, it is also likely that Gay–Berne fluids I and II will attain the orientation parallel to the vorticity plane rather than the orientation parallel to the shear plane even at low shear rates when the director is parallel to the streamlines in the initial configuration if the system is large enough.
It should also be noted that the presence of the transition between the orientations parallel to the shear plane and parallel to the vorticity plane in a simulation of a microscopic system does not prove that this transition will necessarily take place in the corresponding macroscopic system, since the elastic torque caused by the periodic boundary conditions decreases with the system size. If the orientation parallel to the shear plane is stable in a macroscopic system, this is due to the presence of some other torque, such as, for example, surface torques or anchoring torques among other things.
Finally, in many experimental systems and in some simulations, the above-mentioned transition is accompanied by an undulation instability but this instability is not observed in the simulations in the present work. The reason for this could be that the smectic layers are very stiff, so that larger systems are needed to observe them.
Conflicts of interest
There are no conflicts of interest to declare.
Appendix 1: the SLLOD equations of motion at constant pressure
The general form of the SLLOD equations of motion for shear flow, where one or more components of the pressure are kept constant is given by| | 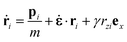 | (A1a) |
and| | ṗi = Fi − ![[small epsi, Greek, dot above]](https://www.rsc.org/images/entities/b_char_e0a1.gif) ·pi − γpziex − αpi, ·pi − γpziex − αpi, | (A1b) |
where ri and pi are the position and peculiar momentum, i.e. the momentum relative to the streaming velocity, of molecule i, m is the molecular mass, γ = ∂ux/∂z is the shear rate, i.e. there is a streaming velocity ux in the x-direction varying linearly in the z-direction, ex is the unit vector in the x-direction, Fi is the force exerted on molecule i by the other molecules and ![[small epsi, Greek, dot above]](https://www.rsc.org/images/entities/b_char_e0a1.gif) is the dilation rate. The Gaussian thermostatting multiplier α is given by the constraint that the linear peculiar kinetic energy is a constant of motion,
is the dilation rate. The Gaussian thermostatting multiplier α is given by the constraint that the linear peculiar kinetic energy is a constant of motion,| | 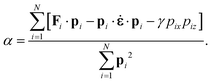 | (A1c) |
Then, the total pressure can be kept constant by using the following Nosé–Hoover feedback mechanism, where the diagonal elements of the dilation rate are equal,| | ![[small epsi, Greek, dot above]](https://www.rsc.org/images/entities/b_char_e0a1.gif) = = ![[small epsi, Greek, dot above]](https://www.rsc.org/images/entities/i_char_e0a1.gif) 1, 1, | (A2a) |
| | 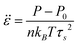 | (A2b) |
| | ![[V with combining dot above]](https://www.rsc.org/images/entities/i_char_0056_0307.gif) = 3 = 3![[small epsi, Greek, dot above]](https://www.rsc.org/images/entities/i_char_e0a1.gif) V, V, | (A2c) |
where P is the actual pressure, P0 is the desired pressure, n = N/V is the number density of the system, kB is Boltzmann's constant, T is the absolute temperature and τs is a time constant, which is arbitrary within certain limits.
It is often desirable to keep the pressure components in the different directions constant separately, for example in the z-direction on the one hand and in the x- and y-directions together on the other hand. This can be achieved by using the following equations,
| | ![[small epsi, Greek, dot above]](https://www.rsc.org/images/entities/b_char_e0a1.gif) = = ![[small epsi, Greek, dot above]](https://www.rsc.org/images/entities/i_char_e0a1.gif) ‖‖ezez + ‖‖ezez + ![[small epsi, Greek, dot above]](https://www.rsc.org/images/entities/i_char_e0a1.gif) ⊥⊥(exex + eyey), ⊥⊥(exex + eyey), | (A3a) |
| | 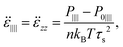 | (A3b) |
| | 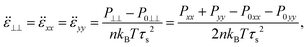 | (A3c) |
| | ![[L with combining dot above]](https://www.rsc.org/images/entities/i_char_004c_0307.gif) z = z = ![[small epsi, Greek, dot above]](https://www.rsc.org/images/entities/i_char_e0a1.gif) ‖‖Lz, ‖‖Lz, | (A3d) |
| | Ȧxy = ![[small epsi, Greek, dot above]](https://www.rsc.org/images/entities/i_char_e0a1.gif) ⊥⊥Axy, ⊥⊥Axy, | (A3e) |
where the components of the dilation rate are
![[small epsi, Greek, dot above]](https://www.rsc.org/images/entities/i_char_e0a1.gif) ‖‖
‖‖ =
![[small epsi, Greek, dot above]](https://www.rsc.org/images/entities/i_char_e0a1.gif) zz
zz and
![[small epsi, Greek, dot above]](https://www.rsc.org/images/entities/i_char_e0a1.gif) ⊥⊥
⊥⊥ =
![[small epsi, Greek, dot above]](https://www.rsc.org/images/entities/i_char_e0a1.gif) xx
xx =
![[small epsi, Greek, dot above]](https://www.rsc.org/images/entities/i_char_e0a1.gif) yy
yy,
Lz is the length of the system in the
z-direction and
Axy is the area of the system in the
xy-plane. If these equations are applied to a smectic phase with the layer normal or the director parallel to the
z-direction and the smectic layers parallel to the
xy-plane, the system is able to attain the equilibrium layer spacing.
Appendix 2
The most straightforward way of deriving the constraint eqn (6) is to apply Gauss's principle of least constraint.5,42,43 Then the constraints are written as functions of the accelerations whereas they are written as functions of the coordinates when the ordinary Lagrangian formalism is used. Thus, we constrain the director angular acceleration, 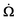 , to be zero since it is a function of the molecular angular accelerations,
, to be zero since it is a function of the molecular angular accelerations, 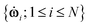 , where N is the number of molecules,
, where N is the number of molecules,| | 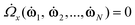 | (A4a) |
and| | 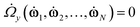 | (A4b) |
According to Gauss's principle, the equations of motion are obtained by minimising a quantity known as the square of the curvature with respect to the accelerations, subject to the above constraints,
| | 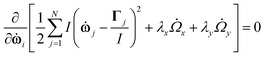 | (A5) |
or
| | 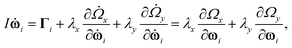 | (A6) |
where the last equality is obtained by noting that the director angular acceleration is a linear function of the molecular angular accelerations. By inserting
eqn (A6) into the constraint
eqn (A4a) and (A4b), a linear system of equations with the multipliers
λx and
λy as unknowns is obtained, which can be expressed in terms of the molecular angular velocities and unit vectors parallel to the axis of revolution of the molecules {
ωi,
ûi; 1 ≤
i ≤
N}.
Appendix 3: practical implementation of the director constraint algorithm for the evaluation of torques
If the constraint eqn (6) or eqn (A6) is applied directly, the director will slowly drift away from the desired orientation due to numerical inaccuracy. Therefore, we have augmented the Gaussian constraint multipliers by two proportional feedback multipliers,| | 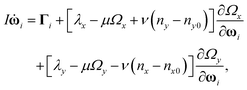 | (A7) |
where μ and ν are the feedback multipliers, nx and ny are the actual values of the x- and y-components of the director and nx0 and ny0 are the corresponding desired values; Ωx and Ωy are the actual values of the x- and y-components of the director angular velocity and their desired values are zero. The values of the multipliers μ and ν are usually set to be about 1.0 in reduced units. The absolute values of Ωx, Ωy, nx − nx0 and ny − ny0 are equal to zero if the numerical method is exact and in practice, they barely exceed 10−8, which is considerably less than the magnitudes of λx and λx. Thus, the effect of the proportional feedback multipliers μ and ν on the phase space trajectories and the ensemble averages of the phase functions is negligible.
Acknowledgements
We gratefully acknowledge Vetenskapsrådet (Swedish Research Council) (Project number: 2014-4694) for their financial support. The simulations were performed using resources provided by the Swedish National Infrastructure for Computing (SNIC) at PDC, HPC2N and NSC. AL thanks for a partial support by a grant of Ministry of Research and Innovation of Romania, CNCS–UEFISCDI, project number PN-III-P4-ID-PCCF-2016-0050, within PNCDI III.
References
-
S. Chandrasekhar, Liquid Crystals, Cambridge University Press, Cambridge, 1992 Search PubMed.
-
P. G. DeGennes and J. Prost, The Physics of Liquid Crystals, Clarendon Press, Oxford, 1993 Search PubMed.
- S. Sarman and A. Laaksonen, J. Comput. Theor. Nanosci., 2011, 8, 1081 CrossRef CAS.
- S. Sarman, Y.-L. Wang and A. Laaksonen, Phys. Chem. Chem. Phys., 2015, 17, 16615 RSC.
- S. Sarman, D. J. Evans and P. T. Cummings, Phys. Rep., 1998, 305, 1 CrossRef CAS.
- M. Goulian and S. T. Milner, Phys. Rev. Lett., 1995, 74, 1775 CrossRef CAS PubMed.
- G. K. Auernhammer, H. R. Brand and H. Pleiner, Rheol. Acta, 2000, 39, 215 CrossRef CAS.
- G. K. Auernhammer, H. R. Brand and H. Pleiner, Phys. Rev. E: Stat., Nonlinear, Soft Matter Phys., 2002, 66, 061707 CrossRef PubMed.
- O. Henrich, K. Stratford, D. Marenduzzo, P. V. Coveneya and M. E. Catesc, Soft Matter, 2012, 8, 3817 RSC.
- C. R. Safinya, E. B. Sirota and R. J. Piano, Phys. Rev. Lett., 1991, 66, 1986 CrossRef PubMed.
- C. R. Safinya, E. B. Sirota, R. F. Bruinsma, C. Jeppesen, R. J. Plano and L. J. Wenzel, Science, 1993, 261, 588 CrossRef CAS PubMed.
- S. H. J. Idziak1, C. R. Safinya, R. S. Hill, K. E. Kraiser, M. Ruths, H. E. Warriner, S. Steinberg, K. S. Liang and J. N. Israelachvili, Science, 1994, 264, 1915 CrossRef PubMed.
- P. Panizza, P. Archambault and D. Roux, J. Phys. II, 1995, 5, 303 CrossRef CAS.
- K. Negita, M. Inoue and S. Kondo, Phys. Rev. E: Stat., Nonlinear, Soft Matter Phys., 2006, 74, 051708 CrossRef CAS PubMed.
- Z.-R. Chen, J. A. Kornfield, S. D. Smith, J. T. Grothaus and M. M. Satkowski, Science, 1997, 277, 1248 CrossRef CAS.
- D. Maring and U. Wiesner, Macromolecules, 1997, 30, 660 CrossRef CAS.
- J. Zipfel, J. Berghausen, G. Schmidt, P. Lindner, P. Alexandridis, M. Tsianoud and W. Richtering, Phys. Chem. Chem. Phys., 1999, 1, 3905 RSC.
- J. Penfold, E. Staples, A. Khan Lodhi, I. Tucker and G. J. T. Tiddy, J. Phys. Chem. B, 1997, 101, 66 CrossRef CAS.
-
Tribology and the Liquid-Crystalline State, ed. G. Biresaw, ACS Symposium Series, 441, American Chemical Society, Washington DC, USA, 1990 Search PubMed.
- F.-J. Carrión, G. Martínez-Nicolás, P. Iglesias, J. Sanes and M.-D. Bermúdez, Int. J. Mol. Sci., 2009, 10, 4102 CrossRef PubMed.
- T. Amann, C. Dold and A. Kailer, Soft Matter, 2012, 8, 9840 RSC.
- H. Guo, K. Kremer and Th. Soddemann, Phys. Rev. E: Stat., Nonlinear, Soft Matter Phys., 2002, 66, 061503 CrossRef PubMed.
- Th. Soddemann, G. K. Auernhammer, H. Guo, B. Dünweg and K. Kremer, Eur. Phys. J. E: Soft Matter Biol. Phys., 2004, 13, 141 CrossRef CAS PubMed.
- H. Guo, J. Chem. Phys., 2006, 124, 054902 CrossRef PubMed.
- H. Guo, J. Chem. Phys., 2006, 125, 214902 CrossRef PubMed.
- K. Kremer and G. S. Grest, J. Chem. Phys., 1990, 92, 5057 CrossRef CAS.
-
R. B. Bird, et al., Dynamics of Polymeric Liquids, Wiley, New York, 1977, vol. 1 and 2 Search PubMed.
- F. Müller-Plathe, Phys. Rev. E: Stat., Nonlinear, Soft Matter Phys., 1999, 59, 4894 CrossRef.
- J. G. Gay and B. J. Berne, J. Chem. Phys., 1981, 74, 3316 CrossRef CAS.
- M. A. Bates and G. R. Luckhurst, J. Chem. Phys., 1996, 104, 6696 CrossRef CAS.
- M. A. Bates and G. R. Luckhurst, J. Chem. Phys., 1999, 110, 7087 CrossRef CAS.
- M. A. Bates and G. R. Luckhurst, J. Chem. Phys., 2004, 120, 394 CrossRef CAS PubMed.
- S. Sarman, J. Chem. Phys., 1998, 108, 7909 CrossRef CAS.
- S. Sarman and A. Laaksonen, J. Chem. Phys., 2009, 131, 144904 CrossRef PubMed.
- G. V. Paolini, G. Ciccotti and M. Ferrario, Mol. Phys., 1993, 80, 297 CrossRef CAS.
- G. Cinacchi, L. De Gaetani and A. Tani, J. Chem. Phys., 2005, 122, 184513 CrossRef PubMed.
-
D. J. Evans and G. P. Morriss, Statistical mechanics of nonequilibrium liquids, ANU Press, Canberra, 2007 Search PubMed.
- S. Sarman, Y.-L. Wang and A. Laaksonen, Comp. Meth. Sci. Technol., 2017, 23, 239 Search PubMed.
-
D. J. Evans, D. J. Searles and S. R. Williams, Fundamentals of Classical Statistical Thermodynamics: Dissipation, Relaxation and Fluctuation Theorems, Wiley-VCH, 2016 Search PubMed.
- H. Irving and J. G. Kirkwood, J. Chem. Phys., 1950, 18, 817 CrossRef.
- D. J. Evans, Mol. Phys., 1977, 34, 314 Search PubMed.
- S. Sarman, J. Chem. Phys., 1996, 104, 342 CrossRef CAS.
- S. Sarman, J. Chem. Phys., 1994, 101, 480 CrossRef CAS.
- A. Stukowski, Visualization and analysis of atomistic simulation data with OVITO – the Open Visualization Tool, Modell. Simul. Mater. Sci. Eng., 2010, 18, 015012 CrossRef.
- S. Bair, C. McCabe and P. T. Cummings, Phys. Rev. Lett., 2002, 88, 058302 CrossRef PubMed.
- C. McCabe, S. Cui and P. T. Cummings, Fluid Phase Equilib., 2001, 183, 363 CrossRef.
|
| This journal is © the Owner Societies 2019 |
Click here to see how this site uses Cookies. View our privacy policy here.  *a,
Yong-Lei
Wang
*a,
Yong-Lei
Wang
 b and
Aatto
Laaksonen
b and
Aatto
Laaksonen
 acd
acd
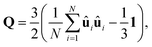
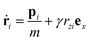
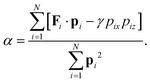
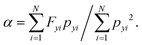
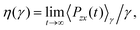
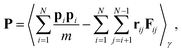
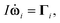
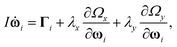
![[capital Gamma, Greek, circumflex]](https://www.rsc.org/images/entities/i_char_e132.gif) x in the direction of the streamlines is given by
x in the direction of the streamlines is given by![[capital Gamma, Greek, circumflex]](https://www.rsc.org/images/entities/i_char_e132.gif) x = 〈λx〉γ/V = 2Pax,
x = 〈λx〉γ/V = 2Pax,![[capital Gamma, Greek, circumflex]](https://www.rsc.org/images/entities/i_char_e132.gif) xel, is formally defined as the derivative of the elastic free energy, Eel, with respect to the angle between the director and the velocity gradient, θ,
xel, is formally defined as the derivative of the elastic free energy, Eel, with respect to the angle between the director and the velocity gradient, θ,![[capital Gamma, Greek, circumflex]](https://www.rsc.org/images/entities/i_char_e132.gif) xel = ∂Eel/∂θ.
xel = ∂Eel/∂θ.![[capital Gamma, Greek, circumflex]](https://www.rsc.org/images/entities/i_char_e132.gif) xshear, must remain unchanged when the shear rate changes sign, i.e. γ → −γ, be zero when θ is equal to an integer multiple of 90 degrees and be a periodic function of θ due to symmetry. This means that it can be expanded in a series of even powers of γ and a Fourier series of sine functions of even multiples of θ,
xshear, must remain unchanged when the shear rate changes sign, i.e. γ → −γ, be zero when θ is equal to an integer multiple of 90 degrees and be a periodic function of θ due to symmetry. This means that it can be expanded in a series of even powers of γ and a Fourier series of sine functions of even multiples of θ,![[capital Gamma, Greek, circumflex]](https://www.rsc.org/images/entities/i_char_e132.gif) xshear ∼ γ2
xshear ∼ γ2![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) sin
sin![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 2θ + higher order terms.
2θ + higher order terms.![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) θ = m/L or cos
θ = m/L or cos![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) θ = l/L, where θ is the angle between the director and the normal of one of the faces of the simulation cell, m is the number of layers intersecting the x-axis and l is the number of layers intersecting the y-axis, see Fig. 2a and b. Consequently, there are two skew director orientations where there are no elastic deformations. This also means that the constraint torques needed to fix the director in these orientations to a large extent are free from elastic contributions and thus they should be better estimates of the shear-induced torque in the absence of elastic deformations.
θ = l/L, where θ is the angle between the director and the normal of one of the faces of the simulation cell, m is the number of layers intersecting the x-axis and l is the number of layers intersecting the y-axis, see Fig. 2a and b. Consequently, there are two skew director orientations where there are no elastic deformations. This also means that the constraint torques needed to fix the director in these orientations to a large extent are free from elastic contributions and thus they should be better estimates of the shear-induced torque in the absence of elastic deformations.
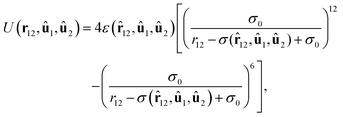
![[r with combining circumflex]](https://www.rsc.org/images/entities/b_char_0072_0302.gif) 12 is the unit vector in the direction of r12 and r12 is the length of r12. The parameter σ0 is the length of the axis perpendicular to the axis of revolution, i.e. the minor axis of a prolate ellipsoid. The strength and range parameters are given by
12 is the unit vector in the direction of r12 and r12 is the length of r12. The parameter σ0 is the length of the axis perpendicular to the axis of revolution, i.e. the minor axis of a prolate ellipsoid. The strength and range parameters are given by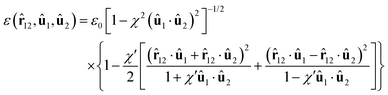
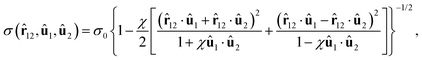
![[r with combining circumflex]](https://www.rsc.org/images/entities/b_char_0072_0302.gif) 12, û1 and û2 are perpendicular to each other, i.e. the cross configuration, χ = (κ2 − 1)/(κ2 + 1), κ is the ratio between the axis of revolution and the axis perpendicular to this axis, i.e. the length-to-width ratio of prolate ellipsoids, χ′ = (κ′ − 1)/(κ′ + 1) and κ′ is the ratio of the potential energy minima of the side-by-side and end-to-end configurations. The parameter κ has been given the value 4.4 and we have used two values of the parameter κ′, namely 20 (I) and 201/2 ≈ 4.472 (II). These values of κ′ enhance the attraction in the side-by-side configuration, thereby stabilising the smectic layers. The first parameterisation has been comprehensively studied by Bates and Luckhurst30–32 and the second one has been applied by the present authors.3,33,34 The moments of inertia around the axes perpendicular to the axis of revolution have been given the value mσ02, where m is the molecular mass.
12, û1 and û2 are perpendicular to each other, i.e. the cross configuration, χ = (κ2 − 1)/(κ2 + 1), κ is the ratio between the axis of revolution and the axis perpendicular to this axis, i.e. the length-to-width ratio of prolate ellipsoids, χ′ = (κ′ − 1)/(κ′ + 1) and κ′ is the ratio of the potential energy minima of the side-by-side and end-to-end configurations. The parameter κ has been given the value 4.4 and we have used two values of the parameter κ′, namely 20 (I) and 201/2 ≈ 4.472 (II). These values of κ′ enhance the attraction in the side-by-side configuration, thereby stabilising the smectic layers. The first parameterisation has been comprehensively studied by Bates and Luckhurst30–32 and the second one has been applied by the present authors.3,33,34 The moments of inertia around the axes perpendicular to the axis of revolution have been given the value mσ02, where m is the molecular mass.
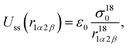
![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1. A similar system has been studied by Paolini et al.35 and by Cinacchi et al.36 The mass of the molecule is equal to m and the moment of inertia has been set equal to 5mσ02/2. This value was obtained by assuming that the mass of each sphere is concentrated at its centre of symmetry and equal to m/11. Note, however, that other realistic mass distributions are possible.
1. A similar system has been studied by Paolini et al.35 and by Cinacchi et al.36 The mass of the molecule is equal to m and the moment of inertia has been set equal to 5mσ02/2. This value was obtained by assuming that the mass of each sphere is concentrated at its centre of symmetry and equal to m/11. Note, however, that other realistic mass distributions are possible.
![[capital Gamma, Greek, circumflex]](https://www.rsc.org/images/entities/i_char_e132.gif) * =
* = ![[capital Gamma, Greek, circumflex]](https://www.rsc.org/images/entities/i_char_e132.gif) σ03/ε0, γ* = γτ and η* = ησ03/ε0τ, respectively.
σ03/ε0, γ* = γτ and η* = ησ03/ε0τ, respectively.
![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 988 ellipsoids forming 15 smectic layers. These numbers of particles and layers were also used in Gay–Berne system II when the torque density was calculated, and 65
988 ellipsoids forming 15 smectic layers. These numbers of particles and layers were also used in Gay–Berne system II when the torque density was calculated, and 65![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 536 ellipsoids forming 18 layers were used when the viscosity was evaluated. In the case of the soft sphere strings, 12
536 ellipsoids forming 18 layers were used when the viscosity was evaluated. In the case of the soft sphere strings, 12![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 800 strings with a total of 140
800 strings with a total of 140![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 800 soft spheres were employed giving eight smectic layers when the viscosity was evaluated and 25
800 soft spheres were employed giving eight smectic layers when the viscosity was evaluated and 25![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 000 strings with a total of 275
000 strings with a total of 275![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 000 spheres forming 10 layers were used when the torque density was obtained. The above parameters are shown in Table 1. The reason why we wanted 15 and 10 layers when the torque density was evaluated was that these two numbers are Pythagorean numbers, allowing two skew orientations of the smectic layer planes where the layer spacing is equal to the equilibrium layer spacing, see Section 2.5.
000 spheres forming 10 layers were used when the torque density was obtained. The above parameters are shown in Table 1. The reason why we wanted 15 and 10 layers when the torque density was evaluated was that these two numbers are Pythagorean numbers, allowing two skew orientations of the smectic layer planes where the layer spacing is equal to the equilibrium layer spacing, see Section 2.5.![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 988
988![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 536
536![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 988
988![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 800
800![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 000
000
![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) γτ (degrees), see Fig. 5, so that a nonequilibrium smectic C phase arises. In contrast to Gay–Berne fluid I and to the system studied in ref. 22–25, there is no transition to the orientation parallel to the vorticity plane. At higher shear rates, the smectic layer structure breaks down and there is a gradual transition to a nonequilibrium nematic phase.
γτ (degrees), see Fig. 5, so that a nonequilibrium smectic C phase arises. In contrast to Gay–Berne fluid I and to the system studied in ref. 22–25, there is no transition to the orientation parallel to the vorticity plane. At higher shear rates, the smectic layer structure breaks down and there is a gradual transition to a nonequilibrium nematic phase.![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) γτ (degrees), see Fig. 5, so that in this case too, the smectic A phase is transformed to a nonequilibrium smectic C phase. Note that the angle is considerably larger than that for the Gay–Berne fluids possibly because the smectic layers do not interpenetrate. At a shear rate of about 0.0045τ−1, there is a gradual transition to a nonequilibrium nematic liquid crystal. There is no transition to the orientation parallel to the vorticity plane in this case either and thus this system too behaves differently to that studied by Guo et al. in ref. 22–25. The behaviour at constant pressure is more or less the same as that at constant volume. If the soft spheres are replaced by attractive Lennard-Jones spheres, the system behaves qualitatively in the same way, at least at some state points.
γτ (degrees), see Fig. 5, so that in this case too, the smectic A phase is transformed to a nonequilibrium smectic C phase. Note that the angle is considerably larger than that for the Gay–Berne fluids possibly because the smectic layers do not interpenetrate. At a shear rate of about 0.0045τ−1, there is a gradual transition to a nonequilibrium nematic liquid crystal. There is no transition to the orientation parallel to the vorticity plane in this case either and thus this system too behaves differently to that studied by Guo et al. in ref. 22–25. The behaviour at constant pressure is more or less the same as that at constant volume. If the soft spheres are replaced by attractive Lennard-Jones spheres, the system behaves qualitatively in the same way, at least at some state points.![[capital Gamma, Greek, circumflex]](https://www.rsc.org/images/entities/i_char_e132.gif) * = (Γ/V)/ε0σ0−3, when the director is confined to the plane perpendicular to the streamlines, as a function of the reduced shear rate, γ*, when the angle between the director and the velocity gradient is equal to the Pythagorean angles θ, of 36.9 and 53.1 degrees in Gay–Berne fluid I. (b) As in (a) but the system is Gay–Berne fluid II. (c) As in (a) but the system is the soft sphere string-fluid
* = (Γ/V)/ε0σ0−3, when the director is confined to the plane perpendicular to the streamlines, as a function of the reduced shear rate, γ*, when the angle between the director and the velocity gradient is equal to the Pythagorean angles θ, of 36.9 and 53.1 degrees in Gay–Berne fluid I. (b) As in (a) but the system is Gay–Berne fluid II. (c) As in (a) but the system is the soft sphere string-fluid
![[capital Gamma, Greek, circumflex]](https://www.rsc.org/images/entities/i_char_e132.gif) */10−3 (θ = 36.9°)
*/10−3 (θ = 36.9°)![[capital Gamma, Greek, circumflex]](https://www.rsc.org/images/entities/i_char_e132.gif) */10−3 (θ = 53.1°)
*/10−3 (θ = 53.1°)![[capital Gamma, Greek, circumflex]](https://www.rsc.org/images/entities/i_char_e132.gif) */10−3 (θ = 36.9°)
*/10−3 (θ = 36.9°)![[capital Gamma, Greek, circumflex]](https://www.rsc.org/images/entities/i_char_e132.gif) */10−3 (θ = 53.1°)
*/10−3 (θ = 53.1°)![[capital Gamma, Greek, circumflex]](https://www.rsc.org/images/entities/char_e132.gif) */10−3 (θ = 36.9°)
*/10−3 (θ = 36.9°)![[capital Gamma, Greek, circumflex]](https://www.rsc.org/images/entities/char_e132.gif) */10−3 (θ = 53.1°)
*/10−3 (θ = 53.1°)![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1 and the potential well depth ratio of the side-by-side and end-to-end configuration is equal to 20 (I) and 201/2 ≈ 4.472 (II), respectively, and the soft sphere string-fluid consisting of linear rigid strings of 11 spheres separated by a sphere radius giving a length-to-width-ratio of 6
1 and the potential well depth ratio of the side-by-side and end-to-end configuration is equal to 20 (I) and 201/2 ≈ 4.472 (II), respectively, and the soft sphere string-fluid consisting of linear rigid strings of 11 spheres separated by a sphere radius giving a length-to-width-ratio of 6![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1.
1.
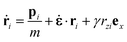
![[small epsi, Greek, dot above]](https://www.rsc.org/images/entities/b_char_e0a1.gif) ·pi − γpziex − αpi,
·pi − γpziex − αpi,![[small epsi, Greek, dot above]](https://www.rsc.org/images/entities/b_char_e0a1.gif) is the dilation rate. The Gaussian thermostatting multiplier α is given by the constraint that the linear peculiar kinetic energy is a constant of motion,
is the dilation rate. The Gaussian thermostatting multiplier α is given by the constraint that the linear peculiar kinetic energy is a constant of motion,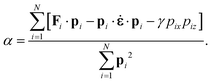
![[small epsi, Greek, dot above]](https://www.rsc.org/images/entities/b_char_e0a1.gif) =
= ![[small epsi, Greek, dot above]](https://www.rsc.org/images/entities/i_char_e0a1.gif) 1,
1,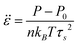
![[V with combining dot above]](https://www.rsc.org/images/entities/i_char_0056_0307.gif) = 3
= 3![[small epsi, Greek, dot above]](https://www.rsc.org/images/entities/i_char_e0a1.gif) V,
V,![[small epsi, Greek, dot above]](https://www.rsc.org/images/entities/b_char_e0a1.gif) =
= ![[small epsi, Greek, dot above]](https://www.rsc.org/images/entities/i_char_e0a1.gif) ‖‖ezez +
‖‖ezez + ![[small epsi, Greek, dot above]](https://www.rsc.org/images/entities/i_char_e0a1.gif) ⊥⊥(exex + eyey),
⊥⊥(exex + eyey),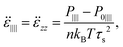
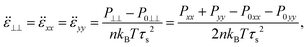
![[L with combining dot above]](https://www.rsc.org/images/entities/i_char_004c_0307.gif) z =
z = ![[small epsi, Greek, dot above]](https://www.rsc.org/images/entities/i_char_e0a1.gif) ‖‖Lz,
‖‖Lz,![[small epsi, Greek, dot above]](https://www.rsc.org/images/entities/i_char_e0a1.gif) ⊥⊥Axy,
⊥⊥Axy,![[small epsi, Greek, dot above]](https://www.rsc.org/images/entities/i_char_e0a1.gif) ‖‖ =
‖‖ = ![[small epsi, Greek, dot above]](https://www.rsc.org/images/entities/i_char_e0a1.gif) zz and
zz and ![[small epsi, Greek, dot above]](https://www.rsc.org/images/entities/i_char_e0a1.gif) ⊥⊥ =
⊥⊥ = ![[small epsi, Greek, dot above]](https://www.rsc.org/images/entities/i_char_e0a1.gif) xx =
xx = ![[small epsi, Greek, dot above]](https://www.rsc.org/images/entities/i_char_e0a1.gif) yy, Lz is the length of the system in the z-direction and Axy is the area of the system in the xy-plane. If these equations are applied to a smectic phase with the layer normal or the director parallel to the z-direction and the smectic layers parallel to the xy-plane, the system is able to attain the equilibrium layer spacing.
yy, Lz is the length of the system in the z-direction and Axy is the area of the system in the xy-plane. If these equations are applied to a smectic phase with the layer normal or the director parallel to the z-direction and the smectic layers parallel to the xy-plane, the system is able to attain the equilibrium layer spacing.
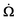 , to be zero since it is a function of the molecular angular accelerations,
, to be zero since it is a function of the molecular angular accelerations, 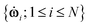 , where N is the number of molecules,
, where N is the number of molecules,