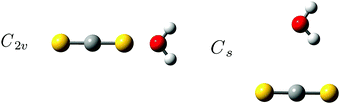THz spectroscopy of weakly bound cluster molecules in solid para-hydrogen: a sensitive probe of van der Waals interactions

Abstract

The present work demonstrates that 99.9% enriched solid para-H₂ below 3 K provides an excellent inert and transparent medium for the exploration of large-amplitude intermolecular vibrational motion of weakly bound van der Waals cluster molecules in the THz spectral region. THz absorption spectra have been generated for CO₂/H₂O and CS₂/H₂O mixtures embedded in enriched solid para-H₂ and numerous observed transitions associated with large-amplitude librational motion of the weakly bound binary CO₂⋯H₂O and CS₂⋯H₂O van der Waals cluster molecules have been assigned together with tentative assignments for the ternary CS₂⋯(H₂O)₂ system. The interaction strength, directionality and anharmonicity of the weak van der Waals “bonds” between the molecules can be characterized via these THz spectral signatures and yield rigorous benchmarks for high-level ab initio methodologies. It is suggested that even a less stable linear conformation of the ternary CS₂⋯(H₂O)₂ system, where one H₂O molecule is linked to each S atom of the CS₂ subunit, may be formed due to the kinetics associated with the mobility of free H₂O molecules in the soft para-H₂ medium. In addition, the spectroscopic observations confirm a linear and planar global intermolecular potential energy minimum for the binary CS₂⋯H₂O system with C_2v symmetry, where the O atom on the H₂O molecule is linked to one of the S atoms on the CS₂ subunit. A semi-experimental value for the vibrational zero-point energy contribution of 1.93 ± 0.10 kJ mol⁻¹ from the class of large-amplitude intermolecular vibrational modes is proposed. The combination with CCSD(T)/CBS electronic energy predictions provides a semi-experimental estimate of 5.08 ± 0.15 kJ mol⁻¹ for the binding energy D₀ of the CS₂⋯H₂O van der Waals system.

---

1. Introduction

One of the ultimate challenges for the physical sciences is to explore and accurately describe how remarkable properties of macroscopic phenomena known from the energy, materials and life sciences emerge from the interplay between specific non-covalent forces such as directional intermolecular hydrogen bonds, long-range London dispersion forces and short-range Pauli repulsion between the involved molecules. These weak non-covalent interactions between molecules are both responsible for the thermodynamic properties of condensed bulk matter, the mechanical properties of functional materials and the complex 3-D folding dynamics of macromolecules governing the molecular organization of biological systems. The interplay between non-covalent intermolecular forces emerges already at the level of the smallest isolated weakly bound cluster molecules. If one is able to isolate and spectroscopically characterize these smallest relevant molecular building blocks, molecule by molecule, it becomes possible to provide accurate experimental observables and further develop reliable theoretical models for the description of more complex supra-molecular systems such as gas hydrates, functional polymers and active drugs.

The vibrational motion involving the strong covalent bonds of stable molecules, the intra-molecular vibrational transitions, is detected in the infrared (IR) spectral region. The non-covalent forces involved in the formation of weakly bound cluster molecules are 10 to 100 times weaker than covalent bonds. The large-amplitude inter-molecular vibrational motion introduced by the complexation between molecules is accordingly probed in the terahertz (THz) spectral region. Both the interaction strength, directionality and anharmonicity of intermolecular hydrogen bonds and van der Waals interactions can be probed via this class of large-amplitude modes arising from the hindered rotational motion of the molecular subunits.^1–3 The associated THz spectral signatures help to characterize the intermolecular potential energy surfaces spanned by the involved molecules and also capture the dominating parts of the highly anharmonic vibrational zero-point energies, which are notoriously challenging to predict accurately by quantum chemical methods. The combination of these experimental vibrational zero-point energy contributions and high-level ab initio interaction energies D_e then enables the determination of accurate semi-experimental binding energies D₀.^4,5

The THz spectral region, the region of the electromagnetic spectrum with wavelengths between 3 mm and 30 μm, is often called the “the gap of the electromagnetic spectrum” as it has been extremely challenging to produce tunable radiation sources covering this entire region. The development of tunable THz laser technologies has enabled extensive investigations of large-amplitude vibrational–rotational–tunneling motion for isolated water clusters owing to the realization of high sensitivity and high spectral resolution.^6,7 The scanning bandwidths, however, are limited for many of these laser-based THz spectrometers and solely minor fractions of the spectrum can be sampled within a reasonable time period. Alternatively, highly brilliant broadband synchrotron radiation sources coupled with conventional Fourier transform interferometry^8–11 as well as far-infrared/ultraviolet ion-dip spectroscopy employing broadband free-electron laser sources^12,13 have provided complementary broadband THz/far-infrared approaches to probe large-amplitude hydrogen bond motion of cluster molecules in the gas phase.

An alternative low-resolution experimental approach, which is not relying on highly brilliant broadband free-electron lasers or synchrotron radiation sources, is conventional matrix isolation spectroscopy.^14,15 In this complementary approach, competitive spectroscopic sensitivities are achieved employing conventional energy-limited thermal radiation sources owing to the generation of large number densities of the unstable molecular systems of interest in cryogenic rare gas environments. The major disadvantage is usually severe perturbations of the resulting spectral signatures relative to those observed in the gas phase and/or molecular beams. However, several investigations of small molecules as H₂O,^16–19 CH₄^20–23 and CH₃OH²⁴ embedded in solid para-H₂ have indicated minor dielectric effects from this medium and revealed almost free overall rotational (H₂O and CH₄) or large-amplitude internal rotational (CH₃OH) motion of these guest molecules.

In the present contribution, we demonstrate how enriched solid para-H₂ provides an excellent inert medium for the exploration of large-amplitude librational motion of weakly bound (CO₂)_n⋯(H₂O)_m and (CS₂)_n⋯(H₂O)_m van der Waals cluster molecules in the THz region. The almost complete absence of more “reactive” ortho-H₂ molecules (I = 1) results in very weak interactions between the cluster molecules and the freely rotating spherically symmetric para-H₂ (I = 0) host molecules.²⁵ In addition, owing to the large-amplitude zero-point lattice vibrations of the para-H₂ crystal, the available matrix cages offer substantially larger space (39 ų) relative to solid neon (22 ų) for guest molecules helping to prevent the appearance of disturbing rotational-translation-coupling transitions in the relevant spectral region below 3 THz.¹⁵

2. Experimental section

Highly enriched para-H₂ samples were prepared from regular H₂ (Air Liquide, 99.999%) employing a laboratory-built ortho–para-H₂ conversion dip-stick apparatus similar to the approach described by Andrews and co-workers.²⁶ Regular H₂ gas was initially transferred to a gas handling system including a dip-stick tube containing ca. 5 grams of a paramagnetic hydrated iron(III) oxide catalyst (Sigma Aldrich, catalyst grade, 30–50 mesh) in a “conversion chamber” mounted at the end of the tube. This chamber was then iteratively immersed into cold helium gas over liquid helium to regulate the temperature of the H₂ gas above and below the H₂ triple point at 13.6 K for around 1.5 hour. The enriched para-H₂ gas was subsequently transferred into a 10 L Duran flask at 14 K to avoid significant conversion back to ortho-H₂ prior the matrix deposition procedure. The ortho/para-H₂ conversion efficiency was quantified accurately by means of mid-infrared absorption spectra recorded for solid films of the converted samples at 3 K employing the low-temperature matrix isolation apparatus described below. The relative integrated line intensities of the solid state induced ro-vibrational S₁(0) and Q₁(0) transitions have proven to provide accurate estimates of the para-H₂ enrichment.^26,27 The average S₁(0)/Q₁(0) line intensity ratios in the order of 50 indicates purities of para-H₂ close to 99.9% (see ESI†).

For the preparation of doped para-H₂ matrices, approximately 0.02 mol of liquid nitrogen pre-cooled para-H₂ sample was deposited manually from the 10 L Duran sample flask via a Swagelok low-flow metering valve onto a gold-plated oxygen-free high thermal conductivity (OFHC) copper mirror at 3.4 K in the cold head of a specially designed immersion helium cryostat (IHC-3).^3,28 The para-H₂ matrices are soft even at this temperature and the matrices are lost above 5 K. The para-H₂ host gas was doped with CO₂ (Sigma-Aldrich, 99.999%), CS₂ (Sigma-Aldrich, 99.9%) and H₂O (Milli-Q) and D₂O gas (Sigma-Aldrich, 99.5% atom D) and mixtures of these gases via separate inlet tubing systems resulting in mixing ratios in the order of (1 : 500 to 1 : 3000). A LakeShore temperature controller (Model 325) kept the mirror temperature at 2.8 ± 0.1 K by the use of resistive heating and feedback electronics before and after the deposition procedures. Interchangeable CsI and polymethylpentene (TPX) windows were mounted onto the vacuum shroud surrounding the cold head of the helium cryostat. THz single-beam sample spectra were recorded by a Bruker IFS 120 FTIR vacuum spectrometer via a specially designed optical arrangement guiding the focused probe beam onto the cold mirror in the cryostat. The spectra between 50 and 370 cm⁻¹ were all generated by a liquid helium cooled Si-bolometer in combination with a 6 μm multilayer Mylar beam splitter and a conventional water-cooled globar radiation source. The single-beam background spectra of the evacuated cryostat were all collected before and after the sample measurements. A spectral resolution in the range from 0.1 to 1.0 cm⁻¹ was selected depending on the observed band widths.

3. Exploratory quantum chemical calculations

The ORCA (v. 4.0.1.2)²⁹ quantum chemistry package has been employed for ab initio electronic structure calculations. The potential energy minima geometries and corresponding harmonic intra- and inter-molecular force fields of both the monomers and binary (m = n = 1) and selected ternary (m = 1, n = 2) (CS₂)_m⋯(H₂O)_n van der Waals cluster molecules have been predicted employing all-electron second-order Møller–Plesset perturbation theory with resolution of the identity approximation (RI-MP2)³⁰ combined with the aug-cc-pCVXZ^31–33 basis set family (with 5-ζ level for the binary systems and Q-ζ level for the ternary systems). The RI-JK approximation was employed with appropriate auxiliary basis sets.^34,35 The Molpro (ver. 2012.1)^36,37 quantum chemistry package was subsequently employed to compute electronic interaction energies (D_e) at the frozen-core coupled-cluster single and double with perturbative triple excitations CCSD(T)³⁸ level by (X = Q, 5, 6) three-point extrapolations in the Dunning's aug-cc-pVXZ basis set family as described by Řezáč.³⁹ In addition, the potential energy minima geometries and corresponding harmonic intermolecular force fields and electronic interaction energies D_e were calculated for the binary CS₂⋯H₂O system with the explicitly correlated CCSD(T)-F12b/cc-pVQZ-F12^40,41 approach with scaling of (T)^42,43 contributions as implemented in Molpro.

4. THz absorption spectra of (CO₂)_n⋯(H₂O)_m van der Waals systems

THz absorption spectra have recently been obtained for several weakly bound (CO₂)_m⋯(H₂O)_n (m = n = 1 and m + n = 3) van der Waals systems embedded in solid neon in two independent investigations.^28,44 A strongly IR-active large-amplitude intermolecular out-of-plane H₂O wagging mode (H₂O a-axis libration) observed at 101.6 cm⁻¹ and a weaker in-plane H₂O rocking mode (H₂O c-axis libration) observed at 166.6 cm⁻¹ have both been assigned independently for the binary CO₂⋯H₂O system as shown in Fig. 1. The assignment of the in-plane H₂O rocking mode in solid neon has been verified by the small observed isotopic red-shift of 1.9 cm⁻¹ upon ¹⁶O/¹⁸O substitution (not shown) and the substantially larger observed isotopic red-shifts of 12.6 cm⁻¹ and 19.6 cm⁻¹ upon single and double H/D substitution of the H₂O subunit. An otherwise forbidden transition associated with the large-amplitude intermolecular H₂O torsional mode (H₂O b-axis libration) has also been observed at 128.4 cm⁻¹ and assigned for the isotopic CO₂⋯HDO variant of the system with the lower C_s symmetry due to the uneven vibrational displacements of the H and D atoms (Fig. 1). The observation and unambiguous assignment of these three different intermolecular vibrational transitions in the spectral region below 5 THz associated with large-amplitude librational modes have confirmed the global potential energy minimum of the CO₂⋯H₂O system predicted by the high-level 5D coupled-cluster potential energy surface by Makarewicz.⁴⁵ The minimum structure has a planar and T-shaped geometry of C_2v symmetry with the oxygen atom of H₂O connected to the C atom and the H atoms pointing away from the CO₂ molecule.^45–56 Nevertheless, the isotopic red-shifts of the out-of-plane H₂O wagging mode predicted below 3 THz could not be verified in the solid neon environment due to the severe spectral overlap with the strong band observed at 79.5 cm⁻¹ associated with the rotational–translation-coupling (RTC) motions of H₂O (Fig. 1).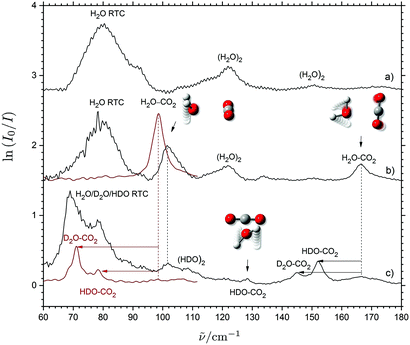

Fig. 1 THz absorption spectra of H₂O (trace a), CO₂/H₂O (trace b) and CO₂/D₂O/H₂O (trace c) embedded in solid neon (black traces, taking from ref. 28) and para-H₂ (red traces). The proposed band assignments for the binary CO₂⋯H₂O system are indicated by animations of the associated large-amplitude librational motion and isotopic spectral shifts indicated by arrows. The vibrational–rotational-coupling transitions for H₂O/HDO/D₂O in neon are denoted RTC.

The red traces of Fig. 1 show the present THz absorption spectra of CO₂/H₂O/D₂O mixtures embedded in solid para-H₂ and the absence of any strong RTC transitions in the spectral region below 100 cm⁻¹ owing to the larger matrix cages in solid para-H₂ relative to solid neon. In the solid para-H₂ medium doped with CO₂/H₂O with a mixing ratio of 4 : 1 to suppress the formation of (H₂O)₂, a distinct band is revealed at 98.6 cm⁻¹, which can easily be assigned to the strong H₂O out-of-plane wagging band of the regular CO₂⋯H₂O system. The band origin is shifted by 3 cm⁻¹ to the red relative to the corresponding transition observed in solid neon (101.6 cm⁻¹). This minor spectral shift is ascribed to slightly more repulsive steric interactions in the smaller matrix cages of the solid neon environment relative to the para-H₂ medium.^4,15 In the THz spectrum obtained for a CO₂/H₂O/D₂O mixture doped in para-H₂ having a (16 : 1 : 4) mixing ratio, two new distinct bands are identified at 78.4 and 71.0 cm⁻¹. The two bands are easily assigned to the red-shifted HDO and D₂O out-of-plane wagging transitions for the isotopic CO₂⋯HDO and CO₂⋯D₂O systems, respectively. The observed isotopic spectral red-shifts are in qualitative agreement with the predictions reported in our previous investigation²⁸ based on the A rotational constants of H₂O/HDO/D₂O.⁴⁶ These new observations perfectly demonstrate the extended spectroscopic window offered by para-H₂ below 3 THz (∼100 cm⁻¹) owing to the lack of disturbing rotational–translation-coupling motions of the dopants.

5. THz absorption spectra of (CS₂)_n⋯(H₂O)_m van der Waals systems

The more weakly bound binary van der Waals system formed between CS₂ and H₂O has been predicted to have two intermolecular potential energy minima with almost equal energy; a linear structure with the O atom on the H₂O subunit linked to one of the S atoms of the CS₂ molecule of C_2v symmetry and another planar T-shaped structure with the H atom on the H₂O subunit pointing towards the C atom on the CS₂ molecule as shown in Fig. 2.⁵⁷ A pulsed beam Fourier transform microwave study by Lovas et al.,⁵⁸ the only experimental investigation of this system reported in the literature so far to our knowledge, has solely identified the linear conformation with C_2v symmetry. Both conformations of the binary CS₂⋯H₂O system are predicted to have significantly lower binding energy than the CO₂⋯H₂O system. The corresponding large-amplitude librational H₂O band origins are therefore expected to be completely overlapped by the strong RTC transition of H₂O in the solid neon environment. This binary weakly bound CS₂⋯H₂O van der Waals system is thus an ideal candidate for the demonstration of the extended THz capability offered by the para-H₂ medium.

Fig. 2 The predicted intermolecular potential energy minima for the two conformations of the binary CS₂⋯H₂O van der Waals system. (left) A linear conformation with the O atom on the H₂O subunit linked to one of the S atoms of the CS₂ molecule having C_2v symmetry. (right) A planar T-shaped structure with the H atom on the H₂O subunit pointing towards the C atom on the CS₂ molecule.

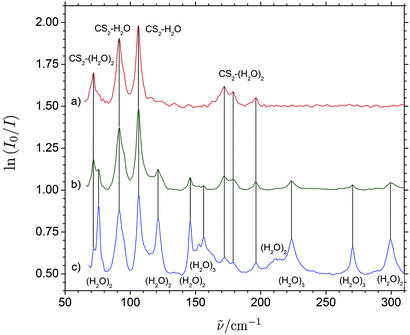
Fig. 3 shows a series of THz absorption spectra obtained for different CS₂/H₂O mixtures with varying mixing ratios embedded in enriched solid para-H₂. The THz spectrum obtained for a CS₂/H₂O mixing ratio of 1 : 2 shows a wealth of distinct vibrational bands in the entire THz region from 50 to 300 cm⁻¹ range. The excess of H₂O relative to CS₂ in this experiment favors the formation of H₂O clusters as these hydrogen-bonded molecular systems are more strongly bound than the (CS₂)_n⋯(H₂O)_m van der Waals systems. THz absorption spectra of the (H₂O)₂ and (H₂O)₃ systems embedded in para-H₂ have been investigated previously by Ceponkus et al.⁵⁹ and extensive vibrational assignments have been proposed. The distinct bands observed at 156.3, 223.5, 270.3 and 299.1 cm⁻¹ have all previously been assigned to transitions associated with large-amplitude intermolecular vibrational modes of (H₂O)₃, whereas other distinct bands observed at 75.7, 121.2, 145.8, 211.0 cm⁻¹ previously have been assigned to transitions of (H₂O)₂.

Fig. 3 THz absorption spectra of CS₂/H₂O/para-H₂ mixtures with varying mixing ratios (10 : 1 : 2000 for trace a, 6 : 3 : 2000 for trace b and 3 : 6 : 2000 for trace c) embedded in solid para-H₂ with proposed band assignments for the (H₂O)₂, (H₂O)₃, CS₂⋯H₂O and CS₂⋯(H₂O)₂ systems. The absorbance scale have been normalized relative to the two bands assigned for the binary CS₂⋯H₂O system.

The THz spectrum of the H₂O-rich para-H₂ matrix shows additional six distinct bands, which cannot be attributed to (H₂O)₂ or (H₂O)₃ and suggest assignments to CS₂-containing cluster molecules. THz absorption spectra obtained for two different CS₂/H₂O mixtures with excess of CS₂ relative to H₂O in para-H₂ shown in Fig. 3 reproduce these bands and the CS₂/H₂O mixing ratio of (10 : 1) almost completely suppress the formation of H₂O aggregates. The six observed bands can be divided into several different categories based on their relative concentration dependencies, which are shown in more details in the ESI.† The two strong reproduced bands at 91.5 and 106.1 cm⁻¹ appear to have the same slower concentration dependency suggesting at first sight assignments to the binary CS₂⋯H₂O system. The three bands observed at 72.1, 172.0 and 178.6 cm⁻¹ may all be attributed to larger ternary (CS₂)_m⋯(H₂O)_n (m + n = 3) systems based on their significantly steeper concentration dependencies (see ESI†). The concentration dependence of the final band observed at 196.2 cm⁻¹ seems slightly smaller but is hard to access. The low intensity of the band makes the relative band intensity more influential of potential small baseline drifts. Nevertheless, this weak 196.2 cm⁻¹ band still seems to have a consistent steeper concentration dependence in three independent experiments than the two bands at 91.5 and 106.1 cm⁻¹ (see ESI†) and may tentatively be assigned to larger ternary (CS₂)_m⋯(H₂O)_n (m + n = 3) systems. In order to explore the origin and the nature of the vibrational motion associated with these observed THz spectral signatures further, the effects of isotopic H/D substitutions on the H₂O subunit have been investigated along with exploratory quantum chemical calculations.

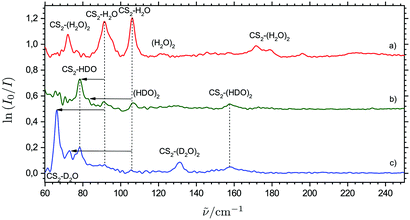
Fig. 4 shows a series of THz absorption spectra obtained for different isotopic CS₂/H₂O/D₂O mixtures with varying relative D₂O content doped in para-H₂. The THz spectrum obtained for a mixture of equal amounts of H₂O and D₂O and a huge excess of CS₂ (mixing ratio of 1.5 : 1.5 : 9) still shows weak traces of the proposed CS₂⋯H₂O dimer bands at 91.5 and 106.1 cm⁻¹, whereas there are no traces of the four proposed bands attributed tentatively to ternary cluster molecules. Instead, a new weak band appears at 157.6 cm⁻¹ together with a strong distinct band at 78.4 cm⁻¹ having a weak shoulder at 81.1 cm⁻¹. In the THz spectrum obtained for a CS₂/D₂O mixture (mixing ratio of 9 : 2), where the combined gas handling and inlet tubing systems have been purged intensively with D₂O to promote H/D exchange on all surfaces, there are no longer any traces of the six bands observed for the CS₂/H₂O mixtures. However, the two bands at 157.6 and 78.4 cm⁻¹ observed in the spectrum for the CS₂/H₂O/D₂O mixture are still visible together with two new bands at 131.1 cm⁻¹ and 66.1 cm⁻¹, where the latter band has a shoulder at 72.9 cm⁻¹.

Fig. 4 THz absorption spectra of CS₂/H₂O/para-H₂ (6 : 2 : 2000, trace a), CS₂/H₂O/D₂O/para-H₂ (9 : 1.5 : 1.5 : 2000, trace b) and CS₂/D₂O/para-H₂ (9 : 2 : 2000, trace c) mixtures embedded in solid para-H₂ with proposed band assignments and isotopic spectral shifts indicated by arrows.

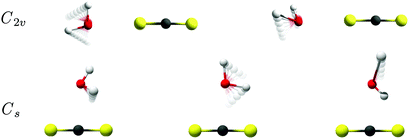
The intermolecular harmonic force fields for the two different potential energy minima for the binary CS₂⋯H₂O system shown in Fig. 2 have been investigated by exploratory quantum chemical calculations at the RI-MP2/aug-cc-pCV5Z level (see ESI†). The important findings from these calculations relate to the actual number of large-amplitude vibrational modes with significant infrared activity. The planar T-shaped structure with the O atom on the H₂O subunit linked to the C atom on the CS₂ molecule have three different transitions associated with large-amplitude librational motion of H₂O with significant band intensity; one very localized out-of-plane librational mode involving the “bound” H atom of H₂O predicted at 187 cm⁻¹, a second in-plane H₂O rocking mode (H₂O c-axis libration) predicted at 152 cm⁻¹ and a third very localized out-of-plane librational mode involving the “free” H atom of H₂O predicted at 74 cm⁻¹. On the other hand, the linear conformation with C_2v symmetry is predicted to have only two strongly IR-active large-amplitude librational modes: one in-plane H₂O rocking mode (H₂O c-axis libration) predicted at 96 cm⁻¹ and one out-of-plane H₂O wagging mode (H₂O a-axis libration) predicted at 91 cm⁻¹. The predicted harmonic fundamental band origins for the two different conformations of the CS₂⋯H₂O system are listed in Table 1 and animations of the highly infrared active large-amplitude intermolecular vibrational modes are shown in Fig. 5. The prediction of only two infrared active librational transitions close in energy for the C_2v symmetric CS₂⋯H₂O conformation suggests the existence of this conformation in the solid para-H₂ environment, which is further supported by the isotopic spectral shift predictions for these librational degrees of freedom described below. In addition, the observed strong band at 72.1 cm⁻¹ in the THz spectra has a significantly steeper concentration dependence than the two bands observed at 91.5 and 106.1 cm⁻¹ (see ESI†). This band therefore cannot be assigned to the strongly IR-active out-of-plane librational mode involving the “free” H atom of H₂O predicted for the less stable Cs conformation of the binary CS₂⋯H₂O system.

Table 1 Predicted vibrational fundamental band origins (units of cm⁻¹) and corresponding IR band intensities (units of km mol⁻¹) for CS₂, H₂O and the two C_2v and C_s conformations of the binary CS₂⋯H₂O system in the double harmonic approximation at the RI-MP2/aug-cc-pCV5Z level. In addition, harmonic vibrational band origins (units of cm⁻¹) at the CCSD(T)-F12b/cc-pVQZ-F12 level are given in square brackets for the most stable C_2v conformation

Mode	ω(H2O)	ω(CS2)	ω(CS2⋯H2O) C2v	ω(CS2⋯H2O) Cs
			Intra-molecular	Intra-molecular
Asym OH stretch	3976.4 (81.2)		3968.7 (86.1) [3941.1]	3952.3 (143.1)
Sym OH stretch	3849.3 (6.6)		3842.6 (12.3) [3831.2]	3821.1 (25.1)
HOH bend	1630.8 (74.8)		1631.8 (23.4) [1650.0]	1633.2 (165.6)
Asym CS stretch		1631.1 (561.3)	1623.4 (629.4) [1552.7]	1627.6 (422.9)
Sym CS stretch		683.4 (0.0)	680.4 (1.2) [669.3]	683.1 (0.4)
SCS bend		403.0 (5.0)	411.4 (6.1) [407.4]	407.0 (8.1)
		403.0 (5.0)	410.2 (5.1) [406.1]	401.1 (5.1)
			Inter-molecular	Inter-molecular
			95.8 (56.6) [96.2]	187.2 (49.8)
			90.8 (223.2) [56.8]	152.2 (115.3)
			78.2 (1.0) [75.9]	75.2 (9.2)
			27.0 (3.0) [26.6]	74.3 (134.0)
			19.0 (8.1) [24.8]	37.5 (4.0)

---

Fig. 5 Animations of the active large-amplitude librational modes of the two different conformations of the binary CS₂⋯H₂O system: (top) the H₂O in-plane rocking (left) and out-of-plane wagging (right) modes for the linear conformation of C_2v symmetry. (bottom) The three H₂O librational modes for the planar T-shaped conformation of C_s symmetry (see text).

In the harmonic approximation, the band origin associated with a specific large-amplitude H₂O librational mode of CS₂⋯H₂O is directly proportional to the square root of the corresponding rotational constant for an isolated H₂O molecule. The inspection of known rotational constants C and A for H₂O, HDO and D₂O thus suggests that the relative spectral red-shift associated with a large-amplitude HDO rocking mode is almost twice as large as the relative spectral red-shift associated with a large-amplitude HDO wagging mode, whereas the corresponding relative spectral red-shifts for the large-amplitude D₂O rocking and wagging modes (relative to H₂O) are more or less of the same size. Based on the varying degree of H/D substitution in two independent experiments and the observed isotopic spectral red-shifts, the bands observed at 106.5, 81.1 and 72.9 cm⁻¹ are then unambiguously assigned to the large-amplitude rocking modes and the bands observed at 91.5, 78.4 and 66.1 cm⁻¹ are unambiguously assigned to the large-amplitude wagging modes for the linear conformations of the CS₂⋯H₂O, CS₂⋯HDO and CS₂⋯D₂O systems, respectively, as indicated in Fig. 4. The harmonic RI-MP2/aug-cc-pCV5Z predictions qualitatively support these isotopic spectral red-shifts and also confirm qualitatively that the relative band intensity between the rocking and wagging modes decreases with the H/D substitution of the H₂O subunit as observed experimentally (see ESI†).

The remaining four distinct bands observed at 72.1, 172.0, 178.6 and 196.2 cm⁻¹ are tentatively assigned to different conformations of the ternary CS₂⋯(H₂O)₂ van der Waals system based both on the steeper observed concentration dependencies and the exploratory quantum chemical predictions given in the ESI.† A single potential energy minimum has been found for the ternary (CS₂)₂⋯H₂O system and the corresponding harmonic force field predictions indicate clearly that this ternary system is not observed in the present experiments. However, multiple intermolecular potential energy minima have previously been suggested theoretically for the ternary CS₂⋯(H₂O)₂ van der Waals system,⁵⁷ which can be divided into two different categories. In the first category, three different conformations of the ternary CS₂⋯(H₂O)₂ system are basically composed of strongly hydrogen-bonded (H₂O)₂ units interacting with single CS₂ molecules (see ESI†). These three conformations may be formed by the diffusion of free H₂O molecules in close vicinity of other H₂O molecules already linked to CS₂ molecules. The heavy CS₂ molecules are trapped in the matrix cages, whereas the lighter H₂O molecules can diffuse between the trapping sites in the matrix environment. The free H₂O molecules can then either approach existing CS₂⋯H₂O dimers from the H₂O fragment side or the unbound S-site. In the latter scenario, a linear and much less stable conformation of the ternary CS₂⋯(H₂O)₂ system (conformation 4, see ESI†) may be formed entirely due to kinetics, where both S atoms on a CS₂ molecule are linked to completely separated H₂O molecules in a similar fashion as observed for the binary CS₂⋯H₂O system.

The four different intermolecular potential energy minima of the relevant ternary CS₂⋯(H₂O)₂ system optimized by the RI-MP2/aug-cc-pCVQZ methodology are shown in the ESI.† The predicted harmonic band origins for the most infrared active large-amplitude vibrational modes of the most stable of these conformations (denoted Conformation 1) all fall in the range from 150 to 200 cm⁻¹, with three strongly active vibrational fundamental transitions predicted for this optimized potential energy minimum structure. These intermolecular force field predictions are thus in qualitative accordance with the 150–200 cm⁻¹ region in the observed THz absorption spectra (Fig. 3). The three distinct bands observed at 172.0, 178.6 and 196.2 cm⁻¹ may then tentatively be assigned to the predicted vibrational transitions (the harmonic approximation) at 157.8, 163.8 and 188.6 cm⁻¹, respectively. As discussed for the binary CS₂⋯H₂O system, the harmonic predictions of the fundamental transitions anomalously seem to underestimate the observed (anharmonic) transition energies. However, the three tentatively vibrational assignments for this global intermolecular potential energy minimum of the CS₂⋯(H₂O)₂ system are qualitatively supported by the experiments done with isotopically substituted samples. In the THz spectrum obtained for solid para-H₂ doped simultaneously with CS₂ and D₂O, only one distinct “ternary” band is observed at 130 cm⁻¹ in qualitative agreement with the predicted isotopic spectral shifts (Fig. 4). The harmonic calculations for the corresponding CS₂⋯(D₂O)₂ conformation predict only two significantly active overlapped fundamental transitions associated with large-amplitude motion at 119.1 and 124.8 cm⁻¹. This THz spectrum also shows evidence of a another broad “ternary” band around 155 cm⁻¹ (Fig. 4), which is observed more clearly in the THz spectrum obtained for para-H₂ doped simultaneously with CS₂/H₂O/D₂O and may tentatively be assigned to overlapped fundamental transitions for the corresponding CS₂⋯(HDO)₂ conformation.

The fourth local intermolecular potential energy minimum concerned with the linear conformation ternary CS₂⋯(H₂O)₂ system has also been optimized by the RI-MP2/aug-cc-pCVQZ methodology as shown in the ESI† (denoted Conformation 4). This linear conformation with the O atoms of two H₂O molecules linked to the two S atoms on the CS₂ subunit has D_2h symmetry and is significantly less stable than the other three intermolecular potential energy minima based on the (H₂O)₂ system. However, due to the diffusion of the lighter H₂O molecules in the soft para-H₂ medium, this less stable conformation may form due to kinetics when free H₂O molecules approach the S atoms on CS₂ molecules, which have already H₂O molecules linked to the other S atoms in the opposite end of the molecules. The harmonic intermolecular force field calculations for this linear conformation supportingly predict two highly infrared active transitions associated with large-amplitude H₂O rocking and wagging modes at 72.1 and 70.0 cm⁻¹, respectively, as observed also for the binary CS₂⋯H₂O system (see ESI†). Both of these transitions gain enormous band intensity relative to the binary CS₂⋯H₂O system (552.6 km mol⁻¹ altogether for these two overlapping H₂O rocking and wagging modes). These harmonic predictions tentatively support the origin of the fourth distinct band at 72.1 cm⁻¹ reproduced in the THz spectra with a concentration dependency larger than the two bands assigned for the binary CS₂⋯H₂O system. Both transitions are predicted to have significant spectral red-shifts upon H/D substitution in agreement with the observation that this 72.1 cm⁻¹ band vanishes completely in the THz spectra obtained for para-H₂ doped simultaneously with CS₂/H₂O/D₂O (Fig. 4). In the only converged potential energy minimum for the ternary (CS₂)₂⋯H₂O system (see ESI†), the H₂O molecule is “sandwiched” in between the two CS₂ subunits. The formation of this ternary system in the matrices is probably kinetically unfavored as only the lighter H₂O molecules undergo diffusion in the para-H₂ medium.

As pointed out during the peer-review correspondence, it would be desirable to support the proposed kinetic schemes involved in the formation of the different conformations of the ternary CS₂⋯(H₂O)₂ system by dedicated annealing experiments. However, several series of THz spectra obtained during the entire hold time of our immersion helium cryostat (8 hours) have not revealed significant changes of relative band intensities. It appears that the para-H₂ medium “self-anneal” during the deposition procedure due to the heat load coming from the “warm” para-H₂ suggesting that the cluster formation steps due to diffusion of the light H₂O molecules must take place already during the deposition procedure. A similar behavior has been observed for doped neon matrices, where only the first annealing step (from 3 K to 10 K and back to 3 K) triggers the formation of more cluster molecules. In subsequent annealing steps of doped neon matrices, any spectral changes are rarely observed suggesting that the vast majority of the free H₂O molecules in the close vicinity of neighboring sample molecules already combine with the sample molecules during the first annealing step in solid neon.

6. A semi-experimental binding energy for the CS₂⋯H₂O system

The observation of two large-amplitude librational modes (H₂O rocking and wagging) of the most stable C_2v conformation of the binary CS₂⋯H₂O system enables the determination of a reliable semi-experimental value for the change of vibrational zero-point energy ΔZPE upon complexation arising from the class of large-amplitude vibrational motion. These two observed large-amplitude H₂O librational fundamental bands alone constitute ca. 60% of the total vibrational zero-point energy of the complete set of five intermolecular vibrational fundamental modes of the most stable CS₂⋯H₂O conformation according to the harmonic RI-MP2/aug-cc-pCV5Z predictions listed in Table 1. Besides the observed transitions associated with the large-amplitude intermolecular H₂O rocking and wagging modes, an almost forbidden large-amplitude intermolecular stretching fundamental transition and two very weak and low-energy fundamental transitions associated with large-amplitude in-plane and out-of-plane CS₂ librational modes exist for this global potential energy minimum. The harmonic RI-MP2/aug-cc-pCV5Z predictions of fundamental energies provide a value of 1.86 kJ mol⁻¹ in total for this change of intermolecular vibrational zero-point energy. In addition, the complexation between CS₂ and H₂O is predicted to result in minor spectral shifts of the intramolecular vibrational modes adding up to −0.05 kJ mol⁻¹ for the change of zero-point energy denoted ΔZPE_intra. This very small value of ΔZPE_intra relative to ΔZPE_inter (ca. 3%) is partly due to the opposite signs of the minor complexation red-shifts associated with the intramolecular OH stretching modes of the H₂O subunit and the minor complexation blue-shifts associated with the intramolecular bending modes of the CS₂ subunit.

The highly anharmonic nature of the large-amplitude vibrational motion for the CS₂⋯H₂O system challenges the employed harmonic approximation severely. The shallow potential energy surface of van der Waals cluster molecules furthermore prevents standard anharmonic treatments such as the second-order vibrational perturbational theory (VPT2) implementation by Barone,^60,61 making reliable theoretical predictions of the intermolecular vibrational band origins notoriously challenging. This is clear from the comparison between theory and experiment in relation to the two large-amplitude H₂O librational modes (rocking and wagging). The observed origin of the large-amplitude rocking band is surprisingly 11% higher than the harmonic prediction and the observed origin of the large-amplitude wagging band is also slightly higher (1%) than the harmonic prediction. Harmonic intermolecular force field predictions usually overshoot the actual (anharmonic) intermolecular transition energies associated with large-amplitude vibrational modes of hydrogen-bonded cluster molecules by 15–25%^62–64 and point at some severe cancellation of errors in the present harmonic calculations. However, similar anomalous harmonic MP2 intermolecular force field predictions have been described for the closely related CO₂⋯H₂O^28,44 and OCS⋯H₂O⁶⁵ van der Waals cluster molecules. In the latter investigation, even harmonic predictions employing the benchmark CCSD(T)-F12 methodology fails to describe the large-amplitude out-of-plane wagging mode (the H₂O a-axis libration) of the weakly bound OCS⋯H₂O system. The out-of-plane wagging band origin for the OCS⋯H₂O system was calculated to 83 cm⁻¹ by harmonic MP2/aug-cc-pVTZ predictions, whereas harmonic CCSD(T)-F12a/aug-cc-pVTZ calculations predicted this band origin to 50 cm⁻¹. Unfortunately, an experimental verification of this large-amplitude H₂O wagging band origin was not possible in the latter neon matrix isolation study due to the RTC motion of H₂O in neon.⁶⁵ The same dependence on methodology is observed for the large-amplitude H₂O wagging mode of the CS₂⋯H₂O van der Waals system. The complementary harmonic CCSD(T)-F12b/cc-pVQZ-F12 calculations shown in Table 1 predict the H₂O wagging band origin at 56.8 cm⁻¹, which is 34 cm⁻¹ lower than the harmonic RI-MP2/aug-cc-pCV5Z prediction. The large-amplitude in-plane H₂O rocking band origin of CS₂⋯H₂O, however, is predicted only 0.4 cm⁻¹ higher by the harmonic CCSD(T)-F12b/cc-pVQZ-F12 calculations. This methodology-dependence on the intermolecular force field predictions for the OCS⋯H₂O and CS₂⋯H₂O van der Waals systems may be concerned with subtle differences in the description of the involved lone pairs on the O atom in the course of the large-amplitude librational motion. The large-amplitude in-plane H₂O rocking motion does not rearrange the lone pairs of the O atom significantly in the vicinity of the interacting S atom on the CS₂ subunit, whereas both these two lone pairs are rearranged significantly in the course of the large-amplitude out-of-plane H₂O wagging motion (Fig. 5). The present experimental findings thus invite for the theoretical development of high-level intermolecular potential energy surfaces for these weakly bound OCS⋯H₂O and CS₂⋯H₂O van der Waals systems, which may shed further light on the significant methodology-dependence for the description of these in-plane and out-of-plane librational coordinates. The most reliable (semi-experimental) value for the intermolecular vibrational zero-point energy for the CS₂⋯H₂O system thus involves the present THz observations of the H₂O wagging and rocking fundamentals (contribution of 1.18 kJ mol⁻¹) in combination with the harmonic predictions for the three remaining low-energy intermolecular vibrational fundamentals (contribution of 0.74 kJ mol⁻¹ at the RI-MP2/aug-cc-pCV5Z level and 0.76 kJ mol⁻¹ at the CCSD(T)-F12b/cc-pVQZ-F12 level) denoted ΔZPE_{inter,semi-exp} in Table 2. The resulting semi-experimental value of 1.88 ± 0.10 kJ mol⁻¹ is then obtained for the total change of vibrational zero-point energy (ΔZPE_{inter,semi-exp} + ΔZPE_intra [RI-MP2/aug-cc-pCV5Z]), where the indicated error bar of ±0.10 accounts both for potential minor matrix perturbations for the two observed fundamental bands and mechanical anharmonicity of the three remaining unobserved low-energy intermolecular vibrational fundamentals.

Table 2 Predicted electronic interaction energies D_e, change of vibrational zero-point energies ΔZPE and resulting van der Waals binding energies D₀ for the two C_2v and C_s conformations of the binary CS₂⋯H₂O system (units of kJ mol⁻¹)

Quantity	CS2⋯H2O C2v	CS2⋯H2O Cs
a Optimized geometries at RI-MP2/aug-cc-pCV5Z and electronic energies at CCSD(T)/CBS. b The harmonic approximation. c Based on semi-experimental intermolecular fundamental transition energies (see text). d Harmonic RI-MP2/aug-cc-pCV5Z predictions. e D 0 = De [CCSD(T)/CBS] − ΔZPEintra [RI-MP2/aug-cc-pCV5Z] − ΔZPEinter,semi-exp. f D 0 = De [CCSD(T)/CBS] − ΔZPE [RI-MP2/aug-cc-pCV5Z].
D e [CCSD(T)/CBS]^a	6.96	5.66
ΔZPEintra [RI-MP2/aug-cc-pCV5Z]^b	−0.05	−0.31
ΔZPEinter,semi-exp	1.93 ± 0.10^c	3.15^d
D 0	5.08 ± 0.15^e	2.82^f

---

The electronic interaction energies D_e predicted at the CCSD(T) level for the two conformations of the CS₂⋯H₂O system as a function of basis set (aug-cc-pVXZ, X = T, Q, 5 and 6) complemented by D_e-values computed at the CCSD(T)-F12b/aug-cc-pV5Z level are given in the ESI.† The three-point (Q, 5 and 6) extrapolation to the complete basis set (CBS) limits are given in Table 2 and provide D_e-values close to the CCSD(T)-F12b/aug-cc-pV5Z level. The difference in interaction energy between the two different conformations are predicted to be in the order of 1.3 kJ mol⁻¹ in the CCSD(T)/CBS limit. The incorporation of harmonic vibrational zero-point energy corrections suggest a difference between the resulting binding energies D₀ in the order of 2.3 kJ mol⁻¹ emerging mainly from the differences in the intermolecular force fields for the two conformations. These theoretical predictions support the experimental evidence that only the most stable C_2v conformation of the CS₂⋯H₂O system is formed in the cryogenic para-H₂ environment. The benchmark D_e-value of 6.96 kJ mol⁻¹ predicted by the CCSD(T)/CBS methodology combined with the semi-empirical change of vibrational zero-point energy ΔZPE_{inter,semi-exp} from the present work finally provides an accurate semi-experimental value for the binding energy D₀ of 5.08 ± 0.15 kJ mol⁻¹ for the most stable conformation of the binary CS₂⋯H₂O van der Waals system.

7. Conclusions

In summary, the present work has demonstrated that close to 99.9% enriched samples of para-H₂ provides an inert and transparent matrix host below 3 K for the investigation of large-amplitude hindered rotational motion for the subunits of weakly bound van der Waals cluster molecules in the THz spectral region. These advantages emerge from the absence of “reactive” ortho-H₂ molecules (I = 1) and the large-amplitude zero-point lattice vibrational motion of the para-H₂ crystals. The freely rotating spherically symmetric para-H₂ (I = 0) molecules of the matrix host interact weakly with the embedded cluster molecules and the significantly larger matrix cages in solid para-H₂ relative to solid neon prevent the appearance of disturbing rotational–translation-coupling motions of dopants in the relevant spectral region below 3 THz. THz absorption spectra have been generated for CO₂/H₂O and CS₂/H₂O mixtures embedded in enriched solid para-H₂ and numerous new observed transitions associated with large-amplitude librational motion of weakly bound binary CO₂⋯H₂O and CS₂⋯H₂O and ternary CS₂⋯(H₂O)₂ van der Waals cluster molecules have been assigned (tentative assignments for the ternary CS₂⋯(H₂O)₂ system). The interaction strength, directionality and anharmonicity of the weak van der Waals “bonds” between the molecules can be characterized via these THz spectral signatures and yield rigorous benchmarks for high-level electronic structure methodologies. The present experimental findings identify significant error cancelation effects for harmonic RI-MP2/aug-cc-pCV5Z and CCSD(T)-F12b/cc-pVQZ-F12 vibrational frequency predictions, where the latter approach severely fails to describe large-amplitude H₂O wagging motion. The spectroscopic observations confirm unambiguously a planar global potential energy minimum for the binary CS₂⋯H₂O system with C_2v symmetry, where the O atom on the H₂O molecule is linked to one of the S atoms on the CS₂ subunit. A semi-experimental value for the change of vibrational zero-point energy of 1.93 ± 0.10 kJ mol⁻¹ from the class of large-amplitude intermolecular vibrational modes is proposed. The combination with CCSD(T)/CBS electronic energy predictions provides a semi-experimental estimate of 5.08 ± 0.15 kJ mol⁻¹ for the dissociation energy D₀ of the CS₂⋯H₂O van der Waals system.

Conflicts of interest

There are no conflicts to declare.

Acknowledgements

The authors acknowledge J. Andersen, M. Torsson and R. W. Berg for help with the design of the para-H₂ conversion apparatus and the DTU Computing Center for access to the High Performance Computing services. RWL acknowledges financial support from the Danish Council for Independent Research's Sapere Aude Programme (Grant Ref.: 12-125248).

References

1. F. Kollipost, J. Andersen, D. Mahler, J. Heimdal, M. Heger, M. A. Suhm and R. Wugt Larsen, J. Chem. Phys., 2014, 141, 174314.
2. F. Kollipost, R. Wugt Larsen, A. V. Domanskaya, M. Noerenberg and M. A. Suhm, J. Chem. Phys., 2012, 136, 151101.
3. J. Ceponkus, P. Uvdal and B. Nelander, J. Chem. Phys., 2008, 129(19), 194306.
4. J. Andersen, A. Voute, D. Mihrin, J. Heimdahl, R. W. Berg, M. Torsson and R. Wugt Larsen, J. Chem. Phys., 2017, 146, 244311.
5. J. Andersen, J. Heimdal, B. Nelander and R. Wugt Larsen, J. Chem. Phys., 2017, 146, 194302.
6. K. Tanaka, K. Harada and K. M. Yamada, Handbook of High-Resolution Spectroscopy, John Wiley & Sons, Ltd, 2011.
7. G. A. Blake, K. B. Laughlin, R. C. Cohen, K. L. Busarow, D.-H. Gwo, C. A. Schmuttenmaer, D. W. Steyert and R. Saykally, Rev. Sci. Instrum., 1991, 62, 1701–1716.
8. D. Mihrin, P. W. Jakobsen, A. Voute, L. Manceron and R. Wugt Larsen, Phys. Chem. Chem. Phys., 2018, 20, 8241–8246.
9. A. R. W. McKellar, J. Mol. Spectrosc., 2010, 262, 1–10.
10. R. Wugt Larsen, F. Hegelund and B. Nelander, Mol. Phys., 2004, 102, 1743–1748.
11. R. Wugt Larsen, F. Hegelund and B. Nelander, J. Phys. Chem. A, 2004, 108, 1524–1530.
12. D. J. Bakker, A. Peters, V. Yatsyna, V. Zhaunerchyk and A. M. Rijs, J. Phys. Chem. Lett., 2016, 7, 1238–1243.
13. D. J. Bakker, A. Dey, D. P. Tabor, Q. Ong, J. Mahe, M.-P. Gaigeot, E. L. Sibert and A. M. Rijs, Phys. Chem. Chem. Phys., 2017, 19, 20343–20356.
14. A. J. Barnes, J. Mol. Struct., 2018, 1163(5), 77–85.
15. J. Ceponkus, A. Engdahl, P. Uvdal and B. Nelander, Chem. Phys. Lett., 2013, 581, 1–9.
16. J. Ceponkus, P. Uvdal and B. Nelander, J. Phys. Chem. A, 2011, 115(27), 7921–7927.
17. J. Ceponkus, P. Uvdal and B. Nelander, J. Phys. Chem. A, 2010, 114(25), 6829–6831.
18. M. E. Fajardo and M. Lindsay, J. Chem. Phys., 2008, 128, 014505.
19. M. Fajardo, S. Tam and M. DeRose, J. Mol. Struct., 2004, 695, 111–127.
20. Y. Miyamoto, M. Fushitani, D. Ando and T. Momose, J. Chem. Phys., 2008, 128(11), 114502.
21. T. Momose, M. Fushitani and H. Hoshina, Int. Rev. Phys. Chem., 2005, 24, 533.
22. S. Tam, M. E. Fajardo, H. Katsuki, H. Hoshina, T. Wakabayashi and T. Momose, J. Chem. Phys., 1999, 111(9), 4191.
23. T. Momose, H. Katsuki, H. Hoshina, N. Sogoshi, T. Wakabayashi and T. Shida, J. Chem. Phys., 1997, 107, 7717.
24. Y.-P. Lee, Y.-J. Wu, R. Lees, L.-H. Xu and J. T. Hougen, Science, 2006, 311(5759), 365–368.
25. I. F. Rivera, Rev. Mod. Phys., 1980, 52(2), 393–452.
26. L. Andrews and X. Wang, Rev. Sci. Instrum., 2004, 75, 3039–3044.
27. S. Tam and M. E. Fajardo, Rev. Sci. Instrum., 1999, 70, 1926–1932.
28. J. Andersen, J. Heimdal, D. W. Mahler, B. Nelander and R. Wugt Larsen, J. Chem. Phys., 2014, 140(9), 091103.
29. F. Neese, Wiley Interdiscip. Rev.: Comput. Mol. Sci., 2017, 1–6.
30. D. E. Bernholdt and R. J. Harrison, Chem. Phys. Lett., 1996, 250(5-6), 477–484.
31. T. H. Dunning Jr, J. Chem. Phys., 1989, 90(2), 1007–1023.
32. A. K. Wilson, T. van Mourik and T. H. Dunning Jr, THEOCHEM, 1996, 388, 339–349.
33. K. A. Peterson and T. H. Dunning, J. Chem. Phys., 2002, 117, 10548–10560.
34. F. Weigend, Phys. Chem. Chem. Phys., 2002, 4, 4285–4291.
35. F. Weigend, A. Köhn and C. Hättig, J. Chem. Phys., 2002, 116(8), 3175–3183.
36. H.-J. Werner, P. J. Knowles, G. Knizia, F. R. Manby and M. Schotz, Wiley Interdiscip. Rev.: Comput. Mol. Sci., 2012, 2, 242–253.
37. H.-J. Werner, P. J. Knowles, G. Knizia, F. R. Manby and M. Schütz, Wiley Interdiscip. Rev.: Comput. Mol. Sci., 2012, 2, 242–253.
38. J. A. Pople, M. Head-Gordon and K. Raghavachari, J. Chem. Phys., 1987, 134(87), 5968.
39. J. Řezáč and P. Hobza, J. Chem. Theory Comput., 2013, 9(5), 2151–2155.
40. G. Knizia, T. B. Adler and H.-J. Werner, J. Chem. Phys., 2009, 130, 054104.
41. K. A. Peterson, T. B. Adler and H.-J. Werner, J. Chem. Phys., 2008, 128(8), 084102.
42. O. Marchetti and H.-J. Werner, Phys. Chem. Chem. Phys., 2008, 10(23), 3400–3409.
43. K. A. Peterson, M. K. Kesharwani and J. M. Martin, Mol. Phys., 2015, 113(13–14), 1551–1558.
44. P. Soulard and B. Tremblay, J. Chem. Phys., 2015, 143, 224311.
45. J. Makarewicz, J. Chem. Phys., 2010, 132(23), 234305.
46. Y. Abashkin, F. Mele, N. Russo and M. Toscano, Int. J. Quantum Chem., 1994, 52(4), 1011–1015.
47. J. Altmann and T. Ford, J. Mol. Struct., 2007, 818(13), 85–92.
48. R. J. Wheatley and A. H. Harvey, J. Chem. Phys., 2011, 134(13), 134309.
49. J. Sadlej and P. Mazurek, J. Mol. Struct., 1995, 337(2), 129–138.
50. J. Sadlej, J. Makarewicz and G. Chalasinski, J. Chem. Phys., 1998, 109(10), 3919–3927.
51. C. N. Ramachandran and E. Ruckenstein, Comput. Theor. Chem., 2011, 966(13), 84–90.
52. K. M. de Lange and J. R. Lane, J. Chem. Phys., 2011, 134(3), 034301.
53. M. Kieninger and O. Ventura, J. Mol. Struct., 1997, 390, 157–167.
54. Y. Danten, T. Tassaing and M. Besnard, J. Phys. Chem. A, 2005, 109(14), 3250–3256.
55. A. S. Tulegenov, Chem. Phys. Lett., 2011, 505(21–23), 71–74.
56. J. Makarewicz, T. Ha and A. Bauder, J. Chem. Phys., 1993, 99(5), 3694–3699.
57. K. N. Kirschner, G. M. Hartt, T. M. Evans and G. C. Shields, J. Chem. Phys., 2007, 126, 154320.
58. T. Ogata and F. J. Lovas, J. Mol. Spectrosc., 1993, 162(2), 505–512.
59. J. Ceponkus, P. Uvdal and B. Nelander, J. Phys. Chem. A, 2012, 112, 3921–3926.
60. V. Barone, J. Chem. Phys., 2005, 122, 14108.
61. V. Barone, M. Biczysko, J. Bloino, M. Borkowska-Panek, I. Carnimeo and P. Panek, Int. J. Quantum Chem., 2012, 112, 2185–2200.
62. R. Wugt Larsen and M. A. Suhm, Phys. Chem. Chem. Phys., 2010, 12, 8152–8157.
63. J. Andersen, J. Heimdal and R. Wugt Larsen, Phys. Chem. Chem. Phys., 2015, 17, 23761–23769.
64. J. Andersen, J. Heimdal and R. Wugt Larsen, J. Chem. Phys., 2015, 143, 224315.
65. P. Soulard, B. Madebene and B. Tremblay, J. Chem. Phys., 2017, 146(23), 234303.

---

Footnote

† Electronic supplementary information (ESI) available: The optimized potential energy minimum geometries and corresponding harmonic force fields for CS₂, H₂O and several conformations of the weakly bound binary (m = n = 1) and ternary (m + n = 3) (CS₂)_m⋯(H₂O)_n systems at the RI-MP2/aug-cc-pCVXZ (X = Q, 5) level are given in the ESI with the absolute electronic energies computed employing the CCSD(T) and CCSD(T)-F12b methodologies with Dunning's augmented correlation-consistent aug-cc-pVXZ (X = T, Q, 5 and 6) basis sets. The mid-infrared absorption spectrum of an 99.9% enriched sample of solid para-H₂ is given with the assignments of the solid state induced ro-vibrational S₁(0) and Q₁(0) transitions employed to estimate the conversion efficiency. The stacked and normalized series of THz spectra obtained for different CS₂/H₂O/para-H₂ mixing ratios is given to illustrate the larger pressure dependence for the assigned bands of the ternary CS₂⋯(H₂O)₂ system. See DOI: 10.1039/c8cp05060k

---