Boosting axiality in stable high-coordinate Dy(III) single-molecule magnets

Abstract

A new nine-coordinate, air-stable Dy(III) single-ion magnet has been successfully isolated. Our in silico studies demonstrate that through carefully modulating the ligand electronics, the axiality can be boosted to generate U_cal barriers of over 600 K.

---

Single-Molecule Magnets (SMMs) are fascinating molecular systems, which display the ability to block magnetisation via an energy barrier, U_eff, resulting in the appearance of magnetic hysteresis of molecular origin.¹ Importantly, the design of viable SMMs strongly correlates with the control of the coordination environment at the level of a single metal ion.² The use of Dy(III) to generate a strong axial magnetic anisotropy,³ a realisation achieved through the vital combination of theory and experiment, has led to a new generation of complexes with impressive energy barriers⁴ and high blocking temperatures⁵ with coercivity up to 80 K (i.e. above the boiling point of liquid nitrogen).⁶ Potential applications will require not only the ability to function at higher temperatures, but also to be chemically stable in air or when exposed to heat.⁷ However, finding an approach towards coordination environments that promote strong magnetic behaviour in 4f-SMMs and, at the same time, display robust chemical stability under ambient conditions has only recently begun to be addressed. In this regard, we recently reported two pentagonal bipyramidal Dy(III) single-ion magnets (SMMs containing only one metal ion), [Dy(H₂O)₅(HMPA)₂]Cl₃·HMPA·H₂O and [Dy(H₂O)₅(HMPA)₂]I₃·2HMPA (HMPA = hexamethylphosphoramide), with blocking temperatures of ∼10 K, and we emphasized the important role of the second coordination sphere in controlling the magnetisation reversal barrier.⁸ In fact, complexes with higher coordination numbers (≥9) that also possess high energy barriers are rare and tuning such an environment in a way that promotes high axiality whilst offering good stability to air, heat and moisture is a challenging task. For this reason, we were intrigued by the complexes [Ln^IIILF](CF₃SO₃)₂·H₂O (L = 1,4,7,10-tetrakis(2-pyridylmethyl)-1,4,7,10-tetraaza-cyclododecane) and, in particular, the notable absence of the Dy(III) analogue along with the lack of magnetic data on any of the reported complexes.⁹ The Dy ion geometry is extremely important in order to obtain higher blocking temperatures and we reasoned that the combination of the pseudo D_4d {DyN₈} cage with a strong axial ligand should show interesting SMM characteristics.¹⁰ Herein, we report the synthesis, magnetic characterisation and ab initio studies of [Dy^IIILF](CF₃SO₃)₂·H₂O (1). Furthermore, we demonstrate an elegant strategy for improving the magnetic behaviour of high-coordinate 4f complexes. By carefully modulating the ligand environment in silico, we show how the calculated energy barrier, U_cal, can be increased, thus making 1 an extremely attractive system to probe the effects of the high-coordinate ligand environment on the dynamics of the magnetisation. Compound 1 (Fig. 1 and Fig. S6, S7, ESI†) was isolated under aerobic conditions from aqueous solution (see ESI†)⁹ and the stability of 1 to ∼350 °C is verified by TGA analysis (Fig. S5, ESI†).

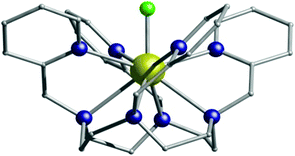Fig. 1 The structure of 1. Dy, gold; N, blue; F, green; C, grey. Hydrogen atoms, counter-ions and the co-crystallised water molecule are omitted for clarity.

We also report the isostructural (but not isomorphous) lanthanum analogue, [La^IIILF](CF₃SO₃)₂·H₂O (2) (Table S1 and Fig. S1, S2, S11, ESI†) and the Dy-doped lanthanum analogue (3) (Fig. S4, ESI†). The nine coordinate Dy(III) centre sits on a C₂ symmetry axis, coincident with the Dy–F bond. Continuous shape measures analysis,¹¹ which estimates the distortion from the perfect polyhedron, gives a value of 1.429 (where 0 corresponds to the ideal structure) for a muffin geometry (Fig. S8 and Tables S4, S5, ESI†). The ninth coordination site is occupied by a strong electronegative fluoride ion, with a relatively short Dy–F bond length of 2.123(2) Å (Table S3, ESI†). Intermolecular hydrogen bonding between the triflate counter-ions and the water molecule is present (Fig. S9, ESI†). In addition, the C–H⋯F intermolecular interactions between neighbouring molecules of 1 create a 1D columnar structure along the c-axis with the closest Dy⋯Dy distance of 7.757 Å (Fig. S10, ESI†).

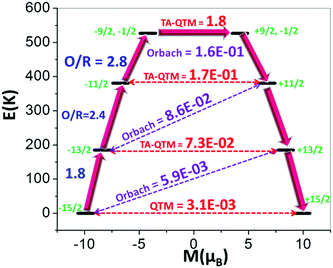
For 1, the eight Kramers Doublets (KDs), corresponding to the ⁶H_15/2 ground state, span an energy range of 808 K (see ESI† for computational details). The transverse components of the ground state (m_J = ±15/2) are found to be negligible (g_xx = 0.006, g_yy = 0.012, Table S7, ESI†), establishing a strong magnetic anisotropy axis (g_zz = 19.837), lying along the Dy–F bond (Fig. S28, ESI†). This can be explained using LoProp¹² charges computed using the CASSCF wavefunction. The charge on the axial F atom is found to be nearly three times larger compared to the nitrogen atoms of the cage ligand, (Fig. S28, ESI†) and this dictates the direction of g_zz axis. Similarly, the axial nature is also observed for the first and second exited states (m_J = ±13/2, g_xx = 0.212, g_yy = 0.228, g_zz = 16.800 and m_J = ±11/2, g_xx = 0.468 g_yy = 0.583, g_zz = 13.380, respectively, Table S7, ESI†), which are found to lie at 185 K and 381 K, respectively above the ground state. Notably, the larger g_xx/g_yy values obtained for the third-exited state (m_J = ±9/2; ±1/2, g_xx = 5.213 g_yy = 5.565, g_zz = 8.350) yield a larger magnetic moment matrix element of 1.8 μ_B (Fig. 2) which is sufficient to promote magnetic relaxation via this state, giving the maximum calculated relaxation barrier (U_cal) of ∼527 K. It is important to note that a small transverse magnetic moment is calculated for the first three KDs (3.1 × 10⁻³, 7.3 × 10⁻² and 1.7 × 10⁻¹μ_B, respectively), suggesting the presence of weak Quantum Tunnelling of the Magnetisation (QTM) and again, relaxation via the third exited state. The Orbach processes related to the m_J and m_J + 1 excited states of opposite magnetization for the first four KDs are found to be very small (<0.16, Fig. 2). Furthermore, thorough analysis of the g-tensor (Table S7, ESI†) reveals axiality up to the third excited state (KD4).

Fig. 2 Ab initio calculated relaxation dynamics for complex 1. The arrows show the connected energy states with the number representing the matrix element of the transverse moment (see text for details). Here, QTM = quantum tunnelling of the magnetisation, TA-QTM = thermally assisted QTM, O/R = Orbach/Raman process. The numbers above each arrow represent corresponding transverse matrix elements for the transition magnetic moments.

The dc magnetic susceptibility measurements for 1 (Fig. S13, ESI†) show that the experimental χ_MT value of 14.1 cm³ mol⁻¹ K (at 300 K) is in close agreement with the theoretical value (14.2 cm³ mol⁻¹ K) for a single Dy(III) ion (⁶H_15/2, S = 5/2, L = 5, g = 4/3). Upon cooling, χ_MT decreases steadily to a value of 11.1 cm³ mol⁻¹ K at 20 K, due to thermal depopulation of the m_J levels, before increasing to 12.0 cm³ mol⁻¹ K at 2.8 K. This low temperature increase is consistent with the presence of weak ferromagnetic intermolecular interactions. Furthermore, the χ_MT data of the diluted sample 3 instead decreases between 50–2 K, which further supports the hypothesis of weak ferromagnetic intermolecular interactions in 1 (Fig. S14, ESI†). Alternating current (ac) susceptibility measurements between 0.6–800 Hz, under zero external dc field, were performed in order to investigate the dynamics of the magnetisation for 1 and the Dy-doped lanthanum analogue, 3. Under zero external dc field, the out-of-phase, χ_M′′ magnetic susceptibility data exhibit well-defined maxima as a function of frequency (Fig. 3 and Fig. S17, ESI†) and temperature with χ_M′′ peaks clearly observable up to 12 K for 1 (Fig. S15, ESI†) and up to 20 K for 3 (Fig. S16, ESI†).

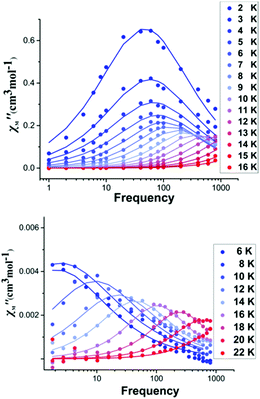Fig. 3 Frequency dependent out-of-phase ac susceptibility signals for complex 1 (upper) and 3 (lower) in zero dc field. The solid lines correspond to the best fit.

For 1, the plots of χ_M′ and χ_M′′ vs. temperature show a rapid increase in the low temperature region (Fig. S15, ESI†). Additionally, the low temperature set of peaks in the χ_M′′(v) curves exhibit little temperature dependence (Fig. 3 upper), which could be attributed to faster relaxation effects (QTM).¹³ For the diluted sample 3, the χ_M′′(T) maxima under zero dc field, are shifted to higher temperatures and the signal at lower temperatures is significantly reduced, suggesting a slower relaxation of the magnetisation (Fig. S16, ESI†). The relaxation times, τ, were extracted from the fit of the Argand plots of χ_M′′ vs. χ_M′ using the generalized Debye model (Fig. S18, ESI†).¹⁴ The α parameters found are relatively large in the range of 0.01–0.29 (2–13 K) for 1, and 0.01–0.41 (6–22 K) for 3, indicating a relatively wide distribution of relaxation times.¹ Thus, the Arrhenius plots are fitted considering more than one possible relaxation process yielding an energy barrier of U_eff = ∼110 K for 1 (Fig. S19 and Table S9, ESI†) and U_eff = ∼290 K for the diluted sample 3 (Fig. S20 and Table S9, ESI†). Importantly, it should be noted that these values are among the highest for high-coordinate lanthanide single-ion magnets (see Table S6, ESI†). To explore the role of low-lying vibrational levels that could enhance relaxation and lower the U_cal barrier, we analysed the N–Dy–F bending mode which lies at 115 cm⁻¹ (Fig. S29, ESI†). Calculations performed on selected vibrational modes corresponding to this frequency reveal a significant reduction in the estimated barrier height (see Fig. S29, ESI†). To assess the strength of the intermolecular interactions, further calculations were performed which yielded small dipolar and intermolecular magnetic exchange couplings (0.02 cm⁻¹ and 0.08 cm⁻¹ respectively). These are expected to further enhance relaxation (see Fig. S30, ESI†).¹⁵

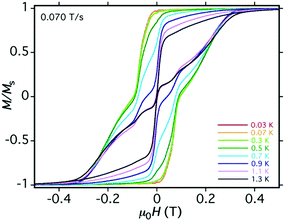
Magnetisation vs. field hysteresis loops were performed on 1 and 3 in light of the large energy barriers observed. Low-temperature hysteresis studies were performed on a single crystal of 1 using an array of micro-SQUIDs.¹⁶ The increase in coercivity with decreasing temperature (Fig. 4) and increasing scan rate (Fig. S26, ESI†) confirms 1 to be a SMM.

Fig. 4 Temperature dependence of single crystal magnetisation versus field hysteresis loops for 1.

The M vs. H loops suggest the presence of QTM and have steps that are somewhat smeared out at low temperatures, possibly due to a distribution of local environments (e.g. disordered solvent molecules, crystals defects) and/or intermolecular interactions. For the diluted powder sample 3 more pronounced butterfly-like loops are observed until 3 K (average sweep rate of ∼10 mT s⁻¹) (Fig. S27, ESI†). The promising magnetic properties and the high stability of 1, combined with the ability to modify either the axial ligand or the polydentate cage ligand, led us to study the effect on the magnetic dynamics of modulating the ligand environment in silico (Fig. 5). To do this, we have created a family of different model systems and used ab initio calculations to show how the ligand electronics can be used to tune and improve the relaxation properties (Fig. S31, S32 and Table S8, ESI†).

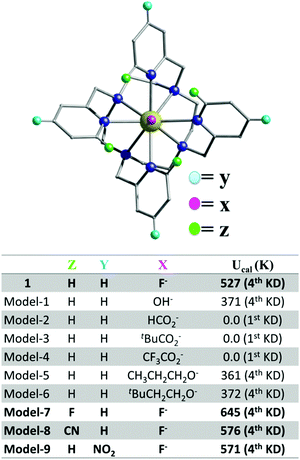Fig. 5 In silico models based on 1 showing how the U_cal barrier can be increased by tuning the ligand electronics.

Substitution of the axial F⁻ ion by monodentate formate or substituted carboxylates (models 2–4 Fig. 5) destroys the U_cal barrier. These weaker axial groups reduce the crystal field splitting significantly, leading to smaller barrier heights (Fig. 5 and Fig. S31, ESI†) and due to smaller charges compared to the nitrogen atoms of the polydentate ligand, the g_zz direction changes (Fig. S32, ESI†). Stronger ligands (⁻OR, models 1, 5 and 6 Fig. 5) maintain the g_zz direction, but with smaller U_cal values than 1. This suggests that axial substitution is detrimental in 1 with the F⁻ ion being the most promising, as was recently shown by Norel et al.¹⁷ We reasoned that if the coordination by the ligand nitrogen atoms is weakened, this should further enhance the barrier height, by moving towards a pseudo Dy–F environment.¹⁸ Hence, we have substituted the -ortho and -para H atoms of the pyridinic ring with strong electron withdrawing groups (models 7–9 Fig. 5). For these models, the computed transverse anisotropy (see Table S8, model-7, model-8 and model-9, ESI†) is found to be significantly reduced, causing an impressive increase to give a U_cal energy barrier of 645 K (for X = F, Z = F, Y = H, see Fig. 5).

Furthermore, the transverse matrix elements for the transition magnetic moments are reduced (see Fig. S31, ESI†) and hence the probability of QTM/TA-QTM is decreased. This suggests a promising route to realise higher barriers for magnetization reversal. Importantly, the models investigated were designed taking into consideration their likely future experimental realisation; i.e. they do not show strong steric hindrance and/or have low coordination numbers. To check further the effect of the transverse field we have rotated the –N₄ plane by ±6 degrees in a model complex (Fig. S33, ESI†) and in the presence of the strong axial F ion, changes in the calculated U_cal values are found to be negligible (Fig. S34, ESI†). Efforts are currently underway to synthesise substituted analogues of the polydentate cage ligand in our laboratory and as a proof-of-concept we also report the crystal structure of a new ligand (Fig. S12 and Table S2, ESI†) where the electron withdrawing CN group, has been included in the ortho position of each pyridinic ring (Fig. 5 model-8, Fig. S31, S32 and Table S8, ESI†). Hence, future work will focus on the realisation of the above exciting family of complexes with high energy barriers along with good air and heat stability.

The UK Engineering and Physical Sciences Research Council are thanked for financial support (grant ref. EP/N01331X/1). The data which underpin this work are available at http://dx.doi.org/10.5525/gla.researchdata.789. G. R. thanks the SERB (EMR/2014/00024) for funding. MKS thanks IIT Bombay for a fellowship.

Conflicts of interest

There are no conflicts to declare.

Notes and references

1. A. Dey, P. Kalita and V. Chandrasekhar, ACS Omega, 2018, 3, 9462; A. K. Bar, P. Kalita, M. K. Singh, G. Rajaraman and V. Chandrasekhar, Coord. Chem. Rev., 2018, 367, 163; Z. Zhu, M. Guo, X.-L. Li and J. Tang, Coord. Chem. Rev., 2019, 378, 350; M. Feng and M.-L. Tong, Chem. – Eur. J., 2018, 24, 7574; S. G. McAdams, A.-M. Ariciu, A. K. Kostopoulos, J. P. S. Walsh and F. Tuna, Coord. Chem. Rev., 2017, 346, 216; B. M. Day, F.-S. Guo and R. A. Layfield, Acc. Chem. Res., 2018, 51, 1880; S. K. Gupta and R. Murugavel, Chem. Commun., 2018, 54, 3685.
2. L. Sorace, C. Benelli and D. Gatteschi, Chem. Soc. Rev., 2011, 40, 3092; J. Wu, J. Jung, P. Zhang, H. Zhang, J. Tang and B. Le Guennic, Chem. Sci., 2016, 7, 3632; K. Katoh, S. Yamashita, N. Yasuda, Y. Kitagawa, B. K. Breedlove, Y. Nakazawa and M. Yamashita, Angew. Chem., Int. Ed., 2018, 57, 9262; Y.-C. Chen, J.-L. Liu, L. Ungur, J. Liu, Q.-W. Li, L.-F. Wang, Z.-P. Ni, L. F. Chibotaru, X.-M. Chen and M.-L. Tong, J. Am. Chem. Soc., 2016, 138, 2829; J. Liu, Y.-C. Chen, J.-L. Liu, V. Vieru, L. Ungur, J.-H. Jia, L. F. Chibotaru, Y. Lan, W. Wernsdorfer, S. Gao, X.-M. Chen and M.-L. Tong, J. Am. Chem. Soc., 2016, 138, 5441; S. K. Gupta, T. Rajeshkumar, G. Rajaraman and R. Murugavel, Chem. Sci., 2016, 7, 5181.
3. S. T. Liddle and J. van Slageren, Chem. Soc. Rev., 2015, 44, 6655; L. Ungur and L. F. Chibotaru, Phys. Chem. Chem. Phys., 2011, 13, 20086; J. D. Rinehart and J. R. Long, Chem. Sci., 2011, 2, 2078.
4. S.-D. Jiang, B.-W. Wang, H.-L. Sun, Z.-M. Wang and S. Gao, J. Am. Chem. Soc., 2011, 133, 4730; Y.-S. Meng, L. Xu, J. Xiong, Q. Yuan, T. Liu, B. W. Wang and S. Gao, Angew. Chem., Int. Ed., 2018, 57, 1; K. L. M. Harriman, J. L. Brosmer, L. Ungur, P. L. Diaconescu and M. Murugesu, J. Am. Chem. Soc., 2017, 139, 1420; Y.-S. Ding, N. F. Chilton, R. E. P. Winpenny and Y.-Z. Zheng, Angew. Chem., Int. Ed., 2016, 55, 16071; Y.-S. Ding, K.-X. Yu, D. Reta, F. Ortu, R. E. P. Winpenny, Y.-Z. Zheng and N. F. Chilton, Nat. Commun., 2018, 9, 3134; S. Demir, M. I. Gonzalez, L. E. Darago, W. J. Evans and J. R. Long, Nat. Commun., 2017, 8, 2144; M. Gregson, N. F. Chilton, A.-M. Ariciu, F. Tuna, I. F. Crowe, W. Lewis, A. J. Blake, D. Collison, E. J. L. McInnes, R. E. P. Winpenny and S. T. Liddle, Chem. Sci., 2016, 7, 155; P. E. Kazin, M. A. Zykin, V. V. Utochnikova, O. V. Magdysyuk, A. V. Vasiliev, Y. V. Zubavichus, W. Schnelle, C. Felser and M. Jansen, Angew. Chem., Int. Ed., 2017, 56, 1; F. Liu, D. S. Krylov, L. Spree, S. M. Avdoshenko, N. A. Samoylova, M. Rosenkranz, A. Kostanyan, T. Greber, A. U. B. Wolter, B. Buchner and A. A. Popov, Nat. Commun., 2017, 8, 16098.
5. A. P. Goodwin, F. Ortu, D. Reta, N. F. Chilton and D. P. Mills, Nature, 2017, 548, 439; A. P. Goodwin, D. Reta, F. Ortu, N. F. Chilton and D. P. Mills, J. Am. Chem. Soc., 2017, 139(51), 18714; F.-S. Guo, B. M. Day, Y.-C. Chen, M.-L. Tong, A. Mansikkamaki and R. A. Layfield, Angew. Chem., Int. Ed., 2017, 56, 11445; K. R. McClain, C. A. Gould, K. Chakarawet, S. J. Teat, T. J. Groshens, J. R. Long and B. G. Harvey, Chem. Sci., 2018, 9, 8492.
6. F.-S. Guo, B. M. Day, Y.-C. Chen, M.-L. Tong, A. Mansikkamäki and R. A. Layfield, Science, 2018, 362, 1400.
7. R. Vincent, S. Klyatskaya, M. Ruben, W. Wernsdorfer and F. Balestro, Nature, 2012, 488, 357; E. M. Pineda, C. Godfrin, F. Balestro, W. Wernsdorfer and M. Ruben, Chem. Soc. Rev., 2018, 47, 501; C. Godfrin, A. Ferhat, R. Ballou, S. Klyatskaya, M. Ruben, W. Wernsdorfer and F. Balestro, Phys. Rev. Lett., 2017, 119, 187702.
8. A. B. Canaj, M. K. Singh, C. Wilson, G. Rajaraman and M. Murrie, Chem. Commun., 2018, 54, 8273.
9. O. A. Blackburn, A. M. Kenwright, A. R. Jupp, J. M. Goicoechea, P. D. Beer and S. Faulkner, Chem. – Eur. J., 2016, 22, 8929; L. S. Natrajan, N. M. Khoabane, B. L. Dadds, C. A. Muryn, R. G. Pritchard, S. L. Heath, A. M. Kenwright, I. Kuprov and S. Faulkner, Inorg. Chem., 2010, 49, 7700; A. Wada, B. Watanabe, Y. Yamanoi and H. Nishihara, Chem. Commun., 2008, 1671; O. A. Blackburn, N. F. Chilton, K. Keller, C. E. Tait, W. K. Myers, E. J. L. McInnes, A. M. Kenwright, P. D. Beer, C. R. Timmel and S. Faulkner, Angew. Chem., Int. Ed., 2015, 54, 10783; O. A. Blackburn, A. M. Kenwright, P. D. Beer and S. Faulkner, Dalton Trans., 2015, 44, 19509.
10. T. Gupta and G. Rajaraman, Eur. J. Inorg. Chem., 2018, 3402.
11. M. Llunell, D. Casanova, J. Cirera, J. M. Bofill, P. Alemany and S. S. Alvarez, SHAPE (version 2.1), Barcelona, 2013.
12. L. Gagliardi, R. Lindh and G. Karlstrom, J. Chem. Phys., 2004, 121, 4494.
13. J.-L. Liu, Y.-C. Chen and M.-L. Tong, Chem. Soc. Rev., 2018, 47, 2431.
14. D. Gatteschi, R. Sessoli and J. Villain, Molecular Nanomagnets, Oxford Univ. Press, 2006.
15. E. Rousset, M. Piccardo, M.-E. Boulon, R. W. Gable, A. Soncini, L. Sorace and C. Boskovic, Chem. – Eur. J., 2018, 24, 14768.
16. W. Wernsdorfer, Adv. Chem. Phys., 2001, 118, 99; W. Wernsdorfer, Supercond. Sci. Technol., 2009, 22, 064013; W. Wernsdorfer, N. E. Chakov and G. Christou, Phys. Rev. B: Condens. Matter Mater. Phys., 2004, 70, 132413.
17. L. Norel, L. E. Darago, B. L. Guennic, K. Chakarawet, M. I. Gonzalez, J. H. Olshansky, S. Rigaut and J. R. Long, Angew. Chem., Int. Ed., 2018, 57, 1.
18. L. Ungur and L. F. Chibotaru, Inorg. Chem., 2016, 55, 10043.

---

Footnote

† Electronic supplementary information (ESI) available: Experimental and computational data; CIFs for 1, 4 and 2 CCDC 1889693–1889695. For ESI and crystallographic data in CIF or other electronic format see DOI: 10.1039/c9cc00965e

---