Effects of lipid composition on membrane distribution and permeability of natural quinones

Abstract

Natural quinones are amphiphilic molecules that function as mobile charge carriers in biological energy transduction. Their distribution and permeation across membranes are important for binding to enzymatic complexes and for proton translocation. Here, we employ molecular dynamics simulations and free energy calculations with a carefully calibrated classical force-field to probe quinone distribution and permeation in a multi-component bilayer trying to mimic the composition of membranes involved in bioenergetic processes. Ubiquinone, ubiquinol, plastoquinone and menaquinone molecules with short and long isoprenoid tails are simulated. We find that penetration of water molecules bound to the polar quinone head increases considerably in the less ordered and porous bilayer formed by di-linoleoyl (18:2) phospholipids, resulting in a lower free energy barrier for quinone permeation and faster transversal diffusion. In equilibrium, quinone and quinol heads localize preferentially near lipid glycerol groups, but do not perform specific contacts with lipid polar heads. Quinone distribution is not altered significantly by the quinone head, tail and lipid composition in comparison to a single-component bilayer. This study highlights the role of lipid acyl chain unsaturation for permeation and transversal diffusion of polar molecules across biological membranes.

---

Introduction

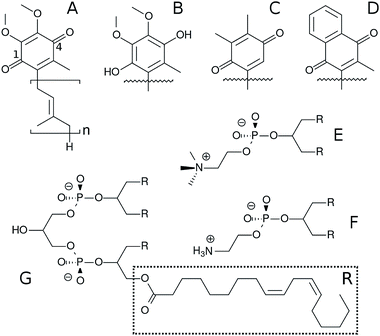
Electron transfer chains (ETC) involved in biological energy transduction rely on natural quinones and their redox-coupled quinols (Q molecules‡, Fig. 1) to shuttle electrons between protein complexes and translocate protons across phospholipid membranes, contributing to generation of an electrochemical gradient.^1–4 Clearly, the mechanisms for molecular recognition and binding of Q by respiratory and photosynthetic enzymatic (super)complexes^5,6 depend on the membrane distribution of Q molecules.^7–9

Fig. 1 Chemical structure of Q molecules and lipids studied here. (A) is ubiquinone (UQ_n), (B) is ubiquinol (UQ_nH₂), (C) is plastoquinone (PQ_n), (D) is menaquinone (MQ_n). The n subscript is the number of bound isoprenoid units, shown only for UQ_n which also displays positions 1 and 4 of the Q-ring. (E) is 1,2-dilinoleoyl-sn-glycero-3-phosphatidylcholine (DLPC), where R is the linoleoyl (18:2) acyl chain. (F) is 1,2-dilinoleoyl-sn-glycero-3-phosphatidylethanolamine (DLPE) and (G) is 1′-3′-bis[1,2-dilinoleoyl-sn-glycero-3-phospho]-sn-glycerol (cardiolipin, LCL).

Diffusion of Q in the membrane has also been suggested to control ETC turnover rates.^10–13 In redox loops translocating protons across the membrane directly through a quinone/quinol pair (or pool), as in the Q-cycle,^14,15 at least two events of Q permeation, or transversal diffusion, occur. In the mitochondrial ETC, quinol production in respiratory complexes I, II and III take place at the membrane N-side, but the Q_o site for quinol oxidation in complex III is at the P-side.^16–18 Alternative oxidases cytochrome bo¹⁹ and cytochrome bd²⁰ in bacteria also carry out quinol oxidation at the membrane P-side. Thus, quinone/quinol recycling depends on Q permeating the membrane back-and-forth and it is important to understand this molecular process in detail.

Most of these proposals focused on Q lateral diffusion over the membrane, a fast and essentially diffusional process.²¹ But transversal diffusion is an activated process and hence much slower.^22–25 Unfavorable desolvation and dielectric interactions (with associated energetic barriers) have to be overcome when the polar Q-head penetrates the lipid bilayer.^18,26

Membrane distribution and lateral diffusion of Q have been experimentally studied (and debated) for decades.^{21,25,27–32} Transversal diffusion is harder to measure accurately and has received less attention.^24,25 Molecular dynamics (MD) simulation is a powerful technique to probe both membrane distribution and permeation, but the quality of the results heavily depend on the force-field description of molecular interactions.^33,34 Recently, MD simulations were used to investigate the permeation of ubiquinone on a 1-palmitoyl-2-oleoyl-sn-glycero-3-phosphatidylcholine (POPC) single-component bilayer and found the Q-head preferentially localizes near lipid glycerol groups.²⁶

Lipid composition modulates the properties of membranes and embedded molecules.^35,36 For instance, the fraction of unsaturation (double bond) in lipid acyl chains changes membrane fluidity and permeability so that cells have evolved to homeostatically control this property through the biosynthesis of fatty acids.^36,37 Bioenergetic membranes are enriched with the anionic cardiolipin and its role on the distribution of ubiquinone in a more realistic multi-component lipid bilayer has been explored by simulation.³⁸ The distribution of natural quinones in membranes with mixed lipid composition was also investigated with more approximate coarse-grained simulations.^39,40

Here, we employ MD simulations with an all-atom force-field carefully calibrated for Q molecules²⁶ to investigate the effects of lipid composition and unsaturation of acyl chains on Q distribution and permeation using a multi-component bilayer mimicking membranes involved in bioenergetic processes. Ubiquinone, ubiquinol, menaquinone and plastoquinone (Fig. 1) are studied to probe the role of the Q-head on membrane localization.

Methods

Set-up for molecular dynamics simulations

Six model bilayers were studied here, composed by 240 DLPC (Fig. 1), 208 DLPE, 64 cardiolipins (LCL di-anion), 16 Q (UQ₂, UQ₂H₂, UQ₁₀, UQ₁₀H₂, PQ₉ or MQ₉) molecules symmetrically divided between each leaflet, 128 Na⁺ cations and 21 728 water molecules. This is the same lipid composition used previously by Róg et al.³⁸ In umbrella sampling simulations, 37 435 water molecules were used to allow for sampling of complete UQ₂ partitioning into the aqueous phase.

The initial configuration for the UQ₁₀H₂ bilayer was kindly provided by Prof. Tomasz Róg as used in their publication.³⁸ Initial geometries for all other bilayers were derived from this configuration by deleting or “mutating” Q-head atoms and adapting the atomic connectivity accordingly.

Force-field parameters for lipids and Na⁺ were taken from CHARMM36.⁴¹ Water was described by TIP3P.⁴² Our CHARMM^43,44 compatible force-field previously obtained by careful calibration²⁶ was used for Q molecules. Additional parameters necessary for MQ and PQ heads were taken directly from the CHARMM specification with partial charges and atom types shown in Table S1 and Fig. S1 (see ESI†). Complete topologies and parameters are available from the authors upon request.

All MD simulations were carried out with GROMACS⁴⁵ versions 4.6.7 for equilibrium trajectories and 5.1.3 for free-energy calculations. The NPT ensemble was used and temperature kept at 310 K with the Bussi thermostat⁴⁶ and a coupling constant of 0.1 ps with two separate coupling groups (water and everything else). Pressure was kept at 1.0 bar with a weak coupling scheme with a compressibility of 0.5–1.0 10⁻⁵ bar⁻¹ and a coupling constant of 1 ps. Semi-isotropic coupling in the direction normal to the bilayer was applied. Electrostatics were handled by PME method⁴⁷ with a real space cutoff of 1.2 nm, grid spacing of 0.13 nm and quartic interpolation. All covalent hydrogen bonds were constrained using LINCS⁴⁸ and van der Waals interactions were truncated from 1.0 to 1.2 nm. No dispersion corrections were applied.⁴⁹ The integration time step was set to 2 fs and the nonbonded list was updated every 20 fs.

Unrestrained MD simulations were performed for 300 ns, frames were recorded every 20 ps and the initial 50 ns were discarded to allow for equilibration in the trajectories analyzed here. Mean area was computed as the ratio between the average area of the membrane plane and the number of lipid heavy atoms per leaflet. Atoms instead of molecules were used to allow comparison with multi-component bilayers. Normalized mass densities were calculated to ease comparison between groups with different number of atoms. Contacts between Q atoms and solvent molecules were defined with a 0.3 nm cut-off. Order parameters for methylene units of acyl chains were also calculated.⁵⁰ The convergence of calculated properties was checked as shown in Fig. S2.†

Free energy calculations

Umbrella sampling (US)⁵¹ was used to compute the free energy profile for UQ₂ permeation across the membrane normal. The distance between the UQ₂ head center-of-mass (COM) and the membrane COM along its normal (z-axis) was used as the reaction coordinate. The membrane COM was computed from a sum over the lipid atoms within a cylinder centered in the quinone and a 2.0 nm radius. This cylinder scheme helps to avoid artifacts due to membrane undulations, which are common in large membranes.⁵²

Each simulation box contained 16 UQ₂ molecules, so 16 different windows were computed simultaneously in each US simulation. To avoid spurious interactions between UQ₂ molecules (for instance, aggregation when in the water phase), an artificial repulsive interaction was included between each Q-head C6 atom pair, using a specific Lennard-Jones pair with zeroed dispersion. Initial configurations for US were obtained at t ∼ 200 ns from the UQ₂ unrestrained MD trajectory described above.

US windows were chosen equally spaced by 0.250 nm in the ranges z = [0.125,1.375] nm and [3.10,4.35] nm, and spaced by 0.125 nm in the range z = [1.500,2.875] nm. The umbrella potential was set with k_umb = 1000 kJ mol⁻¹ nm⁻¹ and a total of 48 windows (obtained from 3 separate US simulations) were used to cover UQ₂ permeation over the complete membrane normal (24 windows for each leaflet). Each US simulation was ran for 300 ns. The reaction coordinate was recorded every 0.2 ps. Free energy profile was symmetrized and calculated with WHAM.^53,54 The initial 30 ns were discarded for equilibration and the remaining 270 ns were used for data accumulation on each window. Statistical uncertainties were estimated as 95% confidence intervals by bootstrap analysis.⁵⁵

Results & discussion

Quinone composition and multi-component lipid membranes do not change the Q-head equilibrium distribution

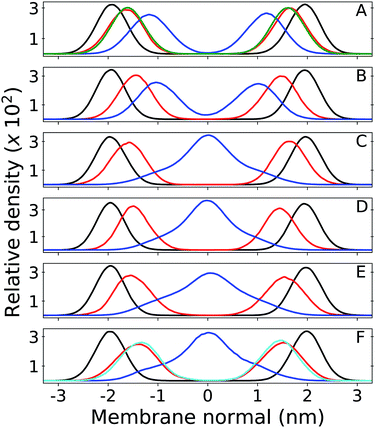
Results from unrestrained molecular dynamics simulations for six membranes with different Q composition are presented in this section. Mass density profiles for lipid groups are shown in Fig. 2. Density distributions in each leaflet are fairly symmetrical (negative or positive membrane normal) which indicates good equilibration and sampling of MD trajectories. Densities of phosphate (P) and acyl glycerol (shown only in Fig. 2A) groups are unaltered in all membranes and suggest that Q composition does not perturb the membrane structure. The multi-component membrane is well mixed and no lipid clusters or domains are found (Fig. S3†).

Fig. 2 Relative mass density of multi-component bilayers with different quinone analogue (Q) composition. Phosphate group of DLPC + DLPE is shown in black, Q-head in red and Q-tail in blue. Panel (A) shows the bilayer containing ubiquinone-2 (UQ₂), where the green profile indicates density of the DLPC + DLPE glycerol group; (B) is ubiquinol-2 (UQ₂H₂); (C) is ubiquinone-10 (UQ₁₀); (D) is ubiquinol-10 (UQ₁₀H₂); (E) is plastoquinone-9 (PQ₉) and (F) is menaquinone-9 (MQ₉), where the cyan profile indicates density of the first Q-ring (6C atoms) only and the full Q-head (10C atoms) is in red. Zero of the membrane normal corresponds to the bilayer center. Data were not symmetrized between the two leaflets.

Density peaks for the Q-head change only 0.3 nm (from 1.4 to 1.7 nm in modulus) between all Q. Density peaks indicate the Q-head equilibrium position across the membrane normal and are in agreement with equilibrium positions previously determined for ubiquinone and ubiquinol in POPC membranes.²⁶ Q-head density distributions also do not depend on isoprenoid chain length (for instance, compare Fig. 2A and C). For short isoprenoid chains (n = 2), the Q-tail density localizes around 1 nm. For longer chains (n = 9,10), the Q-tail density peaks at the membrane center and spreads through most of the lipid phase. UQ_nH₂ (n = 2,10) is slightly more buried, with Q-head peak density 0.2 nm lower than ubiquinone and with more penetration of Q-tail density towards the membrane center. This behavior was also observed in POPC membranes and is a consequence of the intramolecular hydrogen bonds (H-bond) often observed between phenolic hydrogen and methoxy oxygen in ubiquinol.^26,56 These H-bonds stabilize the Q-head when it is desolvated and allow for a higher permeation of UQ_nH₂.

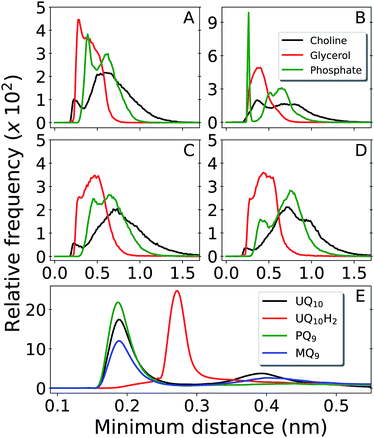
Fig. 3 shows contacts performed by the Q-head O1 with different lipid groups and solvent. H-bond acceptors display shorter water contacts as the minimum distance shown in Fig. 3E is computed between O1 and any of the water atoms. More interestingly, MQ₉ shows the smallest first hydration peak and only UQ₁₀ and MQ₉ show a secondary water peak at a distance of ∼0.4 nm, corresponding to configurations that O1 is not forming an H-bond with water but the other ketonic O4 is. Similar distributions but with smaller differences between Q molecules are observed for contacts with the Q-head O4, except for MQ₉ which is significantly more hydrated in O4 (data not shown here).

Fig. 3 Distribution of minimum distances around the Q-head oxygen O1 of multi-component bilayers with different Q composition. Contacts with DLPC choline group are shown in black, DLPC + DLPE glycerol in red and DLPC + DLPE phosphate in green. Panel (A) is UQ₁₀, (B) is UQ₁₀H₂, (C) is PQ₉ and (D) is MQ₉. Panel (E) shows water contacts for UQ₁₀ in black, UQ₁₀H₂ in red, PQ₉ in green and MQ₉ in blue. Data obtained from unrestrained MD simulations.

The H-bond donor UQ₁₀H₂ frequently makes an H-bond with the anionic phosphate group in DLPC + DLPE (peak at 0.26 nm at Fig. 3B) or in cardiolipins (not shown). H-bond acceptors (UQ₁₀, PQ₉ and MQ₉) do not show frequent contacts with phosphates, neither interact closely with the positive choline groups in DLPC (Fig. 3A, C and D). Almost no H-bonds are observed between any of the Q molecules and either the ethylamine group in DLPE or the bridge glycerol in cardiolipins (not shown). Instead, the Q-head is located near acyl glycerol groups (Fig. 2A). This is very similar to the equilibrium location and contacts performed by Q in a POPC bilayer.²⁶

Results for MQ₉ suggest the two rings in the naphtoquinone head have similar average location across the membrane normal (Fig. 2D), but are probably orthogonal to the bilayer plane with O1 less solvated (pointing towards the membrane) and the opposite O4 more often in contact with water (pointing to the water phase). For PQ₉, the Q-tail density has the lowest peak and spreads more evenly than other Q with long tails. Thus, PQ₉ may have more conformational flexibility which explains the lack of secondary solvation peak (Fig. 3E), without disturbing the average Q-head location.

In comparison to our previous simulations of Q in POPC membranes,²⁶ both density profiles and contacts performed by the Q-head do not change significantly in this multi-component membrane. The Q-head preferentially resides at the bilayer interface, near the membrane normal occupied by either POPC or DLPC + DLPE glycerol groups (Fig. 2A). No specific contacts have been found between Q and polar lipid heads, except for H-bonds between ubiquinol and phosphate groups which are present in any phospholipid. The equilibrium distribution and location of Q on the membrane models studied so far result from the balance of hydrophobic interactions by the Q-tail and hydration of the Q-head, corresponding to a typical amphiphilic molecule.⁵⁷

Increased membrane permeability and penetration of water bound to the Q-head

Free energy profiles and analysis obtained from umbrella sampling simulations for UQ₂ permeation across the membrane are presented in this section. An analogue with only two isoprenoid units was used because it is computationally more efficient to sample and reliable experimental partition coefficients are available for comparison.^58,59

The calculated free energy profile in Fig. 4A shows three important aspects: the minimum across the membrane normal, which represents the equilibrium position of the Q-head, is located at 1.75 nm as expected from the Q-head density peak in Fig. 2A and close to the minimum observed for UQ₂ permeation in the POPC bilayer (1.65 nm).²⁶ The insertion or binding free energy for UQ₂ in the multi-component membrane is −22 ± 2 kJ mol⁻¹, in excellent agreement with experiment (Table 1) and with the binding free energy in POPC (−21 ± 1 kJ mol⁻¹).²⁶ However, the free energy barrier for UQ₂ permeation in the multi-component membrane, given by the free energy difference between the minimum (at 1.75 nm) and the maximum near the center of the bilayer (0 nm), is only 19 ± 1 kJ mol⁻¹, much lower than the barrier computed for permeation in POPC (47 ± 2 kJ mol⁻¹).²⁶

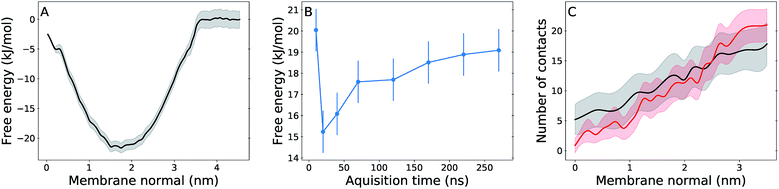Fig. 4 Free energy and hydration profiles for UQ₂ permeation. Panel (A) shows the free energy profile with statistical uncertainty (gray shadow) for UQ₂ insertion across the membrane normal. (B) shows the convergence of the permeation barrier with increasing acquisition time and fixed 30 ns of initial equilibration discarded from analysis. (C) shows the average number of water contacts with the Q-head for permeation in the multi-component membrane (black) and in the pure POPC membrane (red),²⁶ with standard deviations shown in shadow. Data obtained from umbrella sampling simulations and symmetrized between the two leaflets.

Table 1 Experimental and simulated binding free energies (in kJ mol⁻¹) between ubiquinone analogues and multi-component membranes. Experimental free energies were obtained from partition coefficients assuming a temperature of 310 K. Values from Róg et al.³⁸ were estimated from their Fig. 3

Molecule	Experimental	Róg^38	Here
UQ1	−17 (ref. 59), −20 (ref. 58)	−34 ± 4
UQ2	−21 (ref. 58), −24 (ref. 59)		−22 ± 2

---

Fig. 4B shows the permeation barrier converges to within one statistical uncertainty in 200 ns of simulation (170 ns of data acquisition) per US window. In total, 50% more data (300 ns) were collected in each window, supporting the quality of the barrier computed here. Experimental estimates of rates for Q permeation or “flip-flop” by NMR linewidth²⁵ and redox titration of substrates trapped inside vesicles²⁴ only suggested rate upper bounds and for lipids with fully saturated acyl chains. To our knowledge, there are not measurements of Q transversal diffusion for bilayers composed of unsaturated acyl chains to compare with the properties determined here. But, we also calculated a local transversal diffusion⁶⁰ and a permeation coefficient P = 20 cm s⁻¹ (Fig. S4†). This is 4 to 5 fold the P value obtained from simulation of polar aromatic molecules such as phenol and benzoic acid, which have similar (15–20 kJ mol⁻¹) permeation free energy barriers, in di-oleoyl phosphatidylcholine membranes.⁶¹

Thus, Q permeation is observed more frequently in the multi-component membrane than in POPC. Although we have not computed profiles for permeation of the other Q studied here, spontaneous flip-flops were observed for UQ₂H₂, PQ₉ and MQ₉ at least once during the 300 ns of unrestrained MD simulations presented in the previous section. Given that UQ_n did not show spontaneous flip-flops, we can speculate that the other Q analogues will show smaller permeation barriers.

Then, what is different in this multi-component membrane that allows permeation more frequently? The mean area per lipid heavy atom is 0.0126 nm² per atom in the multi-component membrane versus 0.0119 nm² per atom in POPC.²⁶ The two unsaturations (positions 9 and 12) in the linoleoyl acyl chain composing all lipids in the multi-component membrane result in a less ordered lipid phase, as shown by lower methylene order parameters computed for linoleoyl chain in comparison to palmitoyl and oleoyl in POPC (Fig. 5). Lower lipid ordering result in a more porous membrane in which molecules can penetrate with a cheaper cavitation energy cost.^22,62

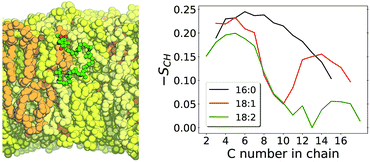Fig. 5 Left panel shows a structural snapshot of the multi-component membrane with UQ₁₀ in its equilibrium position. LCL is shown in orange, DLPC in yellow, DLPE in beige and UQ₁₀ in green (carbons) and red (oxygens). Right panel shows carbon–hydrogen bond vector order parameters (S_CH) calculated with unrestrained MD for acyl chains POPC palmitoyl in black and oleoyl in red,²⁶ and for DLPC + DLPE linoleoyl acyl chains in green.

Accordingly, more water contacts and H-bonds with the Q-head are performed inside the lipid phase for UQ₂ permeation in the multi-component membrane (normal <1 nm in Fig. 4C), leading to less desolvation of the polar Q-head and a lower permeation barrier than in POPC. Water arrest inside the lipid phase during the permeation of polar solutes has been observed in other simulations.^33,63 It should be noted that no water penetration is observed in equilibrium for both POPC or multi-component membranes. But in the rare event of Q permeation, it is easier for water bound to the Q-head to penetrate into a membrane composed by fatty acids with a higher fraction of unsaturations.

A comparison with the simulations performed by Róg et al. shows large and important qualitative differences, specially for ubiquinone which was reported to make no contacts with solvent or lipid head groups and localize in the center of the bilayer.³⁸ It seems unlike that the polar head group in UQ_n, with four oxygen H-bond acceptors, will be stable in the middle of the lipid phase. Their calculated binding free energy for UQ₁ is in large disagreement with experimental partition coefficients (Table 1). For ubiquinol, Q-head location and contacts are similar to ours, but strangely depend on the number of isoprenoid units. The lack of symmetry between the two leaflets in the density profiles shown and the irregular dependence of calculated densities and contacts with the number of isoprenoid units question whether appropriate equilibration and sampling were reached in their work.³⁸ Exactly the same lipid composition and similar simulation procedures were employed here. Thus, most of the qualitative differences found should be due to force-fields. The OPLS derived force-field used by Róg et al. has been shown to artificially overbind Na⁺ cations⁶⁴ and describe lipid order parameters in disagreement with NMR measurements.⁶⁵ On the other hand, the CHARMM36 force-field used here has consistently one of the best performances describing these properties as well as several other membrane structural, thermodynamical and diffusional observables,^41,66,67 including binding free energies and lateral diffusion constants for Q molecules.²⁶

Transversal diffusion of Q may limit turnover of electron transfer chains

Fig. 6 shows the equilibrium position of the Q-head in the multi-component membrane also matches the normal position (in modulus) of entrance sites for Q binding in respiratory complexes, as noted previously for the POPC bilayer.²⁶ An initial encounter complex formed after membrane diffusion of Q and collision into a respiratory complex will frequently have the appropriate geometry in the membrane normal. Fig. 6 also shows membrane permeation has to occur for quinone/quinol recycling as their sites of reduction/oxidation are placed at opposite membrane sides.

Fig. 6 Entrance sites for Q binding in respiratory complexes I–III. Sites for quinone reduction shown in blue and for quinol oxidation in red. Bilayer is represented in solid gray and equilibrium or preferential position of the Q-head across the membrane normal (±1.75 nm) shown with a dashed line. Structures were taken from PDB ID 4HEA⁶⁸ for complex I, 2H88 (ref. 69) for complex II and 2QJP⁷⁰ for complex III.

Bilayers with a low fraction of unsaturated chains, such as POPC,²⁶ may slow down transversal diffusion by up to five orders of magnitude, in comparison to the bilayer with 2 unsaturations per chain studied here. This steep relation is due to the activated nature of the permeation process.^22,23 A low fraction of unsaturation (<20%) may slow Q permeation up to a point it becomes rate-limiting for ETC or even blocks cellular growth.¹³ Yet another reason for the high content of cardiolipins, composed mostly by unsaturated acyl chains, in membranes involved in biological energy transduction⁷¹ might be the increment of Q permeability gained by lipid unsaturation.

Conclusions

Molecular dynamics simulations for ubiquinone, ubiquinol, plastoquinone and menaquinone and free energy calculations for permeation of UQ₂ in a multi-component bilayer mimicking the composition of bioenergetic membranes were presented.

Densities of Q-head and Q-tail (of similar length) across the membrane normal change little between each Q studied. The Q-head preferentially localizes near acyl glycerol groups and no specific contacts between the Q-head and polar lipid heads were observed, except for H-bonds formed between ubiquinol and phosphate groups. This is equivalent to the localization and contacts found for Q in a POPC bilayer. The binding free energy and equilibrium position estimated for UQ₂ partition into the multi-component bilayer are also in agreement to what was found in POPC.²⁶

We may conclude the equilibrium distribution of Q across model bilayers recently studied by molecular simulation^26,38 do not change significantly with lipid composition, even when containing the anionic cardiolipin. The equilibrium structure and thermodynamics of embedded Q are determined by Q-head hydration and the hydrophobic effect of the isoprenoid tail. This should not be entirely unexpected given that similar partition coefficients have been measured for ubiquinone (with the same number of isoprenoid units) in biological membranes with varied composition.^58,59

However, permeation of Q across the membrane changes considerably with lipid composition, specially the fraction of acyl chain unsaturation. Lipids with two unsaturations per acyl chain are less ordered, giving a more porous bilayer. Thus, the polar Q-head may carry water molecules during a flip-flop event with a lower free energy barrier, resulting in much faster transversal diffusion across the multi-component membrane studied here.

Membrane permeability modulated by the fraction of acyl chain unsaturation is important for efficient quinone/quinol recycling in opposite membrane sides and for translocation of protons by Q redox loops. Permeability may even limit turnover rates for biological ETC if the fraction of lipid unsaturation is too low. Results in the multi-component bilayer also confirm our previous observation that the equilibrium position of the Q-head across the membrane normal is similar to the position of protein sites for entrance of Q into respiratory complexes.²⁶ Finally, it should be mentioned that lipid composition may also influence the structure of bioenergetic membranes⁷² and of respiratory complexes⁷³ and their reactivity.^74–76

Conflicts of interest

There are no conflicts to declare.

Acknowledgements

Funding from FAPESP (project 16/24096-5), CNPq (fellowship number 142112/2015-1) and computational resources from the SDumont cluster in the National Laboratory for Scientific Computing (LNCC/MCTI) are gratefully acknowledged.

References

1. P. Mitchell, Chemiosmotic coupling in oxidative and photosynthetic phosphorylation, Biochim. Biophys. Acta, 2011, 1807, 1507–1538.
2. G. W. Canters and E. Vijgenboom, Biological Electron Transfer Chains: Genetics, Composition and Mode of Operation, Springer Netherlands, Dordrecht, 1998.
3. R. E. Blankenship, Molecular Mechanisms of Photosynthesis, Wiley-Blackwell, USA, 1st edn, 2002.
4. D. G. Nicholls and S. J. Ferguson, Bioenergetics, Academic Press, Boston, 4th edn, 2013.
5. M. Iwai, K. Takizawa, R. Tokutsu, A. Okamuro, Y. Takahashi and J. Minagawa, Isolation of the elusive supercomplex that drives cyclic electron flow in photosynthesis, Nature, 2010, 464, 1210–1213.
6. R. Guo, J. Gu, S. Zong, M. Wu and M. Yang, Structure and mechanism of mitochondrial electron transport chain, Biomed. J., 2018, 41, 9–20.
7. F. J. Van Eerden, M. N. Melo, P. W. Frederix, X. Periole and S. J. Marrink, Exchange pathways of plastoquinone and plastoquinol in the photosystem II complex, Nat. Commun., 2017, 8, 1–8.
8. J. Warnau, V. Sharma, A. P. Gamiz-Hernandez, A. D. Luca, O. Haapanen, I. Vattulainen, M. Wikstrom, G. Hummer and V. R. I. Kaila, Redox-coupled quinone dynamics in the respiratory complex I, Proc. Natl. Acad. Sci. U. S. A., 2018, 115, E8413–E8420.
9. M. H. Teixeira and G. M. Arantes, Balanced internal hydration discriminates substrate binding to respiratory complex I, bioRxiv, 2019, 572404.
10. P. R. Rich, A Generalised Model for the Equilibration of Quinones Pools with their Biological Donors and Acceptors in Membrane-Bound Electron Transfer Chains, FEBS Lett., 1981, 130, 173–178.
11. B. Chazotte and C. R. Hackenbrock, Lateral Diffusion as a Rate-limiting Step in Ubiquinone-mediated Mitochondrial Electron Transport, J. Biol. Chem., 1989, 264, 4978–4985.
12. G. Lenaz and M. L. Genova, Mobility and function of Coenzyme Q (ubiquinone) in the mitochondrial respiratory chain, Biochim. Biophys. Acta, 2009, 1787, 563–573.
13. I. Budin, T. de Rond, Y. Chen, L. J. G. Chan, C. J. Petzold and J. D. Keasling, Viscous control of cellular respiration by membrane lipid composition, Science, 2018, 362, 1189.
14. P. Mitchell, The protonmotive Q cycle: a general formulation, FEBS Lett., 1975, 59, 137–139.
15. M. Wikström, V. Sharma, V. R. I. Kaila, J. P. Hosler and G. Hummer, New Perspectives on Proton Pumping in Cellular Respiration, Chem. Rev., 2015, 115, 2196–2221.
16. K. Fiedorczuk, J. A. Letts, G. Degliesposti, K. Kaszuba, M. Skehel and L. A. Sazanov, Atomic structure of the entire mammalian mitochondrial complex I, Nature, 2016, 538, 406–410.
17. E. Maklashina and G. Cecchini, The quinone-binding and catalytic site of complex II, Biochim. Biophys. Acta, 2010, 1797, 1877–1882.
18. W. Cramer, S. S. Hasan and E. Yamashita, The Q cycle of cytochrome bc complexes: A structure perspective, Biochim. Biophys. Acta, 2011, 1807, 788–802.
19. J. Abramson, S. Riistama, G. Larsson, A. Jasaitis, M. Svensson-Ek, L. Laakkonen, A. Puustinen, S. Iwata and M. Wikström, The structure of the ubiquinol oxidase from Escherichia coli and its ubiquinone binding site, Nat. Struct. Biol., 2000, 7, 910–917.
20. S. Safarian, C. Rajendran, H. Müller, J. Preu, J. D. Langer, S. Ovchinnikov, T. Hirose, T. Kusumoto, J. Sakamoto and H. Michel, Structure of a bd oxidase indicates similar mechanisms for membrane-integrated oxygen reductases, Science, 2016, 352, 583–586.
21. M. Afri, B. Ehrenberg, Y. Talmon, J. Schmidt, Y. Cohena and A. A. Frimer, Location and Mobility of Ubiquinones of Different Chain Lengths in Artificial Membrane Vesicles, Chem. Phys. Lipids, 2004, 131, 107–121.
22. R. J. Pace and S. I. Chan, Molecular motions in lipid bilayers. III. Lateral and transverse diffusion in bilayers, J. Chem. Phys., 1982, 76, 4241–4247.
23. A. Imparato, J. C. Shillcock and R. Lipowsky, Lateral and transverse diffusion in two-component bilayer membranes, Eur. Phys. J. E, 2002, 11, 21–28.
24. A. Futami, E. Hurt and G. Hauska, Vectorial redox reactions of physiological quinones I. Requirement of a minimum length of the isoprenoid side chain, Biochim. Biophys. Acta, 1979, 547, 583–596.
25. P. B. Kingsley and G. W. Feigenson, 1H-NMR study of the location and motion of ubiquinones in perdeuterated phosphatidylcholine bilayers, Biochim. Biophys. Acta, 1981, 635, 602–618.
26. V. V. Galassi and G. M. Arantes, Partition, orientation and mobility of ubiquinones in a lipid bilayer, Biochim. Biophys. Acta, 2015, 1847, 1345.
27. H. Katsikas and P. Quinn, The Polyisoprenoid Chain Length Influences the Interaction of Ubiquinones with Phospholipid Bilayers, Biochim. Biophys. Acta, 1982, 689, 363–369.
28. B. A. Cornell, M. A. Keniry, A. Post, R. N. Robertson, L. E. Weir and P. W. Westerman, Location and Activity of Ubiquinone 10 and Ubiquinone Analogues in Model and Biological Membranes, Biochemistry, 1987, 26, 7702–7707.
29. G. Lenaz, B. Samori, R. Fato, M. Battino, G. P. Castelli and I. Domini, Localization and Preferred Orientations of Ubiquinone Homologs in Model Bilayers, Biochem. Cell Biol., 1992, 70, 504–514.
30. M. Jemiola-Rzeminska, J. Kruk, M. Skowronek and K. Strzalka, Location of Ubiquinone Homologues in Liposome Membranes Studied by Fluorescence Anisotropy of Diphenyl-Hexatriene and Trimethylammonium-Diphenyl-Hexatriene, Chem. Phys. Lipids, 1996, 79, 55–63.
31. S. Di Bernardo, R. Fato, R. Casadio, P. Fariselli and G. Lenaz, A High Diffusion Coefficient for Coenzyme QIH Might be Related to a Folded Structure, FEBS Lett., 1998, 426, 77–80.
32. I. Llorente-Garcia, et al., Single-Molecule in Vivo Imaging of Bacterial Respiratory Complexes Indicates Delocalized Oxidative Phosphorylation, Biochim. Biophys. Acta, 2014, 1837, 811–824.
33. C. Neale and R. Pomès, Sampling errors in free energy simulations of small molecules in lipid bilayers, Biochim. Biophys. Acta, 2016, 1858, 2539–2548.
34. D. J. Smith, J. B. Klauda and A. J. Sodt, Simulation Best Practices for Lipid Membranes, Living Journal of Computational Molecular Science, 2018, 1, 5966–5996.
35. S. Ladha, A. R. Mackie, L. J. Harvey, D. C. Clark, E. J. A. Lea, M. Brullemans and H. Duclohier, Lateral Diffusion in Planar Lipid Bilayers: A Fluorescence Recovery after Photobleaching Investigation of Its Modulation by Lipid Composition, Cholesterol, or Alamethicin Content and Divalent Cations, Biophys. J., 1996, 71, 1364–1373.
36. G. van Meer, D. R. Voelker and G. W. Feigenson, Membrane lipids: where they are and how they behave, Nat. Rev. Mol. Cell Biol., 2008, 9, 112–124.
37. S. Ballweg and R. Ernst, Control of membrane fluidity: the OLE pathway in focus, Biol. Chem., 2017, 398, 215–228.
38. P. Kaurola, V. Sharma, A. Vonk, I. Vattulainen and T. Róg, Distribution and dynamics of quinones in the lipid bilayer mimicking the inner membrane of mitochondria, Biochim. Biophys. Acta, 2016, 1858, 2116–2122.
39. D. H. de Jong, N. Liguori, T. van den Berg, C. Arnarez, X. Periole and S. J. Marrink, Atomistic and Coarse Grain Topologies for the Cofactors Associated with the Photosystem II Core Complex, J. Phys. Chem. B, 2015, 119, 7791–7803.
40. F. J. van Eerden, D. H. de Jong, A. H. de Vries, T. A. Wassenaar and S. J. Marrink, Characterization of thylakoid lipid membranes from cyanobacteria and higher plants by molecular dynamics simulations, Biochim. Biophys. Acta, 2015, 1848, 1319–1330.
41. J. B. Klauda, R. M. Venable, J. A. Freites, J. W. O‘Connor, D. J. Tobias, C. Mondragon-Ramirez, I. Vorobyov, A. D. MacKerell and R. W. Pastor, Update of the CHARMM All-Atom Additive Force Field for Lipids: Validation on Six Lipid Types, J. Phys. Chem. B, 2010, 114, 7830–7843.
42. W. L. Jorgensen, J. Chandrasekhar, J. D. Madura, R. W. Impey and M. L. Klein, Comparison of simple potential functions for simulating liquid water, J. Chem. Phys., 1983, 79, 926–935.
43. A. D. MacKerell Jr, et al., All-Atom Empirical Potential for Molecular Modeling and Dynamics Studies of Proteins, J. Phys. Chem. B, 1998, 102, 3586–3616.
44. K. Vanommeslaeghe, E. Hatcher, C. Acharya, S. Kundu, S. Zhong, J. Shim, E. Darian, O. Guvench, P. Lopes, I. Vorobyov and A. D. Mackerell Jr, CHARMM general force field: A force field for drug–like molecules compatible with the CHARMM all–atom additive biological force fields, J. Comput. Chem., 2010, 31, 671–690.
45. S. Pronk, S. Pall, R. Schulz, P. Larsson, P. Bjelkmar, R. Apostolov, M. R. Shirts, J. C. Smith, P. M. Kasson, D. van der Spoel, B. Hess and E. Lindahl, GROMACS 4.5: a high-throughput and highly parallel open source molecular simulation toolkit, Bioinformatics, 2013, 29, 845–854.
46. G. Bussi, D. Donadio and M. Parrinello, Canonical sampling through velocity rescaling, J. Chem. Phys., 2007, 126, 014101.
47. T. Darden, D. York and L. Pedersen, Particle mesh Ewald: An N·log(N) method for Ewald sums in large systems, J. Chem. Phys., 1993, 98, 10089–10092.
48. B. Hess, H. Bekker, H. J. C. Berendsen and J. G. E. M. Fraaije, LINCS: A Linear Constraint Solver for Molecular Simulations, J. Comput. Chem., 1997, 18, 1463–1472.
49. C. Anézo, A. H. de Vries, H. Höltje, D. P. Tieleman and S. Marrink, Methodological Issues in Lipid Bilayer Simulations, J. Phys. Chem. B, 2003, 107, 9424–9433.
50. T. D. Romo, N. Leioatts and A. Grossfield, Lightweight Object Oriented Structure Analysis: Tools for Building Tools to Analyze Molecular Dynamics Simulations, J. Comput. Chem., 2014, 35, 2305–2318.
51. G. M. Torrie and J. P. Valleau, Nonphysical Sampling Distributions in Monte Carlo Free-Energy Estimation: Umbrella Sampling, J. Comp. Physiol., 1977, 23, 187–199.
52. N. Nitschke, K. Atkovska and J. S. Hub, Accelerating potential of mean force calculations for lipid membrane permeation: System size, reaction coordinate, solute-solute distance, and cutoffs, J. Chem. Phys., 2016, 145, 125101.
53. S. Kumar, J. M. Rosenberg, D. Bouzida, R. H. Swendsen and P. A. Kollman, The Weighted Histogram Analysis Method for Free-Energy Calculations on Biomolecules. I. The Method, J. Comput. Chem., 1992, 13, 1011–1021.
54. B. Roux, The calculation of the potential of mean force using computer simulations, Comput. Phys. Commun., 1995, 91, 275–282.
55. R. W. Johnson, An introduction to the bootstrap, Teach. Stat., 2001, 23, 49–54.
56. P. R. Rich and R. Harper, Partition coefficients of quinone and hydroquinones and their relation to biochemical reactivity, FEBS Lett., 1990, 269, 139–144.
57. H. A. L. Filipe, M. J. Moreno, T. Róg, I. Vattulainen and L. M. S. Loura, How To Tackle the Issues in Free Energy Simulations of Long Amphiphiles Interacting with Lipid Membranes: Convergence and Local Membrane Deformations, J. Phys. Chem. B, 2014, 118, 3572–3581.
58. R. Fato, M. Battino, M. D. Esposti, G. P. Castelli and G. Lenaz, Determination of Partition and Lateral Diffusion Coefficients of Ubiquinones by Fluorescence Quenching of n-( 9-Anthroy1oxy)stearic Acids in Phospholipid Vesicles and Mitochondrial Membranes, Biochemistry, 1986, 25, 3378–3390.
59. R. Fato, E. Estornell, S. Di Bernardo, F. Pallotti, G. P. Castelli and G. Lenaz, Steady-State Kinetics of the Reduction of Coenzyme Q Analogs by Complex I (NADH:Ubiquinone Oxidoreductase) in Bovine Heart Mitochondria and Submitochondrial Particles, Biochemistry, 1996, 35, 2705–2716.
60. G. Hummer, Position-dependent diffusion coefficients and free energies from Bayesian analysis of equilibrium and replica molecular dynamics simulations, New J. Phys., 2005, 7, 34.
61. M. Palaiokostas, W. Ding, G. Shahane and M. Orsi, Effects of lipid composition on membrane permeation, Soft Matter, 2018, 14, 8496–8508.
62. J. Tomasi and M. Persico, Molecular Interactions in Solution: An Overview of Methods Based on Continuous Distributions of the Solvent, Chem. Rev., 1994, 94, 2027–2094.
63. C. Neale, W. F. D. Bennett, D. P. Tieleman and R. Pomés, Statistical Convergence of Equilibrium Properties in Simulations of Molecular Solutes Embedded in Lipid Bilayers, J. Chem. Theory Comput., 2011, 7, 4175–4188.
64. A. Catte, M. Girych, M. Javanainen, C. Loison, J. Melcr, M. S. Miettinen, L. Monticelli, J. Määttä, V. S. Oganesyan, O. H. S. Ollila, J. Tynkkynen and S. Vilov, Molecular electrometer and binding of cations to phospholipid bilayers, Phys. Chem. Chem. Phys., 2016, 18, 32560–32569.
65. A. Botan, et al., Toward Atomistic Resolution Structure of Phosphatidylcholine Headgroup and Glycerol Backbone at Different Ambient Conditions, J. Phys. Chem. B, 2015, 119, 15045–15088.
66. D. Poger, B. Caron and A. E. Mark, Validating lipid force fields against experimental data: Progress, challenges and perspectives, Biochim. Biophys. Acta, 2016, 1858, 1556–1565.
67. O. H. S. Ollila and G. Pabst, Atomistic resolution structure and dynamics of lipid bilayers in simulations and experiments, Biochim. Biophys. Acta, 2016, 1858, 2512–2528.
68. R. Baradaran, J. M. Berrisford, G. S. Minhas and L. A. Sazanov, Crystal structure of the entire respiratory complex I, Nature, 2013, 494, 443–448.
69. L.-S. Huang, J. T. Shen, A. C. Wang and E. A. Berry, Crystallographic studies of the binding of ligands to the dicarboxylate site of Complex II, and the identity of the ligand in the “oxaloacetate-inhibited” state, Biochim. Biophys. Acta, 2006, 1757, 1073–1083.
70. L. Esser, M. Elberry, F. Zhou, C.-A. Yu, L. Yu and D. Xia, Inhibitor-complexed structures of the cytochrome bc1 from the photosynthetic bacterium Rhodobacter sphaeroides, J. Biol. Chem., 2008, 283, 2846–2857.
71. J. Comte, B. Maisterrena and D. C. Gautheron, Lipid composition and protein profiles of outer and inner membranes from pig heart mitochondria, Biochim. Biophys. Acta, 1976, 419, 271–284.
72. E. K. Eriksson, V. A. Hernández and K. Edwards, Effect of ubiquinone-10 on the stability of biomimetic membranes of relevance for the inner mitochondrial membrane, Biochim. Biophys. Acta, 2018, 1860, 1205–1215.
73. S. S. Hasan, E. Yamashita, C. M. Ryan, J. P. Whitelegge and W. A. Cramer, Conservation of Lipid Functions in Cytochrome bc Complexes, J. Mol. Biol., 2011, 414, 145–162.
74. T. H. Haines and N. A. Dencher, Cardiolipin: a proton trap for oxidative phosphorylation, FEBS Lett., 2002, 528, 35–39.
75. P. A. Postila, K. Kaszuba, P. Kuleta, I. Vattulainen, M. Sarewicz, A. Osyczka and T. Róg, Atomistic determinants of co-enzyme Q reduction at the Q_i-site of the cytochrome bc₁ complex, Sci. Rep., 2016, 6, 33607.
76. A. H. de Vries, A. E. Mark and S. J. Marrink, The Binary Mixing Behavior of Phospholipids in a Bilayer: A Molecular Dynamics Study, J. Phys. Chem. B, 2004, 108, 2454–2463.

---

Footnotes

† Electronic supplementary information (ESI) available: Additional analysis of convergence, lipid mixture and local diffusion, and atom types and charges used in simulations. See DOI: 10.1039/c9ra01681c

‡ Abbreviations: Q is used in general for quinone or quinol analogues with any oxidation state and number of isoprenoid units. Q-head is the aromatic ring and bound groups except for the Q-tail, which is the full isoprenoid chain. UQ_n is oxidized ubiquinone, PQ_n is plastoquinone and MQ_n is menaquinone, where the n subscript is the number of bound isoprenoid units. UQ_nH₂ is reduced ubiquinol. POPC is 16:0,18:1 phosphatidylcholine, DLPC is di-18:2 phosphatidylcholine, DLPE is di-18:2 phosphatidylethanolamine, LCL is tetra-18:2 cardiolipin, ETC is electron transfer chain, MD is molecular dynamics, US is umbrella sampling and COM is center-of-mass.

---