Open Access Article
Open Access ArticleCreative Commons Attribution 3.0 Unported Licence
Measuring optical activity in the far-field from a racemic nanomaterial: diffraction spectroscopy from plasmonic nanogratings†
Christian
Kuppe
 a,
Xuezhi
Zheng
*b,
Calum
Williams
c,
Alexander W. A.
Murphy
a,
Joel T.
Collins
a,
Sergey N.
Gordeev
d,
Guy A. E.
Vandenbosch
b and
Ventsislav K.
Valev
a,
Xuezhi
Zheng
*b,
Calum
Williams
c,
Alexander W. A.
Murphy
a,
Joel T.
Collins
a,
Sergey N.
Gordeev
d,
Guy A. E.
Vandenbosch
b and
Ventsislav K.
Valev
 *ad
*ad
aCentre for Photonics and Photonic Materials and Centre for Nanoscience and Nanotechnology, University of Bath, Bath, BA2 7AY, UK. E-mail: v.k.valev@bath.ac.uk
bDepartment of Electrical Engineering (ESAT-TELEMIC), KU Leuven, Kasteelpark Arenberg 10, BUS 2444, Heverlee, 3001, Belgium. E-mail: xuezhi.zheng@esat.kuleuven.be
cElectrical Engineering Division, Department of Engineering, University of Cambridge, 9 JJ Thomson Avenue, Cambridge, CB3 0FA, UK
dCentre for Nanoscience and Nanotechnology, University of Bath, Bath, BA2 7AY, UK
First published on 10th May 2019
Abstract
Recent progress in nanofabrication has redrawn the boundaries of the applicability of chiroptical (chiral optical) effects. Chirality, often expressed as a twist in biomolecules, is crucial for pharmaceuticals, where it can result in extremely different chemical properties. Because chiroptical effects are typically very weak in molecules, plasmonic nanomaterials are often proposed as a promising platform to significantly enhance these effects. Unfortunately, the ideal plasmonic nanomaterial has conflicting requirements: its chirality should enhance that of the chiral molecules and yet it should have no chiroptical response on its own. Here, we propose a unique reconciliation to satisfy the requirements: a racemic plasmonic nanomaterial, consisting of equal amounts of opposite chiral unit cells. We show how diffraction spectroscopy can be used to unveil the presence of chirality in such racemic nanogratings in the far-field. Our experiments are supported by numerical simulations and yield a circular intensity difference of up to 15%. The physical origin is demonstrated by full wave simulations in combination with a Green's function – group-theory-based analysis. Contributions from Circular Dichroism in the Angular Distribution of Photoelectrons (CDAD) and pseudo/extrinsic chirality are ruled out. Our findings enable the far-field measurement and tuning of racemic nanomaterials, which is crucial for hyper-sensitive chiral molecular characterization.
New conceptsChiral plasmonic nanomaterials have revolutionized chirality, with new theoretical parameters that enable superchiral light and negative refractive index materials. There are many potential applications, such as ultra-thin-film optical components, nanorobotics, and especially enhanced optical processes with chiral molecules. In order for the chiral nanostructures to enhance the optical activity in molecules without affecting it themselves, the nanostructures need to be in a racemic mixture, i.e. a 50![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) : :![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 50 ratio of enantiomorphs, with zero net optical activity. Yet, the chirality of these same nanostructures needs to be tailored to that of the chiral molecules. Which leads to a contradiction: how to tailor the optical activity in a material with zero optical activity? Our answer appears from looking at the question from a new direction. We show that diffraction spectroscopy can be used to unveil the presence of chirality, in such racemic nanomaterials, even in the far-field. We show very large values for the optical activity in diffracted beams and we provide a rigorous theoretical and conceptual support for our findings. This work creates opportunities to explore and tailor the interactions between plasmonic nanoparticles and chiral molecules: it removes an important roadblock for the entire research field. 50 ratio of enantiomorphs, with zero net optical activity. Yet, the chirality of these same nanostructures needs to be tailored to that of the chiral molecules. Which leads to a contradiction: how to tailor the optical activity in a material with zero optical activity? Our answer appears from looking at the question from a new direction. We show that diffraction spectroscopy can be used to unveil the presence of chirality, in such racemic nanomaterials, even in the far-field. We show very large values for the optical activity in diffracted beams and we provide a rigorous theoretical and conceptual support for our findings. This work creates opportunities to explore and tailor the interactions between plasmonic nanoparticles and chiral molecules: it removes an important roadblock for the entire research field.
|
Introduction
Recently, the field of chirality has experienced a paradigm shift, driven by experimental progress in nanofabrication1,2 and by theoretical insights into the chirality parameters.3–6 These parameters include geometric and optical chirality that both lead to fascinating physical properties, such as negative refractive index7,8 and superchiral light states.9,10 In turn, these concepts are enabling applications, including super-lenses and hyper-sensitive molecular characterization.10Molecular chirality is ubiquitous in bio-organisms and, hence, a crucial topic for pharmacology.11,12 Indeed, the mirror images (or enantiomers) of many bio-molecules can have very distinct functions.13 However, molecular synthesis usually yields an equal proportion of both enantiomers (or a racemic mixture).14 Additional chemical processes are therefore required to separate the enantiomers and at each step their ratio needs to be measured.2,15
Since the very discovery of molecular chirality, optical activity (OA) has been used to measure the ratio of enantiomers (or enantiomeric excess). OA results from the difference in interaction between enantiomers with left- or right-hand circularly polarized light (CPL). Although OA is widely used in chemistry, the effect is typically very weak; this is because the chiral pitch of CPL is orders of magnitude larger than the chiral pitch in molecules.13 Metal nanostructures bridge this gap. These nanostructures benefit from surface plasmon resonances; whereby coherent oscillations of the surface electrons can be excited by visible light.16 These oscillations occur at the same frequency, but with a much shorter wavelength, which effectively confines light at the nanoscale and therefore enhances the interaction with molecules.17–19 As a consequence, chiral plasmonic nanomaterials exhibit pronounced chiral optical (chiroptical) effects, which can unfortunately overshadow the molecular response.20–24
Although achiral plasmonic nanoparticles have been demonstrated to successfully enhance the chiroptical response of some molecules, such as cysteine and riboflavin,20,25 this enhancement is not optimal, as it does not benefit from the chirality of the plasmonic fields. By contrast, a racemic mixture of chiral plasmonic nanostructures has no net OA, but strong local chirality in the plasmonic near-field that chiral molecules can couple to. The response from such racemic nanomaterials can be highly sensitive to the enantiomeric excess of molecules.26 However, the lack of chiroptical response in the far-field makes it difficult to tailor the material to molecules.27–29
Here, we demonstrate for the first time a detection scheme that allows the measurement of the chiroptical response of a racemic nanograting in the far-field. We show that racemic nanogratings can yield extremely large chiroptical responses of up to 15%, comparable to previously reported OA for chiral nanogratings.23,30–33 Previous work has focused on circular intensity difference spectroscopy from individual diffraction beams.23,30–34 Here, we present a comprehensive analysis of up to four orders of diffraction and the physical origin of the measured far-field response is exploited by full-wave electromagnetic simulations. The measured far-field response is studied in the framework of a Green's function – group-theory-based approach. We discuss and rule out contributions from false chirality, such as the Circular Dichroism in the Angular Distribution of Photoelectrons (CDAD) or pseudo/extrinsic chirality.
Results
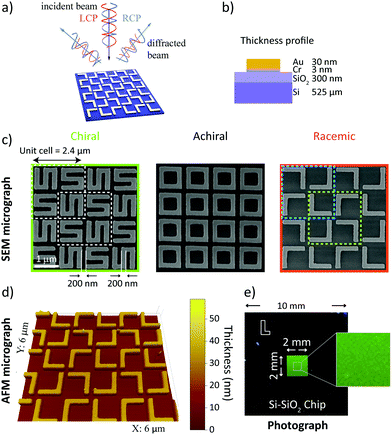
In Fig. 1a, left- and right-circularly polarized (LCP and RCP) light is used to illuminate gold nanogratings. The spatial period of the nanogratings was chosen to produce multiple diffraction order beams in the visible spectrum. Those diffracted beams are analyzed using circular intensity difference (CID) spectroscopy. The gold nanogratings studied in this work were fabricated using electron beam lithography on a silicon-silicon dioxide wafer (dioxide layer thickness of 300 nm). The gold layer (30 nm thickness) was stabilized using a chromium adhesion layer (3 nm thick). The thickness profile is presented schematically in Fig. 1b and the fabrication details are given in the Methods section. The period of the gratings was 2.4 μm. Each square unit cell consists of a 2 × 2 arrangement of gold elements and each element is 1 μm large. The nanowire width, and the nearest neighbor separation is 200 nm. Furthermore, each element is rotated by 90° with respect to its neighbor. The individual nanoelements assemble into three different chiral states – chiral (S-shaped), achiral (square-rings) and racemic (L-shaped). The different gratings were characterized with scanning electron microscopy (SEM) and are shown in Fig. 1c. The L-shaped nanostructures naturally result in unit cells with opposite handedness (highlighted with cyan and yellow dashed lines, in Fig. 1c) and are therefore macroscopically racemic. The racemic nanogratings were further characterized via atomic force microscopy (AFM) and the associated micrograph is presented in Fig. 1d. On a larger scale, the good homogeneity of the total nanograting array (area 4 mm2) is demonstrated by the uniformity of the nanostructured area in the photograph image shown in Fig. 1e.The apparatus used to study the nanogratings is shown schematically in Fig. 2a, with a detailed description in the Methods section. A supercontinuum light source was used to generate coherent white light, with a linear polarizer and an achromatic waveplate to control its polarization state. Since all our nanogratings exhibit C4 symmetry (unchanged when rotated by 90° about its normal axis), the investigation was limited to the in-plane horizontal diffraction orders. Because these diffracted beams are the same on both sides of the incident beam, we focused our attention on the positive diffracted order beams (m = 1, 2, etc.), as indicated in Fig. 2a. The diffracted light was measured with a light detection (LD) scheme, consisting of a microscope objective and an optical fiber connected to a spectrometer for analysis. For the individual nanogratings, the resulting diffraction patterns are shown in Fig. 2b–d; presented as intensity heatmaps. The spatial distribution of the diffracted beams is in good agreement with the predicted spatial distribution from the grating equation (green lines).34 The effective period of the S-shaped and square-ring nanogratings is halved to 1.2 μm as a consequence of the unit cell design shown in Fig. 1c. While the normalized intensity for the L-shaped gratings produces four distinct diffraction orders (m = 1 to 4), the first and third order beams are approximately 50 times less intense than the second and fourth order beams; barely visible in the intensity heatmaps.
 | ||
| Fig. 2 Our nanogratings of chiral, achiral and racemic nanomaterials exhibit multiple diffraction beams in the visible part of the spectrum. The apparatus used to study the circular intensity difference (CID) in diffraction, and intensity pattern for each nanograting, is schematically shown in (a). The polarization state of the incident coherent white light was controlled by a linear polarizer and a quarter-waveplate (QWP), the beam was directed at normal incidence with respect to the nanograting. The diffraction pattern in reflection was measured in the horizontal plane using a fiber-based light detection (LD) system rotated around the sample. Since the nanogratings exhibit C4 symmetry only the positive diffraction orders between 10–90° were measured. The resulting intensities for left circularly polarized (LCP) light are shown on the bottom. The intensities for the samples, shown in Fig. 1c, are represented by normalized heatmaps with the wavelength on the x- and the diffraction angle on the y-axis. The green lines show the predicted position of the diffracted order beams for periods of 1.2 μm (for S- and square-ring shaped samples) and 2.4 μm (for L-shaped samples) are given and agree with the experimental results. | ||
The optical activity of the nanogratings was determined by measuring the CID in each diffraction order beam. CID is defined as
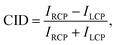 | (1) |
Additionally, to corroborate the experimental results and further explain the physical origins of the observed effects, finite difference simulations were carried out using Lumerical35 (detailed description in the Methods section). The measured and simulated far-field response of the nanogratings are presented in Fig. 3. The results from the experimental and numerical analysis are in excellent agreement for both the spatial distribution and the CID response for each nanograting. The chiral S-shaped nanogratings (Fig. 3a) exhibit a large CID of up to 20% and a change of sign between the first and second diffracted order beams. For the associated mirrored S-shaped nanogratings, the response is opposite in sign, as expected from chirality (see Fig. S1, ESI†). The results are in good agreement with the numerical simulations.
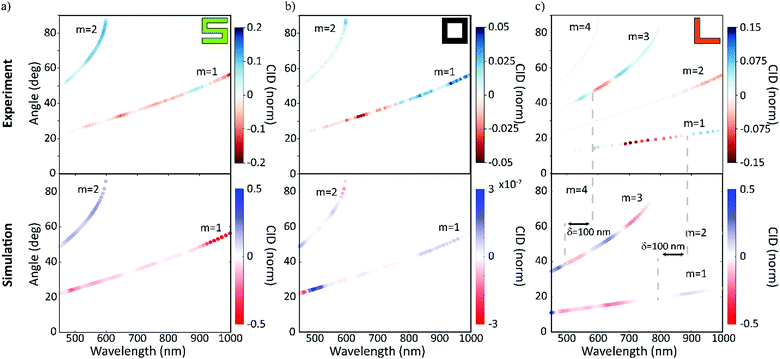 | ||
| Fig. 3 In diffraction, the response of our racemic nanomaterials is similar to that of the chiral nanomaterials. The results for the circular intensity difference (CID) spectroscopy measurements for the three chiral cases – with chiral (green ‘S’), achiral (black ‘square-ring’) and racemic (orange ‘L’). The measured wavelength is shown on the x- and the diffraction angle on the y-axis. The diffracted order beams are numbered, and the color represents the strength and sign of the measured CID signals. The experimental results (top row) are compared with numerical simulations (bottom row) and are in very good agreement. For the racemic case, it should be highlighted that the second and fourth order diffracted beams exhibit no CID, although their intensities are dominant (Fig. 2d). While the chiral and achiral cases agree with our expectations, the racemic case, surprisingly, exhibits a CID comparable to the chiral case. | ||
The achiral square-ring-shaped nanogratings (Fig. 3b) should exhibit no CID and therefore, the measured response indicates the noise level in both the experiments and the numerical simulations. Experimentally, the maximum CID is just below 5%, which is significantly lower than the response obtained for the chiral nanogratings. For the simulations, the numerical noise level is as low as 10−7. Sources for the experimental error are thought to be fabrication imperfections, detection uncertainties and small differences in the fiber coupling efficiency.
Unlike the achiral nanogratings, the racemic L-shaped nanogratings, do exhibit CID. Our experimental results (Fig. 3c) demonstrate a large response of up to 15%, comparable to the S-shaped nanogratings with up to 20%. This counter-intuitive result is in good agreement with the numerical simulations, especially the strong responses in the first and third order diffracted beams. A slight spectral shift (red-shift) between the experimental and numerical results can be observed, due to the difference between the nominal sample geometry (ideally realized in a simulation) and the nanofabricated samples, prone to defects, see AFM micrograph in Fig. 1d. The robustness of the far-field response from the racemic L-shaped nanogratings was further investigated by measuring the effect of sample rotation with respect to the input beam. This investigation shows no significant net-effect on the observed results (see Fig. S2, ESI†).
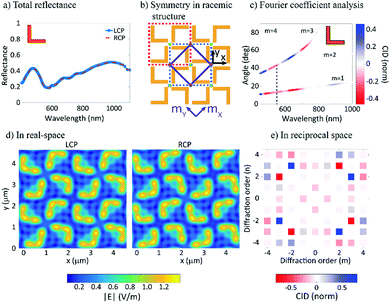
In order to explain the CID effects from the racemic L-shaped nanostructures, a near-field to far-field transformation procedure (see Note 1, ESI†) is employed. In the implementation, the near-field is first decomposed into propagating and non-propagating spatial Fourier modes with their Fourier coefficients being calculated. Then, all the modes are propagated and projected onto an observation plane, so that physical quantities of interests can be obtained, such as electromagnetic fields, power, etc. The reflectance spectrum from the racemic sample is identical under LCP and RCP illumination (see Fig. 4a). This might seem surprising, given that the sample unit cells lack mirror symmetry. However, a careful examination of the sample reveals two additional axes of reflection that do not pass through the rotation centers of the unit cells (see Fig. 4b). Mathematically, these mirroring symmetries, together with the four-fold rotational symmetries, form a D4 point group. By further considering translational symmetries in the square lattice, the sample actually holds a p4g (wallpaper) group.36 Especially, due to the axes of reflection, the optical response for LCP and RCP illumination in the experiment can always be transformed into each other by a mirroring operation with respect to the axes of reflection (see Fig. 4d). This transformation leads to, at most, a phase difference and results in identical reflectance spectra for LCP and RCP illumination. The above statements have also been rigorously proven by using an integral equation representation37–39 in combination with the group representation theory40 (see Notes 1 and 2, ESI†).
In contrast to the reflectance spectrum, which describes the effect of all the (propagating) Fourier modes, diffraction spectroscopy enables the precise examination of each Fourier mode, thereby revealing the symmetry of the structure. As shown in Fig. 4c, the calculated CID agrees well with our experimental data (Fig. 3c). The CID can be mathematically attributed to the fact that when evaluating the Fourier coefficients (see Notes 3 and 4, ESI†) for a given direction of diffraction, the phase term ei(kxx+kyy) may have a different symmetry than the sample. This observation therefore results in different Fourier coefficients for the LCP and RCP illuminations and further corroborates our argument from the reciprocity point of view.
Lastly, it should be pointed out that the square lattice supports only three wallpaper groups:36 the p4 group, which is generated by the C4 point group and is exactly the case of the S-shape sample; the p4m group, which is generated by the D4 point group, whose axes of reflection coincide with the rotational centers of the unit cells and which is exactly the case of the square-ring sample; and the p4m group which is the case of the L-shape sample. By following the same analysis for the L-shape structure, the CID features for the other two cases can be readily derived and are summarized in the Table 1. It is readily seen that reflectance and diffraction circular intensity difference spectroscopy in combination provide us with the powerful capability of identifying the symmetries of a unit cell in the square lattice, without having to analyze the intricate near-field.
| S-shape | L-shape | Square-ring-shape | |
|---|---|---|---|
| Reflectance | ✓ | × | × |
| Diffraction | ✓ | ✓ | × |
Discussion
It is important to distinguish our results from cases of false chirality,41 whereby chirality in the experiment can be measured instead of chirality in the samples. The Circular Dichroism in the Angular Distribution of Photoelectrons (CDAD) effect was first predicted by Ritchie, in a series of publications.42–45 CDAD is very different from the CD effect. The CD effect is often small, as it requires contributions from both the electric and the magnetic dipoles, with the latter being usually very small. By contrast, the CDAD effect can originate from electric dipoles only,46 and as a consequence it was calculated to be much larger than CD, reaching up to 100% of asymmetry.47 The CDAD effect was first demonstrated experimentally in 1989, by Westphal et al.48 and the reported results were in good agreement with the theoretical predications.49–52Importantly, whereas CD requires chirality, CDAD does not.53 CDAD arises from the interaction of three vectors: the wave vector ![[k with combining circumflex]](https://www.rsc.org/images/entities/i_char_006b_0302.gif) , the surface normal
, the surface normal ![[n with combining circumflex]](https://www.rsc.org/images/entities/i_char_006e_0302.gif) and the direction of photoemission
and the direction of photoemission ![[p with combining circumflex]](https://www.rsc.org/images/entities/i_char_0070_0302.gif) . Large dichroic effects are observed as a function of the angle between k and
. Large dichroic effects are observed as a function of the angle between k and ![[n with combining circumflex]](https://www.rsc.org/images/entities/i_char_006e_0302.gif) . Crucially, the effect is only allowed as long as
. Crucially, the effect is only allowed as long as ![[k with combining circumflex]](https://www.rsc.org/images/entities/i_char_006b_0302.gif) ,
, ![[n with combining circumflex]](https://www.rsc.org/images/entities/i_char_006e_0302.gif) and
and ![[p with combining circumflex]](https://www.rsc.org/images/entities/i_char_0070_0302.gif) are not co-planar. In our experimental configuration, where these vectors are co-planar, the CDAD effect is forbidden. Therefore, our results cannot be attributed to CDAD. There is however another case of false chirality, where these vector can be co-planar; this effect is referred to as “pseudo chirality”54 or “extrinsic chirality”.55
are not co-planar. In our experimental configuration, where these vectors are co-planar, the CDAD effect is forbidden. Therefore, our results cannot be attributed to CDAD. There is however another case of false chirality, where these vector can be co-planar; this effect is referred to as “pseudo chirality”54 or “extrinsic chirality”.55
Pseudo/extrinsic chirality is another case of “chirality of the experiment” and can be observed in achiral samples. It too arises from three vectors, two of which are the same as in CDAD: the wave vector ![[k with combining circumflex]](https://www.rsc.org/images/entities/i_char_006b_0302.gif) and the surface normal
and the surface normal ![[n with combining circumflex]](https://www.rsc.org/images/entities/i_char_006e_0302.gif) . The third vector is the direction of the curvature
. The third vector is the direction of the curvature ![[R with combining circumflex]](https://www.rsc.org/images/entities/i_char_0052_0302.gif) on the sample. Here again, large dichroic effects are observed as a function of the angle between
on the sample. Here again, large dichroic effects are observed as a function of the angle between ![[k with combining circumflex]](https://www.rsc.org/images/entities/i_char_006b_0302.gif) and
and ![[n with combining circumflex]](https://www.rsc.org/images/entities/i_char_006e_0302.gif) , and the observed dichroism was found to be proportional to (1/R)(
, and the observed dichroism was found to be proportional to (1/R)(![[R with combining circumflex]](https://www.rsc.org/images/entities/i_char_0052_0302.gif) ·
·![[k with combining circumflex]](https://www.rsc.org/images/entities/i_char_006b_0302.gif) ×
× ![[n with combining circumflex]](https://www.rsc.org/images/entities/i_char_006e_0302.gif) ).56 However, in our experiment
).56 However, in our experiment ![[k with combining circumflex]](https://www.rsc.org/images/entities/i_char_006b_0302.gif) is parallel to
is parallel to ![[n with combining circumflex]](https://www.rsc.org/images/entities/i_char_006e_0302.gif) , leading to
, leading to ![[k with combining circumflex]](https://www.rsc.org/images/entities/i_char_006b_0302.gif) ×
× ![[n with combining circumflex]](https://www.rsc.org/images/entities/i_char_006e_0302.gif) = 0. Therefore, pseudo/extrinsic chirality is also forbidden and our results cannot be attributed to it.
= 0. Therefore, pseudo/extrinsic chirality is also forbidden and our results cannot be attributed to it.
It is worth mentioning that the idea to separate intrinsic chiral contributions from CDAD by adopting a co-planar experimental configuration has been explored by Attard et al.57 However, whereas Attard et al. “tentatively” reported asymmetry values of 2% (±1%), our values rise up to 15% and are well-above the noise-level. Attard et al. reported clear asymmetry in the CDAD experimental geometry. This is in agreement with our own calculations presented in Fig. 4e, where the diagonal diffraction beams (non-co-planar configuration) show the largest CID/asymmetry and reverse sign across the plane of incidence.
Methods
Sample fabrication
10 mm × 10 mm × 525 μm single-side polished Si (p-doped)-SiO2 (300 nm) samples are sonicated in successive baths of acetone and IPA (isopropyl alcohol) for 10 minutes, blow dried with compressed ultra-high purity (UHP) N2 and dehydrated on a hotplate (200 °C, 20 min). UV1116-0.5 (Dow Chemical Company) chemically amplified positive-tone photoresist is spin-coated (5,500 rpm, 45 s) and soft-baked on a hotplate (130 °C, 2 min), resulting in a final thickness of ∼350 nm. 80 kV electron beam lithography (Nanobeam nB1) is used for the high-resolution patterning, with exposure conditions: pattern optimized area dose between 40–100 μC cm−2, 1.8 nA operating current and a 38 μm main field.58 A post-exposure bake on a hotplate is performed at 130 °C, 90 s. The samples are developed in MF-CD-26 for 10 s, followed by a de-ionized (DI)-water rinse for 3 min and N2. Physical vapour deposition of Cr/Au (3/30 nm) is performed using a thermal evaporator (Edwards E306) at a base pressure ∼1 × 10−6 mbar, at an evaporation rate ∼0.1 nm s−1. Resist lift-off is carried out in NMP (N-methyl-2-pyrrolidone) at an elevated temperature of 60 °C for 4 hours, followed by fresh NMP sonication for 2 min, acetone, IPA rinse and UHP N2 blow dry. For nanoscale surface quality inspection, a Zeiss LEO 1530 VP Scanning Electron Microscope (SEM) operating at 5 keV was used and the SEM micrographs are shown in Fig. 1.Experimental methods
The experimental setup consisted of a Fianium SC400-2 2 W laser source with a 1064 nm output wavelength and 20 MHz repetition rate and a 5 ps pulse spliced to an in-house fabricated supercontinuum fiber, described in ref. 59 providing a spectrum between 450 and 1050 nm. Two achromatic linear Glan-Laser polarizers were used to control the power output and a remotely controlled quarter-waveplate (QWP) to selectively produce LCP and RCP light. The QWP was chosen for its broad wavelength range as well as its negligible beam deviation (>1 arcsec), which has been tested – shown in Fig. S3 (ESI†). The sample was mounted on an alignment disk, which in turn was mounted on x–y translation stage placed in the center of an optical breadboard. The breadboard was mounted on a remotely controlled rotation stage. The diffracted light from the sample was collected via a 200 μm core diameter multimode fiber (0.22 NA), which was mounted on a fiber launch system, which in turn was mounted on the breadboard at a distance of 15 cm and measured with an Ocean Optics QE Pro spectrometer. The light coupling into the fiber was optimized with a 20× microscope objective with 0.4 NA and 9 mm focal length. The automated setup used a step size of 0.5°; the spectrometer used an integration time of 30 ms and was averaged over 50 scans. The atomic force microscopy micrograph in Fig. 1d was acquired with a Multimode Scanning Probe Microscope (VEECO) operating in contact mode.Numerical methods
The full-wave simulations were conducted by an FDTD solver, Lumerical.35 In the simulations, the incident LCP and RCP plane waves are generated by superposing two 90 degrees phased plane waves which are linearly polarized along the x and y directions. All layers in the sample have been take into account. In detail, the Au layer is modeled by the material data from Johnson and Christy,60 the Cr layer and the Si layer is modeled by the material data from Palik61 and the reflective index of the SiO2 layer is assumed to be 1.5. It should be noted that instead of using the nominal thickness, the Au layer is assumed to be 50 nm. Two simulation regions are used. On the one hand, the FDTD simulation region is assumed to have periodic boundary conditions along the x and y directions and perfect matching layers (48 layers) along the z direction. On the other hand, a mesh refinement region including both the Au and Cr layers is imposed to the S-shape structures, the L-shape structures, and the square-rings. The mesh steps along x, y and z directions are 10 nm, 10 nm and 1.5 nm, respectively.Conclusions
In summary, we have demonstrated for the first time that diffraction circular intensity spectroscopy can be used to measure a strong chiroptical response for racemic nanogratings. We report chiroptical CID values of up to 15%. Our experimental findings are supported by a rigorous Fourier modal analysis. The analysis can identify the chiroptical response of each individual diffracted order beam. The observed chiroptical behavior in the diffracted beams can be seen as a reciprocal to the extrinsic 2D chirality effect. Furthermore, our results enable the distinction of different unit cells (chiral, achiral and racemic) in a square lattice. Our findings allow the tailoring of far-field features of racemic nanostructures to that of molecules, which is key for developing hyper-sensitive chiral molecular characterization.Conflicts of interest
There are no conflicts to declare.Acknowledgements
V. K. V. acknowledges support from the Royal Society through the University Research Fellowships. We acknowledge Royal Society grants CHG\R1\170067, PEF1\170015 and RGF\EA\180228, as well as STFC grant ST/R005842/1 and EPSRC grant EP/L015544/1. C. W. acknowledges financial support from Cancer Research UK (CRUK) Pioneer Award (C55962/A24669) and Wolfson College, Cambridge, UK. C. W. further acknowledges research support from S. Bohndiek, T. Wilkinson and G. Gordon. X. Z. and G. A. E. V. are grateful for the financial support from the FWO (G090017N) and KU Leuven internal research funds (C24/15/015). All data supporting this study are openly available from the University of Bath data archive at DOI: 10.15125/BATH-00592.References
- M. Kuwata-Gonokami, N. Saito, Y. Ino, M. Kauranen, K. Jefimovs, T. Vallius, J. Turunen and Y. Svirko, Phys. Rev. Lett., 2005, 95, 1–4 CrossRef PubMed.
- M. Hentschel, M. Schäferling, X. Duan, H. Giessen and N. Liu, Sci. Adv., 2017, 3, e1602735 CrossRef PubMed.
- R. Mohammadi-Baghaee and J. Rashed-Mohassel, J. Solution Chem., 2016, 45, 1171–1181 CrossRef CAS.
- S. Yoo and Q.-H. Park, Sci. Rep., 2015, 5, 14463 CrossRef CAS PubMed.
- H. S. Park, T.-T. Kim, H.-D. Kim, K. Kim and B. Min, Nat. Commun., 2014, 5, 5435 CrossRef PubMed.
- A. Canaguier-Durand and C. Genet, Phys. Rev. A: At., Mol., Opt. Phys., 2015, 92, 043823 CrossRef.
- I. Liberal and N. Engheta, Nat. Photonics, 2017, 11, 149–158 CrossRef CAS.
- J. B. Pendry, Y. Luo and R. Zhao, Science, 2015, 348, 521–524 CrossRef CAS PubMed.
- Y. Tang and A. E. Cohen, Phys. Rev. Lett., 2010, 104, 163901 CrossRef PubMed.
- Y. Tang and A. E. Cohen, Science, 2011, 332, 333–336 CrossRef CAS PubMed.
- F. Hong, F. Zhang, Y. Liu and H. Yan, Chem. Rev., 2017, 117, 12584–12640 CrossRef CAS PubMed.
- J. T. Collins, C. Kuppe, D. C. Hooper, C. Sibilia, M. Centini and V. K. Valev, Adv. Opt. Mater., 2017, 5, 1700182 CrossRef.
- V. K. Valev, J. J. Baumberg, C. Sibilia and T. Verbiest, Adv. Mater., 2013, 25, 2517–2534 CrossRef CAS PubMed.
- E. Meggers, Chem. Commun., 2015, 51, 3290–3301 RSC.
- B. Bai, Y. Svirko, J. Turunen and T. Vallius, Phys. Rev. A: At., Mol., Opt. Phys., 2007, 76, 023811 CrossRef.
- B. K. Canfield, S. Kujala, K. Laiho, K. Jefimovs, J. Turunen and M. Kauranen, Opt. Express, 2006, 14, 950 CrossRef PubMed.
- J. M. Slocik, A. O. Govorov and R. R. Naik, Nano Lett., 2011, 11, 701–705 CrossRef CAS PubMed.
- V. K. Valev, N. Smisdom, A. V. Silhanek, B. De Clercq, W. Gillijns, M. Ameloot, V. V. Moshchalkov and T. Verbiest, Nano Lett., 2009, 9, 3945–3948 CrossRef CAS PubMed.
- K. Konishi, B. Bai, Y. Toya, J. Turunen, Y. P. Svirko and M. Kuwata-Gonokami, Opt. Lett., 2012, 37, 4446 CrossRef PubMed.
- B. M. Maoz, Y. Chaikin, A. B. Tesler, O. Bar Elli, Z. Fan, A. O. Govorov and G. Markovich, Nano Lett., 2013, 13, 1203–1209 CrossRef CAS PubMed.
- H. Zhang and A. O. Govorov, Phys. Rev. B: Condens. Matter Mater. Phys., 2013, 87, 075410 CrossRef.
- P. Pagliusi, C. Provenzano, A. Mazzulla, L. Giorgini and G. Cipparrone, Appl. Spectrosc., 2008, 62, 465–468 CrossRef CAS PubMed.
- I. De Leon, M. J. Horton, S. A. Schulz, J. Upham, P. Banzer and R. W. Boyd, Sci. Rep., 2015, 5, 13034 CrossRef PubMed.
- S. N. Volkov, K. Dolgaleva, R. W. Boyd, K. Jefimovs, J. Turunen, Y. Svirko, B. K. Canfield and M. Kauranen, Phys. Rev. A: At., Mol., Opt. Phys., 2009, 79, 043819 CrossRef.
- R. Y. Wang, P. Wang, Y. Liu, W. Zhao, D. Zhai, X. Hong, Y. Ji, X. Wu, F. Wang, D. Zhang, W. Zhang, R. Liu and X. Zhang, J. Phys. Chem. C, 2014, 118, 9690–9695 CrossRef CAS.
- J. García-Guirado, M. Svedendahl, J. Puigdollers and R. Quidant, Nano Lett., 2018, 18, 6279–6285 CrossRef PubMed.
- G. K. Larsen, Y. He, W. Ingram and Y. Zhao, Nano Lett., 2013, 13, 6228–6232 CrossRef CAS PubMed.
- Y. He, K. Lawrence, W. Ingram and Y. Zhao, ACS Photonics, 2015, 2, 1246–1252 CrossRef CAS.
- M. Schäferling, Springer Series in Optical Sciences, Springer International Publishing, Cham, 2017, vol. 205, pp. 87–100 Search PubMed.
- A. Papakostas, A. Potts, D. M. Bagnall, S. L. Prosvirnin, H. J. Coles and N. I. Zheludev, Phys. Rev. Lett., 2003, 90, 107404 CrossRef CAS PubMed.
- S. L. Prosvirnin and N. I. Zheludev, Phys. Rev. E: Stat., Nonlinear, Soft Matter Phys., 2005, 71, 037603 CrossRef CAS PubMed.
- A. Potts, W. Zhang and D. M. Bagnall, Phys. Rev. A: At., Mol., Opt. Phys., 2008, 77, 043816 CrossRef.
- T. Roy, A. E. Nikolaenko and E. T. F. Rogers, J. Opt., 2013, 15, 085101 CrossRef.
- C. Kuppe, C. Williams, J. You, J. T. Collins, S. N. Gordeev, T. D. Wilkinson, N.-C. Panoiu and V. K. Valev, Adv. Opt. Mater., 2018, 1800098, 1–6 Search PubMed.
- https://www.lumerical.com/ .
- M. S. Dresselhaus, G. Dresselhaus and A. Jorio, Group Theory: Application to the Physics of Condensed Matter, Springer Berlin Heidelberg, Berlin, Heidelberg, 2008 Search PubMed.
- X. Zheng, V. K. Valev, N. Verellen, Y. Jeyaram, A. V. Silhanek, V. Metlushko, M. Ameloot, G. A. E. Vandenbosch and V. V. Moshchalkov, IEEE Photonics J., 2012, 4, 267–282 Search PubMed.
- X. Zheng, V. Volskiy, V. K. Valev, G. A. E. Vandenbosch and V. V. Moshchalkov, IEEE J. Sel. Top. Quantum Electron., 2013, 19, 4600908 Search PubMed.
- X. Zheng, V. K. Valev, N. Verellen, V. Volskiy, L. O. Herrmann, P. Van Dorpe, J. J. Baumberg, G. A. E. Vandenbosch and V. V. Moschchalkov, IEEE Photonics J., 2014, 6, 1–13 Search PubMed.
- X. Zheng, N. Verellen, D. Vercruysse, V. Volskiy, P. Van Dorpe, G. A. E. Vandenbosch and V. Moshchalkov, IEEE Trans. Antennas Propag., 2015, 63, 1589–1602 Search PubMed.
- L. D. Barron, Molecular Light Scattering and Optical Activity, Cambridge University Press, Cambridge, 1982 Search PubMed.
- B. Ritchie, Phys. Rev. A: At., Mol., Opt. Phys., 1975, 12, 567 CrossRef.
- B. Ritchie, Phys. Rev. A: At., Mol., Opt. Phys., 1976, 13, 1411 CrossRef.
- B. Ritchie, Phys. Rev. A: At., Mol., Opt. Phys., 1976, 14, 359 CrossRef CAS.
- B. Ritchie, Phys. Rev. A: At., Mol., Opt. Phys., 1976, 14, 1396 CrossRef CAS.
- N. A. Cherepkov, Chem. Phys. Lett., 1982, 87, 344 CrossRef CAS.
- R. L. Dubs, S. N. Dixit and V. McKoy, Phys. Rev. Lett., 1985, 54, 1249 CrossRef CAS PubMed.
- C. Westphal, et al. , Phys. Rev. Lett., 1989, 63, 151 CrossRef CAS PubMed.
- C. Westphal, J. Bansmann, M. Getzlaff and G. Schiinhense, J. Electron Spectrosc. Relat. Phenom., 1990, 52, 613 CrossRef CAS.
- C. Westphal, J. Bansmann, M. Getzlaff and G. Schiinhense, Vacuum, 1990, 41, 87 CrossRef CAS.
- G. Schiinhense, Phys. Ser., 1990, 31, 255 CrossRef.
- G. Schiinhense, Vacuum, 1990, 41, 506 CrossRef.
- G. Schöhense, C. Westphal, J. Bansmann, M. Getzlaff, J. Noffke and L. Fritsche, Surf. Sci., 1991, 251, 132–135 CrossRef.
- T. Verbiest, M. Kauranen, Y. Van Rompaey and A. Persoons, Phys. Rev. Lett., 1996, 77, 1456 CrossRef CAS PubMed.
- E. Plum, X.-X. Liu, V. A. Fedotov, Y. Chen, D. P. Tsai and N. I. Zheludev, Phys. Rev. Lett., 2009, 102, 113902 CrossRef CAS PubMed.
- A. Belardini, M. C. Larciprete, M. Centini, E. Fazio, C. Sibilia, D. Chiappe, C. Martella, A. Toma, M. Giordano and F. Buatier de Mongeot, Phys. Rev. Lett., 2011, 107, 257401 CrossRef CAS PubMed.
- G. A. Attard, D. Watson, E. A. Seddon, S. M. Cornelius, E. Herrero and J. Feliu, Phys. Rev. B: Condens. Matter Mater. Phys., 2001, 64, 115408 CrossRef.
- C. Williams, R. Bartholomew, G. Rughoobur, G. S. D. Gordon, A. J. Flewitt and T. D. Wilkinson, Nanotechnology, 2016, 27, 485301 CrossRef PubMed.
- J. M. Stone and J. C. Knight, Opt. Express, 2008, 16, 2670–2675 CrossRef CAS PubMed.
- P. B. Johnson and R. W. Christy, Phys. Rev. B: Condens. Matter Mater. Phys., 1972, 6, 4370–4379 CrossRef CAS.
- E. Palik, Handbook of Optical Constants of Solids, Academic Press, 1998 Search PubMed.
Footnote |
| † Electronic supplementary information (ESI) available. See DOI: 10.1039/c9nh00067d |
| This journal is © The Royal Society of Chemistry 2019 |