Open Access Article
Open Access ArticleCreative Commons Attribution 3.0 Unported Licence
Interplay between H2O and CO2 coadsorption and space-charge on Y-doped BaZrO3 surfaces†
Jonathan M.
Polfus‡
 *ab,
Jing
Yang‡
*ab,
Jing
Yang‡
 b and
Bilge
Yildiz
*bc
b and
Bilge
Yildiz
*bc
aSINTEF Industry, Sustainable Energy Technology, PO Box 124 Blindern, NO-0314 Oslo, Norway. E-mail: jonathan.polfus@sintef.no
bDepartment of Materials Science and Engineering, Massachusetts Institute of Technology, 77 Massachusetts Avenue, Cambridge, MA 02139, USA
cDepartment of Nuclear Science and Engineering, Massachusetts Institute of Technology, 77 Massachusetts Avenue, Cambridge, MA 02139, USA. E-mail: byildiz@mit.edu
First published on 19th November 2018
Abstract
The present work quantifies the equilibrium defect and adsorbate chemistry on oxide surfaces in the presence of multiple gas components at elevated temperatures and sub-surface space charge. The concentrations of chemisorbed H2O and CO2 as well as surface protons and oxygen vacancies were calculated for Y-doped BaZrO3 using a thermodynamic framework with input from first-principles calculations. The overall energy of the system was minimized based on contributions from gas adsorption, interactions between defects and adsorbates, segregation of point defects and space-charge formation, as well as configurational entropy. The coverage dependent adsorption energies were found as −1.44 + 0.34ΘH2O eV and −2.25 + 1.21ΘCO2 eV for chemisorption of H2O and CO2, respectively. The interaction between the adsorbates was found to follow 1.72ΘH2OΘCO2 eV. The coverage of surface protons was above 0.3 up to 1000 K under most considered conditions (0.01–1 bar H2O, 4 × 10−4–1 bar CO2) due to a favorable interaction with both surface hydroxide and CO2 adsorbates. Most importantly, the results show that the coadsorption, adsorbate interactions or space-charge formation each played a major role in the obtained defect concentrations and surface coverages. Thus, the approach in this work demonstrates the importance of considering quantitatively each of these aspects in obtaining accurately the surface equilibria on complex catalytic oxides.
1. Introduction
Perovskite oxides based on barium zirconate are applicable as proton conducting ceramic electrolytes for intermediate temperature fuel cells,1–4 electrolysis cells5,6 and electrochemical catalytic membrane reactors for steam-methane reforming7 and dehydrogenation processes.8,9 Most of these devices operate at temperatures from about 350 to 800 °C in H2O and CO2 containing atmospheres and the equilibrium surface chemistry can be expected to be significantly affected by the operating environment.10,11 It is therefore of importance to understand quantitatively how the surface composition and defect chemistry may influence the properties of the oxide surface for catalytic activity, chemical stability and coke resistance. For instance, Huang et al. recently demonstrated significantly enhanced CO2 and H2O exchange kinetics on oxide ion conducting perovskites and fluorites, as well as enhanced oxygen exchange rates in the presence of H2O or CO2 in addition to O2 on electronically conducting Sr-doped LaMnO3.12,13 Duan et al.14 recently reported excellent performance and durability of BaZrO3-based protonic ceramic fuel cells with a range of hydrocarbon fuels and a steam-to-carbon ratio of 2.5![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1 at 500–600 °C.
1 at 500–600 °C.
As a proton conducting oxide, Y-doped BaZrO3 (BZY) readily dissolves protons from water vapor by hydration of oxygen vacancies.15 Both the BaO and ZrO2 terminations of the preferred (0 0 1) surface exhibit strong affinity for H2O, and dissociative adsorption predominates according to computational studies.16,17 The hydroxide and protonic species remain at the surface at higher temperatures than in the bulk due to a more exothermic adsorption enthalpy compared to the bulk hydration enthalpy. Furthermore, these charged surface species,  and
and 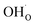 respectively in Kröger–Vink notation,18 are central in the formation of space-charge layers at the surface.19,20 In this respect, protons have been found to be particularly stable at the surface leading to a positive surface charge that is charge compensated by hydroxide adsorbates and a subsurface space-charge region.
respectively in Kröger–Vink notation,18 are central in the formation of space-charge layers at the surface.19,20 In this respect, protons have been found to be particularly stable at the surface leading to a positive surface charge that is charge compensated by hydroxide adsorbates and a subsurface space-charge region.
Adsorption of CO2 has recently been shown to be particularly exothermic for the (0 0 1) surfaces by chemisorption of carbonate species, CO32−.21 The calculated surface coverage as functions of temperature and pCO2 showed that a full carbonate overlayer was stable under ambient 400 ppm CO2 up to 400 K and that significant coverage could be retained up to 2000 K under 1 bar CO2. While the overall chemical stability of bulk BaZrO3 towards CO2 has been demonstrated,21,22 recent studies have shown surface reactivity with CO2 to form BaCO3 by accommodating Ba-deficiency in the subsurface region.23
Considering the strong adsorption of both H2O and CO2, interactions between the adsorbed species must be taken into account in order to appropriately describe the equilibrium surface coverages. Furthermore, the defect chemistry of the surface and subsurface must also be accounted for since all surface species – including neutral and charged adsorbates and point defects – interact and compete for the same surface sites. Accordingly, the gas adsorption equilibria will be influenced by the surface defect chemistry, and conversely the subsurface defect chemistry, or the space-charge region, will be affected by the adsorbates.
In the present work, we utilize first-principles calculations to investigate the concentration of adsorbates and defects on the BaO-terminated (0 0 1) surface of BZY under H2O and CO2 containing atmospheres. A thermodynamic model comprising gas adsorption equilibria, segregation of point defects and formation of a subsurface space-charge layer was implemented. As a result, surface coverages and subsurface space-charge behavior were obtained as a function of environmental variables. The individual contributions to the overall energy minimization of the system have been discussed in order to understand the interplay between gas adsorption equilibria and surface defect chemistry.
2. Computational approach
The DFT calculations were performed using VASP with the PBE generalized gradient approximation functional and projector-augmented wave pseudopotentials.24–26 The plane-wave cut-off energy was 500 eV and the k-point sampling was equivalent to 8 × 8 × 8 for the cubic BaZrO3 unit cell. BaO-terminated (0 0 1) surfaces were constructed as symmetric 11-layer slabs. Adsorbates were considered at coverages of 0.11, 0.25, 0.5 and 1.0 with 2 × 2 and 3 × 3 expanded slabs (up to 243 atoms), and coadsorbate interaction was evaluated for equal coverages of 0.25 and 0.5 on 2 × 2 slabs, i.e., half and full coverage, respectively. Y-acceptors were not explicitly included in the computational cells since the surface was BaO-terminated and any interactions between adsorbates and subsurface Y-dopants can be expected to be minor compared to interactions between adsorbates or between adsorbates and point defects. The adsorption thermodynamics were evaluated based on the adsorption energy, configurational entropy and vibrational properties of the adsorbates obtained by the finite displacement method. The adsorption energy, ΔEadsi, was calculated as the total energy differences of the adsorption reactions. The equilibrium constant of the adsorption reactions was given by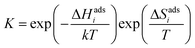 | (1) |
The computed adsorption energies and segregation energies were fed into a thermodynamic framework to obtain the equilibrium concentrations of all adsorbates and defects by minimizing the total energy of the system.28 Effects of defect interaction and formation of subsurface space-charge layers were taken into account.
The energy of the adsorption layer can be separated into the energy of H2O adsorbates, CO2 adsorbates and an interaction term. The energy of the H2O/CO2 adsorption layer without inter-adsorbate interactions was calculated by
| Eadsi = Θi(ΔHadsi − TΔSadsi − Δμi) | (2) |
![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) ln(p/p0) is the chemical potential of the gas phase at varying partial pressure, and the coverage, Θi, represents the number of adsorbed molecules. The interaction between adsorbed H2O and CO2 was obtained from the difference in adsorption energy of the coadsorbates and the individual adsorbates (see Table 2), and described as
ln(p/p0) is the chemical potential of the gas phase at varying partial pressure, and the coverage, Θi, represents the number of adsorbed molecules. The interaction between adsorbed H2O and CO2 was obtained from the difference in adsorption energy of the coadsorbates and the individual adsorbates (see Table 2), and described as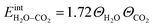 | (3) |
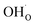 and
and 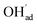 , respectively. For charged surfaces, the concentration of excess surface protons segregated from bulk was defined as
, respectively. For charged surfaces, the concentration of excess surface protons segregated from bulk was defined as 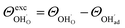 when
when 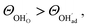 and zero otherwise. The
and zero otherwise. The 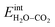 interaction energy was then described as
interaction energy was then described as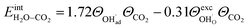 | (4) |
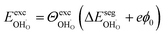 | (5) |
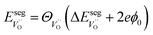 | (6) |
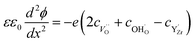 | (7) |
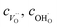 and
and 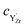 denote the subsurface concentrations of oxygen vacancies, protons and Y-dopants, respectively.
denote the subsurface concentrations of oxygen vacancies, protons and Y-dopants, respectively. 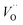 and
and 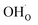 were treated as mobile species that can redistribute within the space-charge region at distance x from the surface according to
were treated as mobile species that can redistribute within the space-charge region at distance x from the surface according to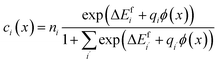 | (8) |
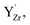 were considered immobile with a fixed concentration of 0.2. The total energy of the space-charge layer was represented as
were considered immobile with a fixed concentration of 0.2. The total energy of the space-charge layer was represented as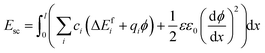 | (9) |
 and
and 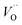
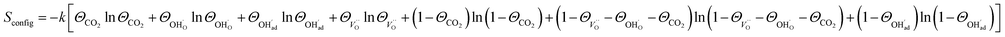 | (10) |
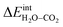 according to eqn (3) showed R2 = 0.999
according to eqn (3) showed R2 = 0.999
| H2O | CO2 | |
|---|---|---|
| ΔEads/eV | −1.44 + 0.34 ΘH2O | −2.25 + 1.21 ΘCO2 |
| ΔZPE/eV | 0.091 | 0.117 |
| ΔSads/eV K−1 | −6.37 × 10−4 | −8.78 × 10−4 |
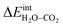 /eV /eV |
1.72 ΘH2OΘCO2 | |
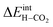 /eV /eV |
−0.31 eV (ref. 21) | |
| Adsorption site | Ba + O | O |
The above set of equations form a thermodynamic framework describing the total energy of the system, including the adsorption layer, segregation layer and subsurface space-charge layer. The system was solved for each environmental condition (temperature and partial pressures) by variation of ϕ0 to minimize the total energy of the system, and thus obtain the equilibrium concentrations of surface defects and adsorbates, 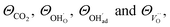 the surface potential ϕ0, as well as the subsurface concentration profiles in a self-consistent way. The constraint for the energy minimization was the global charge neutrality condition
the surface potential ϕ0, as well as the subsurface concentration profiles in a self-consistent way. The constraint for the energy minimization was the global charge neutrality condition
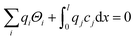 | (11) |
3. Results
Fig. 1 shows relaxed structures of dissociatively adsorbed H2O on the BaO-terminated BaZrO3 (0 0 1) surface at coverages from 0.11 to 1 monolayer. The H2O adsorbate was found to be most stable with surface hydroxide, denoted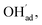 bridged between two barium, and surface protons,
bridged between two barium, and surface protons,  directed towards the oxide ion of
directed towards the oxide ion of  (Fig. 1a). The lowest energy configurations consisted of evenly spaced adsorbates at half coverage (Fig. 1b) and alternating rows with different symmetry at full coverage (Fig. 1c).
(Fig. 1a). The lowest energy configurations consisted of evenly spaced adsorbates at half coverage (Fig. 1b) and alternating rows with different symmetry at full coverage (Fig. 1c).
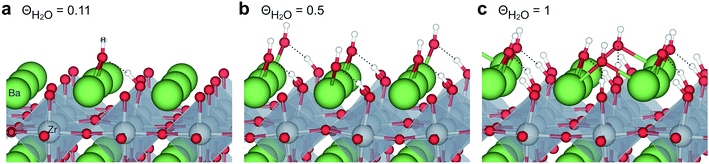 | ||
| Fig. 1 Dissociatively adsorbed H2O at coverages of (a) 0.11, (b) 0.5 and (c) 1 monolayer of the surface oxide ion sites on BaZrO3 (0 0 1). | ||
The interaction between H2O and CO2 adsorbates was evaluated for total surface coverages of 0.5 and 1. With respect to structural interactions, no significant changes were observed due to coadsorption of H2O and CO2 in the case of half coverage (Fig. 2a). On the other hand, a molecular H2O adsorbate formed by association between  and
and 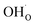 on the fully covered surface as shown in Fig. 2b.
on the fully covered surface as shown in Fig. 2b.
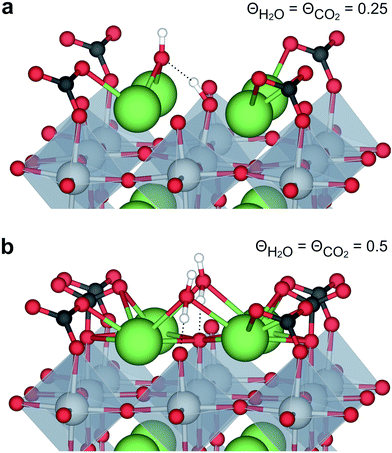 | ||
| Fig. 2 Coadsorption of H2O and CO2 on BaZrO3 (0 0 1) at total coverages of (a) 0.5 and (b) 1 monolayer. | ||
The energetics of H2O and CO2 adsorption that comprise the main input from the first-principles calculations to the thermodynamic model are summarized in Table 2. The adsorption energy of H2O ranged from −1.4 to −1.1 eV for coverages of 0.11 to 1, respectively. These values are similar albeit somewhat less exothermic than previously reported values of −1.5 to −1.3 eV for half and full coverage, respectively.16 Calculations for the ZrO2-terminated surface exhibited similar energies for dissociative adsorption of H2O in range of −1.1 to −1.4 eV.17,20 The adsorption energy of CO2 was more exothermic than that of H2O at low coverage, −2.20 eV at ΘCO2 = 0.06. However, stronger adsorbate interactions resulted in a slightly lower adsorption energy for CO2 than for H2O at full coverage.21 The zero-point energy contribution to the adsorption enthalpy was quite small for both H2O and CO2, which can be ascribed to the rather similar bond relationships for the adsorbed species and gaseous molecules.
The interaction energy between the coadsorbates, 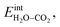 was found to be quite similar to the average interaction energy of the individual adsorbates from the coverage dependent adsorption enthalpies. For instance, the average increase in interaction energy from half to full coverage was 0.39 eV for adsorption of H2O or CO2, and 0.43 eV in the case of coadsorption. It should be noted that the stabilizing interaction between CO2,ad and
was found to be quite similar to the average interaction energy of the individual adsorbates from the coverage dependent adsorption enthalpies. For instance, the average increase in interaction energy from half to full coverage was 0.39 eV for adsorption of H2O or CO2, and 0.43 eV in the case of coadsorption. It should be noted that the stabilizing interaction between CO2,ad and  only refers to excess
only refers to excess 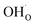 since the interaction between
since the interaction between 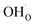 and
and 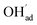 is included in the H2O adsorption energy.
is included in the H2O adsorption energy.
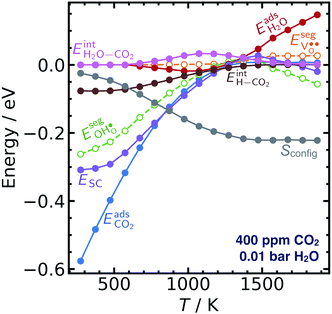
Fig. 3 shows the contributions to the overall energy of the BaZr0.8Y0.2O3 system at equilibrium coverages as a function of temperature at ambient conditions, i.e., 0.01 bar H2O and 400 ppm CO2. The strong adsorption enthalpy of CO2 predominates the stabilization of the system at temperatures below 800 K. Formation of the space-charge layer – driven mainly by the segregation of protons – also exhibits a significant contribution in this temperature range. Notably, the adsorption of H2O is almost negligible despite the strongly exothermic adsorption of H2O (see Table 2). This can be understood from the comparatively large interaction energy between H2O and CO2, 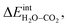 combined with the favorable coupling between CO2,ad and
combined with the favorable coupling between CO2,ad and 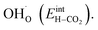 The configurational entropy plays an increasingly important role as temperature increases due to the lower coverage and larger number of configurations of the surface species.
The configurational entropy plays an increasingly important role as temperature increases due to the lower coverage and larger number of configurations of the surface species.
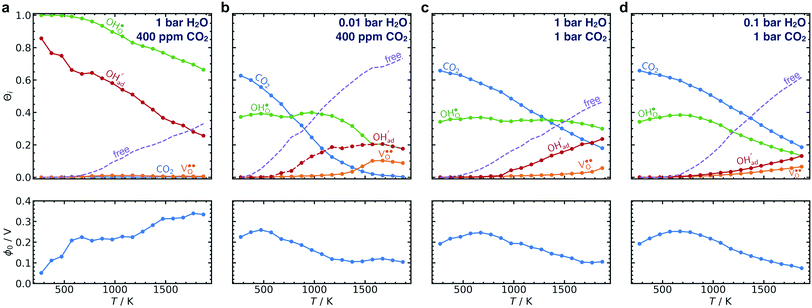
The calculated equilibrium coverages of adsorbates and defects are shown as a function of temperature in Fig. 4 including a subsurface space-charge with a corresponding potential. Under 1 bar H2O and 400 ppm CO2, the surface is predominated by protons partly charge compensated by hydroxide, i.e., dissociatively adsorbed H2O and excess 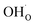 segregated from the bulk (Fig. 4a). The surface attains a positive charge over the whole temperature range with a potential of up to about 0.3 V mainly due to excess
segregated from the bulk (Fig. 4a). The surface attains a positive charge over the whole temperature range with a potential of up to about 0.3 V mainly due to excess 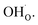 The surface remained free of CO2,ad despite the strong adsorption enthalpy of CO2 due to the unfavorable
The surface remained free of CO2,ad despite the strong adsorption enthalpy of CO2 due to the unfavorable 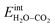 interaction term (Table 2). This behavior is shown graphically in contour maps of the contributions to the energy of the charge-neutral system spanning the complete ranges of ΘH2O and ΘCO2 in Fig. S1 (ESI, Section 2†).
interaction term (Table 2). This behavior is shown graphically in contour maps of the contributions to the energy of the charge-neutral system spanning the complete ranges of ΘH2O and ΘCO2 in Fig. S1 (ESI, Section 2†).
By reducing the H2O pressure to 0.01 bar, ΘCO2 predominates up to 800 K and remains significant to even higher temperatures (Fig. 4b). Protons become the predominant surface species above 800 K, but the coverage of 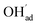 is considerably lower which leads to a surface potential of up to 0.26 V at 500 K. At equal H2O and CO2 pressures of 1 bar, the surface is predominated by carbonate species up to about 1300 K (Fig. 4c). Fig. 4d shows a similar trend with 0.1 bar H2O where CO2,ad remains the predominant species over the whole temperature range.
is considerably lower which leads to a surface potential of up to 0.26 V at 500 K. At equal H2O and CO2 pressures of 1 bar, the surface is predominated by carbonate species up to about 1300 K (Fig. 4c). Fig. 4d shows a similar trend with 0.1 bar H2O where CO2,ad remains the predominant species over the whole temperature range.
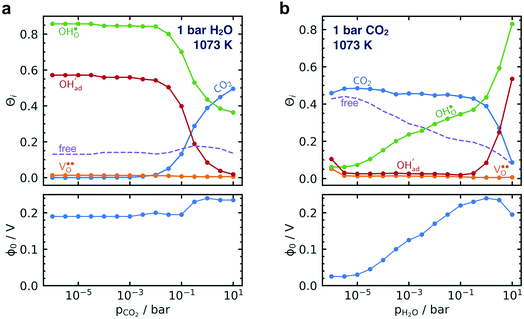
Fig. 5 shows coverage isotherms at 1073 K as function of pH2O and pCO2 under 1 bar CO2 and H2O, respectively. Under these conditions, the coverage of CO2 is negligible below 0.01 bar CO2 (Fig. 5a). From Fig. 5b it becomes apparent that the space-charge potential to a large extent follows the segregation of 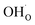 with a significant contribution above 1 × 10−5 bar H2O at this temperature. The potential increases with pH2O up to a pressure of 1 bar where
with a significant contribution above 1 × 10−5 bar H2O at this temperature. The potential increases with pH2O up to a pressure of 1 bar where 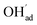 increasingly charge compensates the surface protons. Notably, the coverage of
increasingly charge compensates the surface protons. Notably, the coverage of 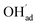 exhibits an inverse relationship with that of CO2 as the coverage of
exhibits an inverse relationship with that of CO2 as the coverage of 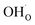 surpasses ΘCO2 at around 0.5 bar H2O (Fig. 5b). This behavior can be explained by the unfavorable interaction between CO2 and
surpasses ΘCO2 at around 0.5 bar H2O (Fig. 5b). This behavior can be explained by the unfavorable interaction between CO2 and 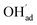 (Eq. (4)).
(Eq. (4)).
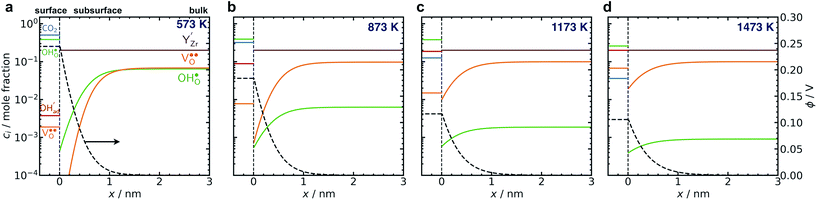
Fig. 6 shows the concerted changes of the surface concentrations and the subsurface space-charge regions under 0.01 bar H2O and 400 ppm CO2 at 573–1473 K. The depletion of protons and oxygen vacancies in the subsurface space-charge region becomes less prominent as the potential is reduced from 0.25 V (Figure 6a) to 0.11 V (Fig. 6d). While the bulk becomes increasingly dehydrated above 573 K, segregated surface protons predominate the surface even at 1473 K due to the favorable proton segregation energy (Table 1). It has previously been shown that inclusion of an Y-segregation profile may significantly affect the space-charge properties of BZY surfaces and interfaces.20,29 In the present case, equilibration of 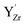 to the potential profile, i.e., Gouy-Chapman approximation, lead to a slight increase in the potential while the surface proton concentration increased significantly at 1073 K in 1 bar H2O and 1 bar CO2 (Fig. S2, ESI Section 3†).
to the potential profile, i.e., Gouy-Chapman approximation, lead to a slight increase in the potential while the surface proton concentration increased significantly at 1073 K in 1 bar H2O and 1 bar CO2 (Fig. S2, ESI Section 3†).
4. Discussion
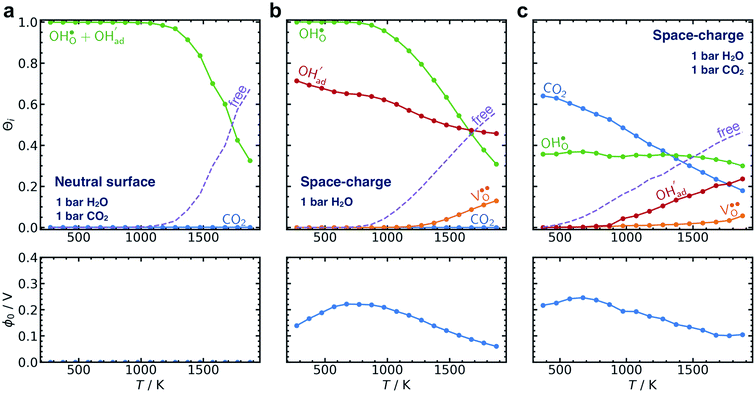
The present results show that interactions between coadsorbates, charged surface species and sub-surface space-charge formation can play a predominant role in the calculated surface coverages. The effect of not taking into account all aspects of the surface equilibria and space-charge formation is therefore evaluated next. Fig. 7 shows the calculated coverages at 1 bar H2O and 1 bar CO2 compared with coverages obtained without considering space-charge formation and without taking into account competitive adsorption of CO2. Without space-charge, the calculated surface coverage was dominated by chemisorbed H2O since excess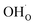 was not included in this model (Fig. 7a). On the other hand, in the absence of competitive CO2 coadsorption, the surface was saturated by
was not included in this model (Fig. 7a). On the other hand, in the absence of competitive CO2 coadsorption, the surface was saturated by 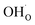 partly charge compensated by
partly charge compensated by 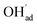 (Fig. 7b). It is clear that these shortcomings of not taking into account space-charge or coadsorption significantly affect the calculated surface coverages in comparison to the results obtained with the complete model in Fig. 7c. By only considering space-charge formation in the absence of H2O and CO2 adsorbates (while
(Fig. 7b). It is clear that these shortcomings of not taking into account space-charge or coadsorption significantly affect the calculated surface coverages in comparison to the results obtained with the complete model in Fig. 7c. By only considering space-charge formation in the absence of H2O and CO2 adsorbates (while 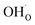 was allowed due to segregation from bulk), a surface potential of 0.68 V was obtained due to a
was allowed due to segregation from bulk), a surface potential of 0.68 V was obtained due to a 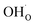 coverage of 0.66. Thus, it is clear that adsorption of uncharged gas species can also significantly affect the space-charge properties because of inter-adsorbate interactions and surface site limitations.
coverage of 0.66. Thus, it is clear that adsorption of uncharged gas species can also significantly affect the space-charge properties because of inter-adsorbate interactions and surface site limitations.
It was confirmed that the predominance of H2Oad over CO2,ad obtained in Fig. 4a and 7a did not occur when removing the interaction between H2Oad and CO2,ad, i.e., 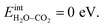 In this case, ΘH2O and ΘCO2 were similar as expected due to their comparable adsorption energetics as well as the increased configurational entropy associated with coadsorption. These coverages were similar to those obtained by Tutuianu et al. for the structurally equivalent BaO (0 0 1) surface without interactions between coadsorbates or surface defects.30 However, Kwon et al. obtained a low interaction energy between chemisorbed H2O and CO2 on BaO (0 0 1) even for a total coverage of 0.5.31 The apparent difference in
In this case, ΘH2O and ΘCO2 were similar as expected due to their comparable adsorption energetics as well as the increased configurational entropy associated with coadsorption. These coverages were similar to those obtained by Tutuianu et al. for the structurally equivalent BaO (0 0 1) surface without interactions between coadsorbates or surface defects.30 However, Kwon et al. obtained a low interaction energy between chemisorbed H2O and CO2 on BaO (0 0 1) even for a total coverage of 0.5.31 The apparent difference in 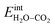 may be associated with a lower basicity of the BaO-terminated BaZrO3 surface due to the presence of zirconium, which reduces the capacity for charge transfer to the adsorbates upon chemisorption.31
may be associated with a lower basicity of the BaO-terminated BaZrO3 surface due to the presence of zirconium, which reduces the capacity for charge transfer to the adsorbates upon chemisorption.31
It is interesting to note that the calculated coverage of the 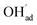 adsorbate increases with temperature under some conditions (e.g., Fig. 7c), which can seem counter intuitive due to the negative entropy of adsorption. Such behavior of
adsorbate increases with temperature under some conditions (e.g., Fig. 7c), which can seem counter intuitive due to the negative entropy of adsorption. Such behavior of 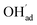 has been predicted previously for BZY surfaces based on an increasingly positive space-charge potential at higher temperatures which thereby stabilized the negatively charged adsorbate.20 However, the calculated space-charge potential becomes less positive at higher temperatures in the present work, and the increased
has been predicted previously for BZY surfaces based on an increasingly positive space-charge potential at higher temperatures which thereby stabilized the negatively charged adsorbate.20 However, the calculated space-charge potential becomes less positive at higher temperatures in the present work, and the increased 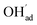 coverage may instead be associated with the rather strong adsorbate interactions which become lower as ΘCO2 decreases.
coverage may instead be associated with the rather strong adsorbate interactions which become lower as ΘCO2 decreases.
In terms of the functional properties of Y-doped BaZrO3 as a proton conducting electrolyte, the present result show that the surface exhibits a high coverage of protons in the form of 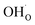 under all the considered conditions. The presence of H2O prevents the formation of a carbonate overlayer which is assumed to be detrimental to both performance and stability.21,23 Similar results were recently obtained for SrO-terminated SrTiO3 based on DFT calculations and in situ FTIR analysis, although a relatively less exothermic chemisorption of CO2 led to generally lower coverages of CO2.32 The favorable interaction between surface
under all the considered conditions. The presence of H2O prevents the formation of a carbonate overlayer which is assumed to be detrimental to both performance and stability.21,23 Similar results were recently obtained for SrO-terminated SrTiO3 based on DFT calculations and in situ FTIR analysis, although a relatively less exothermic chemisorption of CO2 led to generally lower coverages of CO2.32 The favorable interaction between surface 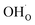 and
and 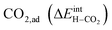 implies that there will be relatively large concentrations of protons available for incorporation into the electrolyte also in carbonate rich areas of the surface. The strong coadsorption may also correspond to an increased stability of the Y-doped BaZrO3 surface with respect to formation of Ba(OH)2 and BaCO3, as well as coke deposition.14
implies that there will be relatively large concentrations of protons available for incorporation into the electrolyte also in carbonate rich areas of the surface. The strong coadsorption may also correspond to an increased stability of the Y-doped BaZrO3 surface with respect to formation of Ba(OH)2 and BaCO3, as well as coke deposition.14
5. Conclusion
The present work demonstrates quantitatively the crucial role of adsorbate interactions and space-charge formation simultaneously in determining the equilibrium surface chemistry of oxides in the presence of multiple gas components. Despite the favorable H2O chemisorption on Y-doped BaZrO3, the calculated H2O coverage was quite low due to the more exothermic CO2 chemisorption and unfavorable interaction between H2O and CO2 adsorbates. However, the coverage of surface protons was found to be considerable up to 1500 K under most conditions due to a favorable interaction with both hydroxide and CO2 adsorbates. The calculated coverages were found to be significantly affected by the interactions between surface species, in particular between surface protons and CO2. Competitive adsorption and space-charge formation were also determined to play major roles in the obtained coverages and concentration of defects.Conflicts of interest
There are no conflicts to declare.Acknowledgements
The Research Council of Norway is acknowledged for financial support through the FOXCET project (Nano2021, 228355), and the Norwegian CCS research centre (NCCS, 257579). Computational resources were provided through the NOTUR under the project nn9259k. J. Y. and B. Y. thank for support from the Consortium for Advanced Simulation of Light Water Reactors (CASL), an Energy Innovation Hub for Modeling and Simulation of Nuclear Reactors under U.S. Department of Energy Contract No. DE-AC05-00OR22725.References
- K. D. Kreuer, S. Adams, W. Münch, A. Fuchs, U. Klock and J. Maier, Proton Conducting Alkaline Earth Zirconates and Titanates for High Drain Electrochemical Applications, Solid State Ionics, 2001, 145(1–4), 295–306 CrossRef CAS.
- Y. Yamazaki, R. Hernandez-Sanchez and S. M. Haile, High Total Proton Conductivity in Large-Grained Yttrium-Doped Barium Zirconate, Chem. Mater., 2009, 21(13), 2755–2762 CrossRef CAS.
- C. Duan, J. Tong, M. Shang, S. Nikodemski, M. Sanders, S. Ricote, A. Almansoori and R. O'Hayre, Readily Processed Protonic Ceramic Fuel Cells with High Performance at Low Temperatures, Science, 2015, 349(6254), 1321–1326 CrossRef CAS PubMed.
- S. Choi, C. J. Kucharczyk, Y. Liang, X. Zhang, I. Takeuchi, H.-I. Ji and S. M. Haile, Exceptional Power Density and Stability at Intermediate Temperatures in Protonic Ceramic Fuel Cells, Nat. Energy, 2018, 3, 202–210 CrossRef CAS.
- L. Bi, S. P. Shafi and E. Traversa, Y-Doped BaZrO3 as a Chemically Stable Electrolyte for Proton-Conducting Solid Oxide Electrolysis Cells (SOECs), J. Mater. Chem. A, 2015, 3, 5815–5819 RSC.
- R. Strandbakke, E. Vøllestad, S. A. Robinson, M.-L. Fontaine and T. Norby, Ba0.5Gd0.8La0.7Co2O6-δ Infiltrated in Porous BaZr0.7Ce0.2Y0.1O3 Backbones as Electrode Material for Proton Ceramic Electrolytes, J. Electrochem. Soc., 2017, 164(4), F196–F202 CrossRef CAS.
- H. Malerød-Fjeld, D. Clark, I. Yuste-Tirados, R. Zanón, D. Catalán-Martinez, D. Beeaff, S. H. Morejudo, P. K. Vestre, T. Norby, R. Haugsrud, J. M. Serra and C. Kjølseth, Thermo-electrochemical production of compressed hydrogen from methane with near-zero energy loss, Nat. Energy, 2017, 2, 923–931 CrossRef.
- S. Hamakawa, T. Hibino and H. Iwahara, Electrochemical Methane Coupling Using Protonic Conductors, J. Electrochem. Soc., 1993, 140(2), 459–462 CrossRef CAS.
- S. H. Morejudo, R. Zanon, S. Escolastico, I. Yuste-Tirados, H. Malerød-Fjeld, P. K. Vestre, W. G. Coors, A. Martinez, T. Norby and J. M. Serra, et al., Direct Conversion of Methane to Aromatics in a Catalytic Co-Ionic Membrane Reactor, Science, 2016, 353(6299), 563–566 CrossRef CAS PubMed.
- Z. A. Feng, C. Balaji Gopal, X. Ye, Z. Guan, B. Jeong, E. Crumlin and W. C. Chueh, Origin of Overpotential-Dependent Surface Dipole at CeO2-x/Gas Interface during Electrochemical Oxygen Insertion Reactions, Chem. Mater., 2016, 28(17), 6233–6242 CrossRef CAS.
- A. K. Opitz, A. Nenning, C. Rameshan, M. Kubicek, T. Götsch, R. Blume, M. Hävecker, A. Knop-Gericke, G. Rupprechter and B. Klötzer, et al., The Surface Chemistry of Perovskite-Type Electrodes during High Temperature CO2 Electrolysis Investigated by Operando Photoelectron Spectroscopy, ACS Appl. Mater. Interfaces, 2017, 9(41), 35847–35860 CrossRef CAS PubMed.
- Y.-L. Huang, C. Pellegrinelli, A. Geller, S.-C. Liou, A. Jarry, L. Wang, Y. Yu, H. Bluhm, E. J. Crumlin and K. J. Gaskell, et al., Direct Observation of Enhanced Water and Carbon Dioxide Reactivity on Multivalent Metal Oxides and Their Composites, Energy Environ. Sci., 2017, 919–923 RSC.
- Y.-L. Huang, C. Pellegrinelli and E. D. Wachsman, Oxygen Dissociation Kinetics of Concurrent Heterogeneous Reactions on Metal Oxides, ACS Catal., 2017, 7(9), 5766–5772 CrossRef CAS.
- C. Duan, R. J. Kee, H. Zhu, C. Karakaya, Y. Chen, S. Ricote, A. Jarry, E. J. Crumlin, D. Hook and R. Braun, et al., Highly Durable, Coking and Sulfur Tolerant, Fuel-Flexible Protonic Ceramic Fuel Cells, Nature, 2018, 557(7704), 217–222 CrossRef CAS PubMed.
- K. D. Kreuer, Aspects of the Formation and Mobility of Protonic Charge Carriers and the Stability of Perovskite-Type Oxides, Solid State Ionics, 1999, 125(1), 285–302 CrossRef CAS.
- A. V. Bandura, R. A. Evarestov and D. D. Kuruch, Hybrid HF–DFT Modeling of Monolayer Water Adsorption on (001) Surface of Cubic BaHfO3 and BaZrO3 Crystals, Surf. Sci., 2010, 604(19–20), 1591–1597 CrossRef CAS.
- R. A. Evarestov and A. V. Bandura, LCAO Calculation of Water Adsorption on (001) Surface of Y-Doped BaZrO3, Solid State Ionics, 2011, 188(1), 25–30 CrossRef CAS.
- F. A. Kröger and H. J. Vink, Relations between the Concentrations of Imperfections in Crystalline Solids, Solid State Phys., 1956, 3(C), 307–435 Search PubMed.
- J.-S. Kim, J.-H. Yang, B.-K. Kim and Y.-C. Kim, Proton Conduction at BaO-Terminated (001) BaZrO3 Surface Using Density Functional Theory, Solid State Ionics, 2015, 275, 19–22 CrossRef CAS.
- J. M. Polfus, T. S. Bjørheim, T. Norby and R. Bredesen, Surface Defect Chemistry of Y-Substituted and Hydrated BaZrO3 with Subsurface Space-Charge Regions, J. Mater. Chem. A, 2016, 4, 7437–7444 RSC.
- J. M. Polfus, B. Yildiz, H. L. Tuller and R. Bredesen, Adsorption of CO2 and Facile Carbonate Formation on BaZrO3 Surfaces, J. Phys. Chem. C, 2018, 122(1), 307–314 CrossRef CAS.
- K. H. Ryu and S. M. Haile, Chemical Stability and Proton Conductivity of Doped BaCeO3-BaZrO3 Solid Solutions, Solid State Ionics, 1999, 125(1), 355–367 CrossRef CAS.
- R. Sažinas, C. Bernuy-López, M.-A. Einarsrud and T. Grande, Effect of CO2 Exposure on the Chemical Stability and Mechanical Properties of BaZrO3-Ceramics, J. Am. Ceram. Soc., 2016, 99(11), 3685–3695 CrossRef.
- P. E. Blöchl, Projector Augmented-Wave Method, Phys. Rev. B: Condens. Matter Mater. Phys., 1994, 50(24), 17953–17979 CrossRef.
- J. Perdew, K. Burke and M. Ernzerhof, Generalized Gradient Approximation Made Simple, Phys. Rev. Lett., 1996, 77(18), 3865–3868 CrossRef CAS PubMed.
- G. Kresse and D. Joubert, From Ultrasoft Pseudopotentials to the Projector Augmented-Wave Method, Phys. Rev. B: Condens. Matter Mater. Phys., 1999, 59(3), 1758–1775 CrossRef CAS.
- S. Ricote, N. Bonanos, A. Manerbino, N. P. Sullivan and W. G. Coors, Effects of the Fabrication Process on the Grain-Boundary Resistance in BaZr0.9Y0.1O3-δ, J. Mater. Chem. A, 2014, 2(38), 16107–16115 RSC.
- D. S. A. Mebane, Variational Approach to Surface Cation Segregation in Mixed Conducting Perovskites, Comput. Mater. Sci., 2014, 103, 231–236 CrossRef.
- J. M. Polfus, T. Norby and R. Bredesen, Proton Segregation and Space-Charge at the BaZrO3 (0 0 1)/MgO (0 0 1) Heterointerface, Solid State Ionics, 2016, 297, 77–81 CrossRef CAS.
- M. Tutuianu, O. R. Inderwildi, W. G. Bessler and J. Warnatz, Competitive Adsorption of NO, NO2, CO2, and H2O on BaO(100): A Quantum Chemical Study, J. Phys. Chem. B, 2006, 110(35), 17484–17492 CrossRef CAS PubMed.
- S.-C. Kwon, W.-R. Lee, H.-N. Lee, J.-H. Kim and H.-L. Lee, Competitive Adsorption of CO2 and H2O Molecules on the BaO (100) Surface: A First-Principle Study, Bull. Korean Chem. Soc., 2011, 32(3), 988–992 CrossRef CAS.
- A. Staykov, S. Fukumori, K. Yoshizawa, K. Sato, T. Ishihara and J. Kilner, Interaction of SrO-Terminated SrTiO3 Surface with Oxygen, Carbon Dioxide, and Water, J. Mater. Chem. A, 2018, 6, 22662–22672 RSC.
Footnotes |
| † Electronic supplementary information (ESI) available. See DOI: 10.1039/c8ta09491h |
| ‡ Equally contributing authors. |
| This journal is © The Royal Society of Chemistry 2018 |