Design and performance analyses of solar arrays towards a metric of energy value†
Adrian B.
Boivin
,
Timothy M.
Westgate
and
Jonathan F.
Holzman
*
School of Engineering, University of British Columbia, Kelowna, British Columbia V1V 1V7, Canada. E-mail: jonathan.holzman@ubc.ca
First published on 17th July 2018
Abstract
In this work, the contemporary approach of analyzing and optimizing solar technology according to conversion efficiency is expanded upon to recognize an emerging paradigm for supply and demand of solar power. The analyses and optimizations are carried out with respect to energy value density, in units of dollars per metre-squared, rather than simple energy density, in units of watt hours per metre-squared, given an emerging trend in electricity prices that has become known as the duck curve. Such an approach is motivated by economic factors, in areas such as California, where dynamic solar power generation leads to high supply during mid-day hours, when the demand is low, and low supply during early- and late-day hours, when the demand is high. With this in mind, the metric of energy value density is analyzed for three silicon-based solar arrays: the flat-panel array, as an established benchmark, the V-groove array, as an array with enhanced conversion efficiency, and the U-groove array, as a newly-proposed array with strong performance for energy value density. Experimental characterizations and theoretical analyses are shown for the arrays' energy value density over July 2012 to June 2018. It is shown that the U-groove array yields the greatest performance in terms of energy value density – and the extent of its outperformance is growing. Over the last year of the study, the U-groove array generated 0.36% more value than the V-groove array and 8.76% more value than the flat-panel array. The prospects for such findings to the solar industry are discussed.
Introduction
The diminished output of solar generation systems during hours of peak demand is a fundamental challenge for contemporary electrical utilities. The challenge arises during morning and evening hours, when there is increased demand for electrical power and little solar-generated power. This challenge has been exacerbated by the growing reliance on solar generation systems1 and the fact that solar generation systems are not easily complemented by traditional steam-turbine-based power plants, since such plants cannot be quickly ramped up or down throughout the day.2 In California, for example, within which there is a great deal of solar-generated power, a trend has emerged in electricity prices. The trend shows high prices during the morning and evening hours, when there is low supply and high demand for solar-generated power, and it shows low (and even negative) prices during the day, when there is high supply and low demand for solar-generated power. The trend is of growing concern and has become known as the duck curve, given the shape of the electrical price curve over the course of the day.3While the underlying cause of the duck curve is relatively clear—in that the low-supply and high-demand hours during the morning and evening are not in sync with the high-supply and low-demand hours during the day—its resolution has remained elusive. As one response, researchers have developed various forms of solar tracking systems, as reviewed by Lee et al.4 and Mousazadeh et al.5 The systems use mechanical motion to yield enhanced solar power generation for both the (low-supply and high-demand) hours during the morning and evening and the (high-supply and low-demand) hours during the day. However, such systems also have high installation and operational costs, in comparison to their static counterparts,6 and this has limited their widespread use. As a second response, researchers have developed various solar materials to improve the efficiency of solar power generation, as reviewed by Bett et al.7 However, such systems have traditionally been constrained by high material costs, in comparison to that of standard silicon solar cells. For this reason, 90% of production capacity in 2015 involved standard silicon solar cells.8 Moreover, such systems provide an overall increase in efficiency, rather than tailoring their improved performance to achieve high supply during the high-demand hours. They must therefore meet the heightened needs for electrical power during the low-supply and high-demand hours of the morning and evening via energy storage, typically with batteries, and in doing so a great deal of power is lost due to poor conversion efficiencies.9 As a third response, researchers have developed a variety of engineered solar structures to improve the efficiency of solar power generation. Engineered solar structures are advantageous in that they can incorporate standard silicon solar cells and thereby utilize existing manufacturing facilities, which is an important concern given the high capital costs of photovoltaic manufacturing.10 Noteworthy examples include the V-groove array11,12 put forward by Li et al.13 and the Solar Tower put forward by Bernardi et al.14 These structures have been optimized for conversion efficiency alone, however, and such optimizations neglect their reliance upon energy storage to supply electrical power during the low-supply and high-demand hours of the morning and evening. While the increased ability of corrugated arrays to capture low-angle light has previously been noted,12,15 it is not known if any of the existing engineered solar structures provide strong performance for solar power generation during these critical hours – or if any new forms of engineered solar structures can be realized towards such a goal.
In this work, the contemporary approach of optimizing engineered solar structures according to conversion efficiency is expanded upon to recognize the emerging supply-versus-demand paradigm for solar power generation. Experimental characterizations and theoretical analyses are carried out to optimize solar structures according to a metric of energy value density, which considers both the quantity and time for solar power generation. In general, solar power that is generated during low-supply and high-demand hours, at higher electricity prices, is given greater energy value in comparison to solar power that is generated during high-supply and low-demand hours, at lower electricity prices. The energy value density serves as a metric for evaluating both the revenue generated by the arrays, as economic performance, and the effectiveness of the arrays in offsetting the emerging duck curve trend, as a greater benefit to the public.
The structures take the form of three solar arrays: the standard flat-panel array, as an established benchmark; the V-groove array, as an existing structure yielding enhanced conversion efficiency; and a newly-proposed U-groove array, as an array exhibiting strong performance for the metric of energy value density due to its greater generation during low-supply and high-demand hours. The following sections introduce the solar arrays, describe their characterizations and analyses, and present the results. A discussion and concluding remarks on the future impact of these findings are then given.
The solar arrays
The energy value density that is used in this work must be carefully defined as a metric for the three solar arrays. Such definitions are given in this section. Descriptions of the analyzed solar arrays themselves are subsequently given.The energy value density is defined by summing the product of time-varying electricity price, in units of United States (US) dollars per watt hour, and generated electrical power density, in units of watts per metre-squared, over the course of a day or year to yield the daily energy value density and yearly energy value density, respectively.
The first factor for energy value density, being the time-varying electricity price, depends upon the location being studied. For this work, the state of California is selected for the location, given its heavy reliance on solar power generation and its growing concern for the duck curve. The day-ahead locational marginal pricing is used for the pricing data, having been obtained from the California Independent System Operator's Open Access Same-Time Information System (OASIS).16 The electricity prices were collected from OASIS for locations across California at one hour intervals for a period of six years starting July 1, 2012, and then averaged over all locations, while treating negative prices as zero. The average was then time-interpolated with the hourly prices taken as the midpoint of each hour to establish a net electricity price for California at two-minute intervals.
The second factor for energy value density, being the time-varying generated electrical power density for a given solar array, is the generated electrical power per unit area. The generated electrical power is defined in this work by experimental characterizations of a typical square silicon solar cell, having a side-length of a = 78 mm, and the application of these characterizations to an analytical model of the solar arrays. The motivation for this tandem experimental-theoretical approach is twofold. First, it becomes possible to characterize the performance of arrays with a wide range of geometries and illumination conditions. Second, it becomes possible to characterize the performance of arrays in terms of their captured, incident, and reflected optical powers – with knowledge of contributions from internal reflections. Such knowledge cannot be gained when the electrical output power alone is measured. The generated electrical power density is defined as a density with respect to the installation area because the generated electrical powers of the arrays scale in proportion to this area.
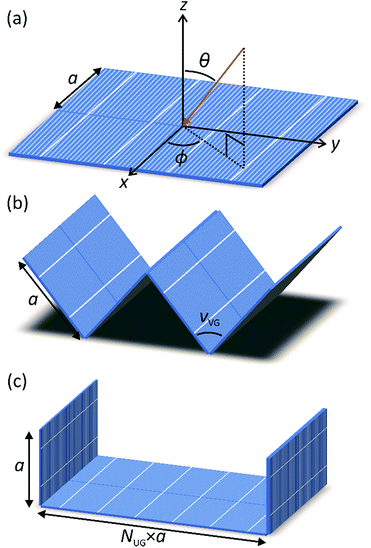
The generated electrical power density is calculated for the changing illumination conditions over the course of a day. The incident sunlight is defined in terms of an azimuth angle with respect to south, ϕ, and a zenith angle, θ, as shown in Fig. 1a on a Cartesian coordinate system. The coordinate system has its x-direction aligned with south, its y-direction aligned with east, and its z-direction aligned vertically, upwards. The solar irradiance is defined by a magnitude of I0 and an incident ray (unit) vector of (α, β, γ). The directional cosines within the ray vector are linked to the azimuth and zenith angles by
α = cos![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) ϕ ϕ![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) sin sin![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) θ, θ, | (1) |
β = sin![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) ϕ ϕ![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) sin sin![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) θ, θ, | (2) |
γ = cos![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) θ. θ. | (3) |
Given these definitions, the generated electrical power density can be analyzed for varying illumination conditions of the three solar arrays described here.
The flat-panel array
The flat-panel array, shown in Fig. 1a, is the typical arrangement of solar cells, and it is used here as a benchmark. It is a planar array of solar cells, each with a side-length of a. The flat-panel array lies within the horizontal plane with its surface normal directed up. While other orientations are possible for this array, for example, by implementing it with staggered solar panels angled towards the mid-day sun, the proposed orientation is studied because it avoids inter-solar-cell shadowing and the reduced coverage of staggered solar panels.17 Results for south-facing orientations would be similar, however, since the angular reflectance is nearly constant across all but the steepest angles of incidence (for an ideal silicon solar cell with 5% normal reflectance, the reflectance is below 10% until the angle of incidence between the solar irradiance and surface normal goes beyond 60°).The V-groove array
The V-groove array, while not commonly used, has been studied extensively. The array, shown in Fig. 1b, is a corrugated structure that is made up of discrete numbers of silicon solar cells with a side-length of a arranged into V-shaped grooves. For this study, the grooves run parallel to the north–south direction. The key design parameter for the V-groove array is the V-angle, νVG, being the internal angle between the sides of the grooves. Several V-angles, varying from νVG = 15° to νVG = 120°, are analyzed to facilitate a fair comparison of this array to the other arrays and identify the optimal V-angle according to the metric of energy value density.The U-groove array
The U-groove array, shown in Fig. 1c, consists of a planar array of solar cells, on top of which run vertical walls of double-sided solar cells. Such a structure forms U-shaped grooves. The walls run parallel to the north–south direction, as this preferentially allows for trapping of low-angled light that illuminates the walls of the array early and late in the day via internal reflections. The key design parameter for the U-groove array is the aspect ratio, NUG. It is the ratio of the spacing between the walls to the height of the walls. For this study, with discrete numbers of solar cells having a side-length of a, the height of the walls is set at a, and the separation between the walls is varied over integer multiples of a. This restriction on the height of the walls to the side-length of one solar cell reduces the design complexity and wasted space of a support structure. Aspect ratios of NUG = 1, 2, 3, and 4 are used in the analysis to compare varying forms of this array to the other arrays and identify the effects of this ratio on the metric of energy value density.Characterizations and analyses
This study applies experimental characterizations, to identify the key parameters of the solar cells used within the three solar arrays, and an analytical model of the three arrays, to define their performance. The experimental characterizations and analytical model are presented in this section.The reflectance is the first parameter to be defined for the solar cells – although its generalized understanding presents a challenge. Notably, the surfaces of commercial solar cells often have textured active areas that yield varying levels of diffuse and specular reflection.18 Thus, it is difficult to generalize the reflective response of a typical solar cell. However, solar cells are often covered by a protective layer of glass or epoxy that creates a specular reflection.19 As such, it is assumed in this work that the reflective properties of the solar cell are defined by specular reflection off the protective layer and negligible reflection from the underlying textured surface. With this in mind, the reflectance of a solar cell with a protective layer of tempered glass was measured with a 650 nm laser beam at normal incidence. It was found to be 3.96%. The reflectance is applied to the analytical model by defining an effective refractive index of neff = (10 + (3.96)1/2)/(10 − (3.96)1/2) ≈ 1.497, which represents a typical refractive index value for glass, and a corresponding angular-dependent reflectance for unpolarized light of
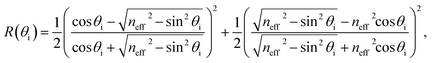 | (4) |
The short-circuit current density is the second parameter that must be defined for the solar cells. It was defined for a monocrystalline solar cell with a side-length of a = 78 mm. The short-circuit current was measured for varying levels of incident irradiance. The linear relationship between the short-circuit current density and incident irradiance was established and used to define the short-circuit current density for standard test conditions, i.e., with 1000 W m−2 incident irradiance.20 This gave a short-circuit current density of Jsc = 203.5 A m−2, for standard test conditions, which is comparable to values seen in the literature.21
The saturation current density is the third and final parameter that must be defined for the solar cells within the three solar arrays. It was found by measuring the short-circuit current and open-circuit voltage of the (above) solar cells, for repeated measurements with differing levels of incident irradiance, and using these values within the ideal diode equation.22 This gave a saturation current density of Jsat = 8 × 10−9 A m−2, which is typical of values in the literature.21
The above solar cell parameters are used in an analytical model of the flat-panel, V-groove, and U-groove arrays with certain assumptions for their physical and electrical characteristics. In terms of physical characteristics, it is assumed that the arrays are sufficiently large in size to have negligible effects from the ends of the arrays. In terms of electrical characteristics, it is assumed that the solar cells are connected through blocking diodes and a single Maximum Power Point Tracking (MPPT) unit to the load. The MPPT unit carries out impedance matching between the solar cells and load to maximize the transfer of electrical power.23 The use of a single MPPT unit for each array is a subtle – but potentially important – point for the arrays. This is because the individual solar cells within the V-groove and U-groove arrays will often capture differing levels of optical power throughout the course of a day. This can yield differing impedances and varying levels of success in matching the impedances of the solar cells to the single load.
The analytical model defines the time-varying captured optical power density and generated electrical power density for the three solar arrays and uses these results to define the accumulated (daily and yearly) energy value densities. For each array, under the illumination conditions for a given time interval, the model is used to compute the captured optical power density for each solar cell in an array as the net power that is not reflected divided by its area, i.e., the solar cell's silicon area. The model is then used to compute the generated electrical power density for each array as the net generated electrical power normalized with respect to the installation area. The product of the electricity price and generated electrical power density is then computed and summed over the course of the day and year to produce the accumulated daily energy value density and yearly energy value density, respectively. The array-specific details for the implementation of the analytical model are summarized in the remainder of this section, with further information given in the ESI.†
The captured optical power density of each solar cell in the flat-panel array is easily computed. It is simply the product of the magnitude of the uniform irradiance I0 and the directional cosine γ.
The captured optical power density of each solar cell in the V-groove array is found by an iterative process. The process makes use of a single structural unit, called a V-cell, which consists of two opposing solar cells. The V-cell is uniformly illuminated by the irradiance of I0 along the unit vector (α, β, γ). For each of the two solar cells within the V-cell, the directional cosines within the unit vector are used to compute three quantities: the angle of incidence, θi, the area of illumination, and the (total) incident optical power. These quantities are then used to calculate the reflected optical power and captured optical power, for each of the two solar cells within the V-cell, using the angle of incidence, θi, within the reflectance expression in eqn (4). The angle of reflection, area of illumination, and reflected optical power for each solar cell are then used to project a reflection onto the solar cells on the opposing side of the groove. This leads to reflected illumination within the same V-cell as well as neighbouring V-cells. These calculations are performed in multiple iterations to characterize the cascading reflections of optical power through the V-shaped groove, and they continue until the cascading reflections exhibit negligible optical power. Note that the alignment of the V-groove array along the x-axis has this process be independent of the directional cosine α, aside from its use in calculating the reflectance. This is because any reflected optical power exiting a V-cell in the x-direction is matched by an identical amount of reflected optical power entering the opposing side of that V-cell. Ultimately, the total captured optical power on each solar cell in the V-cell is extracted and normalized with respect to the silicon area to define the captured optical power densities.
The captured optical power density of each solar cell in the U-groove array is found through a similar iterative process, although its implementation depends upon whether the illumination is steep enough to directly illuminate the solar cells on the bottom of the groove. For the case in which the illumination is not this steep, calculations similar to those used for the V-groove array are employed to find the captured optical power densities. The fact that the sides are parallel simplifies such calculations, given that the angle of incidence becomes constant. However, the additional reflection off the bottom of the U-groove array creates an extra step in the process that must be accounted for, because it allows a small amount of optical power to be captured by one or more of the solar cells on the bottom. For the case in which the illumination is steep enough to directly illuminate the solar cells on the bottom of the groove it becomes necessary to consider two subcases. The first subcase applies when |γ/β| > 2/NUG. Here, the bottom and one wall of the groove both receive direct illumination and reflections from each other, while the opposing wall receives no illumination. The second subcase applies when 2/NUG > |γ/β| > 1/NUG. This subcase is similar to the previous one, but it differs in that the case with less steep illumination causes light to be reflected onto the shadowed wall of the U-groove array. With these subcases, it is possible to form tractable (non-iterative) solutions for the captured optical power densities of the U-groove array.
Once the captured optical power density of each solar cell has been calculated, it can be converted into an electrical power using a single MPPT unit. The current from each solar cell is approximated by the ideal diode equation22 as
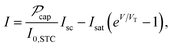 | (5) |
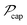 is the captured optical power density of the solar cell, I0,STC = 1000 W m−2 is the incident irradiance for standard test conditions, Isc = Jsca2 and Isat = Jsata2 are the short-circuit and saturation currents calculated from the respective experimentally-determined current densities, V is the array voltage, and VT = 25.7 mV is the thermal voltage of the diode junction. To implement an MPPT unit with each array, the product IV is summed across its solar cells and normalized with respect to the array's installation area. The derivative of this result is then taken with respect to the voltage and set to zero to define the voltage that yields maximal transfer of electrical power to the load. The MPPT unit establishes operation at this maximal condition, and the resulting electrical power defines the generated electrical power density for each solar array.
is the captured optical power density of the solar cell, I0,STC = 1000 W m−2 is the incident irradiance for standard test conditions, Isc = Jsca2 and Isat = Jsata2 are the short-circuit and saturation currents calculated from the respective experimentally-determined current densities, V is the array voltage, and VT = 25.7 mV is the thermal voltage of the diode junction. To implement an MPPT unit with each array, the product IV is summed across its solar cells and normalized with respect to the array's installation area. The derivative of this result is then taken with respect to the voltage and set to zero to define the voltage that yields maximal transfer of electrical power to the load. The MPPT unit establishes operation at this maximal condition, and the resulting electrical power defines the generated electrical power density for each solar array.
Note that eqn (5) does not necessarily produce a positive current. If the captured optical power density is sufficiently small, the reverse current due to diode losses will exceed the light-generated forward current and the solar cell will drain power from the system. This is highly undesirable in practical applications – particularly since this condition can damage the solar cells. To combat this, many systems use blocking diodes to prevent reverse current flow.24 This is implemented in the analytical model by making the current produced by each solar cell equal to the maximum of eqn (5) and zero, which turns the system power density into a piecewise function. Such diodes are assumed to be ideal in the analytical model, since typical systems use several solar cells in series with a single diode, and this limits the effect of any voltage drops.
Results
In order to determine the relative effectiveness of the three solar arrays, the generated electrical power density and accumulated energy value density for the different arrays are calculated first for a single day with a prominent duck curve, and then over the course of several years in order to determine overarching trends and evaluate the performance of each array. As mentioned previously, several variations of the V-groove array and U-groove array were initially tested and compared according to the metric of yearly energy value density over the year of July 2016–June 2017. The optimal variations were found to be the 80° V-groove array and the 3![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1 U-groove array, which gave yearly energy value densities of 5.4978 $ per m2 per year and 5.5152 $ per m2 per year, respectively. It is these variations that are used for the ensuing analyses.
1 U-groove array, which gave yearly energy value densities of 5.4978 $ per m2 per year and 5.5152 $ per m2 per year, respectively. It is these variations that are used for the ensuing analyses.
The single-day analysis is carried out for a date with a significant duck curve characteristic and a location that is representative of the entire state of California. The selected date is the spring equinox, being March 20, 2017. This is because March exhibits dramatic variations in electricity price over the course of a day and thus a strong susceptibility to the duck curve. The selected location has a latitude and longitude of 37° north, 120° west. This location, which is near to Fresno, California, has its latitude and longitude bisect the state of California, and eliminates the offset between apparent solar time and local standard time due to longitude.
Fig. 2 shows the average electricity price in US dollars across California as a function of the time of day on March 20, 2017. The characteristic low mid-day price and high early- and late-day prices of the duck curve can clearly be seen.
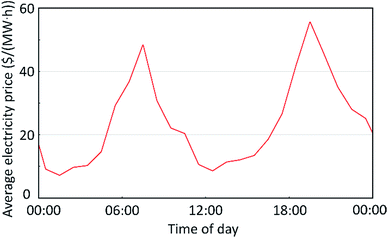 | ||
| Fig. 2 Average electricity price in US dollars per megawatt hour across the state of California as a function of time on March 20, 2017. | ||
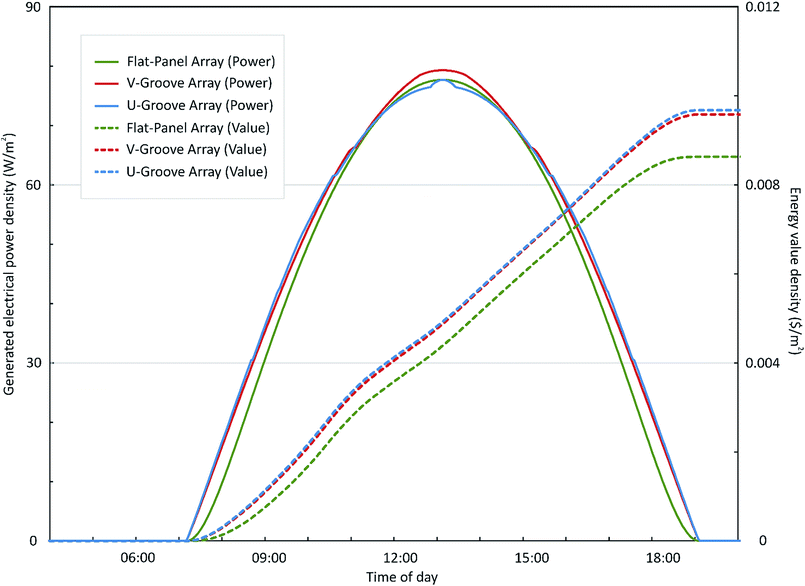
Fig. 3 shows the generated electrical power density as a function of the time of day for the three solar arrays, at the prescribed date (March 20, 2017) and location (37° north, 120° west). Results for the flat-panel array, the V-groove array with νVG = 80°, and the U-groove array with NUG = 3 are plotted as solid curves against the left axis in green, red, and blue, respectively. The curves share a similar (bell) shape that is due to the varying capture cross-section of the arrays as the sun follows its trajectory over the course of the day. However, some differing characteristics can be observed. Notably, the V-groove array obtains the highest generated electrical power densities at mid-day hours, while the U-groove array obtains the highest generated electrical power densities during early- and late-day hours. The superiority of the V-groove array at mid-day hours is because of its angled solar cells, which let this array (and only this array) capture reflections when the sun is to the south, with small azimuth angles. The superiority of the U-groove array at early- and late-day hours is because of its vertical solar cells, which let this array (and the V-groove array to a lesser extent) capture reflections when the sun is to the east and west, with large zenith angles. Fig. 3 also shows the energy value density being accumulated as a function of the time of day for the solar arrays, at the prescribed date (March 20, 2017) and location (37° north, 120° west). Results for the flat-panel array, the V-groove array with νVG = 80°, and the U-groove array with NUG = 3 are plotted as dashed curves against the right axis in green, red, and blue, respectively. The curves approach asymptotic values at the end of the day, which define the daily energy value densities for the three arrays. It is apparent here that the U-groove array and V-groove array outperform the flat-panel array.
At the end of the day, the U-groove array and V-groove array have daily energy value densities of $0.00968 per m2 per day and $0.00958 per m2 per day, respectively, while the flat-panel array has a daily energy value density of $0.00863 per m2 per day. This is due to the U-groove and V-groove arrays' greater ability to capture incident optical power at the early- and late-day hours when the electricity price is high. Overall, the U-groove array exhibits the highest daily energy value density.
It is important to note that the above findings, and the improved performance levels of the U-groove array, manifest themselves during the spring, and to a lesser extent during the fall and winter, when the duck curve is the strongest. However, the majority of solar power is generated during the summer, when the mid-day electricity price is high due to the use of air conditioning. This would enhance the performance of the V-groove array. Thus, for fair comparison, it is necessary to compare the solar arrays over the span of a year. Such a process is carried out here, with the results collected over a period of six years. This extended data collection period is used to accommodate the growing prominence of the duck curve and identify relevant trends (if any).
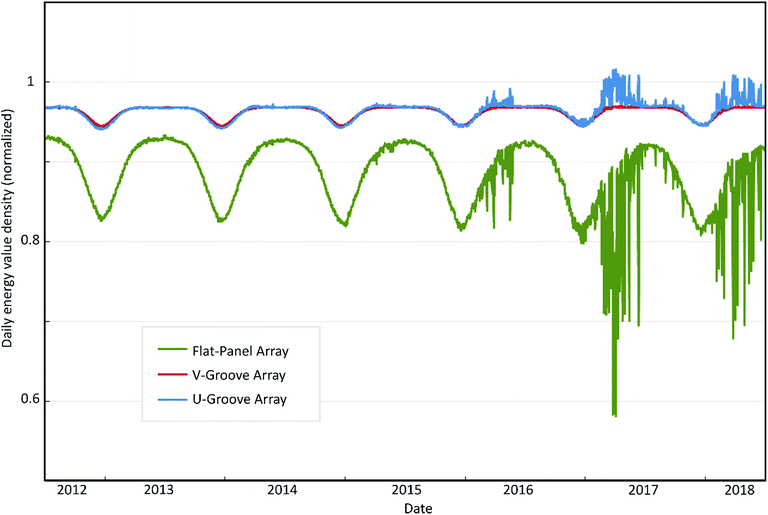
Fig. 4 shows the normalized daily energy value density as a function of the date, spanning July 2012 to June 2018, for each solar array, at the prescribed location (37° north, 120° west). The curves for the flat-panel array, the V-groove array with νVG = 80°, and the U-groove array with NUG = 3 are shown in green, red, and blue, respectively. The results are normalized to compare performance levels and identify trends. The normalization is carried out with respect to results for an idealized flat-panel array having a reflectance of zero. This idealized array is an effective baseline for comparison, but it should not be presumed to be a “perfect” structure. It does not necessarily yield the maximum generated electrical power density. This is because the diode losses are proportional to the silicon area that is not disconnected by the blocking diodes. As such, there can be situations in which the non-flat arrays absorb slightly less power than the idealized flat-panel array but do so while experiencing far lower losses. This can have the non-flat arrays yield greater generated electrical powers than the idealized flat-panel array.
Three key characteristics are evident in Fig. 4. First, the daily energy value density has a cyclical nature with a one-year period and stronger performance during the summer months. The reason for such a characteristic is self-evident. Second, the daily energy value density during the spring, and to a lesser extent the winter and fall, exhibits increasingly strong fluctuations. Such fluctuations come about from the duck curve, which manifests itself as dramatic changes in electricity prices over the course of a day according to the supply and demand of solar-generated power. Third, the duck curve yields its strongest effects on the performance of the flat-panel array, which exhibits deep decreases in the normalized daily energy value density over 2016 (to a small extent), and 2017 and 2018 (to a greater extent). The V-groove array does not exhibit such fluctuations. In stark contrast, the U-groove array exhibits increases in the normalized daily energy value density over 2016 (to a small extent), and 2017 and 2018 (to a greater extent). Such a result manifests itself here because all of the arrays experience the negative effects of the duck curve on the energy value density, including the idealized flat-panel array that is used for normalization, but the U-groove array is able to minimize such effects and thereby maximize the energy value density.
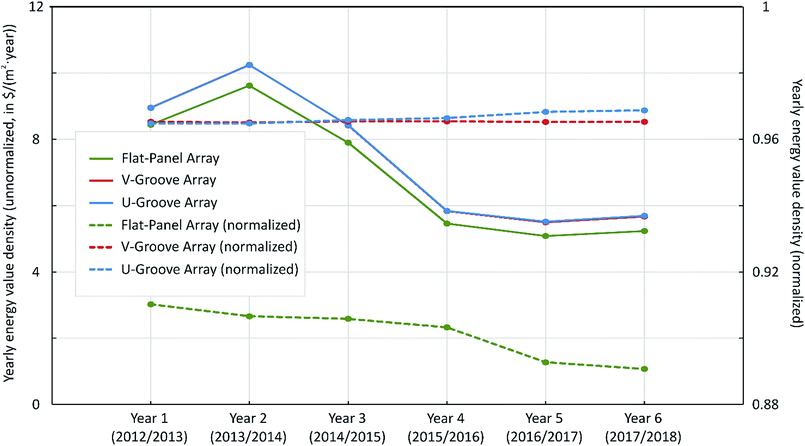
The evolving influence of the duck curve can be quantified for the solar arrays by summing their daily energy value densities over the course of a year to produce a yearly energy value density. The yearly energy value density is shown in Fig. 5 as a function of the year, spanning July 2012 to June 2018, for each of the solar arrays at the prescribed location (37° north, 120° west). Curves for the flat-panel array, the V-groove array with νVG = 80°, and the U-groove array with NUG = 3 are shown in green, red, and blue, respectively. The solid curves, plotted against the left-axis, correspond to unnormalized yearly energy value densities. The dashed curves, plotted against the right-axis, correspond to normalized yearly energy value densities, with respect to the idealized flat-panel array having a reflectance of zero. The unnormalized results in the figure all show a downward trend in the yearly energy value densities for all three arrays over the six-year period. The similar downward trends are due to the resemblance of the generated electrical power density curves in Fig. 3, which show that all three arrays generate most of their power in the mid-day hours, and the increasing influence of the duck curve, which leads to lower electricity prices during those mid-day hours. The influence of the duck curve differs for the three arrays, however, and such differences are best seen following normalization. The normalized results in the figure show that the V-groove array and U-groove array far outperform the flat-panel array and the levels at which they outperform the flat-panel array are increasing. It is also clear that the V-groove array and U-groove array yielded similar performance in the past, but the U-groove array shows improved performance over that of the V-groove array in the latter three years. This is due to its greater capability in capturing optical power during early- and late-day hours, when the electricity prices are high, in tandem with the growing influence of the duck curve. It is likely that the U-groove array will far outperform the other arrays in the future.
Discussion
The results of this study show strong support for the U-groove array in mitigating the effects of the duck curve, but there are several practical points that need to be discussed with respect to the underlying assumptions and the related findings.The first point of discussion relates to the day-ahead locational marginal prices that are used to calculate the value densities generated by the solar arrays. The day-ahead locational marginal prices reflect the value of electricity as estimated a day in advance. However, the actual prices at which electricity is sold can depend upon a Power Purchase Agreement between the owners of the solar installation and the electric utility to which it is connected. Such agreements in California typically use a Net Energy Metering system,25 with identical selling and buying prices. In general, the agreements can set the prices based upon a day-ahead marginal rate (like that used in this study), a time-of-use rate (which can vary), or a flat rate (as the most straightforward). For the time-of-use rate, a value-optimized solar array would still offer benefits like those seen in this study, but the level of gains would depend upon how closely the time-of-use prices match the day-ahead marginal prices. For the flat rate, a value-optimized solar array would also offer benefits, although such benefits would be passed on to the general public, as a lessening on effects of the duck curve, and the electric utility, which would obtain the economic gains of the value-optimized solar arrays. Clearly, a flat rate would reduce the motivation for owners to implement a value-optimized solar array.
The second point of discussion relates to the location of any proposed value-optimized solar arrays. In terms of the geographical location, external factors such as weather conditions, due to frequent overcast days, or accessibility to the grid should be considered. Such factors would impact the generated energy value density and were not factored into this study – given that it used an average of day-ahead marginal prices across the state of California. In terms of the installation location, it is important to consider the field of view of the value-optimized solar array. It should be installed in a location that offers a clear view to the horizon to enable its collection of low-angle and high-value light. Rooftops or open fields, with few buildings or trees, would meet this requirement. It is additionally important to note that this study's optimization of energy value density, with respect to the installation area, makes the findings more applicable to installations on rooftops in dense urban environments, with limited area, rather than open fields, for which the area is less restricted.
The third point of discussion relates to the practical issues of installing V-groove and U-groove arrays – given that such arrays would likely be installed on rooftops. The vertical dimension of these arrays could have wind loading become a concern,26 and so a robust support structure would be necessary. For the V-groove array, the design of the support structure is trivial because it, like existing angled solar panels, can use support structures beneath the arrays. For the U-groove array, the design is more challenging. This array benefits from having thin vertical walls, to maximize the active area of light collection, but such thin walls yield little support. Crossed struts could be used to enhance the support, but these struts would block some fraction of the incident light and reduce the effectiveness of the array. Ultimately, the best way to ensure effective support for the U-groove array is to leverage its ability to be scaled via proportional changes to the horizontal and vertical dimensions. Such scaling comes about because the functionality of the U-groove array is defined by its horizontal-to-vertical aspect ratio, NUG, rather than the absolute dimensions. In this study, the vertical walls' height was set by a single solar cell with a side-length of a = 78 mm. This minimized the absolute height of the array, which allowed it to have thin vertical walls with minimal susceptibility to wind loading. The array would then be scaled to fill the available installation area by tiling, while maintaining a constant height and aspect ratio. In general, U-groove arrays with greater vertical heights could still be used, but such arrays would need to consider the issues of increased wind loading.
The fourth point of discussion relates to a simplification made to the reflectance. As noted earlier, the analytical model characterized specular reflection off the surface of a protective coating and ignored diffuse reflections off the underlying silicon surface. This was done because texturing on this surface makes these diffuse reflections difficult to characterize. Thus, this work assumed that the effects of the diffuse reflections are insignificant. Such an assumption is supported by the literature, given that estimates for this reflectance have it be of a similar magnitude to the reflectance off the protective layer,27 and the fact that oblique reflection off the silicon layer would lead to a large portion of the power being re-captured via total internal reflection off the protective layer. However, additional research on the effects of diffuse reflection on the performance of the three solar arrays is warranted.
A fifth point of discussion relates to the selection of a flat solar array for comparisons. While the flat-panel array is a standard structure and an obvious point of comparison, it would be possible to have its solar cells be angled (typically westward). Such angled arrays were not considered here due to the complexity of optimizing both the design parameters and the large number of orientations of the arrays. However, it can be noted that these angled arrays would outperform the flat-panel array but they would be unlikely to exceed the performance of the U-groove array. This is because the angled arrays are incapable of collecting reflections and would thus suffer from reflection losses during the low-supply and high-demand hours of the morning and evening. The U-groove array experiences these losses to a much lesser extent.
As a sixth and final point, it is useful to note how the metric of energy value density relates to the capital investment (installation) costs and the greater benefits to the general public. With respect to the capital investment costs, it must be noted that the defined energy value density is linked to the solar-generated revenue and so it does not take into account capital installation costs. Thus, there is an implicit assumption here that the installation costs do not vary to a great extent with the area of the array, which would cause them to differ greatly between the different arrays investigated here. This assumption is valid more for smaller arrays, in sites with limited space, where the fixed costs of inverters and installation area outweigh the area-dependent cost of solar cells. Admittedly, the presented work could be revisited as an optimization of energy value density with respect to the active silicon area, rather than installation area. Such an optimization would maximize the solar-generated revenue while minimizing the active silicon area, and this would yield lower installation costs. These results would be valid more for larger arrays, whose installation costs vary to a great extent with the area of the array (if this economic evaluation with respect to the active silicon surface area were carried out for the arrays optimized in this work with respect to the installation area, we would see that the 3![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1 U-groove array, which yields 8.76% more revenue and has 66.67% more silicon than the flat-panel array, and the 80° V-groove array, which yields 8.37% more revenue and has 55.56% more silicon than the flat-panel array, would take longer to have their revenue recover their installation costs). With respect to the benefits to the greater public, it is clear that this work's focus on optimizing energy value density yields clear advantages. This is because it directly confronts the challenge of energy capture during low-supply and high-demand hours – by optimizing for improved matching between the generated electrical power and daily electricity price curves – and thus lessens the prominence of the duck curve.
1 U-groove array, which yields 8.76% more revenue and has 66.67% more silicon than the flat-panel array, and the 80° V-groove array, which yields 8.37% more revenue and has 55.56% more silicon than the flat-panel array, would take longer to have their revenue recover their installation costs). With respect to the benefits to the greater public, it is clear that this work's focus on optimizing energy value density yields clear advantages. This is because it directly confronts the challenge of energy capture during low-supply and high-demand hours – by optimizing for improved matching between the generated electrical power and daily electricity price curves – and thus lessens the prominence of the duck curve.
Conclusions
The presented work differed from contemporary analyses and optimizations of solar technology, which optimize mainly towards conversion efficiency. Instead, analyses and optimizations were carried out with respect to energy value density, to account for the dynamic electricity prices throughout the day according to the duck curve. The metric of energy value density was studied for a flat-panel array, as an established benchmark, a V-groove array, as an array with enhanced conversion efficiency, and a U-groove array, as a newly-proposed array with strong performance for energy value density. Experimental characterizations and theoretical analyses were used to compare the arrays' generated energy value density over a six-year period across the state of California. The U-groove array yielded the greatest performance in terms of energy value density, with the extent of its outperformance growing with each year. The last year of the study had the U-groove array generate 0.36% more value than the V-groove array and 8.76% more value than the flat-panel array. Such findings may become key considerations for deployments of solar infrastructure – given emerging trends in electricity prices and growing demands for solar technology.Conflicts of interest
There are no conflicts of interest to declare.Acknowledgements
This work was supported by the Natural Sciences and Engineering Research Council of Canada (RGPIN-2017-04073), and the Canada Foundation for Innovation (LOF 16659).References
- M. Obi and R. Bass, Renewable Sustainable Energy Rev., 2016, 58, 1082–1094 CrossRef.
- G. Hugg-Glanzmann, Bulk Power System Dynamics and Control-VIII, 2010 iREP Symposium, 2010, pp. 1–7 Search PubMed.
- P. Denholm, M. O'Connell, G. Brinkman and J. Jorgenson, Overgeneration from Solar Energy in California: A Field Guide to the Duck Chart, National Renewable Energy Laboratory, Golden CO, 2015 Search PubMed.
- C. Y. Lee, P. C. Chou, C. M. Chiang and C. F. Lin, Sensors, 2009, 9, 3875–3890 CrossRef PubMed.
- H. Mousazadeh, A. Keyhani, A. Javadi, H. Mobli, K. Abrinia and A. Sharifi, Renewable Sustainable Energy Rev., 2009, 13, 1800–1818 CrossRef.
- R. Eke and A. Senturk, Sol. Energy, 2012, 86, 2665–2672 CrossRef.
- A. W. Bett, S. P. Philipps, S. Essig, S. Heckelmann, R. Kellenbenz, V. Klinger, M. Niemeyer, D. Lackner and F. Dimroth, 28th European Photovoltaic Solar Energy Conference and Exhibition, 2013, pp. 1–6 Search PubMed.
- J. Jean, P. R. Brown, R. L. Jaffe, T. Buonassisi and V. Bulović, Energy Environ. Sci., 2015, 8, 1200–1219 RSC.
- H. Ibrahim, A. Ilinca and J. Perron, Renewable Sustainable Energy Rev., 2008, 12, 1221–1250 CrossRef.
- D. M. Powell, R. Fu, K. Horowitz, P. A. Basore, M. Woodhouse and T. Buonassisi, Energy Environ. Sci., 2015, 8, 3395–3408 RSC.
- S. Sista, Z. Hong, L. M. Chen and Y. Yang, Energy Environ. Sci., 2011, 4, 1606–1620 RSC.
- J. Yoon, K. Kang, S. Kim and J. Kim, Curr. Appl. Phys., 2015, 15, 446–451 CrossRef.
- J. Li, M. Chong, L. Yang, J. Xu, X. F. Duan, M. Gao, F. L. Wang, H. Liu, L. Bian, X. Chi and Y. Zhai, Sol. Energy Mater. Sol. Cells, 2005, 86, 585–591 CrossRef.
- M. Bernardi, N. Ferralis, J. H. Wan, R. Villalon and J. C. Grossman, Energy Environ. Sci., 2012, 5, 6880–6884 RSC.
- J. Kettle, N. Bristow, T. K. N. Sweet, N. Jenkins, G. A. dos Reis Benatto, M. Jørgensen and F. C. Krebs, Energy Environ. Sci., 2015, 8, 3266–3273 RSC.
- California ISO Open Access Same-Time Information System, http://oasis.caiso.com/mrioasis/logon.do, accessed July 2018.
- K. Brecl and M. Topič, Renewable Energy, 2011, 36, 3211–3216 CrossRef.
- C. H. Chang, P. Yu, M. H. Hsu, P. C. Tseng, W. L. Chang, W. C. Sun, W. C. Hsu, S. H. Hsu and Y. C. Chang, Nanotechnology, 2011, 22, 095201 CrossRef PubMed.
- K. S. Han, H. Lee, D. Kim and H. Lee, Sol. Energy Mater. Sol. Cells, 2009, 93, 1214–1217 CrossRef.
- J. F. Randall and J. Jacot, Renewable Energy, 2003, 28, 1851–1864 CrossRef.
- F. Meillaud, A. Shah, C. Droz, E. Vallat-Sauvain and C. Miazza, Sol. Energy Mater. Sol. Cells, 2006, 90, 2952–2959 CrossRef.
- S. A. Kalogiru, Solar Energy Engineering, Elsevier, Oxford, 2014 Search PubMed.
- R. Faranda, S. Leva and V. Maugeri, Power and Energy Society General Meeting – Conversion and Delivery of Electrical Energy in the 21st Century, 2008 IEEE, 2008, pp. 1–6 Search PubMed.
- F. Spertino and J. S. Akilimali, IEEE Xplore: IEEE Transactions on Industrial Electronics, 2009, 56, 4520–4531 Search PubMed.
- R. T. Beach and P. G. McGuire, Evaluating the Benefits and Costs of Net Energy Metering in California, Crossborder Energy, Berkeley CA, 2013 Search PubMed.
- G. A. Kopp, S. Farquhar and M. J. Morrison, Journal of Wind Engineering and Industrial Aerodynamics, 2012, 111, 40–52 CrossRef.
- D. H. Macdonald, A. Cuevas, M. J. Kerr, C. Samundsett, D. Ruby, S. Winderbaum and A. Leo, Sol. Energy, 2004, 76, 277–283 CrossRef.
Footnote |
| † Electronic supplementary information (ESI) available. See DOI: 10.1039/c8se00333e |
| This journal is © The Royal Society of Chemistry 2018 |