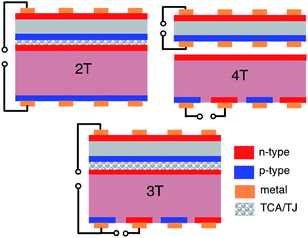
Maximizing tandem solar cell power extraction using a three-terminal design

Abstract

Tandem or multijunction solar cells can greatly increase the efficiency of solar energy conversion by absorbing different energies of the incident solar illumination in semiconductors with different band-gaps, which can operate more efficiently than a single absorber. Many different designs of tandem cells based on high efficiency top cells and Si bottom cells have been proposed, and there is ongoing debate as to whether the sub-cells should be wired in series (to create a tandem device with two terminals) or operated independently (four terminals). An alternative cell configuration that combines some of the strengths of both is a three-terminal device consisting of a top cell optically in series with a modified interdigitated back contact (IBC) Si cell featuring a conductive top contact. Such a configuration can enable improved energy yield while only requiring external wiring on the front and back of the solar cell stack. In this paper, we investigate the operation of three terminal tandems in detail using technology computer aided design (TCAD) device physics simulations. Using III–V top cells as an example case, we show how the addition of a third terminal can deliver comparable power output to a four terminal device, and substantially more power than a two-terminal device, while also enabling power injection and extraction between the two sub-circuits under a variety of spectral conditions.

---

1 Introduction

The field of high-efficiency photovoltaics is experiencing a resurgence of research in the area of hybrid tandem photovoltaics, where two or more dissimilar materials are combined into one device. These tandem cells split the incident solar spectrum into multiple bands, converting each band to electricity more efficiently than a single device alone.¹ Recent advances that have spawned renewed excitement include the development of III–V/Si hybrid tandems that significantly exceed the efficiency of silicon alone and the development of new wide band gap materials, including hybrid organic–inorganic halide perovskites, that may enable lower-cost thin-film tandem devices.^2–4 Most devices are based on a crystalline silicon bottom cell, since these cells are the industry standard and have a narrow band gap (1.1 eV) ideal for the bottom sub-cell of a tandem solar cell.

Tandem cells typically have either two or four terminals, depending on whether each solar cell is contacted individually or the two middle terminals are directly electrically connected to one another. Two-terminal (2T) tandem cells (Fig. 1, 2T), would provide a simple drop-in replacement for a single junction solar cell in a module, but if integrated at the cell level, they require current matching of the two sub-cells, which significantly constrains the choice of top cell materials. Typically, 2T tandem cells have been realized by monolithic/epitaxial growth or wafer bonding. Monolithic growth can be advantageous if high efficiency top cells are compatible with growth directly on Si. In this approach, the interface between the two cells requires a tunnel junction or transparent conductive layer with excellent vertical conductivity, but no lateral conductivity to extract current between cells. Four-terminal (4T) devices (as shown in Fig. 1, 4T), in contrast, can be wired together at the cell or module level and thus have considerably more flexibility in top cell choice and less sensitivity to spectral variations since current matching is not required.^5–7 At the module level they can be integrated as 4T modules, or voltage-matched to produce modules with two terminals.⁸ They also are compatible with textured Si bottom cells. However, 4T cells require intermediate grids or transparent conductive layers between the cells to transport the current laterally to the edge of the cells, increasing optical losses. The sub-cells must be processed separately, which is incompatible with monolithic growth but can enable integration of materials that have processing incompatibilities. So far, the highest efficiencies have been obtained using 4T devices, partially due to the variety of top cells that can be incorporated when the sub-cells do not need to be current matched.²

Fig. 1 Schematics comparing wiring and interconnections of tandem solar cells operated in 2T, 4T, and 3T mode. To enable direct comparison, all devices simulated were based on bottom Si cells with n-type IBC geometries with full-area conductive top contacts. 2T and 3T devices can be connected with a transparent conductive adhesive (TCA) or tunnel junction (TJ), while 4T devices require lateral conduction between the cells.

Here, we present a third option for hybrid tandem photovoltaics: a three-terminal (3T) cell based on an interdigitated back contact (IBC) silicon bottom cell with a conductive top connection to a wider bandgap top cell (Fig. 1, 3T). This monolithic tandem configuration combines the ease of fabrication of a 2T device (only requiring external wiring on the front and back of the solar cell stack) with the flexibility and performance of a 4T device (lower sensitivity to spectral variations, flexibility in choice of top-cell bandgap, compatible with textured Si bottom cells). A bottom cell with an IBC geometry and conductive front-surface-field contact enables the use of three terminals where two of the three are on the back of the cell, providing a platform for high efficiency 3T cells. Similar 3T devices have been proposed but not investigated in depth, nor experimentally verified.^9–12 For instance, Nagashima et al., proposed tandems based on combining a III–V top cell with an IBC–Ge or IBC–Si bottom cell so the two subcells share a common base,^9,12 while Adhyaksa et al. proposed a 3T tandem based on an IBC–Si cell with a “floating front emitter”.¹¹ Prior work by Gee et al.,¹³ and Schulte-Huxel,¹⁴ have demonstrated that it is possible to integrate generic 3T devices into modules without significant performance loss. While the prior modeling has shown there is potential for such a device to produce power, some of the previously proposed 3T tandem structures have never been simulated with device physics software capable of handling semiconductor devices with more than two contacts or the electrical connections between multiple devices, which raises questions about their practical feasibility. Here, we describe for the first time the full operation behavior of single junction 3T Si sub-cell, and the complete operating space of a 3T tandem device.

The 3T tandem concept presented here is fundamentally different from prior “middle contact” 3T approaches that have been fabricated and used as diagnostic tools to address specific cells in a multijunction stack.^15–18 It is also different from a recently proposed “heterojunction bipolar transistor” solar cell that relies on two ideal heterojunction devices to eliminate the need for a tunnel junction in a tandem device.¹⁹ In contrast, in a 3T-IBC device, the Si bottom cell itself has three unique terminals, and therefore cannot be simply described by existing equivalent circuit models. To fully understand the performance of such a 3T cell, we have used rigorous technology computer aided design (TCAD) device modeling to investigate the operating principles of a 3T solar cell both as an independently operated device, and integrated with a top cell. We show that the addition of the extra base contact enables the injection or extraction of excess current in the bottom cell that is present due to current mismatch. Our simulations agree with experimental measurements of 3T Si devices, and have helped with the development of a lumped equivalent circuit model (to be published) to describe 3T device behavior.²⁰ Although our 3T tandem geometry could be achieved by either mechanical integration or heteroepitaxial growth, all simulations presented here are based on experimentally fabricated devices^21,22 and realistic interconnection schemes between the cells based on transparent conductive adhesives (TCAs),^23,24 which enables simulations to be directly compared to experimental results. This will help guide the fabrication and optimization of 3T tandem cells and modules based on high efficiency top cells such as III–Vs or hybrid organic–inorganic halide perovskites.

2 Methods

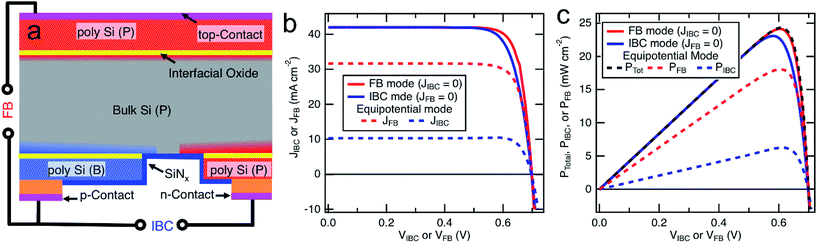
We have modeled a 3T device using a two dimensional TCAD software package (Sentaurus, Synopsis).²⁵ The Si cell was modeled using geometries and doping characteristics based on n-type carrier-selective polysilicon on oxide (POLO) devices fabricated at ISFH (Fig. 2a).^26,27 The cell has an n-type (phosphorus doped) base, with interdigitated back contacts consisting of interfacial SiO₂ layers coated with heavily doped poly-Si (boron or phosphorus doped). The entire front surface of the cell has an n-type poly-Si/SiO₂ passivated contact. A series resistance of 0.5 Ω cm² was used between the subcells, based on experimentally measured properties of a TCA consisting of Ag-coated microspheres embedded in ethylene-vinyl acetate (EVA).²³ A schematic of the simulated Si unit cell is shown in Fig. 2a, and additional details of the simulation parameters can be found in the ESI.†

Fig. 2 (a) Schematic of unit cell used for simulation of 3T Si device; (b, c) limiting J–V and P–V performance for a 3T Si device under unfiltered AM1.5G illumination: front-back (FB), interdigitated back contact (IBC), and equipotential (EP) modes of operation.

Optical generation profiles were calculated using a Monte Carlo ray tracing approach that accounts for coherent effects in thin films for a variety of input spectra generated with SMARTs.^28,29 Separate profiles were generated for Si cells without top cells and Si cells that operate below a 1 μm thick GaInP cell device stack including antireflective coatings, contact layers, and a TCA layer (see ESI† for details of the optical simulation).²¹ To accurately predict the performance of a realistic device, all physical models recommended in a recent review of numerical simulations of Si solar cells by Altermatt were incorporated into the simulation with the exception of Auger recombination, where the improved model proposed by Richter was implemented.^30,31 A two-terminal III–V top cell can be accurately described by a single diode model.³² In the case of a TCA-interconnected tandem device, the top cell influences the bottom cell optically by determining the incident illumination profile, and electrically by imposing a current matching condition as a series-connected circuit element. Thus, top cells were electronically simulated using a single diode model fit of experimental data, and optically simulated using experimentally determined layer thicknesses and optical properties. More details of the simulations of 2T and 4T tandems can be found in the ESI.†

3 Results and discussion

In the proposed 3T tandem device, the top cell design and operation are unchanged from a more conventional 2T or 4T tandem, as the cell still has two contacts and is simply connected in series with the top contact of the Si bottom cell. The Si cell has three unique contacts and thus has more complicated current–voltage (J–V) behavior than a typical 2T solar cell. We first investigate the performance of a 3T Si device without a top cell, so that the performance can be compared to standard Si devices. We then add a GaInP top cell and discuss the additional constraints this adds to the system.

3.1 Three terminal Si devices

The addition of a third conductive contact present in a 3T Si device adds an additional degree of freedom compared to a standard 2T solar cell, so the system cannot be fully described by one external voltage (i.e. a single J–V curve). The currents or voltages at two different contacts must be defined simultaneously to fully define the operation of the cell. We first look at the limiting cases of performance to validate our model with the known performance of 2T Si devices. When no current is collected from the top contact, the cell is effectively operating as an IBC cell, with all current collected between the p-emitter and back n-contacts (referred to as “IBC” mode). When no current is collected from the back n-contact, the cell effectively operates as a selective back-junction device (referred to as “front-back” or “FB” mode). Finally, another limiting case occurs when the back n- and top n-contact are at the same potential (referred to as “equipotential” or “EP” operation of the 3T Si device).

The simulated J–V and power–voltage (P–V) behavior of the 3T Si cell in each of the above limiting cases under AM1.5G illumination (no top III–V cell) is shown in Fig. 2b and c to enable comparison to the performance of a standard Si cell with 2 terminals. The 3T Si cell has nearly identical performance operating in either FB or IBC mode, similar to experimental measurements of an experimental 3T device (Fig. S2†).²⁰ The maximum simulated 1-sun efficiency of the device is 24.3%, in good agreement with the experimentally measured 25.0% efficiency for an IBC POLO device without a poly-Si layer at the front of the cell.²⁶ In the simulations, the only difference between the two modes is a slightly lower fill factor in the IBC case, which is likely due to lateral current transport, current crowding, or higher series resistance at the back n-contact, and could be optimized by changing the geometry or cell design at the rear side of the device.³³ In EP mode, a finite amount of current flows to each of the n-type contacts, creating two separate power producing circuits (dashed lines in Fig. 2b).

To compare all of the different operating states of the cell, it is more useful to plot the total power produced in the cell, by adding the power–voltage curves in each circuit, as the J–V curves in the two different circuits depend on different voltages. The full operation space of a 3T Si device was mapped by explicitly defining the potentials of all of the contacts and fully solving Poisson's equations over a wide range of values. Fig. 3a shows a contour plot of the total power of the system (P_FB + P_IBC) under standard illumination conditions in the region where the net power production of the cell is positive as a function of V_IBC (the potential difference between the back p-type emitter and the back n-contact) and V_FB (the potential difference between the back p-type emitter and the front n-contact).

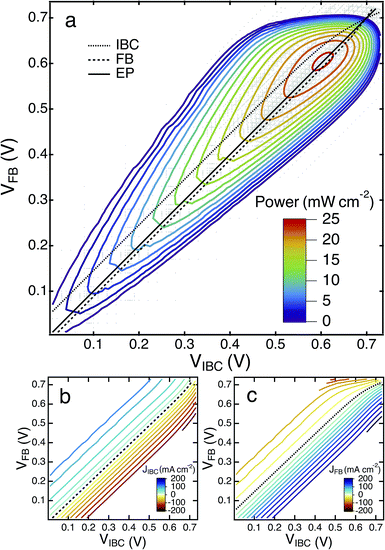Fig. 3 (a) Contour plot of total 3T Si power under AM1.5G illumination plotted vs. the voltages of each sub-circuit. (V_IBC is the potential difference between the back p-type emitter and the back n-contact and V_FB is the potential difference between the back p-type emitter and the front n-contact). The black lines correspond to the voltage behavior of each sub-circuit during the FB, IBC, or EP cases shown in Fig. 2, and gray dots represent each individual simulation used to construct the contours; (b, c) contour plots of the current densities through the IBC and FB circuits of the 3T Si device at all simulated values of V_FB and V_IBC (dashed lines show J = 0 mA cm⁻² contours).

For each of the limiting cases (FB, IBC, EP) discussed above, the voltages of each sub-circuit can be represented on the contour plot in Fig. 3a. Even when no current is passing through one of the n-type contacts, their potentials are inter-dependent. It can easily be seen that the highest overall cell performance is achieved for the EP case where the potentials of the front and back contacts are equal (i.e. V_FB = V_IBC). At any operating state where there is a potential difference between the two n-contacts (i.e. V_FB ≠ V_IBC), the overall cell performance decreases due to the excess current flow between the heavily doped contacts (poly-Si/SiO₂) through the wafer base. Since the contact and base resistivities are relatively low, even a small voltage difference between the two contacts leads to significant excess currents (see Fig. 3b and c) and thus to power dissipation within the cell. This takes place in all areas away from the equipotential mode line in Fig. 3a, and explains why the total efficiency for the two terminal modes of operation (FB, IBC) is lower than the EP case.

This ability to have reversible current flow at each n-contact has a very interesting application for tandem cell performance. In situations where the Si subcell has excess photocurrent relative to the top-cell, adding a third contact enables the extraction of excess photocurrent from the bottom cell. However, under certain conditions this contact can also be used to inject current into the device. In a situation where the bottom sub-cell in a tandem becomes current limiting, due to a narrower bandgap topcell or a temporary system fluctuation, it would be possible to stabilize the power output of the 2T tandem circuit by injecting current through the third terminal. This is shown in Fig. 3b and c, in the regions where the FB current is positive, but the IBC current is negative (the J = 0 line in each plot is indicated by a dotted line). Further work is needed to fully understand the implications of such an operating mode of a tandem device, but it presents a new opportunity on how to think about power extraction from tandem solar cells.

3.2 Three-terminal GaInP/Si tandem devices

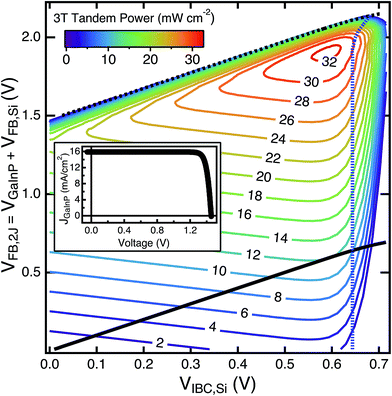
In 3T tandem operation, the current entering the Si cell from the top n-contact (J_FB) must be equal to the current extracted from the top cell because these two devices are connected in series. However, the IBC back n-contact provides an extra degree of freedom to the system, making it possible to extract excess photocurrent or inject external current using the IBC circuit. This extra contact makes it possible to optimize the performance of the Si cell regardless of the current generated from the top cell. Thus, for given current in the top cell, V_IBC can be adjusted along constant J_FB contours (similar to those in Fig. 3c) to maximize the tandem efficiency. It also makes it complicated to plot current density vs. voltage behavior of the tandem cell, because at any operating point of the cell, the third Si contact can be used to influence the performance of the overall device. Using the same approach taken above for a 1J 3T Si device, the full power–voltage space of a 3T GaInP/Si and the Si sub-cell cell is shown in Fig. 4.

Fig. 4 Contour plots of total AM1.5G power density of a 3T GaInP/Si tandem (inset shows the GaInP top-cell J–V data). The black lines superimposed on the 3T tandem power map represents the limiting tandem performance of the GaInP top cell at V_oc (dashed) and J_sc (solid). The blue dotted line indicates the J_Si,IBC = 0 contour of the system (i.e. the performance in 2T mode).

The performance of the Si sub-cell under filtered illumination is similar to the 1J 3T case, just shifted to lower power density due the lower total photon flux incident upon the sub-cell. However, the addition of a standard GaInP top cell with two terminals adds constraints to the operation of the overall tandem device. Just as we only analyzed the modes of operation that produce power for the Si device, we also only consider operation of the tandem cell where power is produced, which corresponds to the power-producing quadrant of the J–V behavior of GaInP top-cell shown in inset (note the tandem efficiency calculated here is semi-empirical, as the GaInP top cell performance is based directly on experimental data fit with a diode model).³² As a stand-alone 1J device, we showed that it is possible for current to flow in both directions from each of the n-contacts of the 3T Si device (Fig. 3c). In tandem operation, adding a top cell in series with the top n-contact adds the constraint that the direction of current flow in the 2J FB circuit can no longer be reversed and still produce power, which corresponds to the V_oc of the GaInP cell, represented by the dashed black line in Fig. 4. The J_SC of the GaInP top cell is also shown (solid black line in Fig. 4). Even when the top cell is in reverse bias (below the solid line in Fig. 4), the Si cell can supply enough power for the tandem system to produce positive power.

Interestingly, although the photogeneration in the Si cell is greater than the top cell in a GaInP/Si tandem, there are still some operation conditions in Fig. 4 where current is being injected into the 2J FB circuit from the Si IBC circuit. When a large voltage is applied to the IBC sub-circuit and a small voltage is applied to the FB sub-circuit, the Si FB sub-circuit can still be current matched to the GaInP by injecting, rather than extracting, current through the Si–IBC circuit (the dashed blue line in Fig. 4 indicates the J_Si,IBC = 0 contour of the system). Although this region of operation does not maximize the overall power production of the tandem cell, it hints at the versatility of cell operation under real world conditions where maximum power point tracking is required.

Although the fully allowable operation space of a 3T GaInP/Si tandem is complex, it is relatively simple to compare the maximum attainable power of the 3T tandem to other potential sub-cell configurations (e.g. current-matched 2T and 4T, Table 1). For the 2T case, the system is described by a single J–V curve, making it straightforward to find the maximum total power of the tandem cell. For 3T tandem cells, the total power production is optimized when the front cell operates at its maximum power point and the Si IBC circuit is then maximized. For the 4T case, the sub-cells are optimized independently with the Si cell in IBC mode, because the TCA interconnection between the sub-cells does not allow for lateral current extraction from the Si cell front contact, and fingers are not included in the optical ray-tracing model. In practice, mechanically stacked 4T devices can use IBC Si cells^22,34 or standard front contacted cells, and at a laboratory scale (1 cm² devices) there is no substantial power loss due to lateral extraction of current through a metal grid in the front-contacted case,² but these losses are likely to become significant at the module scale.³⁵

Table 1 Comparing performance of the same GaInP/Si tandem cell configured in 2T, 3T, and 4T mode under AM1.5G illumination simulated from SMARTS (total spectral power 100.45 mW cm⁻²). For devices where the FB subcircuit includes both subcells, V_FB = V_GaInP,FB + V_Si,FB

Configuration	V FB,mpp (mV)	V IBC,mpp (mV)	J mpp (mA cm^−2)	Eff. (%)
2T (GaInP + Si–FB)	1940	—	15.8	30.6
4T (GaInP)	1310	—	15.8	20.6
4T (Si–IBC)	—	585	20.2	11.8
4T (total)	—	—	—	32.4
3T (FB)	1890	—	15.8	29.8
3T (Si–IBC)	—	594	4.49	2.66
3T (total)	—	—	—	32.5

---

The simulation results shown in Table 1 are in good agreement with experimental measurements of 4T tandem devices. Recently reported mechanically stacked GaInP/Si tandem cells produced a total efficiency of 32.5% using a Si-heterojunction device and 31.5% using a POLO IBC device under AM1.5G illumination.^2,22 Simulation of a 4T tandem cell with the bottom cell operating in IBC mode under the same spectrum had an efficiency of 32.4%. As shown in Table 1, the simulated efficiency of the 3T tandem actually exceeds the 4T tandem considered here. This is due to the reduced FF when the Si cell is operated in IBC mode compared to that of a cell fully optimized for 4T operation. This might be alleviated with optimization of the contact geometries for IBC operation. By enabling current to flow to both n-type contacts simultaneously, the 3T case is closer to the idealized “EP” mode than independent operation in either 2T mode, giving the slight performance advantage seen in Table 1.

3.3 Spectral performance

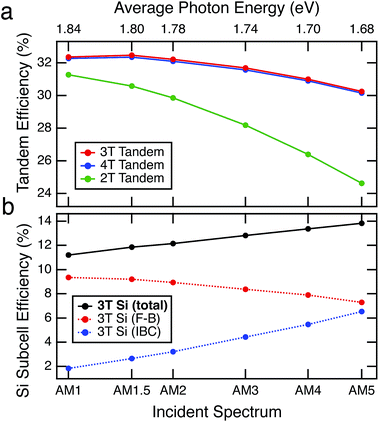
Under real-world conditions, variations in spectrum, temperature, or illumination intensity will impact the performance of a tandem solar cell,^7,36 and 4T tandem devices have been shown to have advantages over 2T tandems because there is no current-matching requirement.⁵ The ability to simultaneously extract power from two different circuits connected to a 3T Si device enables a 3T tandem to maintain the same advantages as a 4T tandem under varying spectral and illumination intensity conditions. If the top cell performance is limited due to fewer available high energy photons, the excess photo-generation in the bottom cell can still be collected through the IBC circuit. To demonstrate this phenomena, we have run tandem device simulations for the GaInP/Si tandem discussed previously under a variety of standard spectra (AM1–AM5) comparing 2T, 3T, and 4T operation of the same device. For each simulation, a unique generation profile was created with raytracing and the top cell performance was scaled based on the EQE of experimental devices. Fig. 5a compares 2T, 3T, and 4T tandem performance for different spectra. Total cell efficiency is plotted vs. the average photon energy of each spectrum considered.

Fig. 5 (a) Total tandem efficiency for GaInP/Si tandem under different incident spectra with 2, 3, or 4 terminal interconnections between cells; (b) efficiency of each component of the 3T Si sub-cell under different incident spectra.

The trends in the data on different spectral conditions show that 2T cells produce significantly less energy as the average photon energy decreases, but 3T cells show the same spectral insensitivity as 4T devices. Under higher air masses, the average photon energy of the incident illumination shifts to lower energies, reducing the photocurrent generated in the GaInP top cell. In 2T mode, the two sub-cells must be current matched, so the tandem performance also decreases. In 4T mode the cells are operated independently, so the Si is able to convert longer wavelength photons that are not captured by the top cell. In 3T mode, the performance of each sub-circuit in the Si device must be considered (Fig. 5b). While the efficiency of the FB circuit decreases due to the current matching requirement with the top cell, the IBC circuit is able to collect the excess photocarriers, and actually becomes more efficient as the average photon energy of the incident illumination decreases.

4 Conclusions and outlook

We have used TCAD simulations to investigate the performance of 3T Si and GaInP/Si tandem solar cells under a wide range of operating conditions. Our simulations are based on realistic experimental parameters for Si and III–V devices and a TCA-based cell interconnection scheme that does not require grids between the two sub-cells. This provides guidelines for the future fabrication of monolithic 3T tandem devices. The behavior of a 3T device cannot be described by a simple I–V curve, and therefore we investigated the full operating space of 3T devices, both as independent and tandem solar cells. We show that the theoretical performance of the 3T tandem device considered here maintains the same spectral advantage over 2T tandem devices as a 4T tandem. The extra terminal in the 3T Si sub-cell enables excess photocurrent to be extracted when the top cell is current limiting, or injected from an external source if the Si sub-cell becomes limiting, which may enable power stabilization at the cell level due to spectral variations, soiling, or degradation of one of the sub-cells.

While this work has focused on a specific implementation of a well-characterized top cell, a Si 3T IBC bottom cell has the potential to work with a wide range of other top cell materials in a tandem device. The 3T IBC design alleviates the current matching conditions of a 2T cell, reducing constraints on the bandgap of the top cell and enabling operation in a wide variety of conditions. However, it maintains the fabrication advantages of a 2T tandem, avoiding the need for lateral conduction between the two cells and potentially providing a mechanism to improve the power conversion of monolithically grown tandem devices that are not current matched. Thus, the design presented here represents a powerful platform for the development of tandem modules, incorporating the fabrication advantages of a 2T tandem with the performance advantages of a 4T design.

Conflicts of interest

There are no conflicts to declare.

Acknowledgements

The authors would like to thank Manuel Schnabel, Jake Atkins, Henning Schulte-Huxel, Ana Kavence, and Andrew Tam for helpful discussions about data analysis and Sentaurus simulations. Dan Friedman provided help with generating illumination using SMARTs. This work was supported by the U.S. Department of Energy under contract no. DE-AC36-08GO28308 with Alliance for Sustainable Energy, LLC, the Manager and Operator of the National Renewable Energy Laboratory. Funding was provided by the U.S. Department of Energy Office of Energy Efficiency and Renewable Energy Solar Energy Technologies Office under DE-EE00030299. Funding at ISFH was provided by the German State of Lower Saxony, the German Federal Ministry for Economics and Energy (BMWi) within the research project “EASi” (FKZ0324040) and EU's FP7 within the research project “HERCULES” (608498). The U.S. Government retains and the publisher, by accepting the article for publication, acknowledges that the U.S. Government retains a nonexclusive, paid up, irrevocable, worldwide license to publish or reproduce the published form of this work, or allow others to do so, for U.S. Government purposes.

References

1. Z. J. Yu, M. Leilaeioun and Z. Holman, Nat. Energy, 2016, 1, 16137.
2. S. Essig, C. Allebé, T. Remo, J. F. Geisz, M. A. Steiner, K. Horowitz, L. Barraud, J. S. Ward, M. Schnabel, A. Descoeudres, D. L. Young, M. Woodhouse, M. Despeisse, C. Ballif and A. Tamboli, Nat. Energy, 2017, 2, 17144.
3. R. Cariou, J. Benick, P. Beutel, N. Razek, C. Flötgen, M. Hermle, D. Lackner, S. W. Glunz, A. W. Bett, M. Wimplinger and F. Dimroth, IEEE J. Photovoltaics, 2017, 7, 367–373.
4. K. A. Bush, A. F. Palmstrom, J. Y. Zhengshan, M. Boccard, R. Cheacharoen, J. P. Mailoa, D. P. McMeekin, R. L. Z. Hoye, C. D. Bailie, T. Leijtens and others, Nat. Energy, 2017, 2, 17009.
5. H. Liu, Z. Ren, Z. Liu, A. G. Aberle, T. Buonassisi and I. M. Peters, Opt. Express, 2015, 23, A382.
6. J. P. Mailoa, M. Lee, I. M. Peters, T. Buonassisi, A. Panchula and D. N. Weiss, Energy Environ. Sci., 2016, 9, 2644–2653.
7. M. T. Hörantner and H. J. Snaith, Energy Environ. Sci., 2017, 10, 1983–1993.
8. S. MacAlpine, D. C. Bobela, S. Kurtz, M. P. Lumb, K. J. Schmieder, J. E. Moore, R. J. Walters and K. Alberi, J. Photon. Energy, 2017, 7, 1.
9. T. Nagashima, K. Okumura, K. Murata and Y. Kimura, Proceedings of the 28th IEEE PVSC, 2000, pp. 1193–1196.
10. J. C. Jimeno, R. Gutierrez, V. Fano, A. Habib, C. del Cañizo, M. A. Rasool and A. Otaegi, Energy Procedia, 2016, 92, 644–651.
11. G. W. P. Adhyaksa, E. Johlin and E. C. Garnett, Nano Lett., 2017, 17, 5206–5212.
12. T. Nagashima, K. Hokoi, K. Okumura and M. Yamaguchi, 2006 IEEE 4th World Conference on Photovoltaic Energy Conference, 2006, pp. 655–658.
13. J. M. Gee, Sol. Cell., 1988, 24, 147–155.
14. H. Schulte-Huxel, E. L. Warren, M. Schnabel, P. Stradins, D. J. Friedman and A. C. Tamboli, Proceedings of the 44th IEEE PVSC, 2017.
15. N. Ito, T. Uesugi, S. Sakai, M. Umeno and S. Hattori, Jpn. J. Appl. Phys., 1981, 20, 121–125.
16. M. A. Steiner, M. W. Wanlass, J. J. Carapella, A. Duda, J. S. Ward, T. E. Moriarty and K. A. Emery, Prog. Photovoltaics Res. Appl., 2009, 17, 587–593.
17. T. Soga, M. Yang, T. Jimbo and M. Umeno, Jpn. J. Appl. Phys., 1996, 35, 1401–1404.
18. M. Emziane and R. J. Nicholas, J. Appl. Phys., 2007, 102, 074508.
19. A. Martí and A. Luque, Nat. Commun., 2015, 6, 6902.
20. M. Rienäcker, E. L. Warren, M. Schabel, H. Schulte-Huxel, A. Merkle, S. Kajari-Schöder, R. Niepelt, R. Brendel, P. Stradins, A. Tamboli and R. Peibst, 2018, In Prep..
21. J. F. Geisz, M. A. Steiner, I. García, S. R. Kurtz and D. J. Friedman, Appl. Phys. Lett., 2013, 103, 041118.
22. M. Rienäcker, M. Schnabel, E. Warren, H. Merkle, A. Schulte-Huxel, T. Klein, M. van Hest, M. Steiner, J. Geisz, S. Kajari-Schröder, R. Niepelt, J. Schmidt, R. Brendel, P. Stradins, A. Tamboli and R. Peibst, Proceedings of the 2017 EUPVSEC, 2017.
23. T. Klein, B. Lee, M. Schnabel, E. Warren, P. Stradins, A. Tamboli and M. F. A. M. van Hest, ACS Appl. Mater. Interfaces, 2018, 10, 8086–8091.
24. T. Klein, B. Lee, M. Schnabel, E. Warren, P. Stradins, A. Tamboli and M. van Hest, Proceedings of the 44th IEEE PVSC, 2017.
25. Synopsys, Optimization of Rear Contact Design in Monocrystalline Silicon Solar-Cell Using 3D TCAD Simulations, TCAD Sentaurus application note, July 2010.
26. F. Haase, F. Kiefer, S. Schäfer, C. Kruse, J. Krügener, R. Brendel and R. Peibst, Jpn. J. Appl. Phys., 2017, 56, 08MB15.
27. M. Rienacker, M. Bossmeyer, A. Merkle, R. Udo, F. Haase, J. Kr, R. Brendel and R. Peibst, IEEE J. Photovoltaics, 2017, 7, 11–18.
28. https://www.pvlighthouse.com.au, last accessed Nov 5, 2017.
29. D. R. Myers and C. A. Gueymard, Proc. SPIE, 2004, 5520, 1–12.
30. P. P. Altermatt, J. Comput. Electron., 2011, 10, 314–330.
31. A. Richter, F. Werner, A. Cuevas, J. Schmidt and S. W. Glunz, Energy Procedia, 2012, 88–94.
32. M. Campanelli, http://pv-fit.com/, last accessed Oct 16, 2017.
33. H. Steinkemper, F. Feldmann, M. Bivour and M. Hermle, IEEE J. Photovoltaics, 2015, 5, 1348–1356.
34. M. Schnabel, M. Rienäcker, A. Merkle, T. Klein, N. Jain, S. Essig, M. van Hest, J. F. Geisz, J. Schmidt, R. Brendel, R. Peibst, P. Stradins and A. Tamboli, Proceedings of the 44th IEEE PVSC, 2017.
35. S. E. Sofia, N. Sahraei, J. P. Mailoa, T. Buonassisi and I. M. Peters, IEEE J. Photovoltaics, 2017, 7, 934–940.
36. M. H. Futscher and B. Ehrler, ACS Energy Lett., 2016, 1, 863–868.

---

Footnote

† Electronic supplementary information (ESI) available: Simulation parameters, power calculations, experimental comparison. See DOI: 10.1039/c8se00133b

---