Open Access Article
Open Access ArticleCreative Commons Attribution 3.0 Unported Licence
Reversible coordination of N2 and H2 to a homoleptic S = 1/2 Fe(I) diphosphine complex in solution and the solid state†
Laurence R.
Doyle
a,
Daniel J.
Scott
a,
Peter J.
Hill
a,
Duncan A. X.
Fraser
a,
William K.
Myers
 *b,
Andrew J. P.
White
a,
Jennifer C.
Green
b and
Andrew E.
Ashley
*b,
Andrew J. P.
White
a,
Jennifer C.
Green
b and
Andrew E.
Ashley
 *a
*a
aDepartment of Chemistry, Imperial College London, London SW7 2AZ, UK. E-mail: a.ashley@imperial.ac.uk
bInorganic Chemistry Laboratory, University of Oxford, Oxford OX1 3QR, UK
First published on 18th July 2018
Abstract
The synthesis and characterisation of the S = 1/2 Fe(I) complex [Fe(depe)2]+[BArF4]− ([1]+[BArF4]−), and the facile reversible binding of N2 and H2 in both solution and the solid state to form the adducts [1·N2]+ and [1·H2]+, are reported. Coordination of N2 in THF is thermodynamically favourable under ambient conditions (1 atm; ΔG298 = −4.9(1) kcal mol−1), while heterogenous binding is more favourable for H2 than N2 by a factor of ∼300. [1·H2]+[BArF4]− represents a rare example of a well-defined, open-shell, non-classical dihydrogen complex, as corroborated by ESR spectroscopy. The rapid exchange between N2 and H2 coordination under ambient conditions is unique for a paramagnetic Fe complex.
Introduction
Recent years have seen great interest in the pursuit of well-defined transition metal (TM) complexes capable of catalysing the reduction of N2 to NH3 or N2H4.1 One of the most compelling rationales for studying such systems is that their mechanistic details can be more readily discerned, in comparison with the complex proton-coupled electron transfer (PCET) steps operative within nitrogenase enzymes.2 The utility of Fe in biological N2 fixation,3 and the anthropogenic Haber–Bosch process,4 has prompted researchers to target Fe complexes as potential synthetic catalysts. These ‘artificial’ nitrogenases employ chemical H+ and e− sources to reduce N2 through PCET pathways, although this process competes with proton reduction to H2, which can preferentially sequester active metal sites.5 Facile displacement of H2 by N2 is thus an important aspect to maintaining a productive N2-fixing catalytic cycle, and an understanding of the binding of these small molecules to low-valent Fe centres could lead to more selective and efficient catalysts for the production of azanes. While the coordination chemistry of N2 and H2 to Fe(0) and Fe(II) complexes is well-documented,6 analogous detailed studies containing Fe(I) are scant,7 despite the potential relevance of this low-valent oxidation state in Fe-based synthetic nitrogenases. We recently reported that the Fe(0) bisphosphine complex, Fe(depe)2(N2) [1·N2; depe = Et2PCH2CH2PEt2] is a highly selective catalyst for the PCET-mediated conversion of N2 to N2H4 with H+ and e− equivalents.8 Herein we report the related low-spin Fe(I) species [Fe(depe)2]+ ([1]+) which is shown to reversibly coordinate N2 or H2, with the latter being a rare case of a thoroughly-characterised paramagnetic σ-H2 complex. Furthermore, this behavior is found to occur both in solution and in the solid-state.Methods
The ESR spectroscopic methods used for characterizing molecular structure are based on the following spin Hamiltonian, representing the electron Zeeman, nuclear Zeeman, hyperfine and nuclear quadrupole components, respectively.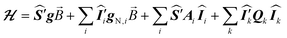 | (1) |
The bold symbols are 3 × 3 tensors (or matrices) and the vector of Cartesian spin operators are defined in appropriate Hilbert space eigenbasis. The third term of the spin Hamiltonian, hyperfine or 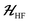 is composed of an isotropic component, aiso, transformed to a 3 × 3 matrix by,
is composed of an isotropic component, aiso, transformed to a 3 × 3 matrix by, 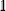 defined as the identity matrix, and an anisotropic component, T.
defined as the identity matrix, and an anisotropic component, T.
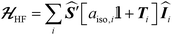 | (2) |
It is the anisotropic tensor component that returns the structural relations of the spin system, based on the summation of dipolar interactions between the position vectors of the central iron atom and surrounding positions, approximated as ligand nuclei position vectors.9
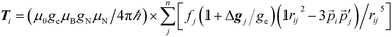 | (3) |
Eqn (3) includes contribution of all centres, pj, of spin density fj at distance rij to the hyperfine interaction matrix for a single nucleus position, pi. The principal axis elements in the limit of an axial tensor are [−T, −T, 2T] where the perpendicular component (eqn (4)) is used to estimate a distance in a single point-dipole approximation:
| T = fFegeffμBgNμN/r3 | (4) |
Analysis of the nuclear quadrupole term of the spin Hamiltonian of eqn (1) for an I = 1 nucleus (relevant to 2H and 14N in this work) can provide useful information on bonding and electronic structure,10 and is given by:
| Q = K × diag[−(1 − η), −(1 + η), 2] | (5) |
| νdq = 2[νef±2 + K2(3 + η2)]1/2 | (6) |
Results and discussion
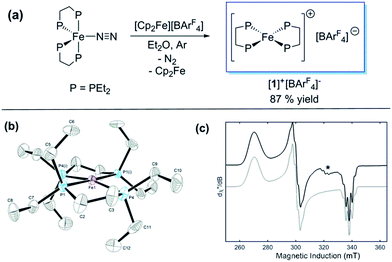
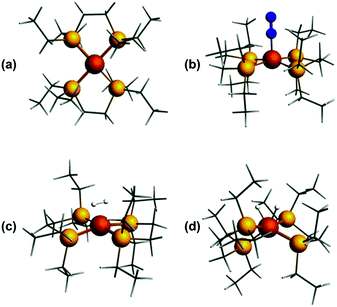
Previously, we showed that N2H4/NH3-producing reactions of 1·N2 with the acid [Ph2NH2]+[TfO]− (TfO = CF3SO3) formed an Fe(I) species, which was shown by X-ray crystallography to be [Fe(depe)2(η1-N2)]+[TfO]− ([1·N2]+[TfO]−).8 Variable-temperature ESR spectra of this compound were complicated, however, which we postulated may be due to competitive N2vs. [TfO]− coordination. In order to suppress the latter, and hence better resolve the behaviour of the [1·N2]+ fragment, we subsequently utilised the more weakly coordinating [BArF4]− (BArF4 = B[3,5-{CF3}2C6H3]4). Thus, oxidation of 1·N2 with 1 eq. [Cp2Fe]+[BArF4]− (Cp = C5H5) produced a deep-blue solution, from which an intensely blue crystalline solid was obtained following work-up and recrystallisation from Et2O/pentane under Ar.13 A single crystal suitable for X-ray diffraction was subsequently isolated which solved and refined as the 15 valence electron (VE), N2-free compound [Fe(depe)2]+[BArF4]− ([1]+[BArF4]−, Fig. 1(a) and (b)). In the structure the [1]+ and [BArF4]− ions are well separated, with no close C or F contacts between the anion and the Fe centre.The [1]+ cation was found to be disordered and, while the structural model is in good agreement with the X-ray crystallographic data (with the molecular connectivity and absence of an N2 ligand being conclusive), the interatomic distances are approximate and will not be discussed in detail.14 The FeP4 unit is pseudo square planar and exhibits a tetrahedral distortion, as seen by a dihedral angle of 12.41(11)° between the two Fe(PP) [Fe(1)P(1)P(4) and Fe(1)P(1i)P(4i)] coordination planes, which is very similar to that observed in the approximately square-based pyramidal [1·N2]+[TfO]− (15.39(9)°). Evidently, coordination of N2 results in minimal reorganisation of the [Fe(depe)2]+ fragment. While two CH3 groups from ligand ethyl groups from each depe moiety are directed towards the vacant axial coordination sites of the Fe centre, large Fe⋯H separations suggest an absence of any agostic or anagostic interactions, which is supported by DFT results (vide infra).15
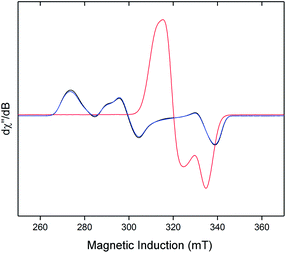
Neither solid samples nor solutions of [1]+[BArF4]− under Ar showed bands attributable to an νNN stretch in their IR or Raman spectra, further confirming the absence of N2 in the complex. [1]+[BArF4]− is insoluble in alkanes, PhH and PhMe, yet highly soluble in THF and in the highly polar, non-coordinating 1,2-difluorobenzene (DFB). 31P NMR spectra (DFB, Ar) of [1]+[BArF4]− are silent, whereas very broad paramagnetically-shifted resonances for the [1]+ moiety feature in the 1H NMR spectrum (see ESI†). The solution-phase magnetic moment (Evans NMR, DFB, 243–298 K, Ar) was found to be 1.75 μB, and the X-band ESR spectrum (PhMe/DFB glass, Ar, 40 K) revealed a rhombic signal (g1 = 2.483, g2 = 2.234, g3 = 1.985) with an isotropic g-value (giso) of 2.23, [giso = (gx + gy + gz)/3; Fig. 1(c)]. These data are consistent with a low-spin (S = 1/2, d7) Fe(I) centre. The strong similarity between the X-band ESR spectrum of a powdered sample of [1]+[BArF4]− (Ar, 1 bar, 40 K) and solution measurements implies that [1]+ is virtually isostructural in solution and the solid state.
Dissolution of [1]+[BArF4]− in N2-saturated solvents (1 atm; DFB or THF) afforded forest-green solutions at room temperature, which became pale yellow upon cooling to −30 °C; either heating these solutions above room temperature, or degassing with Ar, resulted in the rapid reappearance of the characteristic blue colour of [1]+[BArF4]−. An IR active νNN stretch at 2067 cm−1 confirmed coordination of N2 to [1]+ to form [1·N2]+, which is intermediate in value between those seen for 1·N2 and the related Fe(II) [trans-Fe(H)(N2)(depe)2]+ (1975 cm−1 and 2102 cm−1 respectively);16 this trend may be readily accounted for by decreased Fe → N2 π-backbonding as the oxidation state increases.
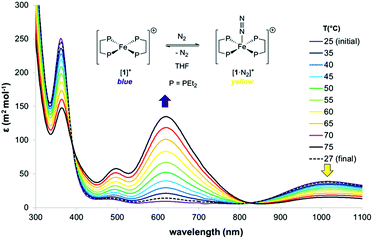
The thermodynamics of N2 coordination were obtained from variable temperature UV-vis spectroscopy by monitoring the concentrations of [1]+ and [1·N2]+via their absorption features (λmax (nm) = 618 and 1018, respectively; Fig. 2).17 N2 association with [1]+ is accordingly found to be exoergic (ΔG298 = −4.9(1) kcal mol−1) with, as expected, a favourable enthalpy (ΔHo = −13.1(1) kcal mol−1) and an unfavourable entropy (ΔSo = −27.6(1) cal K−1 mol−1) contribution; these values compare well with those for N2 binding by (P3B)Co [P = o-(PiPr2)2C6H4; ΔHo = −13.9(7) kcal mol−1, and ΔSo = −32(5) cal K−1 mol−1], which also produces an S = 1/2 dinitrogen complex.18,19
The X-band ESR spectra of rapidly freeze-quenched N2-saturated DFB or THF solutions (40 K) of [1]+[BArF4]− revealed a pseudo-axial signal which differs markedly from the rhombic signal characteristic of the N2-free complex (giso = 2.07; simulated g tensors = 2.0014, 2.0922, 2.125). Additionally, hyperfine coupling to the four 31P nuclei was resolved for the THF glass giving A(31P) = 62.7(1) MHz (Fig. S5†), which is very similar to Aiso(31P) previously obtained for [1·N2]+[TfO]− [66.2(2) MHz].8
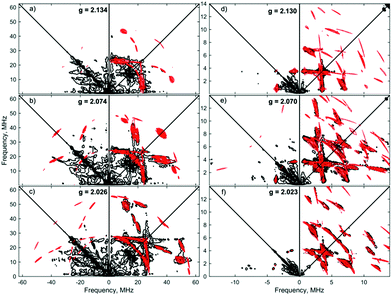
Similar spectroscopic observations have been described for the Fe(I) complex [Fe(DMeOPrPE)2(N2)]+ (DMeOPrPE = R2PCH2CH2PR2; R = CH2CH2CH2OMe), which were attributed to an equilibrium between yellow [Fe(DMeOPrPE)2(N2)]+ and a purple N2-bridged bimetallic S = 1 species {[Fe(DMeOPrPE)2]2(μ-N2)}2+; the latter is favoured at higher temperatures and/or low p(N2).20 We noted that comparable optical absorptions were observed for [1]+ and [1·N2]+ (see Table S1, ESI†), and accordingly 2D-ESR (HYSCORE; HYperfine Sub-level CORrElation) experiments were performed on equivalent 14N2- and 15N2-saturated PhMe/DFB (7![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1) solutions of [1]+[BArF4]−, to fully ascertain the solution-phase coordination mode of N2 to [1]+. As shown in Fig. 3, two 14N signals were clearly detected at the perpendicular field position, in panels a, b, e, f.
1) solutions of [1]+[BArF4]−, to fully ascertain the solution-phase coordination mode of N2 to [1]+. As shown in Fig. 3, two 14N signals were clearly detected at the perpendicular field position, in panels a, b, e, f.
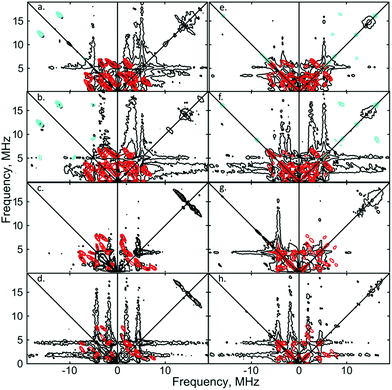 | ||
| Fig. 3 X-band 2D ESEEM spectra of 2.5 mM [1·14N2]+[BArF4]− in THF, with standard 4-pulse HYSCORE (panels (a–d)), and DONUT HYSCORE21 (panels (e–h)), at two fields (3471 G: (a, b, e and f); 3800 G: (c, d, g and h)) and two τ values (200 ns: (a, c, e and g); 132 ns: (b, d, f and h)) while τ2 = 800 ns for DONUT. The samples were frozen glasses at 20 K and measured with pulse lengths of π/2 = 8 ns and π = 12 ns, initial variable delays of 100 ns, and a time step of 20 ns over 200 points in both axes. The microwave frequency was 9.7449 GHz. Experimental data is in black, while separate simulations of two 14N are overlaid in red and cyan. | ||
The proximal nitrogen, 14Np, gives intense double quantum dq, dq correlation peaks in the (−, +) quadrant corresponding to the 14N directly bound to Fe(I) centre, leading to peaks at (∓16.2, ±12.2) MHz and, from eqn (6), Aiso(14Np) may correspondingly be calculated as 14.3 (±0.1) MHz.22 For the distal nitrogen, 14Nd, field-dependent 15N2 simulations of 4-pulse HYSCORE provide Aiso(14Nd) = 4.4 MHz (seen in ESI, Fig. S7†). A clearly-resolved quadrupole interaction of 14Np reveals a very small asymmetry η ∼ 0, which compares well with sp-hybridized 14N found in N![[triple bond, length as m-dash]](https://www.rsc.org/images/entities/char_e002.gif) N and [C
N and [C![[triple bond, length as m-dash]](https://www.rsc.org/images/entities/char_e002.gif) N]−.10a For the 14Nd (red in Fig. 3), it was found that K = 0.9 MHz. In the case of the 14Np, the data was insufficient for a more precise determination, and the quadrupole values of 14Nd were used as an approximation. For ligand atoms directly bonded with covalent character, a point-dipole model can be inaccurate; for 14NdT = 1.2 MHz, and for 14Np the simulation value was T = 0.6 MHz. To confirm that both 14N signals derive from the same molecule (considering that no large 15N hyperfine coupling was observed) close examination of the dq, dq peaks at 3471 G reveals weak multinuclear combination frequency peaks such as {Npα(dq), Npβ(dq), Ndβ(dq)} (seen in Fig. S7†), a signal class previously reported by Stich et al. for Mn2(III/IV) Catalase.23 It is notable that no ‘half-field’ resonance (g ≈ 4) was observed in the CW-ESR experiments, which would be expected for the hypothetical triplet (S = 1) {[Fe(depe)2]2(μ-N2)}2+ due to a formally forbidden ΔMs = 2 transition, as has been documented for other transition metal diradicals.24 Collectively alongside other spectroscopic data, these observations strongly support the solution-phase assignment of [1·N2]+[BArF4]− as [Fe(depe)2(η1-N
N]−.10a For the 14Nd (red in Fig. 3), it was found that K = 0.9 MHz. In the case of the 14Np, the data was insufficient for a more precise determination, and the quadrupole values of 14Nd were used as an approximation. For ligand atoms directly bonded with covalent character, a point-dipole model can be inaccurate; for 14NdT = 1.2 MHz, and for 14Np the simulation value was T = 0.6 MHz. To confirm that both 14N signals derive from the same molecule (considering that no large 15N hyperfine coupling was observed) close examination of the dq, dq peaks at 3471 G reveals weak multinuclear combination frequency peaks such as {Npα(dq), Npβ(dq), Ndβ(dq)} (seen in Fig. S7†), a signal class previously reported by Stich et al. for Mn2(III/IV) Catalase.23 It is notable that no ‘half-field’ resonance (g ≈ 4) was observed in the CW-ESR experiments, which would be expected for the hypothetical triplet (S = 1) {[Fe(depe)2]2(μ-N2)}2+ due to a formally forbidden ΔMs = 2 transition, as has been documented for other transition metal diradicals.24 Collectively alongside other spectroscopic data, these observations strongly support the solution-phase assignment of [1·N2]+[BArF4]− as [Fe(depe)2(η1-N![[triple bond, length as m-dash]](https://www.rsc.org/images/entities/char_e002.gif) N)]+[BArF4]−.
N)]+[BArF4]−.
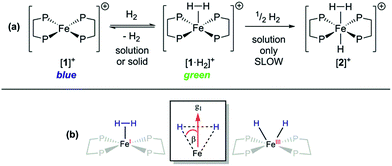
Given that {TM(σ-N2)} and {TM(σ-H2)} fragments are related by the same VE count, numerous diamagnetic metal–ligand platforms have been shown to interconvert these species under N2 and H2 mixtures;25 however, analogous open-shell examples are extremely rare.26 Furthermore, only two thoroughly characterised paramagnetic dihydrogen ligand complexes have been reported to date: (P3B)Co(H2)18 and (P3Si)Fe(H2);7 both of these are idealised C3 symmetric, trigonal bipyramidal S = 1/2 complexes. In spite of the different coordination geometry and cationic charge, admission of H2 (1 atm.) to DFB or THF solutions of [1]+[BArF4]− demonstrated clear reaction (Fig. 4(a)), as evidenced by an immediate colour change to pale green (λmax = 850 nm, εmax ≈ 19 m2 mol−1) and the appearance of a new near-axial ESR signal (X-band, PhMe/DFB, 40 K; g = [2.000, 2.085, 2.160], giso = 2.08, Fig. S6†), which displays more pronounced hyperfine splitting for g2 and g3 than seen for [1·N2]+[BArF4]−.27 The most plausible identities of this species are the Fe(I) adduct [Fe(depe)2(σ-H2)]+ ([1·H2]+) or the Fe(III) oxidative addition product [Fe(depe)2(H)2]+ ([1(H)2]+).28 Using the DFT-optimised structures of [1·H2]+ and [1(H)2]+ (vide infra), the angle (β) between the g1 principal axis and the Fe–H vectors was calculated to be 16° and 31°, respectively.
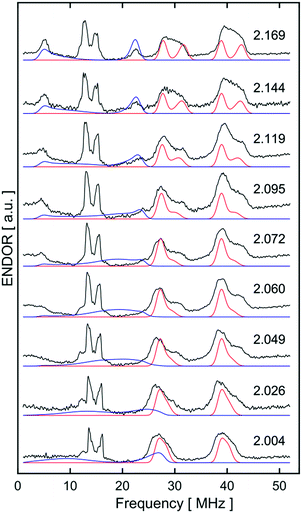
Orientation-selective ENDOR has previously been used to differentiate between Fe(H2) and Fe(H)2 formulations using electron–1H dipolar hyperfine coupling interactions, where only small β angles (<15°; see Fig. 4(b)) were able to reproduce the observed experimental lineshape.7,29 The 1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 2
2![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1 hyperfine seen at the five negative 31P peaks of gmin in CW-ESR of Fig. S6,† was interrogated more closely with H2/D2-saturated solutions of [1]+[BArF4]− using 1H Davies ENDOR (Electron-Nuclear DOuble Resonance) and both 1H & 2H HYSCORE experiments (see Fig. 5). Fits to data from both techniques used two H hyperfine interaction values, for 1H A(1H) = [−17.99, −19.93, 26.58]/MHz, while the values were scaled by the nuclear g-factor ratio gn(2H)/gn(1H) = 0.1535 for the 2H HYSCORE simulation, revealing a dipolar component of T = 15.2 MHz. The Fe–H distance, rFeH (Å), can thus be obtained from rFeH (Å) = ∛(ρ(Fe)79.06/T), using a spin density of ρ(Fe) ∼ 0.83 as remainder of the large isotropic 31P hyperfine interactions;30,31 this coupling is consistent with an Fe–H bond distance of 1.64 Å. Considering the spin density at Fe and the coordinating ligand atoms and DFT coordinates (vide infra), eqn (3) was used to fit an angle of 2β = H–Fe–H, β = 5.5°, using the empirical principal dipolar values [−14.2, −16.2, 30.4] MHz (written as [−T(1 − δ), −T(1 + δ), 2T], with δ as the rhombicity parameter); this value is in excellent agreement with that found for (P3Si)Fe(H2) (β = 6°),7 which was interpreted as indicative of partial rotational averaging of the dipolar interaction. However, the angle β = 5.5° includes spin density on opposing 1,2H, and Morris et al., has shown that rotational motion can reduce H–H dipolar interactions by up to a factor of four, implying that β = 5.5° should be considered an upper limit.32
1 hyperfine seen at the five negative 31P peaks of gmin in CW-ESR of Fig. S6,† was interrogated more closely with H2/D2-saturated solutions of [1]+[BArF4]− using 1H Davies ENDOR (Electron-Nuclear DOuble Resonance) and both 1H & 2H HYSCORE experiments (see Fig. 5). Fits to data from both techniques used two H hyperfine interaction values, for 1H A(1H) = [−17.99, −19.93, 26.58]/MHz, while the values were scaled by the nuclear g-factor ratio gn(2H)/gn(1H) = 0.1535 for the 2H HYSCORE simulation, revealing a dipolar component of T = 15.2 MHz. The Fe–H distance, rFeH (Å), can thus be obtained from rFeH (Å) = ∛(ρ(Fe)79.06/T), using a spin density of ρ(Fe) ∼ 0.83 as remainder of the large isotropic 31P hyperfine interactions;30,31 this coupling is consistent with an Fe–H bond distance of 1.64 Å. Considering the spin density at Fe and the coordinating ligand atoms and DFT coordinates (vide infra), eqn (3) was used to fit an angle of 2β = H–Fe–H, β = 5.5°, using the empirical principal dipolar values [−14.2, −16.2, 30.4] MHz (written as [−T(1 − δ), −T(1 + δ), 2T], with δ as the rhombicity parameter); this value is in excellent agreement with that found for (P3Si)Fe(H2) (β = 6°),7 which was interpreted as indicative of partial rotational averaging of the dipolar interaction. However, the angle β = 5.5° includes spin density on opposing 1,2H, and Morris et al., has shown that rotational motion can reduce H–H dipolar interactions by up to a factor of four, implying that β = 5.5° should be considered an upper limit.32
Simulations of ENDOR data for [1·H2]+ in Fig. 6 are consistent with the DFT structure (vide infra), in having two classes of 31P hyperfine interaction, aiso(31P) = 69.3 MHz of P in-plane orthogonal to the Fe(I)–H2 bond and aiso(31P) = 66.3 MHz for the P bent out-of-plane; furthermore the P–Fe–P depe ligand angle of 85.5° suggests that the symmetry lies closer to 2-fold than 4-fold. Correspondingly, these results provide strong evidence that [1·H2]+ is best described as a non-classical σ-H2 adduct.
Freshly-prepared solutions of [1·H2]+ are sufficiently stable for detailed in situ characterisation and, as with solutions under N2, vacuum/Ar-degassing resulted in regeneration of spectroscopic signals attributed to [1]+, demonstrating reversible coordination of H2. Nevertheless, attempts to obtain thermochemical information for H2 binding were unfortunately frustrated by slow and irreversible formation of the Fe(II) trishydride trans-[Fe(depe)2(H)(H2)]+, [2]+.33 Appreciating that ligation of N2 or H2 to [1]+ results in minimal deformation of the [Fe(depe)2]+ core,34 we speculated that binding of these gases might also be reversible in the solid state, as in solution. Gratifyingly, admission of either N2 or H2 to powdered samples of [1]+[BArF4]− led to comparable colour changes (deep blue to yellow or green, respectively), consistent with clean conversion to [1·(N2/H2)]+[BArF4](s)−. ESR spectra closely matched those obtained in solution, strongly suggesting that the geometry of the [Fe(depe)2]+ core is preserved in both phases upon N2 and or H2 coordination. Crucially, removal of N2/H2 from these samples under vacuum led to complete restoration of the original ESR signal of [1]+ (Fig. 7 and S2†), confirming that binding is fully reversible (over multiple cycles) in the solid state; importantly, no loss in signal intensity was observed (which would be expected from formation of diamagnetic [2]+) under H2. Furthermore, ready exchange of the N2 ligand for H2 is achieved via simple evacuation of N2 and replacing with H2, and vice versa.
ESR spectra of [1]+[BArF4]− obtained in the presence of a single equivalent of N2 or H2 allow for a quantitative comparison of the binding affinities of the two gases; the ratio [1·L]+/[1]+ (L = N2 or H2; determined by signal intensity at 303 K) is significantly larger for H2 (44) than N2 (0.15), revealing that binding of the former is almost 300 times more favourable at ambient temperature.35 For comparison, (P3B)Co(L) (L = N2, H2) are in rapid dissociative equilibrium in solution under similar conditions, whereas (P3Si)Fe(L) species require several days to interconvert (proposed to proceed via an associative mechanism involving partial dechelation of the P3Si ligand);7,18 both demonstrate a preference for H2 binding, albeit to differing degrees (KH2/KN2 ≈ 2 and 50 for Co and Fe, respectively). This difference in exchange kinetics was postulated to result from the poorer π-backbonding capability of Co vs. Fe which leads to weaker M–L interactions. Hence it is plausible that the ready reversibility of N2 and H2 exchange for [1]+ relative to (P3Si)Fe could also be due (in part) to poorer π-donation from the former, by virtue of its cationic charge, which is also manifest in the higher νNN stretch value of the former (2067 vs. 2003 cm−1).
Computational calculations
In order to probe the structure and electronic properties of [1]+, [1·N2]+, and [1·H2]+, density functional calculations were carried out using the ADF program suite version 2014.1.36 The Slater-type orbital (STO) basis sets were of triple-ζ quality augmented with a one polarization function (ADF basis TZP). Core electrons were frozen (C, N 1s; Fe 2p) in our model of the electronic configuration for each atom. The local density approximation (LDA) by Vosko, Wilk and Nusair (VWN)37 was used together with the exchange correlation corrections of Becke and Perdew (BP86).38Optimized geometries were ascertained as local minima via frequency calculations. Geometry optimisation of base-free [1]+ with S = 1/2 resulted in a D2 structure consistent with X-ray crystallographic data, with an angle of approximately 7° between the two iron-ligand Fe(PP) coordination planes (Fig. 8(a)); fixing the spin state to S = 3/2 showed the alternative high-spin structure to be some 0.77 eV (approximately 17.8 kcal mol−1) higher in energy. Geometry optimisation of [1·N2]+ results in a structure of C2 symmetry with a slightly increased angle between the two Fe(PP)2 planes of 19° (Fig. 8(b)). The coordination geometry around Fe is square-based pyramidal with P–Fe–Nα angles of 94.8° and 95.6°. The calculated stretching frequency for the bound N2 ligand was 2059 cm−1, which is in good agreement with experiment (2067 cm−1). Geometry optimisation of [1·H2]+ (Fig. 8(c)) gave a σ-complex with a H–H bond length of 0.899 Å (cf. free H2: 0.74 Å)6 and an average Fe–H distance of 1.61 Å, which correlates well with 2D-ESR data. An alternative [1·(H)2]+ isomer (Fig. 8(d)), corresponding to the product of H2 oxidative addition and containing two well-separated hydride ligands (H⋯H = 1.57 Å and Fe–H distances of 1.51 Å), could also be located, albeit 12 kcal mol−1 higher in energy than [1·H2]+ (see Table S2 in ESI for further details†).
Since all compounds had unpaired spins the DFT calculations were unrestricted, with different orbitals for α and β spins. The energies of the α spin electrons, of which there are more, tended to be lower than those of the β spin electrons in corresponding orbitals because of exchange stabilization (Fig. 9).
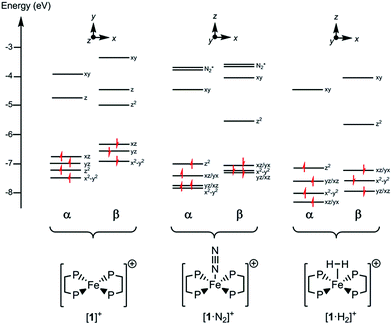 | ||
| Fig. 9 Electronic energy levels and their occupancy for [1]+, [1·N2]+ and [1·H2]+. The principal Fe character is indicated. | ||
The unpaired electron in the three cases, [1]+, [1·N2]+, and [1·H2]+, occupies an orbital of primarily d(z2) character; in the case of [1·N2]+ and [1·H2]+ this is also hybridized with the Fe 4p(z) orbital (Fig. 10), and is antibonding with respect to the coordinated N2 or H2, thus explaining the weak association of these ligands to the [Fe(depe)2]+ core. Of particular interest is the virtual orbital (z) of [Fe(depe)2]+, the isosurface of which is shown in Fig. 10; its AO composition is predominantly Fe 4p(z) and P 3p.
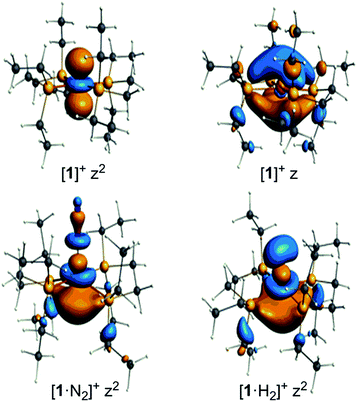 | ||
| Fig. 10 Selected Kohn–Sham isosurfaces for [1]+, [1·N2]+ and [1·H2]+ showing the z2 occupancy of the unpaired electrons and the virtual orbital for [1]+ of primarily 4pz character. | ||
Time-dependent DFT (TDDFT) was used to calculate the electronic absorption spectra of [1]+, [1·N2]+ and [1·H2]+ (see Table S3 and Fig. S15 in the ESI†). The numerical agreement with experiment is only moderate, with the bands being calculated at higher energy than measured experimentally. All three compounds have as their lowest energy bands d–d transitions, with a β spin electron being excited into the hole in the d(z2) orbital. However those bands of [1]+ have effectively zero oscillator strength on account of its high symmetry. The d–d transitions are of longer wavelength for [1]+ than for [1·N2]+ and [1·H2]+, which fits with the smaller HOMO–LUMO gap in the former (see Fig. 9). The subsequent set of bands calculated at 587, 548 and 503 nm for [1]+ fit well with the features found at 500 and 618 nm experimentally; they are of significantly higher oscillator strength than the d–d bands of [1·N2]+ and [1·H2]+ and correspond to excitation from the occupied 3d orbitals into the Fe 4pz orbital. In [1·N2]+ and [1·H2]+, the corresponding band is absent as a consequence of ligand binding along the z axis, hence their respective absorption spectra have no analogous feature. Thus, in spite of the lack of numerical agreement for the d–d bands, many features of the calculated spectra give a good account of those observed.
Conclusions
In conclusion, we have synthesised and fully characterised an open-shell, cationic Fe(I) complex, [1]+[BArF4]−, and demonstrated the readily reversible coordination of N2 and H2 to the S = 1/2 Fe centre. Remarkably, this facile exchange between N2 and H2 coordination occurs in either solution or solid states under ambient conditions, likely due to the very small structural change in transitioning between square planar [1]+ and square-based pyramidal [1·(N2/H2)]+ species. Furthermore, [1·H2]+[BArF4]− is a rare example of a well-defined paramagnetic σ-H2 complex, as corroborated by ESR spectroscopy and DFT calculations. These results reveal that reversible coordination of these small molecules to open-shell complexes is neither restricted to neutral compounds nor C3 molecular symmetries, which until now, have been the only known examples. Given the importance of Fe in catalytic N2 fixation, this work is of significant relevance to the ongoing development and investigation of well-defined transition metal catalysts for N2 reduction, mediated by H+/e− sources or (ideally) H2 as the terminal reductant.Conflicts of interest
There are no conflicts to declare.Acknowledgements
We thank the EPSRC for providing a PhD studentship (P. J. H) and postdoctoral funding (L. R. D and D. J. S), the Royal Society for a University Research Fellowship (A. E. A.), and the Centre for Advanced ESR spectrocopy (CAESR) at the University of Oxford (EP/L011972/1).Notes and references
- For recent reviews, see: (a) Y. Tanabe and Y. Nishibayashi, Chem. Rec., 2016, 16, 1549 CrossRef PubMed; (b) K. C. MacLeod and P. L. Holland, Nat. Chem., 2013, 5, 559 CrossRef PubMed; (c) S. Hinrichsen, H. Broda, C. Gradert, L. Söncksen and F. Tuczek, Annu. Rep. Prog. Chem., Sect. A: Inorg. Chem., 2012, 108, 17 RSC; (d) C. Köthe and C. Limberg, Z. Anorg. Allg. Chem., 2015, 641, 18 CrossRef.
- B. M. Hoffman, D. Lukoyanov, Z.-Y. Yang, D. R. Dean and L. C. Seefeldt, Chem. Rev., 2014, 114, 4041 CrossRef PubMed.
- Y. L. Hu and M. W. Ribbe, J. Biol. Inorg Chem., 2015, 20, 435 CrossRef PubMed.
- R. Schlögl, in Catalytic Ammonia Synthesis Fundamentals and Practice, ed. J. R. Jennings, Plenum Press, New York, 1st edn, 1991, ch. 2, pp. 19–108 Search PubMed.
- The higher absolute entropy of N2vs. H2 can offset favourable TM–(N2) vs. TM–(H2) bond enthalpies, becoming more important at higher temperatures: A. A. Gonzalez and C. D. Hoff, Inorg. Chem., 1989, 28, 4295 CrossRef.
- See: G. J. Kubas, Chem. Rev., 2007, 107, 4152 CrossRef PubMed and references therein.
- Y. Lee, R. A. Kinney, B. M. Hoffman and J. C. Peters, J. Am. Chem. Soc., 2011, 133, 16366 CrossRef PubMed.
- P. J. Hill, L. R. Doyle, A. D. Crawford, W. K. Myers and A. E. Ashley, J. Am. Chem. Soc., 2016, 138, 13521 CrossRef PubMed.
- (a) A. Bachmeier, J. Esselborn, S. V. Hexter, T. Krämer, K. Klein, T. Happe, J. E. McGrady, W. K. Myers and F. A. Armstrong, J. Am. Chem. Soc., 2015, 138, 5381 CrossRef PubMed; (b) A. Schweiger and G. Jeschke, Principles of Pulsed Electron Paramagnetic Resonance, Oxford University Press, Oxford, 2003 Search PubMed; (c) R. Drago, Physical Methods for Chemists, Surfside Scientific Publishers, Gainesville, 1992 Search PubMed.
- (a) G. A. Jeffrey and T. Sakurai, Prog. Solid State Chem., 1964, 1, 380 CrossRef; (b) C. H. Townes and B. P. Dailey, Determination of electronic structure of molecules from nuclear quadrupole effects, J. Chem. Phys., 1949, 17, 782 CrossRef.
- S. A. Dikanov and Y. D. Tsvetkov, Electron Spin Echo Envelope Modulation (ESEEM) Spectroscopy, CRC Press, Inc., Boca Raton, 1992 Search PubMed.
- H. L. Flanagan and D. J. Singel, J. Chem. Phys., 1987, 87, 5606 CrossRef.
- The synthesis of a ‘light blue’ salt “[1·N2]+[BAr4F]−” was briefly described in a recent publication; however only limited characterisation data (under N2) were provided. In light of the comprehensive study reported herein, we believe that this salt in fact likely comprises a mixture of predominantly [1]+[BAr4F]− and [1·N2]+[BAr4F]−. See: J. B. Geri, J. P. Shanahan and N. K. Szymczak, J. Am. Chem. Soc., 2017, 139, 5952 CrossRef PubMed , and related ESI.†.
- The disorder arises due to a mismatch between the lower symmetry of the cation (D2) and the site symmetry of its location in the crystal (S4), hence only the Fe atom (which sits directly on the latter) is strictly ordered. See ESI† for full crystallographic details.
- M. Brookhart, M. L. H. Green and G. Parkin, Proc. Natl. Acad. Sci. U. S. A., 2007, 104, 6908 CrossRef PubMed.
- L. R. Doyle, P. J. Hill, G. G. Wildgoose and A. E. Ashley, Dalton Trans., 2016, 45, 7550 RSC.
- THF was selected for these experiments as the solubility of N2 is known in this medium, in contrast to DFB. See: R. Battino, T. R. Rettich and T. Tominaga, J. Phys. Chem. Ref. Data, 1984, 13, 563 CrossRef.
- D. L. M. Suess, C. Tsay and J. C. Peters, J. Am. Chem. Soc., 2012, 134, 14158 CrossRef PubMed.
- The solution-phase free energy of N2 binding to a [P4(amine)2] Fe(I)-tetraphosphine complex has been recently disclosed (see: D. E. Prokopchuk, E. S. Wiedner, E. D. Walter, C. V. Popescu, N. A. Piro, W. S. Kassel, R. M. Bullock and M. T. Mock, J. Am. Chem. Soc., 2017, 139, 9291 CrossRef PubMed ). In contrast to [1]+, N2 binding was found to be endoergic (ΔG298 = +0.4(5) kcal mol−1), which may arise from their use of poorer aryl-phosphine donors vs. alkyl-phosphines in [1]+, translating to a weaker Fe–N2 bond.
- C. G. Balesdent, J. L. Crossland, D. T. Regan, C. T. López and D. R. Tyler, Inorg. Chem., 2013, 52, 14178 CrossRef PubMed.
- D. Goldfarb, V. Kofman, J. Libman, A. Shanzer, R. Rahmatouline, S. Van Doorslaer and A. Schweiger, J. Am. Chem. Soc., 1998, 120, 7020 CrossRef.
- R. D. Britt, J. L. Zimmermann, K. Sauer and M. P. Klein, J. Am. Chem. Soc., 1989, 111, 3522 CrossRef.
- (a) T. A. Stich, J. W. Whittaker and R. D. Britt, J. Phys. Chem. B, 2010, 114, 14178 CrossRef PubMed; (b) Simultaneous simulations of both 14N in Fig. S7† are important for a full description of the signal in Fig. 3, yet these are beyond the scope of the present work.
- S. S. Eaton, K. M. More, B. M. Sawant and G. R. Eaton, J. Am. Chem. Soc., 1983, 105, 6560 CrossRef.
- J. Ballmann, R. F. Munhá and M. D. Fryzuk, Chem. Commun., 2010, 46, 1013 RSC.
- R. H. Crabtree, Chem. Rev., 2016, 116, 8750 CrossRef PubMed.
- Use of D2 in place of H2 did not lead to any change in the 1H NMR spectrum, nor did any new resonances appear in the 2H NMR spectrum (other than D2 itself). These data are consistent with H/D being directly bound to the paramagnetic Fe centre.
- Yellow/green crystals form upon cooling (−35 °C) saturated solutions of [1]+[BArF4]− in Et2O under N2/H2, respectively. However, attempts to obtain structural data from these (presumably of [1·N2/H2]+[BArF4]−) were thwarted by a rapid loss in crystallinity during handling.
- W. A. Gunderson, D. L. M. Suess, H. Fong, X. Wang, C. M. Hoffmann, G. E. Cutsail III, J. C. Peters and B. M. Hoffman, J. Am. Chem. Soc., 2014, 136, 14998 CrossRef PubMed.
- O. M. Usov, P. S.-T. Choi, J. P. Shapleigh and C. P. Scholes, J. Am. Chem. Soc., 2006, 128, 5021 CrossRef PubMed.
- Exact determination of the fraction of spin on the central Fe(I) ion and the fractions of spin on ligating 31P nuclei is non-trivial due to the nature of the particular s-orbital and p-orbital character of the molecular orbital, and these differ by a factor 36.5 for implications of ligand spin density. See: J. R. Morton and K. F. Preston, J. Magn. Reson., 1969, 30, 577 Search PubMed.
- (a) R. H. Morris and R. Wittebort, Magn. Reson. Chem., 1997, 35, 243 CrossRef; (b) G. A. Facey, T. P. Fong, D. Gusev, P. M. Macdonald, R. H. Morris, M. Schlaf and W. Xu, Can. J. Chem., 1999, 77, 1899 CrossRef.
- Diamagnetic trans-[Fe(depe)2(H)(H2)]+[BArF4]− was identified by 1H and 31P{1H} NMR spectroscopy. See: M. Bautista, K. A. Earl, R. H. Morris and A. Sella, J. Am. Chem. Soc., 1987, 109, 3780 CrossRef; M. V. Baker, L. D. Field and D. J. Young, J. Chem. Soc., Chem. Commun., 1988, 546 RSC . The rate of conversion was observed to be somewhat variable (depending on solvent, trace impurities etc.), and promoted by elevated temperatures and/or extended periods. The mechanism is currently under investigation.
- Computational data for [1·H2]+ predict a similar dihedral angle between Fe(PP) planes (16.9°) as that for [1·N2]+ (18.9°). DFT calculations on [1]+ and [1·N2]+ were in good agreement with experimental X-ray crystallographic data (see ESI†).
- Unfortunately the difficulty of ensuring a consistent temperature throughout the headspace of the sample tube, and the inability to accurately deconvolute the overlapping ESR signals of [1]+, [1·N2]+ and [1·H2]+ (which become increasingly isotropic at elevated temperatures, likely due to phase change behaviour), precluded a solid-state thermodynamic analysis of binding.
- Theoretical Chemistry, ADF2016, SCM, Vrije Universiteit, Amsterdam, The Netherlands, http://www.scm.com Search PubMed.
- S. H. Vosko, L. Wilk and M. Nusair, Can. J. Phys., 1980, 58, 1200 CrossRef.
- A. D. Becke, Phys. Rev. A: At., Mol., Opt. Phys., 1988, 38, 3098 CrossRef.
Footnote |
| † Electronic supplementary information (ESI) available: Full experimental details and characterisation data. CCDC 1451414. For ESI and crystallographic data in CIF or other electronic format see DOI: 10.1039/c8sc01841c |
| This journal is © The Royal Society of Chemistry 2018 |