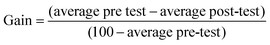A new multimedia application for teaching and learning chemical equilibrium

Abstract

This study presents a method for teaching the subject of chemical equilibrium in which students engage in self-learning mediated by the use of a new multimedia animation (SEQ-alfa©). This method is presented together with evidence supporting its advantages. At a microscopic level, the simulator shows the mutual transformation of A molecules into B molecules and vice versa for the reversible one-step chemical reaction, A(g) ⇔ B(g). The user defines the reaction as endothermic or exothermic and sets a given reaction temperature; SEQ-alfa© then calculates the kinetic constants of the forward and reverse reactions. Based on initial given concentrations, the animation then evaluates the respective rates and concentrations, as well as the concentration quotient value, as the reaction progresses towards its equilibrium state. SEQ-alfa© also demonstrates the effects of concentration and temperature alterations on the reaction's progress and the value of the reaction quotient until equilibrium is reached, thus giving the equilibrium constant. In addition, a validation of this new approach was carried out with 27 teachers. A pre-test and post-test of students’ understanding of the basic concepts of chemical equilibrium were conducted. Tested groups attained a 50% average learning gain (n_exp = 130, n_ctrl = 26). Those students with little or no previous knowledge acquired a better understanding of chemical equilibrium. In addition, 80% of teachers agreed that the multimedia resource and its complementary activities had positive effects.

---

Introduction

Research on improving the teaching of chemical equilibrium (CE) has been conducted for the past 40 years (Burke, 1977; Hackling and Garnett, 1985), in particular, identifying different conceptions of chemical equilibrium held at the secondary and university levels (Tyson et al., 1999). To enhance learning, research suggests emphasising quantitative aspects so that students can visualise the relationship between concentrations in a system in CE, broadening the variety of examples when dealing with Le Chatelier's principle by visualising CE displacements through changes in temperature or concentration, and using graphs to show how concentrations change over time to reach chemical equilibrium.

However, despite these suggestions, which are supported by research aiming to make changes to curricula in secondary and university education, the same alternative conceptions persist today in the teaching and learning of chemical equilibrium (Bergquist and Heikkinen, 1990; Cloonan et al., 2011; Bindel, 2012). It is not sufficient to show students how to recognise and correct their mistakes, as this does not change their ideas. Students’ understanding of CE must be monitored in order to develop strategies that fit with their preconceived ideas. Tyson et al. (1999) showed that there are three important issues in teaching equilibrium:

• Students use multiple explanations to predict the effect of changes induced to mixtures in equilibrium.

• There are many words that have different meanings for teachers, students and textbooks.

• The sophisticated nature of CE has a significant effect on its teaching.

Hence, at a secondary education level, three levels of explanation can be used to predict what will happen when a system in equilibrium is altered: (1) Le Chatelier's principle, (2) equilibrium law, comparing Q with K_eq, and (3) the analysis of reaction rates by collision theory.

Teaching chemical equilibrium

At the Universidad Técnica Federico Santa María, the course ‘Chemistry and Society’ is given in the first year of the curriculum to all engineering students. Approximately 1000 students take the course each semester. One area that is typically difficult for the students is chemical equilibrium. Nevertheless, this area is complicated for many students all over the world (Banerjee, 1991; van Driel and Gräber, 2002). For different reasons, students have reported a series of incorrect concepts that together lead to a misunderstanding of reversible reactions and the state of equilibrium attained in these reactions (Wheeler and Kass, 1978; Hackling and Garnett, 1985; Anamuah-Mensah, 1987). As a result, several research studies on chemical equilibrium have covered understanding of the basic concepts and the development of techniques to facilitate problem-solving regarding chemical equilibrium.

Analogies based on different didactic types of games (e.g., cards, coins, tiles, and matches) have been used to represent particles in a chemical system that is trying to reach equilibrium (Wilson, 1998; Bindel, 2012; Ghirardi et al., 2014). However, these games require a set amount of time to be carried out during a class, and they generally require several iterations to allow conclusions to be drawn. This requirement detracts from the feasibility of implementing such methods, considering the limited number of classroom sessions available to cover the subject matter. On the other hand, since students work with everyday objects, it is difficult to relate microscopic events occurring in a system that is attempting to attain equilibrium with macroscopic properties that can be observed.

Due to the widespread and growing use of technology, models associated with the teaching of different chemistry concepts are needed. Recently, Park et al. (2017) studied the use of computational models in science and reported that they have a positive influence on test results (in terms of their understanding of the model) and on students’ learning progress (Park et al., 2017).

By exploring different models, students can build their own ideas about certain events. Visualisation through symbols, graphs, mathematical equations, animations, simulations and other representations could help students describe and explain some systems’ behaviour and relate a macroscopic problem to an analogous problem on a microscopic level (Linn, 1993; Talanquer, 2011). Many interactive simulations have been developed to represent chemical equilibrium, e.g., the PhET chemistry simulation (https://phet.colorado.edu/en/simulations/category/chemistry) and the interactive chemical thinking tool from the University of Arizona (http://cbc.arizona.edu/~jpollard/fido/fido.html), among others.

In contrast, other researchers have facilitated students’ understanding of problems by developing spreadsheets of calculations from experiments similar to those developed with the games using objects and default transfer rates. In general, the forward and reverse reaction rate constants are assumed to be predetermined without establishing a correlation with temperature. The spreadsheets show how the resulting concentrations change spontaneously until equilibrium is reached, including the effect of altering a system at equilibrium (either by changing the concentrations or temperature) and graphing the variations in concentration (Paolini and Bhattacharjee, 2010; Raviolo, 2012; Serrano, 2016). Only a few authors have reported the results of assessments obtained with some of these techniques, although they have mentioned that students' chemical equilibrium learning is improved.

From our teaching experience over the years, we have identified several misconceptions students have about chemical equilibrium. They are not clear about the characteristics of a reversible reaction and the dynamic character of the equilibrium state, including (among other things) the fact that the concentrations of the species at equilibrium are equal, the value of K_eq depends on the initial concentration, and the reaction rate is often linear. The present study aims to contribute to this research through the development of an animation (SEQ-alfa©) to enhance understanding of the causal relationship between microscopic representation and symbolic microscopic representation (Johnstone, 1982; Bernhard, 2003; Arellano et al., 2014) in the context of chemical equilibrium. SEQ-alfa© provides calculations, graphs and a visual analogy representing microscopic processes. Additionally, the present study aims to describe the preliminary learning impact of the animation, which was given to first-year engineering students under the guidance of a teacher and supported by a series of inquiry activities to facilitate autonomous learning of the basic concepts of chemical equilibrium. This teaching approach was an adaptation of the POGIL (Process Oriented Guided Inquiry Learning) strategy (Hein, 2012).

SEQ-alfa© multimedia application

SEQ-alfa© is a simple digital recourse to enhance understanding of the basic concepts of chemical equilibrium in first-year engineering students. Its design (Fig. 1) includes an animation that represents one analogy of the dynamic nature of equilibrium through visualisation of an idealised elementary reversible chemical reaction A(g) ↔ B(g) that is either endothermic or exothermic. The gaseous compounds’ molecules are represented as spheres of different colours (molecules of A = green spheres and B = blue spheres). They move from one side to the other of a one-litre container, representing microscopic transformations from A to B and from B to A as jumps over a “barrier” and colour changes. However, it should be explained to students that the barrier has no physical meaning and is only intended to facilitate visual representation of the forward and reverse reaction because, in a real system, all molecular species are mixed within the reactor.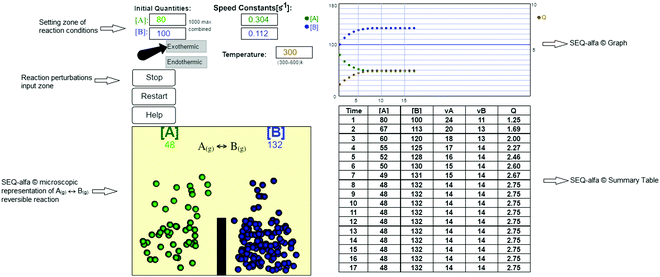

Fig. 1 SEQ-alfa© multimedia application. http://www.oeaquimicaysociedad.usm.cl/actividad password: UDARN.

Additionally, SEQ-alfa© generates a table, analogous to a spreadsheet, that displays the following reaction characteristics for each unit of time [s]: the concentration of A and of B [molecules L⁻¹]; simultaneous forward (A → B) and reverse (A ← B) reaction rate values [in terms of molecules L⁻¹ s⁻¹]; and the reaction quotient 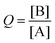. Additionally, it displays a graph showing the evolution over time of the concentration of A, the concentration of B and the value of Q. SEQ-alfa© integrates the contributions of different existing resources into a single digital object and at the same time adds a visual representation of the events taking place at a microscopic level.

The values of the reaction rate constants for the forward reaction (k_A) and the reverse reaction (k_B) were fictional. They were calculated using an Arrhenius-like equation 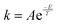(where T is the selected temperature, and A and E are constants whose values are fictitious). Nevertheless, students were able to establish a directly proportional relationship between temperature and the reaction rate constant, i.e., as the temperature increases, both constants (k_A and k_B) increase in value, irrespective of whether the reaction is exothermic or endothermic. For this elementary reaction, the ratio of the forward and reverse reaction rate constants determines the value of K_eq for the system.

SEQ-alfa© allows the user to choose the reaction type (endothermic or exothermic), set the reaction temperature (from 300 to 600 [K]), and set the initial number of A and B molecules per L (recommended over 90 molecules; see Appendix 1). Furthermore, perturbations of concentrations or temperature can be introduced to modify a system at equilibrium.

SEQ-alfa© supported activities

SEQ-alfa© allows and promotes self-learning, which is relevant to a student's education today. To use the multimedia application, students follow a predetermined sequence of experiments and solve the proposed activities, either in class or as homework (in our case, the study was performed during class time). In this way, they can observe, analyse, discuss and draw conclusions regarding basic concepts of chemical equilibrium.

Methodology

SEQ-alfa© and its proposed activities can be carried out by an individual student or cooperatively on a computer, tablet or mobile phone in any browser that supports Flash. We recommend using a PC or Mac computer (desktop or laptop with a mouse for ease of viewing and operation) with the Chrome browser. We believe that SEQ-alfa© is a significant contribution to teaching and learning the complex subject of chemical equilibrium in secondary education and at the initial learning stage of chemistry on the university level. The aim of the present study was to evaluate this new multimedia animation (SEQ-alfa) for the teaching of chemical equilibrium in first-year engineering students.

Participant sample

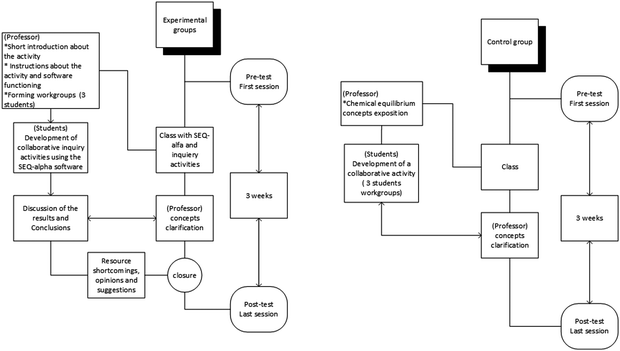
Prior to the study, this study was presented to and approved by the University ethics committee. All participants signed an informed consent agreement (Appendix 4). First-year engineering students performed the interactive classwork collaboratively in small teams of two or three students during a 90 minute class session, learning and discussing conclusions regarding chemical equilibrium concepts. This approach was an adaptation of the POGIL strategy (Hein, 2012) under the teacher's guidance and motivation.

A quasi-experimental design was adopted, comprising a control group and five test groups. All students were evaluated by pre- and post-tests within a 3 week period (each diagnostic test lasted 15 minutes).

The control group (C) contained 24 students who continued with active classes of 90 minutes, which included the exposition of concepts by the professor and a collaborative activity resolution (Fig. 2). Typically, collaborative activity was performed over a 45 minute period working in small student teams. The five experimental groups (A, B, D, E and F), containing a total of 130 students (averaging approximately 26 students per group), worked for 90 minutes with SEQ-alfa©, solving problems and engaging in self-construction of knowledge (Fig. 2). Before beginning, the teacher gave a brief introduction to the animation functions and the aim of each activity.

Fig. 2 Experimental and control class design.

Four activities were implemented in pre-printed form, with spaces to fill in. These activities included a brief description or inquiry and its purpose (Table 1).

Table 1 Purpose of each activity for understanding chemical equilibrium, as well as the corresponding animation and inquiry activities

Activity	Specific purpose
1	To understand that equilibrium is a dynamic process.
2	To analyse the behaviour of the forward and reverse reaction rates when reaching equilibrium and to understand what happens to the concentrations of the agents at equilibrium.
	To deduce the value of Keq with respect to initial concentrations at a constant temperature.
	To analyse the evolution of Q leading up to equilibrium, as well as the spontaneous reaction direction (forward or reverse) before reaching equilibrium.
3	To predict which direction the reaction favours (forward or reverse) using the equilibrium law.
4	To deduce the value of Keq with respect to reaction temperature for exothermic and endothermic systems.

---

Students were expected to use observation and analysis of the information generated in the animation when doing the activities and to draw conclusions concerning the following general aims, which were evaluated through diagnostic tests (words in parentheses are abbreviations for each aim):

(1) To understand that equilibrium is a dynamic process (dynamic).

(2) To analyse the behaviour of forward and reverse reaction rates when they reach equilibrium and what happens to the concentrations of the agents at equilibrium ([ ]_eq).

(3) To determine the influence of the initial concentrations on the value of the equilibrium constant (K_eq − [ ]_ini).

To determine the influence of temperature on the value of the equilibrium constant in exothermic and endothermic processes (K_eq − T).

The effect of the use of SEQ-alfa© in achieving these objectives was validated by the results of pre- and post-tests (Appendix 2). Results from the experimental groups can also be contrasted with those of the control group. Although no tests were given during the classroom activities, each group can assess whether they have performed the task correctly, as the teacher briefly summarises the major expected results of the problem situation and answers any questions that have arisen.

Additionally, 27 chemistry teachers participated in the validation of SEQ-alfa© and its associated activities. After they performed the activities using the instrument, they completed a survey asking their opinion on the learning resource.

Activity: influence of initial concentrations on the value of K_eq

The following section examines activity 2 as an example of one of the activities (see the full list of activities in Appendix 3). The temperature is set to 300 K (k_A = 0.304 and k_B = 0.112), and an exothermic reaction is selected. The student simulates three experiments: for each one, different initial concentration values of A and B are input, as shown in Table 2, and the table is completed with the results from SEQ-alfa©.

Table 2 Summary table for activity 2 results

T = 300 K	Exp. 1	Exp. 2	Exp. 3
[A]ini	80	0	700
[B]ini	100	200	216
Q ini	1.25	∞	0.31
v Aini	24	0	213
v Bini	11	22	24
v Aeq	14	16	75
v Beq	14	16	75
[A]eq	48	54	247
[B]eq	132	146	669
K eq	2.75	2.70	2.71

---

Once the three experiments have been run, the student answers a series of questions in order to reach certain conclusions in accordance with the objectives of the activity. It is natural that the animation (SEQ-alfa©) should provide slightly different values for K_eq for experiments carried out at the same temperature (in general, discrepancies less than 2%). It must be explained to students that, analogous to every experimental procedure, SEQ-alfa© has an associated error since the concentrations are calculated with discrete numbers of molecules that cannot be fractionated.

Given the summary table from activity 2 and the answers to the presented questions, students can conclude the following:

(a) At a set temperature, the values obtained for K_eq are practically equal, with discrepancies approximately 1.9 to 0.4% (<2%).

(b) At equilibrium, the forward and reverse reaction rates become equal.

(c) At the set temperature, the value of Q_ini is different in each experiment, but when equilibrium is reached (i.e., Q = K_eq), the ratio 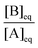will have the same value.

(d) Concentrations of A and B vary over time, and this variation directly influences the reaction rate, where v_At−1 = k_A[A]_t−1 and v_Bt−1 = k_B[B]_t−1 with [A]_t = [A]_t−1 + v_Bt−1 − v_At−1 and [B]_t = [B]_t−1 + v_At−1 − v_Bt−1.

(e) The rate of the forward reaction A → B (v_A) increases, while the rate of the reverse reaction A ← B (v_B) decreases when Q_ini > K_eq. As an example, in experience 2 of this activity [A] increases from its initial value (0 to 54), and [B] decreases from its initial value (200 to 146), indicating that the reverse reaction, in which A is formed, is favoured. When Q_ini < K_eq (Exp. 1 and 3), the rate of the forward reaction A → B (v_A) decreases, while the rate of the reverse reaction A ← B (v_B) increases, i.e., [A] decreases from its initial value (Exp. 1: 80 to 48) and [B] increases from its initial value (Exp. 1: 100 to 132). These changes indicate that the forward reaction, in which B is formed, is favoured. In summary, if Q_ini = K_eq, the system is at equilibrium; if Q_ini < K_eq, the forward reaction is favoured, forming more B; and if Q_ini > K_eq, the reverse reaction is favoured, forming more A.

Discussion

The results of the pre- and post-tests show the percentage of students who had prior knowledge of the class objective and the percentage who acquired the knowledge after (a) their usual active classes (control group) or (b) the experimental class using the didactic self-learning resource with teacher guidance (experimental groups).

According to Benegas (Benegas and Zavala, 2013; Zavala, 2013; Benegas and Sirur Flores, 2014), the gain is converted into a parameter that measures course knowledge irrespective of the initial level of knowledge, thus allowing comparison of the effectiveness of the didactic resource across groups with different levels of prior knowledge. This approach is appropriate for the present situation due to the heterogeneity of the different groups involved in the study. The normalised gain was calculated as follows:

Table 3 shows results obtained on the pre- and post-tests given to each group for each general aim evaluated (see the Methodology section for details).

Table 3 Pre and post-test results

Aims	C (25)^a			A (29)^a			B (27)^a			D (27)^a			E (22)^a			F (26)^a
	Pre (%)	Post (%)	Gain	Pre (%)	Post (%)	Gain	Pre (%)	Post (%)	Gain	Pre (%)	Post (%)	Gain	Pre (%)	Post (%)	Gain	Pre (%)	Post (%)	Gain
% correct answers;a (X) number of evaluated students; Pre: pre-test; Post: post-test.
1(dynamic)	25	46	0.28	21	90	0.87	48	59	0.21	19	52	0.41	18	86	0.83	19	96	0.95
2 ([ ]eq)	4	79	0.78	34	93	0.89	22	96	0.95	59	81	0.55	32	91	0.87	12	85	0.83
3 (Keq − [ ]ini)	29	46	0.24	3	34	0.32	41	33	−0.13	48	44	−0.07	41	18	−0.38	12	19	0.09
4 (Keq − T)	54	79	0.55	72	93	0.75	67	100	1.0	81	93	0.6	73	100	1.0	81	85	0.20

---

As seen in Table 3, the aim of visualising equilibrium as a dynamic process (aim 1) was, in general, satisfactorily achieved, with an average gain of 0.65 for experimental groups relative to the control group. This pattern was similar to results obtained for aim 4, which dealt with the influence of temperature on the value of K_eq, where the average gain was over 0.70. Although students of experimental group F already had knowledge concerning the aim (with 81% accuracy on the pre-test), the use of SEQ-alfa© increased learning by 20% in the subset of students in this group that had little knowledge about this objective.

The animation was successful for visualising chemical equilibrium at the microscale by analogy. However, the results of aim 3 demonstrate one of the limitations of this first version of the resource. Students were unable to understand that the quotients of whole numbers (in the calculation of K_eq) frequently involve answers with fractions, leading to a discrepancy of approximately 2% between cases (when working under the recommended conditions, as shown in Appendix 1); however, working with higher initial amounts of “molecules” decreased the error. Therefore, this issue will be clarified in subsequent activities because it is necessary that the students are aware that every experimental procedure is subject to a small degree of error. The error calculation was added as part of subsequent activities, demonstrating the model's fallibility to students since models are only a representation to facilitate the understanding of certain event (Table 3). We hope that misunderstanding concerning the influence of initial concentrations on the value of K_eq can be avoided.

Data analysis

The analysis of data obtained from the diagnostic pre- and post-tests did not follow a normal distribution (Anderson–Darling tests, P < 0.10). Therefore, in order to identify any significant differences between the median values of the experimental groups (A, B, D, E and F) and the control group (C), the nonparametric Mann–Whitney U test was applied (Table 4). This test allowed comparison of the medians of independent groups with different sample sizes at a significance level of α = 0.05. Significant differences were observed only between the medians of the control group (C) and experimental groups B and D on the initial test and between the medians of group C and experimental group A on the post-test. These findings indicate that, in general, there were no significant differences in medians on the diagnostic tests between the methodology used by the control group and that used by the experimental groups. It can be inferred that most of the students in each group, including controls, attained a score close to 75 (median) in the post-test.

Table 4 Median p-values for α = 0.05 using nonparametric Mann–Whitney U-tests

	p-Value	Median
* Values with significant differences: Pre: pre-test; Post: post-test.
Apre/Cpre	0.4116	25/25
Bpre/Cpre	0.0361*	50/25
Dpre/Cpre	0.0010*	50/25
Epre/Cpre	0.0861	37.5/25
Fpre/Cpre	0.9686	25/25
Apost/Cpost	0.0063*	75/75
Bpost/Cpost	0.1670	75/75
Dpost/Cpost	0.3106	75/75
Epost/Cpost	0.0666	75/75
Fpost/Cpost	0.1706	75/75

---

Fig. 3 illustrates between-groups comparisons for pre- and post-tests, using box-and-whisker plots to illustrate how the distributions of data varied around the medians and whether there was greater or lesser dispersal of the data. The experimental and control groups were very heterogeneous, but all exhibited a general improvement in learning, with median shifts (Table 4) towards better scores on the post-test and a reduction in dispersion. Additionally, the right graph (post-test results) shows a general decrease in dispersion for the experimental groups, in contrast to the control group. This fact may indicate an increase in knowledge concerning chemical equilibrium in the experimental groups.

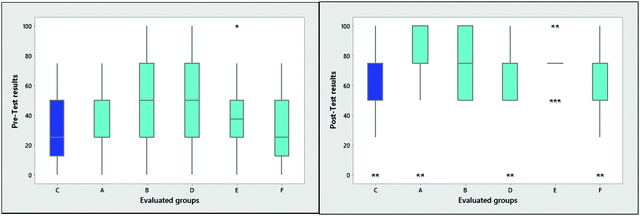Fig. 3 Box and whisker plot of pre- (left) and post-test (right) results for the control (C) and experimental groups.

There was a notably high percentage of low scores on the pre-test (an average of 54% of students earned grades in the range from 0 to 25 out of 100 points), indicating that many students have little or no knowledge about this area of chemistry (which is the type of student at which our self-learning resource is typically aimed). Nevertheless, post-test results demonstrated that students with little or no knowledge of chemical equilibrium improved their grades and acquired a greater understanding of the subject. The percentage of students demonstrating improvement was 90% in the experimental groups and 70% in the control group. The use of analogies to improve learning of chemical equilibrium has been reported by other researchers. For example, Huddle et al. (2000) used cards to represent different equilibrium situations and concluded that students with prior knowledge were able to refine that knowledge, but that students with little knowledge of the subject saw no improvements (Huddle et al., 2000). In the present case, though there was an average gain (0.5) in the total of the test results, the participants that benefited most were students with little prior knowledge of the subject.

The use of SEQ-alfa© as a self-learning resource resulted in a normalised gain of more than 0.50 for the experimental groups, despite the misunderstanding generated in relation to objective 3, which required clarification by the teacher. This value is within the range of normalised gains reported by Benegas for achievement based on active methods (Benegas and Zavala, 2013). At the same time, the control group attained a normalised gain of nearly 0.40, which was expected, as this group participated in an active class.

Statistically, there were no significant differences between the control and experimental groups. The experimental groups worked collaboratively, as did the control group; however, it is remarkable that students in the experimental groups did not receive the concepts from the teacher. They were able to explore concepts by observation, examining the data and engaging in discussion to develop their own mental constructs.

Based on the experiments, students concluded that the resource was useful to them, but they needed more time than the amount given for the proposed activities to gain a full understanding of how SEQ-alfa© works.

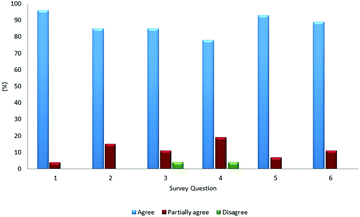
Additionally, 27 chemistry teachers who give classes to first-year university students performed the designed activities using the SEQ-alfa© animation. Fig. 4 shows the results of a survey given to these 27 teachers after having completed the experiences. More than 85% of the teachers considered SEQ-alfa© an attractive, game-oriented, and dynamic resource appropriate for teaching chemical equilibrium. The numbers on the x-axis of the graph indicate the questions in the survey: (1) Does SEQ-alfa© allow students to visualise the dynamic nature of equilibrium at a microscopic level? (2) Does it allow students to verify that when equilibrium is attained, forward and reverse reaction rates are equal, and the concentrations at equilibrium remain constant? (3) Does it allow students to analyse the effect of changes in initial concentrations on the value of K_eq? (4) Does it allow students to analyse the effect of changes in temperature on the value of K_eq? (5) Does it demonstrate the changes that occur when a homogeneous system in equilibrium is altered by introducing or removing a reagent and/or product? (6) Does it demonstrate the changes that occur when a homogeneous system in equilibrium is altered by varying the temperature of the system?

Fig. 4 Results of SEQ-alfa© validation survey given by 27 chemistry teachers.

The teachers also found the insufficient time allotted for each activity to be the primary difficulty, and they reported other difficulties in formulating a subset of questions associated with the complementary activities.

These findings have been taken into account to improve the methodology proposed in the present study. Furthermore, application of the resource revealed that 7% of the teachers incorrectly perceived the concept of reaction rate as indicating the movement of particles and not the number of particles transformed during a set time. This finding was useful for clarifying this concept and instructing teachers to better understand the model, as found in the conclusion of Park et al. (2017).

Conclusions

Our tool is a useful didactic resource to promote understanding of the basic concepts of chemical equilibrium, allowing students to build these concepts through self-learning guided by activities designed to achieve this aim. After using SEQ-alfa©, the learning gain percentage increased 50% and the number of students who were able to comprehend the concepts related to each objective also increased. It can be concluded that the students with some prior knowledge also benefited from the use of the resource, as did the students with little or no prior conceptions of chemical equilibrium. The next step is to combine the use of this improved self-learning resources in an inverted active class and thus achieve even greater strengthening and refinement of the difficulties that students can find in understanding chemical equilibrium, giving them an opportunity to perform activities with SEQ-alfa© in accordance with individual learning speeds.

The work was delivered to engineering students. Would there be a difference in approach if used with students specialising in chemistry? Would the latter have more sophisticated ideas and be better equipped to engage with the material?

Looking at the future use of the resource, it has now been perfected based on this first study, following the opinions and suggestions of students and teachers and thus decreasing the possibility that students acquire incorrect notions. In addition, other activities with the use of the simulator have been created for the experiments in which an alteration (in concentration or temperature) is introduced into a system in equilibrium.

Implication for learning

This package deals with an elementary reversible first order reaction. It is the most straightforward example developed for first year or secondary level students understanding of the basic chemical equilibrium concepts. But, is not representative of more complex reactions like those commonly met in industrial production of chemicals. On the other hand, to avoid misunderstanding SEQ-alfa must be used under teacher's guidance or following its instructions. In a future project, we intend to develop a resource that considers more complex cases.

Conflicts of interest

The authors have no conflicts of interest to declare.

Appendix 1 Calculations in SEQ-alfa©

SEQ-alfa© represents a reversible single-step reaction A_(g) ↔ B_(g) as spheres that represent molecules switching side and changing colour. In order to provide a microscopic view of the reaction, it is considered that each sphere represents a molecule. Therefore, the calculations work only with discrete amounts, implying rounding the results to whole numbers. k_A and k_B are the respective reaction rate constants for the forward reaction (A → B) and the reverse reaction (A ← B). The simulator calculates k_A and k_B using an equation similar to the Arrhenius equation (e.g.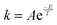; where: A and E are constants, and T is the temperature in Kelvin (K) set by the user). The values that appear in the table are as follows:

• [A] and [B] are the concentrations of A and B evaluated as [molecules L⁻¹] and calculated as [A]_t = [A]_t−1 − v_At−1 + v_Bt−1 and [B]_t = [B]_t−1 − v_Bt−1 + v_At−1 (with t = 0, 1, …, n in [s]); the initial values ([A]_i and [B]_i) are selected by the user.

• v_At and v_Bt as expressed in [molecules L⁻¹ s⁻¹] and are, respectively, the transformation rates of A to B and B to A, and they are calculated as k_A[A]_t and k_B[B]_t.

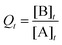• (when Q reaches a constant value, then Q_eq = K_eq).

In all experimental measurements, a degree of error in the values obtained is accepted. Therefore, a graph was drawn up of the discrepancies generated by the simulator when calculating the equilibrium constant, Fig. 5, at constant temperature and different numbers of initial molecules per L (for a total range of molecules per L between zero and 600). The aim was to identify the range of errors which remains below 2%, and therefore the optimal working conditions.

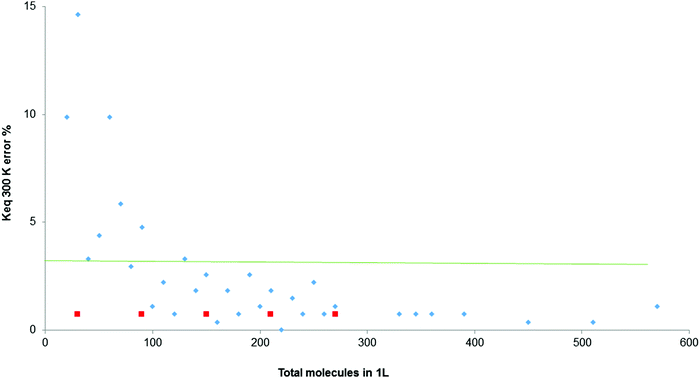Fig. 5 Percentage error in the calculation of K_eq for the total molecules between 0 and 600, at 300 K (orange line denotes 2% of error).

In Fig. 5, only above 250 molecules per L does the error remain under 2%. The red squares indicate that for these amounts of total molecules, K_eq fluctuates between two values.

This gave us two options: (1) abandon the representation of the reaction at a microscopic level, which was one of the objectives of the development of the simulator, and make calculations for continuous quantities [mol], fully solving the problem; or (2) keep the microscopic representation and modify the algorithms to minimise errors. The second option was chosen, altering some algorithms and including more variables to eliminate the fluctuation and minimise error. After inputting these improvements, a second graph of the error was calculated against total molecules per L, this time for 4 separate temperatures, giving Fig. 6.

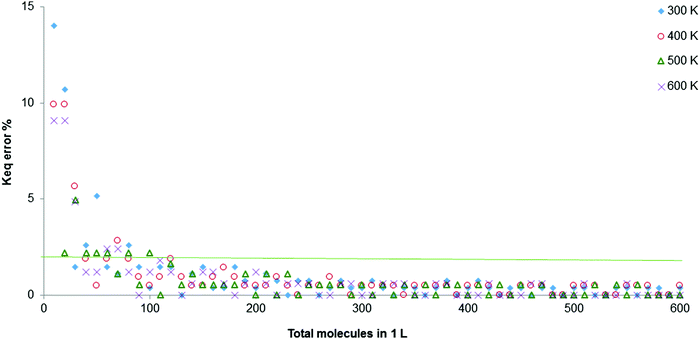Fig. 6 Percentage error in the calculation of K_eq for the total molecules between 0 and 600, at T from 300 to 600 K (orange line denotes 2% of error).

In Fig. 6, it can be seen that above 90 spheres (molecules) the percentage error remains below 2%. The oscillation between two values has been completely removed. It would also be possible to work between 50 and 90 molecules in the 1 L container to achieve a better visualisation of the different experiments, thus the values of the equilibrium constants would be equal. The recommended ranges are 90 to 500 total initial molecules per L and a temperature between 300 and 600 K.

Appendix 2. Chemical equilibrium concepts: diagnostic test

Mark with an X the options that you consider correct

1. In a reversible reaction:

• The reaction always happens in the sense of reactants to products (forward).

• The reaction occurs first from the reactants to products (forward) and subsequently from reactants to products (reverse) until reaching equilibrium.

• Both forward and reverse reactions occur simultaneously, even when the system is at equilibrium.

2. What happens when the system reaches equilibrium?

• The reactants are finished when the system reaches equilibrium.

• The forward reaction rate increases and the reverse rate decreases at equilibrium.

• The concentrations of reactants and products are equal.

• The rates of forward and reverse reactions are equal at equilibrium.

• The concentrations of reactants and products are constants.

3. Does the initial concentration of reactants and products affect the value of the equilibrium constant and equilibrium concentration?

• No, initial concentrations do not influence either the value of the equilibrium constant or the equilibrium concentration.

• No, initial concentrations do not influence the value of the equilibrium constant, but they affect the value of equilibrium concentration.

• Yes, initial concentrations influence the value of the equilibrium constant but do not affect the value of the equilibrium concentrations.

• Yes, initial concentrations affect both the value of the equilibrium constant and the equilibrium concentration.

4. Does temperature influence the value of the equilibrium constant?

• No, the equilibrium constant only changes with concentration.

• No, temperature does not influence the value of the equilibrium constant.

• Yes, temperature changes the value of the equilibrium constant.

Appendix 3. Activities

Activity 1

The students are asked to conduct a simulation up to time t = 30 and complete the following table (Table 5) by observing the simulator, the table and the graph for an exothermic system at 300 K.

Table 5 Summary results for activity 1

t [s]	[A]	[B]	v A	v B	Q
0	0	200	0	22	∞
2	22	178	7	20	8.09
4	42	158	13	18	3.76
6	50	150	14	16	3.00
8	53	147	14	15	2.77
10	54	146	14	14	2.70
20	54	146	14	14	2.70
30	54	146	14	14	2.70

---

An analysis of what is observed in the simulator at t = 10, 20 and 30 is then performed. Through these observations, the student perceives that although the reaction reached equilibrium in less than half the time allotted, the forward and reverse reactions continue to occur (i.e., the molecules continue transforming from one to the other simultaneously), even though the equilibrium concentrations do not change, and the rates of both reactions are equal. From this activity, the students can reach the following conclusions: (1) at equilibrium, the forward and reverse reaction rates become equal (v_A = v_B = 16 [molecules L⁻¹ s⁻¹]); (2) the equilibrium state is dynamic; (3) the concentrations at equilibrium are stationary ([A]_eq = 53 and [B]_eq = 147 [molecules L⁻¹]); and (4) the forward and reverse reactions occur simultaneously.

Activity 3

In this activity, a challenge was put to the students in the form of this question: how will the system spontaneously move?

Considering again an exothermic reaction at T = 300 K, with an initial [A] = 350 and [B] = 150 [molecules L⁻¹], the students must calculate the value of Q with these initial concentrations using the loss of masses 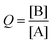. They must compare this estimate of Q with the value of K_eq, deducing that they are the same as in activity 2 since the value of K_eq is the same at a set temperature, even when the initial concentrations vary.

This conclusion can easily be drawn by realising that at the beginning of the experiment the fraction 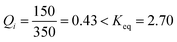. Thus, Q must increase its value. This means that the net process takes place from left to right, favouring the forward reaction (A → B).

The final equilibrium state can be predicted with the simple relationship 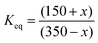. Solving this equation gives x = 215, i.e., the final number of molecules per litre will be 135 for A, whereas for B it will be 365. This is the same result as obtained when students work with the average K_eq value obtained in activities 1 and 2. Students can also perform the simulation and verify these results.

Activity 4

This activity proposes a simulation using the same exothermic system with [A] = 350 and [B] = 150, but the temperature is set to 500 K (higher than previous experiments 1–3). In SEQ-alfa©, students can observe the corresponding constant rates k_A = 0.425 and k_B = 0.233 [s⁻¹] (which are higher than the constant rates of previous activities 1–3; k_A = 0.304 and k_B = 0.112 [s⁻¹]). Students are expected to predict higher reaction rates.

Through this activity, they can see that equilibrium is reached faster (7 [s]) than in activity 3, and K_eq reaches a lower value (1.82) than in activities 1–3. The students can conclude the following: (1) for an exothermic system, higher temperature gives lower K_eq values, and thus the equilibrium constant is indirectly proportional to temperature; and (2) at higher temperatures, higher values are found for the reaction rate constants, and less time is required to reach equilibrium.

The second step of this activity establishes a new reversible chemical endothermic system. In this case, values of [A] = 350 and [B] = 150 [molecules L⁻¹] are initially set. The students perform two experiments, one at 300 K and another at 500 K, maintaining the same initial conditions. The students then complete the following table (Table 6).

Table 6 Summary results for activity 4

	Exp. 1 (300 K)	Exp. 2 (500 K)
Equilibrium time [s]	8	6
K eq	0.67	0.95
v eq	50	80

---

From these results, the following can be concluded: (1) for an endothermic system, higher temperature gives higher K_eq values, and thus the equilibrium constant is directly proportional to temperature; and (2) at higher temperatures, higher values are found for the reaction rates, and less time is required to reach equilibrium.

Appendix 4. Informed consent form: ethical considerations

Address to: students of Chemistry and Society (QUI-010)

Through this informed consent form, you are invited to participate voluntarily this study as part of the OEA-2015 project of the DEA-UTFSM: “Implementation of an application on Moodle platform to stimulate the learning of the students of the course of Chemistry and Society”. In the framework of this project, we investigate the use of an animation (SEQ-alpha) together with inquiry activities to enhance the teaching–learning process of chemical equilibrium. The class activity will take place over two 90 minute sessions.

This modality (an alternative to the usual active class) was developed to improve understanding of the basic concepts of chemical equilibrium and to foster transversal competencies such as the use of digital resources, learning autonomy, collaborative work, and observing, identifying, interpreting, drawing conclusions about, and communicating results.

Your participation is voluntary and, in case of publication, your personal information is confidential and will not be published. Some of the groups will contribute to the study by receiving an active class that includes the development of other collaborative activities without the use of SEQ-alpha.

The aim is to evaluate and validate the use of this resource, where you, as students, may issue comments and suggestions for improvement of this teaching–learning resource.

We emphasise that neither your learning nor your score will be affected if you decline to participate in the activity.

If you wish to participate in this research study, give your name and USM role on the activity form.

Acknowledgements

The researchers gratefully acknowledge financial support from The Office of General Teaching at the Universidad Técnica Federico Santa María (DGD) and the Teaching and Learning Office (DEA) as part of the Olivier Espinoza Aldunate (UTFSM-OEA/2015) Education Research Project; and from Fondecyt Project 1150659 from the Chilean Government's National Commission of Science and Technology (CONICYT).

References

1. Anamuah-Mensah J., (1987), Preliminary investigations into students' representations of the state of chemical equilibrium, Chem. Ind., 1(2), 113–117.
2. Arellano M., Jara R. and Merino C., (2014), Macroscopic, submicroscopic and symbolic representations of matter, Educ. Quím., 25(1), 46–55.
3. Banerjee A. C., (1991), Misconceptions of students and teachers in chemical equilibrium, Int. J. Sci. Educ., 13(4), 487–494.
4. Benegas J. and Sirur Flores J., (2014), Effectiveness of Tutorials for Introductory Physics in Argentinean high schools, Phys. Educ. Res., 10, 010110 DOI:10.1103/PhysRevSTPER.10.010110.
5. Benegas J. and Zavala G., (2013), Evaluación del aprendizaje en física, in Benegas J., Pérez de Landazabal M. C. and Otero J. (ed.), El Aprendizaje Activo de la Física Básica Universitaria, Andavira Editora, S.L., pp. 179–192.
6. Bernhard J., (2003), Physics learning and microcomputer based laboratory (MBL) – learning effects of using MBL as a technological and as a cognitive tool, in Psillos D., Kariotoglou P., Tselfes V., Hatzikraniotis E., Fassoulopoulos G. and Kallery M. (ed.), Science education research in the knowledge-based society, Dordrecht, The Netherlands: Kluwer Academic Publishers, pp. 323–331.
7. Bergquist W. and Heikkinen H., (1990), Student ideas regarding chemical equilibrium: what written test answers do not reveal, J. Chem. Educ., 67(12), 1000.
8. Bindel T. H., (2012), Exploring Chemical Equilibrium with Poker Chips: A General Chemistry Laboratory Exercise, J. Chem. Educ., 89(6), 759–762.
9. Burke B. A., (1977), Chemical equilibrium, J. Chem. Educ., 54(1), 29.
10. Cloonan C. A., Nichol C. A. and Hutchinson J. S., (2011), Understanding Chemical Reaction Kinetics and Equilibrium with Interlocking Building Blocks, J. Chem. Educ., 88(10), 1400–1403.
11. Ghirardi M., Marchetti F., Pettinari C., Regis A. and Roletto E., (2014), A Teaching Sequence for Learning the Concept of Chemical Equilibrium in Secondary School Education, J. Sci. Educ., 91, 59–65.
12. Hackling M. W. and Garnett P. J., (1985), Misconceptions of chemical equilibrium, Eur. J. Sci. Educ., 7(2), 205–214.
13. Hein S., (2012), Positive impacts using POGIL in organic chemistry, J. Chem. Educ., 89, 860–864 DOI:10.1021/ed100217v.
14. Huddle P., White M. and Rogers F., (2000), Simulations for Teaching Chemical Equilibrium, J. Chem. Educ., 77(7), 920–926.
15. Johnstone A., (1982), Macro-and micro-chemistry, Sch. Sci. Rev., 64, 377–379.
16. Linn M., (1993), Using technology to teach thermodynamics: achieving integrated understanding, in Ferguson D. (ed.), Advanced educational technologies for mathematics and science, Berlin: Springer-Verlag, pp. 5–60.
17. Paolini C. and Bhattacharjee S., (2010), Solving Chemical Equilibrium Problems Online, J. Chem. Educ., 87, 456.
18. Park M., Liu X., Smith E. and Waight N., (2017), The effect of computer models as formative assessment on student understanding of the nature of models, Chem. Educ. Res. Pract., 18, 572–581.
19. Raviolo A., (2012), Using a Spreadsheet Scroll Bar to Solve Equilibrium Concentrations, J. Chem. Educ., 89, 1411–1415.
20. Serrano A. T., (2016), Simulación del establecimiento del equilibrio químico utilizando una hoja de cálculo, An. Quím., 112, 95–100.
21. Talanquer V., (2011), Macro, Submicro, and Symbolic: The many faces of the chemistry “triplet”, Int. J. Sci. Educ., 33(2), 179–195 DOI:10.1080/09500690903386435.
22. Tyson L., Treagust D. F. and Bucat R. B., (1999), The Complexity of Teaching and Learning Chemical Equilibrium, J. Chem. Educ., 76(4) 554.
23. van Driel J. and Gräber W., (2002), The teaching and learning of chemical equilibrium, in Gilbert J., de Jong O., Justi R., Treagust D. F. and van Driel J. (ed.), Chemical education: Towards research-based practice, Dordrecht: Kluwer Academic Publishers, pp. 271–292.
24. Wheeler A. E. and Kass H., (1978), Student misconceptions in chemical equilibrium, Sci. Educ., 62(2), 223–232.
25. Wilson A., (1998), Equilibrium: A Teaching/Learning Activity, J. Chem. Educ., 75(9), 1176–1177.
26. Zavala G., (2013), An Analysis of learning in a multi-strategy active-learning course of electricity and magnetism for engineering students, in Eleventh LACCEI Latin American and Caribbean Conference for Engineering and Technology (LACCEI’2013). “Innovation in Engineering, Technology and Education”. August 14–16, 2013 Cancun, Mexico.

---