Evaluating students' abilities to construct mathematical models from data using latent class analysis†
Alexandra
Brandriet
 ,
Charlie A.
Rupp
,
Katherine
Lazenby
and
Nicole M.
Becker
,
Charlie A.
Rupp
,
Katherine
Lazenby
and
Nicole M.
Becker
 *
*
Department of Chemistry, University of Iowa, Chemistry Building, Iowa City, Iowa 52242-1002, USA. E-mail: nicole-becker@uiowa.edu
First published on 3rd January 2018
Abstract
Analyzing and interpreting data is an important science practice that contributes toward the construction of models from data; yet, there is evidence that students may struggle with making meaning of data. The study reported here focused on characterizing students’ approaches to analyzing rate and concentration data in the context of method of initial rates tasks, a type of task used to construct a rate law, which is a mathematical model that relates the reactant concentration to the rate. Here, we present a large-scale analysis (n = 768) of second-semester introductory chemistry students’ responses to three open-ended questions about how to construct rate laws from initial concentration and rate data. Students’ responses were coded based on the level of sophistication in their responses, and latent class analysis was then used to identify groups (i.e. classes) of students with similar response patterns across tasks. Here, we present evidence for a five-class model that included qualitatively distinct and increasingly sophisticated approaches to reasoning about the data. We compared the results from our latent class model to the correctness of students’ answers (i.e. reaction orders) and to a less familiar task, in which students were unable to use the control of variables strategy. The results showed that many students struggled to engage meaningfully with the data when constructing their rate laws. The students’ strategies may provide insight into how to scaffold students’ abilities to analyze data.
Introduction
Scientific inquiry is essential for developing an understanding about the natural world, and the process of constructing models based on empirical data is one way to develop this knowledge. Models in science serve as rich predictive or explanatory tools (Lesh et al., 2000). From this perspective, mathematical equations can also be models, because they are predictive tools that, when the appropriate assumptions are considered, can relate real-world quantities (Harrison and Treagust, 2000). For our study, we characterized students’ abilities to analyze initial concentration and rate data using method of initial rate tasks. The students used the data to construct rate laws (e.g. Rate = k[A]2[B]), which are empirically derived mathematical models. Exponents are used to model the predictive influence of the concentration on the rate, and these exponents are commonly referred to as the reaction orders.The Anchoring Concepts Content Map (ACCM), (Holme et al., 2015) developed by the American Chemical Society Exams Institutes (ACS-EI), describes rate laws as empirically constructed tools that have predictive power (VII.B.1.a and b) (Holme et al., 2015). The ACS-EI described that the ACCM was developed by the ACS community (Murphy et al., 2012, p. 716) and is “likely to span the chemistry content taught in many or most college general chemistry courses” (Holme and Murphy, 2012, p. 722). We believe that this ACCM definition of rate laws suggests that professors believe that rate laws provide an avenue for students to engage in deriving mathematical models from data. However, this raises questions about whether students are engaging in these task as we may hope.
While there is limited research on how students approach method of initial rates tasks specifically, previous research in chemical kinetics suggests that students may hold multiple misconceptions about rate laws and how they are constructed (Bain and Towns, 2016). For instance, students believe that reactant concentration influences the rate in zeroth order reactions (Cakmakci et al., 2006; Cakmakci, 2010; Bain and Towns, 2016), that the reaction rate is expressed using reactants and products (Kolomuç and Tekin, 2011; Bain and Towns, 2016), and that the reaction order can be derived using the stoichiometric coefficients from the balanced chemical equation (Cakmakci et al., 2006; Cakmakci, 2010; Turányi and Tóth, 2013; Bain and Towns, 2016). Underlying these difficulties may be multiple factors, including difficulties in understanding how data are used to empirically construct a rate law.
Fewer studies have focused on how students analyze data to determine rate law exponents. In Cakmakci et al. (2006), the authors presented students with a task involving a zeroth order reaction of the catalyzed decomposition of NO(g) that included (1) the chemical equation, (2) a linear graph of the [NO] vs. time, and (3) the rate law expression (i.e. rate = k[NO]0 = k). When asked to predict what would happen to the reaction rate when the [NO]initial increased, many students based their predictions on rate laws they constructed using the stoichiometric coefficients from the chemical equation, even after the interviewer gave a verbal reminder that the reaction was zeroth order in NO. This suggests that students may have a strong reliance on rote-memorized strategies rather than a conceptual grasp of the empirically derived nature of rate law models.
In our own prior work on student's reasoning about method of initial rates tasks, we examined students’ approaches to a method of initial rates task similar to that shown in Fig. 1, Task 1 (Becker et al., 2017). We conducted fifteen semi-structured interviews and analyzed the data using an inductive approach, focusing on the variation in how students used, interpreted, and mathematized relationships in the data. Our interpretation of the data was guided by a developmental perspective (Wilson, 2009; Duschl et al., 2011; Krajcik, 2012), in that we focused on identifying patterns that suggested increasing sophistication in students’ abilities to analyze data and use their interpretations as evidence of their selected reaction order (Becker et al., 2017). We found five themes in students’ approaches to the method of initial rates task that ranged from the use of surface-features, such as stoichiometric coefficients in the construction of a rate law, to more sophisticated interpretations and mathematization of the trends in the data. Notably, we found that engaging students in a task in which they were asked to critique rate laws constructed by hypothetical students, for all but two students, did not support them in deeper interpretation of data or reflection on the appropriateness of the mathematical model they had constructed. In part, we believe this to be because students possessed limited knowledge of how and why models are critiqued and refined.
 | ||
| Fig. 1 The three sets of initial concentration and rate data used to construct the rate laws. The complete assessment can be found in Appendix 1 (ESI†). | ||
The study reported here builds on our prior work by using latent class analysis (LCA) to examine the validity of the five themes described in Becker and colleagues (2017). The current study also provides insight as to the prevalence of these reasoning patterns in a broader sample of students. As in our previous qualitative study, our goal is not to define the “best-practices” for developing students’ abilities to construct models from data, but instead, to canvas the current state of introductory chemistry students’ responses to a task that is frequently taught and tested in traditional courses. This analysis should provide insight to the effectiveness of current practices, and suggestions for supporting students’ deeper engagement in the important practices of analyzing and interpreting data.
Background
Situated learning and science practice perspectives
Our perspective on learning is informed by situated learning, which considers that students learn through internalization of socially accepted forms of a communities’ practices (Lave and Wenger, 1991). In this perspective, learning and doing are interconnected processes (Brown et al., 1989; Lave and Wenger, 1991). Brown et al. (1989) describes an example in which children learn how to use words through discourse with their families, and therefore, the words are situated in “authentic situations” through real-world examples (Brown et al., 1989, p. 33). In contrast, learning to use words from dictionaries neglects the process of meaningful development, because it does not provide the same use in a social context (Brown et al., 1989, p. 33).Analogously, we make the argument that science is a community that engages in a socially negotiated set of practices. The National Research Council (NRC, 2012) has defined eight science practices that scientists engage in when conducting scientific inquiry. A few of these practices include constructing and using models, analyzing and interpreting data, mathematical and computational thinking, and engaging in argumentation from evidence. These practices, in addition to others, are both socially constructed, used in real scientific inquiry, and important components of learning science (NRC, 2012; Osborne, 2014).
Cooper (2015, p. 1273) argues that most undergraduate chemistry classrooms tend to “favor breadth over depth, often trying to provide courses that ‘cover’ everything that might be deemed important for future chemists, even though most students in introductory courses will never take another chemistry course.” The result is often that students rely on rote-memorized strategies, because they are unable to put all of the facts together to form coherent understandings (Cooper, 2015). Despite explicit instruction, many studies have shown that students leave chemistry courses with multiple misconceptions and highly fragmented mental models (e.g., Stefani and Tsaparlis, 2009; Stamovlasis et al., 2013; Brandriet and Bretz, 2014). We argue that engaging students more intentionally in science practices, such as analyzing and interpreting data and constructing mathematical models, may be one route toward helping students develop deeper and more connected understandings of course content (NRC, 2012; Osborne, 2014; Cooper, 2015).
Analyzing and interpreting data
The focus of our study is on how students engage in the practice of analyzing and interpreting data as a route toward constructing a mathematical model. Findings from data are rarely intuitive or obvious; rather scientists must methodically analyze and interpret that data, so that interpretations of data can be used in support of scientific claims (NRC, 2012; Osborne, 2014). Such analyses may include, for instance, looking for patterns and relationships between variables and testing whether trends in data are consistent with initial hypotheses. The NRC (2012) describes the practice of analyzing data as highly intertwined with other practices, such as mathematical thinking and constructing models. For instance, identification of relationships between variables may be aided by tools, such as graphs and mathematics, with mathematics playing a particularly important role in expressing relationships between different variables in a dataset (NRC, 2012).Despite the importance of analyzing and interpreting data in chemistry and other STEM fields (Osborne, 2014), studies have shown that undergraduate students struggle with key aspects of this practice (Heisterkamp and Talanquer, 2015; Zhou et al., 2016). For instance, Heisterkamp and Talanquer (2015) conducted an in-depth, qualitative case study that examined how an introductory chemistry student used models to explain chemical data. They found that the student tended to use non-productive strategies for making sense of the data, such as relying on surface features and trying to apply ideas that were outside of the relevant context.
Others have found that students may struggle to appropriately use the control of variable (COV) strategy when analyzing data. Zhou et al. (2016) investigated Chinese high school and US college-level physics students’ abilities to recognize variables that could be tested using the COV strategy. The authors used two versions of a written test to assess students: one where the students had to identify testable variables using the experimental conditions, while in the other, they were also provided the experimental outcome data. The results suggested that students had more difficulty recognizing testable variables, when they were given both the conditions and the outcome data. The authors inferred that the students were trying to use the outcome data to identify influential relationships across variables, rather than recognizing if the variable was testable. These results suggest that recognizing that a variable is testable using the COV strategy and coordinating outcome data to the experimental conditions are two distinguishable skills with differing levels of sophistication.
In determining a rate law from data, for instance that shown in Fig. 1, Task 1, students would recognize the need to use the COV strategy to hold the concentration of one reactant constant as they investigate the relationship between the reactant concentrations and the rate. With some experimental designs, for instance that shown in Fig. 1, Task 3, it may not be possible to use COV in this way, and thus flexibility with other numerical strategies is important. After deciding how to examine the impact of the [O2] on the rate using the COV strategy, the student must account for how the [O2] influences the rate, while also using the exponents to mathematically model how the [NO] influences the rate. The goal of evaluating students using such a task is to establish how well students can recognize that both the [O2] and the [NO] simultaneously influence the rate, and previous studies have shown that individuals struggle to reason about how multiple variables influence an outcome (Kuhn et al., 2015; Kuhn, 2016).
Ultimately, the goal of a method of initial rate problem is to identify the reaction order (exponents); however, research has shown that students have difficulty with exponentiation, which is mathematically modeling exponential relationships (Nataraj and Thomas, 2017). As an example, some students have difficulty understanding the symbolism, such as describing that x3 is equivalent to 3x (MacGregor and Stacey, 1997). However, difficulty may also stem when reasoning using exponents. Pitta-Pantazi et al. (2007) used LCA to identify three levels of sophistication in high school mathematics students’ reasoning with exponents, where low level responses only considered exponents as repeated multiplication, intermediate level responses could reason about a base value raised to a negative power, and high-level responses could reason about rational numbers as exponents. A total of 26% of the students were at the lowest level of reasoning, which only required a procedural understanding of exponents. Though the work in chemistry contexts is limited, it is reasonable to expect that students may also struggle with exponentiation in the context of method of initial rate tasks.
Assessment frameworks
Assessment experts describe the process of assessment as analogous to constructing a strong argument (Mislevy et al., 2003; NRC, 2014). A claim that educators would like to make about students needs to be grounded in data; however, a valid interpretation of the data is necessary in order to make that claim (Mislevy et al., 2003). The NRC (2001, 2014) describes this process using a model known as the assessment triangle, where the three interrelated vertices of a triangle are termed cognition (i.e. claim), observation (i.e. evidence), and interpretation (i.e. reasoning); therefore, assessments become an argument based on evidentiary reasoning (NRC, 2014). Experts have developed models that attempt to make the process of evidentiary reasoning explicit, and our work draws on two such approaches: evidence-centered design (ECD) (Mislevy and Riconscente, 2005) and the BEAR assessment system (BAS) (Wilson, 2005, 2009). Both approaches are in-depth and multilayered frameworks, and further details are available in Mislevy and Riconscente (2005) and Wilson (2005).In our previous work, we characterized the levels of sophistication in students’ responses, using a method of initial rate task as a prompt during 15 qualitative interviews (Becker et al., 2017). The purpose of the study discussed here was to refine and validate the ordered nature of these levels through large-scale data collection and a greater variety of method of initial rate tasks. Both ECD and BAS frameworks explicitly outline the need to evaluate the quality of data using a measurement model. Latent variable models, such as LCA, are a common way for researchers to approach this step (Mislevy et al., 2003; Mislevy and Riconscente, 2005). We chose to use LCA as our measurement model. LCA is a technique used to identify groups (i.e. classes) of individuals that represent the response patterns in the data. Others in the chemistry education research literature have successfully used LCA to characterize students and teachers based on patterns in assessment data (Stamovlasis et al., 2013; Harshman and Yezierski, 2016; Zarkadis et al., 2017). Identifying groups based on the students’ and teachers’ strategies allows educators to develop targeted interventions to help improve learning outcomes in the classroom.
Research question
In this study, we used LCA to identify groups of students based on their responses to three method of initial rate tasks. We then investigated the possibility of an ordered nature to the student groups. The following research question guided our study:• How do students analyze initial concentration and rate data to construct rate law models?
Methods
Assessments
Task 1 (Fig. 1) was like the prompt used in Becker et al. (2017). In Task 1, we included a second order relationship between the [A] and the rate and included data, such that the rate increased by a factor of 8.8, rather than a whole number. We included this element of error, because in the qualitative study reported in Becker et al. (2017), we observed that some students could quite easily solve a method of initial rates task that involved whole numbers, but struggled to account for even small errors. This is perhaps because the students did not recognize that rate laws model general trends in the data, rather than measured values. We were interested in seeing the extent to which this challenge was reflected in a larger sample of students.
Task 2 included a zeroth order relationship between the [CO] and the rate, and Task 3 included a first order relationship between the [O2] and the rate. In Task 3, while students could use the COV strategy to determine the order with respect to O2, they were unable to do so for the [NO], because there were no two experimental trials in which the [O2] was constant. Therefore, the students had to account for the multivariate influence that both the [O2] and the [NO] had on the rate, which was not commonly discussed in their course instruction. One approach to doing this would be to solve for the order of O2 using a COV approach and then devise an algebraic expression that could be used to solve for the order in NO. The full rate law assessment can be found in Appendix 1 (ESI†).
The TOLT is an assessment that has been commonly used in previous literature (Williamson and Rowe, 2002; Lewis and Lewis, 2007; Underwood et al., 2016), and it has been shown to produce valid and reliable data with introductory chemistry students (Jiang et al., 2010). In our study, we used students’ TOLT scores along with the results from the rate law assessment to examine evidence for the convergent validity of our tasks (AERA et al., 2014). Since we believed that several of the TOLT reasoning skills (i.e. COV, proportional, and correlational reasoning) were necessary to solve the method of initial rate tasks, we investigated how well the students’ responses to the TOLT correlated with their LCA class membership. Both the rate law and the TOLT assessments were administered online using Qualtrics Insight Platform (Qualtrics, 2017).
Participants and data collection
Participants in this study were enrolled in the second-semester of an introductory chemistry course at a large research-intensive university in the Midwest, during either the Fall 2015 or Spring 2016 semesters. A total of 768 students participated in the study. The course served a broad range of academic majors, but most of the students majored in the life and applied sciences (63%); engineering, computer science, and mathematics (21%); or the physical sciences (7%). The course was comprised of 56% female, 42% male, and <1% transgender students (∼2% did not respond), and participants were primarily in their first (54%) or second (35%) year in college.The course was lecture-based and used the 3rd edition of Chemistry: The Central Science by Brown et al. (2015). Chemical kinetics was taught early in the semester, prior to the first of three multiple-choice course exams. Students completed an eighty-minute case study (i.e. pre-laboratory lecture) and a three-hour laboratory focused on determining the initial rate of the decomposition of H2O2, using different types of catalysts. Students also participated in discussion sections, which were led by graduate teaching assistants and typically entailed collaborative problem solving.
We administered the rate law assessment as an online survey the week prior to the final exam (i.e. post-instruction and post-testing on rate law concepts). The TOLT was administered about three to four weeks prior to the rate law assessment. The researchers visited a course lecture and announced that students would be awarded three points in course credit for the completion of each survey. Because the points were awarded based on completion rather than the correctness of the students’ responses, the students could select whether they wanted their data to be used for research purposes. A total of 768 students elected to participate in the study, which equates to an ∼72% response rate across both semesters.
Institutional Review Board approval was obtained before collecting data for this study. To protect the students’ identities, the students’ names were replaced by a random number and either an F or S to indicate the Fall 15 or Spring 16 semesters.
Data analysis
Coding students’ responses using themes from Becker et al. (2017)
We coded students’ responses to the six open-ended questions (two open-ended questions for each task shown in Fig. 1). The development of our coding scheme was an iterative process with multiple rounds of coding. In Becker et al. (2017), we described five themes in the students’ responses that emerged from our analysis of semi-structured interview data. The purpose of the study reported here was to investigate the extent to which the levels from Becker et al. (2017) generalized to a larger sample of students’ responses. To do this, we adapted the themes that emerged from Becker et al. (2017) for use as a deductive coding scheme to analyze the students’ responses to the open-ended questions shown in Fig. 1 and 2. To a large extent, the Becker et al. (2017) coding scheme fit the students’ responses, but because of the large sample size and increased response diversity, it was necessary to adapt some code definitions. Modifications to the coding scheme are described in Appendix 2 (ESI†), and the final coding scheme is summarized in Table 1. To briefly describe the coding categories used, we will illustrate the five categories using student responses pertaining to the order in the [A] from Task 1 as shown in Fig. 2.| Levels | Definitions | Example responses |
|---|---|---|
| 5 |
Interpreting the exponent
Students can interpret the changes in concentration and rate, while holding a variable constant (or accounting for another variable), and appropriately reasoning about how concentration exponentially influences the rate, depending on the order. |
“The concentration of A from experiment 1 to 3 was tripled. The Initial rate in the same experiments went up by a factor of about 9. Three squared equals nine. Thus, A is second order.” (S90, D: Rate = [A]2[B]) |
| 4 |
Interpreting data
Students can appropriately interpret the changes in concentration and rate, while holding a variable constant (or accounting for another variable). However, students have difficulty reasoning about how the exponent relates to the interpretation of the data; this includes (1) no explicit reasoning, or (2) difficulties with exponential reasoning resulting in an incorrect determination of the reaction order. |
“When B is held constant, and A is multiplied by 3, the rate gets multiplied by 9. The rate moves three times what A does.” (S148, B: Rate = k[A]3[B]) |
| 3 |
Relating conc. and rate
Students can recognize that they need to interpret how the concentration and rate vary, while holding another variable constant (or accounting for another variable). However, their reasoning includes incorrect interpretations of the changes in concentration or rate, for instance, by inferring that rate triples while in fact the data suggest a 9-fold increase. |
“As the rate between exp 1 and exp 3 triples, the concentration of A also tripled.” (F111, E: “Rate = k[A][B]”) |
| 2 |
Low level use of data
Students use the experimental data as evidence for determining the exponents; however, their arguments and/or use of the data is low-level. Students in this level are (1) using procedures without interpreting the change in concentration and rate in terms of the exponent (e.g. 22 = 4), (2) only focusing on concentration or rate, but not both, or (3) providing an argument that only includes the experimental trials used, or (4) failing to hold one variable constant when they interpret the data (or accounting for the change in O2 in Task 3). |
“reactant A would be 3 because between experiment 2 and 3, A increases by *3.” (F101, B: Rate = k[A]3[B]) |
| 1 |
Incorrect evidence
Students reason using surface features of the problem without attempting to use the provided data to infer reaction orders. Most of the students in this category used the coefficients in the chemical equation to determine the order or conflated a rate law with an equilibrium constant. |
“A would be 4 because that is the coefficient in front of A in the equation.” (F280, C: Rate = [C]2/[A]4[B]3) |
| 0 | I don’t know, restating claim only, not enough information, or generic responses about how to solve the problem without specifics for the exponent in question. | “I am not sure I do not remember without looking at notes.” (F123, D: Rate = k[A]2[B]) |
Level 1 responses suggested that the students struggled to identify the appropriate evidence (i.e. the data) necessary to infer the order; students focused on the coefficients in the chemical equation or other surface features from the prompt (e.g. units given for the rate).
Level 2 responses suggested that students attempted to use concentration and rate data, but in what we refer to as a low-level manner. We considered data use “low-level” if there was limited evidence of intentional selection of both concentration and rate data as would be necessary to infer the relationship between the two. Consider, for example, response F101:
“[the exponent for] reactant A [in the rate law] would be 3 because between experiment 2 and 3, [A] increases by *3.” (F101, Task 1, Selected rate law: Rate = k[A]3[B])
Here, student F101 focused only on the change in the concentration and did not examine the impact of the changing [A] on the rate, as would be necessary to infer the correct order.
Level 3 responses suggested an intentional approach to selecting both concentration and rate data (e.g. using the COV strategy) and an attempt to interpret the relationship between the concentration and the rate. However, Level 3 responses reflected incorrect interpretations of the magnitude of changes in the concentration and rate, and often, incorrect reasoning about how the trend in the data related to the selected exponent. For example, consider the following response:
“As the rate between exp 1 and exp 3 triples, the concentration of A also tripled.” (F111, Task 1, Selected rate law: Rate = k[A][B])
Here, student F111 described the rate as tripling when, in fact, it increased by a factor of ∼9 (Task 1 in Fig. 1). Accordingly, the student selected an exponent of 1 for the [A] in the rate law, when an exponent of 2 would have more appropriately modeled the trend in the data.
Level 4 responses reflected an intentional approach to data selection and an appropriate comparison of the changes in the concentration and the rate, but limited or incorrect reasoning about how the patterns in the data informed the selection of the reaction order. As an example, student S148's response is shown below:
“When B is held constant, and A is multiplied by 3, the rate gets multiplied by 9. The rate moves three times what A does.” (S148, Task 1, Selected rate law: Rate = k[A]3[B])
Here, the student correctly identified that the [A] changed by a factor of 3 and the rate changed by a factor of 9. However, they attempted to model this change using an exponent of 3 for A in the rate law, when in fact an exponent of 2 would be appropriate.
Some students chose the correct order but neglected to provide their reasoning for how their interpretation of the data informed their selection of the order. We defined these responses as Level 4+. Finally, Level 5 responses appropriately identified the patterns in the data and provided appropriate reasoning that linked the data back to their order. An example of a Level 5 response is shown in Table 1.
Additionally, we defined Level 0 responses as those in which students responded with “I don’t know,” provided off-topic information, or gave insufficient detail about their reasoning process.
In all cases, students’ responses were assigned to the reasoning level that best fit their response to the open-ended prompt, regardless of whether they chose the correct rate law or not. Conversely, some students selected an incorrect response to the multiple-choice prompt, but gave appropriate reasoning in the open-ended prompt. Here too, responses were assigned to the level that most closely fit their response to the open-ended prompt.
Inter-rater reliability study
To evaluate how consistently we applied our coding scheme to the data, we conducted an inter-rater reliability study. The first author acted as the primary coder, while the second and third authors each coded a subset of the data. The second author coded 170 student responses from the Fall 15 dataset and the third author coded 150 of the student responses from the Spring 16 dataset; the student responses were chosen at random and were spread relatively evenly across the six open-ended tasks. The first author trained both the second and third authors on the coding scheme using example student quotes that were not part of the specific set of responses in the inter-rater reliability study. The second and third authors coded their responses using the Levels 0–5 coding scheme shown in Table 1, independently of the first author. To make the coding scheme as consistent as possible, minor revisions to the code definitions were made throughout the study. The percent agreement and inter-rater reliability values are shown in Table 2, and reflect the final agreed upon coding scheme, which is shown in Table 1. After the inter-rater reliability of the coding was established, the first author independently coded the additional responses in the datasets.Cohen's κ is an inter-rater reliability statistic that measures the extent to which raters agree within a coding structure, but corrects for the possibility that raters may agree by chance (Cohen, 1960, 1968). Two versions of Cohen's κ are shown in Table 2: one that assumed that Levels 0–5 in the coding scheme were nominal (unordered categories) and another that assumed the levels were ordinal (ordered categories). The ordinal version of κ penalizes disagreements that are further away more severely than disagreements that are closer in value. The penalties were applied using linear weights (Gwet, 2014). Since one of the goals of our study was to evaluate the ordered nature of the coding scheme, we evaluated inter-rater reliability based on both statistics. Cohen's κ values that exceed 0.80 are commonly accepted as evidence for excellent consistency in the data (Landis and Koch, 1977), which we saw in the results shown in Table 2.
Results
Latent class analysis (LCA) and model selection
LCA is a technique that can help researchers identify a set of latent classes (i.e. groups of people) with similar response patterns to a set of tasks (Collins and Lanza, 2010). This approach assumes that the latent variable (i.e. something that cannot be directly observed) influences how individuals respond to a set of observed variables or assessment questions. In this way, LCA is part of a set of techniques known as structural equation modeling; however, in LCA, the latent variable is categorical and composed of groups known as classes.Each LCA model produces several parameters. These include item-response probabilities, which are the probability that an individual will respond in a specific manner conditional upon having membership in a certain class; and latent class prevalences, or the probability of having a specific class membership (Collins and Lanza, 2010). These parameters can be used to interpret the patterns in an LCA model. We used the PROC LCA command (The Methodology Center, 2015) in SAS 9.4 to conduct our analyses.
In this study, we used LCA to examine students’ response patterns across the three method of initial rates tasks that involved zeroth, first, and second order relationships between the concentration and rate data. Our goal was to determine if there were underlying challenges in terms of the nature of the tasks (e.g. difficulties with mathematizing numerical relationships, or difficulties in using the COV strategy) that were common across groups of students. To assess this, we used our classifications of student reasonings summarized in Table 1 (i.e. Levels 1–5) as input for our LCA model.
LCA assumes that the observed variables in the model (i.e. students’ responses to the assessment questions) are independent of each other; this assumption is referred to as local independence (Collins and Lanza, 2010). In our preliminary analyses, we found that students’ responses to the two reaction order questions per task were highly interrelated. Thus, we opted to use students’ levels of responses to one question per task (three questions total) to reduce the possibility of violating the local independence assumption in our model. Specifically, we chose students’ responses to the open-ended questions about A in Task 1 (i.e. second order), CO in Task 2 (i.e. zeroth order), and O2 in Task 3 (i.e. first order). Our intent was to include 0th, 1st, and 2nd order reactant questions, because our earlier work suggested that differences in reaction order may present different levels of difficulty for students (Becker et al., 2017).
We used the full-information maximum likelihood (FIML) parameter estimation method for our analysis (Collins and Lanza, 2010; Lanza et al., 2015). This approach to LCA allows inferences to be made from cases (i.e. students) with missing responses. Of the 768 respondents who provided usable (non-blank or Level 0) responses for at least one of the three questions, 37% had a missing response for at least one of the three questions. Additionally, we chose to treat Level 0 responses as missing data, because we did not consider Level 0 to reflect a distinct type of knowledge and skill. Therefore, including Level 0 would unnecessarily increase the complexity of our LCA model.
Overall, we ran six LCA models that fit 2–7 latent classes to the data. Ultimately, we selected the five-class solution as the best fit for our data, based on statistical output (Table 3), parsimony, and interpretability (Collins and Lanza, 2010). Full details related to our model selection process can be found in Appendix 3 (ESI†).
| Classes | Log likelihood | df | G 2 | p-Value | AIC | BIC | Percent of best fitted model (%) |
|---|---|---|---|---|---|---|---|
| a n = 768. b Convergence criterion set at <0.000001000; all models converged to a solution. c Poorly identified model with best model with less than 25% of seeds (Dziak and Lanza, 2015), based on 1000 random starting values. | |||||||
| 2 | −2154.84 | 99 | 241.2 | <0.001 | 291.2 | 407.3 | 100 |
| 3 | −2068.85 | 86 | 69.2 | 0.907 | 145.2 | 321.7 | 100 |
| 4 | −2054.21 | 73 | 40.0 | 0.999 | 142.0 | 378.8 | 100 |
| 5 | −2047.63 | 60 | 26.8 | >0.999 | 154.8 | 452.0 | 40 |
| 6 | Not well identifiedc | ||||||
| 7 | Not well identifiedc | ||||||
Fig. 3 shows the latent class prevalence estimates and Fig. 4 shows the item response probability estimates for the five-class solution. The gradual increase in the probability of higher level responses across each class, shown in Fig. 4, suggests a potential ordering of the latent classes. We used the item response probability estimates to distinguish patterns across classes and to identify descriptive labels for each class (shown in Fig. 4).
LCA does not make assumptions about the ordered nature of the observed variables (i.e. Levels 1–5) or the classes that emerged from the model (i.e. Classes 1–5). Therefore, the numbers that are assigned to the latent classes are arbitrary, so the authors re-assigned values to the classes in Fig. 4 to better match the general patterns in the level of the responses for each class.
The following analysis of the five-class model was centered on the assignment of students to latent classes using posterior probability estimates, which describe the probability that a student belongs in a specific class (Collins and Lanza, 2010); these assignments are shown in Fig. 5. We then compared students’ latent class memberships to other variables, such as their TOLT responses, to inform our interpretation of each class.
 | ||
| Fig. 5 The percent of student responses at each level of reasoning for task A, CO, and O2 within each class. The students were classified in each class using the posterior probabilities estimated from the LCA model. Fig. 5 shows that a large portion of the Level 4 responses were Level 4+, which suggests that many students were able to identify the changes in concentration and rate and select the correct order, but did not communicate their reasoning. | ||
Characteristics of the latent classes
As we have noted, in part, the current work was aimed at examining the validity of the patterns in students’ reasoning described in Becker et al. (2017). We identified a five-class solution that we believe reflects five themes with varying levels of sophistication in how students analyze and interpret data to construct rate laws.“In order to account for the differing coefficients in a balanced equation, the coefficients must be translated into the rate law. This can be done by raising each reactant to its respective stoichiometric coefficient obtained from the balanced equation. Since, in the equation, species A is preceded by the number 4, the coefficient for A is 4. In the rate law, the reactant A would be raised to the power of 4. This is shown as: [A]4” (F147, Task 1, Rate law: Rate = k[A4][B3], Class 1 Level 1)
This student derived the order based on the stoichiometric coefficients in the chemical equation, rather than using the data. They did so consistently across the three rate law tasks. Interestingly in Task 3, the student chose the correct rate law; however, their reasoning made it clear that they did not use the data to derive the reaction order.
This approach may reflect limited recognition of the empirical basis of rate laws and possible confusion across curricular tasks that are on the surface similar. For instance, this approach to constructing a rate law may reflect confusion about when to apply the Law of Mass Action, in which stoichiometric coefficients of a proposed elementary reaction step may be used as coefficients in the rate law (Cakmakci et al., 2006; Cakmakci, 2010; Turányi and Tóth, 2013). Alternately, students may confuse writing rate laws with the approach used for writing equilibrium constant expressions (Becker et al., 2017).
The latent class prevalence for Class 1 was the largest of the five classes (Fig. 3) with a value of 0.379 or an approximately 38% probability that a student would be characterized as using coefficients to derive the order. This implies that it was common for students to struggle to identify the appropriate evidence.
Three common types of low-level data use included (1) the selection of data without an attempt to control for the second concentration variable, (2) the use of concentration or rate data only or (3) the use of an algorithmic approach for determining the reaction orders without evidence that the data were selected intentionally and with an understanding of what would be needed to infer the reaction order.
To illustrate the second approach to low-level data use, Student S366's response is shown below:
“When the concentration of NO2is held constant in two experiments, the values of CO for the same experiments triple.” (S366, Task 2, Selected rate law: Rate = k[NO2]2[CO]3, Class 2 Level 2)
Here, Student S366 concluded that since the [CO] tripled when the [NO2] was held constant, the order in CO would be three. While they seemed to recognize the need to hold the concentration of the second concentration variable constant, they examined only the change in concentration (and not the corresponding change in reaction rate). This perhaps suggests that some students may be using COV without understanding the underlying rationale behind the strategy.
Alternately, other students in Class 2 attempted to apply an algorithmic approach to determine the reaction order, such as the “divide two trials approach.” This approach, which had been demonstrated in the lecture portion of the course, involved writing a rate law for each trial, filling in the measured rates and concentrations used, and then dividing out the expression. If two trials are selected such that one concentration is held constant, it would be possible to solve for the unknown exponent that represents the reaction order.
Some of our participants who attempted the “divide two trials” algorithm either selected data without attention to holding one reactant concentration constant (making it difficult to determine the reaction order), or became confused about what they were solving for. For example, in the following excerpt, Student F225 selected data to control for the influence of the [B] on the rate and set up an expression in which they divided values from the two experimental trials.
“Take the ratios from experiment 1 and 3. Since both k values will be the same, they do not need to be included. It will look like . Then, using the values given, it will look like
. Then, using the values given, it will look like . Since both B values are the same they cancel out. The remaining value is
. Since both B values are the same they cancel out. The remaining value is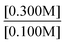 . This will then be multiplied by chemical scenario 1's initial rate. The new equation will be
. This will then be multiplied by chemical scenario 1's initial rate. The new equation will be . The order of the reaction is 3.” (F225, Task 1, Rate law: Rate = k[A]3[B]2, Class 2 Level 2)
. The order of the reaction is 3.” (F225, Task 1, Rate law: Rate = k[A]3[B]2, Class 2 Level 2)
Here, Student F225 solved for the rate for the third experiment, rather than the unknown exponent and identified this quantity as the order with respect to A.
Though this student arrived at an incorrect order for A, there were some students in Class 2 who were able to use this approach and solve for the correct answer. However, if participants used this approach and did not interpret the exponent relative to the patterns in the data, we considered it a more algorithmic approach for solving the problem consistent with lower-level use of the data for our coding scheme.
Overall, the types of low-level data use used by students in Class 2 were like those observed in Becker et al. (2017) and what we referred to as Level 2 reasoning. In this study, Class 2 was a moderately sized class, with a latent class prevalence of 0.112, or a 11% probability that a student would be characterized as using the data in a low-level manner.
As an example, when the [A] increased by a factor of three, the rate increased by a factor of 8.8, rather than a whole number; not surprisingly, students seemed to struggle to distinguish this change in rate more than any other task. As an example:
“Between experiment and 1 and experiment 3 shows that the initial rate greatly increases with a higher concentration of [A]. I am not sure of what the exponent should be, and my best guess is 2.” (F016, Task 1, Selected rate law: Rate = k[A]2[B]2, Class 3 Level 3)
Student F016 examined both the change in the rate and concentration, but seemed unable to interpret the magnitude of the increase in the rate and concentration in a way that would support mathematical modeling of this trend (e.g. concentration triples, rate increases by approximately nine). Several students in Class 3 had difficulty identifying the increase in rate, likely because the rate increased by 8.8 rather than a whole number. Ultimately, Student F016 correctly guessed the reaction order in A, but in contrast, this student responded to Tasks 2 and 3 quite well. This suggests that some Class 3 students struggled to grasp the element of experimental error that we introduced in the [A] in Task 1. Like Class 2, Class 3 was a moderately sized class, with a latent class prevalence of 0.164, or a 16% probability that a student would be characterized by Class 3.
One of the most common heuristics involved taking the ratio of the change in the rate to the change in the concentration to determine the reaction order. As an example, Student S018's response is shown below, with the heuristic reasoning components highlighted in bold.
“Looking at the concentrations of A and B, I first looked at the two concentrations that B had in common, which was experiment 1 and 3. From this, I saw that the concentration of A tripled and the initial rate of reaction went up by 9,so dividing 9 by 3, you get 3for the exponent of A since the rate went up by 9 as the concentration went up by 3.” (S018, Task 1, Selected rate law: Rate = k[A]3[B], Class 4 Level 4)
Here, Student S018 divided the change in rate by the change in concentration to determine the reaction order. Student S018 did not appear to recognize that the selected exponent would not fit the trend in the data.
Interestingly, in the O2 task, students could use the “divide change in rate by change in concentration” approach and arrive at a correct reaction order since the reaction order was 1. A clear implication is that tasks that require students to select the reaction order without also explaining their reasoning may not enable instructors to identify instances of heuristic reasoning that may become problematic in other contexts.
Some students obtained the correct reaction order, but did not include reasoning describing the relationship between the trend in the data and the rate. We considered these responses a subgroup within Level 4 called Level 4+. The following is an example of a Level 4+ student response from Task 2:
“There is no change in the initial rate when NO2is constant and CO increases by a factor of 3.” (F222, Task 2, Selected rate law: Rate = k[NO2]2, Class 4 Level 4+)
While this student was able to describe the changes in the concentration and rate, they did not provide reasoning, leaving us to infer whether they understood the connection between the exponents in the rate law and the patterns in the data.
In this study, Class 4 was the smallest class, with a latent class prevalence of 0.058, or a 6% probability that a student would not include explicit reasoning about how the they determined the reaction order, or include incorrect mathematical reasoning (or the use of heuristics) for relating the change in rate and concentration to the reaction order.
To illustrate a typical response from a student in Class 5, consider student S233's response below.
“To figure out this problem, you have to look at experiments 1 and 3. In these experiments, [B] is the same, so it is constant. This is good because it's the change in [A] that we want to see the effect of. We can see that when [A] is tripled, the initial rate is ×9.To get from 3 to 9 we have to square it, so the exponent for A is 2.” (S233, Task 1, Selected rate law: Rate = k[A]2[B], Class 5 Level 5).
Student S233 explicitly discussed how they identified two trials that would enable them to examine the impact of one reactant on the rate, they described the pattern they saw in the data, and they modeled that pattern using an exponent of 2 in the rate law.
Rather than describing how the selected exponent fit the trends in the data, students often discussed a first order relationship as a linear relationship, a “1 to 1” relationship, or a directly proportional relationship. For example, Student S418 selected an exponent of 1 for O2 based on their recognition of what they described as a linear relationship between the concentration and rate.
“As we hold [NO] constant and double [O2], going from experiment 1 to experiment 2, we see the initial reaction rate doubles,leading us to infer a linear relationship between [O2] and initial reaction rate.” (S418, Task 3, Selected rate law: Rate = k[O2][NO]2, Class 5 Level 5)
In Task 2, there was a zeroth order relationship between the [CO] and the rate. Typical reasoning for omitting CO from the rate law included discussions about how the [CO] did not influence the rate:
“The concentration of CO is tripled between experiments 1 and 2 (while the concentration of NO2was kept the same), but did not produce a change in the reaction rate.Therefore, the concentration of CO has no effect on the rateand can be left out of the rate law entirely (or be given an exponent of 0).” (S499, Task 2, Selected rate law: Rate = k[NO2]2, Class 5 Level 5)
We recognize that these forms of non-exponential reasoning do not provide explicit evidence for how the students arrived at a reaction order of 0 or 1, in the same way that stating 30 = 1 (CO in Task 2) or 21 = 2 (O2 in Task 3) does. However, we view these as appropriate ways to characterize the relationships between the concentration and the rate.
Prevalence of reasoning levels within classes
Overall, the five classes align well with the five levels of reasoning described in Becker et al. (2017). Fig. 5 shows the percent of students assigned to each class that responded at a specific level within our coding scheme. | ||
| Fig. 6 Average TOLT reasoning skill score (0–2 points) for each latent class. Students were assigned to classes using the posterior probability estimates. | ||
Examining evidence for the ordered nature of the latent classes
To further evaluate whether Classes 1 through 5 were ordered in terms of the sophistication of students’ responses, we compared the students’ class memberships to their responses from the TOLT. We expected that if our classes were sensitive enough to distinguish different levels of sophistication in students’ abilities to use these forms of reasoning, then it should correlate with some of the skills measured by the TOLT. Specifically, we focused on proportional reasoning, correlational reasoning, and control of variable reasoning.In most cases, we saw a slight increase in the average TOLT scores for each reasoning skill across each increasingly sophisticated class (Fig. 6). Table 4 shows the Spearman rho (ρ) correlation coefficients associated with the students’ assigned class number and their TOLT scores for each reasoning skill. The correlations between the students’ class membership and their reasoning scores were significant, with proportional reasoning, COV, and correlational reasoning having the greatest correlations with the class number. Therefore, we believe that this provides some evidence for the ordering that we assigned to the latent classes.
Students’ responses to reaction order versus class membership
Fig. 7 shows the proportions of students with correct and incorrect reaction orders for each of the five latent classes for each task. Most of the students who responded with correct orders for tasks A (2nd order) and CO (0th order), were in Class 5 (56.0% of 266 students for A and 52.3% of 421 students for CO), which was the most sophisticated class that emerged from our data. However, it is also worth noting that there was a large percentage of students who provided less sophisticated responses (i.e. Classes 2–4), but ultimately selected the correct answer (44.0% for A and 47.7% for CO). Thus, for many students, communicating clear reasoning for how the trend in the data informed their selection of a rate law was challenging.The results for the order of O2 from Task 3 shows a somewhat different trend in that 76.8% (n = 428) of the students who chose the correct order were in Classes 1–4. In this task, there were several ways for students to choose the correct answer (i.e. first order) without using the exponent to model the pattern in the data. As an example, students may have used the coefficient in the chemical equation or reasoned about the order as the ratio of the changes in rate and concentration (i.e. 2/2 = 1), and as such, this is a limitation of our task.
Of the 185 students that selected an incorrect answer for O2 in Task 3, 166 students indicated that it was impossible to determine the rate law (response option D in Task 3, shown in Appendix 1, ESI†). When students chose response D in Task 3, they were given a single open-ended prompt to explain why they believed this to be impossible. Unfortunately, most of these students did not provide the order for O2. Instead, they described that they could not determine the order for NO, because there were no experimental trials in which O2 was constant; therefore, they were categorized with an incorrect multiple-choice answer (response D in Task 3, shown in Appendix 1, ESI†). We recognize this as a limitation of our analysis, and the reader should interpret the results for O2 in Fig. 7c with caution.
Students’ responses to the NO prompt versus class membership
Task 3 (order in O2 and NO) was distinct from Tasks 1 and 2 because the students were unable to use a COV strategy to determine the reaction order for the [NO]. This led to some interesting insights into how students responded when asked to reason about how the two concentration variables influenced the rate. The following quote is an example of a student with a high-level response:“Comparing experiments 3 and 4, [NO] is multiplied by 2 and [O2] is multiplied by 2 and the initial rate is multiplied by 8. Since we already know the initial rate is multiplied by 2 because of the [O2], then the initial rate is multiplied by an additional 4 because of [NO]. So, 2 squared is 4 so the order is 2nd order with respect to NO.” (S404, Task 3, Rate law: k[O2][NO]2, Class 5 Level 5)
However, reasoning in this manner was difficult for many students. In fact, 23.7% (n = 182) of the students chose that it was impossible to determine the rate law and most often cited that there were no two trials in which the [O2] was constant. As an example:
“The concentration of [O2] is never held constant, so we can not [sic] tell the effect that changing the concentration of NO has on the rate.” (S196, Selected response: “It is impossible to determine the rate law with the information provided”, Task 3, Class 5 Level 2)
Many students categorized as Level 2 (shown in Table 1) struggled to use the COV strategy when describing the patterns in the data. However, in Classes 4 and 5, students rarely responded at Level 2 (shown in Fig. 5), which implies that these students were often able to use the COV strategy. However, when faced with the NO task, we noticed that a much larger percentage of students in Classes 4 and 5 responded at Level 2 (Fig. 8), most often because they felt that they could not account for the [O2] in their analysis. Therefore, while it seemed that many students could use the COV strategy in the [A] and the [CO] tasks, they struggled to reason about how two variables (i.e. both the [O2] and [NO]) simultaneously influenced the rate.
It was not particularly surprising that students struggled with the NO task, because it was not commonly used in their chemistry course. However, these results suggest that students struggle to reason beyond the COV in multivariate contexts. It is possible that some students may be using the COV strategy without having a fundamental understanding of its purpose, and even students in Class 5 may be applying it as a rote-memorized procedure to some extent.
Discussion and conclusions
In this study, we used LCA to identify groups (i.e. classes) of students with varying difficulties analyzing initial concentration and rate data. Our results indicated that the classes were qualitatively distinct and characterized the increasingly sophisticated levels in students’ abilities to construct rate laws from data; this assertion is based on the gradual increase in the levels of reasoning (i.e.Table 1) across the five classes (Fig. 4), and that students’ class membership was, to some extent, correlated with their reasoning skills (Fig. 6), as measured by the TOLT. These results suggest a potentially ordered nature to the identified classes, in which students’ responses varied from lower- to higher-levels of sophistication.Overall, we found some alignment between the five levels in our coding scheme (Table 1) and the classes that emerged from our model. However, the characterization of students using the latent classes provided information beyond the levels coding scheme, because it allowed us to identify patterns in students’ levels of reasoning across multiple tasks (i.e. A, CO, and O2 tasks). As an example, Class 1 students consistently described determining the reaction order using the coefficients in the chemical equation across all three tasks. We believe this approach may reflect limited understanding of the fact that rate laws are empirically derived. Class 1 was the least sophisticated group, and unfortunately, it was also the largest (latent class prevalence value of 0.379). We considered Class 2 to be more sophisticated than Class 1, because Class 2 students recognized the need to analyze the given data to determine their rate laws. However, students in this class tended to use rote-memorized approaches to analyzing the data or struggled to use the COV strategy appropriately.
Class 3 included more heterogeneous response patterns across the three method of initial rates tasks (A, CO, and O2). Students often provided lower-level responses to task A in comparison to the other questions, likely because A had a second order relationship with the rate, which is more challenging to recognize and mathematically model than a zeroth or first order relationship. As a result, we labeled this class “Transitional,” because students’ responses seemed to be dependent on the difficulty of the task. Many of the Class 4 responses appropriately discussed the patterns in the data but either lacked or provided incorrect reasoning related to how their analysis of the data led to their selection of a reaction order.
Class 5 represented the second largest class of students, with a latent class prevalence of 0.287. We viewed Class 5 as the most sophisticated class, since these students were the most consistent in their use of appropriate strategies for determining reaction order across the three method of initial rate tasks. However, Class 5 responses to Task 3 (the NO question) suggested that some students in Class 5 had difficulty constructing a rate law when the COV strategy could not be used.
A large portion of our students used recalled strategies to solve the problems, such as deriving the order from the coefficient in the chemical equation, rather than interpreting the mathematical relationship between concentration and rate. Relatively few students showed evidence that they engaged in analyzing and interpreting data. Even the strategies most commonly used in Class 5 responses could potentially be completed in an algorithmic manner (e.g. 32 = 9 for task A). As a result, there was little evidence that students understood the nature and purpose of mathematical models and the process of modeling that this task mirrors.
For many students, the use of rote-memorized procedures may be essential for students to navigate the “mile wide and inch deep” approach used in many curricular models (NRC, 2012; Cooper, 2015). Instructors and researchers should consider developing instruction and assessments that engage students more deeply in constructing mathematical models from data in ways that go beyond recalled problem-solving strategies.
Limitations
The results of our study are based on students’ written responses to open-ended questions; therefore, our interpretations were limited by the amount of detail that students chose to articulate. As an example, in Level 4, some students did not describe their reasoning for how their analysis of the data was linked to their reaction order. Therefore, we have no way of knowing if the students used appropriate reasoning, or if they simply guessed. Similarly, in Level 1, the students may have used the coefficients in the chemical equation, because they thought the reaction was an elementary step, but chose not to articulate this reasoning. However, since none of the students communicated this, we think this type of implicit reasoning was unlikely to be prevalent for the students who used the coefficient strategy.In general, it is unclear exactly why some students neglected their reasoning; however, McNeill et al. (2006) suggests that the reasoning component can be especially difficult for students to communicate. Similarly, the students in this course were assessed using multiple-choice tests. As a result, it is likely that the students were not familiar with articulating their thoughts in this way.
Another challenge that we faced was a substantial amount of missing data. A total of 37% of the students had a missing response across at least one of the three tasks used in our LCA model. Many of these missing responses were related to the O2 task. When students chose response D in Task 3 (i.e. “It is impossible to determine the rate law with the information provided”), they were given a single box to explain their reasoning. Unfortunately, many students only discussed NO in their responses and neglected O2. Similarly, some students were missing responses to the TOLT, the reaction orders, or the NO prompt, so we only used the available data for these analyses.
For our LCA model, we were able to minimize the impact of this limitation by estimating the parameters using the FIML method, which analyzes the model parameters based on the available data. However, this method assumes that the missing data is missing completely at random (MCAR), which means the propensity of the missing data is completely random, or missing at random (MAR), which means that the missing data are related to another related observed variable (Enders, 2010). These are in contrast to missing not a random (MNAR), which means that missing data are related to the variable itself; however, evaluating whether the data is MNAR is difficult without knowing the missing responses (Enders, 2010). However, in reality, the propensity for missing data is likely motivated by a combination of all three missing data mechanisms (Collins and Lanza, 2010).
Implications
Developmental assessment structures, like the levels of sophistication scheme shown here, have the potential to be used to characterize students’ abilities to engage in science practices, like constructing models and analyzing data. We assessed students using a task that is common in traditional, college-level chemistry instruction, and using the ACS-EI's ACCM as evidence, we believe that this task is meant to engage students in constructing a mathematical model through an analysis of the data. While this task is a worthwhile step toward engaging students in the practices of constructing mathematical models, and analyzing/interpreting data, further work is necessary to develop more authentic contexts for students to engage in these practices that are largely missing from many classrooms.One way that instructors and researchers may consider helping students engage in such practices is using model-focused curricula that facilitates opportunities to engage students in model-based reasoning. Examples of model-based instruction can be found in the physics (Schwarz and White, 2005; Schwarz et al., 2009) and mathematics (Lesh et al., 2000; Doerr and English, 2003) education research literature. Lesh et al. (2000) describes the importance of shifting instructional emphasis from applied problem solving to activities that elicit mathematical model-based reasoning. They describe that model-eliciting activities include educational scenarios that emphasize the conceptual foundations of mathematical skills and abilities that are useful in the real world. In comparison to applied problem solving, much like our method of initial rate problem, students learn to use heuristics, which arguably are less likely to help them transfer these ideas to new situations or help them build skills in higher-order thinking (Lesh et al., 2000). While a few model-focused pedagogical interventions exist in chemistry, such as the Model–Observe–Reflect–Explain (MORE) laboratory modules (Tien et al., 2007), we are unaware of any pedagogy that explicitly focuses on mathematical models.
Since students’ engagement with course content is highly tied to how they are evaluated in the course, it is critical that instructors and researchers consider assessments’ role in the evaluation of students’ learning. As an example, the results from this study showed that many students were able to identify the correct answer to the questions, but struggled to provide appropriate reasoning. In this course, the students were assessed using multiple-choice assessment tasks that asked the students to identify the reaction order for a specific species, and as a result, it is likely that they were unaccustomed to articulating their reasoning, like they were asked to do in our study. Several resources are available that highlight ways to assess students’ meaningful engagement in course content through the use of three-dimensional learning, which includes science practices, cross-cutting concepts, and disciplinary core ideas (NRC, 2012, 2014; Laverty et al., 2016).
Assessment structures, like the levels of reasoning coding scheme shown here, provide a developmental perspective for gauging the growth in students’ abilities, rather than a snap-shot of the pieces of students’ knowledge at any single time (Wilson, 2009). We argue that our levels of reasoning coding scheme could be used as an initial starting point for assessing students’ ideas but should be refined and redeveloped with new tasks that may be beneficial for helping students more completely engage with mathematical models. We suggest that future research focus on developing curricular activities and well-aligned assessments that facilitate mathematical modeling, and analyzing and interpreting data, with the goal of providing rich learning experiences in the classroom.
Conflicts of interest
There are no conflicts of interest to declare.Acknowledgements
We would like to thank Dr. Jordan Harshman for his help writing the R code used to calculate the inter-rater reliability statistics.References
- American Educational Research Association, American Psychological Association and National Council on Measurement in Education (AERA, APA and NCEM), (2014), Standards for educational and psychological testing, Washington, DC: Joint Committee on the Standards for Educational and Psychological Testing.
- Bain K. and Towns M. H., (2016), A review of research on the teaching and learning of chemical kinetics, Chem. Educ. Res. Pract., 17(2), 246–262.
- Becker N., Rupp C. and Brandriet A., (2017), Engaging students in analyzing and interpreting data to construct mathematical models: an analysis of students' reasoning in a method of initial rates task, Chem. Educ. Res. Pract., 18(4), 798–810.
- Brandriet A. R. and Bretz S. L., (2014), The development of the redox concept inventory as a measure of students’ symbolic and particulate redox understandings and confidence, J. Chem. Educ., 91(8), 1132–1144.
- Brown J. S., Collins A. and Duguid P., (1989), Situated cognition and the culture of learning, Educ. Res., 18(1), 32–42.
- Brown T. L., LeMay H. E., Bursten B. E., Murphy C. J., Woodward P. M. and Stoltzfus M. W., (2015), Chemistry: The central science, 13th edn, Upper Saddle River, NJ: Pearson Education.
- Cakmakci G., (2010), Identifying alternative conceptions of chemical kinetics among secondary school and undergraduate students in Turkey, J. Chem. Educ., 87(4), 449–455.
- Cakmakci G., Leach J. and Donnelly J., (2006), Students’ ideas about reaction rate and its relationship with concentration or pressure, Int. J. Sci. Educ., 28(15), 1795–1815.
- Cohen J., (1960), A coefficient of agreement for nominal scales, Educ. Psychol. Meas., 20(1), 37–46.
- Cohen J., (1968), Weighted kappa: nominal scale agreement provision for scaled disagreement or partial credit, Psychol. Bull., 70(4), 213–220.
- Collins L. M. and Lanza S. T., (2010), Latent class and latent transition analysis: with applications in the social, behavioral, and health sciences, Hoboken, NJ: John Wiley and Sons, Inc.
- Cooper M. M., (2015), Why ask why? J. Chem. Educ., 92(8), 1273–1279.
- Doerr H. M. and English, L. D., (2003), A modeling perspective on students’ mathematical reasoning about data, J. Res. Math. Educ., 34(2), 110–136.
- Duschl R., Maeng S. and Sezen A., (2011), Learning progressions and teaching sequences: a review and analysis, Stud. Sci. Educ., 47(2), 123–182.
- Dziak J. J. and Lanza S. T., (2015), SAS graphics macros for latent class analysis users’ guide (Version 2), University Park: The Methodology Center, Penn State, retrieved from http://methodology.psu.edu.
- Enders C. K., (2010), Applied missing data analysis, New York, NY: Guilford Press.
- Gwet K. L., (2014), Handbook of inter-rater reliability: the definitive guide to measuring the extent of agreement among raters, 4th edn, Gaithersburg, MD: Advanced Analytics, LLC.
- Harrison A. G. and Treagust D. F., (2000), A typology of school science models, Int. J. Sci. Educ., 22(9), 1011–1026.
- Harshman, J. and Yezierski, E., (2016), Characterizing high school chemistry teachers’ use of assessment data via latent class analysis, Chem. Educ. Res. Pract., 17(2), 296–308.
- Heisterkamp K. and Talanquer V., (2015), Interpreting data: the hybrid mind, J. Chem. Educ., 92(12), 1988–1995.
- Holme T. and Murphy K., (2012), The ACS exams institute undergraduate chemistry anchoring concepts content map I: general chemistry, J. Chem. Educ., 89(6), 721–723.
- Holme T., Luxford C. and Murphy K., (2015), Updating the general chemistry anchoring concepts content map, J. Chem. Educ., 92(6), 1115–1116.
- Jiang B., Xu X., Garcia A. and Lewis J. E., (2010), Comparing two tests of formal reasoning in a college chemistry context, J. Chem. Educ., 87(12), 1430–1437.
- Kolomuç A. and Tekin S., (2011), Chemistry teachers’ misconceptions concerning concept of chemical reaction rate, Eur. J. Phys. Chem. Educ., 3(2), 84–101.
- Krajcik J. S., (2012), The importance, cautions and future of learning progression research, in Alonzo A. C. and Gotwals A. W. (ed.), Learning Progressions in Science, The Netherlands: Sense Publishers, pp. 27–36.
- Kuhn D., (2016), What do young science students need to learn about variables? Sci. Educ., 100(2), 392–403.
- Kuhn D., Ramsey S. and Arvidsson T. S., (2015), Developing multivariable thinkers, Cognit. Dev., 35, 92–110.
- Landis J. R. and Koch G. G., (1977), The measurement of observer agreement for categorical data, Biometrics, 33(1), 159–174.
- Lanza S. T., Dziak J. J., Huang L., Wagner A. and Collins L. M., (2015), PROC LCA & PROC LTA users’ guide (Version 1.3.2), University Park: The Methodology Center, Penn State, retrieved from http://methodology.psu.edu.
- Lave J. and Wenger E., (1991), Situated learning: legitimate peripheral participation, New York, NY: Cambridge University Press.
- Laverty J. T., Underwood S. M., Matz R. L., Posey L. A., Carmel J. H., Caballero M. D., Fata-Hartley C. L., Ebert-May D., Jardeleza S. E. and Cooper M. M., (2016), Characterizing college science assessments: the three-dimensional learning assessment protocol, PLoS One, 11(9), e0162333.
- Lesh R., Hoover M., Hole B., Kelly A. and Post T., (2000), Principles for developing thought-revealing activities for students and teachers, in Kelly A. and Lesh R. (ed.), Research Design in Mathematics and Science Education, Mawah, NJ: Lawrence Erlbaum Associates, pp. 591–646, retrieved from http://www.cehd.umn.edu/ci/rationalnumberproject/00_2.html.
- Lewis S. E. and Lewis J. E., (2007), Predicting at-risk students in general chemistry: comparing formal thought to a general achievement measure, Chem. Educ. Res. Pract., 8(1), 32–51.
- MacGregor M. and Stacey K., (1997), Students’ understanding of algebraic notation: 11–15, Educ. Stud. Math., 33(1), 1–19.
- McNeill K. L., Lizotte D. J., Krajcik J. and Marx R. W., (2006), Supporting students’ construction of scientific explanations by fading scaffolds in instructional materials, J. Learn. Sci., 15(2), 153–191.
- Mislevy R. J. and Riconscente M. M., (2005), Evidence-centered assessment design: layers, structures, and terminology, PADI Technical Report No. 9, Menlo Park, CA: SRI International, pp. 1–38.
- Mislevy R. J., Almond R. G. and Lukas J. F., (2003), A brief introduction to evidence-centered design, RR-03-16, Princeton, NJ: Educational Testing Service, pp. 1–29, retrieved from http://onlinelibrary.wiley.com/doi/10.1002/j.2333-8504.2003.tb01908.x/abstract.
- Murphy K., Holme T., Zenisky A., Caruthers H. and Knaus K., (2012), Building the ACS exams anchoring concept content map for undergraduate chemistry, J. Chem. Educ., 89(6), 715–720.
- Nataraj M. S. and Thomas M., (2017), Teaching and learning middle school algebra: valuable lessons from the history of mathematics, in Stewart S. (ed.), And the Rest is Just Algebra, Switzerland: Springer International Publishing, pp. 131–154.
- National Research Council, (2001), Knowing what students know: The science and design of education assessment (Committee on the Foundations of Assessment. Board on Testing and Assessment, Center for Education, Division of Behavioral and Social Sciences and Education), Washington, DC: The National Academies Press.
- National Research Council, (2012), A framework for k-12 science education: practices, crosscutting concepts, and core ideas (Committee on a Conceptual Framework for New K-12 Science Education Standards. Board on Science Education, Division of Behavioral and Social Sciences and Education), Washington, DC: The National Academies Press.
- National Research Council, (2014), Developing assessments for the Next Generation Science Standards (Committee on Developing Assessments of Science Proficiency in K-12. Board on Testing and Assessment and Board on Science Education), Washington, DC: The National Academies Press.
- Osborne J., (2014), Teaching scientific practices: meeting the challenge of change, J. Sci. Teach. Educ., 25(2), 177–196.
- Pitta-Pantazi D., Christou C. and Zachariades T., (2007), Secondary school students’ levels of understanding in computing exponents, Journal of Mathematical Behavior, 26(4), 301–311.
- Qualtrics, (2017), Welcome to the new Qualtrics, retrieved June 8, 2017, from http://https://www.qualtrics.com/support/explore-the-new-qualtrics/.
- Schwarz C. V. and White B. Y., (2005), Metamodeling knowledge: developing students’ understanding of scientific modeling, Cognit. Instruct., 23(2), 165–205.
- Schwarz C. V., Reiser B. J., Davis E. A., Kenyon L., Achér A., Fortus D., Shwartz Y., Hug B. and Krajcik J., (2009), Developing a learning progression for scientific modeling: making scientific modeling accessible and meaningful for learners, J. Res. Sci. Teach., 46(6), 632–654.
- Stamovlasis D., Papageorgiou G. and Tsitsipis G., (2013), The coherent versus fragmented knowledge hypotheses for the structure of matter: an investigation with a robust statistical methodology, Chem. Educ. Res. Pract., 14(4), 485–495.
- Stefani C. and Tsaparlis G., (2009), Students’ levels of explanations, models, and misconceptions in basic quantum chemistry: a phenomenographic study, J. Res. Sci. Teach., 46(5), 520–536.
- The Methodology Center, (2015), PROC LCA and PROC LTA (Version 1.3.2), University Park: Penn State, retrieved from http://methodology.psu.edu.
- Tien L. T., Teichert M. A. and Rickey D., (2007), Effectiveness of a more laboratory module in prompting students to revise their molecular-level ideas about solutions, J. Chem. Educ., 84(1), 175–181.
- Tobin K. G. and Capie W., (1981), The development and validation of a group test of logical thinking, Educ. Psychol. Meas., 41(2), 413–423.
- Turányi T. and Tóth Z., (2013), Hungarian university students’ misunderstandings in thermodynamics and chemical kinetics, Chem. Educ. Res. Pract., 14(1), 105–116.
- Underwood S. M., Reyes-Gastelum D. and Cooper M. M., (2016), When do students recognize relationships between molecular structure and properties? A longitudinal comparison of the impact of traditional and transformed curricula, Chem. Educ. Res. Pract., 17(2), 365–380.
- Williamson V. M. and Rowe M. W., (2002), Group problem-solving versus lecture in college-level quantitative analysis: the good, the bad, and the ugly, J. Chem. Educ., 79(9), 1131–1134.
- Wilson M., (2005), Constructing measure: an item response modeling approach, Mahwah, NJ: Lawrence Erlbaum Associates, Inc.
- Wilson M., (2009), Measuring progressions: assessment structures underlying a learning progression, J. Res. Sci. Teach., 46(6), 716–730.
- Zarkadis N., Papageorgiou G. and Stamovlasis D., (2017), Studying the consistency between and within the student mental models for atomic structure, Chem. Educ. Res. Pract., 18(4), 893–902.
- Zhou S., Han J., Koenig K., Raplinger A., Pi Y., Li D., Xiao H., Fu Z. and Bao L., (2016), Assessment of scientific reasoning: the effects of task context, data, and design on student reasoning in control of variables, Think. Skills Creat., 19, 175–187.
Footnote |
| † Electronic supplementary information (ESI) available: Appendices. See DOI: 10.1039/c7rp00126f |
| This journal is © The Royal Society of Chemistry 2018 |





