Open Access Article
Open Access ArticleInfluence on ferric chloride aqueous solution caused by external electrostatic field: a molecular dynamics simulation study
Shi Zhibo *ab,
Li Liyia,
Han Yongc and
Bai Jieb
*ab,
Li Liyia,
Han Yongc and
Bai Jieb
aDepartment of Electrical Engineering, Harbin Institute of Technology, Harbin, 150001, China
bCollege of Electronic Information and Automation, Civil Aviation University of China, Tianjin 300300, China. E-mail: zhiboshi2012@126.com; Tel: +86-22-2409 2714
cMeasurement Technology and Instrumentation Key Laboratory of Hebei Province, School of Electrical. Engineer, Yanshan University, 438 Hebei Street, Hai Gang, Qinhuangdao 066004, China
First published on 16th November 2018
Abstract
A detailed analysis of structural properties and dynamic properties of ferric chloride aqueous solution under external electrostatic fields with different intensities was performed by molecular dynamics (MD) simulations. The effects on the ferric chloride aqueous solution caused by using an electrostatic field were examined in terms of the radial distribution function of the Fe3+ ion and water molecule/Cl−, coordination number of water/Cl− around the Fe3+ ion, characteristics of hydrogen bonds, solution viscosity, and how these effects influence the hydrolysis process of the Fe3+ ion. The goal behind the study is to attain additional insights into the mechanism of electrocoagulation when ferric chloride is used as coagulant, and provide a fundamental basis for the practical use of this technology.
Introduction
Flocculation is an effective method in many water treatment engineering fields. Adding coagulant is the most important step in the flocculation process. The most widely used coagulants are aluminium salt and ferric salt. Aluminium salt has a certain biological toxicity to human beings, which has a correlation with the occurrence of Alzheimer's disease.1,2 Therefore the use of aluminium salt coagulant may cause the secondary pollution of raw water. Compared with the aluminium salt coagulant, the ferric salt coagulant has the advantages of no biological toxicity, higher coagulation and settlement rate, better dewatering of sludge and shorter water treatment time.3 However, in the practical application of ferric salt coagulant, there are still many disadvantages such as the high dosage required, high cost and secondary environmental pollution. Therefore, an enhanced electrocoagulation technique has been developed. The enhanced electrocoagulation technique can effectively improve coagulation efficiency and significantly reduce coagulant dosage. At present, the enhanced electrocoagulation technique has been widely used in the treatment of many kinds of wastewater, such as dye and non-ferrous waste water, oily wastewater and municipal wastewater, which has achieved good results. Many researchers have done a lot of research on the mechanism and optimization method of the enhanced electrocoagulation technique,4–9 but most of the research only stays in the stage of observing and analysing experimental phenomena and does not obtain the reliable intrinsic micro mechanism. This is mainly due to the rapid hydrolysis reaction when the coagulant is dissolving in the water,3 and this process is difficult to observe and measure through experimental methods. Therefore, studying the influence of electrostatic field on the hydrolysis process of ferric salt is important to explore the mechanism of electrocoagulation.Ferric chloride is the most widely used ferric salt coagulant. It is a kind of Fe(III) salt. When the Fe(III) salt enters the water, it will generate Fe3+ through ionization. But the Fe3+ is not stable in the water, which is quickly combined with the water molecules to form Fe(H2O)63+. Then the Fe(H2O)63+ will show a strong tendency to hydrolyse in water and form various hydroxyl iron ions.10,11 When external electrostatic field is present, the process of Fe3+ combining with the water molecules will be influenced.
Therefore, in the present article the ferric chloride solution was taken as the study object, and the influence on the ferric chloride solution system caused by external electrostatic field during the time slot before the chemical reaction of Fe3+ and water molecules was studied. Since molecular dynamics (MD) simulation can cover up a time span of micro-seconds or nano-seconds, we used MD simulation to study the water shell radius of the hydrated Fe3+, the coordination number of water molecules, the average residence time of water molecules in water shell of Fe3+, the self-diffusion coefficient of Fe3+ and water molecules, the hydrogen bond structural parameters and the changes of solution viscosity under electrostatic fields with different intensity. The potential effects of these changes on the hydrolysis of Fe3+ and the condensation process of Fe3+ complexes were also analyzed.
The detailed description of the simulation
The changes of ferric chloride aqueous solution under electrostatic field were investigated by equilibrium molecular dynamics. The simulations were performed in the NPT ensemble (at constant particle number, pressure and temperature) using the GROMACS package.12 All the simulated temperatures were set at 300 K by using Berendsen temperature coupling method. The pressures were set at 1 atm. Since the chemical reaction of Fe3+ and water molecules doesn't begin at that initial time slot, the water molecules will not be broken. In addition, SPC/E model is one of the most popular water models for the remarkable accuracies of various properties over wide temperatures and pressures. In particular, this model reproduces the dielectrostatic constant quite well as compared with other models, which is very important for the salt–water mixtures. Therefore, according to the simulation method of salt–water system,13–15 the SPC/E model was adopted for water molecules in our work. The ferric chloride solution with a concentration of 1.03 mol kg−1 was selected as the research object. According to the requirement of the composition ratio of ferrous chloride in ferric chloride coagulant in the Chinese national standard GB-4482-2006 “water treatment agent ferric chloride”, 2 ferrous chloride molecules were added into the system. According to the concentration of the solution, the whole simulation system consisted of 3765 water molecules, 70 Fe3+ ions, 2 Fe2+ ions and 214 Cl− ions (a total of 4051 particles), which were placed in the box of 5 nm × 5 nm × 5 nm. The periodic boundary condition was used. In this paper, the GROMOS force field was used to calculate the interaction between iron ions and water molecules.15 When calculating the Lennard-Jones interaction, the cut-off was set as 1 nm. Fast Particle-Mesh ESD electrostatic method (PME)16 was used to calculate the electrostatic interaction with a real space cut-off of 0.7 nm. The value of Fourier spacing was 0.12 nm. The time step length used for all simulations was 2 fs,15 and the simulation time of each electrostatic field intensity was 20 ns. The Lennard-Jones potential parameters of each particle are listed in Table 1, and the potential parameters of Fe3+ and Fe2+ are referred in ref. 17. The electrostatic field intensity employed in the simulation process was set as 105 V m−1, 106 V m−1, 107 V m−1, 108 V m−1, respectively, and the direction of electrostatic field was along the direction of the Y axis. The finished system model is shown in Fig. 1. Since the parameters will change easily during the whole simulation time, it is necessary to evaluate the degree of numerical fluctuation in this process. The results of the parameters were obtained from the last 10 ns of every simulation. The 10 ns was divided into ten segments, and we obtained 10 parameter values from each segment. The final result of parameter was obtained from the average of the 10 parameter values. In addition, the volatility of the data was measured by standard deviation marked as error bar in the figures.| ε (kJ mol−1) | σ (nm) | |
|---|---|---|
| Fe3+ | 2.166 | 0.191 |
| Fe2+ | 2.106 | 0.191 |
| Cl− | 1.2889 | 0.3470 |
| O | 0.6502 | 0.3166 |
In order to verify the correctness of the simulation method, the self-diffusion coefficient of two kinds of iron ions, the self-diffusion coefficient of water molecules, the first peak position of the radial distribution function of the iron ion–water molecules and the water molecule coordination number of hydrated Fe3+ ion were calculated without external electrostatic field. The solution temperature was set as 300 K and the solution concentration was set as 0.11 mol kg−1. The results were compared with the simulation and experimental results in other literatures. The results are shown in Table 2.
| M1 | M2 | M3 | |
|---|---|---|---|
| a M1 is from our work, M2 is the result by other simulate method, M3 is from experiments.b From ref. 18 using MD simulation.c From ref. 17 using MD simulation.d From ref. 19 using diaphragm cell method.e From ref. 20 using diaphragm cell method.f From ref. 21 using X-ray. | |||
| DFe(III) (cm2 s−1 × 10−5) | 0.52 | 0.53b, 0.50c | 0.56d |
| DFe(II) (cm2 s−1 × 10−5) | 0.61 | 0.56b, 0.69c | 0.7e |
| nFe(III)–H2O | 6.21 | 6b, 6.46c | 6f |
| nFe(II)–H2O | 5.96 | 6b, 6.23b | 6f |
| Location of first peak of the gFe(III)–H2O(r) (nm) | 0.202 | 0.196b, 0.195c | 0.198f |
| Location of first peak of the gFe(II)–H2O(r) (nm) | 0.208 | 0.209b, 0.212c | 0.210f |
As can be seen from Table 2, the calculation results of DFe(III), DFe(II), nFe(III)–H2O, nFe(II)–H2O, location of the first peak of the gFe(III)–H2O(r) and gFe(II)H2O(r) are close to the results of other literatures, which proves that the MD simulation method in this paper is more reasonable and can be used to study the change of solution properties of ferric chloride solution under external electrostatic field.
Results and discussion
Radial distribution function
In this section, the values of PFe(III)–H2O (first peak value), PFe(III)–Cl, RFe(III)–H2O, nFe(III)–H2O, RFe(III)–Cl, nFe(III)–Cl were calculated under the external electrostatic field with intensity of 105 V m−1, 106 V m−1, 107 V m−1 and 108 V m−1, respectively, and the results were compared with that under no external electrostatic field. The radial distribution function was calculated according eqn (1):22
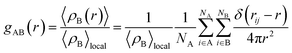 | (1) |
The water molecule coordination number of Fe3+ is calculated according to eqn (2):23
 | (2) |
The chloride ions coordination number of Fe3+ is calculated according to eqn (3):
 | (3) |
The calculation results of radial first peak position of Fe3+–H2O and PFe(III)–H2O are shown in Table 3 and Fig. 2. The results of RFe(III)–H2O and nFe(III)–H2O are shown in Fig. 3 and 4. The RFe(III)–H2O was obtained from the location of the first local minimum of gFe–H2O(r).
| Electrostatic field strength | 0 V m−1 | 105 V m−1 | 106 V m−1 | 107 V m−1 | 108 V m−1 |
|---|---|---|---|---|---|
| Radial first peak position of Fe3+–H2O (nm) | 0.206 | 0.206 | 0.206 | 0.206 | 0.206 |
| PFe(III)–H2O | 21.952 | 21.768 | 21.667 | 21.663 | 21.517 |
 | ||
| Fig. 4 The number of coordination water around Fe3+ under electrostatic field with different intensity. | ||
According to Table 3 and Fig. 2 it can be seen that under electrostatic field with different intensity the position of first peak of gFe–H2O(r) are all 0.206 nm, which is consistent with the that under no electrostatic field. This indicates that electrostatic field has no influence on the position of first peak of gFe–H2O(r). But the external electrostatic field decreases the value of PFe(III)–H2O, and this value decreases with the increase of electrostatic field intensity. When the electrostatic field intensity are 0 V m−1, 105 V m−1, 106 V m−1, 107 V m−1 and 108 V m−1, the PFe(III)–H2O values are 21.952, 21.768, 21.667, 21.663, 21.517 respectively. From Fig. 3, it is known that the value of RFe(III)–H2O decreases notably under electrostatic field. It can be seen that except for the value of RFe(III)–H2O is 0.264 nm when electrostatic field intensity is 108 V m−1, under other electrostatic fields the RFe(III)–H2O values are all 0.268 nm, which is only less 0.002 nm than that under no electrostatic field. Therefore, the external electrostatic field has little influence on the radius of hydrated Fe3+ ion. As shown in Fig. 4, compared with no external electrostatic field the value of nFe(III)–H2O under electrostatic field increases, and as electrostatic field intensity increases the value of nFe(III)–H2O is obviously increased.
When external electrostatic field is present the value of PFe(III)–H2O decreases, which indicates that the number of water molecule in the position of the first peak (0.206 nm) is reduced. But the ionic radius of the hydrated Fe3+ ion is not affected by electrostatic field, and the number of coordination water molecule of the hydrated Fe3+ ion is increased. The changes above indicate that the external electrostatic field makes more water molecules become the coordination water of Fe3+ ions, which means the external electrostatic field can enhance the interaction between Fe3+ ions and the nearby water molecules. This enhanced interaction is beneficial to the hydrolysis of Fe3+ ions in water. Hedstrom10 confirmed the existence of FeOH2+, Fe(OH)2+ and Fe2(OH)24+ during the hydrolysis process of Fe(III) salt, and measured their hydrolysis equilibrium constants. Biederman11 found that except the above hydrolytic ions, Fe3(OH)45+ (a kind of trimer) also existed. The equations of possible hydrolytic reaction of Fe3+ ions in water shows as below:
 | (4) |
Under normal conditions the complex form of the ferric monomer produced by hydrolysis intensively tends to be polymerized, and the most likely product is the dipolymer Fe2(OH)24+, because dipolymer Fe2(OH)24+ has significant stability.10,11,24,25 No matter what forms of hydrolysates produced by hydrolysis of Fe3+, water molecules are the main reactants. The electrostatic field enhances the interaction and the reaction probability of the Fe3+ and surrounding water molecules, which facilitates the polymerization of the complex form of the ferric monomer. This is beneficial to the enhancement of the coagulation effect of the ferric chloride coagulant.
The interaction between the Fe3+ and the surrounding water molecules is enhanced by the external electrostatic field, and it can be indirectly reflected from the distribution of the anion around the Fe3+. Fig. 5 and 7 show the value of PFe(III)–Cl, RFe(III)–Cl, nFe(III)–Cl under electrostatic field with different intensity.
From Fig. 5, it can be seen that the first peak position of the radial distribution function of Fe3+–Cl− is 0.232 nm no matter whether there is external electrostatic field or not. But the electrostatic field reduces the value of PFe(III)–Cl, and as the intensity of the electrostatic field increases, the value of PFe(III)–Cl is getting smaller. When the electrostatic field intensity is 0 V m−1, 105 V m−1, 106 V m−1, 107 V m−1 and 108 V m−1, the PFe(III)–Cl values are 19.332, 18.554, 16.837, 16.545, 15.395 respectively. From Fig. 6 and 7, the electrostatic field has little influence on the value of RFe(III)–Cl. No matter whether there is electrostatic field or not, the value is about 0.254 nm. But electrostatic field significantly reduces the coordination number of Cl− around the Fe3+, and the coordination number decreases with the increase of the electrostatic field intensity.
 | ||
| Fig. 7 The number of coordination Cl− around Fe3+ under electrostatic field with different intensity. | ||
According to Debye–Huckel Theory proposed by Debye and Huckel in 1923, on the one hand, the Coulomb force between the Fe3+ and the Cl− makes the ions tend to be orderly arranged as in the lattice. On the other hand, the Brownian motion will make the ions in a random distribution. Since Brownian motion is not strong enough to counteract the Coulomb force, the result of the interaction between these two forces is bound to form such a situation: around a Fe3+ (central ion), the Cl− ions are more likely to appear than other Fe3+ ions. Therefore, it can be considered that the Cl− ions with negative charges are relatively concentrated around the Fe3+ central ions. Comparing with Fig. 2 the reduction in value of PFe(III)–Cl is much more than PFe(III)–H2O with increase in the strength of the electrostatic field. This may because that the interaction between Fe3+ and H2O is electrostatic interaction, but the interaction between Fe3+ and Cl− is composed of electrostatic interaction and ionic polarization interaction. Electrostatic interaction and ionic polarization interaction are all caused by the electric field of electron cloud. Therefore the interaction between Fe3+ and Cl− is easier to be influenced by external electric field than the interaction between Fe3+ and H2O. In addition, the PFe(III)–H2O is higher as compared to the one given in ref. 26. Also in present study, the PFe(III)–H2O is higher as compared to PFe(III)–Cl whereas in ref. 26, the trend is opposite. We believe that this phenomenon may be caused by the difference of solution concentration. Our solution concentration is 1.03 mol kg−1, but the concentration in the reference is 4.1 mol kg−1. We also run another simulation with the FeCl3 concentration of 4.1 M for verification. The result showed that the intensity was higher for PFe(III)–Cl as compared to PFe(III)–H2O, which met with the result in the reference.
From Fig. 5 and 7, it is found that PFe(III)–Cl and nFe(III)–Cl are reduced simultaneously under the electrostatic field, which indicates that the electrostatic field weakens the Coulomb force between the central Fe3+ and the surrounding Cl− ions and reduces the number of Cl− ions around the Fe3+. In the meantime, since there are only Cl− and water molecules around Fe3+ ions, the vacancies produced by reduced Cl− ions are replaced by water molecules. This also indirectly confirmed the increase of number of coordination water around Fe3+.
Diffusivity
In this section, the values of the self-diffusion coefficient of Fe3+ DFe(III) and water molecules DH2O are calculated when the external electrostatic field intensity is 105 V m−1, 106 V m−1, 107 V m−1 and 108 V m−1 respectively, and these values are compared with that under no external electrostatic field. The self-diffusion coefficient is calculated according to eqn (5) ‘Einstein relation’:27
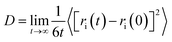 | (5) |
As shown in Fig. 8, compared with the value of DFe(III) (0.0895 × 10−5 cm2 s−2) under no electrostatic field, the DFe(III) increases under external electrostatic field. As the intensity of the electrostatic field increases, the value of DFe(III) is bigger. However, it can be seen from Fig. 9 that, contrary to the change trend of DFe(III), the self-diffusion coefficient of water molecules DH2O becomes smaller with the intensity of the electrostatic field, which means the value of DH2O is inversely proportional to the electrostatic field intensity.
The diffusion coefficient is an important parameter to study the thermodynamic properties of ferric chloride solution, and its change reflects the activity change of particles in solution, which will directly affect the equilibrium of the hydrolysis reaction. The results in Fig. 8 show that the electrostatic field enhances the activity of Fe3+ ions in the solution, which contributes to increase the collision probability of the Fe3+ with the water molecules, thus increases the probability of the Fe3+ to capture the coordination water and promotes the initial hydrolysis of the Fe3+. In addition, while the Fe3+ is hydrolyzing, the polymerization between different Fe3+ ions will also occur, which can produce the ferric complexes in the form of polymer.10,11 The increase of the self-diffusion coefficient of Fe3+ also increases the collision probability between different Fe3+ and complex monomers, thus promotes the formation of polymers. The positive charge of the polymer is generally higher such as Fe2(OH)24+ (dipolymer) with 4 positive charges and Fe3(OH)45+ (tripolymer) with 5 positive charges. The more charges can make stronger adsorption capacity. In addition, it is known from Fig. 9 that the effect of electrostatic field reduces the self-diffusion coefficient of water molecules, mainly because the interaction between Fe3+ and water molecules is enhanced by the electrostatic field, which means that the binding effect of Fe3+ on water molecules is enhanced.
Residence time of water molecules in the first water shell of Fe3+
The dynamical residence time of water molecules is an important parameter describing the effect of solute on water solvent. It can reflect the migration characteristics and stability of water molecules in the presence of solute.28,29 Residence time of water molecules is the average time for water molecules to stay in the first water shell of solute ions.30 In this paper, the residence time of water molecules was calculated by eqn (6):31
 | (6) |
 | (7) |
The calculation results of the residence time of water molecules under electrostatic field with different intensity are shown in Fig. 10.
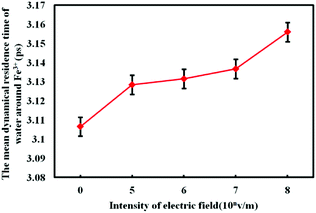 | ||
| Fig. 10 Average residence time of H2O molecules around Fe3+ under electrostatic field with different intensity. | ||
As shown in Fig. 10, the residence time γres of the water molecules under different electrostatic field is larger than that without electrostatic field. And with the increase of electrostatic field intensity, γres shows an upward trend. The external electrostatic field prolongs the residence time of water molecule, which is also related to the enhanced interaction between Fe3+ and water molecules. The results obtained above show that the electrostatic field can effectively enhance the electrostatic interaction between Fe3+ and water molecules, which makes Fe3+ to attract more water as the coordination water molecules. Then more water molecules' mobility is limited, thus the diffusivity of water molecules is reduced. The diffusion of water molecules has direct relation with the residence time of water molecules,32 the decrease of the diffusion of water molecules will reduce the frequency of water molecules entering and leaving the first water shell of Fe3+. According to eqn (7) it is known that the reduction of the frequency of entering and leaving the first water shell will prolong the residence time of each water molecule, which makes the mean residence time of water molecules prolonged.
Hydrogen bond
Hydrogen bond plays a important part during the process of hydrolysis, polymerization and adsorption. The hydrogen bond network structure in the solution directly affects the adsorption properties of polymeric ferric chloride.33 Therefore, in this section the strength characteristics of hydrogen bond network are studied, including the number of hydrogen bonds (nHB) and the average lifetime of hydrogen bonds (τHB), which is due to the positive relationship between these two parameters and the strength of the hydrogen bond network.34In the Gromacs software, hydrogen bonding is defined from two aspects: the distance between donor (D) and receptor (A), and the angle of hydrogen-donor–acceptor. The specific definition is as follows:
(1) The distance between donor and acceptor is less than van der Waals distance (3.5 A).
(2) The angle of hydrogen-donor–acceptor is less than 30°.
In this simulation, the donor and acceptor are oxygen atoms in different water molecules. The angle of the hydrogen-donor–acceptor is expressed by ∠HD-OD–OA.
Hydrogen bonds exist widely among water molecules in water. Due to the dynamic characteristics of water molecules, the hydrogen bonds between the water molecules are constantly forming and breaking at the same time.35 Therefore, hydrogen bond lifetime represents the average time of hydrogen bond in this dynamic process. The hydrogen bond lifetime τHB can be calculated by eqn (8).36
 | (8) |
| C(τ) = 〈hi(t)hi(t + τ)〉 | (9) |
The number of hydrogen bonds (nHB) and the percentage of water molecules with n hydrogen bonds (fn) were investigated, where n = 0, 1, 2, 3. The lifetime and the number of hydrogen bonds in solutions under different intensities of electrostatic field are shown in Tables 4 and 5.
| Electrostatic field intensity | |||||
|---|---|---|---|---|---|
| 0 V m−1 | 105 V m−1 | 106 V m−1 | 107 V m−1 | 108 V m−1 | |
| Hydrogen bond life (ps) | 7.53 | 7.53 | 7.53 | 7.52 | 7.50 |
| Electrostatic field intensity | |||||
|---|---|---|---|---|---|
| 0 V m−1 | 105 V m−1 | 106 V m−1 | 107 V m−1 | 108 V m−1 | |
| f0 (%) | 47.40 | 47.43 | 47.49 | 47.52 | 47.53 |
| f1 (%) | 35.54 | 35.56 | 35.56 | 35.59 | 35.62 |
| f2 (%) | 14.20 | 14.16 | 14.16 | 14.14 | 14.11 |
| f3 (%) | 2.81 | 2.81 | 2.81 | 2.80 | 2.78 |
| nHB | 2722.38 | 2721.14 | 2718.70 | 2716.35 | 2713.53 |
It can be seen from Table 4 that the average lifetime of hydrogen bond in the solution decreases under the effect of electrostatic field, but the decrease is not obvious. Only when the intensity of the electrostatic field is large (108 V m−1), the average lifetime of hydrogen bond decreases from 7.53 ps to 7.50 ps. Therefore, the external electrostatic field has little effect on the average life of hydrogen bonds. However, according to Table 5 the number of hydrogen bonds decreases with the increase of electrostatic field intensity. The total number of water molecules involved in the bond formation decreases from 2722.38 to 2713.53. As the electrostatic field intensity rises from 0 V m−1 to 108 V m−1, the proportion of the water molecules which do not participate in forming hydrogen bond rises from 47.40% to 47.53%, the proportion of water molecules involved in forming 1 hydrogen bonds rises from 35.54% to 35.62%, the proportion of water molecules involved in forming of 2 hydrogen bonds decreased from 14.20% to 14.11%, and the proportion of water molecules involved in forming 3 hydrogen bonds declined from 2.81% to 2.78%.
The change of the hydrogen bond structure parameters indicates that the electrostatic field has little influence on the hydrogen bond average life, but has a significant influence on the number of hydrogen bonds. The electrostatic field can effectively destroy the hydrogen bond inside the water cluster in the solution, and reduce the number of water molecules involved in the formation of multiple hydrogen bonds. In addition, the rise of the proportion of water molecules involved in forming 0 and 1 hydrogen bonds means that the number of monomer water molecules and dipolymers water molecules increased under electrostatic field, and this effect tends to be more significant with the increase of electrostatic field intensity. The increase in the number of monomer water molecules and dipolymers water molecules is beneficial to increase the diffusivity and permeability of water molecules. However, the result of the previous study shows that the self-diffusion coefficient of water molecules in the solution decreases under electrostatic field, which is mainly ascribed to the enhanced binding to water molecules caused by Fe3+. Therefore, the change of hydrogen bond structure in the solution also proves the enhancement of the binding effect of Fe3+ ions on water molecules under the electrostatic field.
Viscosity
The dynamic viscosity of the solution is an important parameter for the conformation change of the solution. The change of viscosity of ferric chloride solution will affect the Brown motion characteristics of the ferric complex formed by hydrolysis and the rate of particles collision probability, thus affect the polymerization. It has been confirmed that electrostatic field can influence the dynamic viscosity of solution.37 The dynamic viscosity of the solution can be obtained by eqn (10):
 | (10) |
ax = A![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) cos(kz), k = 2π/lz cos(kz), k = 2π/lz
| (11) |
 | (12) |
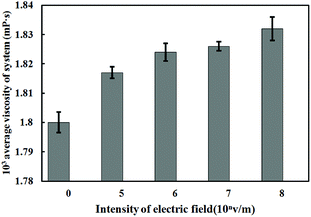
The viscosity value of solution under electrostatic field with different intensity is shown in Fig. 11.
From the calculation results of the viscosity of Fig. 11, it is found that the viscosity of ferric chloride solution increases under the action of electrostatic field, and it is positive correlation between viscosity of the solution and electrostatic field intensity. As the electrostatic field intensity rises from 0 V m−1 to 108 V m−1, the viscosity of the solution rises from 1.8 mPa to 1.832 mPa s. The viscosity of the solution is a parameter to measure the friction between the fluid layers in the solution system. The viscosity is a macroscopic property to reflect the friction effect of all the particles in the solution, which is related to the number of hydrocarbon bonds in the solution and the molecular weight of the particles. Since there is no hydrocarbon bond in the solution system, the change of solution viscosity directly reflects the change of internal structure and kinetic parameters of the water solvent. The Bakker's study result38 shows that the change of the viscosity of the ionic solution is directly related to the residence time of water molecules in the first water shell of the hydrated ion. If the residence time is prolonged, the viscosity of the solution will correspondingly increase.
According to the results in Fig. 10, the external electrostatic field can significantly prolong the residence time of water molecules, thus increasing the viscosity of the solution. In addition, the results of Fig. 11 are consistent with the calculation results of the diffusion coefficient of the water molecules under the electrostatic field in Fig. 9. There is a negative correlation between the diffusion of water molecules and the viscosity of the solution, which means the decrease of the diffusion of water molecules can lead to the increase of solution viscosity. The increase of solution viscosity is not conducive to the destabilization and collision aggregation of colloid particles during the later reaction. Therefore, viscosity increase should be relieved during the application of the technique of electrocoagulation, such as using the method of adjusting the reaction temperature.
In our previous work,32 we discussed the impact of an electrostatic field and impurity Mg2+ ions on CaCl2 solution. The results in the previous paper shows that under electrostatic field the DCa increased, which meets with the DFe in the present article. But the viscosity trend in the two studies is opposite. The experimental results from previous ref. 39 showed that the electric field (magnetic field) can reduce surface tension of pure water, which means the electric field can reduce the viscosity of pure water. But the presence of metal cations will increase the viscosity of solution because of the bound effect to the water molecules. So there will be two opposite effects to the water molecules, one (from electric field) can increase the activity and the other (from metal cations) can impair the activity. The DH2O in the previous paper increased under electrostatic field, but decreases in the present article. This may because Fe3+ has a much bigger attraction to water molecule than Ca2+, and electrostatic field enhances this attraction of Fe3+, which means the inhibition effect gains the upper hand. Therefore, the lower DH2O under electrostatic field in the present study leads to a longer average residence time of H2O molecules around Fe3+, and the enhanced attraction from Fe3+ leads to a less number of hydrogen bonds between water molecules.
Conclusions
In the present article, the change of microscopic properties of ferric chloride solution under electrostatic fields with different intensity was studied by equilibrium molecular dynamics simulations for investigating the mechanism of enhanced electrocoagulation technique. The results show that external electrostatic field can change the distribution characteristics of water molecules around Fe3+. When electrostatic field is present, the first peak position of Fe3+–H2O radial distribution function almost has no change, but the first peak value decreases, and the number of coordinated water molecules increases. The electrostatic field can change the diffusion characteristics of Fe3+ and water molecules in solution. Under the effect of electrostatic field, the self-diffusion coefficient of Fe3+ increases, but the self-diffusion coefficient of water molecules decreases, and the average residence time of water molecules in the first water shell of Fe3+ increases. The electrostatic field can change the structure of hydrogen bond network in solution. Under the effect of electrostatic field, the average lifetime of hydrogen bond in the solution has no obvious change, but the number of hydrogen bonds decreases, and the proportion of water molecules that do not participate in bonding and to participate in the formation of 1 hydrogen bond has increased. The change amplitude of the parameters above is bigger with the increase of electrostatic field intensity. The changes of these parameters show that the electrostatic field can enhance the interaction between Fe3+ and water molecules, and promote the hydrolysis of Fe3+ and the polymerization of ferric ion complex, which is beneficial to the enhancement of the effect of ferric chloride coagulant. In addition, the external electrostatic field increases the viscosity of the solution. This change is not conducive to the interaction of colloid particles in the solution. Therefore, the viscosity of solution should be controlled during the practical application of the technique of electrocoagulation.Conflicts of interest
There are no conflicts to declare.Greek symbols and nomenclature
| gA–B | Radial distribution function, nm |
| nA–B | Particle B coordination number around particle A |
| D | Diffusion coefficient, cm2 s−1 |
| P | First peak intensity of gAB |
| γ | Residence time of water molecules, ps |
| τHB | Hydrogen bond lifetime, ps |
| C(τ) | Hydrogen bond correlation function |
| hi(t) | Heaviside unit step function |
| ρ | Density of solution |
| ν | Velocity of solution |
| η | Viscosity value of solution, mP s−1 |
Acknowledgements
This work was financially supported by the National Natural Science Foundation of China (Grant No. 51408525).References
- Y. Cui and J. Xiao, Environ. Sci. Pollut. Res., 1998, 20(3), 39 CAS.
- G. Q. Fan, China Water & Wastewater, 1998, 14(3), 42 Search PubMed.
- H. Zheng, T. Long and X. Shu, Chongqing Enviroment Science, 2000, 22(3), 51 Search PubMed.
- O. T. Can, M. Bayramoglu and M. Kobya, Ind. Eng. Chem. Res., 2002, 42, 3391 CrossRef.
- N. Daneshvar, A. H. Sorkhabi and M. B. Kasiri, J. Hazard. Mater., 2004, B1122, 55 CrossRef PubMed.
- L. S. Calvo, J. P. Leclerc and G. Tanguy, Environ. Prog., 2003, 22(1), 57 CrossRef CAS.
- M. F. Pouet and F. Persin, Water Sci. Technol., 1992, 25(12), 247 CrossRef CAS.
- N. V. Nikolaev, A. S. Kozlovsii and I. I. Utkin, Sov. J. Water Chem. Technol., 1983, 4(3), 70 Search PubMed.
- N. S. Abuzaid, A. A. Bukhari and Z. M. Hamouz, Adv. Environ. Res., 2002, 6(3), 325 CrossRef CAS.
- B. O. A. Hedstrom, Ark. Kemi, 1953, 5, 1 Search PubMed.
- G. Biederman and P. Schindler, Acta Chem. Scand.Acta Chem. Scand., 1957, 11, 731 CrossRef.
- V. D. Spoel, D. Lindahl, E. Hess, B. Groenhof, G. Mark and A. E. Berendsen, J. Comput. Chem., 2005, 26(16), 1701 CrossRef PubMed.
- H. J. C. Berendsen, J. R. Grigera and T. P. Straatsma, J. Phys. Chem., 1987, 91, 6269 CrossRef CAS.
- Z. Zhang and Z. Duan, Phys. Earth Planet. Inter., 2005, 149(4), 335 CrossRef CAS.
- M. Li, Z. Duan and Z. Zhang, Mol. Phys., 2008, 106(24), 26857 Search PubMed.
- M. P. Allen and D. J. Tildesley, Computer Simulation of Liquids, Oxford Clarendon Press, 1989 Search PubMed.
- X. Li and Z. Yang, J. Theor. Comput. Chem., 2006, 5, 341 CrossRef CAS.
- S. Amira, D. Spangberg, M. Probst and K. Hermansson, J. Phys. Chem. B, 2004, 108, 496 CrossRef CAS.
- A. J. Easteal, R. Malhotra, W. E. Price and L. A. Woolf, J. Solution Chem., 1991, 20(3), 319 CrossRef CAS.
- W. E. Price and L. A. Woolf, J. Solution Chem., 1992, 21(3), 239 CrossRef CAS.
- B. S. Brunschwig, C. Creutz, D. H. Macartney, T. K. Sham and N. Sutin, Faraday Discuss. Chem. Soc., 1982, 74, 113 RSC.
- D. M. York, T. A. Darden and L. G. Pedersen, J. Chem. Phys., 1993, 99, 8345 CrossRef CAS.
- A. A. Chialvo and J. M. Simonson, J. Chem. Phys., 2003, 119, 8052 CrossRef CAS.
- C. M Flynn, Chem. Rev., 1984, 84(1), 31 CrossRef.
- J. Y. Bottero, A. Manceau, F. Villieras and D. Tchoubar, Langmuir, 1994, 10(1), 316 CrossRef CAS.
- H. Zhang, G. A. Waychunas and J. F. Banfield, J. Phys. Chem. B, 2015, 119, 10630 CrossRef CAS PubMed.
- T. Darden and D. J. York, Chem. Phys., 1993, 98, 1008 Search PubMed.
- H. J. Bakker, Chem. Rev., 2008, 108, 1456 CrossRef CAS PubMed.
- Y. Zhu, X. Lu and H. Ding, Mol. Simul., 2003, 29, 767 CrossRef CAS.
- M. Li, Z. Duan and Z. Zhang, Mol. Phys., 2008, 106, 2685 CrossRef CAS.
- M. J. Wei, L. Zhang and L. Lu, Phys. Chem. Chem. Phys., 2012, 14, 16536 RSC.
- L. Zhu, Y. Han, C. Zhang, R. Zhao and S. Tang, RSC Adv., 2017, 7, 47583 RSC.
- W. Hu, Chemical engineering thermodynamics, Chemical Industry Press, Beijing, 2001, p. 61 Search PubMed.
- X. Zhang, Q. Zhang and D. X. Zhao, Acta Phys.-Chim. Sin., 2011, 27(11), 2547 CAS.
- A. Luzar and D. Chandler, Nature, 1996, 379, 55 CrossRef CAS.
- W. F. V. Gunsteren, Biomolecular Simulation: The GROMOS96 Manual and User Guide, Groningen, 1996 Search PubMed.
- B. Hess, J. Chem. Phys., 2002, 116, 209 CrossRef CAS.
- H. J. Bakker, Chem. Rev., 2008, 108(4), 1456 CrossRef CAS PubMed.
- Y. I. Cho and S. H. Lee, Int. J. Heat Mass Transfer, 2005, 32, 1 CrossRef CAS.
| This journal is © The Royal Society of Chemistry 2018 |