Effects of temperature on the fracture and fatigue damage of temperature sensitive hydrogels

Abstract

As an excellent model material for fundamental studies on temperature-sensitive hydrogels, poly(N-isopropylacrylamide) (NIPA) hydrogel has been applied in drug delivery, tissue engineering, and soft robotics. However, the lack of study on fracture and fatigue hinders further development of hydrogels for applications where cyclic loading–unloading is unavoidable. In this study, the fracture and fatigue damage of the NIPA hydrogel were studied for the first time by pure shear tests at different temperatures. Fracture behaviors were investigated under monotonic load from 31 °C to 39 °C. It is found that the fracture energy increases with the increase in temperature. The fracture energy is approximately 20 J m⁻² near the volume phase transition temperature. Temperature also significantly influences the fatigue life. By fitting the experimental data, the fatigue limit λ_f is determined. The results obtained from the experimental tests would be important for the engineering applications of the NIPA hydrogels.

---

Introduction

Hydrogels are a type of soft and wet material that consist of cross-linked macromolecules and water.^1,2 Due to the softness and high water absorption ability, hydrogels have drawn considerable attention in different fields, such as tissue engineering,^3–5 matrices for biological studies,^6–8 and drug delivery.^9,10 Moreover, hydrogels undergo reversible volume change by absorbing or exuding water in response to a variety of external stimuli,^1,11,12 such as temperature, light, magnetic field, pH, ionic strength, and chemical reactions. Based on the volume changes, actuating and sensing properties of hydrogels have been broadly studied.¹ With the application fields of hydrogels being further extended, it is imperative to understand the mechanical properties of hydrogels. Although the tensile-compression properties of hydrogels are studied extensively,¹³ the studies on fracture and fatigue properties are rather insufficient.

In 2017, Tang et al.¹⁴ first initiated a study of the fatigue fracture of hydrogels. By choosing the polyacrylamide hydrogel as a model material, fast fracture, delayed fracture and fatigue fracture were studied under monotonic, static, and cyclic loads, respectively. In the same year, Bai et al.¹⁵ published a paper on the fatigue fracture of tough hydrogels. They observed that the stress–stretch curve would reach a steady state after 2000 cycles. From the experimental results, it was found that the fracture energy and the threshold of fatigue fracture were approximately 10 000 J m⁻² and 53 J m⁻², respectively. More recently, Zhang et al.¹⁶ initiated the study of the fatigue behaviour of double network hydrogels. They observed that internal damage accumulated over thousands of cycles until a steady state was reached under cyclic stretches for a sample without a pre-cut crack. For a sample with a pre-cut crack, the crack propagated over several cycles if the maximum stretch was larger than a critical value. Furthermore, the crack would not propagate over several cycles if the energy release rate was below a threshold, around 200–400 J m⁻², which varied with the concentration of PAAM. Bai et al. (2018)¹⁷ also studied the fatigue fracture of self-recovery hydrogels. They found that the stress–stretch curve recovered after thousands of cyclic stretches for a sample without a pre-cut crack. The covalent network played a critical role in determining the threshold of fatigue fractures, while the noncovalent interactions slowed down the extension of the crack under cyclic loads. Zhang et al. (2018)¹⁸ studied the effect of water on the fatigue fracture of nearly elastic hydrogels by choosing the polyacrylamide hydrogel as a model material. They found that the water content largely influenced the fracture energy and fatigue thresholds.

In the aforementioned studies, the fatigue fracture for several types of hydrogels has been studied by pure shear tests, and the energy release rate was characterized as a function of the extension of crack length per cycle. In addition, the fatigue fracture threshold for corresponding hydrogels was obtained. However, all the existing researches concentrated on the fatigue fracture of hydrogels, while few studies focused on the fatigue damage of hydrogels. The effects of temperature on the fracture and fatigue of hydrogels remain unexplored. The lack of such a study hinders the further development of applications of hydrogels, particularly in fields that require their longevity under cyclic load conditions.

In this paper, we focused on the study of the fracture and fatigue behaviours of NIPA hydrogels by pure shear tests and tried to reveal the effects of temperature on the fracture and fatigue mechanism of temperature-sensitive hydrogels. Fracture behaviours were investigated under monotonic load from 31 °C to 39 °C. It was found that the fracture energy increases with the increase in temperature. The fracture energy was approximately 20 J m⁻² near the volume phase transition temperature. Temperature also significantly influenced the fatigue life. By fitting the experimental data, the fatigue limit (λ_f) was determined. The findings on the fracture and fatigue of temperature-sensitive hydrogels would provide some guidelines for possible applications in practical engineering.

Experiments

Thus far, there are many types of temperature-sensitive hydrogels that can be synthesized successfully, such as poly(N-isopropylacrylamide) (NIPA), methyl vinyl ether (MVE), and methacrylic acid (MAAC). Among those hydrogels, NIPA is the most excellent model material for fundamental studies on the temperature sensitivity of hydrogels. Furthermore, the volume phase transition temperature (VPTT) lies between 30 °C and 35 °C from experimental studies. The exact temperature is a function of the detailed microstructure of the macromolecule.^19,20 Above the VPTT, the hydrogel is collapsed and hydrophobic, while it is swollen and hydrophilic below the VPTT. In this study, we selected NIPA hydrogel as a model material to study the fracture and fatigue damage of temperature sensitive hydrogels. It was synthesized via a free radical copolymerization, and the synthetic scheme was a modified scheme of Suzuki and Ishii.²¹

Sample preparation

We chose N-isopropylacrylamide (NIPA, monomer), N,N′-methylenebisacrylamide (BIS, crosslinker), N,N,N′,N′-tetramethylethylenediamine (TEMED, accelerator) and ammonium persulfate (APS, initiator) as the main precursors. The detailed preparation process is shown as follows. (1) Initially, 3.9 g of purified NIPA monomer was dissolved in 50 g deionized water with 66.5 mg N,N′-methylenebisacrylamide as the crosslinker. (2) The as-prepared solution was refrigerated at 4 °C for 8 hours to dissolve sufficiently. (3) Then, 120 μL of TEMED was added as an accelerator into the solution. (4) Furthermore, 20 mg of ammonium persulfate (APS) was added as an initiator for the condensation reaction. (5) The product was injected into a clean glass mould with 1 mm silicon spacer. In order to prevent the NIPA monomer from being separated at room temperature, the injection process was performed as quickly as possible. (6) The mould was refrigerated at 4 °C, and the gelation process was performed for more than 24 hours for sufficient gelation. (7) The NIPA gel sheet was carefully removed from the glass mould and washed using deionized water to get rid of residual chemicals and unreacted monomers. (8) The prepared gel samples were immersed in deionized water at room temperature for 7 days to reach the equilibrium swollen state.

The VPTT test of the self-prepared NIPA hydrogel shows the VPTT ranging from 34.5 °C to 35.2 °C. Because of the hysteresis of swelling–deswelling, the VPTT from the heating process slightly differs with that from the heating process. Moreover, the slightly fluctuated VPTT value is attributed to mechanical constraints.²²

Pure shear test

For pure shear tests, the fully saturated samples were machined into rectangular sheets with dimensions of 5.0 cm × 3.5 cm using a laser cutting machine. One type of obtained samples was used to test strain energy density and fatigue life, while the other samples with a 0.5 cm-crack in the middle edge were used to test the critical stretch and calculate fracture energy (Fig. 1).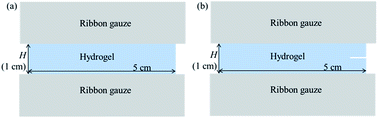

Fig. 1 Schematic of two types of samples for pure shear tests. (a) Sample without a pre-cut crack; (b) sample with a pre-cut crack near the middle of the edge.

In the pure shear test, the tensile tester (SHIMADZU AGS-X, Shimadzu Corporation, Japan) with a load cell of 50 N was used for all of the tests. The lower side of the sample was fixed on the bottom of the water bath and the upper side was clamped using the metallic grippers of the tensile tester. To prevent the specimen from breaking or sliding during the tension process, the lower and upper sides of the gel were attached with ribbon gauze. The valid length (H) of the sample between the fixed bottom and the upper gripper was set as 1.0 cm. Under monotonic load, the samples are loaded until rupture in the water bath with a strain rate of 5 mm min⁻¹ for each temperature (stepwise from 31 °C to 39 °C with 2 °C increments).

Due to the fact that the stress change is quite small when compared with the strain change after the yielding of the hydrogel, it is more reasonable to use strain (or stretch) as the control variable for the fatigue property tests. Therefore, in this study, stretch was adopted to study the fatigue of the NIPA hydrogel. For each test under different maximum stretch (λ_max), the number of cycles was increased until the sample ruptured. Fatigue life is defined as the maximum cycles corresponding to λ_max. Considering no distinct rate dependence for the NIPA hydrogel²² and the time-consuming process of the cyclic tests, a larger loading strain rate of 30 mm min⁻¹ was used in the mechanical cyclic tests. Fatigue tests were conducted at 31 °C and 37 °C to show the fatigue damage below the VPTT and above the VPTT, respectively.

Fracture behaviours

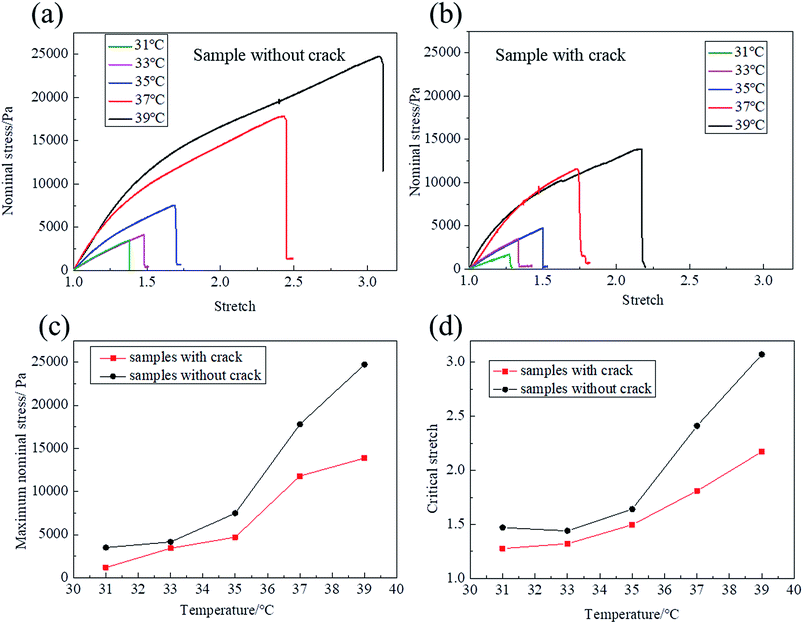
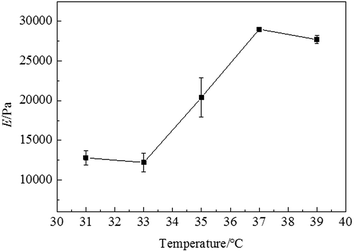
To calculate the fracture energy of the NIPA hydrogel, the stress–stretch curves of samples with/without the pre-cut crack were measured at different temperatures through the VPTT by pure shear tests at a loading strain rate of 5 mm min⁻¹. In Fig. 2(a) and (b), it is clearly shown that the stress–stretch curves change with different temperatures. With the increase in temperature, the hydrogel undergoes a phase transition: the amount of water in the hydrogel in equilibrium varies with the change in temperature.²² Both the maximum nominal stress and maximum stretch increase with the increase in temperature (Fig. 2(c) and (d)). It can be clearly found that the increase in rate of the maximum nominal stress and maximum stretch below the VPTT are smaller than those above the VPTT. Due to non-homogeneous deformation and phase discontinuity, the samples were easily ruptured in a small stretch at 35 °C. The values of maximum nominal stress and maximum stretch at 35 °C are close to the values below the VPTT. For samples without the pre-cut crack, the maximum nominal stress at 31 °C is around 5 kPa, while the value at 39 °C is about 25 kPa (Fig. 2(c)). The critical maximum stretch (λ_c) at 39 °C can be up to 3, which is twice of the λ_c at 31 °C (Fig. 2(d)). As the NIPA hydrogel is rather sensitive to cracking, the mechanical properties of samples with the pre-cut crack are significantly weaker than the samples without the pre-cut crack in terms of maximum nominal stress and critical stretch (Fig. 2(c) and (d)).

Fig. 2 Fracture characteristics of NIPA hydrogels under monotonic load. (a) Stress–stretch curves for samples without the crack under different temperatures; (b) stress–stretch curves for samples with the crack under different temperatures; (c) the relationship between maximum nominal stress and temperature; and (d) the relationship between critical stretch and temperature.

We calculated the Young's modulus (E) from the slope of the stress–stretch curves of samples without the pre-cut crack in 10% strain by assuming that the NIPA hydrogel is in an elastic state within 10% deformation. The Young's modulus (E) below the VPTT is about 13 kPa, while the Young's modulus (E) above the VPTT is approximately 28 kPa. With the increase in temperature through the phase transition, the Young's modulus (E) increases drastically (Fig. 3).

Fig. 3 Young's modulus (E) of the NIPA hydrogels at different temperatures.

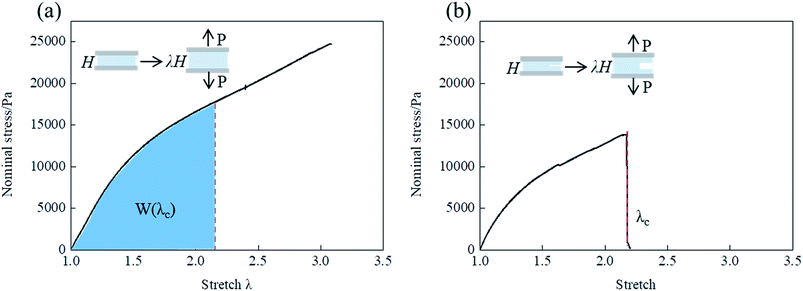
According to the results of Fig. 2, we calculate the fracture energy of the NIPA hydrogel at different temperatures. The calculation method of fracture energy is shown in Fig. 4. The area under the stress–stretch curve gives the strain energy density W(λ) (Fig. 4(a)). In the pure shear tests, W(λ) is the energy per volume of the uncut samples. The energy release rate G is calculated as follows:²³

G = HW(λ) (1)

where H is the sample length between the fixed bottom and the upper gripper when the sample is undeformed, and λ is the vertical stretch. The fracture energy is defined as the critical energy release rate from crack initiation to propagation. Therefore, the fracture energy is calculated from eqn (1) when the stretch λ equals the critical stretch λ_c of the samples with the pre-cut crack (Fig. 4(b)).

Fig. 4 Calculation of strain energy density W(λ_c) by pure shear tests: (a) the stress–stretch curve of samples without the pre-cut crack; and (b) the stress–stretch curve of samples with the pre-cut crack.

The calculated fracture energy at different temperatures is shown in Fig. 5. The fracture energy of the NIPA hydrogels is approximately 10 J m⁻² at temperatures below the VPTT. The fracture energy increases rapidly when the temperature is higher than the VPTT. The fracture energy can be up to 150 J m⁻² at 39 °C. In comparison with the existing research results (e.g., the fracture energy of the polyacrylamide hydrogel is around 50 J m⁻²,¹⁴ the fracture energy of PAMPS/PAAM double-network hydrogels is nearly 3000 J m⁻² (ref. 15) and the fracture energy of tough hydrogels is close to 10 000 J m⁻² (ref. 24)), the fracture energies of NIPA hydrogels are quite different. This might have originated from the hydrogen bonding and hydrophobicity of the NIPA hydrogels.

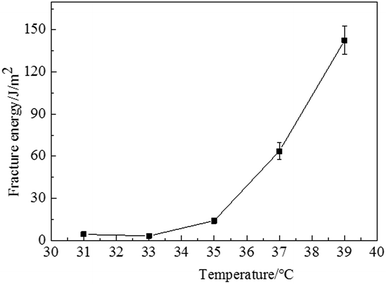Fig. 5 Fracture energy of the NIPA hydrogels at different temperatures. The data represent the mean ± standard deviation of three experimental results.

The fracture energy increases rapidly when the temperature is higher than the VPTT, mainly because of the intrinsic properties of the NIPA hydrogel. Above the VPTT, the hydrophobic interactions become dominant, and the hydrogel shrinks (or undergoes deswelling) and turns into a collapsed and hydrophobic state expelling water. Therefore, the water content of the hydrogels above the VPTT is lower than that below the VPTT. In ref. 18, it was found that the fracture energy reduces with the increasing in water content. To some extent, the findings in this study further verify the effects of water content on fracture energy.

Fatigue damage

The fatigue of hydrogels is commonly studied by pure shear tests using samples with/without a pre-cut crack. Bai et al.¹⁷ defined fatigue damage as the irreversible change in the mechanical property for a sample without a pre-cut crack subject to a cyclic load, while fatigue fracture was defined as the gradual crack propagation for a sample with a pre-cut crack subject to a cyclic load. Herein, we focused on the study of fatigue damage of the NIPA hydrogel. The life of the fatigue damage (N_f) is defined as the maximum cycles when the nucleates are generated but not completely fractured. The VPTT clearly influences the mechanical properties of the NIPA hydrogels. Therefore, the fatigue damage was studied at temperatures above the VPTT and below the VPTT.

From the information presented in Fig. 2(d), it is observed that the critical stretch increases with the increase in temperature. To improve the efficiency of tests as much as possible, a temperature (37 °C) slightly higher than the VPTT was set to study fatigue damage above the VPTT. According to the loading mode shown in Fig. 6(a), fatigue damage tests were conducted with a prescribed stretch (λ_max) ranging from 1.2 to 1.8. We loaded the hydrogel without stopping until the crack was observed by the naked eye and recorded the evolution of stress–stretch curves over cycles. Fig. 6(b) shows that the maximum nominal stress of each cycle varies with the number of cycles. The maximum nominal stress within 1000 cycles reduced rapidly, and then increased with the increase in number of cycles until the generation of nucleates (i.e., the maximum nominal stress suddenly reduced over cycles). The evolution of stress–stretch curves over cycles for NIPA hydrogels still did not reach a relatively steady state, while the robust polyacrylamide–alginate hydrogel would reached a steady state after approximately 2000 cycles.¹⁶ In comparison, the stress–stretch curves for the polyacrylamide hydrogel remained nearly the same with cycling.¹⁴ Distinct mechanical softening was observed within 1000 cycles due to the breakage of weak bonds and viscoelasticity. The evolution of maximum stress over cycles indicates that the mechanical properties are first weakened and then strengthened over cycles until fatigue damage occurs for the NIPA hydrogels.

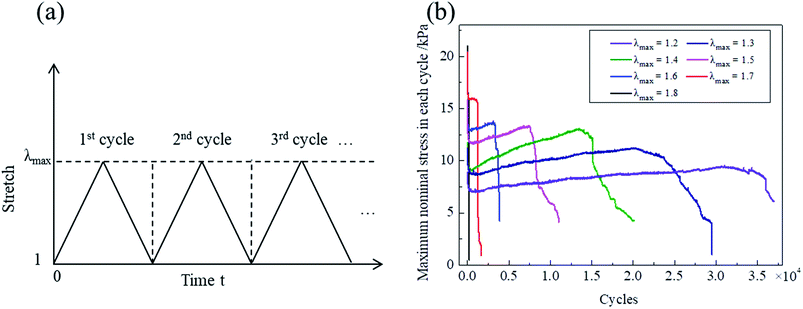Fig. 6 The loading mode under cyclic load (a) and the maximum nominal stress measured with cycles at 37 °C (b).

As illustrated in Fig. 6(b), the maximum nominal stress becomes 0 shortly after the generation of nucleates for larger maximum stretch cases (i.e., λ_max = 1.8, 1.7, and 1.6). This infers that the fatigue propagation life is approximately 0 in comparison with the fatigue damage life (N_f). For smaller maximum stretch cases (i.e., λ_max = 1.2, 1.3, 1.4, and 1.5), the maximum nominal stress reduces as number of cycles increases after the peak value. This indicates that the NIPA hydrogel is not very sensitive to nucleates or flaws at a smaller maximum stretch under cyclic loading. Nonetheless, the fatigue propagation life is clearly smaller than the fatigue damage life (N_f). Therefore, the fatigue life of the NIPA hydrogel is described by the fatigue damage life (N_f) in this study.

Fatigue damage tests below the VPTT were also conducted using the same loading model as in Fig. 6(a) with a prescribed stretch (λ_max) ranging from 1.1 to 1.27. A temperature (31 °C) slightly lower than the VPTT was chosen to study fatigue damage for NIPA hydrogels below the VPTT. By observing the recordings of the evolution of stress–stretch curves over cycles, it was found that the evolution features of maximum nominal stress in each cycle over cycles were similar to the evolution features above the VPTT. However, there were several differences on the stress–stretch curves because the responses of the polymer network under a cyclic load at different temperatures were different.²⁰ Although the hysteresis between the loading and unloading curves is generated due to the damage of the polymers network, the hysteresis loop is clearly smaller than that above the VPTT. Furthermore, the hysteresis loop in the first cycle is mostly identical to that of subsequent cycles. Residual strain is also observed at the end of the initial hundreds of cycles. After hundreds of cycles, the residual strain completely disappears as the stress is larger than 0 when the stretch returns to 1 for smaller λ_max cases.

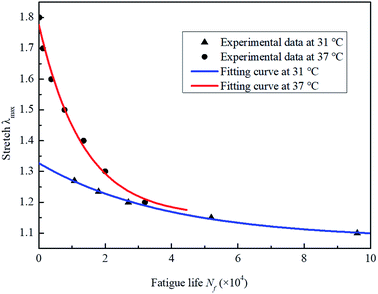
The number of cycles (N_f) corresponding to the maximum nominal stress for different λ_max cases was obtained, as shown in Fig. 6(b). The experimental data is shown using black dots and triangles in Fig. 7. It is clearly observed that the fatigue life under the same stretch at 37 °C is larger than that at 31 °C. It seems that N_f is exponentially reduced with the increase in stretch. The experimental data were fitted using the following equation:

λ = λ_f + A₀e^−N_f/B₀ (2)

where λ is stretch, λ_f is fatigue limit, N_f is fatigue life, and A₀ and B₀ are the two fitting parameters.

Fig. 7 The relationship of λ–N_f for the NIPA hydrogel at 31 °C and 37 °C.

The fitting curves are shown in Fig. 7 in red and blue for the cases of 37 °C and 31 °C, respectively. It seems that the fitting curve agrees well with the experimental data. The fitting parameters are λ_f = 1.15, A₀ = 0.624 and B₀ = 1.343 × 10⁴ for the case of 37 °C, while they are λ_f = 1.08, A₀ = 0.247 and B₀ = 3.904 × 10⁴ for the case of 31 °C.

By analysis of the fatigue life of the NIPA hydrogels at different temperatures, it was found that the fatigue life should be in the order of magnitude of 4. By comparison, the fatigue life of rubber should be approximately 107. λ_f varies with temperature. It was found that λ_f above the VPTT is larger than that below the VPTT. The fatigue life above the VPTT is also larger than that below the VPTT. Hence, it is noted that the fatigue limit λ_f should be determined by the lowest temperature to prevent the NIPA hydrogels from fracturing during the fatigue life.

Conclusions

By pure shear tests, the fracture behaviours and fatigue damage of the NIPA hydrogels at different temperatures were obtained. The fracture energy measured under monotonic load increases with the increase in temperature. Moreover, the fracture energy is approximately 10 J m⁻² below the VPTT, while the fracture energy is up to 150 J m⁻² at 39 °C. The analysis of the evolution of stress–stretch curves over numerous cycles indicates that the mechanical properties of the NIPA hydrogel under cyclic load are first weakened and then strengthened until fatigue damage occurs. The fatigue life (N_f) increased with the increase in temperature. By fitting the experimental data using the equation λ = λ_f + A₀e^−N_f/B₀, it was found that the fitting curve agreed well with the experimental data as the fatigue limit λ_f was 1.15 and 1.08 at 37 °C and 31 °C, respectively. The fatigue limit (λ_f) should be determined by the lowest temperature to prevent the NIPA hydrogels from fracturing during the fatigue life due to the variation in fatigue limit (λ_f) with temperature. The findings in this study might be important for the engineering applications of NIPA hydrogels.

Conflicts of interest

There are no conflicts to declare.

Acknowledgements

This study was supported by the National Natural Science Foundation of China (11372236 and 11572236).

Notes and references

1. J. P. Gong, Why are double network hydrogels so tough?, Soft Matter, 2010, 6(12), 2583–2590.
2. Z. S. Liu, W. Toh and T. Y. Ng, Advances in Mechanics of Soft Materials: A Review of Large Deformation Behavior of Hydrogels, Int. J. Appl. Mech., 2015, 7, 1530001.
3. C. M. Hassan and N. A. Peppas, Structure and applications of poly (vinyl alcohol) hydrogels produced by conventional crosslinking or by freezing/thawing methods, in Biopolymers·PVA Hydrogels, Anionic Polymerisation Nanocomposites, Springer, 2000, pp. 37–65.
4. K. Y. Lee and D. J. Mooney, Hydrogels for tissue engineering, Chem. Rev., 2001, 101(7), 1869–1880.
5. P. S. Lienemann, M. P. Lutolf and M. Ehrbar, Biomimetic hydrogels for controlled biomolecule delivery to augment bone regeneration, Adv. Drug Delivery Rev., 2012, 64(12), 1078–1089.
6. J. W. Jeong, M. K. Kim, H. Cheng, W. H. Yeo, X. Huang, Y. Liu, Y. Zhang, Y. Huang and J. A. Rogers, Capacitive Epidermal Electronics for Electrically Safe, Long-Term Electrophysiological Measurements, Adv. Healthcare Mater., 2014, 3(5), 642–648.
7. J. Li, A. D. Celiz, J. Yang, Q. Yang, I. Wamala, W. Whyte, B. R. Seo, N. V. Vasilyev, J. J. Vlassak, Z. Suo and D. J. Mooney, Tough adhesives for diverse wet surfaces, Science, 2017, 357(6349), 378–381.
8. Y. R. Zhang, L. Q. Tang, B. X. Xie, Z. J. Xu, K. J. Liu, Y. P. Liu, Z. Y. Jiang and S. B. Dong, Int. J. Appl. Mech., 2017, 9, 1750044.
9. R. Langer, Drug delivery and targeting, Nature, 1998, 392(6679), 5–10.
10. P. Ferreira, J. Almeida, J. Coelho and M. Gil, Photocrosslinkable Polymers for Biomedical Applications, INTECH Open Access Publisher, 2011.
11. S. J. Zheng, Z. Q. Li and Z. S. Liu, The fast homogeneous diffusion of hydrogel under different stimuli, Int. J. Mech. Sci., 2018, 137, 263–270.
12. S. Xu, Y. Wang, J. Y. Hu and Z. S. Liu, Int. J. Appl. Mech., 2016, 8, 1640002.
13. J. H. Wu, P. F. Li, C. L. Dong, H. T. Jiang, B. Xue, X. Gao, M. Qin, W. Wang, B. Chen and Y. Cao, Rationally designed synthetic protein hydrogels with predictable mechanical properties, Nat. Commun., 2018, 9(620), 1–11.
14. J. Tang, J. Li, J. J. Vlassak and Z. G. Suo, Fatigue fracture of hydrogels, Extreme Mech. Lett., 2017, 10, 24–31.
15. R. B. Bai, Q. Yang, J. Tang, X. P. Morelle, J. Vlassak and Z. Suo, Fatigue fracture of tough hydrogels, Extreme Mech Lett., 2017, 15, 91–96.
16. W. L. Zhang, X. Liu, J. K. Wang, J. D. Tang, J. Hu, T. Q. Lu and Z. G. Suo, Fatigue of Double-Network Hydrogels, Eng. Fract. Mech., 2018, 187, 74–93.
17. R. B. Bai, J. W. Yang, X. P. Morelle, C. H. Yang and Z. G. Suo, Fatigue Fracture of Self-Recovery Hydrogels, ACS Macro Lett., 2018, 7, 312–317.
18. E. R. Zhang, R. B. Bai, X. P. Morelle and Z. G. Suo, Fatigue fracture of nearly elastic hydrogels, Soft Matter, 2018, 14, 3563–3571.
19. S. J. Zheng and Z. S. Liu, Phase transition of temperature sensitive hydrogel under mechanical constraint, J. Appl. Mech., 2018, 85, 021002.
20. H. G. Schild, Poly(N-isopropylacrylamide): experiment, theory and application, Prog. Polym. Sci., 1992, 17, 163–249.
21. A. Suzuki and T. Ishii, Phase coexistence of neutral polymer gels under mechanical constraint, J. Chem. Phys., 1999, 110(4), 2289–2296.
22. N. Zhang, S. J. Zheng, Z. Z. Pan and Z. S. Liu, Phase Transition Effects on Mechanical Properties of NIPA Hydrogel, Polymers, 2018, 10(358), 1–11.
23. R. S. Rivlin and A. G. Thomas, Rupture of rubber. I. Characteristic energy for tearing, J. Polym. Sci., 1953, 10(3), 291–318.
24. J. Y. Sun, X. H. Zhao, W. R. K. Illeperuma, O. Chaudhuri, K. H. Oh, D. J. Mooney, J. J. Vlassak and Z. G. Suo, Highly stretchable and tough hydrogels, Nature, 2012, 489, 133–136.

---