Open Access Article
Open Access ArticleEffect of pressure on the structural, electronic and mechanical properties of ultraincompressible W2B
Zhen Qin,
Weiguang Gong,
Xianqi Song,
Menglong Wang,
Hongbo Wang * and
Quan Li
* and
Quan Li *
*
Key Laboratory of Automobile Materials of MOE, State Key Laboratory of Superhard Materials, Department of Materials Science, Jilin University, Changchun 130012, China. E-mail: liquan777@jlu.edu.cn; whb2477@jlu.edu.cn
First published on 18th October 2018
Abstract
The crystal structures of W2B have been extensively investigated by the swarm structure searching method at ambient and high-pressure conditions. Our calculated thermodynamic enthalpy data suggests that the tetragonal phase with I4/m symmetry is the most stable at 0–50 GPa. The theoretical elastic properties and phonon spectroscopy confirmed that I4/m W2B is both mechanically and dynamically stable. The calculated band structure and density of states show that I4/m W2B is metallic and the electronic properties are sensitive to changes in external pressure with the occurrence of an electronic topological transition. The simulated high elastic modulus, hardness and strain–stress relationships reveal that W2B exhibits excellent ultraincompressible properties and high strength. The combination of superior conductivity and mechanical properties reveals that W2B can be used for hard coatings and electrical measurements.
1. Introduction
Tungsten borides are exemplary materials with covalent-bonds formed by light elements (LE) and transition metals (TM), and exhibit excellent performance in terms of their chemical inertness, hardness, and stability; thus, they have been widely used as cutting tools and wear-resistant coatings.1–4 The high hardness and high strength of these TM borides benefit from not only the contributors to the macroscopic hardness, but also the determinants of the relative hardness of structurally related borides and the anisotropic hardness of W borides.4–13 It is widely expected that with higher concentration of the B atoms, the compounds will possess higher hardness. Several tungsten borides with outstanding mechanical properties have been synthesized with inexpensive starting materials, and economical experimental conditions (e.g., ambient-pressure and high temperature conditions).5,14–16 A comprehensive understanding of the mechanical mechanism for tungsten borides with various boron content has been plagued by the complex structural arrangements due to their flexible bonding ability. Recently, the structural determination of these tungsten borides has been widely explored by the latest first-principles structural search techniques and Rietveld refinement of the X-ray powder patterns.17–19 It is essential to understand the structural and mechanical response under various loading conditions and examine the influence of B content on the strength and hardness of these tungsten borides. Based on the prototypes of boron-rich tungsten borides, our previous calculations show that WB2 phases with relatively lower boron content exhibit better overall strength, and the increase in the B content does not lead to higher strength and hardness.19 A pressing task is to explore the fundamental atomistic mechanisms for the structural and mechanical response under various conditions for tungsten borides with the lowest B content ratio, i.e., W2B (γ-W2B). The measured Vickers hardness of W2B reaches 24 GPa at 0.49 N.20 W2B has been thought to have a tetragonal Al2Cu-type structure with I4/mcm symmetry for several decades.8,21–23 However, our recent results have clarified and corrected previous structural assignments for W2B18 and identified a new I4/m structure that is energetically stable at ambient conditions. Thus, the corresponding physical properties and functional performance of γ-W2B should be reexamined. It is known that these potential superhard materials mainly serve under load conditions, e.g., high pressure, which is a very effective means to modulate the crystal structures and physical properties for condensed materials.24–27 Therefore, we have systematically explored the underlying structural, electronic and mechanical properties for W2B at ambient and high-pressure conditions. Our calculations show that I4/m![[4 with combining macron]](https://www.rsc.org/images/entities/char_0034_0304.gif) u W2B is the most stable structure at the entire pressure range of 0–50 GPa. Dynamical stability has been identified by the calculated phonon spectrum. The calculated high bulk modulus, shear modulus and hardness data show that W2B possesses excellent mechanical properties. Furthermore, W2B exhibits a metallic feature, and the band structure is sensitive to changes in external pressure. A pressure-induced electronic topological transition has been predicted in W2B, which can cause anomalies in a wide range of physical properties, such as resistivity, thermoelectric power, and the Hall coefficient. The calculated stress–strain results show that W2B has small elastic anisotropy in the elastic range. W2B, with both superior conductivity and mechanical properties, can be used for many applications such as hard coatings and electrical measurements.
u W2B is the most stable structure at the entire pressure range of 0–50 GPa. Dynamical stability has been identified by the calculated phonon spectrum. The calculated high bulk modulus, shear modulus and hardness data show that W2B possesses excellent mechanical properties. Furthermore, W2B exhibits a metallic feature, and the band structure is sensitive to changes in external pressure. A pressure-induced electronic topological transition has been predicted in W2B, which can cause anomalies in a wide range of physical properties, such as resistivity, thermoelectric power, and the Hall coefficient. The calculated stress–strain results show that W2B has small elastic anisotropy in the elastic range. W2B, with both superior conductivity and mechanical properties, can be used for many applications such as hard coatings and electrical measurements.
2. Computational methods
The first-principles energetic calculations were performed using the density functional theory with the Perdew–Burke–Ernzerhof generalized gradient approximation (GGA) exchange-correlation potential28 as implemented in the Vienna ab initio simulation package (VASP).29 Global structural predictions were performed using the CALYPSO method,30–33 which has successfully predicted the stable and metastable structures of various systems.34–36 The ion–electron interaction was treated by the projector augmented-wave (PAW) technique,37 where 5d46s2 and 2s22p1 were adopted as valence electrons for W and B atoms, respectively. The electronic wave functions were expanded in a plane-wave basis set. The desirable cutoff energy of 600 eV and appropriate Monkhorst–Pack k point meshes16 for Brillouin zone sampling were chosen to ensure that the total energies converged to be better than 1 meV per atom for all cases. Phonon calculations were conducted using a supercell approach as implemented in the PHONOPY code.38 Elastic constants were calculated by adopting the strain–stress method and the three-dimensional models of modulus were built using Elastic Anisotropy Measures (ELAM) code39 to manifest anisotropy of the perfect single crystal. The bulk (B) and shear moduli (G) for corresponding isotropic polycrystalline were derived from the Voigt–Reuss–Hill averaging scheme.40 The relaxed loading path and quasi-static ideal strength were determined using a previously established method41 with the lattice vectors manually deformed in the direction of the applied strain and the other independent strain tensors simultaneously relaxed.3. Results and discussion
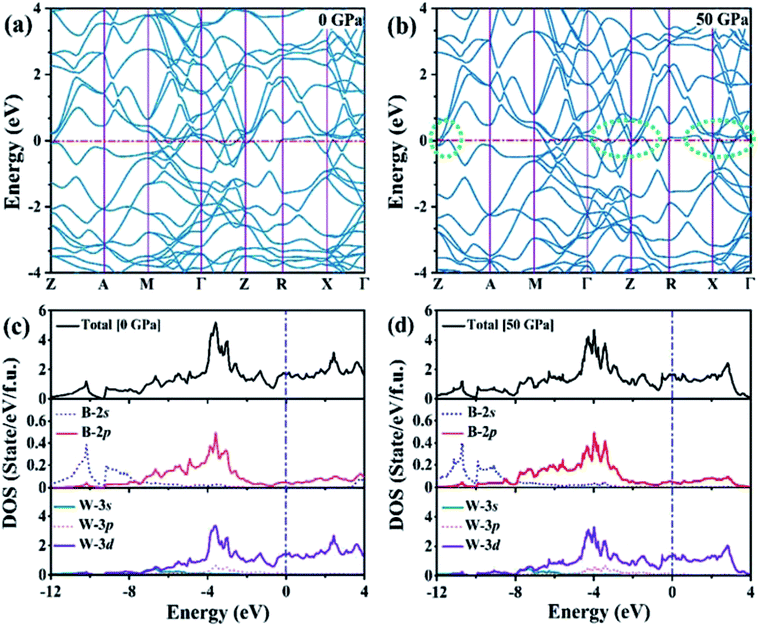
Using the variable-cell CALYPSO method, the structural search for W2B was performed with cell sizes of 1–4 formula units at 0–50 GPa. The current analysis on thermodynamic enthalpy confirmed that the tetragonal phase with I4/m symmetry is most stable at ambient and high-pressure conditions. Lattice parameters of the I4/m structure from theoretical calculations are a = b = 5.580 Å and c = 4.756 Å, accompanied by equilibrium atomic Wyckoff positions of 8h (0.176, 0.664, 0.0) for W atoms and 4e (0.0, 0.0, 0.221) for B atoms. Perspective structural screenshots from diverse views of W2B are shown in Fig. 1. Each tungsten atom is surrounded by four boron atoms as well as three tungsten atoms with two approximately equal W–W bond lengths of 2.688 and 2.693 Å [Fig. 1(a)], which are slightly smaller than those in pure tungsten metal (2.747 Å). Furthermore, each boron atom has an eightfold coordinate with tungsten atoms with two analogous bond lengths of 2.365 and 2.420 Å [Fig. 1(b)].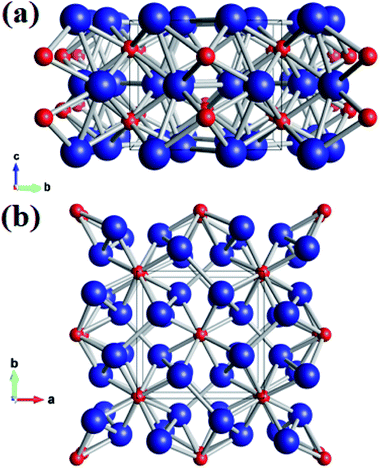 | ||
| Fig. 1 (a) Front view and (b) top view of the I4/m structure of W2B under ambient pressure. Large blue and small red spheres represent tungsten and boron atoms, respectively. | ||
Based on harmonic approximation, the calculated phonon dispersion curves exhibiting vibration modes of the I4/m structure of W2B have been shown in Fig. 2(a). There is no imaginary frequency in the entire Brillouin zone, i.e., all the phonon frequencies are positive, which demonstrates that the I4/m structure of W2B is dynamically stable under ambient pressure. The current results are in good agreement with previous calculations.42 We have further checked the phonon spectra for I4/m symmetry of W2B at high-pressure conditions to further identify its dynamical stability [Fig. 2(b)]. The blue shift of phonon peaks with the increase in pressure originates from the enhanced force constants affected by atomic distances. An interesting phenomenon is found in the phonon dispersion curves of the W2B. They possess apparent gaps between the high and low frequency areas. We further analyzed the contribution of tungsten and boron atoms to phonon frequency by means of the phonon density of the states of W2B, as shown in Fig. 2(c and d). Our results show that the vibrations of tungsten atoms and boron atoms correspond to low and high phonon frequency areas, respectively, which stems from the greater mass of the tungsten atom than that of the boron atom.
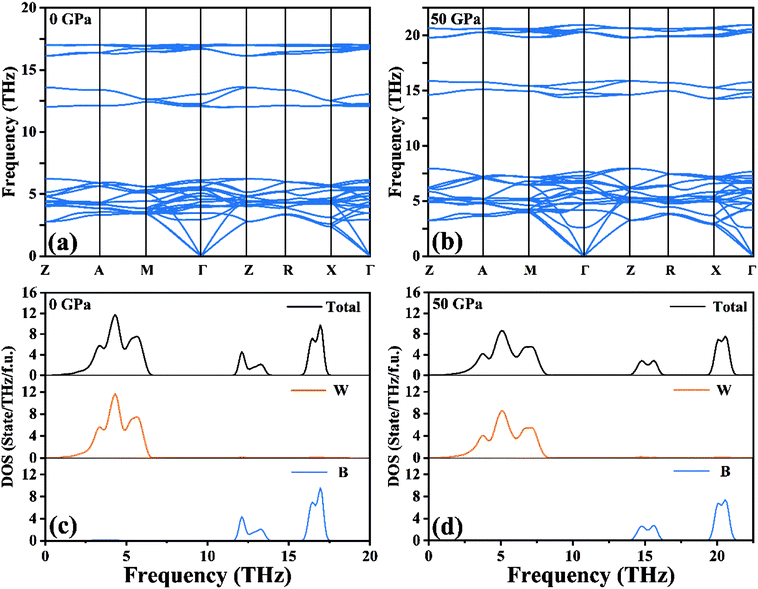 | ||
| Fig. 2 (a and b) Calculated phonon dispersion curves and (c and d) phonon density of states for W2B at 0 GPa and 50 GPa, respectively. | ||
We analyzed the electronic band structure, density of states (DOS) and topological nature of the Fermi surface for exhibiting electronic properties of the I4/m phase at atmospheric and high pressure. The distinct crossover behavior between the valence and the conduction bands indicates that I4/m W2B is metallic, as shown in Fig. 3. Our results, as shown in Fig. 3(a), indicate that the delocalized W-3d orbitals dominate the electronic density of the states around the Fermi level. The substantial overlap of the W-3d and B-2p states [Fig. 3(c and d)] demonstrates the strong covalent bonding states between boron atoms and tungsten atoms. It is noted that a deep energy valley (pseudogap) is shown in the calculated electronic DOS below the Fermi level at about −0.7 eV. It has been confirmed that the pseudogap separates the localized and delocalized electrons, where the electrons of the valence bands above (below) the pseudogap are delocalized (localized). The presence of the pseudogap indicates that the covalent bonds play the dominant role in W2B, which has been to effectively enhance its mechanical properties, e.g., high bulk modulus, shear modulus, and hardness. With the increase in pressure, the crossing behavior of the electronic band structure near the Fermi energy evidently changed near the Z point and X–Γ directions, which are highlighted by the dotted circles in Fig. 3(b). The significant changes in the Fermi surface profiles in Fig. 4 demonstrate the occurrence of a pressure-induced electronic topological transition, which causes anomalies in a wide range of physical properties, such as resistivity, thermoelectric power, and the Hall coefficient. The 3D Fermi surfaces [Fig. 4], with some visible nesting features, are very complex in the entire Brillouin zone, which may be responsible for the superconductivity of W2B at 3.1 K.43
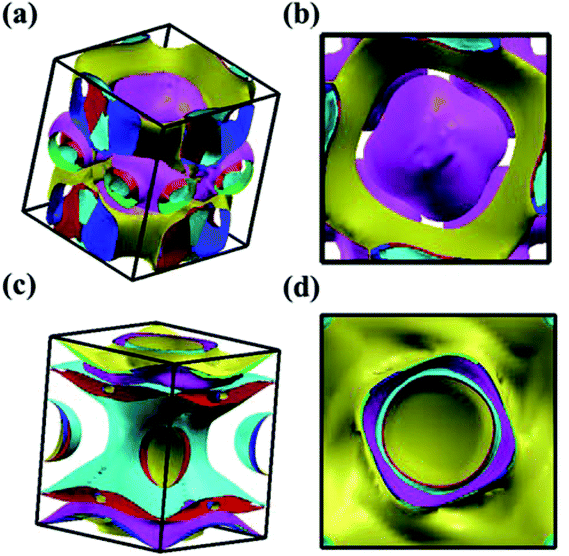 | ||
| Fig. 4 Screenshots for the calculated Fermi surface of I4/m W2B from different directions at 0 GPa (a and b) and 50 GPa (c and d), respectively. | ||
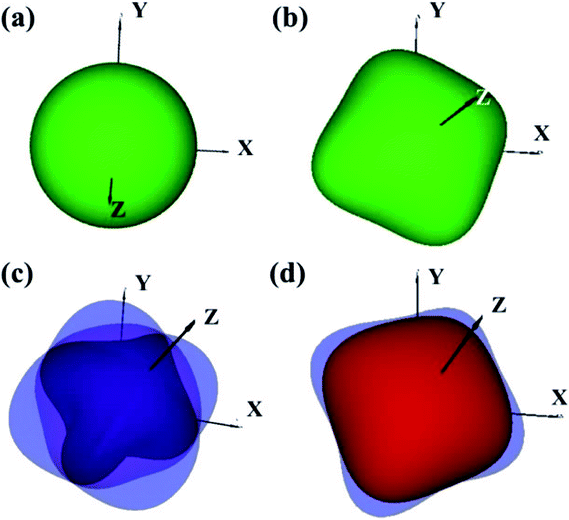
The elastic constants of the I4/m W2B were calculated by the strain–stress method at a small strain of 0.3%. Our results show that the independent elastic constants satisfy the mechanical stability criteria,44 suggesting that I4/m W2B is elastically stable. In order to visually reflect anisotropy of elastic moduli, the three-dimensional models of linear compressibility, Young's modulus, Poisson's ratio and shear modulus were calculated. As shown in Fig. 5, W2B exhibits excellent mechanical properties with low elastic anisotropy at small strain. The simulated bulk modulus, shear modulus and Young's modulus of W2B reach 338.5, 165.0 and 425.7 GPa, respectively, as listed in Table 1. The theoretical elastic properties show that the W2B exhibits an unusual incompressibility, but is relatively weak to resist shear deformation. Poisson's ratio has also been calculated to describe the response of the transverse strain to the longitudinal strain. The calculated Poisson's ratio (Pr) reaches 0.29, indicating that W2B is a typical isotropic engineering material (0.2 < Pr < 0.5) near the equilibrium, and its interatomic forces are predominantly central forces.45 Based on the revised hardness model,46,47 the simulated Vickers hardness value of the I4/m structure is 15.1 GPa, which is comparable to that of aluminum nitride (AlN, 15–17 GPa).48,49 Our results show that pressure significantly enhances the mechanical properties of W2B, as listed in Table 1, which is a key requirement for the application of hard materials.
| Phase | Pressure | C11 | C33 | C44 | C66 | C12 | C13 | B | G | E | Pr | Hv |
|---|---|---|---|---|---|---|---|---|---|---|---|---|
| I4/m | 0 GPa | 568 | 550 | 156 | 178 | 205 | 237 | 338 | 165 | 426 | 0.29 | 15.1 |
| 50 GPa | 799 | 756 | 226 | 269 | 302 | 352 | 485 | 234 | 605 | 0.29 | 19.1 |
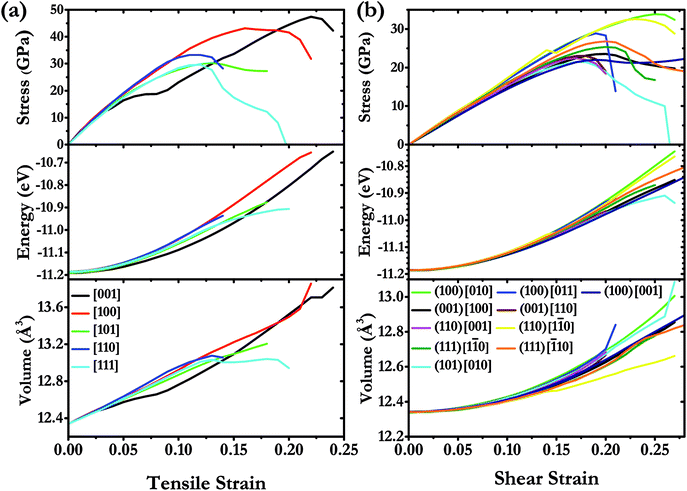
We have systematically investigated the ideal strength for I4/m W2B in various tension and shear directions at large strain by first-principle calculations. The stress response relationships along diverse crystallographic directions are shown in Fig. 6. The weakest tensile stress for W2B appears in the [111] direction, accompanied by a numerical value of ideal strength of 29.6 GPa with the corresponding strain of 0.12. At small strains, the tensile stress appears to rise almost linearly with large slopes, indicating that the equilibrium structure possesses large elastic constants. The stress responses along different directions are almost identical at strains below 5%, which is consistent with the 3D representations of elastic properties [Fig. 5]. The minimum shear stress of 21.4 GPa for W2B is obtained along the (101) [010] crystal orientation with a strain of 0.17. At small strains, the slopes of the shear stress–strain curve are gentler than those of the tensile stress–strain curves, which is consistent with the results of the elastic modulus near the equilibrium. The particular stress peaks as well as corresponding strains are listed in Table 2. It is noted that the strain–stress relations for traditional superhard materials, e.g., diamond and c-BN, show a sudden break at stress peaks. Herein, W2B presents a behavior of meandering decline that produces better ductility and extended elasticity than traditional superhard materials. In order to provide a more detailed description of the stress–strain process, we show the calculated energy and volume in various tensile, and shear deformation directions (Fig. 6). With an increase instress, the calculated energy increases monotonously and quickly. For tensile strain along the [111] direction, the volume increases first and then, the enhancement is minor with a small variation in strain from 0.12 to 0.20. The shear process is the opposite, that is, the volume rises during the entire process along the (101) [010] crystal direction. Therefore, the failure mechanisms under tensile and shear deformations are significantly different.
| Tensile direction | Strain | Stress (GPa) | Shear direction | Strain | Stress (GPa) |
|---|---|---|---|---|---|
| [001] | 0.22 | 47.4 | (001) [100] | 0.20 | 23.5 |
| [100] | 0.16 | 43.1 | (001) [110] | 0.18 | 23.0 |
| [101] | 0.13 | 30.3 | (110) [1![[1 with combining macron]](https://www.rsc.org/images/entities/char_0031_0304.gif) 0] 0] |
0.23 | 32.6 |
| [110] | 0.12 | 33.3 | (110) [001] | 0.17 | 22.4 |
| [111] | 0.12 | 29.6 | (111) [1![[1 with combining macron]](https://www.rsc.org/images/entities/char_0031_0304.gif) 0] 0] |
0.20 | 25.3 |
(111) [![[1 with combining macron]](https://www.rsc.org/images/entities/char_0031_0304.gif) 10] 10] |
0.20 | 26.8 | |||
| (100) [010] | 0.25 | 33.8 | |||
| (100) [011] | 0.19 | 28.8 | |||
| (100) [001] | 0.31 | 23.1 | |||
| (101) [010] | 0.17 | 21.4 |
4. Conclusion
In summary, we have systematically explored the thermodynamically stable structures for W2B at pressure ranging from 0 to 50 GPa using the CALYPSO method. Our results indicate that W2B with I4/m symmetry is energetically and dynamically stable under atmospheric and high pressure. We have systematically studied the pressure effect on its intrinsic electronic structure, elastic properties and stress response relations. The calculated band structure and density of states show that I4/m W2B is metallic and the electronic properties are sensitive to changes in external pressure with the occurrence of an electronic topological transition. The simulated high elastic modulus, hardness and strain–stress relationships reveal that W2B exhibits excellent ultraincompressible properties, high hardness, and high strength. The superior conductivity and mechanical properties reveal that W2B is expected to be used in many fields such as hard coatings for electrical devices or anvils of large volume press for electrical measurements.Conflicts of interest
There are no conflicts to declare.Acknowledgements
The authors acknowledge the funding support from the National Natural Science Foundation of China under Grant No. 11622432, 11474125 and 11704044, the National Key Research and Development Program of China under Grant No. 2016YFB0201200, the Science Challenge Project (TZ2016001), and program for JLUSTIRT. Part of the calculation was performed in the high-performance computing center of Jilin University and at Tianhe2-JK in the Beijing Computational Science Research Center.References
- J. C. Crowhurst, A. F. Goncharov, B. Sadigh, C. L. Evans, P. G. Morrall, J. L. Ferreira and A. J. Nelson, Science, 2006, 311, 1275–1278 CrossRef CAS PubMed.
- A. F. Young, C. Sanloup, E. Gregoryanz, S. Scandolo, R. J. Hemley and H. Mao, Phys. Rev. Lett., 2006, 96, 155501 CrossRef PubMed.
- H. Y. Chung, M. B. Weinberger, J. B. Levine, A. Kavner, J. M. Yang, S. H. Tolbert and R. B. Kaner, Science, 2007, 316, 436 CrossRef CAS PubMed.
- R. Mohammadi, A. T. Lech, M. Xie, B. E. Weaver, M. T. Yeung, S. H. Tolbert and R. B. Kaner, Proc. Natl. Acad. Sci. U. S. A., 2011, 108, 10958–10962 CrossRef CAS PubMed.
- M. Xie, R. Mohammadi, Z. Mao, M. M. Armentrout, A. Kavner, R. B. Kaner and S. H. Tolbert, Phys. Rev. B: Condens. Matter Mater. Phys., 2012, 85, 064118 CrossRef.
- Q. Gu, F. Krauss and W. Steurer, Adv. Mater., 2008, 20, 3620–3626 CrossRef CAS.
- R. Kiessling, Acta Chem. Scand., 1947, 1, 893–916 CrossRef CAS.
- H. Itoh, T. Matsudaira, S. Naka, H. Hamamoto and M. Obayashi, J. Mater. Sci., 1987, 22, 2811–2815 CrossRef CAS.
- S. Okada, K. Kudou and T. Lundström, Jpn. J. Appl. Phys., 1995, 34, 226 CrossRef CAS.
- H. P. Woods, F. E. Wagner Jr and B. G. Fox, Science, 1966, 151, 75 CrossRef CAS PubMed.
- M. Kayhan, E. Hildebrandt, M. Frotscher, A. Senyshyn, K. Hofmann, L. Alff and B. Albert, Solid State Sci., 2012, 14, 1656 CrossRef CAS.
- J. Lei, M. T. Yeung, P. J. Robinson, R. Mohammadi, C. L. Turner, J. Yan, A. Kavner, A. N. Alexandrova, R. B. Kaner and S. H. Tolbert, J. Phys. Chem. C, 2018, 122, 5647–5656 CrossRef CAS.
- P. J. Robinson, G. Liu, S. Ciborowski, C. Martinez-Martinez, J. R. Chamorro, X. Zhang, T. M. McQueen, K. H. Bowen and A. N. Alexandrova, Chem. Mater., 2017, 29, 9892–9896 CrossRef CAS.
- H.-Z. Chen, Y.-Y. Zhang, X. Gong and H. Xiang, J. Phys. Chem. C, 2013, 118, 2333 CrossRef.
- M. Xie, R. Mohammadi, C. L. Turner, R. B. Kaner, A. Kavner and S. H. Tolbert, Phys. Rev. B, 2014, 90, 104104 CrossRef.
- H. J. Monkhorst and J. D. Pack, Phys. Rev. B: Condens. Matter Mater. Phys., 1976, 13, 5188 CrossRef.
- A. T. Lech, C. L. Turner, R. Mohammadi, S. H. Tolbert and R. B. Kaner, Proc. Natl. Acad. Sci. U. S. A., 2015, 112, 3223–3228 CrossRef CAS PubMed.
- Q. Li, D. Zhou, W. Zheng, Y. Ma and C. Chen, Phys. Rev. Lett., 2013, 110, 136403 CrossRef PubMed.
- Q. Li, D. Zhou, W. Zheng, Y. Ma and C. Chen, Phys. Rev. Lett., 2015, 115, 185502 CrossRef PubMed.
- G. Akopov, M. T. Yeung and R. B. Kaner, Adv. Mater., 2017, 29, 1604506 CrossRef PubMed.
- B. Armas and F. Trombe, Sol. Energy, 1973, 15, 67–73 CrossRef CAS.
- S. Stadler, R. P. Winarski, J. M. MacLaren, D. L. Ederer, J. vanEk, A. Moewes, M. M. Grush, T. A. Callcott and R. C. C. Perera, J. Electron Spectrosc. Relat. Phenom., 2000, 110–111, 75–86 CrossRef CAS.
- E. Zhao, J. Meng, Y. Ma and Z. Wu, Phys. Chem. Chem. Phys., 2010, 12, 13158–13165 RSC.
- Y. Zhou, Q. Xu, C. Zhu, Q. Li, H. Liu, H. Wang and J. S. Tse, RSC Adv., 2016, 6, 66721–66728 RSC.
- F. Peng, Y. Sun, C. J. Pickard, R. J. Needs, Q. Wu and Y. Ma, Phys. Rev. Lett., 2017, 119, 107001 CrossRef PubMed.
- Y. Ma, M. Eremets, A. R. Oganov, Y. Xie, I. Trojan, S. Medvedev, A. O. Lyakhov, M. Valle and V. Prakapenka, Nature, 2009, 458, 182 CrossRef CAS PubMed.
- C. Chen, Y. Xu, X. Sun, S. Wang and F. Tian, RSC Adv., 2014, 4, 55023–55027 RSC.
- J. P. Perdew, K. Burke and M. Ernzerhof, Phys. Rev. Lett., 1996, 77, 3865 CrossRef CAS PubMed.
- G. Kresse and J. Furthmüller, Phys. Rev. B: Condens. Matter Mater. Phys., 1996, 54, 11169 CrossRef CAS.
- Y. Wang, J. Lv, L. Zhu and Y. Ma, Phys. Rev. B: Condens. Matter Mater. Phys., 2010, 82, 094116 CrossRef.
- Y. Wang, J. Lv, L. Zhu and Y. Ma, Comput. Phys. Commun., 2012, 183, 2063–2070 CrossRef CAS.
- H. Wang, Y. Wang, J. Lv, Q. Li, L. Zhang and Y. Ma, Comput. Mater. Sci., 2016, 112, 406–415 CrossRef CAS.
- X. Zhang, Y. Wang, J. Lv, C. Zhu, Q. Li, M. Zhang, Q. Li and Y. Ma, J. Chem. Phys., 2013, 138, 114101 CrossRef PubMed.
- Y. Li, X. Feng, H. Liu, J. Hao, S. A. T. Redfern, W. Lei, D. Liu and Y. Ma, Nat. Commun., 2018, 9, 722 CrossRef PubMed.
- X. Zhong, H. Wang, J. Zhang, H. Liu, S. Zhang, H.-F. Song, G. Yang, L. Zhang and Y. Ma, Phys. Rev. Lett., 2016, 116, 057002 CrossRef PubMed.
- H. Zhang, Y. Li, J. Hou, K. Tu and Z. Chen, J. Am. Chem. Soc., 2016, 138, 5644–5651 CrossRef CAS PubMed.
- G. Kresse and G. D. JoubertKresse, Phys. Rev. B: Condens. Matter Mater. Phys., 1999, 59, 1758 CrossRef CAS.
- A. Togo, F. Oba and I. Tanaka, Phys. Rev. B: Condens. Matter Mater. Phys., 2008, 78, 134106 CrossRef.
- A. Marmier, Z. A. Lethbridge, R. I. Walton, C. W. Smith, S. C. Parker and K. E. Evans, Comput. Phys. Commun., 2010, 181, 2102–2115 CrossRef CAS.
- R. Hill, Proc. Phys. Soc., London, Sect. A, 1952, 65, 349 CrossRef.
- D. Roundy, C. Krenn, M. L. Cohen and J. Morris Jr, Phys. Rev. Lett., 1999, 82, 2713 CrossRef CAS.
- M. Wang, C. Liu, M. Wen, Q. Li and Y. Ma, Phys. Chem. Chem. Phys., 2017, 19, 31592–31598 RSC.
- G. F. Hardy and J. K. Hulm, Phys. Rev., 1954, 93, 1004–1016 CrossRef CAS.
- Z.-j. Wu, E.-j. Zhao, H.-p. Xiang, X.-f. Hao, X.-j. Liu and J. Meng, Phys. Rev. B: Condens. Matter Mater. Phys., 2007, 76, 054115 CrossRef.
- H. Fu, D. Li, F. Peng, T. Gao and X. Cheng, Comput. Mater. Sci., 2008, 44, 774–778 CrossRef CAS.
- X.-Q. Chen, H. Niu, D. Li and Y. Li, Intermetallics, 2011, 19, 1275–1281 CrossRef CAS.
- Y. Tian, B. Xu and Z. Zhao, Int. J. Refract. Met. Hard Mater., 2012, 33, 93–106 CrossRef CAS.
- D. M. Teter, MRS Bull., 1998, 23, 22–27 CrossRef CAS.
- F. Gao, J. He, E. Wu, S. Liu, D. Yu, D. Li, S. Zhang and Y. Tian, Phys. Rev. Lett., 2003, 91, 015502 CrossRef PubMed.
| This journal is © The Royal Society of Chemistry 2018 |