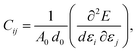Open Access Article
Open Access ArticleAssessment of the mechanical properties of monolayer graphene using the energy and strain-fluctuation methods†
Siby Thomasa,
K. M. Ajith *b,
Sang Uck Lee
*b,
Sang Uck Lee *ac and
M. C. Valsakumard
*ac and
M. C. Valsakumard
aDepartment of Bionano Technology, Hanyang University, Ansan 15588, Korea. E-mail: sulee@hanyang.ac.kr
bDepartment of Physics, National Institute of Technology Karnataka (NITK), PO: Srinivasnagar, Mangalore, India – 575025
cDepartment of Chemical & Molecular Engineering, Hanyang University, Ansan 15588, Korea
dDepartment of Physics, Indian Institute of Technology Palakkad (IIT Palakkad), Ahalia Campus, Kozhipara, Palakkad, Kerala, India – 678557
First published on 31st July 2018
Abstract
Molecular statics and dynamics simulations were performed to investigate the mechanical properties of a monolayer graphene sheet using an efficient energy method and strain-fluctuation method. Using the energy method, we observed that the mechanical properties of an infinite graphene sheet are isotropic, whereas for a finite sheet, they are anisotropic. This work is the first to report the temperature-dependent elastic constants of graphene between 100 and 1000 K using the strain-fluctuation method. We found that the out-of-plane thermal excursions in a graphene membrane lead to strong anharmonic behavior, which allows large deviations from isotropic elasticity. The computed Young's modulus and Poisson's ratio of a sheet with an infinite spatial extent are 0.939 TPa and 0.223, respectively. We also found that graphene sheets with both finite and infinite spatial extent satisfy the Born elastic stability conditions. We extracted the variation in bending modulus with the system size at zero kelvin (0.83 eV) using a formula derived from the Foppl–von Karman approach. When the temperature increases, the Young's modulus of the sample decreases, which effectively reduces the longitudinal and shear wave velocities.
Introduction
Graphene is a perfect example of a true two-dimensional (2D) single-layer atomic crystal in which carbon atoms are arranged in a honeycomb non-Bravais lattice.1 Although graphene contains a single type of carbon atoms, it has two sub-lattices with pseudo-spins that cause the electron velocity to become very high, which in turn leads to an increase in electron mobility. It is the first truly 2D material with a planar sp2 arrangement of carbon atoms and has greatly influenced the scientific community through its exceptional electronic and thermo-mechanical properties, such as its large theoretical specific area, high melting point, and outstanding electrical properties.2–5 Due to its extremely high crystal and electronic quality, graphene shows unique optical properties and a high thermal conductivity value of 4100 ± 500 W m−1 K−1, which is quite large compared with any other known material.6 The semi-metallic character and unique electronic properties of graphene can be effectively used in high-speed integrated devices, field effect transistors, gas sensors, flexible electronics, supercapacitors, and nano-composites.7,8An understanding of the temperature-dependent physical properties of materials is a prerequisite for advanced device-fabrication technology. Several groups have performed atomistic simulations and experimental analyses to calculate the mechanical properties of monolayer graphene. Using the atomic force microscopy (AFM)-nanoindentation technique, Lee et al. measured the elastic modulus of graphene and reported that it is the hardest known material, with an extraordinary Young's modulus of 1.0 TPa.3 Mortazavi et al. reported that highly ordered defect-free graphene is one of the thinnest membranes, with a hardness a hundred times greater than steel.9 They also used AFM to calculate the intrinsic stress of a monolayer graphene sheets and found it to be 130 ± 10 GPa, which corresponds to a strain of 0.25. Min et al. studied the mechanical properties of graphene extensively using atomistic simulation methods and compared those results with experimental analyses.10 Even though the elastic moduli of a monolayer graphene sheet are comparable to those of a graphite crystal, significant changes have been reported in the Young's modulus and Poisson's ratio.11 The superior mechanical properties of graphene have also been explained in terms of bond energy,12,13 and the observed bond energy14 of sp2-hybridized graphene with C–C bonds is higher than that of diamond with sp3 hybridized bonds.15
In density functional theory studies, Kudin et al. reported the isotropy of the elastic moduli of graphene along the armchair (n, n) and zigzag (n, 0) directions, with an observed elastic modulus value of 1.150 TPa.16 Using ab initio calculations, Liu et al. determined the phonon-induced instability of graphene under tension and reported a zero-temperature Young's modulus of 1.050 TPa.17 Using molecular dynamics and the tight binding method, Zhao et al. reported a Young's modulus for graphene nanoribbons of 1.010 TPa and 0.910 TPa, respectively.18 In general, 2D materials produce strong anharmonic effects that become more notable at high temperatures due to the excitation of high-energy phonon modes. From the intrinsic thermal mean square vibration amplitude, Jiang et al. investigated the Young's modulus of graphene using molecular dynamics simulations.19 They observed a room temperature elastic modulus of 1.050 TPa using both experimental and theoretical studies. By combining the first principles calculation and a quasi-harmonic approximation, Shao et al. observed the temperature dependent elastic constants and Young's modulus of graphene at zero kelvin and reported a Young's modulus value of 1.208 TPa.20 Jian et al. performed molecular dynamics simulations to investigate graphene's mechanical properties and reported the non-linear elastic behavior of pristine and defective graphene sheets.21
In this paper, we use the energy and strain-fluctuation methods to report the elastic constants of a free-standing graphene sheet. We also computed the elastic moduli and acoustic wave velocities from the obtained elastic constants and investigated the system size-dependence of those properties. An attempt has also been made to gauge the temperature dependence of the elastic constants using a strain-fluctuation method derived from the fluctuation–dissipation theorem.22 To the best of our knowledge, this is the first independent analysis of the temperature-dependent elastic constants of graphene using a classical molecular dynamics simulation technique. We expect that our results will furnish ideas for new practical applications.
Theoretical background for the calculation
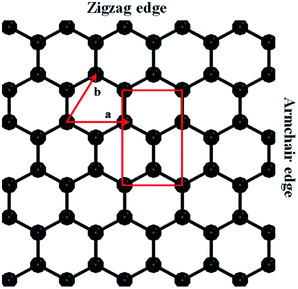
The atomic arrangement of the simulated graphene sheet with primitive lattice vectors a and b is shown in Fig. 1. The top and bottom of the sheet are the zigzag edges, and the left and right sides represent the armchair edges. Two different kinds of atoms (based on the direction of orientation) represent the presence of two sub-lattices in the honeycomb lattice of the graphene. The red rectangular cell represents the unit cell of graphene with two different types of carbon atoms. The positions of the atoms in the sub-lattices are (1/2, 1/6), (0, 2/3) and (0, 1/3), (1/2, 5/6), respectively, for the different kind of atoms. In this work, we calculated the elastic constants of a monolayer graphene sheet in two ways: (i) directly using an efficient energy method23–25 by extracting the energy of the strained graphene layer and fitting it to a polynomial using strain as the variable; and (ii) using the strain fluctuation method,26,27 which considers the averages of the statistical fluctuations in either strain or stress. The detailed theoretical description of these methods can be found in our previous works.25,28 We briefly describe these methods here.When the simulation cell size is very small, the movements of the atoms correlate with those of the neighboring atoms in the proximal edge of the same cell. As the size of the system increases, those correlations decrease. To simulate a system that mimics a sheet of finite size, we have added a large enough empty space to surround the entire sheet. The presence of this large empty space minimizes the atomic interactions during the simulation. We expected the computed elastic constants to be system-size dependent, so we varied the system size systematically from 900 atoms to 360![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 000 atoms. The finite size scaling method has also been carried out along with the molecular dynamics (MD) simulations, and the values are extrapolated to an infinite system-size limit.
000 atoms. The finite size scaling method has also been carried out along with the molecular dynamics (MD) simulations, and the values are extrapolated to an infinite system-size limit.
It is also possible to deduce the elastic constants by studying the fluctuations in the stress or strain in the system at thermal equilibrium without applying any external constraint. To do that, we invoked the appropriate fluctuation–dissipation theorem, which is based on the assumption that in thermodynamic equilibrium, a system's response to a spontaneous fluctuation is the same as its response to a small applied force. We adopted that method22 to calculate the elastic constants at a finite temperature; the fundamental equation used in the strain-fluctuation26,27 method is given by:
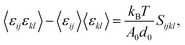 | (1) |
One advantage of using eqn (1) is that it includes only the fluctuations in the h matrix, which is derived from the three angles and sides of the simulation box and provides a technique for computing the elastic constants. We also used in-house codes to calculate the temperature dependent elastic constants from the derived MD data. We performed MD calculations with a time-dependent metric tensor to permit the volume and shape of the MD cell to change over time. We used the method detailed by Parrinello and Rahman to modulate the size and shape of the simulation cell for a system of N particles in a periodically repeating MD cell that varies in shape and volume over time.27,30 The symmetry-equivalent elastic constants are extracted from the statistical fluctuations of the simulation box lengths and the angle. Then the relationship between the instantaneous strain tensor ε and the h matrix can be expressed as,26
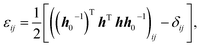 | (2) |
Computational details
We performed the simulations using the classical MD simulation package LAMMPS (Large scale Atomic/Molecular Massively Parallel Simulator).31 Among the various types of empirical interatomic potentials for carbon, the Tersoff32–34 and Tersoff-type35,36 potentials belong to the most successful category. We used the long range bond order potential (LCBOP)37 to model the interactions among the carbon atoms in graphene. Even though we performed the simulations using Tersoff and Tersoff type empirical potentials, along with the Tersoff potential recently tuned by Kinaci et al.38 for studies of graphene-like nanostructures (as reported in Sevik et al.39), our results do not corroborate the experimental results. Monte Carlo simulations by Magnin et al.40 indicated that the LCBOP potential shows the best agreement with their reference data near room temperature. Using classical MD simulations, Anees et al. investigated the temperature-dependent phonon frequency shift and structural stability of graphene using the LCBOP potential41 and reported the importance of LCBOP in describing the bond making and bond breaking mechanisms. The ability of LCBOP to accurately describe various features such as bond distances, conjugation, stretching force constants, elastic constants, and interlayer interaction energy in graphite prompted us to use it to analyze the mechanical properties of a graphene sheet.37 The interaction energy of the LCBOP potential can be expressed as:
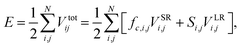 | (3) |
Results and discussion
The computed nearest neighbor distance of carbon atoms in the honeycomb lattice of graphene (Fig. S1†) is 1.42 Å. While applying a longitudinal strain to a finite system of 900 atoms, we observed considerable changes in bond length (1.44 Å) and angle compared to an infinite system subjected to the same strain (1.42 Å). The system size-dependence of the in-plane elastic moduli of graphene had not been studied experimentally until a recent experimental analysis seemed to report that such a size dependence does exist for graphene.42–44 Even though experimental evidence is still lacking, finite size-scaling plays a pivotal role in understanding the material's behavior. Recently, experimental confirmation of the scaling behavior of bending rigidity with system size has been reported,45 providing firm support for theoretical46 and atomistic simulations.47 We also found a finite size-scaling effect for the elastic properties of hexagonal boron nitride (h-BN) in accordance with a power law.25Elastic constants using molecular statics analysis
This section explains the results of the computed elastic constants of graphene at zero kelvin by means of molecular statics simulations. In a graphene sheet, the carbon atoms experience strong covalent bonding within the layers, and they experience weak (3.34 Å) van der Waal's interactions across the layers.16 The elastic properties of graphene have a strong relationship with its mechanical stability; essentially, they indicate the material's response to a given external strain. We studied the cell-size dependence of the anisotropy in the in-plane elastic moduli of graphene by changing the system size from a 15 × 15 × 1 supercell (900 atoms) to a 300 × 300 × 1 supercell (360![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 000 atoms). First, we considered a rectangular simulation cell of the honeycomb lattice in which we took one of the basis vectors to be the basis vector along the x-direction. We took the other basis vector along the y-direction and set its magnitude as
000 atoms). First, we considered a rectangular simulation cell of the honeycomb lattice in which we took one of the basis vectors to be the basis vector along the x-direction. We took the other basis vector along the y-direction and set its magnitude as 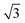 times the lattice parameter of the honeycomb lattice. All the calculations are done in the microcanonical ensemble (constant number of particles, volume and energy), with energy kept constant within one part in 107 for times in the order of 100 ps. Then, we extracted the change in energy upon different types of deformation of the simulation cell and calculated the respective elastic constants.
times the lattice parameter of the honeycomb lattice. All the calculations are done in the microcanonical ensemble (constant number of particles, volume and energy), with energy kept constant within one part in 107 for times in the order of 100 ps. Then, we extracted the change in energy upon different types of deformation of the simulation cell and calculated the respective elastic constants.
In the presence of small deformations, graphene is an isotropic and linear elastic material. During large deformations, graphene shows strain-softening behavior, and the relationship between stress and strain can be established on the basis of the second-order linear elastic modulus E and the third-order nonlinear elastic modulus D.3,48 Then σ = Eε + Dε2. Here, the second-order term leads to a decrease in stiffness at a larger tensile strain, and D becomes less than zero. The intrinsic stress of graphene is calculated from the maximum value of σ, obeying the condition 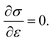 Then the intrinsic strength (maximum stress) and corresponding strain can be written as σintrinsic = −E2/4D and εintrinsic = −E2/2D, respectively. Guoxin Cao49 reported that graphene is a typical brittle-like material, and when εintrinsic becomes high, its lattice becomes unstable.
Then the intrinsic strength (maximum stress) and corresponding strain can be written as σintrinsic = −E2/4D and εintrinsic = −E2/2D, respectively. Guoxin Cao49 reported that graphene is a typical brittle-like material, and when εintrinsic becomes high, its lattice becomes unstable.
The elastic behavior of graphene is characterized by isotropic in-plane interactions, and the elastic matrix of the second-order elastic constants is denoted as:
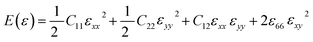 .25 Now, the longitudinal strain along the x-direction can be represented as εxx, that along the y-direction is εyy, and the applied shear strain along the xy plane is εxy. In the Voigt notation, these applied strains are denoted using the symbols ε1, ε2, and ε6, respectively. Here, the x(y) axis is along the zigzag (armchair) direction, εij's are the infinitesimal strain tensors, and Cij's are the corresponding linear elastic constants.50 For the case of a 2D isotropic sheet, the linear elastic constants satisfy the conditions C11 = C22 and 2C66 = C11 − C12, which shows that the Born mechanical stability criterion of graphene becomes C11 > 0, C11 > C12, and C66 > 0.51,52
.25 Now, the longitudinal strain along the x-direction can be represented as εxx, that along the y-direction is εyy, and the applied shear strain along the xy plane is εxy. In the Voigt notation, these applied strains are denoted using the symbols ε1, ε2, and ε6, respectively. Here, the x(y) axis is along the zigzag (armchair) direction, εij's are the infinitesimal strain tensors, and Cij's are the corresponding linear elastic constants.50 For the case of a 2D isotropic sheet, the linear elastic constants satisfy the conditions C11 = C22 and 2C66 = C11 − C12, which shows that the Born mechanical stability criterion of graphene becomes C11 > 0, C11 > C12, and C66 > 0.51,52
For small deformations, the in-plane stiffness matrix of a graphene sheet (generally, any 2D system) using elastic energy can be expressed as,
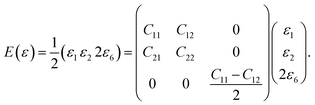 | (4) |
We used the finite size-scaling method to analyze the effect of the simulation cell size on the calculated physical properties of graphene. Initially, we used simulation cells without any vacuum space at the boundaries, essentially mimicking an infinite system. We found that the calculations using an infinite sheet with 10![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 000 atoms in a simulation cell were quite adequate to obtain convergence with respect to the simulation cell size (or system size). Because all the atoms in the simulation cell are surrounded by atoms, no surface effects occur in the simulation. To calculate the finite size properties, we varied the size of the simulation cell from 900 atoms to 360
000 atoms in a simulation cell were quite adequate to obtain convergence with respect to the simulation cell size (or system size). Because all the atoms in the simulation cell are surrounded by atoms, no surface effects occur in the simulation. To calculate the finite size properties, we varied the size of the simulation cell from 900 atoms to 360![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 000 atoms, providing sufficient vacuum space at the boundaries. When the system size reached ∼122
000 atoms, providing sufficient vacuum space at the boundaries. When the system size reached ∼122![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 500 atoms or more, the finite system produced a very good correlation with the infinite system.
500 atoms or more, the finite system produced a very good correlation with the infinite system.
The in-plane atomic arrangement of graphene in the x − y plane is expressed by the chirality angle θ: 0° ≤ θ ≤ 30°, where θ = 0° corresponds to the zigzag chirality and θ = 30° corresponds to the armchair chirality.49 Then, the Young's modulus and Poisson's ratio along an arbitrary orientation θ using the calculated elastic constants are,48,50
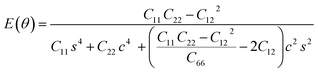 | (5) |
 | (6) |
![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) θ and s = sin
θ and s = sin![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) θ. If we consider the Cauchy relations in eqn (5) and (6), then C11 = C22 and 2C66 = C11 − C12 for an isotropic sheet. If we use θ = 0° (corresponding to the zigzag chirality), then
θ. If we consider the Cauchy relations in eqn (5) and (6), then C11 = C22 and 2C66 = C11 − C12 for an isotropic sheet. If we use θ = 0° (corresponding to the zigzag chirality), then
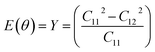 | (7) |
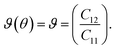 | (8) |
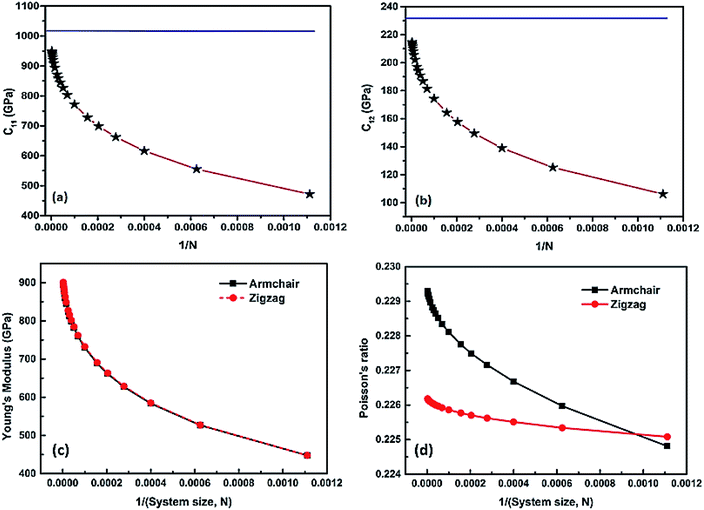
The elastic constants are extracted from the total energy by fitting it as a function of various specific strains. Our calculations show that the elastic constants of a graphene sheet with an infinite system size are C11 = C22 = 0.989 TPa, C12 = 0.221 TPa, and C66 = 0.380 TPa, which clearly depicts the isotropy of the material. We also made a direct comparison of the obtained C66 value with the theoretical value using the Cauchy relation for a hexagonal system and obtained 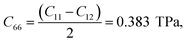 which is comparable to the result from the energy analysis method (C66 = 0.380 TPa). We continued the simulation using finite system sizes in which the simulation cells are surrounded on all sides by a vacuum of an appropriate thickness and calculated the system-size dependence of the Young's modulus and Poisson's ratio of graphene using eqn (5) and (6). The direction-dependent anisotropy in the elastic constants is observed and calculated using θ = 0° for the zigzag direction and θ = 30° for the armchair direction. The values of C11 and C12 for each system size are fitted to the equation P(N) = α − β/Nq, and the results are plotted as a function of 1/N. The variation of C11 and C12 is inverse to the system size, as shown in Fig. 2(a) and (b), respectively. We also found that both C11 and C12 increase with the system size in accordance with the power law, reaching a saturated value when the simulation cell size becomes very high.
which is comparable to the result from the energy analysis method (C66 = 0.380 TPa). We continued the simulation using finite system sizes in which the simulation cells are surrounded on all sides by a vacuum of an appropriate thickness and calculated the system-size dependence of the Young's modulus and Poisson's ratio of graphene using eqn (5) and (6). The direction-dependent anisotropy in the elastic constants is observed and calculated using θ = 0° for the zigzag direction and θ = 30° for the armchair direction. The values of C11 and C12 for each system size are fitted to the equation P(N) = α − β/Nq, and the results are plotted as a function of 1/N. The variation of C11 and C12 is inverse to the system size, as shown in Fig. 2(a) and (b), respectively. We also found that both C11 and C12 increase with the system size in accordance with the power law, reaching a saturated value when the simulation cell size becomes very high.
Furthermore, we noticed that the graphene sheet shows considerable variation in the computed Young's modulus and Poisson's ratio at small system sizes. As the system size increases, the Young's modulus converges to a value of ∼1 TPa, which corresponds to an infinite sheet. When the simulation cell size increases, the anisotropy of the Young's modulus and Poisson's ratio progressively decrease, as shown in Fig. 2(c) and (d), respectively. A detailed comparison of our computed Young's modulus with that in earlier studies is presented in Table 1. A comparison of the calculated Young's modulus and Poisson's ratio of the graphene sheet with other atomistic analysis using LAMMPS code is tabulated in Table S1.† The relative energy–strain response graph for calculating the elastic constants is shown in Fig. S2 in the ESI.† A finite system of 900 atoms subject to periodic boundary conditions and a vacuum space of 20 Å is shown in Fig. S2(a).† The computed elastic constants with 40![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 000 atoms and 122
000 atoms and 122![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 500 atoms differed significantly, as shown in Fig. S2(b) and (c),† respectively. As the system size increases, the finite system tends to mimic an infinite sheet (10
500 atoms differed significantly, as shown in Fig. S2(b) and (c),† respectively. As the system size increases, the finite system tends to mimic an infinite sheet (10![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 000 atoms), as shown in Fig. S2(d).† The obtained Young's moduli for systems with 900, 40
000 atoms), as shown in Fig. S2(d).† The obtained Young's moduli for systems with 900, 40![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 000, 122
000, 122![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 500, and 360
500, and 360![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 000 atoms are 0.447, 0.827, 0.873, and 0.939 TPa, respectively. The obtained elastic constants are positive values that ensure the mechanical stability of a graphene sheet.
000 atoms are 0.447, 0.827, 0.873, and 0.939 TPa, respectively. The obtained elastic constants are positive values that ensure the mechanical stability of a graphene sheet.
| Reference | Year | Method | Y (TPa) | ϑ |
|---|---|---|---|---|
| Present study | 2018 | MD (LCBOP) | 0.939 | 0.223 |
| Gao et al.55 | 2015 | Elastic shell model | 1.028 | 0.150 |
| Shao et al.20 | 2012 | DFT-QHA | 1.208 | — |
| Jian et al.21 | 2012 | MD | 1.090 | — |
| Hajgato et al.57 | 2012 | DFT | 1.050 | — |
| Shen et al.58 | 2012 | MD | 1.025 | — |
| Jing et al.59 | 2012 | MD (COMPASS) | 1.032 | — |
| Zhang et al.60 | 2012 | MD (AIREBO) | 0.995 | — |
| Terdalkar et al.61 | 2010 | MM (AIREBO) | 0.840 | — |
| Neek-Amal et al.62 | 2010 | MD | 0.800 | — |
| Neek-Amal et al.63 | 2010 | MD indentation | 0.501 | — |
| Jiang et al.19 | 2009 | MD | 0.950 | 0.220 |
| Zhao et al.18 | 2009 | MD (AIREBO) | 1.010 | 0.210 |
| TB | 0.910 | — | ||
| Wei et al.64 | 2009 | Ab initio | 1.037 | — |
| Cadelano et al.48 | 2009 | TB | 0.931 | 0.310 |
| Lu et al.65 | 2009 | MD (REBO) | 0.725 | 0.398 |
| Lee et al.3 | 2008 | Experiment | 1.020 | — |
| Hemmasizadeh et al.66 | 2008 | MM/CM | 0.939 | — |
| Liu et al.17 | 2007 | Ab initio | 1.050 | 0.186 |
| Konstantinova et al.67 | 2006 | DFT | 1.240 | — |
| Reddy et al.68 | 2006 | MM | 0.669 | 0.416 |
| Kudin et al.16 | 2001 | DFT | 1.150 | 0.149 |
| Van Lier et al.69 | 2000 | Ab initio | 1.110 | 0.149 |
The computed elastic constants also satisfy the necessary and sufficient conditions for elastic stability (Born-stability criterion), i.e., C11 > 0 and C11 > |C12|.51
Bending rigidity and thin shell thickness using molecular statics simulation
We used equations derived from Foppl–von Karman plate theory53,54 to determine the zero temperature bending rigidity (k) of a graphene sheet from the computed values of its Young's modulus and Poisson's ratio. The thin shell thickness (ts) characterizes structural flexibility and is used to compute the non-linear structural deformation mechanism in 2D materials.55 The Young's modulus is a material property, whereas tensile stiffness is a structural property of the material that is profoundly influenced by its geometry and composition. First, we calculated the thin shell thickness from the known value for the bending stiffness of graphene. The tensile stiffness D is related to the Young's modulus Y and thin shell thickness (ts) as D = Yts. Then, the thin shell thickness can be expressed as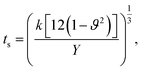 and the bending rigidity of the graphene sheet can be computed from the obtained value of the thin shell thickness. The equation connecting the bending rigidity or bending stiffness of graphene to its Young's modulus, thin shell thickness (ts), and in-plane Poisson's ratio ϑ is:
and the bending rigidity of the graphene sheet can be computed from the obtained value of the thin shell thickness. The equation connecting the bending rigidity or bending stiffness of graphene to its Young's modulus, thin shell thickness (ts), and in-plane Poisson's ratio ϑ is:
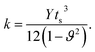 | (9) |
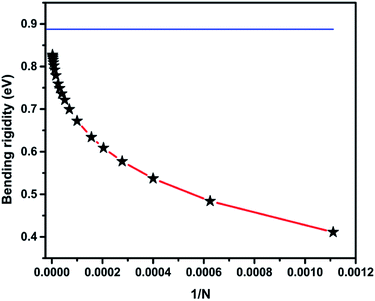
Using the atomistic Monte-Carlo technique, Fasolino et al. investigated the zero kelvin bending rigidity of a pristine graphene sheet (0.82 eV) and found that it increased with temperature.56 We computed the thin shell thickness (ts) value of graphene as 1.1871 Å, which is greater than that of the thickness value (0.89 Å) obtained using density functional theory calculations.55 The obtained thin shell thickness is much smaller than the inter-layer spacing (d = 3.4 Å), which is comparable to earlier reports.55 We extracted the bending rigidity of a graphene sheet of infinite spatial extent at zero kelvin using eqn (9) and found it to be 0.83 eV. We already reported that the zero temperature bending rigidity of an h-BN sheet with an infinite boundary is 0.62 eV, which is lower than the bending rigidity of a graphene sheet.25 Those observations reveal that graphene is both the hardest 2D material and highly flexible. We also observed that k, Y, and ϑ monotonically increase with system size. The variation in bending rigidity, calculated using the computed values of the Young's modulus and Poisson's ratio, is inverse to the system size, as shown in Fig. 3. The blue line in the figure corresponds to the value of the respective bending modulus extrapolated to an infinite system size limit.
Finite temperature elastic constants
During the analysis of finite temperature elastic constants, we used the periodic boundary condition along the x and y directions, whereas, we used a non-periodic boundary condition (more specifically, shrink-wrapping with a minimum value of the simulation cell) along the z-direction. We performed the strain-fluctuation method using a constant temperature and ambient pressure (NPT) ensemble for 0.5 nanoseconds (ns), with the thermodynamic tension and external hydrostatic pressure set to zero. The size and shape of the periodically repeating molecular dynamics simulation cell is controlled using a Lagrangian, and the entire system was equilibrated by coupling it to a Nose–Hoover thermostat. The study of the finite temperature elastic constants of graphene provides new insight into the various intrinsic thermodynamic properties within a range of temperatures.The general belief from harmonic theory predicts that a 2D membrane or crystal is highly unstable in principle. This refutation is solved by including the anharmonic coupling between the bending and stretching modes in the calculation.43 In the harmonic approximation, the correlation function for the out of plane (flexural) displacements in graphene is denoted as h(r) (different from the h considered earlier) which, in Fourier space, is represented as 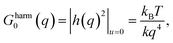 where kB is the Boltzmann constant, T is the temperature, the suffix u = 0 in the average explains the absence of any external strain, and the subscript 0 denotes that we neglect anharmonic coupling between the in-plane stretching and out-of-plane bending modes. The harmonic theory predicts divergence of the mean-square amplitude of the out-of-plane displacements, and it is given by h2harm ∝ L2 or h2harm = CL2, where L is the size of the sample, C is a temperature dependent constant, and h2 = |h(q)|2. This is the well-known result by which the harmonic theory of membranes predicts a crumpled membrane rather than a flat one.
where kB is the Boltzmann constant, T is the temperature, the suffix u = 0 in the average explains the absence of any external strain, and the subscript 0 denotes that we neglect anharmonic coupling between the in-plane stretching and out-of-plane bending modes. The harmonic theory predicts divergence of the mean-square amplitude of the out-of-plane displacements, and it is given by h2harm ∝ L2 or h2harm = CL2, where L is the size of the sample, C is a temperature dependent constant, and h2 = |h(q)|2. This is the well-known result by which the harmonic theory of membranes predicts a crumpled membrane rather than a flat one.
Recent studies reported that Young's modulus is a scale-dependent parameter and that the effective Young's modulus of graphene can be defined by considering the anharmonicities, coupling the lowest order in the in-plane (u(r)) and out-of-plane (h(r)) displacements.43,70 The effect of temperature increases the ripple amplitude and effectively softens the elastic moduli of 2D systems due to the anharmonic coupling between the bending and stretching modes. The observed temperature-dependent, out-of-plane intrinsic buckling (ripples) in graphene is a highly nonlinear phenomenon that profoundly influences its elastic properties. A recent study by Ahmadpoor et al. reported the temperature dependency of the out-of-plane fluctuations in graphene sheet, and explained the variation of elastic stiffness with system size and also the associated nonlinearities.71 We observed that the ripples (Fig. S3†) can effectively soften the elastic moduli, in the sense that stretching a crumpled graphene sheet requires less force than stretching a flat one.72 In this way, we investigated the influence of temperature on the thermal rippling behavior of graphene, which effectively reduces the elastic constants and is completely absent from the zero kelvin molecular statics calculations. Our MD simulations predicted a nonlinear temperature dependence of the elastic constants with significant anharmonic effects. The elastic modulus changes considerably with temperature and also strongly depends on the thermal rippling of the material.
The temperature-dependent elastic constants are derived using the instantaneous strain fluctuations shown in eqn (1) and (2). The variation of the independent elastic constants (C11 and C12) with temperature is shown in Fig. 4. We calculated the Young's modulus and Poisson's ratio of the graphene sheet using eqn (7) and (8), and the analysis shows a decrease in those elastic physical quantities with an increase in temperature, as shown in Fig. 5(a) and (b), respectively. We also calculated the variation in the bulk and shear moduli with temperature using the computed elastic constants, Young's modulus, and Poisson's ratio in eqn (10) and (11), as shown in Fig. 6. The computed temperature-dependent elastic constants completely satisfy the Born mechanical stability criterion in the studied temperature range, which validates our efforts in this study. Even though the slow convergence of the strain-fluctuation method for calculating elastic constants has already been reported,73 this method is quite easy to implement compared with the stress-fluctuation method.
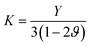 | (10) |
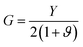 | (11) |
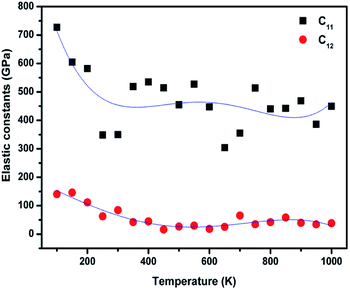 | ||
| Fig. 4 Calculated independent elastic constants of graphene at various temperatures using the strain fluctuation method. | ||
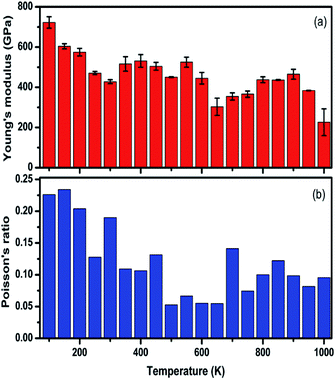 | ||
| Fig. 5 The computed values for the (a) Young's modulus and (b) Poisson's ratio of graphene at various temperatures using the strain fluctuation method. | ||
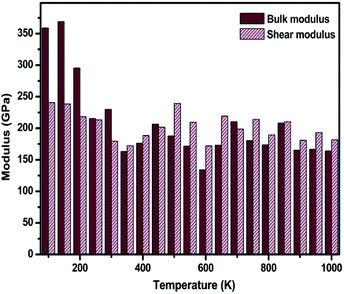 | ||
| Fig. 6 The temperature-dependent variation in computed values for the bulk and shear modulus using the strain-fluctuation method. | ||
In our analysis, we noted a significant decrease in C11 with temperature compared with C12. We emphasize that the lack of proper computational and experimental study of the finite temperature elastic constants of graphene restrict direct comparisons with our results. However, our results are quantitatively in agreement with the general trend, and the significant decrease in computed elastic constants and associated moduli with an increase in temperature is the direct consequence of the ripples intrinsic in 2D materials.28 We suggest that fluctuations in temperature might need to be considered over a longer time, on the order of nanoseconds (ns), to reduce the error bar associated with our calculations.
Longitudinal and shear wave velocities using elastic constants
The longitudinal and shear wave velocities of a monolayer graphene sheet are computed from the derived values of the elastic constants. It is commonly understood that, when applying a small deformation, each individual atom present in a graphene lattice is influenced by the motion of its nearest neighbor, and both the inertial and elastic restoring forces act upon each atom. The mass of the atom is closely related to the density of the material, whereas the spring constant is related to the elastic constants of the material. In graphene, we can generate soundwaves using the volumetric and shear deformations. From the computed values for the elastic constants, Young's modulus, and Poisson's ratio, we calculated two kinds of soundwaves: (1) longitudinal waves (p-waves)—soundwaves generated due to volumetric deformations (compressions) and (2) shear waves (s-waves)—soundwaves generated due to shear deformations. To analyze those sound velocities, we need the corresponding mass density of the graphene sheet. Using the equation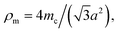 we calculated the two-dimensional mass density of graphene74 as 7.6036 × 10−7 kg m−1,2 where a is the in-plane lattice parameter of graphene, and mc is the atomic mass of a carbon atom. Here, the observed mass density of graphene is almost half the mass density of h-BN, which we reported previously.25,28 The in-plane elastic modulus (Young's modulus), Y; two-dimensional mass density, ρm; Poisson's ratio, ϑ; and in-plane elastic constants, C11 and C12, are used in the following relations to obtain the longitudinal and shear wave velocities:75,76
we calculated the two-dimensional mass density of graphene74 as 7.6036 × 10−7 kg m−1,2 where a is the in-plane lattice parameter of graphene, and mc is the atomic mass of a carbon atom. Here, the observed mass density of graphene is almost half the mass density of h-BN, which we reported previously.25,28 The in-plane elastic modulus (Young's modulus), Y; two-dimensional mass density, ρm; Poisson's ratio, ϑ; and in-plane elastic constants, C11 and C12, are used in the following relations to obtain the longitudinal and shear wave velocities:75,76
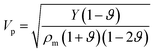 | (12) |
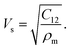 | (13) |
Using eqn (12) and (13), we calculated the longitudinal (Vp) and shear wave (Vs) velocities of a system with an infinite boundary as 21.82 km s−1 and 9.88 km s−1, respectively. For a system with a finite spatial extent, the longitudinal (Vp) and shear wave (Vs) velocities increase as the system size increases. For example, as the system size increases from 900 atoms to 360![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 000 atoms, the Vp value varies from 15.07 km s−1 to 21.40 km s−1, with a corresponding change in Vs is 9.73 km s−1 from 6.84 km s−1. The variation in the Vp and Vs of a finite sheet is inverse to the system size, as shown in Fig. S4(a) and (b),† respectively. As the system size increases, the Young's modulus and Poisson's ratio also increase, and at higher system sizes, those values saturate and mimic an infinite sheet. Those changes lead to an increase in both longitudinal and shear wave velocities. We also noticed that the longitudinal wave possesses a higher velocity than the shear wave in the entire studied range of system size. The Vp/Vs value lies in the range of 2.19 to 2.20. When the temperature increases, the Young's modulus of the sample decreases, which effectively reduces the longitudinal and shear wave velocities, as shown in Fig. 7. Peng et al. reported the advantages of measuring sound velocities in h-BNC heterostructures and predicted that the longitudinal and shear wave velocities could be used to validate the elastic properties of materials. When they introduced the h-BN domains into graphene structures, they found that the sound velocity gradient could be used to form a sound frequency and ranging channel, which they treated as the fundamental functional mechanism in surface acoustic wave sensors and waveguides.76
000 atoms, the Vp value varies from 15.07 km s−1 to 21.40 km s−1, with a corresponding change in Vs is 9.73 km s−1 from 6.84 km s−1. The variation in the Vp and Vs of a finite sheet is inverse to the system size, as shown in Fig. S4(a) and (b),† respectively. As the system size increases, the Young's modulus and Poisson's ratio also increase, and at higher system sizes, those values saturate and mimic an infinite sheet. Those changes lead to an increase in both longitudinal and shear wave velocities. We also noticed that the longitudinal wave possesses a higher velocity than the shear wave in the entire studied range of system size. The Vp/Vs value lies in the range of 2.19 to 2.20. When the temperature increases, the Young's modulus of the sample decreases, which effectively reduces the longitudinal and shear wave velocities, as shown in Fig. 7. Peng et al. reported the advantages of measuring sound velocities in h-BNC heterostructures and predicted that the longitudinal and shear wave velocities could be used to validate the elastic properties of materials. When they introduced the h-BN domains into graphene structures, they found that the sound velocity gradient could be used to form a sound frequency and ranging channel, which they treated as the fundamental functional mechanism in surface acoustic wave sensors and waveguides.76
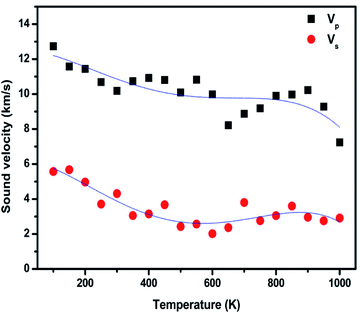 | ||
| Fig. 7 Variation in longitudinal (Vp) and shear wave (Vs) velocities in monolayer graphene using the strain-fluctuation method at different temperatures. | ||
Conclusions
In conclusion, we carried out systematic molecular statics and dynamics simulations to study the mechanical properties of a monolayer graphene sheet. Our analysis of temperature-dependent elastic constants for graphene between 100 and 1000 K is the first independent approach using the strain-fluctuation method. Direction-dependent anisotropic behavior is clearly observed in finite sheets, whereas infinite sheets are isotropic. The computed elastic constants satisfy the Born mechanical stability criterion and satisfy C11 > 0, C11 > C12, and C66 > 0. From the computed values of the Young's modulus and Poisson's ratio, changes in the zero kelvin bending rigidity with system size are deduced using a formula derived from the Foppl–von Karman approach. Thermally excited ripples in graphene lead to strong anharmonic behavior that essentially causes a large deviation from isotropic elasticity. The elastic moduli and associated properties decreased with an increase in temperature. When the temperature increases, the Young's modulus of the sample decreases, which effectively reduces the longitudinal and shear wave velocities. In this paper, we focused only on the elastic and associated properties of a monolayer graphene sheet. Recent studies reported the possibility of creating other 2D carbon allotropes77,78 with better practical applications, including energy storage. Our results provide new information about the mechanical stability of graphene that could be highly useful for the design of integrated electronic devices. Future research might be on a systematic study of defective graphene sheets to analyze the effects of direction-dependent anisotropic behavior on various physical properties. Further analysis into the dependence of mechanical and other properties of pristine and defective allotropes of 2D carbon should be done, along with experimental verification of our results.Conflicts of interest
There are no conflicts to declare.Acknowledgements
This research was supported by grants from the Basic Science Research Program (NRF-2018R1A2B6006320) and the Creative Materials Discovery Program (2015M3D1A1068062) through the National Research Foundation of Korea (NRF) funded by the Ministry of Science, ICT, and Future Planning.References
- K. S. Novoselov, D. Jiang, F. Schedin, T. J. Booth, V. V. Khotkevich, S. V. Morozov and A. K. Geim, Proc. Natl. Acad. Sci. U. S. A., 2005, 102, 10451–10453 CrossRef PubMed.
- A. K. Geim and K. S. Novoselov, Nat. Mater., 2007, 6, 183–191 CrossRef PubMed.
- C. Lee, X. D. Wei, J. W. Kysar and J. Hone, Science, 2008, 321, 385–388 CrossRef PubMed.
- A. A. Balandin, Nat. Mater., 2011, 10, 569–581 CrossRef PubMed.
- Y. W. Zhu, S. Murali, W. W. Cai, X. S. Li, J. W. Suk, J. R. Potts and R. S. Ruoff, Adv. Mater., 2010, 22, 3906–3924 CrossRef PubMed.
- B. Mortazavi, O. Benzerara, H. Meyer, J. Bardon and S. Ahzi, Carbon, 2013, 60, 356–365 CrossRef.
- K. Z. Milowska, M. Woinska and M. Wierzbowska, J. Phys. Chem. C, 2013, 117, 20229–20235 CrossRef.
- M. Sreejesh, N. M. Huang and H. S. Nagaraja, Electrochim. Acta, 2015, 160, 94–99 CrossRef.
- B. Mortazavi and S. Ahzi, Carbon, 2013, 63, 460–470 CrossRef.
- K. Min and N. R. Aluru, Appl. Phys. Lett., 2011, 98, 013113 CrossRef.
- M. Arroyo and T. Belytschko, Phys. Rev. B: Condens. Matter Mater. Phys., 2004, 69, 115415 CrossRef.
- G. M. Rignanese and J. C. Charlier, Phys. Rev. B: Condens. Matter Mater. Phys., 2008, 78, 125415 CrossRef.
- K. S. Novoselov, A. K. Geim, S. V. Morozov, D. Jiang, Y. Zhang, S. V. Dubonos, I. V. Grigorieva and A. A. Firsov, Science, 2004, 306, 666–669 CrossRef PubMed.
- K. Erickson, R. Erni, Z. Lee, N. Alem, W. Gannett and A. Zettl, Adv. Mater., 2010, 22, 4467–4472 CrossRef PubMed.
- D. W. Bullett, J. Phys. C: Solid State Phys., 1975, 8, 2707–2714 CrossRef.
- K. N. Kudin, G. E. Scuseria and B. I. Yakobson, Phys. Rev. B: Condens. Matter Mater. Phys., 2001, 64, 235406 CrossRef.
- F. Liu, P. M. Ming and J. Li, Phys. Rev. B: Condens. Matter Mater. Phys., 2007, 76, 064120 CrossRef.
- H. Zhao, K. Min and N. R. Aluru, Nano Lett., 2009, 9, 3012–3015 CrossRef PubMed.
- J. W. Jiang, J. S. Wang and B. W. Li, Phys. Rev. B: Condens. Matter Mater. Phys., 2009, 80, 113405 CrossRef.
- T. J. Shao, B. Wen, R. Melnik, S. Yao, Y. Kawazoe and Y. J. Tian, J. Chem. Phys., 2012, 137, 194901 CrossRef PubMed.
- J. Zhu, M. He and F. Qiu, Chin. J. Chem., 2012, 30, 1399–1404 CrossRef.
- L. D. Landau, E. M. Lifsic and L. P. Pitaevskij, Statistical physics 1 5., Pergamon Press, Oxford, 1980 Search PubMed.
- N. M. A. Krishnan and D. Ghosh, J. Appl. Phys., 2014, 115, 064303 CrossRef.
- Q. L. Xiong and X. G. Tian, AIP Adv., 2015, 5, 107215 CrossRef.
- S. Thomas, K. M. Ajith and M. C. Valsakumar, J. Phys.: Condens. Matter, 2016, 28, 295302 CrossRef PubMed.
- J. R. Ray, Comput. Phys. Rep., 1988, 8, 111–151 CrossRef.
- M. Parrinello and A. Rahman, J. Chem. Phys., 1982, 76, 2662–2666 CrossRef.
- S. Thomas, K. M. Ajith and M. C. Valsakumar, Superlattices Microstruct., 2017, 111, 360–372 CrossRef.
- P. J. Fay and J. R. Ray, Phys. Rev. A: At., Mol., Opt. Phys., 1992, 46, 4645–4649 CrossRef.
- M. Parrinello and A. Rahman, Phys. Rev. Lett., 1980, 45, 1196–1199 CrossRef.
- S. Plimpton, J. Comput. Phys., 1995, 117, 1–19 CrossRef.
- J. Tersoff, Phys. Rev. B: Condens. Matter Mater. Phys., 1988, 37, 6991–7000 CrossRef.
- J. Tersoff, Phys. Rev. Lett., 1988, 61, 2879–2882 CrossRef PubMed.
- J. Tersoff, Phys. Rev. B: Condens. Matter Mater. Phys., 1989, 39, 5566–5568 CrossRef.
- D. W. Brenner, Phys. Rev. B: Condens. Matter Mater. Phys., 1990, 42, 9458–9471 CrossRef.
- D. W. Brenner, O. A. Shenderova, J. A. Harrison, S. J. Stuart, B. Ni and S. B. Sinnott, J. Phys.: Condens. Matter, 2002, 14, 783–802 CrossRef.
- J. H. Los and A. Fasolino, Phys. Rev. B: Condens. Matter Mater. Phys., 2003, 68, 024107 CrossRef.
- A. Kinaci, J. B. Haskins, C. Sevik and T. Cagin, Phys. Rev. B: Condens. Matter Mater. Phys., 2012, 86, 115410 CrossRef.
- C. Sevik, A. Kinaci, J. B. Haskins and T. Cagin, Phys. Rev. B: Condens. Matter Mater. Phys., 2011, 84, 085409 CrossRef.
- Y. Magnin, G. D. Forster, F. Rabilloud, F. Calvo, A. Zappelli and C. Bichara, J. Phys.: Condens. Matter, 2014, 26, 185401 CrossRef PubMed.
- P. Anees, M. C. Valsakumar and B. K. Panigrahi, 2D Mater., 2015, 2, 035014 CrossRef.
- J. H. Los, A. Fasolino and M. I. Katsnelson, Phys. Rev. Lett., 2016, 116, 015901 CrossRef PubMed.
- G. Lopez-Polin, C. Gomez-Navarro, V. Parente, F. Guinea, M. I. Katsnelson, F. Perez-Murano and J. Gomez-Herrero, Nat. Phys., 2015, 11, 26–31 Search PubMed.
- R. J. T. Nicholl, H. J. Conley, N. V. Lavrik, I. Vlassiouk, Y. S. Puzyrev, V. P. Sreenivas, S. T. Pantelides and K. I. Bolotin, Nat. Commun., 2015, 6, 8789 Search PubMed.
- M. K. Blees, A. W. Barnard, P. A. Rose, S. P. Roberts, K. L. McGill, P. Y. Huang, A. R. Ruyack, J. W. Kevek, B. Kobrin, D. A. Muller and P. L. McEuen, Nature, 2015, 524, 204–207 CrossRef PubMed.
- D. R. Nelson, T. Piran and S. Weingerg, Statistical Mechanics of Membranes and Surfaces, World Scientific, Singapore, 2004 Search PubMed.
- J. H. Los, M. I. Katsnelson, O. V. Yazyev, K. V. Zakharchenko and A. Fasolino, Phys. Rev. B: Condens. Matter Mater. Phys., 2009, 80, 121405(R) CrossRef.
- E. Cadelano, P. L. Palla, S. Giordano and L. Colombo, Phys. Rev. Lett., 2009, 102, 235502 CrossRef PubMed.
- G. X. Cao, Polymers, 2014, 6, 2404–2432 CrossRef.
- Y. Ding and Y. L. Wang, J. Phys. Chem. C, 2013, 117, 18266–18278 CrossRef.
- F. Mouhat and F. X. Coudert, Phys. Rev. B: Condens. Matter Mater. Phys., 2014, 90, 224104 CrossRef.
- J. Zhou and R. Huang, J. Mech. Phys. Solids, 2008, 56, 1609–1623 CrossRef.
- A. Föppl, Vorlesungen über technische Mechanik, ed. B. G. Teubner, Leipzig, Berlin, 1911 Search PubMed.
- T. Von Kármán, Encyklopädie der mathematischen Wissenschaften., 1910 Search PubMed.
- E. L. Gao and Z. P. Xu, J. Appl. Mech., 2015, 82, 121012 CrossRef.
- A. Fasolino, J. H. Los and M. I. Katsnelson, Nat. Mater., 2007, 6, 858–861 CrossRef PubMed.
- B. Hajgato, S. Guryel, Y. Dauphin, J. M. Blairon, H. E. Miltner, G. Van Lier, F. De Proft and P. Geerlings, J. Phys. Chem. C, 2012, 116, 22608–22618 CrossRef.
- Y. K. Shen and H. A. Wu, Appl. Phys. Lett., 2012, 100, 101909 CrossRef.
- N. N. Jing, Q. Z. Xue, C. C. Ling, M. X. Shan, T. Zhang, X. Y. Zhou and Z. Y. Jiao, RSC Adv., 2012, 2, 9124–9129 RSC.
- Y. Y. Zhang, Q. X. Pei and C. M. Wang, Appl. Phys. Lett., 2012, 101, 081909 CrossRef.
- S. S. Terdalkar, S. Huang, H. Y. Yuan, J. J. Rencis, T. Zhu and S. L. Zhang, Chem. Phys. Lett., 2010, 494, 218–222 CrossRef.
- M. Neek-Amal and F. M. Peeters, Phys. Rev. B: Condens. Matter Mater. Phys., 2010, 81, 235421 CrossRef.
- M. Neek-Amal and F. M. Peeters, Phys. Rev. B: Condens. Matter Mater. Phys., 2010, 81, 235437 CrossRef.
- X. D. Wei, B. Fragneaud, C. A. Marianetti and J. W. Kysar, Phys. Rev. B: Condens. Matter Mater. Phys., 2009, 80, 205407 CrossRef.
- Q. Lu and R. Huang, Int. J. Appl. Mech. Eng., 2009, 1, 443–467 CrossRef.
- A. Hemmasizadeh, M. Mahzoon, E. Hadi and R. Khandan, Thin Solid Films, 2008, 516, 7636–7640 CrossRef.
- E. Konstantinova, S. O. Dantas and P. M. V. B. Barone, Phys. Rev. B: Condens. Matter Mater. Phys., 2006, 74, 035417 CrossRef.
- C. D. Reddy, S. Rajendran and K. M. Liew, Nanotechnology, 2006, 17, 864–870 CrossRef.
- G. Van Lier, C. Van Alsenoy, V. Van Doren and P. Geerlings, Chem. Phys. Lett., 2000, 326, 181–185 CrossRef.
- R. Roldan, A. Fasolino, K. V. Zakharchenko and M. I. Katsnelson, Phys. Rev. B: Condens. Matter Mater. Phys., 2011, 83, 174104 CrossRef.
- F. Ahmadpoor, P. Wang, R. Huang and P. Sharma, J. Mech. Phys. Solids, 2017, 107, 294–319 CrossRef.
- S. Chen, Buckling and topological defects in graphene and carbon nanotubes, PhD thesis, University of California, Berkeley, 2012.
- A. A. Gusev, M. M. Zehnder and U. W. Suter, Phys. Rev. B: Condens. Matter Mater. Phys., 1996, 54, 1–4 CrossRef.
- L. J. Karssemeijer and A. Fasolino, Surf. Sci., 2011, 605, 1611–1615 CrossRef.
- L. E. Kinsler and A. R. Frey, Fundamentals of accoustics, Wiley, 1962 Search PubMed.
- Q. Peng, A. R. Zamiri, W. Ji and S. De, Acta Mech., 2012, 223, 2591–2596 CrossRef.
- X. Y. Li, Q. Wang and P. Jena, J. Phys. Chem. Lett., 2017, 8, 3234–3241 CrossRef PubMed.
- Z. H. Wang, X. F. Zhou, X. M. Zhang, Q. Zhu, H. F. Dong, M. W. Zhao and A. R. Oganov, Nano Lett., 2015, 15, 6182–6186 CrossRef PubMed.
Footnote |
| † Electronic supplementary information (ESI) available. See DOI: 10.1039/c8ra02967a |
| This journal is © The Royal Society of Chemistry 2018 |