Open Access Article
Open Access ArticleStrain and screening effects on field emission properties of armchair graphene nanoribbon arrays: a first-principles study
Han Hua,
Siow Mean Lohab,
Tsan-Chuen Leung*a and
Ming-Chieh Lin *c
*c
aDepartment of Physics, National Chung Cheng University, Chia-Yi 62101, Taiwan. E-mail: tcleungtw@gmail.com
bDepartment of Physics, University of Warwick, Coventry CV4 7AL, UK
cMultidisciplinary Computational Laboratory, Department of Electrical and Biomedical Engineering, Hanyang University, Seoul 04763, Korea. E-mail: mclin@hanyang.ac.kr
First published on 20th June 2018
Abstract
The field screening effect on the field-emission properties of armchair graphene nanoribbons (AGNRs) under strain has been studied using first-principles calculations with local density approximation (LDA). Using the zone folding method with the effect of a dipole barrier along with the work function of strained graphene, we can obtain the work function of AGNR of any width under strain, confirmed with the LDA calculations. We have systematically investigated the effects of inter-ribbon distance and ribbon width on the work function of AGNR arrays. It is found that the work function of AGNR arrays increases rapidly as the inter-ribbon distance Dx increases, which is caused by the positive dipole at the edge of the ribbon. Using a simple linear interpolation model, we can obtain the work function of AGNRs of any ribbon-width and inter-ribbon distance. The dependences of the inter-ribbon distance and strain on the field enhancement factor have been determined. The enhancement factor reaches about 90% of its saturated value as the inter-ribbon distance approaches two times the ribbon-width. For a tensile strain, the field enhancement factor increases with applied strain while for a compressive one, the field enhancement factor is nearly independent. The effects of inter-ribbon distance and strain on the enhancement factor can be explained by the interlayer and intralayer screening effects, respectively.
Introduction
Graphene, i.e., a macroscopic single sheet of graphite, has attracted tremendous attention in recent years because of its extraordinary physical, chemical, mechanical, and electrical properties such as high electron mobility (105 cm2 V−1 s−1) and exceptional thermal conductance (3–5 kW m−1 K−1).1–4 More specifically, the graphene nanoribbon (GNR), i.e., a strip cut from a graphene sheet and terminated by hydrogen atoms, with various widths of nanometer size,5–9 has been widely investigated for a variety of applications in nanoelectronic devices.10 Since the structure of GNRs is similar to those of graphene and carbon nanotubes (CNTs), the GNRs are expected to have various similarly extraordinary electronic, magnetic, mechanical, and transport properties. The electronic properties of these GNRs are dominated by the edge structure, ribbon width, and bulk defects.11–13 The geometric and electronic properties of edge-decorated GNRs with elements of an atomic number lower than 30 had been investigated thoroughly by ab initio or first-principles density functional theory (DFT) calculations.10 It was found that the edge decoration of flat GNRs drastically change the electronic and geometric properties. Three optimal or stable structures could be obtained including a zipper-line decorated CNT formed by covalent bonds, an edge-decorated curved GNR made up of a metal chain with interlaced dipole–dipole interactions, and a flat GNR with edge passivation. Most of the decorated systems were classified as conductors while a few were semiconductors with a band gap stemming from the anti-ferromagnetic configuration. The results suggested a possible route to selectively fabricate specific types of edge-decorated geometric structures with desired electronic properties for applications in engineering nanoelectronic devices and thus avoid the difficulties in separating the mixed products obtained in unzipping experiments.10Graphene nanoribbons with zigzag and armchair edges are called ZGNRs and AGNRs, respectively. We refer to a ZGNR (an AGNR) with N dimer lines as an N-ZGNR (N-AGNR). The electrical property of ZGNR becomes half-metallic when an external electric field is applied, as proposed by Son et al.14 In half-metals, electrical current can be completely spin polarized as a result of the coexistence of metallic nature for electrons with one spin orientation and insulating nature for electrons with the other. It was demonstrated by using first-principles DFT calculations that half-metallicity in GNRs is realizable if in-plane homogeneous electric fields are applied across the zigzag-shaped edges of the ZGNRs, and that their magnetic properties can be controlled by the external electric fields. The results suggested a new path to explore spintronics at the nanometre scale, based on graphene14 in spite of Rudberg et al. debated whether this half-metallicity would be removed by a nonlocal exchange effect.15 On the other hand, the electrical property of AGNR is semiconducting and the band gap depends on its ribbon width.12,16 One can develop the application of AGNR by tuning the band gap of AGNR, for instance, the application in optoelectronic device and nanolaser.17,18 Although there are several methods to tune the band gap of AGNR, one effective way is applying an external stress.19–21 Recently, the relation between inversion symmetry breaking and gap opening has been studied,22,23 for instance, asymmetrical strain distributions notably adjust the band structure near the Fermi energy of graphene.24 Furthermore, graphene can be used as an active channel layer.
In the recent years, the wide applications of vacuum electronic devices call for a well development of field emission cathodes. Field emission arrays (FEAs) are good candidates for the use as field emitters. FEAs with their high current densities and fast turn on have been envisioned to be capable of improving the performance of many devices. So far, the field emission due to quantum mechanical tunneling is described by the well-known Fowler–Nordheim (FN) equation,25,26
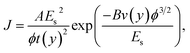 | (1) |
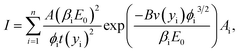 | (2) |
The work function of graphene can determine the band alignment28 and affect the charge injection between graphene and the metallic contact.29,30 The thin nature of vertically standing graphene is a good candidate for field emitter and the emitting current can be dramatically enhanced by a lower work function.31 Previous study showed that the work function of AGNR can be modulated by strain.32 The work function increases and decreases with uniaxial tensile strain and compressive strain, respectively. The Fermi energy shift with strain plays the most important role in the variation of the work function under strain.32 Engineering the work function of a single AGNR using strain and functional species has been proposed and studied by Peng et al. using first principles calculations.33 It was found that the work function of an AGNR can be tuned by strain and edge and surface decorations. Although the effects of different width on the electric properties were studied, the results of the AGNR were limited to one width of 14C atoms with 1 and 2 atomic variations. Barone et al. found that electronic properties of nanoribbons are not only sensitive to the edge terminations but also the ribbon width.34 It was demonstrated that the electronic properties of ribbons with wider width of practical significance can be determined by extrapolation. On the other hand, Nilsson et al.35 demonstrated experimentally and theoretically that emission from high density carbon nanotube arrays is poor because of the field screening effect. The equipotential lines in the vicinity of each tip is screened by the surrounding tubes. The screening effects reduce the field enhancement and thus the field emission current as the intertube distance is decreased. The screening effect is strongly dependent on the relative height of the tubes compared to the intertube distance. Nilsson at el. predicted that the current emission of the CNTs becomes a maximum when the inter-tube distance is about two times of its height. Graphene-based field emission devices can be well developed through further understanding the electronic properties of AGNR arrays. Up to now, there has been no comprehensive systematic study of the effect of inter-ribbon distance and ribbon width on the work function and field enhancement factor of AGNR arrays, and this will be the focus of this work.
In this study, the screening effect on field-emission properties of AGNR arrays under strain has been studied using first-principles DFT calculations. We have systematically investigated the effects of inter-ribbon distance, ribbon-width, and strain on the work function and field enhancement factor of AGNRs. The results indicate that the work function of AGNR will be affected by the surface dipole barrier due to charge transfer between hydrogen atoms and the edge carbon atoms. Using the zone folding method with the effect of dipole barrier along with the work function of strained graphene, we can obtain the work function of AGNR arrays of any width under strain, confirmed with the LDA calculations. Our present study provides valuable insight into the strain and screening effects on the field emission properties of AGNR arrays.
Results and discussion
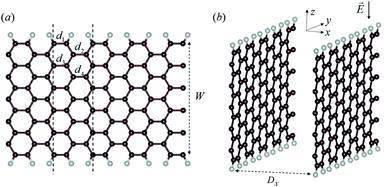
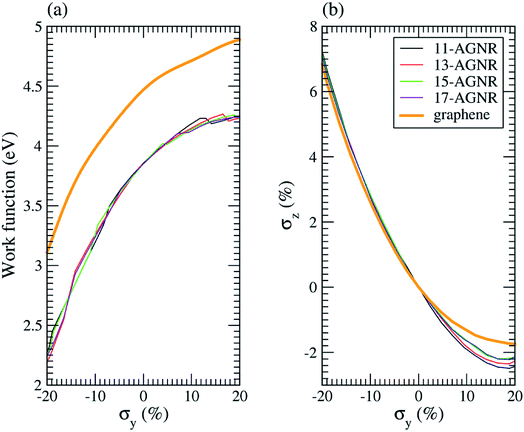
Fig. 1(a) shows the atomic structures of an 11-AGNR, with the coordinate axes defined in Fig. 1(b). We refer to an armchair graphene nanoribbon with N armchair chains as an N-AGNR. The dangling bonds at the edges of the ribbon are passivated by hydrogen atoms. The nanoribbon edge direction is along the y-axis and a manipulated vacuum thickness (Dx) of 10 Å is applied to the x axis, with a vacuum space (Dv) of 25 Å or more along the z direction. The axial bonds of first and second columns in the unit cell are labeled (d1, d3) and (d2, d4), respectively. The ribbon width (W) is defined here as the width without including the hydrogen atoms at the edges. The widths of the N-AGNRs for N = 7, 9, 11, 13, 15, 17, 19, 21, 23, and 25 are listed in Table 1. The strain effect on the work function of AGNR is studied. Fig. 2(a) shows the work function for various AGNRs with N = 11, 13, 15, and 17 as a function of an uniaxial strains (σy) along the y direction by the direct LDA calculation. That of graphene is also given in the figure for comparison. In the LDA calculations of the uniaxial strain effect on graphene, a structure optimization has been done for each applied y-strain to obtain the corresponding induced z-strain. Fig. 2(b) shows the induced strain along the width direction (σz) in various AGNRs as a function of applied strain along the ribbon length (σy). As one can see in Fig. 2(a), the work function of AGNRs increases under tensile strain and decreases under compressive strain while the dependence of the work function of AGNRs on the width of ribbon under strain is weak. It is interesting to note that the work function of unstrained AGNR is almost independent of the width of ribbon. The barriers caused by the surface dipole layers at the edges are positive due to the charge transfer between hydrogen atoms and the edge carbon atoms. Since the electrons will gain energy by passing through the positive dipole layer at the surfaces, the work function will be reduced. The dipole barrier of AGNR is given by the difference between the work function of AGNR and graphene (yellow line), as shown in Fig. 2(a). The curve for graphene is used to represent the case where the width of the ribbon approaches infinity. The dipole barrier for an unstrained AGNR is −0.64 eV. The dipole barrier (D) is inversely proportional to y-strain (smaller y-strain correspond to higher density of dipoles), thus it can be written as| D = −0.64/(1 + 0.01σy). | (3) |
| N | Width (Å) | N | Width (Å) |
|---|---|---|---|
| 7 | 7.28 | 17 | 19.49 |
| 9 | 9.72 | 19 | 21.93 |
| 11 | 12.17 | 21 | 24.37 |
| 13 | 14.61 | 23 | 26.82 |
| 15 | 17.04 | 25 | 29.25 |
The difference in the work function from that of graphene for small carbon nanoribbons is due to the downshift of the Fermi energy relative to the vacuum level.20
The change of work function induced by a passivation or adsorbates can be attributed to the barrier of surface dipoles and Fermi level shifts. In previous study,19 it was found the shift of the Fermi energy relative to the vacuum level is caused by the asymmetry of the slope of the Dirac cone, represented as
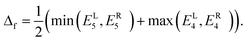 | (4) |
A downshift of the Fermi level causes an upshift in the work function,20 thus, the work function of AGNR (ΦAGNR) as a function of strain is given by
| ΦAGNR = (ΦG + D) − Δf, | (5) |
Now, we investigate how the inter-ribbon distance (Dx) affects the work function of armchair graphene nanoribbons. The work functions are calculated by the difference between the Fermi level and the average potential in the vacuum region where it approaches a constant. For the case of a semiconducting ribbon, the Fermi level is chosen at the middle of the gap. Fig. 4(a) shows the calculated work functions as a function of the inverse ribbon width for various inter-ribbon distances. Our local-density approximation results agree with a previous study.36 For a given inter-ribbon distance, the work function of AGNR increases as the width of the ribbon increases. The trend becomes more obvious for larger inter-ribbon distance. It is of interest to note that the work function is strongly dependent on the inter-ribbon distance. This dependence can be qualitatively explained by the fact that there is a dipole at the edge of the ribbon. Carbon attracts electrons from hydrogen; therefore, the dipole at the edge is positive. A positive dipole layer leads to a decrease in work function. The higher the density of the dipoles, which corresponds to smaller inter-ribbon distance, the lower the work function. This explains the observation that the work function decreases as the inter-ribbon distance decreases. One can see from Fig. 4(a) that the work function varies roughly linearly with 1/W as W ≧ 17.04 Å (corresponding to N ≧ 15). This allows us to extrapolate to 1/W → 0, which will give the work function of a “wide” ribbon. Fig. 4(c) shows the work function of the wide AGNR as a function of inverse inter-ribbon distance calculated by the linear fit of the data in Fig. 4(a). It is of interest to note that the work function of the wide AGNR also varies linearly with 1/Dx. The straight line in Fig. 4(c) is the linear fit to the data for Dx ≧ 25 Å which is given by Φ = 4.3965 − 6.4749/Dx. An extrapolation toward a larger Dx limit gives a value of ∼4.4 eV, which is the work function of an isolated wide AGNR. The theoretical and experimental work functions of graphene are 4.5 eV and 4.6 eV, respectively.37,38 Note that the work function of isolated wide AGNR is lower than that of graphene. This is because the edge of the AGNR is terminated by a hydrogen atom in our calculation. The positive dipole layer at the edge of the ribbon will lower the work function of the system.
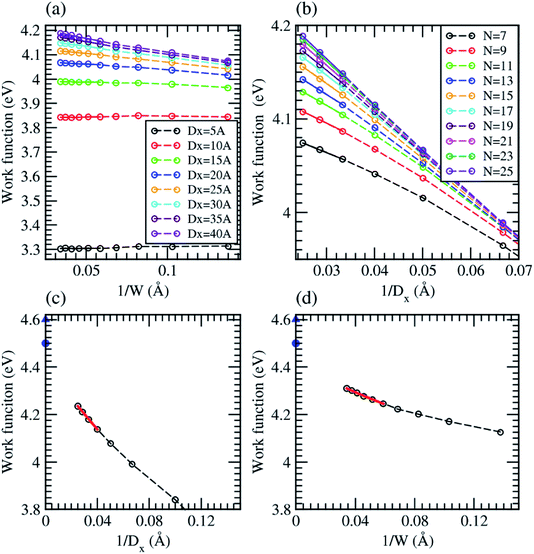 | ||
| Fig. 4 Work function of AGNR, calculated by local density approximation (LDA), as a function of (a) inverse ribbon width 1/W and (b) inverse inter-ribbon distance 1/Dx. The lines in (a) and (b) serve as visual guides. (c) Work function of wide AGNRs, calculated by the linear fit to the results in (a), as a function of inverse inter-ribbon distance. (d) Work function of isolated AGNR, calculated by the linear fit to the results in (b), as a function of inverse ribbon width. The lines in (c) and (d) are the linear fit to the data. The blue circle and triangle in (c) and (d) indicate the theoretical31 and experimental32 work function of graphene. | ||
In order to confirm this observation, the work functions of AGNRs are plotted as a function of inverse inter-ribbon distance for various ribbon widths, as shown in Fig. 4(b). It is found that the work function varies almost linearly with 1/Dx as Dx ≧ 30 Å. The linear fitting results for W ≧ 17.04 Å (corresponding to N ≧ 15) will give the work function of an isolated AGNR with various ribbon widths, as shown in Fig. 4(d). The work function of an isolated AGNR is also linear, as given by Φ = 4.3979 − 2.5979/W. An extrapolation to 1/W → 0 will give the work function of an isolated wide AGNR. The work function of an isolated wide AGNR from Fig. 4(d) agrees well with that from Fig. 4(c). Therefore, the linear interpolation results in Fig. 4(a) and (b) are reliable. This means that we can use the results of linear regression in Fig. 4(a) to obtain the work function of an AGNR of any ribbon-width.
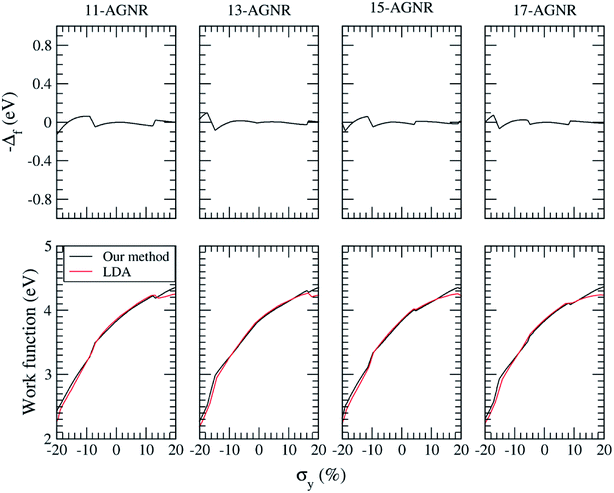
It is worth of mentioning that one can use the zone folding method with the effect of dipole barrier along with the work function of strained graphene to estimate the work function of any strained AGNRs although we use a case of Dx = 10 Å to demonstrate the agreement between our model and the direct LDA calculations, as shown in Fig. 3. In general, eqn (3) can be modified as follows:
| D = −c(W, Dx)/(1 + 0.01σy). | (6) |
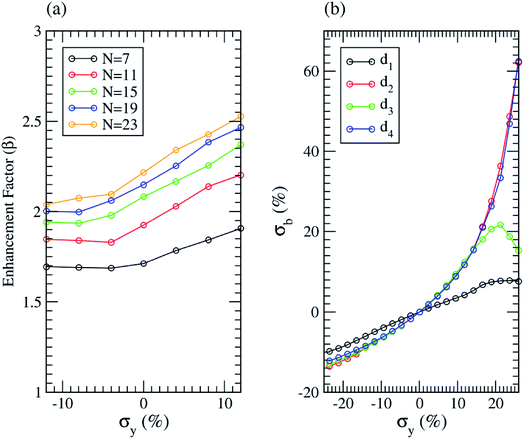
Next, we study how the inter-ribbon distance affects the field enhancement factor of AGNRs. In order to simulate a homogenous external electric field (E) in the z-direction (perpendicular to the edge), as shown in Fig. 1(b), we impose an electric field by applying a classical dipole sheet at the middle of the vacuum region in the z direction. The field enhancement factor (β) is defined as the ratio of the maximum value of the local electric field in the vicinity of the edge of the AGNR to the applied field. The local electric field is determined by the gradient of the Coulomb potential energy difference induced by the applied field. Fig. 5(a) shows the calculated field enhancement factors as a function of inter-ribbon distance for various AGNRs under an electric field of 0.05 V Å−1. When the inter-ribbon distance is smaller than the width of the ribbon, the enhancement factor grows rapidly as Dx increases. When we further increases Dx, the enhancement factor increases slowly and then tends toward saturation. As the inter-ribbon distance becomes much larger than the width of the ribbon, the enhancement factor remains the same as that of an isolated ribbon. This phenomenon is caused by the electrostatic screening effect, which is determined by the width of the ribbons compared to the inter-ribbon distance. When the ribbons are too close to each other for electric field penetration, it will lead to the suppression of the field enhancement. The saturated value of the enhancement factor increases as the ribbon width increases. The dependence of the enhancement factor on the ribbon width W and inter-ribbon distance Dx can be well described by the following expression.39
| β = c1 + c2[1 − exp(−c3(Dx))]. | (7) |
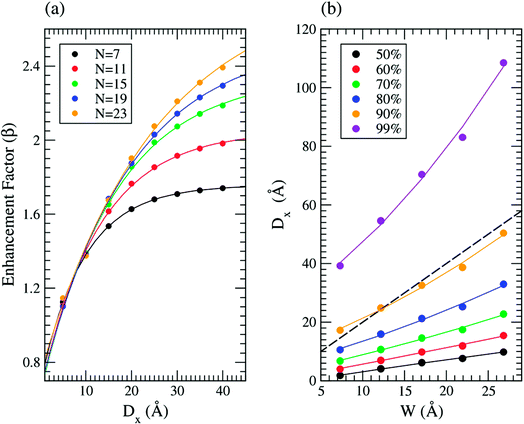 | ||
| Fig. 5 (a) Field enhancement factor β of N-AGNR as a function of inter-ribbon distance under an electric field of E = 0.05 V Å−1. (b) Inter-ribbon distance as a function of ribbon width such that the enhancement factor is 50, 60, 70, 80, 90 and 99% of its saturated value. The solid lines in (a) denote the fitting curves calculated by eqn (1). The solid lines in (b) denote the second degree polynomial curve-fitting results. The dashed line is given by Dx = 2W. | ||
The solid line in Fig. 5(a) is the curve-fitting results. The fitting values of c3 are given by 0.105, 0.077, 0.061, 0.052, and 0.040 Å−1 for N = 7, 11, 15, 19, and 23, respectively. In addition, the saturated β values for AGNR of N = 7, 11, 15, 19, and 23 obtained from the fitting curve are 1.757, 2.051, 2.346, 2.537 and 2.835, respectively. Compared to that of ZGNR40 with a similar width, the saturated field enhancement factor of AGNR is smaller.
In order to describe the screening effect more quantitatively, we calculate the value of Dx such that the enhancement factor is 50, 60, 70, 80, 90 and 99% of its saturated value for various ribbon widths, using the curve-fitting results from Fig. 5(a). The results are shown in Fig. 5(b). The solid line in Fig. 5(b) is the second degree polynomial curve-fitting result. The enhancement factor almost reaches 90% of its saturated value as Dx → 2W. In comparison, for the case of ZGNR, the wider the ribbon, the larger the ratio of the inter-ribbon distance and ribbon width (Dx/W > 2) which is needed to suppress the screening effect.40 However, if one would like to suppress 99% of screening effect (purple line), according to the figure, then the wider the ribbon, the larger the ratio of the inter-ribbon distance and ribbon width (Dx/W) is needed.
Finally, we consider the strain effect on the field enhancement factor of AGNRs. Fig. 6(a) shows the calculated field enhancement factors as a function of strain for various N-AGNRs under an electric field of 0.05 V Å−1. For a tensile strain, the field enhancement factor increases with the applied strain while for a compress one, the field enhancement factor is almost independent. It can be explained by considering the edge distortion of geometry configuration due to the applied strain. In Fig. 1(a), d1 represents the axial bonds on the armchairs, d3 represents that under the armchairs, and d2 and d4 are the bond lengths between the armchairs. As one can see in Fig. 6(b), d2 and d4 are prolonged more than d1 under a tensile strain while the length contractions of the two are similar under a compress strain. For the former case, the local field enhancement effect of the armchair would be enhanced due to the increase of intra-armchair distance (d2 and d4) which suppresses the intralayer screen effect. For the latter case, the variation of these bonds is relatively similar so the field enhancement is nearly independent.
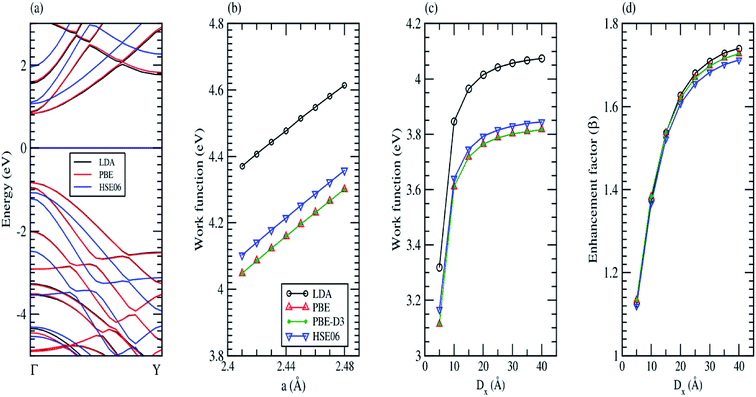
It is well-known that LDA underestimates the band gap of semiconductors. On the other hand, the hybrid function of HSE06 has been shown to accurately reproduce experimental band gaps for a wide variety of materials. In the following, we will investigate how the HSE06 approach affects the effects of the inter-ribbon distance and strain on the work function and field enhancement factor. Because the HSE06 calculations are very time consuming, we will only consider the AGNRs with N = 7. Fig. 7(a) shows the band structure of 7-AGNR with Dx = 10 Å calculated by LDA, PBE, and HSE06. We observe from Fig. 7(a) that there are only slight differences between the LDA bands and the PBE bands. However, the HSE06 calculations show a band gap of 2.13 eV, which is about 1.67 eV larger than the band gap calculated by LDA in good agreement with the previous study.34 It is of interest to note that the valence (conduction) band shift downwards (upwards) without significant change in the band dispersion. Fig. 7(b) shows the work function of graphene as a function of the lattice constant of the unit cell calculated by LDA and PBE. The optimized lattice constant, which was determined by minimizing the total energy of the graphene sheet, are 2.44 Å and 2.46 Å for the calculation of LDA and PBE, respectively. The experimental value of the work function is 4.5 eV. Therefore, LDA provide a better description of the work function of graphene. Fig. 7(c) shows the work function of 7-AGNR as a function of inter-ribbon distance calculated by LDA, PBE, and HSE06. The work functions calculated by PBE are very close to those calculated by HSE06. The work function of 7-AGNR with different inter-ribbon distance calculated by LDA is about 0.25 eV higher than that calculated by PBE, which is consistent with the results of graphene. Fig. 7(d) shows the field enhancement factors of 7-AGNR as a function of inter-ribbon distance calculated by LDA, PBE, and HSE06. The field enhancement factors calculated by the three methods are almost the same. One might wonder the van der Waals force between layers may be important to consider in the AGNRs system. In order to verify this, the method of dispersion correction as an add-on to DFT, namely, DFT-D is used and PBE-D2![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 41,42 and PBE-D3
41,42 and PBE-D3![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 43 are used to study the 7-AGNR arrays for comparison. In order to make sure we correctly use the PBE-D2 and PBE-D3, we used the case of graphite whose equilibrium interlayer distance between graphenes was determined experimentally44 to be 6.707 Å and theoretically to be 8.84 Å and 6.45 Å, respectively, by PBE and PBE-D2.42 In our calculations, we found the equilibrium interlayer distance in graphite is determined to be 6.75 A, 8.85 Å, and 6.45 Å, respectively, using PBE-D3, PBE, and PBE-D2, giving good agreement with the former work. It is expected that the prediction of PBE-D3 is more accurate and very close to the experimental value. Then the PBE-D3 calculations are performed to study the work function of graphene under strain, giving the same result as that calculated by PBE, as shown in Fig. 7(b). The work function and field enhancement factor for the case of 7-AGNR arrays are calculated as a function of inter-ribbon distance using PBE-D3 and the corresponding results are also shown in Fig. 7(c) and (d), respectively. As one can see, the PBE-D3 results agree with the PBE ones very well. This means that the van der Waals force is comparatively weak in the AGNRs as the interlayer distance under study in this work is ranged from 5 Å to 40 Å. However, if one would like to study a closer interlayer distance, then PBE-D2 and PBE-D3 should be considered.
43 are used to study the 7-AGNR arrays for comparison. In order to make sure we correctly use the PBE-D2 and PBE-D3, we used the case of graphite whose equilibrium interlayer distance between graphenes was determined experimentally44 to be 6.707 Å and theoretically to be 8.84 Å and 6.45 Å, respectively, by PBE and PBE-D2.42 In our calculations, we found the equilibrium interlayer distance in graphite is determined to be 6.75 A, 8.85 Å, and 6.45 Å, respectively, using PBE-D3, PBE, and PBE-D2, giving good agreement with the former work. It is expected that the prediction of PBE-D3 is more accurate and very close to the experimental value. Then the PBE-D3 calculations are performed to study the work function of graphene under strain, giving the same result as that calculated by PBE, as shown in Fig. 7(b). The work function and field enhancement factor for the case of 7-AGNR arrays are calculated as a function of inter-ribbon distance using PBE-D3 and the corresponding results are also shown in Fig. 7(c) and (d), respectively. As one can see, the PBE-D3 results agree with the PBE ones very well. This means that the van der Waals force is comparatively weak in the AGNRs as the interlayer distance under study in this work is ranged from 5 Å to 40 Å. However, if one would like to study a closer interlayer distance, then PBE-D2 and PBE-D3 should be considered.
Fig. 8(a) shows the work function of 7-AGNR with Dx = 10 Å as a function of strain calculated by LDA, PBE, and HSE06. The work function of 7-AGNR with different strain calculated by LDA is about 0.25 eV higher than that calculated by PBE while that calculated by HSE06 is slightly larger than PBE. The enhancement factors calculated by LDA, PBE, and HSE06 exhibit a similar dependence on the strain. Fig. 8(b) shows the enhancement factor of 7-AGNR as a function of strain under an electric field of E = 0.1 V Å−1 calculated by LDA, PBE, and HSE06. The enhancement factors calculated by LDA, PBE, and HSE06 exhibit a similar dependence on a compressive strain. Although the LDA shows some discrepancy with PBE and HSE06 under a tensile strain, the qualitative results are the same and the maximum discrepancy is ∼10% for the largest strain we applied in this study. However, it is hard to say which method is more accurate for calculating the local electric fields. In general, we notice that the PBE and HSE06 results show a very similar trend to the LDA results. Therefore, although the LDA calculation underestimated the band gaps of AGNRs, the LDA results shown in Fig. 5 and 6 can provide good qualitative descriptions of the screening and strain effects, respectively, on the field enhancement of AGNR arrays under an external electric field. Similarly, the effects of strain and inter-ribbon distance on work functions of AGNR arrays calculated by the LDA, as shown in Fig. 3 and 4, respectively, will be closer to experimental results than either PBE or HSE06 predictions.
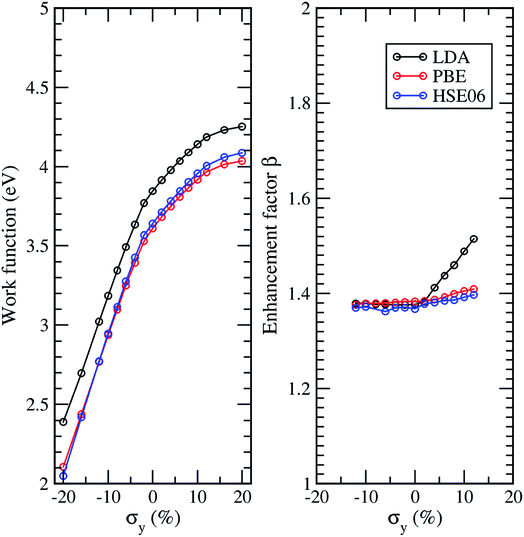 | ||
| Fig. 8 (a) Work function and (b) field enhancement factor β of 7-AGNR as a function of strain under an electric field of E = 0.1 V Å−1 calculated by LDA, PBE, and HSE06. | ||
Conclusions
In conclusion, we have systematically investigated the strain effect on the work function of the armchair graphene nanoribbons using first-principles density functional theory. Using the zone folding method with the effect of dipole barrier along with the work function of strained graphene, we can obtain the work function of AGNR of any width under strain, in good agreement with the direct LDA calculations. The effect of interlayer distance on the work function and field enhancement factor is also investigated. We found that the work function of AGNRs increases rapidly as inter-ribbon distance Dx increases, which is caused by the positive dipole array at the edge of the ribbon. For a given Dx, the work function of AGNRs increases as the width of the ribbon increases. The wider the ribbon, stronger the effect of Dx on the work function. The field enhancement increases rapidly when the inter-ribbon distance increases as long as Dx < W. When we further increase Dx, the field enhancement increases slowly and then tends toward saturation. For a tensile strain, the field enhancement factor increases with the applied strain while for a compress one, the field enhancement factor is nearly independent. The effects of inter-ribbon and strain on enhancement factor can be explained by the interlayer and intralayer screening effects, respectively. Our findings not only provide an insight into understanding the screening effect on the characteristics of the strained AGNRs, but also provide a guideline for their efficient application in field emission devices.Method of calculation
The calculations were performed by the density functional theory (DFT)45 and the local density approximation (LDA)46 using the Ceperley–Alder form of exchange-correlation functional47 with a plane wave cutoff of 286 eV, as implemented in the Vienna ab initio simulation package (VASP).48–50 For Brillouin-zone integrations, the 1 × 20 × 1 k-points mesh with gamma centered grid is utilized for all systems studies. The atomic positions were relaxed until the magnitudes of the forces became less than 0.02 eV Å−1. To investigate how the exchange-correlation functionals affect the effect of the inter-ribbon distance on the work function, field enhancement factor, and band gap as well as the Fermi energy. The generalized-gradient approximation (GGA) with the Perdew–Burke–Ernzerhof functional (PBE)51 and hybrid functional (HSE06)52 together with the projector augmented wave (PAW) method are used to study 7-AGNRs. The method of dispersion correction as an add-on to DFT, namely, DFT-D has been used to verify if the van der Waals force between layers is important in the AGNRs system under study. Both the PBE-D2![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 41,42 and PBE-D3
41,42 and PBE-D3![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 43 are used to study the equilibrium interlayer distance in graphite for comparison while the more accurate PBE-D3 is used to study the 7-AGNR arrays to see the effect of the van der Waals force in the AGNR arrays.
43 are used to study the equilibrium interlayer distance in graphite for comparison while the more accurate PBE-D3 is used to study the 7-AGNR arrays to see the effect of the van der Waals force in the AGNR arrays.
Conflicts of interest
The authors declare no competing financial interests.Author contributions
T. C. Leung and S. M. Loh conceived and initiated the study. H. Hu and S. M. Loh performed first principles calculations and contributed equally to this study. H. Hu, S. M. Loh, T. C. Leung, and M. C. Lin performed the detailed analysis and contributed the discussions. H. Hu, S. M. Loh, T. C. Leung, and M. C. Lin wrote the manuscript. All authors reviewed the manuscript.Acknowledgements
T. C. Leung wishes to acknowledge that his contribution to this study began during a visit to the State Key Laboratory of Surface Physics of Fudan University. The authors acknowledge the National Center for Theoretical Sciences in Taiwan and financial supports from the Ministry of Science and Technology of Taiwan (MOST) under Grant No. MOST-106-2112-M-194-004, Hanyang University (HY-201400000002393), and the National Research Foundation of Korea. The authors are grateful to the National Center for High-Performance Computing (NCHC) for computer time and facilities.References
- X. S. Li, W. W. Cai, J. An, S. Kim, J. Nah, D. X. Yang, R. Piner, A. Velamakanni, I. Jung, E. Tutuc, S. K. Banerjee, L. Colombo and R. S. Ruoff, Science, 2009, 324, 1312 CrossRef PubMed.
- Y. W. Tan, Y. Zhang, K. Bolotin, Y. Zhao, S. Adam, E. H. Hwang, S. D. Sarma, H. L Stormer and P. Kim, Phys. Rev. Lett., 2007, 99, 246803 CrossRef PubMed.
- J. N. Hu, X. L. Ruan and Y. P. Chen, Nano Lett., 2009, 9, 2730 CrossRef PubMed.
- A. A. Balandin, S. Ghosh, W. Z. Bao, I. Calizo, D. Teweldebrhan, F. Miao and C. N. Lau, Nano Lett., 2008, 8, 902 CrossRef PubMed.
- M. Fujita, K. Wakabayashi and K. Nakada, J. Phys. Soc. Jpn., 1996, 65, 1920 CrossRef.
- K. Nakada, M. Fujita, G. Dresselhaus and M. S. Dresselhaus, Phys. Rev. B, 1996, 54, 17954 CrossRef.
- M. Fujita, M. Igami and K. Nakada, J. Phys. Soc. Jpn., 1997, 66, 1864 CrossRef.
- K. Wakabayashi, M. Fujita, H. Ajiki and M. Sigrist, Phys. Rev. B, 1999, 59, 8271 CrossRef.
- K. Wakabayashi and M. Sigrist, Phys. Rev. Lett., 2000, 84, 3390 CrossRef PubMed.
- S. L. Chang, S. Y. Lin, S. K. Lin, C. H. Lee and M. F. Lin, Sci. Rep., 2014, 4, 6038 CrossRef PubMed.
- K. A. Ritter and J. W. Lyding, Nat. Mater., 2009, 8, 235 CrossRef PubMed.
- Y. W. Son, M. L. Cohen and S. G. Louie, Phys. Rev. Lett., 2006, 97, 216803 CrossRef PubMed.
- J. J. Chen, H. C. Wu, D. Yu and Z. M. Liao, Nanoscale, 2014, 6, 8814 RSC.
- Y.-W. Son, M. L. Cohen and S. G. Louie, Nature, 2006, 444, 347 CrossRef PubMed.
- E. Rudberg, P. Salek and Y. Luo, Nano Lett., 2007, 7, 2211 CrossRef PubMed.
- L. Yang, C.-H. Park, Y.-W. Son, M. L. Cohen and S. G. Louie, Phys. Rev. Lett., 2007, 99, 186801 CrossRef PubMed.
- M. Ryzhii and V. Ryzhii, Phys. Rev. B, 2010, 82, 075419 CrossRef.
- V. Ryzhii, M. Ryzhii, N. Ryabova, V. Mitin and T. Otsuji, Infrared Phys. Technol., 2011, 54, 302 CrossRef.
- S. M. Loh, Y. H. Huang, K. M. Lin, W. S. Su, B. R. Wu and T. C. Leung, Phys. Rev. B, 2014, 90, 035450 CrossRef.
- L. Yang and J. Han, Phys. Rev. Lett., 2000, 85, 154 CrossRef PubMed.
- R. Heyd, A. Charlier and E. McRae, Phys. Rev. B, 1997, 55, 6820 CrossRef.
- D. Xiao, W. Yao and Q. Niu, Phys. Rev. Lett., 2007, 99, 236809 CrossRef PubMed.
- W. Yao, D. Xiao and Q. Niu, Phys. Rev. B, 2008, 77, 235406 CrossRef.
- G. Gui, J. Li and J. X. Zhong, Phys. Rev. B, 2008, 78, 075435 CrossRef.
- E. L. Murphy and R. H. Good, Phys. Rev., 1956, 102, 1464 CrossRef.
- C. A. Spindt, I. Brodie, L. Humphrey and E. R. Westerberg, J. Appl. Phys., 1976, 47, 5248 CrossRef.
- M. C. Lin, J. Vac. Sci. Technol., B: Microelectron. Nanometer Struct.--Process., Meas., Phenom., 2007, 25, 493 CrossRef.
- Y. Shi, K. K. Kim, A. Reina, M. Hofmann, L. J. Li and J. Kong, ACS Nano, 2010, 4, 2689 CrossRef PubMed.
- G. Giovannrtti, P. A. Khomyakov, G. Brocks, V. M. Karpan, J. van den Brink and P. J. Kelly, Phys. Rev. Lett., 2008, 101, 026803 CrossRef PubMed.
- P. A. Khomyakov, G. Giovannetti, P. C. Rusu, G. Brocks, J. van den Brink and P. J. Kelly, Phys. Rev. B, 2009, 79, 195425 CrossRef.
- G. Eda, H. E. Unalan, N. Rupesinghe, G. A. J. Amaratunga and M. Chhowalla, Appl. Phys. Lett., 2008, 93, 233502 CrossRef.
- X. H. Peng, F. Tang and A. Copple, J. Phys.: Condens. Matter, 2012, 24, 075501 CrossRef PubMed.
- X. Peng, F. Tang and A. Copple, J. Phys.: Condens. Matter, 2012, 24, 075501 CrossRef PubMed.
- V. Barone, O. Hod and G. E. Scuseria, Nano Lett., 2006, 6, 2748 CrossRef PubMed.
- L. Nilsson, O. Groening, C. Emmenegger, O. Kuettel, E. Schaller, L. Schlapbach, H. Kind, J.-M. Bonard and K. Kern, Appl. Phys. Lett., 2000, 76, 2071–2073 CrossRef.
- D. G. Kvashnin, P. B. Sorokin, J. W. Brüning and L. A. Chernozatonskii, Appl. Phys. Lett., 2013, 102, 183112 CrossRef.
- G. Giovannetti, P. A. Khomyakov, G. Brocks, V. M. Karpan, J. van den Brink and P. J. Kelly, Phys. Rev. Lett., 2008, 101, 026803 CrossRef PubMed.
- C. Oshima and A. Nagashima, J. Phys.: Condens. Matter, 1997, 9, 1 CrossRef.
- P. E. Blöchl, Phys. Rev. B, 1994, 50, 17953 CrossRef.
- H. Hu, T. C. Lin, T. C. Leung and W. S. Su, Phys. Chem. Chem. Phys., 2018, 20, 14627 RSC.
- S. Grimme, J. Comput. Chem., 2006, 27, 1787 CrossRef PubMed.
- T. Bučko, J. Hafner, S. Lebègue and J. Ángyán, J. Phys. Chem. A, 2010, 114, 11814 CrossRef PubMed.
- S. Grimme, J. Antony, S. Ehrlich and H. Krieg, J. Chem. Phys., 2010, 132, 154104 CrossRef PubMed.
- Y. X. Zhao and I. L. Spain, Phys. Rev. B: Condens. Matter Mater. Phys., 1989, 40, 993 CrossRef.
- P. Hohenberg and W. Kohn, Phys. Rev., 1964, 136, B864 CrossRef.
- W. Kohn and L. J. Sham, Phys. Rev., 1965, 140, A1133 CrossRef.
- D. M. Ceperley and B. J. Alder, Phys. Rev. Lett., 1980, 45, 566 CrossRef.
- G. Kresse and J. Hafner, J. Phys.: Condens. Matter, 1994, 6, 8245 CrossRef.
- G. Kresse and J. Furthmüller, Phys. Rev. B, 1996, 54, 11169 CrossRef.
- G. Kresse and D. Joubert, Phys. Rev. B, 1999, 59, 1758 CrossRef.
- J. Perdew, K. Burke and M. Ernzrhof, Phys. Rev. Lett., 1996, 77, 3865 CrossRef PubMed.
- J. Heyd, G. E. Scuseria and M. Ernzerhof, J. Chem. Phys., 2003, 118, 8207 CrossRef.
| This journal is © The Royal Society of Chemistry 2018 |