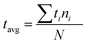Open Access Article
Open Access ArticleEvaporation dynamics of liquid marbles at elevated temperatures†
Kamalalayam Rajan Sreejith,
Chin Hong Ooi,
Dzung Viet Dao and
Nam-Trung Nguyen *
*
Queensland Micro- and Nanotechnology Centre, Griffith University, 170 Kessels Road, 4111 Queensland, Australia. E-mail: nam-trung.nguyen@griffith.edu.au
First published on 24th April 2018
Abstract
Study of evaporation dynamics of liquid marbles at elevated temperature is essential to determine the feasibility of liquid marbles to be used as micro compartments for digital polymerase chain reaction (PCR). We have modified an existing theoretical model of evaporation of a liquid droplet and verified its applicability on the evaporation of liquid marbles. The evaporation dynamics of an individual and a group of liquid marbles are analysed. This paper demonstrates that the evaporation dynamics of liquid marbles obeys the theoretical framework for elevated temperatures. The evaporation of a group of liquid marbles are observed as a coupled function of their diameter, their number in a group, the vapour density of the surrounding atmosphere and their spatial distribution.
1. Introduction
Liquid marbles are formed by coating liquid droplets with fine particles of hydrophobic materials. This coating enables the liquid droplet to hold its spherical shape even under a relatively high mechanical stress. Moreover, the hydrophobic particle coating helps to isolate the liquid droplet from the surrounding environment reducing the possible contamination of the sample inside the liquid marble. Being inert, the hydrophobic material coating does not react with the liquid sample, making it suitable to carry out chemical reactions. The manipulation of liquid marbles in terms of mobility can be effectively achieved by gravitational,1 electrostatic2,3 or magnetic methods.4–7 With these capability, liquid marbles find applications in gas/pollution sensing,8,9 micro-pumps,10 biochemical reactions,4,5 genetic analysis and lab on chip devices.11 Excellent reviews and articles have been published on the properties, applications and mobility manipulation techniques of liquid marbles.12–18 Significant advancement in cell biology, bioengineering and biomedicine have been achieved recently using liquid marbles.13,18–21 Arbatan et al. successfully verified the use of liquid marbles as bioreactor for rapid blood typing.22 Sarvi et al. demonstrated the usage of liquid marbles as a bioreactor for cardio genesis of embryonic stem cells.23 Serrano et al. used liquid marbles as a cryopreservation tool for mammalian cells.24 The porosity of liquid marble surface was successfully utilized by Tian et al. for the cultivation of microorganisms.25Though much advancement has been achieved in exploring the possibilities of liquid marbles as a reactor for biological and chemical reactions, vast application areas are still unexplored, such as polymerase chain reaction (PCR). In terms of technology, there has been a leap in the field of PCR since its invention. Qualitative PCR (qPCR) and digital PCR are the two prominent techniques to perform DNA amplification.26 In qPCR, the products are continuously monitored throughout the reaction cycles using fluorescent dyes. The quantity of a target DNA can be found by comparing the fluorescent output curve with a standard curve. In digital PCR, the reaction mixture is compartmentalised into several smaller units. Each unit undergoes the same thermal cycles as in the case of a conventional qPCR. Each unit is expected to have one or more template DNA and some unit may not even contain a template DNA. The units which had undergone a positive PCR can be identified by fluorescent dyes. A positive florescence from a unit is regarded as ‘1’ while the negative fluorescence (no fluorescence) is considered to be a ‘0’ similar to signals in digital electronics.27,28 Digital PCR techniques are gaining the attention of researchers and practitioners recently.29–33 Better accuracy, high throughput and efficiency in preventing cross contamination are the main reasons behind the popularity of digital PCR techniques. Liquid sample containing PCR reagents along with DNA templates and fluorescent dyes can be coated with hydrophobic particles to form a liquid marble based digital PCR micro reactor. Liquid marbles can be an ideal candidate for being a micro-reactor to carry out PCR because of their self-sustainability, ability to prevent contamination, availability of various manipulation techniques16 and ease of handling. The major constraint in using liquid marble as a micro-compartment for PCR is the possibility of evaporation of reactants through the semi permeable membrane of the liquid marble. Evaporation is expected as the polymerase chain reaction can be only achieved by a sequence of thermal cycling with temperature ranging from 55 °C to 95 °C.34 In this context, it is essential to study the evaporation of liquid marble at elevated temperatures.
It is also essential to understand the evaporation behaviour of a group of liquid marbles at elevated temperatures. The present paper discusses the evaporation behaviour of individual and a group of liquid marbles at elevated temperatures. The paper also demonstrates a method to increase the lifetime of liquid marbles and makes it suitable for biochemical reactions at elevated temperatures such as PCR.
2. Theoretical background
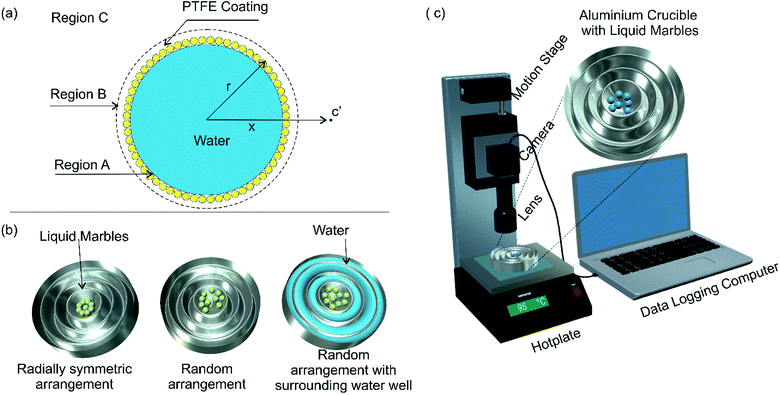
A few studies have been carried out by various research groups on the evaporation of liquid marbles under different conditions. Most of these studies were carried out to analyse the evaporation dynamics of liquid marbles at room temperature and atmospheric pressure.11,35–40 Moreover, not many researchers had attempted to evaluate the evaporation process of a group of liquid marbles. These studies do not provide useful information on the feasibility of liquid marbles for polymerase chain reaction. In this context, we are adapting an existing model of liquid droplet evaporation and modifying it to fit the physical characteristics of liquid marbles. Fig. 1(a) shows the model of a liquid marble. The evaporation mechanism of a liquid marble can be considered as a two-step process. The region close to the liquid marble surface (region B) would be uniformly saturated with liquid vapour if the hydrophobic coating of the marble is thin and uniform.The vapour molecules in region B would be topped up from liquid molecules in region A (liquid state) as the diffusion from B to C progresses, maintaining a dynamic equilibrium of mass transport from A to B and subsequently to C. Therefore, the factor determining the evaporation rate of liquid marble is the diffusion rate from region B to C. We hypothesize that the hydrophobic coating of liquid marble offers a constant resistance to the evaporation process as compared to an ordinary liquid droplet. At any given instance, the mass flux at the radial location x (represented to an arbitrary point c′ in Fig. 1(a)) around a liquid marble can be described as41
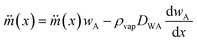 | (1) |
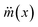 is the mass flux of liquid vapour, wA is the mass fraction of liquid vapour at corresponding point, ρvap is the density of liquid vapour phase, DWA is the binary diffusivity of liquid in the air and
is the mass flux of liquid vapour, wA is the mass fraction of liquid vapour at corresponding point, ρvap is the density of liquid vapour phase, DWA is the binary diffusivity of liquid in the air and 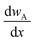 is the mass fraction gradient in space. The total mass of a liquid marble (mLM) is the combined mass of liquid droplet (mL) and mass of the hydrophobic coating (mH).
is the mass fraction gradient in space. The total mass of a liquid marble (mLM) is the combined mass of liquid droplet (mL) and mass of the hydrophobic coating (mH).| mLM = mL + mH | (2) |
Since the mass reduction in liquid marble during evaporation is only due to the evaporation of water, the change in mass of hydrophobic coating, mH over time is zero. Thus the rate of change mass can be represented as
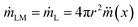 | (3) |
Substituting 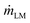 in the expression for
in the expression for 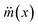 and rearranging result in
and rearranging result in
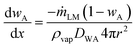 | (4) |
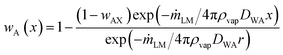 | (5) |
The mass fraction of liquid vapour in the region close to the particle coating (x → r) of the liquid marble is wAS and at infinity (x → ∞) is wA∞. The mass fraction of liquid vapour in the bulk atmosphere is taken as wA∞ in all practical cases. Applying these boundary conditions and solving for mass rate of the liquid marble yield:
 | (6) |
Since the mass reduction is due to the evaporation of the liquid inside the marble, the rate of change of mass can be approximated as
 | (7) |
 | (8) |
 | (9) |
This is similar to the d2 law of droplet evaporation. It shows that the liquid marble obeys d2 law of evaporation and the rate of surface regression depends on the initial diameter of the marble and the mass fraction of vapour at infinity. But this theoretical model has not considered the possible attenuation caused by the thin hydrophobic layer covering the liquid droplet. For a uniform and thin hydrophobic coating, we can assume a constant attenuation. We can then rewrite eqn (9) as
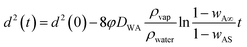 | (10) |
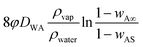 is the surface and known as the regression coefficient (k) that has a dimension of m2 s−1.
is the surface and known as the regression coefficient (k) that has a dimension of m2 s−1.
3. Materials and methods
3.1 Preparation of the aluminium crucible as water reservoir
An aluminium crucible with customized size and shape was made for efficient heat transfer and to ensure repeatability of the experiments. A concentric well-shaped mould was designed in 123D software (Autodesk Inc) and 3D printed using Nobel 1.0 advanced SL printer (XYZ Printing). Heavy duty aluminium foil (Alcan foil Products) of 0.024 mm thickness was pressed over the mould to make aluminium crucible for the experiment. The aluminium crucible thus obtained was fixed on to a 75 × 50 × 2 mm glass plate to avoid accidental physical deformation during the experiments. The central cavity of the crucible was designed to keep the liquids marbles while other surrounding cavities were designed to carry water for later experiments, Fig. 1(b). The diameter of the central cavity was 14 mm. The concentric well shaped structure provides controllability on the amount of water around the liquid marbles.3.2 Preparation of liquid marbles
Liquid marbles were formed by dispensing and subsequent rolling of deionised water droplets on a bed of polytetrafluoroethylene (PTFE) powder (Sigma-Aldrich, 1 μm nominal diameter, ρ = 2.2 g cm−3). A micropipette (model CH 02607 by Thermo electron corporation) was used for droplet dispensing as it provides good controllability on the volume and the diameter of the droplet. Liquid marbles with 2 μl, 5 μl and 10 μl volumes were prepared for the experiments.3.3 Experimental setup and procedures
The required number of liquid marbles for each experiment was transferred to the aluminium crucible. The crucible was subsequently transferred to a hotplate with a stabilised temperature value. The top view of the liquid marbles was recorded with a CMOS USB camera and a telecentric (0.5× and 0.3×) lenses (model: 63074, Edmund Optics). A motorized stage (Zaber technologies T-LS 28M) was used for fine focusing throughout the experiments. Fig. 1(c) shows the schematic of the experimental setup. The diameter of liquid marbles was measured by comparing the liquid marble image with a calibrated scale using ImageJ software. All the experiments were carried out in the air conditioned laboratory environment (24 ± 1 °C temperature, 50 ± 2% relative humidity and atmospheric pressure) until there was a visible buckling on the liquid marbles. The time at which buckling is visible on the liquid marble is termed as buckling time (tb). We consider tb as the lifetime of liquid marble in this paper.4. Results and discussion
4.1 Temperature dependence of evaporation
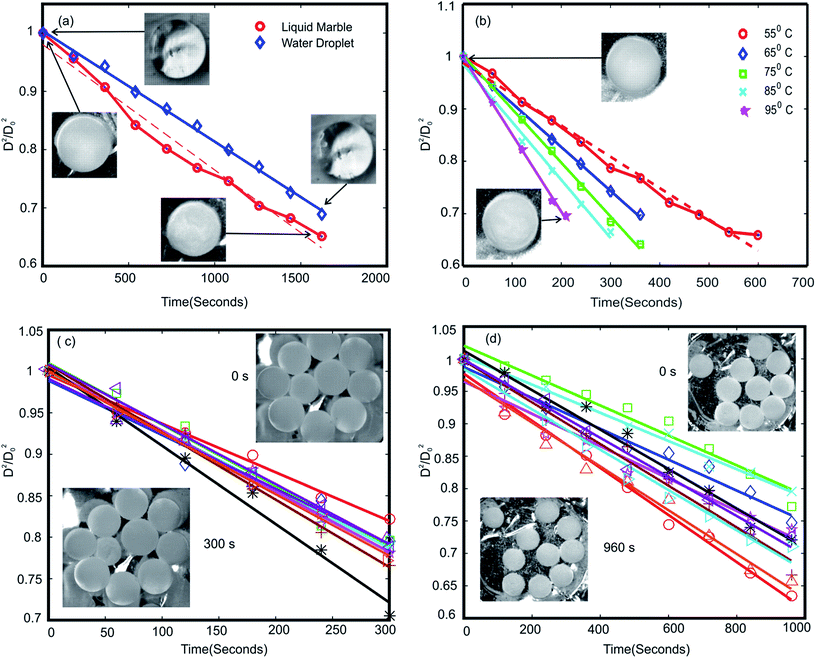
Fig. 2(a) shows the change of the normalised diameter of a water droplet and a liquid marble. The behaviour of water droplet was in accordance with the d2 law, whereas the liquid marble exhibited a nonlinear behaviour. The dotted lines represent the least square fit of liquid marble surface regression. The R2 value of the fitted line was 0.9968 for water droplet and 0.98 for liquid marble. Average surface regression rate (k) observed for the liquid marble is 1.2 times higher than the corresponding water droplet. This indicates that the liquid marble evaporates faster compared to uncoated water droplet of similar volume. A few research groups have reported a longer lifetime for liquid marbles compared to pure droplets of similar volume.11,38 They concluded that the hydrophobic coating is offering a barrier effect for the evaporation of water in the liquid marble which in turn reduces the rate of evaporation. Conversely, Laborie et al. reported a higher evaporation rates for liquid marbles with thin hydrophobic coating compared to similar water droplets. They had pointed out two effects that cause faster drying: (i) water loss rate through a layer of dense micro particles is almost the same as the one from bare interface; (ii) the solid particles lead to incompressibility of the interface whose area remains constant over the drying process. Thus, liquid marbles covered with a monolayer particles exhibit a larger interface than liquid droplets and dry faster.36 From these studies, we conclude that at room temperature the rate of evaporation of a liquid marble compared to a corresponding bare liquid droplet is related to the thickness of the hydrophobic coating. Liquid marbles with a thick hydrophobic coating evaporates slower while that with a thin or monolayer of hydrophobic coating evaporates faster compared to a corresponding uncoated liquid droplet. Our experiment showed a higher surface regression rate for liquid marbles compared to its uncoated counterpart at room temperature.
A heterogeneous hydrophobic coating of liquid marble may lead to non-homogeneous evaporation of water through the coating, in turn causing the marble to deviate from d2 law. At higher temperature, water molecules on the surface will get sufficient kinetic energy to evaporate through the hydrophobic coating, almost uniformly through the hydrophobic surface. This may be the reason for liquid marbles to exhibit constant surface regression rate at higher temperatures. The surface regression rate k of liquid marbles at various temperatures is shown in Table 1. Liquid marbles with 2 μl and 5 μl volume was also tested at 95 °C to ensure the behaviour at elevated temperature. The results exhibited good alliance with d2 law. The buckling time for 2 μl, 5 μl and 10 μl was 2 minutes, 3 minutes and 3.5 minutes (see ESI, Movie S1†) respectively at 95 °C.
| Condition | Number of marbles | Temperature (°C) | k × 10−9 m2 s−1 |
|---|---|---|---|
| 10 μl water droplet | 1 | 25 | 1.4 |
| 10 μl liquid marble | 1 | 25 | 1.7 |
| 55 | 4.5 | ||
| 65 | 6.6 | ||
| 75 | 8.1 | ||
| 85 | 8.7 | ||
| 95 | 11.6 | ||
| 10 | 95 | 5.0 ± 0.7 | |
| 10 μl liquid marble with surrounding water well | 10 | 95 | 2.1 ± 0.4 |
4.2 Evaporation of a group of liquid marbles
Evaporation behaviour of a group of liquid marbles is vital as the PCR application is a high throughput process. Ten liquid marbles with volumes of 5 μl and 10 μl respectively were heated at 95 °C to analyse their group evaporation dynamics. The change in diameter was noted until visible buckling was observed on any one of the liquid marbles in the group. The average change in the square of the diameter is plotted against time, Fig. 2(c). The results showed good agreement with the d2 law model. The average surface regression rate was lesser compared to a single liquid marble with similar volume leading to an extended average buckling time (tavg). The decrease in surface regression rate and rise in average buckling time of grouped liquid marbles compared to their single counterpart can be attributed to the general evaporation dynamics discussed in the theory section. The transport of water molecules from region A to B is governed by the diffusion of water vapour from B to C, Fig. 1(a). In a group setting, region B of the marble group becomes saturated rapidly with very little evaporation from individual liquid marbles whereas the diffusion from B to C remains almost constant. Thus the rate of water loss from individual liquid marble is lower, leading to lower surface regression rate and extended the average buckling time.The above hypothesis can be extended with three further hypotheses: (i) the average buckling time (life time) of a group of liquid marbles can be increased by increasing the number of liquid marbles in the group; (ii) the liquid marbles situated at the edges in a group are expected to buckle faster compared to those in the centre since the diffusion of water vapour from region B to C through their outward facing surface might be higher. This may decrease the average buckling time of the group; (iii) the average buckling time can be extended if the liquid marbles are kept in a vapour saturated environment.
To verify the first hypothesis, a group of 5, 10 and 20 liquid marbles of 5 μl and 10 μl volumes were heated at a constant temperature of 95 °C (see ESI, Movie S2†). The marbles were continuously monitored for visible buckling. Average buckling time was calculated after observing visible buckling on each marble in the group. Average buckling time of the group is calculated as the weighted average time:
| Condition | Volume | Number in a group | Buckling time, tb (minutes) |
|---|---|---|---|
| Random arrangement | 5 μl | 1 | 3 |
| 5 | 4.9 ± 0.42 | ||
| 10 | 4.4 ± 0.39 | ||
| 20 | 6.5 ± 1.43 | ||
| 10 μl | 1 | 3.5 | |
| 5 | 7.5 ± 0.96 | ||
| 10 | 8.3 ± 1.76 | ||
| 20 | 8.8 ± 1.55 | ||
| Radial symmetry arrangement | 10 μl | 9 | 8.8 ± 1.17 |
| Water well | 10 μl | 10 | 25.2 ± 5.18 |
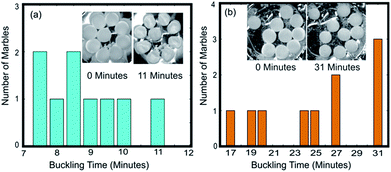
Fig. 3(a–c) show the buckling time histogram of different group of liquid marbles. The histogram shows that 4 out of 5 marbles in the group had buckled between 4.5 and 5 minutes resulting the average buckling time of the group to be 4.9 minutes. On the other hand, 8 out of 10 liquid marbles buckled between 4 and 4.5 minutes leading the weighted average to be 4.4 minutes. We observed that the 8 marbles that buckled during 4–4.5 minutes were relatively distant from the central marble. This observation gives a primary confirmation about the second hypothesis. It can be speculated that the average life time of group of liquid marbles depend on the spatial distribution of liquid marbles.
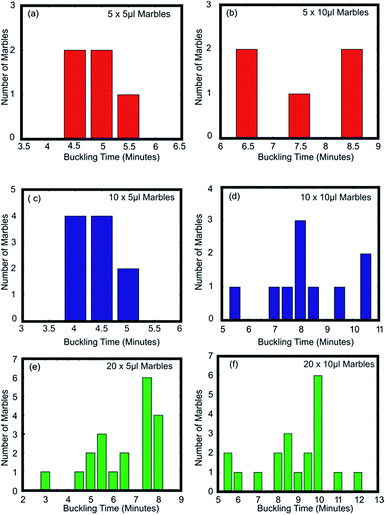 | ||
| Fig. 3 Buckling time histogram of (a) 5 × 5 μl; (b) 5 × 10 μl; (c) 10 × 5 μl; (d) 10 × 10 μl; (e) 20 × 5 μl; and (f) 20 × 10 μl liquid marbles. | ||
We had conducted another experiment to verify the effect of distribution of liquid marbles on their average buckling time and to verify the second hypothesis. Nine liquid marbles of 10 μl each were arranged in the crucible in radial symmetry and heated at a constant temperature of 95 °C (see ESI, Movie S3†). We observed that the rate of change of diameter of the liquid marble at the centre is lower compared to those situated at the edges. The central liquid marble was the last one to buckle. This confirms the second hypothesis. Fig. 4(a) shows the buckling histogram of 9 symmetrically arranged liquid marbles. The average buckling time was noted as 8.8 minutes. The average buckling time of 9 symmetrically arranged liquid marbles is equal to that of 20 randomly distributed marbles and greater than 10 randomly distributed liquid marbles of similar volume. We can conclude that the average buckling time of a group of liquid marbles at elevated temperature is a coupled function of number of liquid marbles and their spatial distribution. It is evident from the experiments that the decrease in average buckling time of a group liquid marbles is due to relative fast evaporation of the liquid marbles on the edge.
4.3 Behaviour of liquid marbles with surrounding water well at elevated temperature
According to the third hypothesis, the average buckling time of the group can be improved by increasing the vapour density in the region around liquid marbles situating at the edges. We conducted the following experiments to verify the effect of increased vapour density on the life time of the liquid marbles.The concentric grooves on the aluminium crucible were filled with water. A single 10 μl liquid marble was kept in the central cavity and the crucible is heated at 95 °C till visible buckling is observed on the marble (see ESI, Movie S4†). The buckling time was 9 minutes whereas the same without surrounding water well was 3.5 minutes. The experiment was repeated with 10 numbers of liquid marbles each with 10 μl volume. The average buckling time of the group was observed as 25.2 minutes whereas it was 8.3 minutes for marbles without surrounding water well. Fig. 4 shows the buckling histogram of the experiment. The average life time of the group was extended three times compared to its counterpart without surrounding water wells. It can also be noted that the buckling of the first liquid marble occurred after 17 minutes while it occurred after 5.5 minutes for the corresponding group without water well. This indicates that the individual buckling time of liquid marbles situating at the edges in group can be extended by providing a vapour saturated environment around it. The extended buckling time of liquid marbles at the edges would extend the average buckling time of the group. We can summarise that the average lifetime of a group of liquid marbles can be extended by heating them in a vapour saturated environment.
5. Conclusions
The present study shows that the evaporation of liquid marbles obeys d2 law at elevated temperatures. The non-homogeneous evaporation of water through the porous hydrophobic coating of the marble might be the reason for liquid marbles to deviate from d2 law at lower temperatures. The d2 law was obeyed for individual as well as grouped liquid marbles from 65 °C to 95 °C. Buckling time of liquid marbles was observed to depend on the number of marbles in the group, vapour density in the surrounding atmosphere and their spatial distribution of liquid marbles in the group. The average buckling time of a group of liquid marbles can be extended by providing a vapour saturated environment around the group of liquid marbles. We conclude that the average life time of a group of liquid marbles and their evaporation behaviour can be accurately predicted with d2 law for liquid marbles with the same diameter and homogeneous spatial distribution under a controlled environment. The present study also reveals the possibility of liquid marbles to survive catastrophic evaporation during the thermal cycles of PCR. More extensive studies on the prediction of life time of grouped liquid marbles and their evaporation dynamics under real PCR thermal cycles would be carried out in future works.Conflicts of interest
There are no conflicts to declare.Acknowledgements
The author acknowledges the Australian Research Council for funding support through the grant DP170100277.References
- L. Mahadevan and Y. Pomeau, Phys. Fluids, 1999, 11, 2449–2453 CrossRef CAS.
- E. Bormashenko, R. Pogreb, R. Balter, O. Gendelman and D. Aurbach, Appl. Phys. Lett., 2012, 100, 151601 CrossRef.
- E. Bormashenko, R. Pogreb, T. Stein, G. Whyman, M. Schiffer and D. Aurbach, J. Adhes. Sci. Technol., 2012, 25, 1371–1377 CrossRef.
- Y. Xue, H. Wang, Y. Zhao, L. Dai, L. Feng, X. Wang and T. Lin, Adv. Mater., 2010, 22, 4814–4818 CrossRef CAS PubMed.
- Y. Zhao, Z. Xu, M. Parhizkar, J. Fang, X. Wang and T. Lin, Microfluid. Nanofluid., 2012, 13, 555–564 CrossRef CAS.
- M. K. Khaw, C. H. Ooi, F. Mohd-Yasin, R. Vadivelu, J. S. John and N. T. Nguyen, Lab Chip, 2016, 16, 2211–2218 RSC.
- L. Zhang, D. Cha and P. Wang, Adv. Mater., 2012, 24, 4756–4760 CrossRef CAS PubMed.
- J. Tian, T. Arbatan, X. Li and W. Shen, Chem. Eng. J., 2010, 165, 347–353 CrossRef CAS.
- J. Tian, T. Arbatan, X. Li and W. Shen, Chem. Commun., 2010, 46, 4734–4736 RSC.
- E. Bormashenko, R. Balter and D. Aurbach, Appl. Phys. Lett., 2010, 97, 091908 CrossRef.
- M. Dandan and H. Y. Erbil, Langmuir, 2009, 25, 8362–8367 CrossRef CAS PubMed.
- D. Quéré and P. Aussillous, Proc. R. Soc. A, 2006, 462, 973–999 CrossRef.
- E. Bormashenko, Langmuir, 2017, 33, 663–669 CrossRef CAS PubMed.
- E. Bormashenko, Curr. Opin. Colloid Interface Sci., 2011, 16, 266–271 CrossRef CAS.
- E. Bormashenko, Soft Matter, 2012, 8, 11018–11021 RSC.
- C. H. Ooi and N.-T. Nguyen, Microfluid. Nanofluid., 2015, 19, 483–495 CrossRef CAS.
- G. McHale and M. I. Newton, Soft Matter, 2015, 11, 2530–2546 RSC.
- N. M. Oliveira, C. R. Correia, R. L. Reis and J. F. Mano, Adv. Healthcare Mater., 2015, 4, 264–270 CrossRef CAS PubMed.
- R. K. Vadivelu, H. Kamble, A. Munaz and N. T. Nguyen, Biomed. Microdevices, 2017, 19, 31 CrossRef PubMed.
- E. Bormashenko, R. Balter and D. Aurbach, Int. J. Chem. React. Eng., 2011, 9, 1 Search PubMed.
- R. K. Vadivelu, C. H. Ooi, R. Q. Yao, J. Tello Velasquez, E. Pastrana, J. Diaz-Nido, F. Lim, J. A. Ekberg, N. T. Nguyen and J. A. St John, Sci. Rep., 2015, 5, 15083 CrossRef CAS PubMed.
- T. Arbatan, L. Li, J. Tian and W. Shen, Adv. Healthcare Mater., 2012, 1, 80–83 CrossRef CAS PubMed.
- F. Sarvi, T. Arbatan, P. P. Y. Chan and W. Shen, RSC Adv., 2013, 3, 14501 RSC.
- M. C. Serrano, S. Nardecchia, M. C. Gutierrez, M. L. Ferrer and F. del Monte, ACS Appl. Mater. Interfaces, 2015, 7, 3854–3860 CAS.
- J. Tian, N. Fu, X. D. Chen and W. Shen, Colloids Surf., B, 2013, 106, 187–190 CrossRef CAS PubMed.
- A. A. Morley, Biomol. Detect. Quantif., 2014, 1, 1–2 CrossRef PubMed.
- Y.-Q. Fan, M. Wang, F. Gao, J. Zhuang, G. Tang and Y.-J. Zhang, Chin. J. Anal. Chem., 2016, 44, 1300–1307 CAS.
- L. Cao, X. Cui, J. Hu, Z. Li, J. R. Choi, Q. Yang, M. Lin, L. Ying Hui and F. Xu, Biosens. Bioelectron., 2017, 90, 459–474 CrossRef CAS PubMed.
- J. Camunas-Soler, H. Lee, L. Hudgins, S. R. Hintz, Y. J. Blumenfeld, Y. Y. El-Sayed and S. R. Quake, Clin. Chem., 2018, 64, 336–345 Search PubMed.
- A. C. Bateman, A. L. Greninger, E. E. Atienza, A. P. Limaye, K. R. Jerome and L. Cook, Clin. Chem., 2017, 63, 761–769 CAS.
- S. Ookawa, M. Wanibuchi, Y. Kataoka-Sasaki, M. Sasaki, S. Oka, S. Ohtaki, S. Noshiro, K. Komatsu, Y. Akiyama, T. Mikami, N. Mikuni, J. D. Kocsis and O. Honmou, World Neurosurg., 2018, 111, e783–e789 CrossRef PubMed.
- Y. K. Wong, H. F. Tsang, V. W. Xue, C. M. Chan, T. C. Au, W. C. Cho, L. W. Chan and S. C. Wong, Expert Rev. Precis. Med. Drug Dev., 2017, 2, 177–186 CrossRef.
- D. Dobnik, T. Demsar, I. Huber, L. Gerdes, S. Broeders, N. Roosens, F. Debode, G. Berben and J. Zel, Anal. Bioanal. Chem., 2018, 410, 211–221 CrossRef CAS PubMed.
- C. D. Ahrberg, A. Manz and B. G. Chung, Lab Chip, 2016, 16, 3866–3884 RSC.
- P. S. Bhosale, M. V. Panchagnula and H. A. Stretz, Appl. Phys. Lett., 2008, 93, 034109 CrossRef.
- B. Laborie, F. Lachaussée, E. Lorenceau and F. Rouyer, Soft Matter, 2013, 9, 4822 RSC.
- C. Aberle, M. Lewis, G. Yu, N. Lei and J. Xu, Soft Matter, 2011, 7, 11314 RSC.
- A. Tosun and H. Y. Erbil, Appl. Surf. Sci., 2009, 256, 1278–1283 CrossRef CAS.
- C. H. Ooi, E. Bormashenko, A. V. Nguyen, G. M. Evans, D. V. Dao and N. T. Nguyen, Langmuir, 2016, 32, 6097–6104 CrossRef CAS PubMed.
- M. D. Doganci, B. U. Sesli, H. Y. Erbil, B. P. Binks and I. E. Salama, Colloids Surf., A, 2011, 384, 417–426 CrossRef CAS.
- S. R. Turns, An Introduction to Combustion - Concepts and Applications, McGraw-Hill, 2nd edn, 2000 Search PubMed.
- A. A. P. Kumar, V. P. Sandireddy, T. Banerjee and D. Bandyopadhyay, Ind. Eng. Chem. Res., 2015, 54, 1131–1141 CrossRef CAS.
Footnote |
| † Electronic supplementary information (ESI) available: Movies S1–S4. See DOI: 10.1039/c8ra02265h |
| This journal is © The Royal Society of Chemistry 2018 |