View PDF VersionPrevious ArticleNext Article

Open Access Article
This Open Access Article is licensed under a Creative Commons Attribution-Non Commercial 3.0 Unported Licence
DOI: 10.1039/C7RA13643A (Paper) RSC Adv., 2018, 8, 8856-8869

The nano heat effect of replacing macro-particles by nano-particles in drop calorimetry: the case of core/shell metal/oxide nano-particles

A. Yakymovych*ab, G. Kaptaycde, H. Flandorfera, J. Bernardif, S. Schwarzf and H. Ipsera
aDepartment of Inorganic Chemistry – Functional Materials, Faculty of Chemistry, University of Vienna, Althanstr. 14, 1090 Vienna, Austria. E-mail: andriy.yakymovych@univie.ac.at
bDepartment of Metal Physics, Ivan Franko National University, Kyrylo and Mephodiy str. 8, 79005 Lviv, Ukraine
cDepartment of Nanotechnology, University of Miskolc, Miskolc-Egyetemváros, Hungary-3515
dMTA-ME Materials Science Research Group, Miskolc-Egyetemváros, Hungary-3515
eBay Zoltan Ltd on Applied Research, BAY-ENG, 2 Igloi, Miskolc, Hungary-3519
fUniversity Service Center for Transmission Electron Microscopy, Vienna University of Technology, Wiedner Hauptstrasse 8-10, A-1040 Vienna, Austria

Received 25th December 2017 , Accepted 20th February 2018

First published on 27th February 2018

Abstract

Experimental results are presented here obtained by a drop calorimetric method, in which Ni and Cu particles, both in bulk and nanosized form, were dropped into a liquid Sn-3.8Ag-0.7Cu solder alloy (in wt%). The molar enthalpies of mixing of the liquid (Sn-3.8Ag-0.7Cu)–Ni(Cu) alloys were measured. An extra exothermic heat effect is observed when dropping nano-particles instead of macro-particles. This is partly due to the loss of the large surface area and the corresponding large surface enthalpy of the nano-particles before their dissolution in the liquid alloy. However, a large additional exothermic heat effect was also found in the case of Cu-nano-particles, due to the exchange chemical reaction between the Cu2O shell of the nano-particles and liquid Sn; this is caused by the fact that the Cu-nano-particles are core–shell particles with an inner metallic Cu core and an outer Cu2O shell. This effect is less significant for Ni nano-particles which have a thinner oxide shell.

Introduction

Nanostructured alloys represent a relatively novel class of materials compared to the conventional bulk ones, with a number of unique and promising features that have attracted an increasing number of scientists and engineers. However, there are still many open issues related to this research topic, such as the thermodynamic stability of the nanosized structures or the changes in properties during transition of the materials from the nanosized to bulk form.

At present, it is possible to produce nanoparticles (NPs) controlling not only their size but also their shape (spheres, plates, rods, etc.) and internal structure (metallic, bimetallic and multicomponent metal NPs), while the main progress in studies of the characteristics of NPs is achieved only in terms of size dependent thermodynamic properties. For instance, the size-dependent changes of the melting temperature, cohesive energy, melting enthalpy and entropy were theoretically predicted and experimentally described in the literature.1–3 At the same time, there are only few studies dealing with changes in various other properties of NPs caused by their shape or internal structure. For instance, there is a number of papers dealing with the investigation of optical properties of metallic4,5 and bimetallic NPs.6–8 The extinction spectra of metal nanoparticles, such as Ag nanodisks and triangular prisms, Au multirods, as well as Au shell NPs with a pinhole (several nm) structure were investigated in ref. 9. A bond-energy model for the calculation of the cohesive energy was developed in order to predict the size and shape dependency of various physical properties of metallic and bimetallic NPs with core/shell structure.10

The explosive growth in the number of studies of some classes of materials is mostly related to their prospective application. For instance, in order to promote new enhanced and customer-friendly lead-free solders, nanocomposite Sn-based alloys with minor additions of metal nanoparticles have been under intensive scientific examination.11–13 Unfortunately, most of these studies refer to mechanical properties14–18 while information related to thermophysical and thermodynamic properties as well as structural features, especially in the liquid state, is scarce.19–21 However, a possible industrial use requires comprehensive data on new nanosized materials with precisely controlled properties. In particular, one needs reliable information on the thermodynamic stability of the employed metal nanoparticles in the bulk solder with respect to their possible dissolution during long time use. Therefore, new studies dealing with chemical and physical properties of metal NPs in a bulk metal matrix, depending on size, shape, composition, and structure of these NPs, are demanded.

In the present study, a drop calorimetric method is used to investigate the “thermodynamic nanoeffects”. A Sn-3.8Ag-0.7Cu alloy (SAC387; in wt%) was employed in the performed study as the main component since SAC387 is a commercially available solder. Many papers are dealing with nanocomposite Sn–Ag–Cu (SAC) solders, attempting to improve their properties by minor additions of metal NPs such as Co, Cu, Fe, Ni, etc.17,22 The nanocomposite SAC solder is reflowed during the soldering process, and reactive metal NPs are dissolved in the liquid Sn-based matrix. Therefore, the present research provides essential data to simulate the soldering process using nanocomposite solders with nano-sized metal additions in a proper way. The heat effects caused by the dissolution of Cu and Ni in bulk as well as in nanosized form were determined and the excess surface enthalpies of the employed NPs were derived. The experimental results are theoretically described taking into account not only the size but also the internal structure of the nanoparticles, i.e. their apparent core–shell (metal core/oxide shell) structure.

Results and discussion

Calorimetric measurements. The present study was started with calorimetric measurements, adding pieces of bulk Cu into a liquid Sn-4.2Ag alloy (in at%) (Table 1), where the molar enthalpy of mixing for the liquid Sn-4.2Ag alloy was taken from Flandorfer et al.23 Since the concentration values in figures and tables are given in at%, the composition of the SAC387 master alloy is also converted to at%, resulting in a composition Sn-4.1Ag-1.3Cu. The measurements were performed at 1073 K and 873 K; they were compared with data calculated by a Redlich–Kister–Muggianu polynomial based on literature data by Luef et al.24
Table 1 Enthalpies of mixing data for the addition of bulk Cu into the liquid Sn-4.2Ag alloy; standard states: pure liquid metals
Mol. Cu dropped Measured enthalpy Partial molar enthalpy Integral molar enthalpy
nCu (10−3) mol

image file: c7ra13643a-t1.tif

(J mol−1)		 xCua ΔMix[H with combining macron]Cu (J mol−1) xCub ΔMixH (J mol−1)
a Average of xCu before and after drop.b Per mole of the mixture.
T = 1073 K; starting amount: nAg = 1.8224 × 10−3 mol; nSn = 41.8071 × 10−3 mol
          93
0.5684 33[thin space (1/6-em)]518 ± 604 0.0064 −506 ± 958 0.0129 91 ± 7
0.4250 33[thin space (1/6-em)]165 ± 513 0.0176 −858 ± 1049 0.0223 82 ± 11
0.4547 33[thin space (1/6-em)]350 ± 552 0.0272 −673 ± 1054 0.0321 73 ± 24
0.5055 33[thin space (1/6-em)]081 ± 609 0.0375 −942 ± 1046 0.0428 62 ± 37
0.5484 33[thin space (1/6-em)]167 ± 622 0.0485 −856 ± 1049 0.0542 51 ± 50
0.5490 32[thin space (1/6-em)]832 ± 656 0.0598 −1191 ± 1038 0.0653 36 ± 64
0.5543 32[thin space (1/6-em)]678 ± 659 0.0708 −1345 ± 1033 0.0763 20 ± 77
0.5728 32[thin space (1/6-em)]278 ± 673 0.0818 −1737 ± 1021 0.0874 −1±90
0.5735 32[thin space (1/6-em)]305 ± 674 0.0928 −1718 ± 1021 0.0982 −21 ± 103
0.5861 32[thin space (1/6-em)]147 ± 686 0.1036 −1876 ± 1016 0.1090 −43 ± 115
0.6221 31[thin space (1/6-em)]584 ± 715 0.1146 −2439 ± 999 0.1201 −73 ± 128
0.6412 31[thin space (1/6-em)]509 ± 735 0.1258 −2514 ± 996 0.1314 −104 ± 141
0.6621 31[thin space (1/6-em)]693 ± 764 0.1370 −2330 ± 1002 0.1427 −133 ± 154
0.6729 31[thin space (1/6-em)]618 ± 774 0.1483 −2405 ± 1000 0.1538 −163 ± 167
0.6982 31[thin space (1/6-em)]383 ± 797 0.1595 −2640 ± 992 0.1651 −196 ± 180
0.6986 30[thin space (1/6-em)]800 ± 783 0.1707 −3223 ± 974 0.1762 −236 ± 192
0.7058 30[thin space (1/6-em)]738 ± 790 0.1816 −3285 ± 972 0.1870 −276 ± 204
0.8912 30[thin space (1/6-em)]456 ± 988 0.1936 −3567 ± 963 0.2003 −330 ± 218
0.9026 30[thin space (1/6-em)]035 ± 987 0.2068 −3989 ± 950 0.2133 −389 ± 232
[thin space (1/6-em)]
T = 873 K; first measurement; starting amount: nAg = 1.7980 × 10−3 mol; nSn = 41.2485 × 10−3 mol
          168
0.2275 26[thin space (1/6-em)]836 ± 367 0.0026 −1445 ± 1077 0.0053 157 ± 8
0.2985 26[thin space (1/6-em)]834 ± 481 0.0087 −1448 ± 1077 0.0121 146 ± 19
0.3254 26[thin space (1/6-em)]633 ± 521 0.0157 −1648 ± 1069 0.0194 133 ± 31
0.3738 26[thin space (1/6-em)]326 ± 591 0.0235 −1955 ± 1056 0.0277 116 ± 44
0.3762 26[thin space (1/6-em)]383 ± 596 0.0318 −1898 ± 1059 0.0359 99 ± 57
0.4031 25[thin space (1/6-em)]741 ± 623 0.0402 −2541 ± 1033 0.0445 76 ± 71
0.4038 25[thin space (1/6-em)]659 ± 623 0.0487 −2622 ± 1030 0.0530 52 ± 84
0.4617 25[thin space (1/6-em)]844 ± 717 0.0577 −2437 ± 1037 0.0625 27 ± 98
0.4643 25[thin space (1/6-em)]883 ± 722 0.0672 −2398 ± 1039 0.0719 3 ± 113
0.4787 25[thin space (1/6-em)]618 ± 737 0.0766 −2663 ± 1028 0.0814 −25 ± 128
0.5448 25[thin space (1/6-em)]135 ± 823 0.0866 −3147 ± 1009 0.0919 −61 ± 143
0.5582 25[thin space (1/6-em)]443 ± 853 0.0972 −2838 ± 1021 0.1025 −93 ± 160
0.5697 24[thin space (1/6-em)]608 ± 842 0.1078 −3674 ± 987 0.1130 −135 ± 175
0.6367 24[thin space (1/6-em)]833 ± 950 0.1188 −3448 ± 996 0.1245 −178 ± 192
0.8346 24[thin space (1/6-em)]284 ± 1218 0.1318 −3997 ± 974 0.1391 −242 ± 213
[thin space (1/6-em)]
T = 873 K; second measurement; starting amount: nAg = 1.7652 × 10−3 mol; nSn = 40.4961 × 10−3 mol
          168
0.5287 27[thin space (1/6-em)]335 ± 736 0.0062 −1056 ± 994 0.0124 150 ± 17
0.5341 26[thin space (1/6-em)]341 ± 717 0.0184 −2049 ± 958 0.0245 123 ± 33
0.5679 26[thin space (1/6-em)]795 ± 775 0.0308 −1595 ± 974 0.0371 100 ± 50
0.5970 26[thin space (1/6-em)]517 ± 807 0.0436 −1873 ± 964 0.0501 74 ± 67
0.6152 25[thin space (1/6-em)]994 ± 815 0.0565 −2396 ± 945 0.0630 40 ± 84
0.6165 26[thin space (1/6-em)]133 ± 821 0.0693 −2257 ± 950 0.0757 9 ± 101
0.6252 25[thin space (1/6-em)]237 ± 804 0.0819 −3153 ± 918 0.0881 −34 ± 117
0.6330 25[thin space (1/6-em)]837 ± 833 0.0943 −2553 ± 939 0.1004 −67 ± 132
0.6442 25[thin space (1/6-em)]443 ± 835 0.1065 −2947 ± 925 0.1126 −106 ± 148
0.6478 24[thin space (1/6-em)]890 ± 822 0.1185 −3500 ± 905 0.1245 −152 ± 163
0.6838 24[thin space (1/6-em)]527 ± 855 0.1306 −3863 ± 892 0.1367 −204 ± 178
0.7186 24[thin space (1/6-em)]314 ± 890 0.1429 −4076 ± 884 0.1492 −260 ± 193
0.7401 24[thin space (1/6-em)]488 ± 924 0.1554 −3902 ± 890 0.1617 −313 ± 208
0.7588 23[thin space (1/6-em)]746 ± 918 0.1679 −4644 ± 863 0.1741 −377 ± 222
0.7771 23[thin space (1/6-em)]671 ± 937 0.1803 −4719 ± 861 0.1865 −442 ± 237

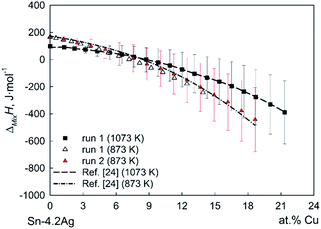
Fig. 1 shows very good agreement between experimental values and calculated curves, taking into account that the experimental data of ref. 24 were obtained at temperatures different from the present ones, namely 773 K, 973 K and 1173 K. The corresponding values of the integral enthalpy of mixing for the liquid Sn-4.1Ag-1.3Cu alloy were then used as the starting values required for the evaluation of ΔMixH of quaternary liquid Ag–Cu–Ni–Sn alloys. As evident from Fig. 1, the deviation from ideal behavior (enthalpy of mixing is equal to zero) is more significant at the lower temperature, in full accord with the general expectation for systems with chemical compounds.25


image file: c7ra13643a-f1.tif
Fig. 1 Integral enthalpy of mixing of liquid (Sn-4.2Ag)100−xCux alloys.

The experimental values for the Ag–Cu–Ni–Sn system are presented in Table 2, and they are compared with literature data by Saeed et al.,26 obtained at 1273 K, in Fig. 2. In order to describe the molar enthalpy of mixing for liquid quaternary alloys, it was suggested to modify the Redlich–Kister–Muggianu polynomial by adding an additional term corresponding to symmetric quaternary interactions.26 As seen from Fig. 2, there is a reasonably good agreement between experimental and calculated data with a maximum difference of less than 1 kJ mol−1.

Table 2 Enthalpies of mixing data for the addition of bulk Ni into the liquid Sn-4.1Ag-1.3Cu alloy; standard states: pure liquid metals
Mol. Ni dropped Measured enthalpy Partial molar enthalpy Integral molar enthalpy
nNi (10−3 mol)

image file: c7ra13643a-t2.tif

(J mol−1)		 xNia ΔMix[H with combining macron]Ni (J mol−1) xNib ΔMixH (J mol−1)
a Average of xNi before and after drop.b Per mole of the mixture.
T = 1073 K; starting amount: nAg = 1.6901 × 10−3 mol; nCu = 0.5285 × 10−3 mol; nSn = 38.5956 × 10−3 mol
          93
1.1040 −9226 ± 667 0.0132 −49894 ± 650 0.0263 −1225 ± 16
1.1889 −9214 ± 718 0.0398 −49882 ± 649 0.0532 −2567 ± 32
1.2866 −10252 ± 864 0.0669 −50920 ± 723 0.0806 −3969 ± 51
1.3084 −10061 ± 863 0.0938 −50729 ± 709 0.1069 −5307 ± 68
1.6360 −11267 ± 1208 0.1224 −51935 ± 794 0.1378 −6919 ± 91
[thin space (1/6-em)]
T = 1073 K; second measurement; starting amount: nAg = 1.7825 × 10−3 mol; nCu = 0.5574 × 10−3 mol; nSn = 40.7056 × 10−3 mol
          93
0.2259 −9155 ± 135 0.0026 −49719 ± 643 0.0052 −169 ± 15
0.2769 −9283 ± 168 0.0084 −49848 ± 652 0.0115 −485 ± 30
0.3012 −9718 ± 191 0.0149 −50282 ± 683 0.0183 −827 ± 45
0.3641 −9669 ± 230 0.0224 −50234 ± 680 0.0264 −1234 ± 60
0.3723 −9784 ± 238 0.0305 −50349 ± 688 0.0345 −1644 ± 75
0.3743 −9825 ± 240 0.0386 −50390 ± 691 0.0426 −2050 ± 90
0.4248 −10111 ± 280 0.0471 −50676 ± 711 0.0515 −2505 ± 105
0.4646 −10129 ± 307 0.0564 −50693 ± 712 0.0612 −2993 ± 119
0.5238 −9884 ± 338 0.0665 −50449 ± 695 0.0718 −3529 ± 133
0.5556 −10511 ± 381 0.0773 −51076 ± 739 0.0828 −4092 ± 147
0.5738 −11319 ± 424 0.0883 −51884 ± 796 0.0938 −4669 ± 162
0.5936 −11034 ± 428 0.0994 −51599 ± 775 0.1050 −5249 ± 176
0.6200 −11567 ± 468 0.1107 −52132 ± 813 0.1164 −5845 ± 190
0.6274 −11251 ± 461 0.1220 −51816 ± 791 0.1276 −6430 ± 204
0.6874 −12276 ± 551 0.1336 −52841 ± 863 0.1396 −7067 ± 218
[thin space (1/6-em)]
T = 873 K; first measurement; starting amount: nAg = 1.7086 × 10−3 mol; nCu = 0.5343 × 10−3 mol; nSn = 39.0184 × 10−3 mol
          152
0.3080 −18322 ± 397 0.0037 −52664 ± 1108 0.0074 −242 ± 10
0.3278 −18316 ± 423 0.0113 −52658 ± 1108 0.0152 −652 ± 20
0.5430 −17950 ± 686 0.0215 −52292 ± 1086 0.0278 −1312 ± 35
0.5684 −18800 ± 752 0.0342 −53142 ± 1137 0.0406 −1997 ± 53
[thin space (1/6-em)]
T = 873 K; second measurement; starting amount: nAg = 3.5225 × 10−3 mol; nCu = 1.1015 × 10−3 mol; nSn = 80.4407 × 10−3 mol
          152
1.2447 −18830 ± 1419 0.0072 −53125 ± 1140 0.0144 −619 ± 16
1.2190 −18733 ± 1383 0.0213 −53029 ± 1135 0.0281 −1349 ± 32
0.4438 −18926 ± 509 0.0306 −53221 ± 1146 0.0331 −1610 ± 38
0.4800 −18996 ± 552 0.0357 −53291 ± 1150 0.0383 −1891 ± 44
0.4846 −18669 ± 548 0.0409 −52965 ± 1131 0.0435 −2169 ± 50
0.5128 −18822 ± 585 0.0463 −53117 ± 1140 0.0490 −2461 ± 56
0.5463 −19068 ± 631 0.0519 −53364 ± 1155 0.0548 −2770 ± 63


image file: c7ra13643a-f2.tif
Fig. 2 Integral enthalpy of mixing of liquid (Sn-4.1Ag-1.3Cu)100−xNix alloys.

The results in Table 3 differ from those in Tables 1 and 2 by the experimental procedure: they were obtained by dropping pieces of Cu or Ni wrapped in a Sn-4.1Ag-1.3Cu foil into the liquid alloy in the calorimeter at 1073 K and 873 K. These measurements were performed to ensure that no significant side effects would be observed when dropping NPs wrapped into such a foil into the calorimeter. As seen from Fig. 3a and b, very good agreement was obtained between experimental results with and without employing the Sn-4.1Ag-1.3Cu foil. It should also be noted that, in contrast to the ternary Ag–Cu–Sn alloys (Fig. 1), the quaternary Ag–Cu–Ni–Sn alloys did not show any significant temperature dependence of the molar mixing enthalpies (Fig. 2 and 3b). The present results of the partial enthalpy of mixing for ternary and quaternary alloys were exothermic in the investigated concentration range at both temperatures while the integral enthalpy of mixing for the ternary (Sn-4.1Ag-1.3Cu)–Cu alloys changes from positive to negative values with increasing Cu content. Furthermore, the experimental data for the ternary (Sn-4.1Ag-1.3Cu)–Cu alloys indicated a clear temperature and concentration dependence of the integral enthalpy of mixing, with a tendency to more exothermic values at lower temperatures and higher Cu contents.

Table 3 Enthalpies of mixing data for the addition of both packed bulk Cu and Ni into the liquid Sn-4.1Ag-1.3Cu alloy; standard states: pure liquid metals
Mol. packed dropped metal Measured enthalpy Partial molar enthalpy Integral molar enthalpy
nCu (10−3 mol)

image file: c7ra13643a-t3.tif

(J mol−1)		 xCua ΔMix[H with combining macron]Cu (J mol−1) xCub ΔMixH (J mol−1)
a Average of xCu/xNi before and after drop.b Per mole of the mixture.
T = 1073 K; starting amount: nAg = 2.0639 × 10−3 mol; nCu = 0.6454 × 10−3 mol; nSn = 47.1327 × 10−3 mol
          93
0.6101 33[thin space (1/6-em)]431 ± 654 0.0060 −427 ± 1072 0.0121 85 ± 13
0.6273 33[thin space (1/6-em)]021 ± 692 0.0181 −837 ± 1103 0.0241 73 ± 26
0.6580 32[thin space (1/6-em)]527 ± 722 0.0302 −1331 ± 1098 0.0363 56 ± 40
0.6816 32[thin space (1/6-em)]532 ± 761 0.0425 −1326 ± 1117 0.0486 38 ± 53
0.7116 32[thin space (1/6-em)]707 ± 790 0.0548 −1151 ± 1110 0.0610 22 ± 67
0.7181 32[thin space (1/6-em)]267 ± 821 0.0670 −1592 ± 1144 0.0731 1 ± 81
0.7284 32[thin space (1/6-em)]090 ± 789 0.0790 −1768 ± 1083 0.0849 −22 ± 94
0.7326 32[thin space (1/6-em)]363 ± 787 0.0907 −1495 ± 1075 0.0965 −42 ± 106
0.7487 31[thin space (1/6-em)]614 ± 862 0.1022 −2244 ± 1152 0.1079 −69 ± 119
0.7657 31[thin space (1/6-em)]775 ± 857 0.1135 −2083 ± 1119 0.1191 −96 ± 132
0.7762 31[thin space (1/6-em)]465 ± 813 0.1247 −2393 ± 1048 0.1302 −125 ± 144
0.7933 31[thin space (1/6-em)]575 ± 877 0.1357 −2284 ± 1105 0.1411 −153 ± 156
0.8448 31[thin space (1/6-em)]104 ± 859 0.1468 −2754 ± 1017 0.1525 −188 ± 167
0.8656 31[thin space (1/6-em)]181 ± 893 0.1582 −2677 ± 1031 0.1638 −222 ± 178
0.8783 30[thin space (1/6-em)]703 ± 853 0.1694 −3155 ± 971 0.1750 −262 ± 189
0.9206 30[thin space (1/6-em)]828 ± 906 0.1807 −3030 ± 984 0.1864 −301 ± 200
0.9556 30[thin space (1/6-em)]679 ± 965 0.1920 −3179 ± 1010 0.1976 −342 ± 211
0.9794 30[thin space (1/6-em)]405 ± 1046 0.2031 −3453 ± 1068 0.2086 −385 ± 223
1.1165 29[thin space (1/6-em)]964 ± 972 0.2149 −3894 ± 871 0.2213 −443 ± 233
1.1578 29[thin space (1/6-em)]959 ± 960 0.2278 −3900 ± 830 0.2343 −501 ± 243
nNi (10−3 mol)

image file: c7ra13643a-t4.tif

(J mol−1)		 xNia ΔMix[H with combining macron]Ni (J mol−1) xNib ΔMixH (J mol−1)
T = 1073 K; starting amount: nAg = 3.6576 × 10−3 mol; nCu = 1.1436 × 10−3 mol; nSn = 83.5197 × 10−3 mol
          93
0.2961 −9558 ± 68 0.0017 −50193 ± 228 0.0033 −77 ± 1
0.6407 −9529 ± 281 0.0069 −50164 ± 438 0.0105 −436 ± 4
0.7048 −9220 ± 337 0.0144 −49855 ± 478 0.0182 −822 ± 8
0.8726 −10072 ± 464 0.0229 −50707 ± 532 0.0276 −1300 ± 13
0.9016 −10140 ± 420 0.0324 −50775 ± 465 0.0371 −1784 ± 18
0.9177 −9371 ± 404 0.0419 −50006 ± 441 0.0466 −2259 ± 22
0.9838 −9552 ± 509 0.0516 −50187 ± 517 0.0566 −2760 ± 28
0.9888 −10474 ± 466 0.0615 −51109 ± 472 0.0663 −3260 ± 33
1.0563 −10137 ± 492 0.0714 −50772 ± 466 0.0765 −3779 ± 38
1.1982 −11081 ± 565 0.0821 −51716 ± 472 0.0878 −4362 ± 43
1.3312 −10262 ± 674 0.0939 −50897 ± 506 0.1000 −4985 ± 50
[thin space (1/6-em)]
T = 873 K; starting amount: nAg = 3.5799 × 10−3 mol; nCu = 1.1194 × 10−3 mol; nSn = 81.7527 × 10−3 mol
          152
0.5236 −18437 ± 498 0.0030 −52800 ± 950 0.0060 −168 ± 6
0.7791 −18687 ± 752 0.0104 −53050 ± 966 0.0148 −637 ± 14
0.8281 −18514 ± 860 0.0194 −52877 ± 1038 0.0240 −1124 ± 24
0.8751 −19025 ± 878 0.0287 −53388 ± 1003 0.0335 −1632 ± 33
0.9304 −18348 ± 906 0.0384 −52711 ± 974 0.0434 −2154 ± 43


image file: c7ra13643a-f3.tif
Fig. 3 Integral enthalpy of mixing of liquid (Sn-4.1Ag-1.3Cu)100−xCux alloys at 1073 K (a) and (Sn-4.1Ag-1.3Cu)100−xNix alloys at 1073 K and 873 K (b).

The microstructure analysis of the samples after calorimetric measurements showed that the intermetallic compounds (IMCs) Ag3Sn, Cu6Sn5 and Ni3Sn4 had been formed during the solidification of the investigated Ag–Cu–Ni–Sn samples (Fig. 4a–d, Table 4). These results are in very good agreement with the quaternary Ag–Cu–Ni–Sn phase diagram.27 According to SEM analyses of the investigated samples, a substitution of Ni and Cu atoms, respectively, was observed in the IMCs Cu6Sn5 and Ni3Sn4. This effect is more pronounced for (Cu,Ni)6Sn5 due to a significantly increasing exothermic enthalpy of formation of this compound on admixture of Ni.28 In the Sn76Ag3Cu21 alloy, two Cu–Sn IMCs were found, namely Cu3Sn and Cu6Sn5. According to the Cu–Sn phase diagram, Cu3Sn should be formed in the investigated alloy during cooling and should decompose under equilibrium conditions into pure Sn and Cu6Sn5 at 681 K.29 However, the cooling of the sample after the calorimetric measurement was certainly not slow enough to reach an equilibrium state, thus Cu3Sn grains are left as can be seen in the microstructure.


image file: c7ra13643a-f4.tif
Fig. 4 BSE micrographs of (Sn-4.1Ag-1.3Cu)100−xCux (a) – Sn76Ag3Cu21; (b) – Sn83Ag4Cu13) and (Sn-4.1Ag-1.3Cu)100−xNix (c) – Sn81Ag4Cu1Ni14; (d) – Sn91Ag4Cu1Ni4) samples after calorimetry.
Table 4 SEM-EDX results of (Sn-4.1Ag-1.3Cu)100−xCux and (Sn-4.1Ag-1.3Cu)100−xNix samples after calorimetry
Sample Temperature of calor. meas. (K) Dropped component Phase 1 Phase 2 Phase 3 Phase 4
  Sn at%   Ag at% Sn at%   Cu at% Ni at% Sn at%   Ni at% Cu at% Sn at%
Sn76Ag3Cu21 1st meas. 1073 bulk Cu βSn 100 Ag3Sn 75 25 Cu6Sn5 53 — 47 — — — —
Cu3Sn 74 — 26   — — —
Sn83Ag4Cu13 2nd meas. 873 nano Cu βSn 100 Ag3Sn 73 27 Cu6Sn5 53 — 47 — — — —
Sn81Ag4Cu1Ni14 1st meas. 1073 bulk Ni βSn 100 Ag3Sn 76 24 (Cu,Ni)6Sn5 34 18 48 (Ni,Cu)3Sn4 39 3 58
Sn91Ag4Cu1Ni4 1st meas. 873 nano Ni βSn 100 Ag3Sn 73 27 (Cu,Ni)6Sn5 34 19 50 (Ni,Cu)3Sn4 40 2 58

After the experiments with bulk Cu and Ni, the corresponding experiments with nano-particles were performed (Tables 5 and 6). The excess enthalpies due to the nano-effect were estimated, similarly as in ref. 19, by comparing the measured enthalpy values obtained with bulk and nanosized particles (Fig. 5 and 6).

Table 5 Enthalpies of mixing data for the addition of nano Cu into the liquid Sn-4.1Ag-1.3Cu alloy; standard states: pure liquid metals
Mol nano-sized Cu dropped Measured enthalpy Partial molar enthalpy Integral molar enthalpy
nCu (10−3 mol)

image file: c7ra13643a-t5.tif

(J mol−1)		 xCua ΔMix[H with combining macron]Cu (J mol−1) xCub ΔMixH (J mol−1)
a Average of xCu before and after drop.b Per mole of the mixture.
T = 1073 K; first measurement; starting amount: nAg = 1.9452 × 10−3 mol; nCu = 0.6083 × 10−3 mol; nSn = 44.4216 × 10−3 mol
          93
0.2233 34[thin space (1/6-em)]199 ± 637 0.0024 14 ± 1104 0.0047 91 ± 13
0.2161 33[thin space (1/6-em)]758 ± 629 0.0069 −427 ± 1127 0.0091 9 ± 26
0.2504 34[thin space (1/6-em)]010 ± 633 0.0116 −175 ± 979 0.0141 −68 ± 39
0.2546 33[thin space (1/6-em)]692 ± 627 0.0166 −492 ± 954 0.0191 −157 ± 51
0.2747 33[thin space (1/6-em)]839 ± 630 0.0217 −346 ± 888 0.0243 −243 ± 63
0.2747 33[thin space (1/6-em)]463 ± 623 0.0268 −722 ± 878 0.0294 −337 ± 74
0.3087 33[thin space (1/6-em)]676 ± 627 0.0321 −509 ± 787 0.0349 −426 ± 85
0.3298 33[thin space (1/6-em)]606 ± 622 0.0378 −579 ± 735 0.0407 −524 ± 96
0.3360 33[thin space (1/6-em)]156 ± 617 0.0436 −1029 ± 712 0.0464 −629 ± 106
0.3482 33[thin space (1/6-em)]233 ± 619 0.0493 −952 ± 688 0.0522 −733 ± 116
0.3544 33[thin space (1/6-em)]470 ± 623 0.0551 −715 ± 681 0.0580 −836 ± 126
0.3562 32[thin space (1/6-em)]910 ± 613 0.0609 −1275 ± 666 0.0637 −943 ± 136
0.3624 33[thin space (1/6-em)]115 ± 617 0.0665 −1069 ± 659 0.0692 −1047 ± 145
0.3691 32[thin space (1/6-em)]364 ± 603 0.0719 −1821 ± 632 0.0746 −1151 ± 153
0.3913 33[thin space (1/6-em)]257 ± 619 0.0775 −928 ± 613 0.0803 −1250 ± 161
0.3954 32[thin space (1/6-em)]276 ± 601 0.0831 −1909 ± 589 0.0860 −1358 ± 169
0.4237 33[thin space (1/6-em)]125 ± 617 0.0889 −1059 ± 564 0.0918 −1462 ± 177
0.4345 32[thin space (1/6-em)]461 ± 604 0.0946 −1724 ± 539 0.0974 −1571 ± 184
0.6205 32[thin space (1/6-em)]701 ± 609 0.1014 −1483 ± 380 0.1054 −1677 ± 190
[thin space (1/6-em)]
T = 1073 K; second measurement; starting amount: nAg = 1.9755 × 10−3 mol; nCu = 0.6177 × 10−3 mol; nSn = 45.1128 × 10−3 mol
          93
0.2332 33[thin space (1/6-em)]688 ± 794 0.0024 −170 ± 882 0.0048 90 ± 16
0.1613 33[thin space (1/6-em)]499 ± 789 0.0064 −359 ± 1296 0.0081 6 ± 32
0.1933 33[thin space (1/6-em)]488 ± 789 0.0100 −370 ± 1058 0.0119 −51 ± 48
0.2653 33[thin space (1/6-em)]506 ± 789 0.0144 −353 ± 772 0.0170 −119 ± 63
0.2273 33[thin space (1/6-em)]140 ± 781 0.0191 −718 ± 891 0.0212 −209 ± 77
0.2760 33[thin space (1/6-em)]028 ± 778 0.0237 −830 ± 731 0.0262 −286 ± 91
0.3389 33[thin space (1/6-em)]049 ± 779 0.0292 −810 ± 596 0.0322 −377 ± 105
0.1684 33[thin space (1/6-em)]079 ± 779 0.0336 −779 ± 1200 0.0350 −484 ± 118
0.2893 32[thin space (1/6-em)]908 ± 775 0.0375 −951 ± 695 0.0399 −536 ± 131
0.3051 32[thin space (1/6-em)]717 ± 771 0.0424 −1142 ± 655 0.0449 −626 ± 143
0.2855 32[thin space (1/6-em)]876 ± 774 0.0472 −982 ± 703 0.0495 −717 ± 155
0.3051 32[thin space (1/6-em)]934 ± 776 0.0519 −925 ± 659 0.0543 −799 ± 167
0.3317 32[thin space (1/6-em)]732 ± 771 0.0569 −1126 ± 603 0.0594 −888 ± 178
0.3277 32[thin space (1/6-em)]491 ± 765 0.0618 −1367 ± 606 0.0643 −981 ± 189
0.3157 32[thin space (1/6-em)]893 ± 775 0.0665 −965 ± 636 0.0688 −1070 ± 200
0.3024 32[thin space (1/6-em)]243 ± 760 0.0709 −1615 ± 651 0.0730 −1154 ± 210
0.3711 32[thin space (1/6-em)]069 ± 755 0.0756 −1789 ± 528 0.0782 −1237 ± 220
[thin space (1/6-em)]
T = 873 K; first measurement; starting amount: nAg = 1.8702 × 10−3 mol; nCu = 0.5848 × 10−3 mol; nSn = 42.7094 × 10−3 mol
          152
0.1134 26[thin space (1/6-em)]783 ± 570 0.0012 −1597 ± 1335 0.0025 144 ± 13
0.1199 26[thin space (1/6-em)]873 ± 572 0.0038 −1508 ± 1266 0.0051 93 ± 25
0.1321 26[thin space (1/6-em)]885 ± 572 0.0065 −1495 ± 1150 0.0079 39 ± 37
0.1296 26[thin space (1/6-em)]849 ± 570 0.0092 −1532 ± 1171 0.0106 −20 ± 49
0.1338 27[thin space (1/6-em)]048 ± 576 0.0120 −1332 ± 1143 0.0134 −75 ± 61
0.1379 26[thin space (1/6-em)]691 ± 568 0.0147 −1689 ± 1094 0.0161 −133 ± 72
0.1462 26[thin space (1/6-em)]922 ± 573 0.0176 −1458 ± 1041 0.0190 −190 ± 83
0.1501 26[thin space (1/6-em)]819 ± 571 0.0205 −1562 ± 1009 0.0220 −251 ± 95
0.1519 26[thin space (1/6-em)]460 ± 563 0.0235 −1921 ± 984 0.0249 −313 ± 105
0.1677 26[thin space (1/6-em)]439 ± 563 0.0265 −1942 ± 891 0.0281 −375 ± 116
0.1779 26[thin space (1/6-em)]667 ± 568 0.0298 −1714 ± 847 0.0314 −442 ± 126
0.1892 26[thin space (1/6-em)]616 ± 566 0.0332 −1765 ± 795 0.0349 −511 ± 136
0.1914 26[thin space (1/6-em)]425 ± 562 0.0366 −1956 ± 780 0.0383 −584 ± 146
0.1980 26[thin space (1/6-em)]148 ± 557 0.0401 −2233 ± 746 0.0418 −658 ± 156
0.2129 25[thin space (1/6-em)]925 ± 552 0.0437 −2455 ± 688 0.0455 −734 ± 164
0.2246 26[thin space (1/6-em)]184 ± 557 0.0474 −2197 ± 659 0.0494 −813 ± 174
0.2343 26[thin space (1/6-em)]097 ± 555 0.0513 −2284 ± 630 0.0533 −895 ± 182
0.3362 26[thin space (1/6-em)]195 ± 558 0.0561 −2186 ± 440 0.0589 −981 ± 190
0.3904 25[thin space (1/6-em)]837 ± 550 0.0621 −2544 ± 374 0.0653 −1104 ± 198
0.0850 25[thin space (1/6-em)]601 ± 545 0.0658 −2780 ± 1702 0.0664 −1234 ± 206
[thin space (1/6-em)]
T = 873 K; second measurement; starting amount: nAg = 1.9152 × 10−3 mol; nCu = 0.5989 × 10−3 mol; nSn = 43.7365 × 10−3 mol
          152
0.3188 27[thin space (1/6-em)]210 ± 571 0.0034 −1143 ± 953 0.0068 140 ± 12
0.3780 26[thin space (1/6-em)]649 ± 559 0.0107 −1704 ± 787 0.0146 −2±24
0.4031 26[thin space (1/6-em)]564 ± 557 0.0185 −1789 ± 736 0.0225 −164 ± 35
0.4044 26[thin space (1/6-em)]627 ± 559 0.0264 −1725 ± 735 0.0303 −329 ± 45
0.4038 26[thin space (1/6-em)]629 ± 559 0.0340 −1723 ± 736 0.0377 −489 ± 55
0.4165 26[thin space (1/6-em)]253 ± 551 0.0414 −2100 ± 706 0.0452 −646 ± 65
0.4239 26[thin space (1/6-em)]231 ± 550 0.0488 −2122 ± 691 0.0525 −803 ± 75
0.4250 25[thin space (1/6-em)]600 ± 537 0.0560 −2753 ± 672 0.0595 −961 ± 83
0.4375 25[thin space (1/6-em)]995 ± 545 0.0630 −2358 ± 663 0.0665 −1113 ± 92
0.4487 25[thin space (1/6-em)]936 ± 544 0.0700 −2416 ± 645 0.0735 −1263 ± 100
0.4675 25[thin space (1/6-em)]889 ± 543 0.0770 −2464 ± 618 0.0806 −1413 ± 108
0.4745 25[thin space (1/6-em)]845 ± 542 0.0840 −2508 ± 608 0.0875 −1565 ± 116
0.4820 25[thin space (1/6-em)]517 ± 535 0.0909 −2835 ± 591 0.0943 −1717 ± 123
0.4834 25[thin space (1/6-em)]315 ± 531 0.0976 −3038 ± 584 0.1010 −1867 ± 130
0.4838 25[thin space (1/6-em)]371 ± 532 0.1042 −2981 ± 585 0.1073 −2015 ± 137
0.4957 25[thin space (1/6-em)]077 ± 526 0.1104 −3276 ± 565 0.1135 −2157 ± 143
0.5133 25[thin space (1/6-em)]438 ± 534 0.1167 −2915 ± 553 0.1199 −2295 ± 149
0.5271 24[thin space (1/6-em)]826 ± 521 0.1231 −3527 ± 526 0.1263 −2440 ± 155
0.5745 25[thin space (1/6-em)]129 ± 527 0.1297 −3223 ± 488 0.1330 −2583 ± 160

Table 6 Enthalpies of mixing data for the addition of nano Ni into the liquid Sn-4.1Ag-1.3Cu alloy; standard states: pure liquid metals
mol nano-sized Ni dropped Measured enthalpy Partial molar enthalpy Integral molar enthalpy
nNi (10−3 mol)

image file: c7ra13643a-t6.tif

(J mol−1)		 xNia ΔMix[H with combining macron]Ni (J mol−1) xNib ΔMixH (J mol−1)
a Average of xNi before and after drop.b Per mole of the mixture.
T = 1073 K; first measurement; starting amount: nAg = 3.6656 × 10−3 mol; nCu = 1.1462 × 10−3 mol; nSn = 83.7083 × 10−3 mol
          93
0.7417 −13861 ± 554 0.0041 −49400 ± 543 0.0083 −318 ± 5
0.7656 −13684 ± 547 0.0124 −49222 ± 516 0.0166 −759 ± 9
0.7858 −13867 ± 555 0.0207 −49406 ± 512 0.0248 −1200 ± 14
1.1022 −13626 ± 545 0.0305 −49164 ± 357 0.0361 −1787 ± 18
0.9587 −13915 ± 556 0.0409 −49453 ± 422 0.0456 −2300 ± 22
0.9615 −13856 ± 554 0.0502 −49394 ± 418 0.0548 −2793 ± 26
1.1326 −14329 ± 573 0.0601 −49867 ± 372 0.0653 −3350 ± 30
1.1366 −14293 ± 572 0.0704 −49832 ± 369 0.0754 −3897 ± 34
1.1458 −13471 ± 539 0.0804 −49010 ± 338 0.0853 −4421 ± 37
1.1778 −14456 ± 578 0.0902 −49994 ± 362 0.0951 −4947 ± 41
1.2029 −14130 ± 565 0.0999 −49669 ± 343 0.1047 −5467 ± 44
1.2095 −14599 ± 584 0.1095 −50137 ± 357 0.1142 −5978 ± 48
1.2590 −14164 ± 566 0.1189 −49702 ± 329 0.1236 −6483 ± 51
1.2684 −15096 ± 604 0.1281 −50635 ± 356 0.1326 −6979 ± 54
1.3939 −14345 ± 574 0.1375 −49884 ± 303 0.1424 −7503 ± 57
1.4623 −15264 ± 610 0.1474 −50803 ± 314 0.1523 −8048 ± 60
1.4931 −15142 ± 606 0.1572 −50681 ± 304 0.1621 −8582 ± 63
1.5044 −14769 ± 591 0.1668 −50308 ± 292 0.1715 −9098 ± 64
[thin space (1/6-em)]
T = 1073 K; second measurement; starting amount: nAg = 1.7663 × 10−3 mol; nCu = 0.5523 × 10−3 mol; nSn = 40.3348 × 10−3 mol
          93
0.4599 −13541 ± 587 0.0053 −49053 ± 918 0.0106 −428 ± 10
0.4871 −13539 ± 587 0.0160 −49051 ± 866 0.0214 −1000 ± 20
0.5091 −13755 ± 596 0.0268 −49267 ± 847 0.0323 −1578 ± 30
0.5175 −13421 ± 581 0.0376 −48933 ± 805 0.0429 −2141 ± 39
0.5516 −13324 ± 577 0.0484 −48836 ± 748 0.0539 −2718 ± 47
0.6021 −13307 ± 577 0.0596 −48820 ± 684 0.0654 −3322 ± 55
0.6275 −14081 ± 610 0.0711 −49594 ± 710 0.0769 −3940 ± 64
0.6496 −13815 ± 599 0.0826 −49327 ± 668 0.0883 −4545 ± 72
0.6757 −14440 ± 626 0.0940 −49952 ± 682 0.0997 −5162 ± 80
0.6847 −15378 ± 666 0.1053 −50891 ± 733 0.1109 −5780 ± 88
0.7012 −15195 ± 658 0.1164 −50707 ± 704 0.1219 −6384 ± 69
0.7162 −15503 ± 672 0.1273 −51015 ± 708 0.1326 −6977 ± 104
0.7427 −15479 ± 671 0.1380 −50991 ± 681 0.1433 −7568 ± 111
0.7497 −14992 ± 650 0.1485 −50504 ± 647 0.1537 −8134 ± 118
[thin space (1/6-em)]
T = 873 K; first measurement; starting amount: nAg = 1.9944 × 10−3 mol; nCu = 0.6236 × 10−3 mol; nSn = 45.5455 × 10−3 mol
          152
0.5701 −21187 ± 669 0.0058 −51159 ± 991 0.0116 −447 ± 12
0.5162 −21731 ± 687 0.0167 −51703 ± 1128 0.0218 −1014 ± 24
0.5665 −21908 ± 692 0.0272 −51880 ± 1038 0.0327 −1612 ± 36
0.8113 −22802 ± 720 0.0401 −52774 ± 759 0.0476 −2441 ± 48
0.8229 −22080 ± 698 0.0549 −52052 ± 721 0.0621 −3248 ± 59
1.0979 −22729 ± 718 0.0714 −52701 ± 559 0.0807 −4279 ± 69
0.6052 −23010 ± 727 0.0856 −52981 ± 1029 0.0905 −4860 ± 80
0.2324 −22454 ± 709 0.0922 −52426 ± 2604 0.0939 −5075 ± 91
[thin space (1/6-em)]
T = 873 K; second measurement; starting amount: nAg = 1.8391 × 10−3 mol; nCu = 0.5751 × 10−3 mol; nSn = 41.9986 × 10−3 mol
          152
0.2662 −21613 ± 474 0.0030 −51585 ± 1005 0.0059 −157 ± 9
0.2395 −21910 ± 481 0.0086 −51882 ± 1135 0.0112 −450 ± 19
0.4425 −22942 ± 484 0.0159 −52014 ± 619 0.0207 −962 ± 28
0.3227 −22008 ± 483 0.0240 −51980 ± 847 0.0273 −1341 ± 37
0.5358 −22191 ± 487 0.0327 −52163 ± 515 0.0382 −1931 ± 46
0.7365 −22375 ± 491 0.0454 −52347 ± 378 0.0526 −2723 ± 54
0.5059 −21987 ± 483 0.0573 −51959 ± 539 0.0620 −3261 ± 62
0.6155 −22840 ± 501 0.0675 −52811 ± 464 0.0731 −3881 ± 69
0.2582 −22827 ± 501 0.0753 −52799 ± 1105 0.0775 −4152 ± 78


image file: c7ra13643a-f5.tif
Fig. 5 Concentration dependencies of the measured enthalpy effect for (Sn-4.1Ag-1.3Cu)100−xCux at 1073 K (a) and 873 K (b) (■ – for additions of bulk Cu; □ – for additions of nanosized Cu).

image file: c7ra13643a-f6.tif
Fig. 6 Concentration dependencies of the measured enthalpy effect for (Sn-4.1Ag-1.3Cu)100−xNix at 1073 K (a) and 873 K (b) (■ – for additions of bulk Ni; □ – for additions of nanosized Ni).

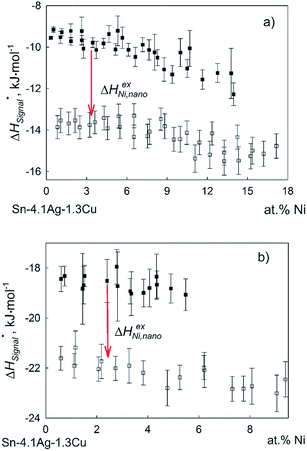
In order to estimate values of the excess enthalpy, the concentration dependencies of the measured enthalpy for additions of Cu and Ni in bulk and nanosized form were plotted as a function of the content of the added element and extrapolated to zero. The estimated value of ΔHexi,nano for Cu additions was found to be about −17.0 ± 1.2 kJ mol−1 at 1073 K and −18.5 ± 1.3 kJ mol−1 at 873 K (Fig. 5). The corresponding value of ΔHexi,nano for Ni was found as about −3.8 ± 1.6 kJ mol−1 at 1073 K and −3.3 ± 1.5 kJ mol−1 at 873 K (Fig. 6).

The TEM analysis together with HAADF STEM (high angle annular dark field – scanning transmission electron microscopy) imaging should bring essential information about the characteristics of the employed Cu and Ni NPs in order to explain the significant difference in the values of the excess surface enthalpy. Fig. 7 and 8 show examples of the TEM micrographs of Cu and Ni NPs which show that the NPs (including oxide shell) are of similar size, considering the original size distribution.


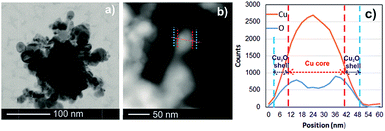image file: c7ra13643a-f7.tif
Fig. 7 TEM bright field image (a) and HAADF STEM image (b) with corresponding EDX linescan (c) of Cu NPs.

image file: c7ra13643a-f8.tif
Fig. 8 TEM bright field image (a) and HAADF STEM image (b) with corresponding EDX linescan (c) of Ni NPs.

Furthermore, EDX elemental mapping of Cu NPs showed an oxide shell (Cu2O) covering a metal core (Fig. 7(a–c)). These data are in a good agreement with XRD analysis indicating the presence of both Cu and Cu2O (cubic, see ref. 30) in the investigated Cu nanopowder (Fig. 9a). In the case of Ni NPs, only traces of NiO (trigonal/rhombohedral, see ref. 31) with very low intensity were found in the XRD pattern (Fig. 9b); only minor amounts of oxygen were found on the surface of the Ni NPs (Fig. 8b and c). The first broad peak in the X-ray patterns is caused by the specimen holder with the polycarbonate cap.


image file: c7ra13643a-f9.tif
Fig. 9 XRD patterns of Cu (a) and Ni NPs (b).

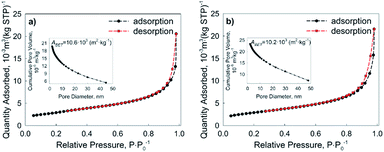
Pore size distributions of Cu and Ni NPs were measured by nitrogen sorption according to the theory of Barrett, Joyner and Halenda (BJH) (Fig. 10a and b). The determined BET surface area of the employed NPs is equal to (10.6 ± 0.4) 103 m2 kg−1 for Cu NPs and (10.2 ± 0.4) 103 m2 kg−1 for Ni NPs.


image file: c7ra13643a-f10.tif
Fig. 10 BET isotherm and BJH pore size distribution of Cu (a) and Ni NPs (b).

Theoretical considerations

The goal of this chapter is to model the observed ΔHexi,nanovalues by applying the principles of nano-thermodynamics.32–34 In a previous paper19 the nano-effect was described as
 
ΔHexi,nano = −ABETMσsg,H,TD, (1)
where ABET (m2 g−1) is the BET surface area of the nano-particles (which is assumed to be negligible for bulk material), M (g mol−1) is the molar mass of the nano-particles, σsg,H,TD (J m−2) is the enthalpy part of the surface energy of the solid nano-particles at the drop temperature. (Note that in the present paper the sign of ΔHexi,nano is kept positive contrary to the previous paper,19 thus a negative sign appears in eqn (1); this is done for two reasons: to avoid predicting anything before the experiments are run, and to make more obvious that the nano-effect is exothermic). The physical meaning of eqn (1) is the loss (see the negative sign) of the enthalpy part of the surface energy of the nano-particles upon dissolution per mole of metal added. The calculated and experimental results for the systems studied in this paper are compared in Table 7.
Table 7 Calculated and measured nano-effects (ΔHexi,nano, kJ mol−1) without considering the influence of the oxide shell on the nano-particles
Metal ABET (m2 g−1) M (g mol−1) σsg,H,TD) J m−2)35 ΔHexi,nano eqn (1) ΔHexi,nano experiment
Cu 10.6 ± 0.4 63.55 1.93 ± 0.19 −1.3 ± 0.2 −17.8 ± 0.8
Ni 10.2 ± 0.4 58.69 2.36 ± 0.23 −1.4 ± 0.2 −3.5 ± 0.3

As follows from Table 7, the experimental values in this case are considerably more negative than the calculated ones, and this difference is especially striking for Cu nanoparticles. This is most probably due to the fact that eqn (1) is strictly valid only for pure metallic nano-particles without any oxide shell. However, as observed by the TEM and XRD investigations of the nano-particles (see Fig. 6–8), the Cu-nano-particles are severely contaminated by oxygen. Actually, instead of Cu-nano-particles we have core/shell nano-particles with a Cu inner core (α) and a Cu2O shell (β), which form together particle γ. A similar oxidation problem exists also for Ni nano-particles, however, to a much smaller extent. Therefore, the previous model in eqn (1) has to be modified to take into account the role of the oxide shells on the metallic nano-particles, too.

When the experiments were performed, it was assumed that n0Me (mole) of pure metal was added into the calorimeter. Instead, the molar part y of these nano-particles was actually oxidized so that in fact the following amounts of matter were added:

 
nα = (1 − y)n0Me, (2)
 
nβ = yn0Me, (3)
where α denotes the added metal, and β denotes its oxide shell MeOx (where the stoichiometry is always written such that the oxide molecule contains one metallic atom, i.e., x can be any positive number). Thus, in addition to eqn (1), there are two additional terms for the enthalpy nano-effect: one is responsible for different heat capacities of α (metal) and β (oxide), while the other one is responsible for the chemical interaction between β and metal atoms in the liquid alloy (in our case these are mostly atoms of Sn), into which the nano-particles are added:
 
ΔHexα/β,nano = −ABETMγσγ,H,TD + y(ΔHCp + ΔrH0), (4)
where Mγ is the average molar mass of the partly oxidized particle as defined by eqn (5), σγ,H,TD is the effective enthalpy part of the surface energy of the partly oxidized particle as defined by eqn (6), and ΔHCp (J mol−1) is the enthalpy difference due to the different heat capacities of the oxide and the metal as defined by eqn (7); ΔrH0 (J mol−1) is the standard molar enthalpy change of the chemical reaction: MeOx + ySn = SnyOx + Me (or, which is the same: β + ySn = SnyOx + α, where the stoichiometry is always written such that the oxide molecule contains one metallic atom, i.e., x can be any positive number):
 
Mγ = (1 − y)Mα + yMβ, (5)
 
image file: c7ra13643a-t7.tif(6)
 
image file: c7ra13643a-t8.tif(7)
where Mα (g mol−1) is the molar mass of the metal core, Mβ (g mol−1) is the molar mass of the oxide shell, σα/β,H,TD (J m−2) is the enthalpy part of the α/β interfacial energy, σβ,H,TD (J m−2) is the enthalpy part of the surface energy of the oxide shell, σα,H,TD (J m−2) is the enthalpy part of the surface energy of the metallic core, d (nm) is the thickness of the oxide shell, δ ≅ 1 nm is the coefficient in the separation dependence of interfacial energies,36 CP,β (J (mol K)−1) is the molar heat capacity of the oxide shell of the nano-particle, CP,α (J (mol K)−1) is the molar heat capacity of the metallic inner core of the nano-particle. When the oxide shell is thin, it is modelled as a shell of constant thickness following the original shape of the nano-particle. If this thickness is much smaller than the radius of the nano-particle, the BET surfacse area of the outer oxide/gas surface and the BET interfacial area of the inner metal/oxide interface are considered equal.

In order to check whether the proposed reactions are exergonic and favorable or not, the free energy change for the reactions was estimated from the Gibbs energy of formation values of the oxides of copper (ΔfGCu2O), nickel (ΔfGNiO) and tin (ΔfGSnO2). In the present case, there are two chemical exchange reactions, i.e. (Cu2O + 1/2Sn[double bond, length as m-dash]1/2SnO2 + 2Cu) and (NiO + 1/2Sn[double bond, length as m-dash]1/2SnO2 + Ni). It is assumed that the Gibbs energy change for the first reaction can be obtained as ΔrG(NiO/SnO2) = 1/2ΔfGSnO2 − ΔfGNiO and that for the second reaction as ΔrG(Cu2O/SnO2) = 1/2ΔfGSnO2 − ΔfGCu2O. The Gibbs energies of formation for the oxides at 1073 K and 873 K were taken from ref. 37 and 38. Based on the obtained results, the calculated Gibbs energy change for the reactions is exothermic at both temperatures and equals −93.3 kJ mol−1 and −86.9 kJ mol−1 for ΔrG(Cu2O/SnO2), and −38.2 kJ mol−1 and −34.5 kJ mol−1 for ΔrG(NiO/SnO2) at 873 K and 1073 K, respectively.

The amount of matter of the oxide shell can be expressed from its geometry as:

 
nβ ≅ ABETdρβn0Me, (8)
where ρβ (g m−3) is the density of the oxide shell. The quantities expressed by eqn (3) and (8) are equal. Consequently, the thickness of the oxide shell (d) can be expressed as function of the mole fraction of the oxidized part of the nano-particle (y), as:
 
image file: c7ra13643a-t9.tif(9)

Let us also mention that for y = 0, eqn (4) becomes identical to eqn (1), being a reasonable boundary condition. Substituting eqn (5)–(7) and (9) into eqn (4), the excess nano heat effect can be calculated as function of y for partly oxidized metallic nano-particles.

The corresponding constants are given in Table 7. In this paper, the selection Sn was made (for the values in the last column of Table 8), as Sn has the highest affinity towards oxygen and the highest mole fraction in the liquid alloy among its components (Sn, Cu, Ag). The results calculated based on Table 8 are compared with experimental data in Fig. 11 and 12.

Table 8 Parameters to calculate the excess nano heat effect ΔHexpi,nano (kJ mol−1) by eqn (4)–(7) and (9)a
Metal ABET (m2 g−1) Mα (g mol−1) βx M (g mol−1) ρβ (g cm−3) σα,H,TD (J m−2) σβ,H,TD (J m−2) σα/β,H,TD (J m−2) T (K) ΔHCp (kJ mol−1) ΔrH0 (kJ mol−1)
a Density is from ref. 39, interfacial energies are from ref. 35 and 40, and enthalpy data are from ref. 41.
Cu 10.6 63.55 0.5 71.55 6.0 1.93 0.7 1.93 873 6.00 −71.05
Cu 10.6 63.55 0.5 71.55 6.0 1.93 0.7 1.93 1073 8.40 −75.01
Ni 10.2 58.69 1 74.69 7.45 2.36 0.9 2.36 873 13.96 −61.84
Ni 10.2 58.69 1 74.69 7.45 2.36 0.9 2.36 1073 18.208 −64.33


image file: c7ra13643a-f11.tif
Fig. 11 Comparison of experimental data (dotted horizontal lines) with theoretical values (bold lines) at two temperatures for the dependence of the excess nano enthalpy effect on the ratio of oxidation of the Cu nanoparticles. Calculated by eqn (5)–(7) and (9) and parameters of Table 8.

image file: c7ra13643a-f12.tif
Fig. 12 Comparison of experimental data (dotted horizontal lines) with theoretical values (bold lines) at two temperatures for the dependence of the excess nano enthalpy effect on the ratio of oxidation of the Ni nanoparticles. Calculated by eqn (4)–(7) and (9) and parameters of Table 8.

As follows from Fig. 11 and 12, the experimental results can be reproduced with y = 0.24 ± 0.02 for Cu-nanoparticles and with y = 0.039 ± 0.004 for Ni-nanoparticles. These values are in qualitative agreement with Fig. 7–9. Thus, our new extended model is able to describe the nano heat effect for the dissolution of partly oxidized nano-particles.

Experimental

The heat effects of small additions of Cu and Ni to the liquid SAC387 alloy were investigated by a drop calorimetric method. The measurements were carried out using a Calvet-type twin microcalorimeter system under high purity Ar (99.9999%) flow (approximately 20–30 ml min−1). The apparatus consists of two thermopiles containing more than 200 thermocouples, a commercial wire wound resistance furnace (HTC-1000, SETARAM, Lyon, France) and a self-made automatic drop device for up to 30 drops. The SAC387 alloy was placed in a BN crucible. The time interval between individual drops was 40 min, and the acquisition interval of the heat flow was 0.5 s. The calorimeter was calibrated by five drops of standard α-Al2O3 provided by NIST (National Institute of Standards and Technology, Gaithersburg, MD) at the end of the drop series of each separate measurement. The microcalorimeter and the mechanical sampler were controlled through a self-provided software using the graphical programming environment LabVIEW. The obtained signals from the thermocouples were recorded and evaluated using the commercial HiQ© software. The microcalorimeter was described in detail elsewhere.42

In general, the measured enthalpy (integrated heat flow at constant pressure) for bulk materials is equal to:

 
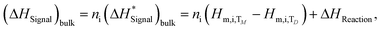image file: c7ra13643a-t10.tif(10)
where ni is the number of moles of the added element i, image file: c7ra13643a-t11.tif is the measured enthalpy in J mol−1, Hm denotes molar enthalpies, TD is the drop temperature, and TM is the calorimeter temperature for the respective measurement in Kelvin. The molar enthalpy difference (Hm,i,TM − Hm,i,TD) was calculated using the SGTE data for pure elements.43

However, in the case of nanosized additions one must also take into account the additional heat effect caused by the excess (surface) enthalpy of the metal nanoparticles. Thus, eqn (10) for the addition in the nanosized form can be rewritten as19:

 
image file: c7ra13643a-t12.tif(11)
where ΔHexi,nano is the excess enthalpy connected with the replacement of bulk material by nano-particles in J mol−1. Therefore, in order to find the heat effect caused by the additions of material in nanosized form we must know the heat effect caused by the addition of the same material in bulk form.

Furthermore, due to the rather small masses of added component i, partial enthalpies can be calculated by:

 
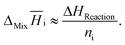image file: c7ra13643a-t13.tif(12)

The integral molar enthalpy of mixing, ΔMixH, was calculated by summing the respective reaction enthalpies and dividing by the total molar amount of substance, where nj stands for the molar amount of substance which was already present in the crucible:

 
image file: c7ra13643a-t14.tif(13)

Prior to the measurements, the SAC387 alloy was prepared from Sn ingot (99.998% metallic purity), Ag shot (99.999% metallic purity) and Cu rods (99.9% metallic purity, all from Alfa Aesar, Karlsruhe, Germany) without further purification. The samples with a total mass between 5 and 10 g were sealed in evacuated quartz glass ampoules and kept in a muffle furnace for 2 weeks at 1173 K. The mass loss of the ingots was less than 0.1 mg.

The measurements were performed by dropping pure Ni or Cu, both in bulk and nanosized form. Ni pieces were obtained from Advent (99.99%; Oxford, UK), Ni and Cu nanopowders from IoLiTec Nanomaterials (Heilbronn, Germany). To avoid severe oxidation, all operations with nano-Ni and nano-Cu were performed in a glovebox (M. Braun, LabMaster 130) under Ar atmosphere (Ar 5.0; O2 and H2O < 5 ppm each). The calorimetric measurements using the metal nanopowders were carried out similar to our previous thermodynamic investigations of nano-Co additions to liquid SAC387 alloys.19 the Ni and Cu nanoparticles were first packed into a SAC387 foil. The employed foil was produced from the same ingot using a foil rolling mill; it had a thickness of about 50 μm. The sample holders of the auto sampling device were loaded with nanopowder samples inside the glovebox and closed in a box, which was only taken out just before the measurement to be transported to the calorimeter. The calorimetric measurements with the packed nanoparticles were started with five drops of SAC387 foil pieces in order to determine and, subsequently, subtract the heat effect of the SAC387 foil from the obtained measured enthalpy. A few measurements with bulk Cu and Ni, packed into the SAC387 foil, were also carried out to prove the accuracy of this procedure.

Various factors must be considered when estimating the random and systematic errors in the measurements, i.e. the calorimeter construction, measuring method, calibration procedure, signal integration and “chemical errors”. Uncertainties of the enthalpy values given in Tables 1–6 were estimated based on the propagation of errors, taking also into account the standard deviation of the calorimeter constant s(k) which was evaluated by five drops of alumina for each run. The uncertainty of the partial enthalpy of mixing for each drop was calculated based on the uncertainties of peak areas of each drop, Ai, of the amount of added component, ni, and s(k); the error of the integrated enthalpy of mixing was taken summarizing the errors of the single drops throughout the final composition. A similar procedure of calculation of the uncertainties of the enthalpy values was employed previously in ref. 44 and 45.

The phase composition and the microstructure of the samples were examined after the calorimetric measurements by powder X-ray diffraction (XRD; Bruker D8 Advance X-ray diffractometer) and scanning electron microscopy (SEM; Zeiss Supra 55 ESEM). The XRD analysis was carried out at ambient temperature using Ni-filtered Cu Kα radiation (accelerating voltage 40 kV, electron current 40 mA). The nanopowders were fixed onto the sample holder using pre-dried petroleum jelly in the Ar-filled glovebox. Rietveld refinement of XRD patterns was performed with the Topas 3 software provided by Bruker AXS. The energy-dispersive X-ray (EDX) detector signal for SEM analysis was calibrated using pure elements as standard materials and Co for the energy calibration.

The Ni and Cu nanoparticles were characterized by XRD analysis (XRD; Bruker D8 Advance X-ray diffractometer) and transmission electron microscopy (TEM; analytical TECNAI F20 field emission TEM). A silicon single crystal sample holder with a matching polymer (polycarbonate) cap was used in order to avoid a possible oxidation of NPs. The EDX mapping of NPs was performed with an energy-dispersive X-ray detector (EDAX TEAM Apollo XLTW SDD).

The surface area of the nanopowders was estimated using the BET technique, whereby N2 adsorption–desorption isotherms of the nanopowders were analyzed using a TriStar II 3020 instrument (Micromeritics). This method is based on a theory developed by S. Brunauer, P. Emmett and E. Teller46 where the name of the theory was taken from the first letter of each author's surnames. According to this method, the surface area of a known mass of a sample was determined by monitoring the mass change by adsorption of nitrogen over time, which is widely used due to its availability in high purity and its strong interaction with most solids. The data collected during the measurement are shown in the form of a BET isotherm, which plots the quantity of gas adsorbed as a function of the relative pressure.

Conclusions

The presented experimental results show clearly that an extra exothermic heat effect (nano-heat effect) is observed when bulk pieces are replaced by nano-particles in drop calorimetric measurements. First of all, this is due to the loss of the large surface area of the nano-particles upon their dissolution. However, when the nano-particles are covered with a surface oxide shell, resulting in an exothermic chemical reaction with the solvent (a liquid alloy in the present case), the measured nano-effect can become even more exothermic, especially if the reaction enthalpy is strongly negative. This effect has been examined here on the example of the core/shell Cu/Cu2O and Ni/NiO nano-particles dropped into Sn-rich liquid alloys.

Conflicts of interest

There are no conflicts to declare.

Acknowledgements

This work was supported by the Austrian Science Fund (FWF) [grant numbers P 26304 and P 27049]. The authors want to acknowledge the help of Prof. M. Zehetbauer and Prof. E. Schafler from the Faculty of Physics, University of Vienna, with the Sn-4.1Ag-1.3Cu foil preparation, Ing. C. Mitterer from the Faculty of Chemistry, University of Vienna, with BET analysis and Dr St. Puchegger from the Faculty of Physics, University of Vienna, with the SEM studies. TEM analysis was performed using the facilities at the University Service Center for Transmission Electron Microscopy at the Vienna University of Technology. The work by G.K. was supported by project GINOP 2.3.2 – 15 – 2016 – 00027 financed in the framework of the Szécheny-plan supported by the European Union.

References

  1. M. Zhang, M. Y. Efremov, F. Schiettekatte, E. A. Olson, A. T. Kwan, S. L. Lai, T. Wisleder, J. E. Greene and L. H. Allen, Phys. Rev. B, 2000, 62, 10548–10557 CrossRef CAS.
  2. S. Y. Xiong, W. H. Qi, Y. J. Cheng, B. Y. Huang, M. P. Wang and Y. J. Li, Phys. Chem. Chem. Phys., 2011, 13, 10652–10660 RSC.
  3. R. Ferrando, Structure and properties of nanoalloys, Elsevier, Amsterdam, 2016, vol 10 Search PubMed.
  4. Y. Hua, K. Chandra, D. H. M. Dam, G. P. Wiederrecht and T. W. Odom, J. Phys. Chem. Lett., 2015, 6, 4904–4908 CrossRef CAS PubMed.
  5. K. S. Lee and M. A. El-Sayed, J. Phys. Chem. B, 2006, 110, 19220–19225 CrossRef CAS PubMed.
  6. N. Dai, L. Zhang, Z. Wang, X. Wang, J. Zhang, H. Gong, H.-B. Han and Y. Han, J. Phys. Chem. C, 2017, 121, 12358–12364 Search PubMed.
  7. I. Papagiannouli, P. Aloukos, D. Rioux, M. Meunier and S. Couris, J. Phys. Chem. C, 2015, 119, 6861–6872 CAS.
  8. S. W. Baek, G. Park, J. Noh, C. Cho, C. H. Lee, M. K. Seo, H. Song and J. Y. Lee, ACS Nano, 2014, 8, 3302–3312 CrossRef CAS PubMed.
  9. E. Hao, G. C. Schatz and J. T. Hupp, J. Fluoresc., 2004, 14, 331–341 CrossRef CAS PubMed.
  10. W. H. Qi, Acc. Chem. Res., 2016, 49, 1587–1595 CrossRef CAS PubMed.
  11. J. Shen and Y. C. Chan, Microelectron. Reliab., 2009, 49, 223–234 CrossRef CAS.
  12. L. Sun and L. Zhang, Adv. Mater. Sci. Eng., 2015, 2015, 639028 Search PubMed.
  13. E. E. M. Noor, A. Singh and T. C. Yap, Soldering Surf. Mount Technol., 2013, 25, 229–241 CrossRef CAS.
  14. A. Yakymovych, Y. Plevachuk, P. Svec, D. Janikovic, P. Sebo, N. Beronska, M. Nosko, L. Orovcik, A. Roshanghias and H. Ipser, J. Mater. Sci.: Mater. Electron., 2017, 28, 10965–10973 CrossRef CAS.
  15. M. N. Bashir, A. S. M. A. Haseeb, A. M. S. Rahman, M. A. Fazal and C. R. Kao, J. Mater. Sci., 2015, 50, 6748–6756 CrossRef CAS.
  16. A. K. Gain and Y. C. Chan, Intermetallics, 2012, 29, 48–55 CrossRef CAS.
  17. L. Zhang and K. N. Tu, Mater. Sci. Eng., R, 2014, 82, 1–32 CrossRef.
  18. S. L. Tay, A. S. M. A. Haseeb, M. R. Johan, P. R. Munroe and M. Z. Quadir, Intermetallics, 2013, 33, 8–15 CrossRef CAS.
  19. A. Yakymoyych, G. Kaptay, A. Roshanghias, H. Flandorfer and H. Ipser, J. Phys. Chem. C, 2016, 120, 1881–1890 Search PubMed.
  20. A. Yakymoyych, Y. Plevachuk, V. Sklyarchuk, B. Sokoliuk, T. Galya and H. Ipser, J. Phase Equilib. Diffus., 2017, 38, 217–222 CrossRef.
  21. A. Yakymovych, S. Mudry, I. Shtablavyi and H. Ipser, Mater. Chem. Phys., 2016, 181, 470–475 CrossRef CAS.
  22. A. T. Tan, A. W. Tan and F. Yusof, Sci. Technol. Adv. Mater., 2015, 16 Search PubMed.
  23. H. Flandorfer, C. Luef and U. Saeed, J. Non-Cryst. Solids, 2008, 354, 2953–2972 CrossRef CAS.
  24. C. Luef, H. Flandorfer and H. Ipser, Z. Metallkd., 2004, 95, 151–163 CrossRef CAS.
  25. G. Kaptay, Metall. Mater. Trans. A, 2012, 43, 531–543 CrossRef CAS.
  26. U. Saeed, H. Flandorfer and H. Ipser, J. Mater. Res., 2007, 22, 3218–3225 CrossRef CAS.
  27. S. W. Chen and C. A. Chang, J. Electron. Mater., 2004, 33, 1071–1079 CrossRef CAS.
  28. C. Schmetterer, M. Rodriguez-Hortala and H. Flandorfer, J. Phase Equilib. Diffus., 2014, 35, 429–433 CrossRef CAS PubMed.
  29. S. Furtauer, D. Li, D. Cupid and H. Flandorfer, Intermetallics, 2013, 34, 142–147 CrossRef CAS PubMed.
  30. W. Wang, Z. G. Liao, Y. Wang, X. A. Wu, F. Y. Qu and X. Zhang, Cryst. Res. Technol., 2011, 46, 300–304 CrossRef CAS.
  31. P. E. Tomaszewski, Phase Transitions, 1992, 38, 127–220 CrossRef CAS.
  32. R. Vallee, M. Wautelet, J. P. Dauchot and M. Hecq, Nanotechnology, 2001, 12, 68–74 CrossRef CAS.
  33. G. Kaptay, J. Nanosci. Nanotechnol., 2012, 12, 2625–2633 CrossRef CAS PubMed.
  34. G. Kaptay, RSC Adv., 2017, 7, 41241–41253 RSC.
  35. L. Z. Mezey and J. Giber, Jpn. J. Appl. Phys., Part 1, 1982, 21, 1569–1571 CrossRef CAS.
  36. G. Kaptay, J. Mater. Sci., 2012, 47, 8320–8335 CrossRef CAS.
  37. R. D. Holmes, H. S. C. O'Neill and R. J. Arculus, Geochim. Cosmochim. Acta, 1986, 50, 2439–2452 CrossRef CAS.
  38. G. Petot-Ervas, R. Farhi and C. Petot, J. Chem. Thermodyn., 1975, 7, 1131–1136 CrossRef CAS.
  39. G. V. Samsonov, Physico-chemical properties of oxides, Metallurgia, Moscow, 1978 Search PubMed.
  40. G. Kaptay, E. Bader and L. Bolyan, Mater. Sci. Forum, 2000, 329–3, 151–156 CrossRef.
  41. I. Barin and F. Sauert, Thermochemical properties of pure substances, Wiley-VCH, New York, 1993 Search PubMed.
  42. H. Flandorfer, F. Gehringer and E. Hayer, Thermochim. Acta, 2002, 382, 77–87 CrossRef CAS.
  43. A. T. Dinsdale, CALPHAD, 1991, 15, 317–425 CrossRef CAS.
  44. A. Yakymovych, S. Furtauer, H. Flandorfer and H. Ipser, Monatsh. Chem., 2014, 145, 1697–1706 CrossRef CAS PubMed.
  45. A. Yakymovych, S. Furtauer, A. Elmahfoudi, H. Ipser and H. Flandorfer, J. Chem. Thermodyn., 2014, 74, 269–285 CrossRef CAS PubMed.
  46. S. Brunauer, P. H. Emmett and E. Teller, J. Am. Chem. Soc., 1938, 60, 309–319 CrossRef CAS.
This journal is © The Royal Society of Chemistry 2018
Click here to see how this site uses Cookies. View our privacy policy here.