Open Access Article
Open Access ArticleMolecular dynamics simulation of the viscoelasticity of polymer nanocomposites under oscillatory shear: effect of interfacial chemical coupling
Ziwei Li a,
Jun Liu*abcd,
Zhiyu Zhanga,
Yangyang Gaoabcd,
Li Liu*abcd,
Liqun Zhang
a,
Jun Liu*abcd,
Zhiyu Zhanga,
Yangyang Gaoabcd,
Li Liu*abcd,
Liqun Zhang abcde and
Binbin Yuanf
abcde and
Binbin Yuanf
aKey Laboratory of Beijing City on Preparation and Processing of Novel Polymer Materials, Beijing University of Chemical Technology, People's Republic of China
bBeijing Engineering Research Center of Advanced Elastomers, Beijing University of Chemical Technology, People's Republic of China
cEngineering Research Center of Elastomer Materials on Energy Conservation and Resources, Beijing University of Chemical Technology, People's Republic of China
dBeijing Advanced Innovation Center for Soft Matter Science and Engineering, Beijing University of Chemical Technology, Beijing 100029, People's Republic of China
eState Key Laboratory of Organic-Inorganic Composites, Beijing University of Chemical Technology, Beijing 100029, People's Republic of China
fThe Second Research Institute of Civil Aviation Administration of China, Chengdu 610000, People's Republic of China
First published on 20th February 2018
Abstract
In this work by adopting coarse-grained molecular dynamics simulation, we focus our attention on investigating the effect of the chemical coupling between polymer and nanoparticles (NPs) on the viscoelastic properties of polymer nanocomposites (PNCs). Firstly we examine the effect of the interfacial chemical coupling on the non-linear behavior, such as the change of the storage moduli, the loss moduli and the loss factor as a function of the strain amplitude. Besides the reinforcing effect contributed by the interfacial chemical interaction, a much smaller loss factor is also observed attributed to less molecular friction and dissipation. Meanwhile, the effects of temperature, frequency, and the interfacial physical interaction between NPs and polymers on the viscoelastic properties are also probed. To uncover the structural and dynamic effect of the interfacial chemical coupling, we calculate the radial distribution function of polymer chains around NPs, the content of the polymer beads in the first layer of the interfacial region under quiescent and dynamic conditions, the incoherent intermediate dynamic structure factor of the polymer beads, which are chemically or physically tethered to the NPs, and all the polymer beads of the system, the quantitative comparison of the mean relaxation time for different interfacial chemical coupling, and the mean-square displacement of the polymer chains. Lastly we analyze the change of the interfacial energy such as the physical and chemical energies during oscillatory shear. Through these analyses, we conclude that with the increase of the interfacial chemical coupling, the change extent of the interfacial physical interaction versus the periodic strain decreases, attributed to a much smaller adsorption–desorption reversible process. This can rationalize the much weaker non-linear behavior or the “Payne effect”. Based on these results, we anticipate that a better molecular-level understanding is provided on the effect of the interfacial coupling on the viscoelastic properties of PNCs.
1. Introduction
Filled elastomers are of great significance and have been extensively used in industrial applications. When subjected to a certain degree of periodic strain, filled elastomers exhibit typical nonlinear behavior, such as the reduction of the modulus as a function of the dynamic strain amplitude, which is commonly called the “Payne effect”.1,2 Payne explained that this effect was attributed to the destruction of the physical interaction between fillers. The fact that the modulus decreases sharply with the increase of the strain is detrimental for filled polymers used under dynamic loading. It is important to understand the nature of the “Payne effect” and attenuate it in some conditions. Since the concept of “Payne effect” is proposed, several models have been presented to illustrate this phenomenon. There is a widely held view that the non-linear strain-dependent behavior of filled rubbers is attributed to the break-down of filler networks. Kraus3 suggested the first phenomenological quantitative model to describe the “Payne effect” relying on the agglomeration–deagglomeration of carbon black agglomerates. Furthermore, Kraus considered that it is the excess forces between particles or between particles and polymers that leads to the non-linear decrease behavior. The van de Walle–Tricot–Gerspacher model4 introduced a weighting function to establish the relationship between G′ and G′′. The NJ-model5 tended to examine the energy dissipation process in junction points between carbon black aggregates and provided a filler network interpretation for modulus increase with increasing filler content. The Links–Nodes–Blobs model6,7 is introduced by Lin and Lee to describe the strain-dependent dynamic properties of filled rubber network caused by the destroying of chain-like structures and aggregates interconnected by weak bonds. Alternatively, Cassagnau8 proposed that the “Payne effect” is associated with the chain disentanglements as well as the filler network breakdown, which are directly related to the silica content and the dynamic strain amplitude. In contrast to the above mechanisms, Maier et al.9 proposed that the “Payne effect” can be produced by the stress-induced debonding of polymer chains from the filler surface. Moreover, Sternstein and Zhu et al.10,11 found that the “Payne effect” still occur at low filler concentrations, in which case the filler network is difficult to form, which results from the release of the trapped polymer entanglement structures at polymer–filler interfaces that determine the viscoelastic behavior of the composite, rather than the breakage of the filler agglomeration or network. Alireza12 declared in his research that the amplitude-dependent dynamic moduli is attributed to disentanglement of bulk polymer chains from those strongly adsorbed to the surface of nanoparticles. This is essentially due to the mismatch between the relaxation times of the free and adsorbed chains and flow-induced disentanglement of adsorbed chains in fast flows. Moreover, Yang et al.13 consider that the microscopic strain of the matrix is the major reason for reinforcement and onset of the “Payne effect” instead of the variations of filler agglomeration. The aforementioned theories reasonably illustrate the “Payne effect” to a certain extent and can be summarized to the following reasons from two aspects: (i) the particle–particle interaction and (ii) the polymer–particle interaction.Up to now, several simulation studies have been carried out to investigate the viscoelasticity of polymer nanocomposites,14–24 because of its fine analysis and characterization at the molecular level compared to experimental tools. Our group has carried out the relevant research before. To be specific, Chen et al.25 provided an insight on the role of polymer–particle interactions in the strain-dependent viscoelasticity, by studying the cross-linked elastomeric systems containing various concentrations of monodispersed NPs with different interfacial interactions via coarse-grained molecular dynamics simulation. Chen concluded the two important factors contributing to the “Payne effect” of filled elastomers, such as the breakage of the rigid polymer shell around NP and the rearrangement of polymer-shell-bridged NP network under oscillatory shear. While in the case of low loading the debonding of polymer monomers from the NP surfaces as well comes into play. Wang et al.26 found that, with the increase of the formed semi-interpenetrating NP network by molecular simulation, the “Payne effect” decreases at small strain amplitude, while the dynamic storage modulus was strengthened, and the energy loss was lowered at large strain amplitude. The result is attributed to the break-up of the aggregation of the NPs and an enhanced interfacial contact area between the polymer chains and NPs which leads to the much friction. Raos et al.27 used the coarse-grained DPD simulation to study the change of the storage modulus of filled elastomers under the oscillatory shear flow. They observed a strain stiffening of the material (anti-Payne behavior), different from those observed experimentally. And in their next study,28 they claimed that the particle–particle interaction does not directly influence the “Payne effect”. Moreover, a dependence of the small-strain nonlinear behavior of filled elastomer was also seen in FEM simulations by Gusev et al.29
Although some simulation work have been carried out to investigate the mechanism of the “Payne effect” and most of them focused on the role of the physical interactions of the polymer–filler and filler–filler. To promote and realize a better dispersion of NPs and corresponding properties in the polymer matrix, the chemical modification technique is widely used, which is favorable to enhance the compatibility of the NPs with the polymer matrix, such as the coupling agent modification30 and the polymer grafting modification.31 Furthermore, some studies32,33 indicated that the coupling agent modification of fillers could weaken the “Payne effect” due to the reduction of filler–filler interaction or the filler network. Qiao et al.34 used epoxy group-functionalized styrene-butadiene rubbers to form a covalent bonding with the hydroxyl groups on the silica surfaces resulting from a ring-opening reaction. The inclusion of just 1.6 wt% of glycidyl methacrylate (GMA) reduces the initial G′ by 75% with the “Payne effect” decreasing significantly. The authors explained this in two factors: (1) the improved dispersion of silica which reduced the filler–filler network; (2) the improved interfacial interaction between rubber and filler which strengthened the filler–rubber network due to the restriction of the mobility of rubber. Nevertheless, other results35,36 showed that if graphene oxide and carbon nanotubes are surface grafted with small molecules or polymer chains, the “Payne effect” may become more prominent. It is because these grafted ligands have much weaker interfacial interaction with the polymer matrix, leading to the formation of the additional filler–filler networks compared with the pristine case. Meanwhile, chain modification can also result in a much weaker “Payne effect” compared with the untreated at the same loading of silica fillers.37 Zhong et al.38 also found that the non-linear strain-dependent lightly increases via vulcanization accelerator grafted the silane modified silica compared to the silane modified, which is induced by the slippage of adsorbed polymer chains on the filler surface during tension.
On the other hand, Gregory et al.39 used molecular dynamics simulation to investigate the viscoelastic properties of polymer nanocomposites composed of polymer-grafted NPs. Results illustrated that the moduli decreased with increasing NP size, and increased with the increase of the NP loading, graft length, grafting density and graft/matrix affinity, which results from the additional distortion of the shear field in the polymer matrix caused by the addition of NP grafts into the polymer matrix. Liu et al.40 found that polymer nanocomposites filled with end-grafted nanoparticles showed a weaker strain-induced nonlinear behavior compared to NPs without any surface modification via molecular dynamics simulation. The phenomenon is more obvious with the increase of the grafted chain length. They further conjectured that the polymer end-grafting of the NPs can enhance the brush/matrix interface thickness, and correspondingly improve the dispersion state and the physical interfacial interaction.
In this work, we focus our attention on the effect of the chemical coupling between NPs and polymers on the viscoelasticity through a non-equilibrium molecular dynamics (NEMD) simulation method. By fixing the filler volume fraction equal to 26.5%, we systematically change the physical parameters such as the interfacial chemical coupling extent, the temperature, and the dynamic periodic shear frequency. Note that the physical interactions between nanoparticles–nanoparticles (εnn) and between polymer–polymer (εpp) are set to be weakly attractively, while we vary the physical interaction strength between polymer and NPs (εnp). The viscoelastic properties of the simulated PNCs under oscillatory shear are obtained with the “Payne effect” decreasing as the chemical coupling increases. The mechanism is illustrated by analyzing the structural parameters such as the distribution function of polymers around NPs and dynamic structural evolution. The reasons of the reduction of the “Payne effect” in this work can be summarized to two aspects: (1) with the introduction of the chemical coupling, the polymers become more tightly to NPs which leads to the reduction of filler–filler network; (2) the variation of interfacial physical interaction as periodic shear proceeds which is corresponding to the adsorption–desorption reversible process.
2. Simulation model and method
A standard Kremer and Grest41 bead-spring model was chosen to represent the polymer chain. Each bead in the polymer chain has the size of σ and the mass of m. Each polymer chain consists of 30 beads, which makes sure that the size of polymer chains is comparable with that of the NPs. And it has been shown that the chains with this length exhibit the static behavior characteristic of long polymers in the melt.40 The adjacent beads on a polymer chain are connected with each other via a strong bonded interaction, finite extensible nonlinear elastic (FENE) potential,
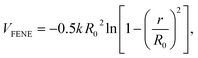 | (1) |
 | (2) |
It should be noted that when mapping the simulation units to experimental ones, the interaction parameter ε is set to be about 2.5–4.0 kJ mol−1 depending on specific polymers.44–46 According to the reported mapping process,47,48 the modeled NP with the diameter equal to 10σ generally maps to silica particles with the diameter of 12.8–28.8 nm. Therefore, the NP with the diameter equal to 4σ in the present simulation model approximately corresponds to silica particles with the diameter of 5–12 nm. Moreover, it is generally assumed that one polymer bead with a diameter of 1 nm roughly corresponds to 5 repeating units of polyethylene for that the carbon–carbon bond length equal to 0.154 nm in the polymer physics. It indicates that one polymer bead with the diameter of 1σ in the current model corresponds to 3–6 bonds of a realistic polymer chain. Furthermore, when mapping the simulation time unit to experimental scale, τ ranges from 1.8 ps for PTHF to 66 ps for PE.40 Thus, our simulation is considered to fall within a realistic range of experiments.49,50
After the fillers were dispersed in the polymer matrix, the chemical coupling between fillers and polymers were introduced. The chemical coupling is composed of the chemical bonds which are randomly created between polymers and NPs, when the distance between them becomes smaller than 2.75σ. The process of the chemical coupling continues until the pre-set interfacial chemical coupling (Nb = 0 to 30) is reached. By statistically averaging the number of connected NPs on each polymer chain, we found that the chemical connection points are evenly distributed along the chain backbone. The chemical bonds between polymer and fillers were described as the same FENE potential with the parameters setting to k = 30ε/σ2 and R0 = 1.5σ. We controlled the number of the chemical bonds between polymers and each NP equal to 0 to 30 (Nb = 0 to 30), respectively, as shown in Fig. 1. Note that the blue beads represent those polymer beads, which are chemically bonded the NPs.
At the beginning, NPs and polymers were placed in a big simulation box with a periodic boundary condition adopted in all three directions. The temperature was fixed at T = 1.0 which is above the glass transition temperature (T = 0.41) of polymer chains by using the Nose–Hoover thermostat and barostat. The NPT ensemble of 5 × 106 steps (5 × 103τ) was adopted here to ensure the number density of the polymer equal to around ρ = 0.85, which corresponds to the density of polymer melts. The velocity-Verlet algorithm was applied to integrate the equations of motion with a timestep of δt = 0.001, where the time was reduced by the LJ time (τ). Following this, chemical bonds between NPs and polymers were generated if their distances were less than 3.0 in the NVT ensemble. The process could be monitored by collecting the statistics of the total number of chemical bonds. After adequate equilibrium of the above system, NEMD simulations in the canonical (NVT) ensemble were performed at T = 1.0 and the algorithm for the oscillatory shear was realized using the SLLOD equations of motion. The shear strain and time-dependent shear rate were respectively expressed as
![[small gamma, Greek, dot above]](https://www.rsc.org/images/entities/i_char_e0a2.gif) xy(t) = γ0 xy(t) = γ0![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) sin(2πνt), sin(2πνt),
| (3) |
![[small gamma, Greek, dot above]](https://www.rsc.org/images/entities/i_char_e0a2.gif) xy(t) = 2πνγ0 xy(t) = 2πνγ0![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) cos(2πνt), cos(2πνt),
| (4) |
σxy(t) = γ0[G′![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) sin(2πνt) + G′′ sin(2πνt) + G′′![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) cos(2πνt)], cos(2πνt)],
| (5) |
![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) δ = G′′/G′). In the current simulations, shear frequency in most simulation systems is 0.01τ−1, followed from the literature.51 Furthermore, we adjusted the frequency to 0.001τ−1 for comparison. The shear strain amplitude γ0 was varied to study the viscoelasticity of the systems as a function of the shear strain. NEMD simulation for each system consisting of 107 steps (104τ) to guarantee the consistency, followed by 106 steps (103τ) to sample the properties. Then the structural and dynamic data were collected for ensemble average. All the MD simulations were conducted using the large scale atomic/molecular massively parallel simulator (LAMMPS) molecular dynamics package.52
δ = G′′/G′). In the current simulations, shear frequency in most simulation systems is 0.01τ−1, followed from the literature.51 Furthermore, we adjusted the frequency to 0.001τ−1 for comparison. The shear strain amplitude γ0 was varied to study the viscoelasticity of the systems as a function of the shear strain. NEMD simulation for each system consisting of 107 steps (104τ) to guarantee the consistency, followed by 106 steps (103τ) to sample the properties. Then the structural and dynamic data were collected for ensemble average. All the MD simulations were conducted using the large scale atomic/molecular massively parallel simulator (LAMMPS) molecular dynamics package.52
3. Results and discussion
3.1 Viscoelastic behavior
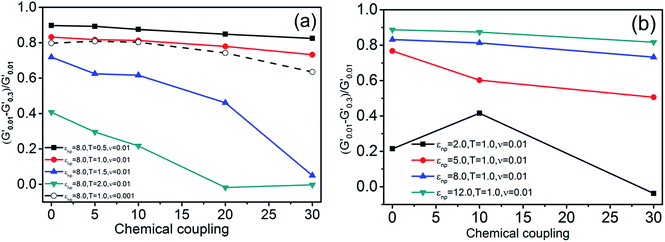
Following our previous work,25 the “Payne effect” is related to the polymer–filler interaction and the filler loading. Firstly we examine the change of the storage moduli, the loss moduli and the loss factor as a function of the strain amplitude for various extent of interfacial chemical coupling, by fixing the interfacial physical interaction εnp = 8.0, the volume fraction of filler equal to 26.5% and the dynamic shear frequency ν = 0.01τ−1, as shown in Fig. 2. It can be observed from Fig. 2(a) and (b) that both G′ and G′′ decrease with the increase of the strain amplitude, and enhance with the increasing interfacial chemical coupling. The decrease of the storage moduli becomes prominent at the strain amplitude greater than 0.02, while at the highest interfacial coupling the storage moduli becomes increased at large strain amplitude. We will interpretate this observation later. Moreover, the beginning strain for the decrease of the loss moduli is around γ0 = 0.1, which demonstrates a relative lag response on the shear strain compared to the storage moduli. Fig. 2(c) reveals that the loss factor decreases with the interfacial chemical coupling, indicating less molecular friction and dissipation. | ||
Fig. 2 (a) Storage modulus G′, (b) loss modulus G′′, and (c) loss factor tan![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) δ, as a function of shear strain amplitude for the systems with different polymer–particle chemical coupling on temperature at 1.0 and frequency at 0.01τ−1. (d) Strain dependence of G′ for CR/m-MWCNT composites with different MWCNT/CMI ratios (ref. 53). δ, as a function of shear strain amplitude for the systems with different polymer–particle chemical coupling on temperature at 1.0 and frequency at 0.01τ−1. (d) Strain dependence of G′ for CR/m-MWCNT composites with different MWCNT/CMI ratios (ref. 53). | ||
We have compared our work with some experimental results in Fig. 2. Jiang et al.53 investigated the effect of the non-covalent modification of carboxylated multi-walled carbon nanotubes (MWCNT) by 1-carboxyethyl-3-methylimidazolium bis(trifluoromethyl sulfonyl)imide (CMI), on the polymer–filler interactions, filler dispersion, and mechanical properties of polychloroprene (CR)/MWCNT composites. Fig. 2(d) shows that by with increasing MWCNT/CMI ratio from 1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 0 to 1
0 to 1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 2, the “Payne effect” of CR composite becomes more pronounced, indicating CMI can effectively strengthen the interactions between MWCNT and CR. However, when the MWCNT/CMI ratio is as high as 1
2, the “Payne effect” of CR composite becomes more pronounced, indicating CMI can effectively strengthen the interactions between MWCNT and CR. However, when the MWCNT/CMI ratio is as high as 1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 8, the ΔG′ decreases because CMI has an obvious plasticizing effect on CR/m-MWCNT composites when the CMI content is very high. It can be assumed that the increase of the physical interaction between polymer and filler enhances the “Payne effect”, and the excessive force such as the chemical interaction may weaken the “Payne effect”.
8, the ΔG′ decreases because CMI has an obvious plasticizing effect on CR/m-MWCNT composites when the CMI content is very high. It can be assumed that the increase of the physical interaction between polymer and filler enhances the “Payne effect”, and the excessive force such as the chemical interaction may weaken the “Payne effect”.
3.2 Structures
In order to realize the essence of role of chemical coupling between polymers and NPs, a series of simulated processes were performed to analyze the internal structures of simulated systems. Fig. 7(a) shows distribution states of polymers around NPs in unsheared systems at five chemical coupling degrees using radial distribution functions (RDFs). The value of the peak at r = 2.65σ which caused by physical adsorption means that there is a packed polymer layer (the first layer) referred to “bound rubber” or “bound shell” in rubber materials55,56 and it declines consistently with the increasing chemical coupling. At the same time, a new peak at r = 2.45σ appears and increases with the increasing chemical bonds. It is interpreted that the chemical coupling converse partial interactions between NPs and polymers from physical adsorption to chemical bonding which makes polymers bound to the NPs' surfaces more tightly. Furthermore, Fig. 7(b) shows the radial distribution functions (RDFs) of NPs around NPs, which reflects the filler dispersion state. The remarkable peak emerging at about r = 5σ indicates that there is a layer of chain molecules between NPs. The remarkable peak emerging at about r = 5σ indicates that there's a layer of polymer molecules between NPs. The value of the peak gradually declines and moves left as the Nb increases, which manifests that the chemical coupling between polymer and NPs makes the NPs closer to each other. | ||
| Fig. 7 (a) Radial distribution function of polymers around NPs, gnp(r); (b) radial distribution function of NP–NP, gnn(r) in the system with εnp = 8.0. | ||
Fig. 8 shows the first layer content of polymers which represents the average number of polymers within a distance of σ from each NP surface with respect to the shear amplitude in quiescent condition. That means if the polymer molecule is bound to any NP within a distance of σ, it will be classified as polymers in the first layer around NP. We average the number of this type of polymer molecules for each NP, which is referred to the value of the first layer content. The value decreases with the shear amplitude increasing uniformly, which means that more polymers separate from the NP surface as the shear amplitude increases. It is also found that the overall value decreases with the increasing chemical coupling. It demonstrates that more polymers without chemical coupling are crowed out of the layer within the distance of σ from the NP surface as the chemical coupling increases, which indicates polymers are more tightly to NPs' surface.
The first layer content generates a periodic variation that the value decreases with the strain increasing in a shearing period of time equal to 100τ as shown in Fig. 9. The lowest value appears at the maximum strain amplitude, which means that the content of polymer chains desorbing from the surface of the NPs becomes the biggest at that point.
Fig. 10 shows the incoherent intermediate dynamic structure functions (Φsq) of polymers which reflects the mobility of polymers. The faster the values decline, the higher the mobility of polymers is. It is obvious that polymers with chemical coupling (the blue lines) have weaker mobility compared to polymers without chemical coupling (the red lines) in the first layer around NPs in each chemical coupling system. Moreover, the function of system Nb = 0 which has no chemical coupling reduces the fastest corresponding to the highest mobility of polymers. Furthermore, the functions of total polymers always behave the same as the functions of polymers without chemical coupling in each system except the system Nb = 30, which is due to that the considerable chemical coupling is enough to affect the total mobility.
Results of MRT curves shown in Fig. 11 demonstrate that the introduction of chemical bonds between NPs and polymers increases the relaxation time of polymers in the first layer but decreases it of total polymers. On one hand, polymers in the first layer become tight to NPs and the relaxation behavior becomes weak as the chemical coupling increases. On the other hand, for total polymers, the mean relaxation time decreases with the number of chemical bonds increasing, which is due to that the tightly limited polymers with chemical coupling around NPs weaken the physical interactions between NPs and all the rest polymers.
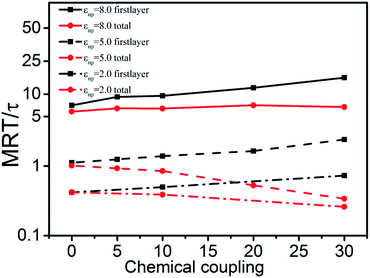 | ||
| Fig. 11 Mean relaxation time (MRT) of polymers in the first layer and that of total polymers as a function of chemical coupling at varies εnp. | ||
Results of mean square displacements which represent the mobility of whole polymer chains are shown in Fig. 12. The mobility of whole polymer chains become weaker with the increasing chemical coupling, which exhibits a similar case to the mobility of polymer monomers results shown in Fig. 7.
 | ||
| Fig. 12 Mean square displacements (MSD) of polymer chains as a function of equilibrium time for systems with different chemical coupling. | ||
3.3 Energy evolution under the oscillatory shear
The interfacial potential energy which reflects the polymers around NPs were monitored under oscillatory shear and presented in Fig. 13. The energy exhibits periodically changes with time obviously which is synchronous with shear strain, which is attributed to polymer chains debonding to particle surface under shear. Partial polymer monomers were bonded to NP surface through chemical coupling and these monomers could not debond under shear. The absolute value overall energy gradually decreases with the increasing chemical coupling from Nb = 0 to Nb = 30, which is corresponding to the gradually weakened physical adsorption–desorption process. It suggests that chemical bonds between polymer and NPs hinder the interfacial physical bonding–debonding effect and consequently weaken the downward trend of G′.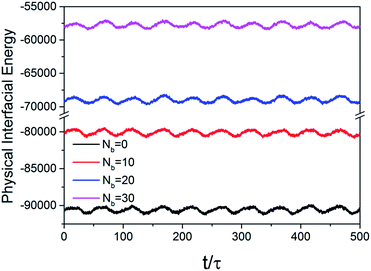 | ||
| Fig. 13 Plot of the physical interaction energy between polymers and NPs as a function of shearing time at shear strain of 30% and εnp = 8.0. | ||
Fig. 14 directly shows the corresponding energy changes of total bonds including bonds on polymer chains and chemical coupling bonds as the shear cycles at varying amplitudes. The cyclic shear period is 100τ, which means the simulation box deforms and returns to the initial state every 50τ with the maximum value of bond energy appears at every maximum strain. Meanwhile, by comparing ordinates of the four graphs, it is found that the peak energy has a significant increase as the chemical coupling increases. Moreover, the changing model of above the equilibrium value depends on the chemical coupling. It illustrates that chemical coupling between polymers and NPs obviously increase bond energy during the shear process, and it attributes to the resulting stress to prevent the destruction of the chemically bonded networks.
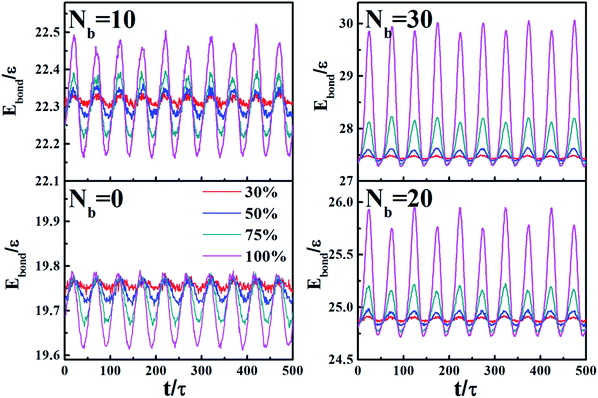 | ||
| Fig. 14 Bond energy (Ebond) of chemical bonds between polymers and NPs during the oscillatory shear, for Nb = 0, 10, 20, and 30. | ||
4. Conclusions
The effect of chemical coupling between polymers and NPs on the viscoelastic properties of polymer nanocomposites (PNCs) has been examined by coarse-grained simulation. The computational results have shown that the formation of chemical coupling weakens the “Payne effect” under various imposed conditions. The decreasing of the “Payne effect” is attributed to the three points: (i) chemical bonds decrease the physical bonding–debonding of polymer chains from the filler surfaces; (ii) the polymer-shell-bridged network becomes more difficult to be destroyed; (iii) the mobility of polymers has been constrained. Moreover, the storage moduli's abrupt rise results from the chemical bond energy increasing sharply at large strain. The above simulation work provides a useful information on how chemical coupling between polymers and nanoparticles influence the “Payne effect” as well as an understanding of structure and viscoelastic properties of filled polymer nanocomposites influenced by grafting NPs that could coupled with polymer chains.Conflicts of interest
There are no conflicts to declare.Acknowledgements
We would like to acknowledge the financial supports from the National 973 Basic Research Program of China 2015CB654700 (2015CB654704), the Foundation for Innovative Research Groups of the NSF of China (51221002 and 51521062), the National Natural Science Foundation of China (51333004, 51403015 and 21674010) and the Major International Cooperation (51320105012) of the National Nature Science Foundation of China. The super-calculation center of “Tianhe number two” and the cloud calculation platform of Beijing University of Chemical Technology (BUCT) are both greatly appreciated.References
- A. R. Payne, J. Appl. Polym. Sci., 1962, 6, 57–63 CrossRef CAS.
- A. R. Payne, J. Appl. Polym. Sci., 1963, 7, 873–885 CrossRef CAS.
- G. J. Kraus, Appl. Polym. Symp., 1984, 39, 75 CAS.
- A. Van de Walle, C. Tricot and M. Gerspacher, KGK-Kaut. Gummi. Kunst., 1996, 49, 172–179 CAS.
- G. Heinrich and M. Klüppel, Adv. Polym. Sci., 2002, 160, 1–44 CrossRef CAS.
- C. R. Lin and Y. D. Lee, Macromol. Theory Simul., 1996, 5, 1075–1104 CrossRef CAS.
- C. R. Lin and Y. D. Lee, Macromol. Theory Simul., 1997, 6, 339–350 CrossRef CAS.
- P. Cassagnau, Polymer, 2003, 44, 2455–2462 CrossRef CAS.
- P. G. Maier and D. Göritz, KGK, Kautsch. Gummi Kunstst., 1996, 49, 18–21 CAS.
- S. S. Sternstein and A. J. Zhu, Macromolecules, 2002, 35, 7262–7273 CrossRef CAS.
- A. J. Zhu and S. S. Sternstein, Compos. Sci. Technol., 2003, 63, 1113–1126 CrossRef CAS.
- A. S. Sarvestani, Macromol. Theory Simul., 2016, 25, 312–321 CrossRef CAS.
- R. Q. Yang, Y. H. Song and Q. Zheng, Polymer, 2017, 116, 304–313 CrossRef CAS.
- G. Allegra, G. Raos and M. Vacatello, Prog. Polym. Sci., 2008, 33, 683–731 CrossRef CAS.
- J. Liu, L. Q. Zhang, D. P. Cao and W. C. Wang, Phys. Chem. Chem. Phys., 2009, 11, 11365–11384 RSC.
- G. D. Smith, D. Bedrov, L. Li and O. Byutner, J. Chem. Phys., 2002, 117, 9478–9489 CrossRef CAS.
- F. W. Starr, J. F. Douglas and S. C. Glotzer, J. Chem. Phys., 2003, 119, 1777–1788 CrossRef CAS.
- T. Kairn, P. J. Daivis, I. Ivanov and S. N. Bhattacharya, J. Chem. Phys., 2005, 123, 194905 CrossRef CAS PubMed.
- V. Pryamitsyn and V. Ganesan, Macromolecules, 2006, 39, 844–856 CrossRef CAS.
- V. Pryamitsyn and V. Ganesan, J. Rheol., 2006, 50, 655–683 CrossRef CAS.
- S. T. Knauert, J. F. Douglas and F. W. Starr, J. Polym. Sci., Part B: Polym. Phys., 2007, 45, 1882–1897 CrossRef CAS.
- J. D. Thomin, P. Keblinski and S. K. Kumar, Macromolecules, 2008, 41, 5988–5991 CrossRef CAS.
- E. Jaber, H. B. Luo, W. T. Li and D. Gersappe, Soft Matter, 2011, 7, 3852–3860 RSC.
- J. T. Kalathi, G. S. Grest and S. K. Kumar, Phys. Rev. Lett., 2012, 109, 198301 CrossRef PubMed.
- Y. L. Chen, Z. W. Li, S. P. Wen, Q. Y. Yang, L. Q. Zhang, C. L. Zhong and L. Liu, J. Chem. Phys., 2014, 141, 1–11 Search PubMed.
- W. H. Wang, G. Y. Hou, Z. J. Zheng, L. Wang, J. Liu, Y. P. Wu, L. Q. Zhang and A. V. Lyulin, Phys. Chem. Chem. Phys., 2017, 19, 15808–15820 RSC.
- G. Raos, M. Moreno and S. Elli, Macromolecules, 2006, 39, 6744–6751 CrossRef CAS.
- G. Raos and M. Casalegno, J. Chem. Phys., 2011, 134, 054902 CrossRef PubMed.
- H. R. Lusti, I. A. Karmilov and A. A. Gusev, Soft Matter, 2003, 1, 115–120 CrossRef CAS.
- R. Yamazakim, N. Karyu, M. Noda, S. Fujii and Y. Nakamura, J. Appl. Polym. Sci., 2016, 133, 43256 Search PubMed.
- S. Rezaei and B. Pourabbas, Polym. Compos., 2015, 36, 1365 CrossRef CAS.
- W. Fu and L. Wang, J. Appl. Polym. Sci., 2016, 133, 43891 Search PubMed.
- C. Siriwong, P. Sae-Oui and C. Sirisinha, Polym. Test., 2014, 38, 64–72 CrossRef CAS.
- H. Qiao, M. Y. Chao, D. Hui, J. Liu, J. C. Zheng, W. W. Lei, X. X. Zhou, R. G. Wang and L. Q. Zhang, Composites, Part B, 2017, 114, 356–364 CrossRef CAS.
- C. W. Wang, Z. J. Liu, S. F. Wang and Y. Zhang, J. Appl. Polym. Sci., 2016, 133, 82907 Search PubMed.
- K. Subramaniam, A. Das, D. Steinhauser, M. Klüppel and G. Heinrich, Eur. Polym. J., 2011, 47, 2234–2243 CrossRef CAS.
- S. Mohapatra, R. Alex and G. B. Nando, J. Appl. Polym. Sci., 2016, 133, 43057 CrossRef.
- B. C. Zhong, Z. X. Jia, Y. F. Luo and D. M. Jia, Compos. Sci. Technol., 2015, 117, 46–53 CrossRef CAS.
- G. D. Hattemer and G. Arya, Macromolecules, 2015, 48, 1240–1255 CrossRef CAS.
- J. X. Shen, J. Liu, H. D. Li, Y. Y. Gao, X. L. Li, Y. P. Wu and L. Q. Zhang, Phys. Chem. Chem. Phys., 2015, 17, 7196–7207 RSC.
- K. Kremer and G. S. Grest, J. Chem. Phys., 1990, 92, 5057–5086 CrossRef CAS.
- J. S. Smith, D. Bedrov and G. D. Smith, Compos. Sci. Technol., 2003, 63, 1599–1605 CrossRef CAS.
- C. Bennemann, W. Paul, J. Baschnagel and K. Binder, J. Phys.: Condens. Matter, 1999, 11, 2179–2192 CrossRef CAS.
- S. Nam, H. W. Cho, S. Lim, D. Kim, H. Kim and B. J. Sung, ACS Nano, 2013, 7, 851–856 CrossRef CAS PubMed.
- P. Gao and H. Guo, Phys. Chem. Chem. Phys., 2015, 17, 31693–31706 RSC.
- P. Gao and H. Guo, Polymer, 2015, 69, 25–38 CrossRef CAS.
- Y. Li, M. Kroger and W. K. Liu, Soft Matter, 2014, 10, 1723–1737 RSC.
- M. Kroger, O. Peleg and A. Halperin, Macromolecules, 2010, 43, 6213–6224 CrossRef.
- A. Ghanbari, T. V. M. Ndoro, F. Leroy, M. Rahimi, M. C. Böhm and F. Müller-Plathe, Macromolecules, 2012, 45, 572–584 CrossRef CAS.
- S. N. Mohammad, Nanotechnology, 2012, 23, 285707 CrossRef PubMed.
- Y. L. Chen, L. Liu, Q. Y. Yang, S. P. Wen, L. Q. Zhang and C. L. Zhong, Langmuir, 2013, 29, 13932–13942 CrossRef CAS PubMed.
- S. Plimpton, J. Comput. Phys., 1995, 117, 1–19 CrossRef CAS.
- G. Y. Jiang, S. Q. Song, Y. H. Zhai, C. Feng and Y. Zhang, Compos. Sci. Technol., 2016, 123, 171–178 CrossRef CAS.
- J. Liu, Y. Y. Gao, D. P. Cao, L. Q. Zhang and Z. H. Guo, Langmuir, 2011, 27, 7926–7933 CrossRef CAS PubMed.
- M. J. Wang, Rubber Chem. Technol., 1998, 71, 520–589 CrossRef CAS.
- J. L. Leblanc, Prog. Polym. Sci., 2002, 27, 627–687 CrossRef CAS.
| This journal is © The Royal Society of Chemistry 2018 |